On the safety of ITER accelerators

Abstract

Three 1 MV/40A accelerators in heating neutral beams (HNB) are on track to be implemented in the International Thermonuclear Experimental Reactor (ITER). ITER may produce 500 MWt of power by 2026 and may serve as a green energy roadmap for the world. They will generate −1 MV 1 h long-pulse ion beams to be neutralised for plasma heating. Due to frequently occurring vacuum sparking in the accelerators, the snubbers are used to limit the fault arc current to improve ITER safety. However, recent analyses of its reference design have raised concerns. General nonlinear transformer theory is developed for the snubber to unify the former snubbers' different design models with a clear mechanism. Satisfactory agreement between theory and tests indicates that scaling up to a 1 MV voltage may be possible. These results confirm the nonlinear process behind transformer theory and map out a reliable snubber design for a safer ITER.

The International Thermonuclear Experimental Reactor (ITER) is configured as a next-generation tokamak machine that is now the flagship facility for the magnetic confinement fusion (MCF) society scheduled to start power-producing tests in 2026¹,². ITER permits safe operation in relevant improved plasma regime by controlling large sawtooth collapses physically³, but now it is judged to be on unsafe ground electrically due to its accelerators. The transformer-structured tokamak device shifts from the fault state of the transformer to a normal state when circuit shorting occurs in the secondary single-turn winding of the tokamak plasma⁴. Thus, reliability, availability, maintainability, and inspectability (RAMI) standards are critical in engineering the MCF roadmap with the transformer-structured tokamak into a power plant after fixing the recent cable event in the ITER central solenoid (CS). The transformer primary winding is known as the ITER “beating heart”. With a wall-plug electrical efficiency of 27–65%⁵, the accelerator-driven heating neutral beam (HNB) has the clearest physical mechanism for fusion plasma, considered as actuators of EU MCF fusion demonstration power plant (DEMO) for 1.33 GWe power stations after the ITER⁵,⁶,⁷,⁸. At present, the HNB-driven Tokamak current reached 1 MA with an injection power of 3.75 MW with a beam energy of 360 keV⁹. Initially, the ITER will use two 1 MeV HNBs and one 100 keV diagnostic NB⁸. In each ITER HNB system, two snubbers based on SF6 gas insulation are currently configured as functional passive protection devices to be inserted between the ITER ion source and its 1 MV acceleration power supply to absorb the stored energy in their respective transmission lines (TLs) and insulation transformer to attenuate the peak fault arc currents and quench these currents when shorting occurs. These HNB accelerators are protected by snubbers for reliable operation where vacuum sparking occurs frequently. However, a recent RAMI analysis of these snubbers leads to another concern regarding ITER safety due to the use of the pure flux matching model, which is an incomplete snubber model. Due to the strong electromagnetic interference (EMI) effects generated by the frequently occurring fault arc current, our studies on the ITER snubber reveal that its present reference design does not guarantee adequate ITER safety based on a logical review of historical studies. By unifying former design models with well-known transformer theory, the nonlinear transformer model is developed specifically for the design of reliable snubbers for ITER safety.

Results

In this study, a complete and accurate model is constructed for the design of an ultra-high-voltage (HV) snubber to protect the expensive ITER machine with a clear logical mechanism: the step-by-step linear approach to the nonlinear transformer cores. Natural iron loss in the cores is revealed as the dominant factor in suppressing the fault arc current for the accelerators, although this loss is designed to be as low as possible to develop common and efficient industry transformers that are now found worldwide. The extreme case is a superconducting transformer with no iron or copper loss. Snubber design is formulated from complete transformer theory to address the ITER's harsh EMI problems caused by its 1 MV accelerators. The parameters of its present structure could be preserved by replacing its core material of FINEMET with DELTAMAX, which will reduce its construction costs by fixing its insulation frame at 1 MeV.

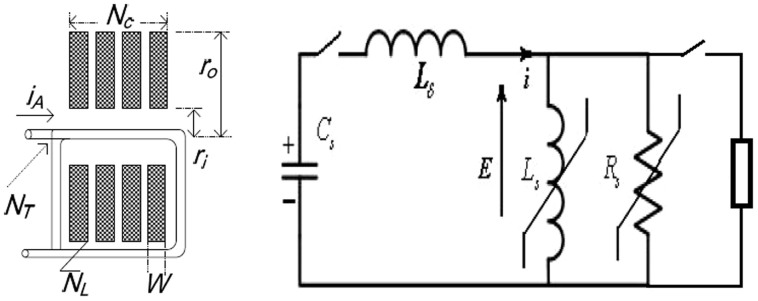
A snubber is generally implemented with cascading transformer cores as configured in Figure 1A. Due to the nature of its transformer character, its precise equivalent circuit is shown in Figure 1B. It has three important elements¹⁰, that are upgraded with a nonlinear resistor R_s and an inductor L_s because of the time-varying nature of its fault protection process. L_δ is the leakage inductance, including the TL's inductance and transformer's leakage inductance, which will never saturate due to the air gap nature of its magnetic path. L_s is the transformer's magnetisation inductance based on the flux matching model used by the current ITER design. R_s is the snubber's resistor, which is the combination of the natural iron loss of the transformer cores analysed by Fink, Baker, and Owren (FBO)¹¹ and the secondary resistor load used in the snubber transformer¹². The former natural iron loss dominates the fault suppression capability (FSC) of snubbers, and the secondary resistor only plays a complementary role.

Figure 1.

(A-left) Snubber Configuration; (B-right) Equivalent Circuit.

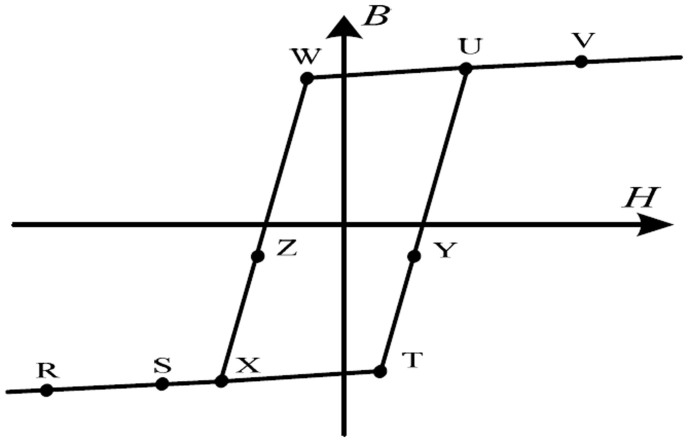
As one special case of nonlinear snubber theory, the flux matching model¹³,¹⁴ that only considers the linear cases of magnetisation inductance L_s and the additional part of the secondary resistor R_s is used to design the ITER reference snubber, leading to its functional invalidation due to oversaturation from its inner layers at −1 MV parameter settings. With the simplified model, the simulation indicates that strong EMI effects of over 10 kA fault current pulses exist in the main HV circuit¹⁶,¹⁷. These currents should be below 0.6 kA for low EMI when vacuum spark-down occurs for better EM compatibility with other tokamak systems based on the experiences of Experimental Advanced Superconducting Tokamak (EAST-the original HT-7U), in China, DIII-D in the USA, and JT-60SA in Japan. Physically, both the secondary resistor R_s and the inductance L_s are dynamically nonlinear in the vacuum sparking process for snubber applications¹¹,¹⁸. This transformer-type snubber is approached with the classical parallel BH curve model¹⁹, which simplifies the complex nonlinear process with a step-by-step linear approach in the suppression process of the fault arc current, as shown in Figure 2.

Figure 2. B-H curve of the magnetic material.

Figure 2 presents the complete BH hysteresis curve of the magnetic material¹⁰,¹⁹ that is generally implemented in the core snubber. The core snubber should operate in a negative saturation region under normal conditions and in the unsaturated interval between −H_s and H_s to have a large inductance when shorting occurs. When a bias current flows in the opposite direction of the core snubber in the main circuit, the core is positioned at point R in Figure 2, which is the deep negative saturation. When the accelerator current in the main circuit is switched on, it operates at point S, near the saturation point. Under normal conditions, this small inductance has a minor impact on the main circuit. When high voltage breakdown occurs, the operation point goes along the S-X-T-Y-Z-X-S cycle. The inductance becomes much larger when transiting from the S-X-T section to the T-Y section. This increase has the function of limiting the amplitude of the discharged arc current to the load of the ion source due to the principle of a flux linkage constant in the short-circuited windings¹⁰. At the same time, the core loss consumes the discharged energy. The snubber cannot exceed point U in Figure 2, which is the positive saturation point; otherwise, the core layer is in the positive saturation region, leading to a reduced dynamic inductance that reversely amplifies the fault current. Unfortunately, this situation might occur in the present ITER design. The fault current cannot be limited, so the material's magnetic flux swing will partly determine the snubber's volume, which is why FINEMET was first selected for the reference design of the ITER snubber¹⁴. Our new work demonstrates that FINEMET is not appropriate for the ITER HNB parameters due to its thickness limitations and the amplified stray capacitance that is caused by its TL structure as designed and solidified in the current ITER construction. FINEMET may lead to the ITER becoming an HV testing field for lighting flashes due to the HV pulses exceeding 5 kV that are simulated to be transferred to the ground¹⁶,¹⁷,²⁰,²¹. This situation will destroy many of the ITER components in its path.

The physical mechanism of a snubber for the ITER fault arc limiter is elaborated using the parallel BH model for a complete nonlinear transformer theory used in its HNB protection. Both inductor and resistor mechanisms should be included for accurate analysis and design. Due to the parallel nature of R_s and L_s, significantly decreasing any one of them will lead to an invalidation of the snubber function. The pure flux-matching model of the snubber is intrinsically incomplete not only in theory but also in engineering practice.

Discussion

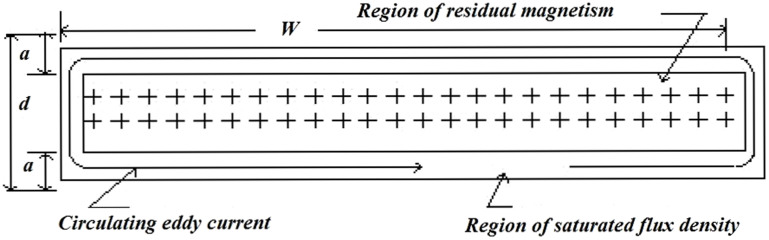
By integrating the eddy loss of all single core layers, as shown in Figure 3, and reformulating the FBO model, which assumes that the snubber core layer never saturates and the inductance L_s is infinite, the discharged fault arc current is derived as¹⁸:

where V₀ and C_s are the initial sparking voltage and stray capacitance, respectively, as shown in Figure 1B. C_s is mainly the TL capacitance between the inner HV floating pole with radii R₁ = 250 mm and the outside shield pole with radii R₂ = 1,500 mm¹⁴. L_TL is the TL length between the HV power supply and its accelerator load located in different ITER buildings currently under construction. This scheme is similar to a coaxial conductor with a total length of over 100 m¹⁴. C_s can be derived as:

C_s is assumed to be 0.4 nF¹³,²² if the total length of the TL is less than 10 m, but ITER engineering does not currently support the data that urgently require a re-design of its buildings and components. Even at 0.4 nF, simulation²² did not take the fault current into the range needed for a ITER like reactor, i.e. within 0.6 kA.

Figure 3. Eddy current of a core tap winding.

γ is the designed character parameter of the snubber, the less, the better which can be further derived as¹⁸:

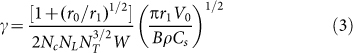Non-saturation core design is the key to have a small γ at given maximum fault voltage.

As shown in Figure 1A, r₁ and r₀ are the inner and outer radii of the core, respectively, W is the width of the core type, and N_c, N_L, and N_T are the number of cores, core type layers, and number of conductor turns around the cores, respectively. ρ is the resistivity of the core material, and B is the swing of the flux intensity of the core material that is modified to 2B_s due to the existence of the snubber bias current. B equals residual magnetism B_r plus saturation flux intensity B_s in the original FBO model.

For more advanced snubber design with a compact structure, we could eliminate the assumption that the eddy current resistance of the core is approximately 2.5 times its logically derived resistance¹⁸. The condition of the core type thickness in the advanced snubber model is further derived as:

The discharged arc time is then upgraded as

Equation (5) is valid only when Equation (4) is satisfied. When the initial voltage is beyond the threshold voltage, saturation develops from the inner layer of the cores, leading to the invalidation of the snubber.

The reformulated snubber equivalent resistance is derived as¹⁸:

At the instant of time that a fault arc current appears, the initial resistance of the snubber is further derived as:

The parallel inductance of the snubber is derived as²³:

where

is the average magnetic path length and

D_e is the total equivalent unsaturated thickness of the core snubber, which is also time varying during the shorting process of the HV circuit¹¹,¹⁸. f is the space filling factor of the core snubber, and μ_r is the relative permeability, which will change from the negative saturation region to the unsaturated region (as illustrated in Figure 2) when the bias current is switched on and shorting occurs. The parameter μ_r is judged as essential for an effective core snubber system¹⁸. This permeability-determined inductance will increase to a very large value when the T point in Figure 2 is reached because the relative permeability could increase over 100 times upon transition from a negative saturation line to an unsaturated line with typical magnetic materials, such as FINEMET and DELTAMAX. These effects limit the shorting current. This inductance will gradually decrease with the increase of the saturated thickness of the first layer. When it reaches point U in Figure 2, its current-limiting function disappears. To effectively protect the ion source and its HVDC power supply, care should be taken in its design to maintain an ample safety margin.

If the concept of a Distributed Core Snubber (DCS)²⁰,²¹ is implemented in above nonlinear theory to replace a large concentrated snubber, C_s could be simply replaced by C_s/n in above equations, where n is the distributed number of concentrated snubbers.

The ITER reference design is now based on the flux matching method developed in JAEA (i.e., the JAEA model), which only considers the total core flux swing and linear secondary resistor in Figure 1B. However, the time-varying nonlinear resistor of core loss is neglected in its transformer model, which is not the natural case of Figure 1B. With only the linear secondary resistor R, it gives the discharged arc time and magnetic flux of the core snubber as

and

respectively. Table 1 lists the ITER snubber design by the JAEA model under different conditions from 1998 to present¹³,¹⁴. The studied ITER stray capacitance is now as high as 5.9 nF¹⁴,¹⁵, which is a reasonable value because its present TL is composed of three TLs: TL1 from the HV power supply to HV deck1 to accommodate the ion source power supplies, TL2 from the HV deck1 to the HV deck2, and TL3 from the HV deck2 to the HV accelerator¹⁴.

Table 1. Design of the ITER NBI snubber.

Characteristics	Parameters13	Parameters14,15
Core width (W)	25.4 mm	25.4 mm
Lamination thickness (d)	0.02 mm	0.02 mm
Stacking factor (f)	0.71	0.71
Inner radius (r1)	200 mm	250/480 mm
Outer radius (r0)	450 mm	750/700 mm
Number of laminations (NL)	8,875	17,750/7,810
Cores (Nc)	13	217/151
Conductor turns (NT)	1	1
Saturation flux density (Bs)	1.35 T	1.35 T
Resistivity (ρ)	1.2 × 10−6 Ω-m	1.2 × 10−6 Ω-m
Magnetic unsaturation relative permeability μr0	3,500 (1 MHz)	3500 (1 MHz)
Initial voltage, V0 (kV)	1,000	1,000
Stray Capacitance Cs (nF)	0.4	3.724/1.2/5.9

ITER requires benign EM environments for safe operation. However, the current ITER reference design raises concerns about future ITER operation due to the strong EMI effects of a fault current of over 10 kA combined with its existing 100 kV fault voltage even with an additional series resistor and core snubbers in its HV circuit¹⁶,¹⁷. The fault pulses could destroy many of its components. This is a well-known fact due to the HV pulse transferred to the common ground. This pulse should be less than 2 kV according to the ITER Electric Design Handbook (EDH). The peak maximum shorting current is suggested to be below 0.6 kA for low EMI when vacuum spark-down occurs. The recommended current has benign EMC with other ITER systems.

Methods

Tests and analysis of the snubber models

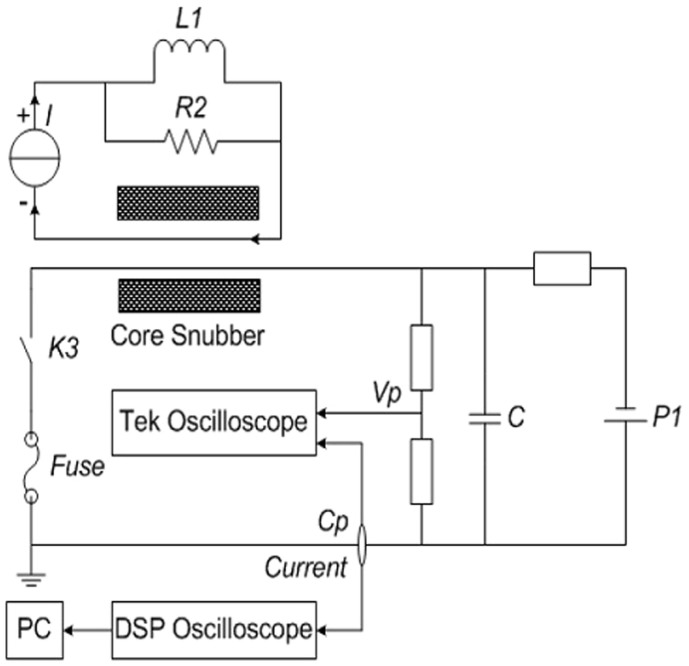
To validate the design equations, snubbers with FINEMET (the present ITER design) and DELTAMAX materials were both fabricated to be tested with the circuit shown in Figure 4. A 200 MHz TPS2024 oscilloscope with four channels was used to synchronously measure the discharged voltage and the current waveforms with an EP-100 K voltage divider and the Pearson™ Current Monitor Model 101. If C_sV₀ is constant, gradually increasing the voltage results in the same peak current as increasing the capacitance based on our unified nonlinear transformer theory expressed in Equation 1. Although the pulse width becomes slightly long. In addition, the voltage can be accurately generated, measured, and controlled to validate the new nonlinear theory experimentally. All of our tests are guided by the nonlinear transformer theory used for snubber design, which eliminates all incompleteness of snubber former models and agrees well with our tests.

Figure 4. HV Snubber Test Circuit.

Test parameters of the FINEMET snubber with increasing stray capacitance are listed in Table 2. Figure 5A presents its discharged arc current with a 76 nF capacitance by loading the 40 Ω additional secondary resistor and setting the number of turns of the primary and secondary windings to four. Further increasing the initial discharged voltage or capacitance beyond the thresholds will significantly increase the shorting current because Equation (4) is not satisfied. The nonlinear voltage effects beyond the threshold are due to the mode transition from the snubber discharging mode to the LCR discharging mode in the same circuit with voltage-determined impedance¹⁸.

Table 2. d = 0.03 mm, ρ = 0.9 × 10⁻⁶ Ω-m, B = 2.5 T,N_T = 4, N_c = 1, N_L = 817, R_L = 40 Ω, Bias Current = 30 A (ON240/170/50 test).

No.	Cs [nF]	Initial voltage [kV]	Peak current (test) [A]	Load [Ω]	Rs0 [Ω]	Peak current (theory) [A]	Arc time TA (theory) [μs]	Arc time TA (test) [μs]	Thickness (theory) [mm]
0207	43	8	160	40	50,066	47.6	4.43	4.0	0.0293
0210	76	8	180,200	40	37,659	63.2	5.88	4.9	0.0307

Figure 5.

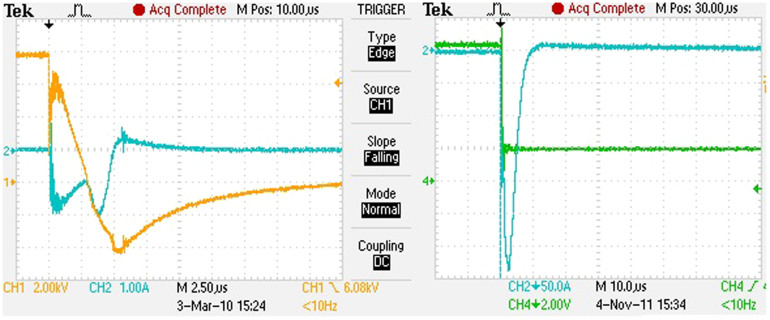
(A-left) FINEMET: The discharged current and voltage pulses for an 8 kV charging voltage with a 76 nF Capacitor (EAST Snubber shot No. 0210: horizontal scale: 1 μs/div, vertical scale: 2 kV/div for CH1, 100 A/div CH2). (B-right) DELTAMAX: The discharged current and voltage pulses for a 42.1 kV charging voltage with a 33 nF Capacitor (EAST Snubber shot No. 0061: horizontal scale: 10 μs/div, vertical scale: 10 kV/div for CH4, 50 A/div CH2).

Figure 5A presents the discharged current and voltage pulses for an 8 kV charging voltage with a 76 nF capacitor, where the second restarted 200 A current peak in the blue line is due to the saturation effects of core tapes. The threshold voltage could not be enhanced further with a 76 nF capacitor discharged at 8 kV. Table 1 also lists the analysis results of the FINEMET snubber mentioned above using Equations (1) to (6). For the FINEMET model, the maximum theoretical thickness is only experimentally extended to 0.0307/0.03 = 1.02 times the actual thickness, even with the 40 Ω secondary resistor. The snubber arc discharge is converted into a LCR discharge beyond the threshold voltage with the same circuit configuration due to the nonlinear impedance effects and amplitude of the shorting arc current in LCR mode becoming much larger than that of the snubber mode. This situation should be avoided in the snubber design due to its strong EMI effects on the other Tokamak system components.

Because the studied ITER stray capacitance is now as high as 5.9 nF, it is very difficult for a FINEMET material to satisfy Equation 4 with the reference configuration, even with the secondary resistor, which occurs in the present reference design for the ITER snubber that was used in 1993²⁴. Thus, a model with DELTAMAX cores, i.e. 50–50 NiFe²⁵ was developed and tested. The typical parameters and test results are listed in Table 3 with its threshold voltage. The results of testing the DELTAMAX material without the secondary resistor and setting the turns of the primary winding to one are listed in Table 3. This configuration leads to a further increase of the threshold voltage of a single pulse discharge to 42.1 kV, as shown in Figure 5B. For the DELTAMAX-based model, the maximum theoretical thickness is experimentally extended to 0.0587/0.0508 = 1.16 times the actual thickness without the secondary resistor for discharging the single shorting current pulse. This value is the optimised factor for the snubber design with the DELTAMAX material. The testing results with Deltamax snubber at 80 kV HNB accelerator was encouraging since it limited all fault currents within 0.45 kA at 80 kV faulting voltage²⁶.

Table 3. d = 0.0508 mm, f = 0.88, ρ = 0.45 × 10⁻⁶ Ω-m, B = 3.0 T,N_T = 1, N_c = 80, N_L = 870, L_s = 28.558 μH (DELTAMAX 253/154/12.7 test).

No.	Cs [nF]	Initial Voltage[kV]	Peak Current (test) [A]	Rs0 [Ω]	Peak Current (theory) [A]	Arc time TA (theory) [μs]	Arc time TA (test) [μs]	Thickness (theory) [mm]
0050	33	10.1	70	99.12	40.2	12.42	10	0.0288
0052	33	17.1	90	76.18	85.4	9.638	10	0.0374
0053	33	30.4	200	57.1	202.5	7.22	10	0.0499
0054	33	31.6	220	55.6	219.8	7.08	10	0.0513
0055	33	34.1	245	53.9	243.8	6.80	10	0.0528
0056	33	36.2	270	52.36	263.2	6.63	10	0.0544
0057	33	38.7	295	50.6	290.9	6.41	10	0.0563
0058	33	35	280	53.2	250.2	6.74	10	0.0535
0061	33	42.1	340	48.55	330.1	6.14	10	0.0587
0063	33/2	45.5	265	66	262.2	4.18	6	0.0432
0064	33/2	61	400	57	407	3.61	6	0.05

Design of the ITER snubber

By considering the above test factors and Equation (4), the minimum core layer thickness in the ITER snubber with DELTAMAX and FINEMET materials is optimised as:

Inserting material data from Tables 1 and 2 into Equations (13) and (14), the core layer thickness requirements of the ITER snubbers of both magnetic materials are computed for the FINEMET and DELTAMAX snubbers and are listed in Table 4. A smaller thickness may lead to invalidation of the snubber due to the principle of the magnetic flux linkage constant¹⁰,¹⁸.

Table 4. Required conditions of the 1 MV ITER core layer thickness given the current geometry.

	Snubber 1	Snubber 2/3/4
Inner radius (r1)	200 mm	250/480/480 mm
Capacitance Cs (nF)	0.4	3.724/1.2/5.9
FINEMET (d/mm)	0.0357	0.0974/0.0399/0.0884
DELTAMAX (d/mm)	0.0168	0.046/0.015/0.042

In summary, the secondary resistor could not significantly increase the snubber threshold voltage when the core layers saturate from the inside in the present ITER reference snubber design with a thickness of only 0.02 mm using FINEMET. Because a 5.9 nF/1 MV stray capacitance is used to study its design¹⁴,¹⁵, it is very difficult to satisfy the thickness requirement of Equation (13) for FINEMET with the present configuration. Due to the flexibility of the DELTAMAX thickness, it may be the more effective material for damping the peak shorting current for the ITER HV circuit to less than 0.6 kA. This change results in a more robust ITER snubber design given the present structural parameters implemented with SF6 insulation after setting its 1 MV vacuum insulation in place²⁷.

For a benign EM environment, system optimisation of the ITER snubbers is still required for safe operation, together with the HV transmission lines in the current RAMI analysis²⁸,²⁹. The EMI trouble in the ITER could be avoided by the proposed method, just as that of the superconducting cable in the ITER “beating heart”³⁰, where the special tokamak transformer is struggling to work safely in its long pulsed DC mode. The difficulty is in reaching good H-mode confinement with the additional 33 MW HNB heating¹,² needed for stable operation from its earlier simple AC mode³¹.