Abstract
Functional connectivity analyses can offer insights into mechanisms of the brain that might not be revealed by traditional fMRI. These analyses compare seed voxels’ activity over time to the activity of other voxels over time and identify correlations between regions. This study is the first to perform functional connectivity analyses in the human medial temporal lobe (MTL) at high enough resolution to resolve the hippocampal subfields. We calculated the average correlation coefficients between the MTL cortices, which include the entorhinal (ERC), perirhinal (PRC), and parahippocampal cortex (PHC), and the hippocampal subfields dentate gyrus/CA3, CA1, and subiculum. We found that the hippocampal subfields had relatively high correlations with each other both within and across hemispheres, but did not have exceptionally strong correlations with the MTL cortices. The opposite was also seen where there was a relatively high correlation coefficient between the ERC and PRC, but both regions had low correlation coefficients with the hippocampal subfields. We also found greater functional connectivity within a hemisphere than across hemispheres. These effects were replicated across multiple datasets which differed in task demands, participants’ age, and scanner sequence/slice acquisition. Notably, all datasets were better correlated to these patterns of intrinsic functional connectivity than to a model based on anatomical constraints. This is consistent with evidence that functional connectivity is not a direct mapping of anatomical connectivity. These patterns of functional connectivity imply a distinction between the MTL cortices and the hippocampus and speak to our understanding of the organization of the MTL.
Keywords: functional connectivity, fMRI, medial temporal lobe, Hippocampus
INTRODUCTION
Functional connectivity measures the correlation of activity over time across different neuroanatomical regions (Friston et al., 1993). Most fMRI functional connectivity investigations have studied correlations of activity in cortical regions (e.g., Biswal, et. al, 1995; Lowe, 2000; Greicius et al., 2003; Fox et al., 2005, 2007; Damoiseaux et al., 2006). Fewer studies have focused on subcortical areas, in particular the hippocampus and adjacent cortical regions of the medial temporal lobe (MTL; though see Stein et al., 2000). None have been performed in the MTL with high enough resolution to investigate the functional connectivity of the hippocampal subfields. This study is the first of its kind to do so. We investigated correlations of activity across subregions of the MTL, including the hippocampal subfields and the MTL cortices (perirhinal, entorhinal, and parahippocampal). We are particularly interested in these regions because of their prominent role in memory processes and the various theories that posit dissociations in function across MTL regions (Squire et al., 2004).
Although the brain accounts for 20% of the body’s energy consumption, traditional fMRI activation studies constitute only a 1–5% change in blood-oxygen-level-dependent (BOLD) activity from baseline (Raichle, 2010). The vast majority of activity is due to spontaneous firing (Raichle and Mintun, 2006). Therefore, in traditional fMRI activation studies it can be difficult to identify significant regions of activity in this sea of “noise”. To circumvent this problem functional connectivity analyses look for correlations in the spontaneous changes in activity that is ignored in traditional fMRI activation studies. The correlational nature of functional connectivity analyses can also provide a broader understanding of the brain by revealing how various parts of the brain potentially interact.
Since the first fMRI functional connectivity study in 1995 (Biswal et al., 1995), functionally connected regions have been found throughout the cortex in the default mode network, sensorimotor cortex, visual cortex, auditory cortex, and other regions (for review, see Rosazza and Minati, 2011). There has been general consistency in functionally connected networks across studies, with different styles of data analysis (e.g., seed style versus ICA; Rosazza and Minati, 2011), and across resting state scans versus the residuals of task-related activity (Fair et al., 2007). In addition, similar functionally connected networks have been identified in deeply anesthetized monkeys (Vincent et al., 2007).
In this study, we performed seed style functional connectivity analyses in ten fMRI datasets from ~200 participants collected in our lab over the span of several years. The datasets differed in task demands, participants’ age, and scanner sequence/slice acquisition (none had been previously analyzed for this kind of connectivity). Across datasets two patterns of functional connectivity emerged. The first was relatively high functional connectivity between the entorhinal (ERC) and perirhinal (PRC) cortex and amongst the hippocampal subfields. However, there was relatively weak functional connectivity between the MTL cortices and the hippocampal subfields and between any region and the parahippocampal cortex (PHC). All datasets were better correlated to this pattern of functional connectivity than to a model of the known anatomical connections. This is not entirely unexpected as there is evidence that functional connectivity is not merely a direct mapping of anatomical connectivity, but rather indicates something specific about functional organization and activity (Lowe, 2000; Van Dijk et al., 2010). Thus, functional connectivity analyses should not be viewed as proxies for anatomical analyses. The second pattern revealed that in areas of high functional connectivity as mentioned above, there was greater functional connectivity within a hemisphere than across hemispheres. Taken together, these results have implications regarding the organization of the MTL and hippocampus and how these regions might interact with each other
METHODS
Participants
Ten fMRI datasets were analyzed. Participants for the first nine datasets were recruited from the University of California, Irvine (Lacy et al., 2011; Mattfeld et al., 2011; Yassa et al., 2011). Participants in the 10th dataset were recruited from Johns Hopkins University (Bakker et al., 2008). Each dataset was comprised of ~20 participants (range n =16–25) for a total of 198 participants. All participants were either healthy young adults (age range, 18–33; mean age, 21) or healthy older adults (datasets, 4 and 6; age range, 60–83; mean age, 71). Written consent was obtained in compliance with the local Institutional Review Boards. All participants were compensated for their time.
Behavioral Tasks
Before any correlational analyses were performed, task events were modeled and then subtracted from the raw fMRI signal leaving the residual activity of task related scans (methods described below under Functional Connectivity Analysis). Theoretically, removing task effects from event-related fMRI data in such a manner leaves residual signal equivalent to resting state data (Fox et al., 2006; Andrews-Hanna et al., 2007; He et al., 2007). However, this may not entirely be the case as Fair et al. (2007) caution that although the functional connectivity in the residuals of event-related activity are qualitatively similar to true resting state data, quantitative differences can still exist. Moreover, even within resting state data, quantitative differences in the functional connectivity can be observed based on whether participants are at rest with their eyes open versus their eyes closed (Van Dijk et al., 2010). Thus, there may be many factors that contribute to subtle differences in the output of functional connectivity analyses and we should not assume that we can remove all modulation by the task. Further, we must also take into account that certain task effects cannot be removed from the data such as attentional state and internal environment during task performance. For all the above reasons, it is important to consider the tasks performed and thus they are described below.
Dataset #1: Image Pair Locations
Twenty-one healthy young adults studied 10 pairs of scene images placed in separate but random locations on the screen and were then tested on their memory for the spatial locations of each pair of images (3 s each with a 0.5 s ISI, 5 s study-test interval). The participants’ task was to indicate via button press whether images were in the same locations or different locations from the study phase. There were three study/test blocks per run for a total of 210 pairs of images studied and tested across seven 4-min runs. Task procedures are further described in Stark et al. (2010).
Dataset #2: Firsts, Lures, and Repeats
Twenty-one healthy young adults incidentally encoded a series of color images of everyday objects (2.4 s each with a 0.3 s ISI) by indicating via button press whether each was an indoor or outdoor object. Images could be new images not previously seen (first presentations), exact repetitions of images previously seen (repetitions), or images similar to those previously seen, but not the exact same (lures). There were a total of 768 trials (192 first presentations, 96 repetitions, 96 lures, and 384 unrelated foil items) divided into eight 4.5-min runs. Task procedures are further described in Lacy et al. (2011).
Dataset #3: Firsts and Lures (Young Participants)
Similar to dataset 2, nineteen healthy young adults incidentally encoded a series of color images of everyday objects (2.4 s each with a 0.3 s ISI) by indicating via button press whether each was an indoor or outdoor object. In this task, images could only be first presentations or lure items. There were no repetitions. There were a total of 768 trials (192 first presentations, 192 lures, and 384 unrelated foil items) divided into eight 4.5-min runs. Task procedures are further described in Yassa et al. (2011).
Dataset #4: Firsts and Lures (Older Participants)
This dataset had the same task and design as Dataset 3, except that it was run in sixteen healthy older adults. Task procedures are further described in Yassa et al. (2011).
Dataset #5: Resting State (Young Participants)
Eighteen healthy young adults remained in a relaxed awake state for ~2 min of fMRI scanning. There was no overt task. Some participants had two sessions of resting state scans on the same day separated by ~40 min of an incidental encoding task similar to the one described in Dataset #2. For these subjects, their resting state scans were concatenated together before being preprocessed and analyzed.
Dataset #6: Resting State (Older Participants)
This dataset had the same design and procedures (there was no overt task) as Dataset 5 except that it was run in 18 healthy older adults.
Dataset #7: A or B Associations, 80% Valid Feedback
Twenty-five healthy young adults participated in a continuous learning task where they had to associate each of four stimuli with either Group A or B. For two of the stimuli, participants received positive feedback for correct answers, but no feedback for incorrect answers. For the other two stimuli, participants received negative feedback for incorrect answers, but no feedback for correct answers. Valid feedback was given on 80% of trials, and invalid feedback was given on 20% of trials. There were 40 learning trials (10 presentations per stimuli, 3 s each with a 1 s ITI) and 20 perceptual baseline trials per 4-min run. Participants completed either four or eight runs. A new stimulus set was presented for every four runs. Task procedures are further described in Mattfeld et al. (2011).
Dataset #8: Four Response Associations, 80% Valid Feedback
Eighteen healthy young adults participated in a continuous learning task where they had to associate each of four stimuli with one of four button box responses. Participants received “Yes” or “No” feedback on correct and incorrect trials respectively (trial duration =3 s with a 1 s ITI). When participants reached criterion on a particular stimulus, that stimulus was removed from the task and was replaced with a new stimulus. Participants were always learning four stimuli concurrently. Correct feedback was given on 80% of trials, and incorrect feedback was given on 20% of trials. Participants learned on average 16.3 stimuli across six 4-min runs.
Dataset #9: Four Response Associations, 100% Valid Feedback
This dataset has the same task and design as Dataset 8 except that correct feedback was given on 100% of trials. To match difficulty with the previous task, participants were required to learn eight stimuli to button box associations at a time. Twenty-two healthy young adults participated in this task. Participants learned on average 31.9 stimuli across six 4-min runs.
Dataset #10: Firsts, Repeats, Lures at Johns Hopkins
Similar to Dataset 2, twenty healthy young adults incidentally encoded a series of color images of everyday objects (2.5 s each with a 0.5s ISI) by indicating via button press whether each was an indoor or outdoor object. Images could be first presentations, exact repetitions, or lures items. There were a total of 1,158 trials divided into eight 5.5-min runs. Task procedures are further described in Bakker et al. (2008).
In summary, Dataset 1 can be thought of as a relatively traditional explicit memory task. Datasets 2, 3, 4, and 10 are variations of an incidental encoding task. Datasets 5 and 6 are resting state scans. Datasets 7, 8, and 9 are continuous learning paradigms. See Table 1 for a summary of the datasets.
TABLE 1.
Summary of Datasets
| Dataset | n | Population | Location | Behavioral task |
|---|---|---|---|---|
| 1 | 21 | Young | UC Irvine | Explicit memory task |
| 2 | 21 | Young | UC Irvine | Incidental encoding |
| 3 | 19 | Young | UC Irvine | Incidental encoding |
| 4 | 16 | Old | UC Irvine | Incidental encoding |
| 5 | 18 | Young | UC Irvine | Resting state scan |
| 6 | 18 | Old | UC Irvine | Resting state scan |
| 7 | 25 | Young | UC Irvine | Continuous learning |
| 8 | 18 | Young | UC Irvine | Continuous learning |
| 9 | 22 | Young | UC Irvine | Continuous learning |
| 10 | 20 | Young | Johns Hopkins | Incidental encoding |
Scanning Procedures
Three different scanning procedures were used for these studies. All were performed on a 3.0 Tesla Philips scanner with an 8-channel SENSE (Sensitivity Encoding) coil in order to acquire high-resolution imaging data of the hippocampus (Kirwan et al., 2007). Distortions of the functional echo-planar image (EPI) signal were controlled by: (1) higher-order shims, which can directly compensate for local field distortions, (2) SENSE parallel imaging, which uses multiple surface coils to undersample k-space with fewer phase encoding steps (Pruessner et al., 2002), and (3) the use of thin slices as artifacts are a function of the number of slices from the inhomogeneity rather than absolute distance (Buxton, 2001). A whole-brain 0.75 mm or 1 mm isotropic magnetization prepared rapid acquisition gradient echo (MPRAGE) structural scan was acquired for datasets 1–9 and dataset 10, respectively.
For Datasets 1–6, oblique EPIs were collected (1.5 mm isotropic voxels, 120 × 120 acquisition matrix, 22 slices) aligned parallel to the principal axis of the hippocampus with a repetition time of 1,500 ms, an echo time of 26 ms, a flip angle of 70°, and a SENSE reduction factor of 2.
For Datasets 7–9, oblique EPIs were collected (1.5 × 1.5 × 2 mm3 voxels, 120 × 120 acquisition matrix, 35 slices) aligned perpendicular to the principal axis of the hippocampus with a repetition time of 2,000 ms, an echo time of 26 ms, a flip angle of 70°, and a SENSE reduction factor of 2.
For Dataset 10, oblique EPIs were collected (1.5 mm isotropic voxels, 64 × 64 acquisition matrix, 19 slices) aligned parallel to the principal axis of the hippocampus with a repetition time of 1,500 ms, an echo time of 30 ms, a flip angle of 70°, and a SENSE reduction factor of 2.
Cross-Participant Alignment
Cross-participant alignment was performed using Region of Interest—Advanced Normalization Tools (ROI-ANTS; Avants et al., 2008; Klein et al., 2009; Lacy et al., 2011; Yassa et al., 2011) based on regional alignment methods developed in our laboratory (Miller et al., 2005; Yassa and Stark, 2009). An affine registration was applied to bring each participant’s structural image into the atlas space of Talairach and Torneaux (1988). This initial registration provides a rough first pass, removing large spatial shifts between participants prior to subsequent fine-tuned cross-participant alignment using Advanced Normalization Tools (ANTs), a powerful diffeomorphic alignment algorithm (Avants et al., 2008). ANTs can be used to create custom central tendency templates as well as to create 3D vector fields to map each participant’s brain into template space. We used the structural scans of 20 healthy young participants and 20 healthy older participants to create custom central tendency templates for young and older participants respectively. Following the template generation, each participant’s MPRAGE was then warped into the appropriate custom template space. The resulting transformation parameters were subsequently applied to the output of analyses of the functional data.
Functional Connectivity Analysis
Data analysis was performed using the Analysis for Functional NeuroImages (AFNI) software (Cox, 1996). As in traditional fMRI activation studies, images were co-registered to correct for within and across-scan head motion. Acquisitions in which a significant motion event occurred (defined as >3° or 2 mm of movement relative to prior acquisition) ±1 TR surrounding the motion event were excluded.
All task effects, including baseline trials, were modeled via general linear model (GLM) using AFNI’s 3dDeconvolve command (Cox, 1996; Fair et al., 2007). The model was used to synthesize the data and this was subtracted from the raw fMRI signal to generate the residuals. Note that for the resting state datasets (5 and 6) only scanner drift was modeled and removed from the raw data. We then performed a seed style correlational analysis on the residual fMRI data. Twelve regions of interest (ROIs) were analyzed: PHC, PRC, ERC, dentate gyrus, and CA3 (DG/CA3, which are combined due to lack of resolution to accurately separate these regions), CA1, and subiculum in each hemisphere. ROIs were anatomically defined with the use of our alignment model. For information on the relative size of these ROIs please see Supporting Information Table 1.
For each functional connectivity analysis, seed regions’ average time series were generated. Global signal, white matter, and cerebral spinal fluid (CSF) time series were also generated and were added to the regression model of each seed region to account for any physiological and any other possible sources of noise that might cause artifactual correlations across regions. The assumption being that physiological noise, e.g. cardiac and respiratory effects, should be captured across the brain in the global signal and there should be little to no true “activity” in the white matter and CSF. Thus, the signal from these regions should be primarily noise. The noise regressors were created for each subject by averaging time series across all voxels in a mask of the brain, white matter, and CSF on their MPRAGE. In one analysis, white matter and CSF regressors were created for each slice to account for possible local physiological noise. Adding additional regressors into the model did not prove to be any more robust than using a single white matter and CSF regressor for the entire acquisition window (see Results).
For each subject, the average correlation coefficient between every pair of ROIs was calculated by finding the average correlation between the time series of seed regions and all the individual voxels in other ROIs. This style of analysis does not provide the noise reduction that averaging time series within ROIs would and thus results in small correlation coefficients. However, we choose this style of analysis because it is not subject to correlations being driven by a few outlier voxels that could dominate a region’s average time series. Instead, by correlating a seed region’s time series to every voxel in another ROI and then averaging over these correlations, each voxel is weighted equally in this overall correlation. Thus this method is more assumption-free than correlating two average time series from different ROIs. We did not perform the even more assumption free analysis of correlating every voxel in a seed region to even voxel in another ROI due to the large number of calculations that would require. These correlation coefficients were then Fisher’s z transformed and averaged across all voxels within each ROI. For each subject, this resulted in a vector of transformed correlation coefficients that corresponded to all possible pairs of ROIs. Group analysis began by averaging correlation coefficients across participants within a dataset and then comparing each dataset to each other via correlation and Pearson’s r.
Permutation Analysis
In order to test the patterns of functional connectivity within each dataset, we performed two permutation analyses. The first analysis was to test the internal consistency of the emergent pattern in each dataset. This began by randomly splitting the participants from each dataset into two halves and creating an average correlation coefficient vector for each half of participants. We randomly permuted the average correlation coefficient vector from the first half of participants 10,000 times and correlated each random permutation with the unaltered vector from the second half of participants. Thus, we created a chance distribution of correlation coefficients between the two halves of the datasets. We then correlated the unaltered vector from the first half of participants to the unaltered vector from the second half of participants to find the true correlation between the two halves of the datasets. Using the mean and standard deviation of the chance distribution of correlation coefficients, we calculated the z score and respective P-value of the real correlation of interest, that is between the unaltered halves of each datasets.
We next sought to determine whether the same patterns that emerged in Dataset 1 were reliably present in each of the other datasets. We created two models of these patterns plus an anatomical model of the connections reported in Lavenex and Amaral (2000; Fig. 1). The first model allowed us to test for the distinction between the MTL cortices and the hippocampal subfields, coding for strong ERC/PRC interactions and strong within-hippocampal interactions only. The second model tested the hemispheric effect within each region. To create a chance distribution of correlation coefficients between the models and the data, we first performed 10,000 permutations of each model and correlated these permutations with each dataset. We then calculated the correlation coefficient between each average dataset and the unaltered models and compared this to the previously generated distribution of chance correlation coefficients to obtain z scores and P-values. Since the models were built off of general observations from Dataset 1, the fit of Dataset 1 to the models was expected and the correlation coefficients of Dataset 1 to the models are simply reported for descriptive purposes. The importance of these models is in testing the reliability of this pattern in the remaining nine datasets. This same sort of permutation analysis was also used to test the correlation between each dataset and the anatomical model.
FIGURE 1.
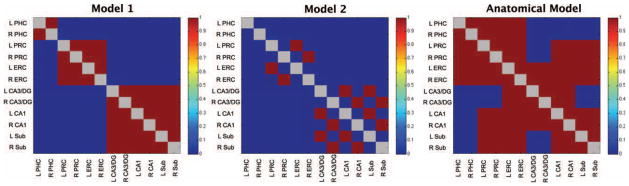
Model 1 models strong functional connectivity between left and right PHC, between bilateral PRC and ERC, and amongst the hippocampal subfields, but weak functional connectivity between the MTL cortices and the hippocampal subfields. Model 2 models strong functional connectivity within hemisphere and weak functional connectivity across hemisphere in areas of high functional connectivity as modeled in Model 1. The Anatomical Model is representation of the anatomical connections of the primate MTL as reported in Lavenex and Amaral (2000).
Lastly, we created a fake dataset by scrambling the average correlation coefficients from dataset 1 twenty times to create 20 fake “participants” and then we averaged the correlation coefficients of these “participants” to create dataset 11. We ran the above mentioned permutation analyses on this averaged scrambled dataset 11.
RESULTS
All participants’ vector of correlation coefficients for Dataset 1 were averaged together and displayed in matrix form (Fig. 2 left). Two patterns of functional connectivity emerged. The first was relatively high correlation coefficients between left and right PHC, between bilateral PRC and ERC, and amongst the hippocampal subfields (Fig. 2 left, boxes outlined in red). Notably, however, there was relatively weak functional connectivity between the MTL cortices and the hippocampal subfields. The second pattern was that in areas of high functional connectivity, there was also a hemispheric effect such that seed regions were better correlated with ROIs within the same hemisphere than the opposite hemisphere (e.g., left DG/ CA3 and left CA1 are better correlated than left DG/CA3 and right CA1).
FIGURE 2.
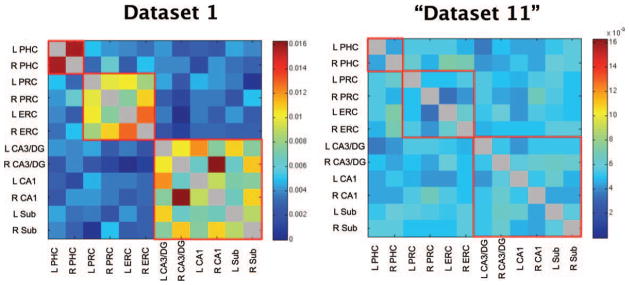
(Left) Z-transformed correlation coefficients averaged across all participants in Dataset 1 for all possible pairs of ROIs. The diagonal is grayed out since seed regions are perfectly correlated with themselves. Regions of high functional connectivity are outlined in red for visualization. Notably, there is relatively weak functional connectivity between the MTL cortices and the hippocampal subfields. (Right) A dataset of 20 fake participants created by scrambling the average correlations coefficients of dataset 1 twenty times. The scrambled “Dataset 11” does not show the same patterns of functional connectivity as dataset 1 or the other datasets (see Fig. 3). L, left; R, right; PHC, parahippocampal cortex; PRC,. perirhinal cortex; ERC, entorhinal cortex; DG, dentate gryus; Sub, subiculum.
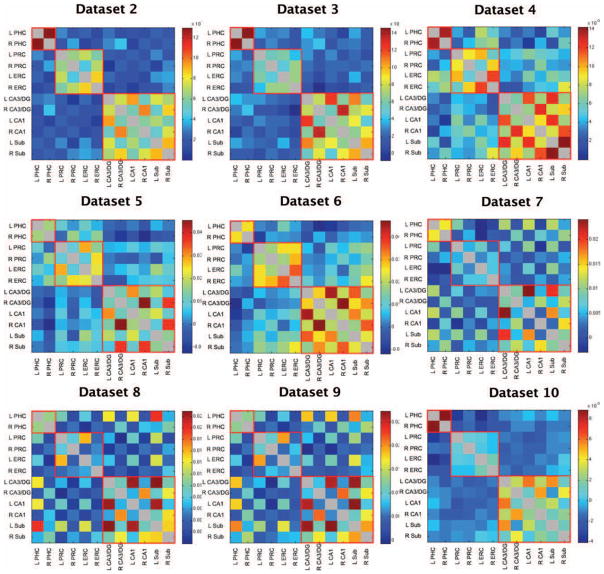
To verify that this was not a coincidental pattern and that each dataset was internally consistent, we performed a permutation analysis. Note that the vector of correlations coefficients used in this analysis (described in Methods) equals one half of each correlation matrix as each matrix is necessarily symmetric. We found that the emergent pattern of functional connectivity in all datasets was statistically significant (all datasets z > 4.8, P < 0.0001, Fig. 3, Table 2). A fake “Dataset 11” did not reveal a significant pattern when tested against itself (z = −0.11, P =0.91, Fig. 1 right). Thus, it is clear that the patterns of functional connectivity seen in Datasets 1–10 did not arise by chance and that each dataset is internally consistent.
FIGURE 3.
Z-transformed correlation coefficients averaged across participants in Datasets 2–10 for all possible pairs of ROIs. Diagonals are grayed out since seed regions are perfectly correlated with themselves. Regions of high functional connectivity are outlined in red for visualization. All datasets show similar patterns of functional connectivity.
TABLE 2.
Within Dataset Permutations
| Dataset | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | “11” |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CorrCoef | 0.8447 | 0.8396 | 0.9260 | 0.6225 | 0.6408 | 0.7754 | 0.8916 | 0.9052 | 0.9545 | 0.8603 | −0.0140 |
| z-score | 6.865 | 6.735 | 7.446 | 5.014 | 5.175 | 6.302 | 7.174 | 7.339 | 7.608 | 6.867 | −0.114 |
| P-value | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | 0.9092 |
To test the validity of the emergent pattern of functional connectivity within each dataset, 10,000 permutations were performed on one half of the data from each dataset and then correlated with the second half of the data from each dataset to create a distribution of correlation coefficients. Reported are the correlation coefficients of the two halves of the datasets to each other, its z-score, and its resulting P-value. Each dataset had a significant pattern of functional connectivity except the fake dataset “11”.
We next sought to determine whether the same general patterns that emerged in dataset 1 were reliably present in each of the other datasets. We created two simplified models of these patterns (Fig. 1) and performed a permutation analysis comparing each dataset to each model (see Methods). Since the models were built off of general observations from Dataset 1, there will necessarily be a clear correlation between Dataset 1 and the models (albeit not a perfect correlation as the models are based on general patterns and not the specific data). The remaining nine datasets, however, were not used to generate the models and are therefore independent of them. Datasets 2–10 were significantly correlated with both models (all z > 3.61, P < 0.0001, Table 3, see Supporting Information Figure 1 for better visualization of the hemispheric effects). Thus, the observed correlation of each dataset to the two models was not the result of chance. The fake “dataset 11” did not correlate with either model (z = −0.17, P =0.87 and z =0.07, P =0.95 respectively, Table 3).
TABLE 3.
(a) Each Dataset Compared With Model 1; (b) Each Dataset Compared With Model 2
| Dataset | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | “11” |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CorrCoef (a) | 0.8553 | 0.8766 | 0.8283 | 0.7626 | 0.6876 | 0.8025 | 0.4512 | 0.4778 | 0.4589 | 0.7502 | −0.0218 |
| z-score | 6.831 | 7.059 | 6.664 | 6.188 | 5.511 | 6.535 | 3.641 | 3.845 | 3.724 | 6.065 | −0.1670 |
| P-value | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | 0.8674 |
| CorrCoef (b) | 0.5998 | 0.5733 | 0.6254 | 0.5911 | 0.8026 | 0.6515 | 0.5987 | 0.6251 | 0.6401 | 0.5590 | 0.0069 |
| z-score | 4.908 | 4.596 | 5.025 | 4.838 | 6.535 | 5.231 | 4.816 | 5.067 | 5.164 | 4.523 | 0.068 |
| P-value | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | 0.9458 |
To test the validity of each pattern of functional connectivity represented by the models, 10,000 permutations of each model were correlated with each dataset to create a distribution of correlation coefficients. Reported are the correlation coefficients of the model to the dataset, its z-score, and its resulting P-value. Since the models were built off of observations from dataset 1, the fit of dataset 1 to the models was expected and the correlation coefficients of dataset 1 to the models are simply reported for descriptive purposes. Each dataset was significantly correlated with both models. The fake “dataset 11” did not correlate with either model.
These patterns of functional connectivity were robust across datasets as all datasets were highly correlated with the models. However, differences still remained amongst the datasets; some datasets were more strongly correlated with the models than others. To further examine these differences and to compare across datasets, we correlated every participants’ vector of correlation coefficients with Model 1. It is clear that even when the correlation to the model was done at the individual subject level, all datasets (save the scrambled “Dataset 11”) showed reliable high correlations (Fig. 4). A one-way ANOVA across Datasets 1–10 showed that there were indeed differences across datasets (F9,187 =12.88, P < 0.0001). Post-hoc Bonferroni’s multiple comparison tests were performed on all pairs of datasets; however, only pairwise tests of specific interest are reported here. There was a significant difference between younger and older participant datasets during an incidental encoding task. Younger participants in Dataset 3 were significantly better correlated to Model 1 than older participants in Dataset 4 (t33 =4.28, P < 0.01). However, there was no difference between how well younger and older participants (Datasets 5 and 6, respectively) were correlated to Model 1 during a resting state scan (t33 =1.89, n.s.). It is also interesting to note that young participants in an incidental encoding task (Dataset 3) were significantly better correlated with Model 1 than an equivalent population of young participants during an resting state scan (Dataset 5; t35 =5.05, P < 0.001), but no difference was seen between older participants during an incidental encoding task or resting state scan (Datasets 4 and 6, respectively; t31 =1.24, n.s.). A two-way ANOVA on these four datasets (3, 4, 5, and 6) revealed a significant task (incidental encoding vs. rest) by age (younger vs. older participants) interaction (F1 =16.49, P < 0.001).
FIGURE 4.
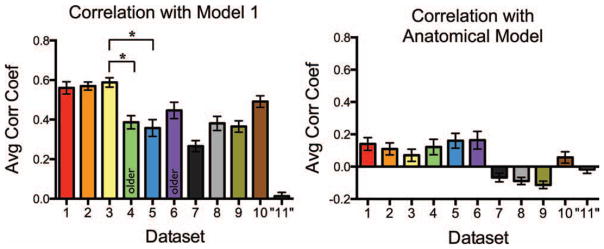
(Left) The average correlation of every participants’ vector to model 1 for each dataset. Since model 1 was built off of general observations from dataset 1, the high correlation of dataset 1 to model 1 is expected and the correlation coefficients of dataset 1 to model 1 are simply reported for descriptive purposes. All datasets were highly correlated with model 1, especially compared to a scrambled dataset “11”, but not all datasets were equal (one-way ANOVA across Datasets 1–10, F9,187 = 12.88, P <0.0001). Post-hoc Bonferroni’s multiple comparison tests were performed on all pairs of datasets; however, only tests of specific interest are reported here. Young participants (Dataset 3) in an incidental encoding task were significantly better correlated to Model 1 than older participants (Dataset 4) in the same exact task (t33 = 4.28, P <0.01). There were also differences in task-related versus resting state data in similar participants. Dataset 3, an incidental encoding task, was significantly better correlated to Model 1 than Dataset 5, a resting state scan (t35 = 6.57, P <0.001), despite both datasets being collected in healthy young adults with the same scanner sequence at the same MRI facility. (Right) The average correlation of every participants’ vector to an anatomical model representing the anatomical MTL connections reported in Lavenex and Amaral (2000). A two-way ANOVA on the correlation of each participants’ vector of coefficients in Datasets 1–10 to Model 1 and the anatomical model was run to compare the fit of each dataset to each model. Post-hoc Bonferroni’s multiple comparison tests revealed that each dataset was better correlated to Model 1 than to the anatomical model (all t >4.08, all P <0.001), suggesting that Model 1 is a better representation of the pattern of functional connectivity within each dataset than known anatomical connections.
Last, we wanted to evaluate how well each dataset’s pattern of functional connectivity correlated with the known anatomical connectivity of the MTL. We created a model (Fig. 1 right) based on the known anatomical connections of the MTL (Lavenex and Amaral, 2000). We then correlated every participants’ vector of correlation coefficients with the anatomical model (Fig. 4). We performed a two-way ANOVA on the correlation of each participants’ vector of coefficients to both Model 1 and the anatomical model to directly compare the fit of each dataset to each model. Post-hoc Bonferroni’s multiple comparison tests revealed that each dataset was better correlated to Model 1 than to the anatomical model (all t > 4.08, all P < 0.001), suggesting that Model 1 is a better representation of the pattern of functional connectivity within each dataset than known anatomical connections. A permutation analysis was also performed on the anatomical model. Only three of the ten datasets were significantly correlated with the anatomical model (z >2.15, P < 0.05, Supporting Information Table 2).
Manipulation Checks
Although the pattern of results was remarkably consistent both within and across datasets, there are several possible sources of artifacts that could lead to the observed patterns. We should note, however, that the findings were replicated across several datasets which included participants of different ages, different tasks (or in the case of the resting scans, no task), and different scan sequences/slice acquisitions. One of these datasets was even collected at a different scanning facility. Furthermore, the MTL cortices vs. hippocampal subfields pattern exists across hemispheres. Although in the rat there are massive commissural connections in the dentate gyrus, this is not the case in primates (Amaral et al., 1984). Thus, the finding that hippocampal ROIs are better correlated to hippocampal ROIs in the opposite hemisphere than MTL cortex ROIs in the same hemisphere (and vice versa) suggests that the correlations are not due to mere proximity. Nevertheless, to account for possible sources of artifact, we performed a number of manipulation checks, all of which were performed on Dataset 1, comparing the resulting correlation between the manipulation check and Dataset 1 with the distribution of chance coefficients.
Physical Proximity of ROIs
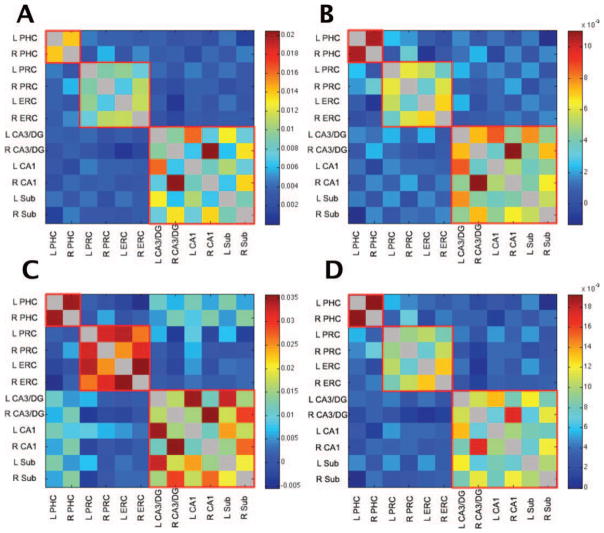
It is possible that spurious correlations between ROIs could be induced by neighboring voxels. For example, CA1 is physically closer to the subiculum than it is to the PHC and any spatial blur can induce a correlation among proximal voxels. Note, however, that this clearly cannot account for the cross-hemisphere effects mentioned above. To address this potential concern, we analyzed the data using eroded versions of the ROIs [the outermost voxel (0.75 mm) along the edges of each ROI were removed from the ROI masks] so that no voxels were touching other ROIs or gray matter/white matter/CSF outside of the ROIs. Using the permutation analysis described earlier to compare the correlation coefficient vectors of eroded ROIs to noneroded ROIs, the results were virtually identical (Fig. 5A; z =7.72, P < 0.0001).
FIGURE 5.
Dataset 1 (A) analyzed with noneroded ROIs, (B) with an additional white matter and CSF regressors for each slice of acquisition, (C) with bandpass filtered (0.01–0.1 Hz) data instead of data with task effects removed via deconvolution, and (D) with task effects left in. All analyses produced similar patterns of functional connectivity and were highly correlated with the original Dataset 1 analysis (see Fig. 1, all z >7.19, all P <0.0001).
Noise Varying Across Slice
Second, it is possible that the noise injected into our data might have a component that is consistent within each slice but that varies across slices. This would induce an elevated correlation within each slice and a reduced correlation across slices. As our slices are typically oblique axials aligned with the hippocampus, this would separate the hippocampus and MTL cortical structures across slices. It is also possible that the global white matter and CSF regressors do not properly account for residual noise and that they might be biased towards or against some regions. To address these potential concerns, we created a white matter and CSF regressors for each slice to replace the global ones used in the initial analysis. The results were again unchanged (Fig. 5B; z > 7.72, P <0.0001).
Bandpass Filtered Data
Last, another common technique for processing event-related fMRI data in functional connectivity analyses is to bandpass filter the data instead of modeling events and removing them via deconvolution as we have done here. To verify that the patterns of functional connectivity revealed were not a result of our method of deconvolution, we bandpass filtered our data from 0.01 to 0.1 Hz instead of removing task effects via deconvolution and then repeated our correlational analyses. Again, the same pattern emerged (Fig. 5C; z > 7.191, P > 0.0001).
Despite these controls, the same two patterns of functional connectivity emerged in all datasets: there was relatively strong functional connectivity between the ERC and PRC and between the hippocampal subfields, but not across the MTL cortices and hippocampal subfields and in the mentioned areas of strong functional connectivity, there was greater functional connectivity within a hemisphere than across hemispheres.
DISCUSSION
We observed two patterns of functional connectivity in the human MTL. The first was relatively high functional connectivity between the left and right PHC, the ERC and PRC bilaterally, and amongst the hippocampal subfields (DG/CA3, CA1, and subiculum) both within and across hemispheres. However, there was relatively weak functional connectivity between the MTL cortices and the hippocampal subfields. Second, we saw greater functional connectivity within a hemisphere than across hemispheres. These patterns were consistent across 10 datasets despite the fact that these datasets differed in task demands, participants’ age, and scanner sequence/slice acquisition. Additionally, only three out of the ten datasets reported were significantly correlated with a model based on the known anatomical connections in the MTL. All ten datasets were more strongly correlated with Model 1 than the anatomical model, suggesting that Model 1 is a better representation of the pattern of functional connectivity in the human MTL than the known anatomical connections. The observed patterns of functional connectivity were not necessarily expected a priori (we would have been less surprised to see a pattern of functional connectivity similar to the anatomical connectivity). However, the robustness of the observed patterns across datasets and the lack of correlation between many datasets and the anatomical model suggest that the observed patterns of functional connectivity represent a real phenomenon. These results have implications regarding the organization of the MTL and hippocampus and how these regions might interact with each other.
Functional Connectivity Versus Anatomical Connectivity
The current findings might lead some to wonder why known anatomical connections, such as those between the ERC and DG or between the PRC and PHC (Amaral, 1993; Lavenex and Amaral, 2000), do not appear to be represented in the functional connectivity of the MTL. Functional connectivity and anatomical connectivity are thought to be highly related as suggested by simultaneous fMRI and DTI studies which show similar functionally and anatomically connected networks (Koch et al., 2002). Additionally, disruptions in anatomical connectivity typically lead to disruptions in functional connectivity (Quigley et al., 2003; Johnston et al., 2008). However, it is possible for regions to have high functional connectivity without direct anatomical projections to each other (Damoiseaux and Greicius, 2009). For example, the default mode network is routinely identified as a functionally connected network despite the lack of a full set of direct anatomical connections (Greicius et al., 2003; Fox et al., 2005).
Functional connectivity should not be thought of as synonymous with anatomical connectivity as previous studies have shown that task effects can change the strength of functional connectivity between regions while the underlying anatomical connections remain constant (Lowe, 2000). Similarly the strength of functional connectivity during resting state scans can be influenced by subtleties such as whether participants are at rest with their eyes open versus their eyes closed—which is obviously unrelated to anatomy (Van Dijk et al., 2010). Similarly, neuromodulatory effects or inhibition of an area could affect the functional connectivity with a downstream region without effecting the underlying anatomy. Further, it is quite possible that the pattern of functional connectivity that one would predict from the anatomy exists, but only for brief periods of time (e.g., as regions become synchronous), with the dominant mode being uncorrelated. Functional connectivity may be described as being anatomically constrained as there must be at least an indirect anatomical connection between functionally connected regions. However, functional connectivity reflects something more than basic structural connectivity. This gives it numerous potential uses as a dependent measure of brain function.
Last, perhaps the anatomical model better captures functional connectivity during task demands and the data driven model is a result of removing task effects. We have evidence that this is unlikely to be the case. When we analyzed dataset 1 with task effects removed and task effects left in, the results are strikingly similar to each other (see Fig. 5D). This suggests that the great majority of correlated activity across regions is not due to the task effects, but rather is more likely driven by some underlying activity. A second possibility is, perhaps, the anatomical model is a true indication of the connectivity between regions during task demands; however, this “true” connectivity is very transient and cannot be picked up with the slow time scale of fMRI. Future experiments with electrophysiological recordings would be better suited to address this possibility.
Organization of the MTL
These patterns of functional connectivity may provide insight into the inherent organization of the MTL. The distinction between the MTL cortices and the hippocampal subfields suggests that these two regions are largely in communication with themselves and less so between each other. That is not to say they are not communicating across the hippocampus versus cortex border, but rather simply that there is a greater correlation of activity within the MTL cortex or the hippocampus than across regions.
This difference in inherent connectivity is consistent with many notions of a division of labor amongst the structures in the MTL as historically, the components of the MTL have often been organized along these lines. For example, Squire et al. (2004) point to the notion that the anatomy suggests the hippocampus “combines and extends” the processing carried out in the MTL cortices. While the specifics of the extension are not clear, this is not a hypothesis of equipotentiality, but rather that the hippocampus is set apart from the MTL cortical structures. Eichenbaum and Cohen’s “relational memory theory” also separated the PRC and PHC (which are thought to encode elements of an event) from the hippocampus (which is thought to encode the relationship between those elements; Eichenbaum et al., 1992; Eichenbaum, 2000). Moreover, Brown and Aggleton (2001) described the PRC and hippocampus as interacting but dissociated units which differed in both the type of memory, recognition and recollection respectively, as well as the level of subjective experience, familiarity and conscious remembering respectively. Computational modeling’s “complementary learning systems” distinguishes the neocortex and hippocampus by their computational processes and thus the speed and efficiency with which these regions can learn new associations. According to this model, the neocortex is a slow, statistical learner that is unable to resolve catastrophic interference. However, the hippocampus rapidly acquires information by assigning distinct representations to stimuli, thus avoiding these interference issues (McClelland et al., 1995; Norman and O’Reily, 2003).
In addition to the MTL cortex versus hippocampus distinction, we also saw that the PHC had relatively weak functional connectivity with all other ROIs including the PRC. This raises the possibility that the PHC performs a function unique to itself that is different from the functions of the PRC. This observation is consistent with the “binding of item in context” (BIC) model which suggests a distinction between the functions of the PRC, PHC, and hippocampus. The BIC model posits that the PRC is involved in item representations, the PHC is involved in context representations, and the hippocampus binds those items in context (Diana et al., 2007; Ranganath, 2010).
The results shown here, that an initial differentiation can be drawn between the hippocampus and the MTL cortical structures and that a secondary differentiation would further separate the PHC, are therefore consistent with many theories of function of MTL. This basic pattern does not speak strongly to which theory is a better account. However, these results do open up a new avenue for hypothesis testing since the datasets differed not only in their design but also in the degree to which the various patterns were shown.
Differences Amongst Datasets
As noted, although all datasets were highly correlated with the models, they were not equally so. One place in which we saw a significant difference was between younger and older participants during an incidental encoding task (Datasets 3 and 4). The pattern of functional connectivity in younger participants was significantly more correlated with Model 1 than the pattern of functional connectivity in older participants. In other words, there was less of a distinction between the MTL cortices and the hippocampus in older participants than younger participants (see Fig. 2). Whether this is beneficial or detrimental is currently unknown because we did not have a behavioral measure of performance and thus cannot evaluate how this relates to functional connectivity. Other studies on Alzheimer’s Disease (AD) patients, however, suggest that behavior and functional connectivity are related since AD patients are reported to have impaired functional connectivity compared to healthy controls (Li et al., 2002; Greicius et al., 2004).
It is interesting to note that we did not see a difference between younger and older participants during resting state scans (Datasets 5 and 6, respectively), but we did see a difference between equivalent populations of younger participants during an incidental encoding task vs. rest (Datasets 3 and 5, respectively). This difference between the younger participant datasets might stem from the fact that resting state scans are intrinsically different from task related activity. Participants are not cognitively inactive during rest, but rather appear to have high levels of activity, which could be due to mind-wandering or self-referential thought (Stark and Squire, 2001). Since there are fewer constraints on participants’ thought processes during rest than during task, it would not be surprising to see greater variance in the BOLD activity of resting state scan participants than task-performing participants. There was a significant task (incidental encoding vs. rest) by age (younger vs. older participants) interaction, suggesting that perhaps the functional connectivity of the MTL changes with age, but only during task-related activity and not so during rest. Future studies with more direct comparisons between age and task may better elucidate how these variables affect patterns of functional connectivity.
Last, Datasets 7, 8, and 9 were less correlated with Model 1 than other datasets (e.g., Dataset 1), which might be due to the continuous learning paradigm that was unique to these datasets. Even though task effects were removed by GLM, task may still have some effect on the emergent patterns of functional connectivity that is unaccounted for, e.g., via attentional state that the task properties set.
Overall, the patterns of functional connectivity revealed were remarkably consistent both within and across datasets despite the fact that these datasets differed by task demands, participants’ age, and scanner sequence/slice acquisition. However, there are many factors that may contribute to subtle differences in the output of functional connectivity analyses. Future directions include further exploring these dataset differences. For example, in certain datasets there appear to be relatively stronger correlation coefficients between the ERC and subiculum (see Fig. 2). We propose using statistical modeling to find the best fit model for individual datasets as well as modulating different components of the models to see how each is affect by participants’ age or task. Further analysis of functional connectivity patterns and better statistical modeling could eventually let to diagnostic capabilities.
CONCLUSIONS
Functional connectivity analyses can inform us in ways that traditional univariate activation-based fMRI cannot. This study is an initial foray into investigating the functional connectivity of the MTL at high enough resolution to visualize the hippocampal subfields. The results of this analysis indicate that there is stronger connectivity within the MTL cortices and the hippocampal subfields than across the MTL cortex and the hippocampus. This does not suggest that the MTL cortex and hippocampus are not communicating with other or even that they might not be highly correlated. It is possible that these regions are highly correlated but only transiently. If this were the case, fMRI may not be adequate to pick up these transient effects, but they could perhaps be observed with electrophysiology. The current results indicate that there is greater overall correlation within these regions than across these regions and that the degree to which this is shown can vary. Notably, this pattern was more robust than an anatomical model of the MTL. Although this pattern of functional connectivity may be initially surprising, these findings have implications for our understanding of the inherent organization of the MTL and suggest a tripartite organization such that the hippocampus, the perirhinal, and entorhinal cortices, and the parahippocampal cortex perform functions that interact with each other but are functionally dissociable. Future research will further elucidate the role of age and task effects on of the functional connectivity of the MTL.
Acknowledgments
Grant sponsor: NIH; Grant numbers: R03 AG032015, R01 AG034613, R01 MH08582, P50 AG 016573; Grant sponsor: NIA; Grant number: 5 T32 AG 96-28.
The authors thank Aaron Mattfeld for his advice and assistance.
Footnotes
Additional Supporting Information may be found in the online version of this article.
References
- Amaral DG. Emerging principles of intrinsic hippocampal organization. Current Opin Neurobiol. 1993;3:225–229. doi: 10.1016/0959-4388(93)90214-j. [DOI] [PubMed] [Google Scholar]
- Andrews-Hanna JR, Snyder AZ, Vincent JL, Lustig C, Head D, Raichle ME, Buckner RL. Disruption of large-scale brain systems in advanced aging. Neuron. 2007;56:924–935. doi: 10.1016/j.neuron.2007.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants B, Duda JT, Kim J, Zhang H, Pluta J, Gee JC, Whyte J. Multivariate analysis of structural and diffusion imaging in traumatic brain injury. Acad Radiol. 2008;15:1360–1375. doi: 10.1016/j.acra.2008.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakker A, Kirwan CB, Miller NI, Stark CEL. Pattern separation in the human hippocampal CA3 and dentate gyrus. Science. 2008;319:1640–1642. doi: 10.1126/science.1152882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Resonance Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Brown MW, Aggleton JP. Recognition memory: What are the roles of the perirhinal cortex and hippocampus? Nat Rev Neurosci. 2001;2:51–61. doi: 10.1038/35049064. [DOI] [PubMed] [Google Scholar]
- Buxton RB. Introduction to Functional Magnetic Resonance Imaging: Principles and Techniques. Cambridge, UK: Cambridge University Press; 2001. [Google Scholar]
- Cox RW. AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Damoiseaux JS, Greicius MD. Greater than the sum of its parts: A review of studies combining structural connectivity and resting-state functional connectivity. Brain Struct Funct. 2009;213:525–533. doi: 10.1007/s00429-009-0208-6. [DOI] [PubMed] [Google Scholar]
- Damoiseaux JS, Rombouts SA, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF. Consistent resting-state networks across healthy subjects. Proc Naltl Acad Sci USA. 2006;103:13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diana RA, Yonelinas AP, Ranganath C. Imaging recollection and familiarity in the medial temporal lobe: A three-component model. TICS. 2007;11:379–386. doi: 10.1016/j.tics.2007.08.001. [DOI] [PubMed] [Google Scholar]
- Eichenbaum H. A cortical-hippocampal system for declarative memory. Nat Rev Neurosci. 2000;1:50. doi: 10.1038/35036213. [DOI] [PubMed] [Google Scholar]
- Eichenbaum H, Otto T, Cohen NJ. The hippocampus—What does it do? Behav Neural Biol. 1992;57:2–36. doi: 10.1016/0163-1047(92)90724-i. [DOI] [PubMed] [Google Scholar]
- Fair DA, Schlagger BL, Cohen AL, Miezin FM, Dosenbach NU, Wenger KK, Fox MD, Snyder AZ, Raichle ME, Petersen SE. A method for using blocked and event-related fMRI data to study “resting state” functional connectivity. NeuroImage. 2007;35:396–405. doi: 10.1016/j.neuroimage.2006.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Raichle ME. Intrinsic fluctuations within cortical systems account for intertrial variability in human behavior. Neuron. 2007;56:171–184. doi: 10.1016/j.neuron.2007.08.023. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Zacks JM, Raichle ME. Coherent spontaneous activity accounts for trial-to-trial variability in human evoked brain responses. Nat Neurosci. 2006;9:23–25. doi: 10.1038/nn1616. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Functional and effective connectivity in neuroimaging: A synthesis. Hum Brain Mapp. 1994;2:56–78. [Google Scholar]
- Friston KJ, Frith CD, Liddle PF, Frackowiak RS. Functional connectivity: The principal-component analysis of large (PET) data sets. J Cereb Blood Flow Metab. 1993;13:5–14. doi: 10.1038/jcbfm.1993.4. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proc Natl Acad Sci USA. 2003;100:253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V. Default-mode network activity distinguishes Alzheimer’s disease from healthy aging: evidence from functional MRI. Proc Natl Acad Sci USA. 2004;101:4637–4642. doi: 10.1073/pnas.0308627101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He BJ, Snyder AZ, Vincent JL, Epstien A, Shulman GL, Corbetta M. Breakdown of functional connectivity in frontoparietal networks underlies behavioral deficiets in spatial neglect. Neuron. 2007;53:905–912. doi: 10.1016/j.neuron.2007.02.013. [DOI] [PubMed] [Google Scholar]
- Johnston JM, Vaishnavi SN, Smyth MD, Zhang D, He BJ, Zempel JM, Shimony JS, Snyder AZ, Raichle ME. Loss of resting interhemispheric functional connectivity after complete section of the corpus callosum. J Neurosci. 2008;28:6453–6458. doi: 10.1523/JNEUROSCI.0573-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirwan CB, Jones C, Miller MI, Stark CEL. High-resolution fMRI investigation of the medial temporal lobe. Hum Brain Mapp. 2007;28:959–966. doi: 10.1002/hbm.20331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, Christensen GE, Collins DL, Gee J, Hellier P, et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage. 2009;46:786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch MA, Norris NG, Hund-Georgiadis M. An investigation of functional and anatomical connectivity using magnetic resonance imaging. NeuroImage. 2002;16:241–250. doi: 10.1006/nimg.2001.1052. [DOI] [PubMed] [Google Scholar]
- Lacy JW, Yassa MA, Stark SM, Muftuler LT, Stark CEL. Distinct pattern separation related transfer functions in human CA3/ dentate and CA1 revealed using high-resolution fMRI and variable mnemonic similarity. Learn Mem. 2011;18:15–18. doi: 10.1101/lm.1971111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavenex P, Amaral DG. Hippocampal-neocortical interaction: A hierarchy of associativity. Hippocampus. 2000;10:420–430. doi: 10.1002/1098-1063(2000)10:4<420::AID-HIPO8>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- Li SJ, Li Z, Wu G, Zhang MJ, Franczak M, Antuono PG. Alzheimer disease: Evaluation of a functional MR imaging index as a marker. Radiology. 2002;225:253–259. doi: 10.1148/radiol.2251011301. [DOI] [PubMed] [Google Scholar]
- Lowe MJ. Correlations in low-frequencey BOLD fluctuations reflect cortico-cortical connections. NeuroImage. 2000;12:582–587. doi: 10.1006/nimg.2000.0654. [DOI] [PubMed] [Google Scholar]
- Mattfeld AT, Gluck MA, Stark CEL. Functional specialization within the striatum along both the dorsal/ventral and anterior/posterior axes during associative learning via reward and punishment. Learn Mem. 2011;18:703–711. doi: 10.1101/lm.022889.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland JL, McNaughton BL, O’Reilly RC. Why there are complementary learning systems in the hippocampus and neocortex: Insights from the successes and failures of connectionist models of learning and memory. Psychol Rev. 1995;102:419–457. doi: 10.1037/0033-295X.102.3.419. [DOI] [PubMed] [Google Scholar]
- Miller MI, Beg MF, Ceritoglu C, Stark C. Increasing the power of functional maps of the medial temporal lobe by using large deformation diffeomorphic metric mapping. Proc Natl Acad Sci USA. 2005;102:9685–9690. doi: 10.1073/pnas.0503892102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman KA, O’Reilly RC. Modeling hippocampal and neocortical contributions to recognition memory: A complementary-learning-systems approach. Psychol Rev. 2003;110:611–646. doi: 10.1037/0033-295X.110.4.611. [DOI] [PubMed] [Google Scholar]
- Pruessner JC, Kohler S, Crane J, Pruessner M, Lord C, Byrne A, Kabani N, Collins DL, Evans AC. Volumetry of temporopolar, perirhinal, entorhinal and parahippocampal cortex from high-resolution MR images: Considering the variability of the collateral sulcus. Cereb Cortex. 2002;12:1342–1353. doi: 10.1093/cercor/12.12.1342. [DOI] [PubMed] [Google Scholar]
- Quigley M, Cordes D, Turski P, Moritz C, Haughton V, Seth R, Meyerand ME. Role of the corpus callosum in functional connectivity. AJNR Am J Neuroradiol. 2003;24:208–212. [PMC free article] [PubMed] [Google Scholar]
- Raichle ME. Two views of brain function. TICS. 2010;14:180–190. doi: 10.1016/j.tics.2010.01.008. [DOI] [PubMed] [Google Scholar]
- Raichle ME, Mintun MA. Brain work and brain imaging. Annu Rev Neurosci. 2006;29:449–476. doi: 10.1146/annurev.neuro.29.051605.112819. [DOI] [PubMed] [Google Scholar]
- Ranganath C. A unified framework for the functional organization of the medial temporal lobes and the phenomenology of episodic memory. Hippocampus. 2010;20:1263–1290. doi: 10.1002/hipo.20852. [DOI] [PubMed] [Google Scholar]
- Rosazza C, Minati L. Resting-state brain networks: Literature review and clinical applications. Neurol Sci. 2011;32:773–785. doi: 10.1007/s10072-011-0636-y. [DOI] [PubMed] [Google Scholar]
- Stark CEL, Squire LR. When zero is not zero: The problem of ambiguous baseline conditions in fMRI. Proc Natl Acad Sci USA. 2001;98:12760–12766. doi: 10.1073/pnas.221462998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark SM, Yassa MA, Stark CEL. Individual differences in spatial pattern separation performance associated with healthy aging in humans. Learn Mem. 2010;17:284–288. doi: 10.1101/lm.1768110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein T, Mortiz C, Quigley M, Cordes D, Haughton V, Meyerand E. Functional connectivity in the thalamus and hippocampus studied with functional MR imaging. AJNR Am J Neuroradiol. 2000;21:1397–1401. [PMC free article] [PubMed] [Google Scholar]
- Squire LR, Stark CEL, Clark RE. The medial temporal lobe. Annu Rev Neurosci. 2004;27:279–306. doi: 10.1146/annurev.neuro.27.070203.144130. [DOI] [PubMed] [Google Scholar]
- Talairach J, Tournoux P. A Co-Planar Stereotaxic Atlas of the Human Brain. New York: Thieme Medical Publisher; 1988. [Google Scholar]
- Van Dijk KR, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. Intrinsic functional connectivity as a tool for human connectomics: Theory, properties, and optimization. J Neurophysiol. 2010;103:297–321. doi: 10.1152/jn.00783.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent JL, Patel GH, Fox MD, Snyder AZ, Baker JT, Van Essen DC, Zempel JM, Snyder LH, Corbetta M, Raichle ME. Intrinsic functional architecture in the anaesthetized monkey brain. Nature. 2007;447:83–86. doi: 10.1038/nature05758. [DOI] [PubMed] [Google Scholar]
- Yassa MA, Mattfeld AT, Stark SM, Stark CEL. Age-related memory deficits linked to circuit-specific disruptions in the hippocampus. Proc Natl Acad Sci USA. 2011;108:8873–8878. doi: 10.1073/pnas.1101567108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yassa MA, Stark CEL. A quantitative evaluation of cross-participant registration techniques for MRI studies of the medial temporal lobe. NeuroImage. 2009;44:319–327. doi: 10.1016/j.neuroimage.2008.09.016. [DOI] [PubMed] [Google Scholar]