Simulating and explaining passive air sampling rates for semi-volatile compounds on polyurethane foam passive samplers

Abstract

Passive air samplers (PAS) including polyurethane foam (PUF) are widely deployed as an inexpensive and practical way to sample semi-volatile pollutants. However, concentration estimates from PAS rely on constant empirical mass transfer rates, which add unquantified uncertainties to concentrations. Here we present a method for modeling hourly sampling rates for semi-volatile compounds from hourly meteorology using first-principle chemistry, physics, and fluid dynamics, calibrated from depuration experiments. This approach quantifies and explains observed effects of meteorology on variability in compound-specific sampling rates and analyte concentrations; simulates nonlinear PUF uptake; and recovers synthetic hourly concentrations at a reference temperature. Sampling rates are evaluated for polychlorinated biphenyl congeners at a network of Harner model samplers in Chicago, Illinois during 2008, finding simulated average sampling rates within analytical uncertainty of those determined from loss of depuration compounds, and confirming quasi-linear uptake. Results indicate hourly, daily and interannual variability in sampling rates, sensitivity to temporal resolution in meteorology, and predictable volatility-based relationships between congeners. We quantify importance of each simulated process to sampling rates and mass transfer and assess uncertainty contributed by advection, molecular diffusion, volatilization, and flow regime within the PAS, finding PAS chamber temperature contributes the greatest variability to total process uncertainty (7.3%).

Introduction

Passive air samplers (PAS) collect atmospheric trace compounds under ambient conditions onto polyurethane foam (PUF), semi-permeable membranes, and polymer resin sampling media.^1–8 This versatile, low-cost technique proves useful for establishing spatial gradients in air toxics and emerging contaminants of concern, and in sampling semi-volatile organic compounds (SVOCs) for which real-time observations remain challenging. Many SVOCs, including polychlorinated biphenyls (PCBs) and polycyclic aromatic hydrocarbons, are known or potential human carcinogens, toxic, bio-accumulative, and subject to long-range chemical transport.² Passive air sampling is also routinely used in atmospheric monitoring for mercury, ammonia, aerosols, and nitrogen dioxide.^{9, 10}

In passive air sampling, ambient air flows through the PAS chamber and the compound’s mass accumulates onto sampling media throughout the sampler’s deployment period. Without the controlled flow rates of active methods, concentrations must be calculated from estimated passive sampling rates. Traditionally, PAS has been described as the uptake of a chemical onto sampling media (e.g. polyurethane foam⁷) as a function of sampling rate (R_s) and the fugacity gradient between the ambient air and the PUF disk, with uptake onto the disk defined as ^{1, 4, 5, 7}:

$$\frac{d{M}_{\mathit{\text{PUF}}}}{dt}=k_{\nu }\cdot A_s\cdot (C_{\mathit{\text{Air}}}-\frac{C_{\mathit{\text{PUF}}}}{K_{\mathit{\text{PUF}}}})$$ (1)

where M_PUF represents the mass of a gaseous or semi-volatile compound on the PUF (ng), k_ν the empirical constant mass transfer coefficient (m s⁻¹), A_s the surface area of the PUF (m²), C_Air the analyte concentration in the air (ng m⁻³), C_PUF the compound’s concentration on the PUF (ng m⁻³), and K_PUF the PUF:air equilibrium partition coefficient (m³ g⁻¹). The product of k_ν × A_s is R_S, which may be determined experimentally from loss of depuration compounds or uptake of native compounds.⁴ For R_S estimation by loss of depuration compounds, the PUF disk is spiked with a known amount of chemical prior to exposure and then the mass transfer coefficient is calculated based on its first order elimination rate during the entire deployment.^{5, 11} Alternatively, the uptake of native compounds entails deploying a series of clean PUF disks in a setting with a known ambient concentration and deriving a linear uptake curve to calculate R_S.^{5, 12}

These two approaches in determining R_S lead to a range of issues regarding concentration observations gathered using PAS. As with the analyzed mass from a PAS, these techniques result in only one R_S value for the entire sampling period, with unquantified uncertainties and unknown variability. Beyond the large quantified and unquantified errors in the analytical approach to calculating R_S for individual samples, empirical R_S values are often used for different periods and different locations from those in which they were originally determined, leading to even greater uncertainties in resultant analyte air concentrations.

Empirical and theoretical studies suggest that much of the uncertainty stems from the effects of meteorology on R_S, primarily with a focus on isolating how individual meteorological parameters such as wind speed¹¹ and temperature¹³ affect observed variability. Klánová et al. found that R_S for gas-phase compounds, including PCBs, exhibits a linear correlation to wind speed and inverse correlation to temperature.¹⁴ The angle at which the ambient air enters the PAS chamber also affects flow within the chamber, with positive angles of 15° and 30° increasing R_S by 30% and 50%, respectively, and a −10° angle leading to a 40% reduction.¹⁵ While studies have attempted to address these issues through computational fluid dynamic modeling,^{15, 16} and theoretical models of the passive sampling uptake process have been developed,¹ no comprehensive process model to date has directly simulated and quantified the comprehensive effects of atmospheric dynamics on observed passive sampling flow rates.

The PCB concentration in air can be experimentally determined from Equation 2:

$$C_{\mathit{\text{Air}}}=\frac{M_{\mathit{\text{PCB}}}}{Rs*t}$$ (2)

where M_PCB is the total accumulated mass on the PUF (ng) and t is the total deployment time (d). This approach assumes that C_Air is constant over the entire sampling period. However, daily observations in urban areas consistently invalidate this assumption.^{17, 18} Hsu et al. showed that variability in ambient air concentration for ∑PCBs in 22 daily samples taken in a 50-day period near Chicago (0.22 to 1.80 ng m⁻³) using active sampling was larger than the average concentration (1.0 ± 0.5 ng m⁻³). ¹⁷ The high short-term variability in PCB analyte air concentration can be explained by the influences of meteorology on volatilization (temperature) and source location (wind); in that study, concentration was highly correlated with daily time series of temperature (r² = 0.46) and slightly correlated with wind speed (0.19) and wind direction (0.17). The assumption of negligible loss from the PUF (i.e., $\frac{C_{\mathit{\text{PUF}}}}{K_{\mathit{\text{PUF}}}}\approx 0$) throughout the deployment period, another necessary precondition for this reduced-form expression of the fundamental passive sampling relationships, may also be invalid for SVOCs depending on the length of the deployment.

In this study, a method to estimate hourly sampling rates, analyte air concentrations (C_Air), and PCB uptake on PAS-PUF samplers (C_PUF) from first principle chemistry, physics, mass transfer, and computational fluid dynamics is presented. Using data from seven deployments of samplers from our PCB sampling network in Chicago^{6, 19} flow rates are calibrated with empirical depuration approaches to refine the model, and process contributions to uncertainties are estimated.

Experimental Methods & Data

Modeling Approach

This model reconsiders the theoretical passive sampling relationship in Equation 1 to incorporate temporal variability in mass transfer, sampling rate, and PUF concentration based on discrete temporal information on ambient air concentrations and meteorology (Equation 3).

$$\frac{d{M}_{\mathit{\text{PUF}}}}{dt}=k_{\nu }(T,WS,WD,P,t)*A_s*(C_{\mathit{\text{Air}}}(T,t)-\frac{C_{\mathit{\text{PUF}}}(t)}{K_{\mathit{\text{PUF}}}})$$ (3)

where C_AIR is a function of both ambient temperature (T) and time (t), C_PUF varies in time due to resolved mass transfer, and k_v varies in time as a result of meteorological conditions known from prior empirical and theoretical studies to impact passive sampling rates, including wind speed (WS), wind direction (WD), temperature and pressure (P). The dependency of the mass transfer coefficient on these ambient parameters is derived from boundary layer mass transfer theory, where the Sherwood number representing the ratio of convective to diffusive mass transfer is dependent on the flow conditions represented by the Reynolds Number and the ratio of the diffusive momentum to the diffusion of mass.²⁰ From this theory, the sampling rate equation becomes

$$R_s=f_{\mathit{\text{PBL}}}*(\gamma *D^{\mathit{1}-\beta }*{\nu }^{\beta -\alpha }*V_A^{\alpha }*L^{\alpha -\mathit{1}})*A_s$$ (4)

where f_PBL is the fraction of ambient analyte air concentration inside the PUF boundary layer, and the first bracket represents the mass transfer coefficient, where γ is an advective mass transfer coefficient specific to the PAS housing and media (dimensionless), D is the molecular diffusivity for each compound (m s⁻¹), ν is the kinematic viscosity (m² s⁻¹), V_A is the air velocity (m s⁻¹), L is the diameter of the PUF disk (m), β represents the differences between momentum transport and mass transport (dimensionless), and α represents the flow regime (laminar or turbulent) as a function of air velocity. We considered α and β values consistent with flow over a flat plate. Expressions and values for each component in Equation 4 are presented in the SI.

Uptake of an SVOC on the PAS is a function of accumulation of mass on the PUF over time and the mass of the PUF, as indicated in Equation 5:

$$C_{\mathit{\text{PUF}}}={\int }_{t-\mathit{1}}^t\frac{dm/dt}{m_{\mathit{\text{PUF}}}}$$ (5)

where dm/dt is the accumulation of SVOC mass onto the PUF for that time period (ng), and m_PUF is mass of the PUF (g). To calculate the C_PUF to K_PUF ratio, K_PUF was computed using a logarithmic relationship between the octanol-air partition coefficient K_OA and K_PUF from Shoeib & Harner⁷ (Equation 6):

$$K_{\mathit{\text{PUF}}}={\mathit{10}}^{(\mathit{0.6366}*\text{log}(K_{OA})-\mathit{3.1774}}$$ (6)

Using this dynamic model, we can predict the meteorology-driven variation in the ambient concentrations of the SVOC during the deployment period. The hourly concentration of SVOCs in the atmosphere at ambient temperature T can be computed by first correcting the measured integrated air concentration to a standard temperature, then modeling the hourly concentrations as a function of hourly meteorology during deployment period. Using Equation 7:

$$C_{\mathit{\text{Air}}}=C_{298}*e^{\frac{\mathit{\Delta }{U}_{OA}}{R}(\frac{1}{T}-\frac{1}{T_{298}})}*\frac{T}{T_{\mathit{\text{PAS}}}}$$ (7)

where C₂₉₈ is the PCB concentration at 298K (ng m⁻³) calculated from the integrated C_PUF and analyzed mass, ΔU_OA is octanol-air enthalpy for PCBs (J/mol), R is the gas constant (J mol⁻¹-K⁻¹), T₂₉₈ is the temperature 298 K, and T_PAS is the PAS internal chamber temperature (K). Since C_Air varies predictably with temperature for SVOCs, the Van’t Hoff relationship explains variability between T and a reference temperature (here, 298 K). The ratio of T to T_PAS considers volatility of PCBs in the conditions within PAS chamber, as temperature within the chamber differs from ambient air temperature due to solar heating during the day and radiative cooling at night,¹³ and is consistent with the temperature of the local built environment.¹³ Thus, the ratio of T/T_PAS ensures that the computed C_Air reflects ambient air concentrations rather than the concentration in the PAS to which the PUF disk was directly exposed. Further details are presented in the Supporting Information (SI).

The fraction of ambient analyte air concentration present in the air flowing immediately over the PUF disk, f_PBL, determines the SVOC mass capable of transfer to the PUF. Computational fluid dynamics modeling found that simulated PCB concentration in the turbulent boundary layer around the PUF disk in a Harner model sampler is lower than that in free flowing air in the PAS chamber, with f_PBL during turbulent flow (internal air velocities ≥ 0.5 m s⁻¹) of approximately 0.5. At lower air velocities, laminar flow prevails, with f_PBL ≈ 1.¹⁶

PAS PUF Observations & Loss of Depuration Compound Experiments

Hourly gas phase R_S were calculated in MATLAB²¹ for 156 PCB congeners and coeluting groups of congeners²² in Chicago during 2008, including two isotope labeled depuration compounds with negligible ambient concentrations, 2,4,4’-trichlorobiphenyl (¹³C₁₂) (C13-PCB 28) and 2,3,3’,5,5’-pentachlorobiphenyl (¹³C₁₂) (C13-PCB 111), representing low and high molecular mass PCB compounds. A total of 83 PAS PUFs were deployed during the study period in Harner model samplers at 32 locations in Chicago, and sampling rates determined from loss of depuration compounds from seven PUF samples at seven sites.¹⁹ The PUF deployments with depuration compounds covered most of 2008, except for an eight week period from mid-September to mid-November, and 11 days in late December and early January. Deployments ranged from 24 to 76 d, with an average of 43 ± 8 d. All samples were extracted and analyzed following methods described by Hu et al. (2008).²³ Using methods described by Persoon et al. (2010),⁶ the depuration compound experiment consisted of spiking clean PUF disks with 40 ng of PCB congeners 28 (13C-PCB 28) and 111 (13C-PCB 111) from a mixture of EPA Method 1668A labeled clean-up standard solution (Cambridge Isotope Laboratories). The PUFs were spiked by placing them in amber jars and then adding the depuration compounds in 20 mL acetone. The PUFs were dried in the jars, capped with Teflon lids, sealed in Ziploc bags and stored in a −20°C freezer until deployment. Each PUF was deployed at one of the seven locations. After deployment, PUF disks were collected and analyzed to determine the remaining PCB mass of each congener. The remaining fraction of the spiked depuration compounds was 29% and 96%, for C13-PCB28 and C13-PCB11, respectively. We determined k_v from difference between the initial spiked tracer mass and final PUF analyzed mass, and then determined R_S from the product of k_v × A_s (Table 1).

Table 1.

Modeled and depuration PCB 28 R_S for each depuration compound sample. R_S and γ reported for sample-specific fit, multiple linear regression, and mean values. A median value for γ of 0.076 is suggested from all samples.

					Average Model RS (m3 d−1)
Site	Sampling Period	Sample Specific γ	MLR γ	Depuration RS (m3 d−1)	Using Median γ (0.076)	Using MLR γ
Dewey	1/17 – 2/26	0.06	0.07	5.00	6.43	6.06
Dawes	2/22 – 4/11	0.08	0.07	5.53	5.55	5.31
Corkery	4/18 – 5/16	0.09	0.06	5.94	5.13	4.28
Gresham	5/16 – 7/31	0.08	0.11	3.84	3.87	5.63
Chase	6/30 – 8/11	0.19	0.18	6.79	2.66	6.28
St. Elizabeth	8/11 – 9/19	0.10	0.09	5.67	4.55	5.52
Webster	11/13 – 12/19	0.06	0.06	5.06	6.51	4.81
	Mean	0.09	0.09	5.40	4.96	5.41

Meteorology

Temporal variability in mass transfer was calculated using hourly modeled and observed meteorology. The Weather Research and Forecasting Model (WRF) version 3.3^{24, 25} was used to simulate meteorology and land surface temperatures at 1.33 km horizontal resolution over Chicago and 12 km over the Upper Midwest and Northeast United States. WRF operates by integrating the atmospheric primitive equations with physics parameterizations, including submodels simulating land surface processes, boundary layer dynamics, convection, microphysics and radiation.²⁶ A detailed description of the WRF configurations is presented in the SI in the Meteorology Simulation section. Results from WRF for this application met or exceeded community standards for atmospheric chemical transport modeling, as presented in SI under Meteorological Evaluation. We also employed hourly observations from Automated Weather Observing System (AWOS) units at 16 local area airports, obtained from the Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory.²⁷ From both WRF and AWOS observations, we used temperature, three-dimensional wind vectors, surface pressure and relative humidity as inputs to the sampling rate model. We employed 2 m ambient air temperature from WRF and AWOS, and used WRF surface temperature (T_SKIN) as a proxy for T_PAS, the sampler’s internal temperature.

As meteorology simulated by numerical weather models includes errors in accuracy that may influence sampling rate, hourly de-biased meteorology was calculated by subtracting the hourly domain-average bias (the average difference between model and observation at the 16 airports) from the WRF simulated meteorology to yield bias-corrected meteorological fields. These bias-corrected fields thus combine the accuracy of hourly observations with the fine spatial features resolved by urban and regional scale modeled meteorology.

The impacts of PAS chamber air velocity on k_v were calculated from the empirical linear relationship determined from wind tunnel experiments relating ambient wind speed V_a to internal air velocity,¹¹ as the Harner design reduces internal wind speed, advection, and in turn R_S. We also employed a polynomial regression on empirical results reported by May et al. from wind tunnel studies, where R_S depends on the angle between the 3D wind vector and the PAS apparatus.¹⁵ We considered wind vectors for swinging tethered samplers as deployed, accounting for sampler mass in an hourly equilibrium angle to the wind. Results differed by less than 1% using this second approach (SI).

Results and Discussion

We first evaluate the model using depuration experiments and quantify hourly variability and process contributions and estimate uncertainty at a representative site. We identify variability between compounds, months, and years at the Chicago sampling network, and extend analysis to simulated spatial patterns across Chicago and the Great Lakes. We then evaluate linearity in hourly PUF-air mass transfer and contextualize R_S uncertainty.

Model Evaluation

We evaluated modeled R_S for the two C13-labeled depuration compounds, C13-PCB 28 and C13-PCB 111. First, values for the advective mass transfer coefficient γ were calibrated to yield an empirical constant relating the observed sampling rates specific to the Harner samplers’ design to first principles mass transfer processes. We fitted γ using Equation 4 at seven sampling sites in Chicago by Euler’s method from C-13 PCB 28 depuration compound R_S (Table 1) and the numerical model. The median γ C13-PCB 28 value from the seven deployments was 0.076. First principles only account for flow over a foam disk floating in space, with no enclosure, so this reduction is expected, especially since the Harner sampler is designed to modulate flow rate. We then estimated modeled R_S for each PUF. Normalized mean difference between modeled and depuration C13-PCB 28 R_S using the median γ value was −5% and normalized mean absolute difference was 22%. These differences are consistently less than or comparable to the estimated analytical uncertainty of 15–25% for congener-specific PCB depuration compounds for our laboratory.²² Thus, model results fall within the contemporary range of analytical uncertainty even when using a single representative median value for γ. Results were similar for C13-PCB 111 (SI), and indicated that γ scales between compounds by the ratio of log(K_OA), with normalized mean difference of −4% and normalized mean absolute difference of 36% using γ values (median = 0.087) scaled from C13-PCB 28. Sample-specific anomalies in fitted γ (Table 1) were investigated further and found to be correlated with both wind speed (R² = 0.76) and temperature (R² = 0.46), suggesting additional process contributions to mass transfer not yet resolved by the model. Multiple linear regression on wind speed and temperature (SI) provide γ estimates tailored to each deployment (MLR γ), which further improve estimates of modeled R_S, (Table 1).

Hourly Compound-Specific Sampling Rates

Using this modeling approach, hourly R_S can be determined anywhere and at any time for all SVOCs from meteorology, K_OA, and molecular weight alone, using empirical mass transfer coefficient γ from prior depuration experiments. The sampling rate R_S is not constant during a deployment period, and is highly dependent on local hourly weather. Modeled hourly R_S for PCB congener 28 vary by a factor of 5 (Figure 1) over a PAS deployment period due to meteorology. Modeled R_S resolves diurnal and synoptic weather cycles in sampling, seen as the small and large amplitude peaks, respectively. Sampling rate was also computed using averaged simulated meteorology during each PUF deployment to determine if average values could be simply scaled from reference conditions based on representative average deployment meteorology. As shown in Figure 1, average meteorology greatly underestimated R_S. Average V_A and T_Skin were approximately 40% and 21% of the hourly variability seen in V_A and T_Skin during the deployment period. Since sampling rate is an exponential function of both V_A and T, the use of average values produces consistently lower advective and diffusive sampling rates.

Figure 1.

R_S at the Dawes sampling site from 2/22/2008 to 4/11/2008 for PCB congener 28, including the hourly Rs predicted from our model (black); average loss of depuration R_S (red); modeled R_S using average meteorology (green); and R_S due to molecular diffusion (blue).

The PCB 28 R_S time series at the Dawes site from 2/22/2008 to 4/11/2008 indicated minimal impact of weather model biases on modeled R_S. We found a 1.8% average difference between debiased and raw model meteorological data. In contrast, temperature plays a vital role in variability in R_S, where using T_Skin rather than ambient T as a proxy for T_PAS leads to a 7.3% average reduction in total R_S. A complete sensitivity analysis is presented in SI.

Diffusive and Advective Contributions to Sampling Rate

Sampling rate was disaggregated into advective and diffusive components to quantify their roles in the net sampling rate. Figure 1 shows hourly total and diffusive sampling, with advective contribution as the difference. The relative contributions vary with wind speed, with higher PAS chamber air velocities leading to a larger contribution by advective mass transfer. The average R_S from diffusion for PCB 28 at the Dawes sampling site during February-April 2008 was 2.73 ± 1.07 m³ d⁻¹, consistent with average reported indoor R_S values of 2.45 for PCB 28 determined by loss of depuration compounds.⁵ Thus, this model might also be used to estimate indoor R_S, due primarily to diffusion, using indoor temperatures and air circulation rates.

Sampling Rate Variability among SVOCs

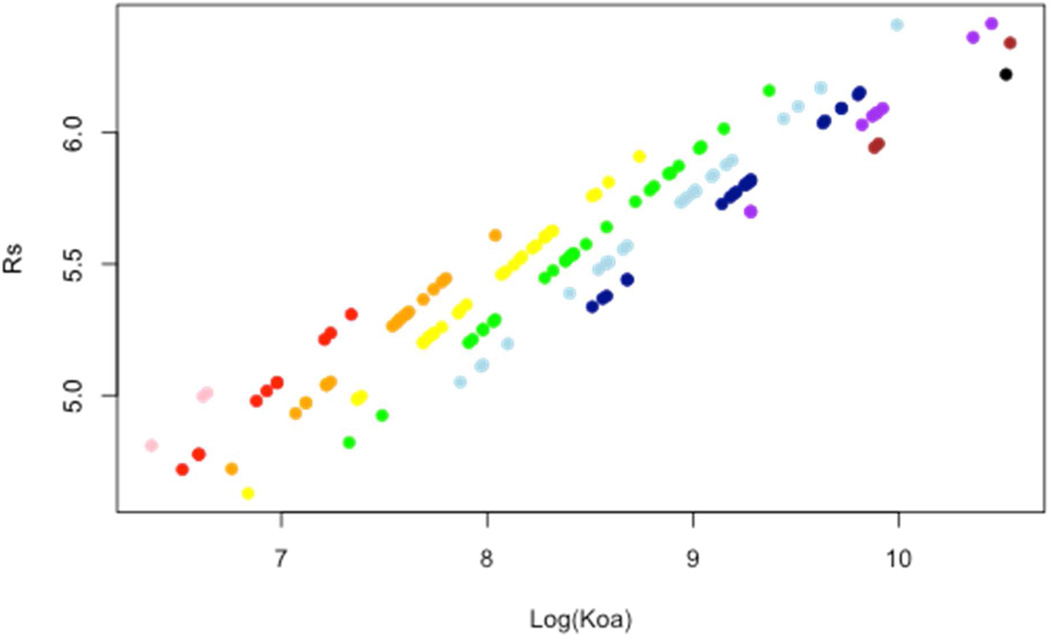
We found simulated R_S to be congener dependent, although the effect is smaller than variability in meteorology. Rs increases with K_OA. There is a consistent 27% range in R_S between low and high molecular weight congeners in each deployment (Figure 2) and a 20% range among homolog groups (Table 2). Sampling rate decreases with increasing molecular weight along K_OA isopleths, indicating that differences in R_S between SVOCs under ambient conditions are due more to variability in K_OA (γ) than to differences in molecular diffusion (D). Therefore, accurate estimation of SVOC concentrations from PAS PUF samples requires compound-specific sampling rates rather than the use or averaging of an arbitrary set of depuration compounds, and highlights this practice as a source of uncertainty in contemporary concentration estimates from passive air sampling. By removing the analytical uncertainty inherent to depuration experiments, these findings explain the variability in R_S values derived for a range of compounds in prior depuration studies,^28–31 and show that the theoretical variability in R_S is of similar magnitude to contemporary analytical uncertainties of ~20–25% for PCBs in ambient air ^{32, 33}.

Figure 2.

R_S dependency on Log(K_OA) and homolog group (colors, from pink = 1 to black = 10) for each PCB congener during the PUF deployment at the Dawes sampling site from 2/22/2008 to 4/11/2008.

Table 2.

Simulated monthly average gas phase R_S (m³ d⁻¹) by homolog group (#Cl) in Chicago for all PUFs deployed in 2008 and 2011, calculated from observed meteorology at Chicago O’Hare Airport. We did not sample in December and hence no R_s is estimated for the 12^th month.

#Cl	1		2		3		4		5		6		7		8		9		10
Month	‘08	‘11	‘08	‘11	‘08	‘11	‘08	‘11	‘08	‘11	‘08	‘11	‘08	‘11	‘08	‘11	‘08	‘11	‘08	‘11
1	6.18		6.27		6.50		6.76		6.95		7.11		7.23		7.57		7.60		7.78
2	5.57	5.15	5.66	5.23	5.86	5.42	6.10	5.64	6.28	5.80	6.41	5.93	6.52	6.03	6.84	6.32	6.86	6.34	7.02	6.49
3	5.52	4.11	5.61	4.17	5.81	4.32	6.04	4.49	6.22	4.62	6.36	4.72	6.47	4.81	6.78	5.04	6.80	5.06	6.96	5.17
4	4.87	4.08	4.94	4.14	5.12	4.29	5.33	4.46	5.48	4.59	5.60	4.69	5.70	4.77	5.97	5.00	6.00	5.02	6.13	5.14
5	4.87	4.82	4.95	4.89	5.13	5.07	5.33	5.27	5.49	5.42	5.61	5.54	5.71	5.64	5.98	5.91	6.00	5.93	6.14	6.07
6	5.17	5.17	5.25	5.24	5.44	5.44	5.66	5.65	5.83	5.82	5.95	5.95	6.06	6.05	6.35	6.34	6.37	6.36	6.52	6.51
7	5.28	5.20	5.36	5.28	5.55	5.47	5.77	5.69	5.95	5.86	6.07	5.98	6.18	6.09	6.47	6.38	6.50	6.40	6.65	6.55
8	5.29	5.29	5.37	5.37	5.56	5.57	5.79	5.79	5.96	5.96	6.09	6.09	6.19	6.19	6.49	6.49	6.51	6.51	6.66	6.66
9		5.34		5.42		5.62		5.84		6.01		6.14		6.25		6.55		6.57		6.73
10		4.85		4.92		5.10		5.30		5.46		5.58		5.68		5.95		5.97		6.11
11	5.81	4.73	5.90	4.80	6.12	4.98	6.36	5.18	6.55	5.33	6.69	5.44	6.81	5.54	7.13	5.80	7.16	5.83	7.33	5.96

Not only is there congener-specific variability in R_S between using regional versus local scale meteorology, there is also seasonal and annual variability, with maxima in winter and summer (~40% greater than boreal spring). There is less than 5% difference in average monthly R_S in the warmest months (July and August) compared to the coldest (January and February), with advection and diffusion each contributing 50 ± 6% to the total. Differences in monthly average R_S between 2008 and 2011 using observed meteorology at Chicago O’Hare Airport varied from <1.5% in summer (June-August) to 25.7% in February, with greater difference in the windier winter months (Table 2). Hence it is important to use meteorology for the specific deployment period.

Seasonal and Spatial Variability in Sampling Rate

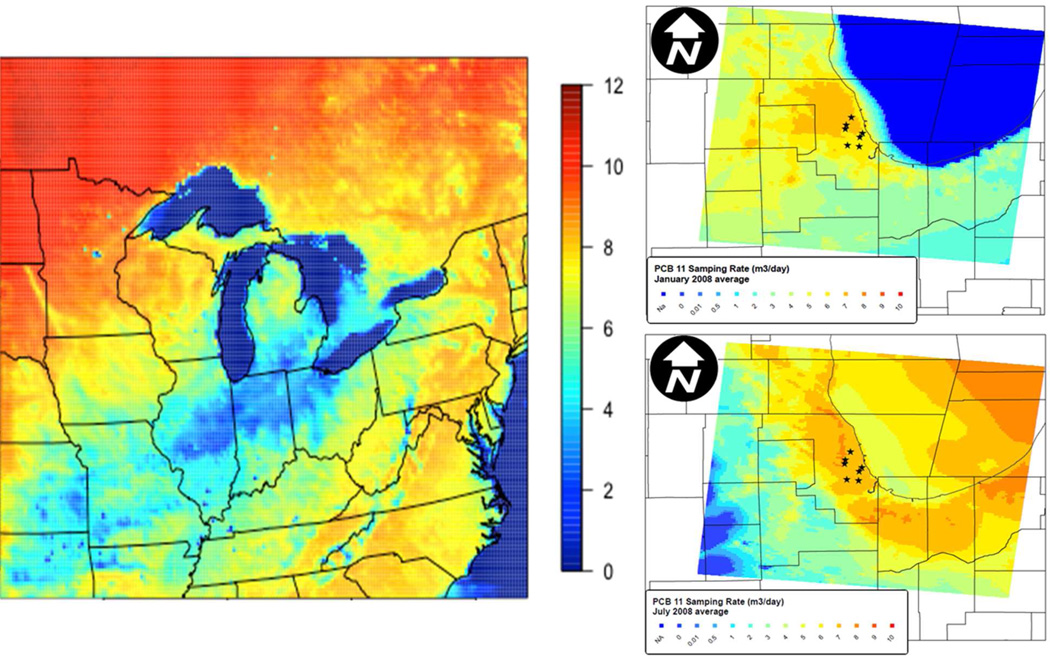
The importance of meteorology is even more evident when considering R_s across regional scales. Seasonal and spatial variability in R_S was assessed using both the regional and urban scale simulated meteorology for PCB 11 (3,3’-dichlorobiphenyl), a compound that is emitted from paint pigment and has observed endemic high concentrations throughout Chicago.^{23, 34} Simulated R_S from the coarse domain (12 km × 12 km) showed order of magnitude regional congener-specific gradients (Figure 3) and revealed local land cover influences, with higher sampling rates near large cities and lower sampling rates along the Appalachian Mountains.

Figure 3.

Spatial variability in sampling rate R_s for PCB 11(m³ d⁻¹). Left plot shows January 2008 from 12 km WRF meteorology; right plots show local variability over the Chicago area for January (top) and July 2008 (bottom), from 1.33 km WRF meteorology.

Sampling rate varies across the Great Lakes region in the month of January, with average R ranging from 1 – 2 m³ d⁻¹ in central Illinois and Indiana to as high as 11 – 12 m³ d⁻¹ in western Ontario. Sampling rates are not yet calculated accurately over water (Figure 3), as the current model implementation assumes that temperature inside the metal PAS is similar to surface temperature. Furthermore, the study included no depuration compound measurements sampling the high wind speeds found over the Great Lakes, so γ values may not be representative.

Sharper gradients in R_S are found using the 1.33 km resolution simulations, which better resolve impacts of the urban environment on local wind gradients and land surface heterogeneity. Estimated PCB 11 R_S for the city of Chicago from regional-scale (12 km) meteorology for January ranges from 3 – 6 m³ d⁻¹, while R_S from local meteorology ranged from 2 – 8 m³ d⁻¹ (Figure 3). Urban land cover impacts R_S through surface roughness and temperature variability. Figure 3 also shows a gradient across Chicago in both the winter and summer due to increased wind speeds at sites closer to Lake Michigan, as well as the heat island impacts of urban land cover on temperature.

To further assess the importance of spatial variability, modeled R_S from all 83 PUFs samples was calculated for each PCB congener using simulated hourly site-specific meteorology and observed hourly meteorology from Chicago O’Hare Airport (ORD). The normalized mean difference in R_s for all 83 samples at 32 sites between site specific and observations at ORD was 13.8%, and ranged from 0.3% to 43.9%. Since the temperature inside the sampler (T_Skin) was not available from observations, ambient T was used as a proxy temperature inside the PUF chamber. As previously noted, the difference between T and T_skin leads to the greatest variability in net process uncertainty and explains roughly half the average difference. Thus, predictions of urban R_S from regional meteorology or from a regional observation with unrepresentative land cover may both underestimate spatial variability. This analysis suggests that site-specific hourly meteorological observations are ideal for determining R_S; however, nearby airport observations can also be used, especially if land cover does not vary greatly.

Quantifying Mass Uptake Rates

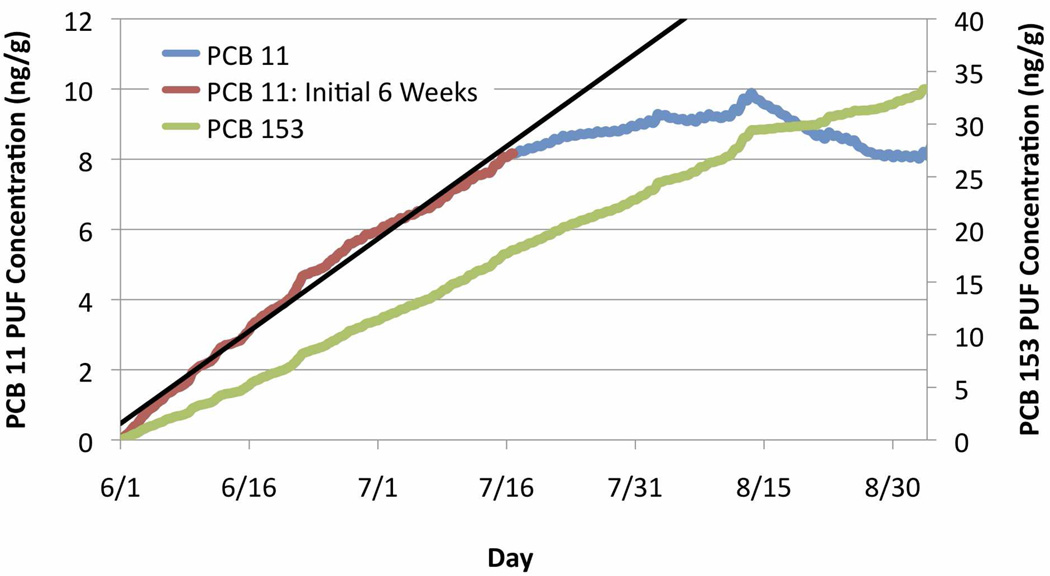
Hourly PCB PUF concentration on the PUF disk was evaluated to assess the assumptions that the PUF:air transfer $(\frac{C_{\mathit{\text{PUF}}}}{K_{\mathit{\text{PUF}}}})$ is negligible and the mass uptake is linear.^{1, 5, 7} Figure 4 depicts mass uptake for PCB congener 11 onto the PUF disk as a mass fraction of the PUF. Concentration increase on the PUF for both low and high molecular weight congeners is approximately linear (R² > 0.97) over 60+ day deployment periods in winter and spring. In the cooler months, hourly uptake follows a staircase pattern, with spikes corresponding to large episodic increases in ambient wind speed and passive sampling rate during synoptic frontal passages, and higher linear uptake rates during sustained periods of high winds. While PUF uptake follows this quasi-linear trend for 12–13 weeks throughout the winter, this is not the case during the warmer months. More volatile and low molecular weight (LMW) compounds begin to saturate after 6 weeks of deployment in the summer, when linear uptake gradually slows, followed by loss in concentration from the PUF into the atmosphere. Sampling rates respond to saturation, and are also sensitive to the dynamic impacts of temperature on saturation levels. After the PUF becomes saturated at high temperatures, LMW compounds volatize off the PUF disk until a new PUF concentration equilibrium point is reached. That equilibrium concentration may reach higher values during cold spells (e.g. near 8/15 in Figure 4), and then lower again as the temperature rises. This trend continues if the PUFs are left out longer than 12 weeks. Saturation can lead to a >20% underprediction of quantified mass for LMW compounds. However, this is only the case for volatile LMW compounds, as linear uptake occurs for less volatile congeners throughout long summer deployments (Figure 4).

Figure 4.

Simulated PUF concentration (ng/g) at the Dawes sampling site from June 1 to August 31 2008: PCB 11 (blue, left axis) and PCB 153 (green, right axis). For low molecular weight congeners, concentration on the PUF during the first 6 weeks (red) increases linearly (black trendline, R² = 0.9).

Modeled mass uptake onto the PUF shows that it is likely that previous methods used for determining C_Air have underpredicted concentrations for LMW compounds during long deployments in warm conditions if one assumes constant linear uptake throughout as PAS PUF deployment. In turn, the quantified analyzed mass may not be representative of the true mass uptake during PAS PUF deployment period. Saturation can be estimated from K_PUF and can be corrected for using temperature, deployment length and k_V from depuration compounds, ^{35, 36} but only if a representative range of such compounds is included on each PUF. In the Great Lakes and other areas with high variability in temperature, cloud cover and wind speed during a PUF deployment, even correcting using daily average temperature may not resolve the effects of PAS internal temperatures within a metal housing under full sunlight. However, nonlinear uptake is not a requirement when using the numerical model described here, as loss can be quantified and C_Air calculated from the linear uptake period.

Remaining Uncertainties in Passive Sampling

This study identifies and quantifies uncertainties in the knowledge of passive air sampling processes, and provides a modular platform for evaluating their impacts on sampling rate in the field. We identify temperature in the PAS chamber as the single most important unresolved condition for predicting seasonality in R_S. The simulated net process uncertainty of <10% from all factors is considerably smaller than the compounding errors contributed by applying depuration R_S values to other SVOC compounds (~30% between PCB congeners) and to PUFs deployed at other places and times (unquantified). After minimizing R_s errors and accounting for saturation, net observational uncertainties in passive sampling reduce to those contributed by analytical methods, which would make them identical to active sampling methods with known R_S. Since PAS integrate concentrations over longer periods of time, they avoid potential representativeness errors from averaging sparse daily observations from high volume active sampling into monthly or seasonal composites. Thus, with greater confidence and demonstrated accuracy in R_S, PAS may ultimately provide an accurate means for long-term environmental monitoring and trends assessment to complement conventional protocols of episodic or infrequent daily active sampling.

Results also highlight the need for computational fluid dynamics experiments that account for the combined effects of wind speed and wind angle on PUF boundary layer dynamics, and quantify their impacts on the observed wind speed differential between the upper and lower sides of the foam disk³⁷. Model processes can be made more complete by accounting for two-stage uptake between surface sorption and observed non-uniform diffusion within the sampling media due to kinetic resistance ³⁵ and sampler configuration ³⁶. This modeling approach can also be extended to sampling for aerosol-phase SVOCs on the foam surface and within the body of the foam disk.