Restricted diffusion of calretinin in cerebellar granule cell dendrites implies Ca²⁺-dependent interactions via its EF-hand 5 domain

Abstract

Ca²⁺-binding proteins (CaBPs) are important regulators of neuronal Ca²⁺ signalling, acting either as buffers that shape Ca²⁺ transients and Ca²⁺ diffusion and/or as Ca²⁺ sensors. The diffusional mobility represents a crucial functional parameter of CaBPs, describing their range-of-action and possible interactions with binding partners. Calretinin (CR) is a CaBP widely expressed in the nervous system with strong expression in cerebellar granule cells. It is involved in regulating excitability and synaptic transmission of granule cells, and its absence leads to impaired motor control. We quantified the diffusional mobility of dye-labelled CR in mouse granule cells using two-photon fluorescence recovery after photobleaching. We found that movement of macromolecules in granule cell dendrites was not well described by free Brownian diffusion and that CR diffused unexpectedly slow compared to fluorescein dextrans of comparable size. During bursts of action potentials, which were associated with dendritic Ca²⁺ transients, the mobility of CR was further reduced. Diffusion was significantly accelerated by a peptide embracing EF-hand 5 of CR. Our results suggest long-lasting, Ca²⁺-dependent interactions of CR with large and/or immobile binding partners. These interactions render CR a poorly mobile Ca²⁺ buffer and point towards a Ca²⁺ sensor function of CR.

Key points

• The dynamics of the second messenger Ca²⁺ are tightly controlled by Ca²⁺-binding proteins (CaBPs).

• The diffusional mobility of a given CaBP, such as calretinin (CR), defines how it affects the range-of-action of Ca²⁺ but, if unexpectedly low, may also indicate that the CaBP acts as a Ca²⁺ sensor, undergoing specific protein interactions.

• Here we quantified the diffusional mobility of CR in dendrites of cerebellar granule cells using microscopic methods.

• We find that CR diffuses unexpectedly slow, that its mobility is further reduced when Ca²⁺ levels are elevated and that a distinct region of CR interacts with specific targets in a Ca²⁺-dependent manner.

• Our findings indicate a new ‘sensor’ role for CR, which may allow for Ca²⁺-dependent feedback control of neuronal excitability.

Introduction

The precise functional roles of most members of the large and diverse group of Ca²⁺-binding proteins (CaBPs) are still poorly understood. While the distinct Ca²⁺-binding kinetics of the different CaBPs are evidently of central importance for their function, other properties also need to be considered to give meaning to the cell type-specific expression of CaBPs, of which some differ little in their Ca²⁺-binding behaviour. Diffusional mobility, interaction with binding partners and possible sensor functions are such properties that define the range of action (Allbritton et al. 1992) and mode of action (Schwaller, 2009) of CaBPs.

Calretinin (CR) is an EF-hand CaBP closely related to calbindin-D28k and calmodulin with well-characterized Ca²⁺-binding kinetics (Faas et al. 2007). It is widely expressed in the nervous system, including the Calyx of Held (Felmy & Schneggenburger, 2004) and cerebellar granule cells (Rogers, 1989; Schwaller et al. 2002). Its absence increases release probability at granule cell terminals (Schmidt et al. 2013) and alters excitability of granule cells (Gall et al. 2003), which at the behavioural level leads to impaired motor co-ordination (Schiffmann et al. 1999). Despite its functional importance and abundant expression, little is known about the mobility and possible interactions of CR within neurons. Some reports point towards immobilization at membranes (Winsky & Kúznicki, 1995; Hack et al. 2000) while others suggest that CR acts as a Ca²⁺ sensor (Kúznicki et al. 1995a, b) that binds to Ca_v2.1 channels (Christel et al. 2012) and other targets (Marilley & Schwaller, 2000).

Mobility and binding of proteins of interest can be quantified with fluorescence recovery after photobleaching (FRAP) (Axelrod et al. 1976), allowing for measurements in spines (Svoboda et al. 1996; Star et al. 2002; Schmidt et al. 2003a, 2005, 2007b), small dendrites (this study), axons (Schmidt et al. 2007a), somata (Brown et al. 1999) and membranes (Feder et al. 1996), i.e. in situations where equations for 1D, 2D and 3D diffusion apply. However, more complex situations such as bounded systems (Sullivan & Brown, 2011) or anomalous subdiffusion (Brown et al. 1999) can also be quantified with adapted diffusion equations. Interactions with cellular targets become evident by prolonged recovery times, especially if the targets are large or immobile and if the interaction has slow off rates (Schmidt et al. 2005). Finally, binding sites can be identified by quantifying the effects of synthetic peptides that resemble putative binding domains (Schmidt et al. 2005).

Here we employed FRAP to study the mobility of CR in dendrites of cerebellar granule cells. We found that molecular movement is better described by anomalous subdiffusion than normal diffusion and that CR showed a strongly reduced mobility when compared to inert tracers. Increasing the intracellular Ca²⁺ concentration ([Ca²⁺]_i) significantly reduced the mobility further, while a peptide consisting of 35 amino acids, containing the sequence of EF-hand 5 of CR, significantly increased the mobility of CR. Our data indicate that CR acts as poorly mobile buffer and possibly as a Ca²⁺ sensor in granule cells.

Methods

Ethical approval

All experiments were carried out in accordance with institutional guidelines for animal experiments, and were approved by the state directorate of Saxony, Germany.

Slice preparation and solutions

Acute cerebellar brain slices were prepared from 21–24-day-old mice of either sex that were killed by decapitation under isoflurane (Curamed, Karlsruhe, Germany) anaesthesia. The vermis was isolated and mounted in a chamber filled with cooled (0–2°C) artificial cerebrospinal fluid. Parasagittal slices (200 μm thick) were cut using a vibratome (HM 650 V; Microm, Walldorf, Germany) and kept in artificial cerebrospinal fluid at 35°C for 40 min before they were transferred to the recording chamber. Experiments were performed at room temperature. Artificial cerebrospinal fluid contained (in mm): 125 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 26 NaHCO₃, 1 MgCl₂, 2 CaCl₂ and 20 glucose, gassed with 95% O₂ and 5% CO₂ (pH 7.3–7.4 at 20–22°C). Unless stated otherwise, all chemicals were from Sigma-Aldrich, Seelze, Germany. For FRAP experiments, the pipette solution was composed of (in mm): 150 potassium gluconate, 10 NaCl, 3 magnesium ATP, 0.3 sodium GTP, 10 Hepes, 0.08 dye-labelled CR (CR*) or 0.5 fluorescein-labelled dextran (FD; 10 or 40 kDa) and 50 μm EGTA dissolved in bidistilled water (Sigma-Aldrich, Seelze, Germany).

We set the concentration of CR to 80 μm because the buffer capacity of granule cells has been estimated to be ∼60 (Brenowitz & Regehr, 2007) and CR is their major endogenous buffer (Schiffmann et al. 1999). Depending on assumptions about concentrations of unknown buffers and the Ca²⁺ affinity of CR (Faas et al. 2007), the CR concentration will be 40–80 μm (Schmidt et al. 2013), a concentration range we expect to be reached after 20 min equilibration time with a pipette solution containing 80 μm CR.

For Ca²⁺ imaging, the pipette solution contained 50 μm of the Ca²⁺-indicator dye Oregon Green BAPTA-1 (OGB-1; Molecular Probes, Eugene, OR, USA) and 50 μm of the Ca²⁺-insensitive dye Atto 637 (Atto-Tec, Siegen, Germany) instead of CR* or FD/EGTA. The pH was adjusted to 7.3 with KOH.

Labelled calretinin and gel electrophoresis

Purified human recombinant CR (266 of 271 amino acids (98%) identical to mouse CR) expressed in Escherichia coli was labelled with Alexa-488 (Molecular Probes) as described previously (Schmidt et al. 2003a). Labelling conditions (pH 9.0) were selected to preferentially label the α-amino group of CR, while ɛ-amino groups were not labelled significantly. The labelled protein was purified on a size exclusion column (20 × 0.8 cm, gel volume 10 ml) containing Bio-Gel P-6 (medium, fractionation range 1–6 kDa; Bio-Rad, Hercules, CA, USA) to remove unbound dye. 0.3–1 ml labelling reaction mixture was applied to the column and eluted with buffer [50 mm (NH₄)HCO₃, 0.1 mm CaCl₂, pH 8.3]. The molecular Alexa/CR ratio was 2.6–4.5. The purity of the protein was tested by gel electrophoresis of dye-labelled and native CR (250 μg each), using a 15% SDS-polyacrylamide gel.

To test for unbound dye in FD solutions, FDs were dissolved in purified water (500 μm) and separated on a 2.5% agarose gel, prepared and run in standard Tris-acetate EDTA buffer solution for 1 h at 50 V. In addition, mixtures of FDs and fluorescein were run on the same gel.

Cell loading and electrophysiology

Patch pipettes were pulled from borosilicate glass (Hilgenberg, Malsfeld, Germany) with a PC-10 puller (Narishige, Tokyo, Japan) to resistances of 10–11 MΩ. Whole-cell patch clamp recordings were obtained with an Axopatch 200A amplifier (Axon Instruments Inc., Union City, CA, USA), a LIH 1600 AD/DA converter and Patch Master 2.2 software (HEKA, Lambrecht, Germany). Seal formation was slightly prolonged by CR* or FDs. The resting membrane potential was held constant by injecting up to –50 pA holding current in the current clamp mode. The cells were equilibrated with the dye-containing pipette solution for at least 20 min before FRAP or Ca²⁺ imaging experiments.

Fluorescence recovery after photobleaching recordings

Two-photon FRAP experiments were performed as described previously (Schmidt et al. 2003a) on granule cell dendrites between 20 and 50 min after the whole cell configuration had been established. Briefly, a custom modified Fluoview 300 laser-scanning microscope (LSM; Olympus, Hamburg, Germany) equipped with a mode-locked Ti:sapphire laser (Tsunami; Spectra Physics, Darmstadt, Germany) set to a centre wavelength of 765 nm was used. The laser light was intensity modulated with a Pockels cell (model 350-80 LA-BR; Conoptics, Danbury, CT, USA; controlled via the AD/DA converter and Patch Master software) and focused on the specimen by a 60×/0.9 NA water immersion objective (Olympus). The fluorescence and laser intensity were recorded simultaneously using the internal photomultiplier tubes (PMTs) of the LSM, and sampled in the point mode (sampling frequency 500 kHz, 1 ms binning).

The baseline fluorescence and the fluorescence recovery were measured at laser intensities of 3–8 mW (measured at the exit of the objective). For bleaching, a 1 ms long, high-intensity laser pulse (20–40 mW) was applied. The specimen and system background were recorded by focusing the laser beam on unstained tissue next to the granule cell dendrite and by completely blocking the laser beam, respectively, using the same intensity protocol as during the FRAP recordings.

Aqueous FRAP recordings of 3, 10, 40 and 70 kDa FD or CR* (50 μm each), were performed in a droplet of intracellular solution, using photon counting instrumentation. The LSM was custom-modified so that two external, photon counting capable PMTs could be attached to the system. The first, red-sensitive PMT (PMC 100-1; Becker & Hickl, Berlin, Germany) was placed close to the scanning mirrors of the LSM and, by detecting scattered laser light, was used to record the excitation intensity. The second, red-insensitive PMT (PMC 100-0; Becker & Hickl) collected the fluorescence signal after it was diverted out of the LSM by a mirror placed into the emission pathway. The PMT signals were recorded using a time-correlated single photon counting board (TimeHarp; PicoQuant, Berlin, Germany) and SymPhoTime 4.2 software (PicoQuant). For each aqueous FRAP experiment, 2500 individual measurements, repeated at 20 Hz, were averaged. The duration of the bleach pulse was reduced to 10 μs, to prevent significant diffusion during bleaching (Brown et al. 1999). Baseline fluorescence was recorded for 1 ms and the recovery for 20 ms. In recording the fluorescence and system background, the intracellular solution was replaced by water or the laser beam was blocked, respectively.

Peptides

In indicated experiments 80 μm of a synthetic peptide (‘EF5-peptide’) or a scrambled control peptide were co-dialysed with 40 μm CR* via the somatic patch pipette.

• EF5-peptide EFNAIFTFYDKDGSGYIDENELDALLKDLYEKNKK

• Scrambled peptide EDNFKLDNLKDYAKELFIAGYLYGEEKFIKTSDDN

The EF5-peptide, assumed to represent the putative binding domain of CR, contained the entire EF-hand domain 5 (the Ca²⁺-chelating loop is marked in bold) and part of the linker EF5 to EF6 (underlined). This 35 amino acid stretch is highly conserved, i.e. 100% identical between rat and mouse. Ninety-four per cent (33 of 35 residues) are identical in the human CR sequence.

Analysis of fluorescence recovery after photobleaching data

FRAP data were analysed with custom written routines in Igor Pro (Wavemetrics, Lake Oswego, OR, USA). The raw fluorescence data were corrected for the specimen background, the laser intensity data for the system background. To correct for non-linear switching artefacts of the Pockels cell, the fluorescence was subsequently divided by the square of the laser intensity (Brown et al. 1999) and, thereafter, normalized to the baseline fluorescence (F/F₀). Data were only accepted for analysis if the initial bleaching during the baseline period was less than 15%.

The first second of the fluorescence recovery in dendrites (F(t)) was fitted with a one-dimensional diffusion equation (Schmidt et al. 2007a) of the form:

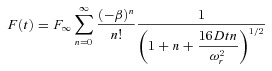(1)

where D is the diffusion coefficient, F_∞ is the postbleach fluorescence after recovery, β is the bleach depth parameter and ω_r is the radial e⁻² radius of the two-photon excitation volume. For our system, ω_r has dimensions of ∼0.53 μm in tissue and ∼0.57 μm in water (Schmidt et al. 2007a). A fit for anomalous subdiffusion was implemented by replacing terms of Dt by D_(t)·t, then by Γ·t^α and finally by (γt)^α (Feder et al. 1996; Brown et al. 1999), where γ is a mobility coefficient and α≤ 1 is the anomalous subdiffusion exponent. This yielded the following equation:

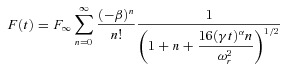(2)

The first 20 ms of the aqueous recovery were described with the free 3D diffusion equation given in Brown et al. (1999):

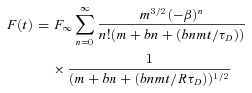(3)

with the characteristic radial diffusion time t_D=ω_r²/8D, and the ratio of the beam dimensions R =ω_z²/ω_r², where ω_z∼1.8 μm (Schmidt et al. 2007a) is the axial e⁻² radius of the two-photon excitation volume. The parameters m and b represent the number of photons absorbed per molecule in a fluorescence and bleaching event, respectively. Assuming two-photon excitation, we used m=b= 2 and ignored possible higher-order processes. During fitting, the series were truncated after the sixth partial sum. The reliability of all fits was judged by inspection of the residuals (i.e. data – fit).

Ca²⁺ imaging

Ca²⁺ signals were recorded at 67 Hz, using 50 μm of the fluorescent Ca²⁺ indicator dye OGB-1. As OGB-1 is dim at resting Ca²⁺ levels, 50 μm of the Ca²⁺ insensitive red fluorescent dye Atto 637 was used in addition. Both dyes were excited at ∼810 nm. The fluorescence signals were split by a 570 nm dichroic mirror. The red fluorescence was filtered with a 645–685 nm bandpass, the green signal with a 510–550 nm bandpass filter (AHF, Tübingen, Germany). In both channels, a 700 nm short-pass filter was used for blocking residual excitation light.

Analysis of Ca²⁺ signals was done using Igor Pro. Changes in intracellular free Ca²⁺ were expressed as background subtracted relative increases in OGB-1 fluorescence (ΔF/F₀). ΔF/F₀ traces were subsequently smoothed using a five-point sliding average algorithm.

Numerical simulations

Numerical simulations were performed according to previously published principles and with previous parameters (see Schmidt et al. 2003b, 2007b, 2013 and references therein). The kinetics of dendritic Ca²⁺ dynamics were described by numerically solving coupled sets of differential equations in a single compartment model using NDSolve of Mathematica 9 (Wolfram Research, Oxfordshire, UK). The model covered Ca²⁺ influx, a surface-based clearance mechanism (K_M 3 μm), binding and diffusion of Ca²⁺, ATP (370 μm, k_on 500 μm⁻¹ s⁻¹, k_off 100,000 s⁻¹), CR (80 μm, k_{on, tense} 1.8 μm⁻¹ s⁻¹, k_{on, relaxed} 310 μm⁻¹ s⁻¹, k_on,V 7.3 μm⁻¹ s⁻¹, k_{off, tense} 53 s⁻¹, k_{off, relaxed} 20 s⁻¹, k_{off, V} 252 s⁻¹) and, during model adjustment, OGB-1 (40 μm, i.e. 80% of the pipette concentration, k_on 430 μm⁻¹ s⁻¹, k_off 140 s⁻¹). Ca²⁺ binding was simulated by second order kinetics, except for binding sites I–IV of CR, for which cooperativity was implemented. The extrusion mechanism was balanced by a Ca²⁺ leak to generate a resting [Ca²⁺]_i of 45 nm; [Mg²⁺]_i was set to 590 μm. The model was adjusted to the measured fluorescence transients using an influx train (Gaussian width 600 μs, 96 Hz average frequency with 6% adaptation factor for the interspike interval). The amplitude of the Ca²⁺ influx and pump velocity were the only variables. During adjustment, a 35% whole cell wash-out reduction for endogenous CR was used. For simulating FRAP recordings, OGB-1 and wash-out correction were removed from the simulation and the fractional Ca²⁺ occupancy of CR was calculated.

Statistics

Unless denoted otherwise average data are given as median and interquartile range (IQR). For comparing groups of non-normally distributed data the Mann–Whitney–Wilcoxon rank sum test (comparison of two groups) or the Kruskal–Wallis ANOVA on ranks (comparison of more than two groups) was used.

Results

The aim of the present study was to analyse the mobility of the endogenous CaBP, CR, in its native neuronal environment using two-photon FRAP (Brown et al. 1999; Schmidt et al. 2003a). For this purpose we chose cerebellar granule cells, which constitute the major fraction of brain neurons (Braitenberg & Atwood, 1958) and are known to strongly express CR (Rogers, 1989; Arai et al. 1991; Resibois & Rogers, 1992). To our knowledge this is the first study of FRAP experiments in granule cells. Thus, in a first set of experiments we established the experimental and theoretical framework of FRAP in dendrites of granule cells using FD. Subsequently, the mobility of CR* was quantified under resting conditions, during neuronal activity and during interference with possible binding partners.

Anomalous subdiffusion of fluorescein dextrans in granule cell dendrites

Granule cells were dialysed with a pipette solution containing either 10 kDa or 40 kDa FDs in the whole cell patch clamp configuration. Within minutes, the morphology of the cells (soma, initial axon segment and dendrites) could be resolved under two-photon excitation (Fig. 1A). Granule cells had three to five dendrites of 6–24 μm length, which terminated in the typical glomerular structure. The single ascending axons originating from the somata or a dendrite were rather dim due to their small diameter. To measure the mobility of FDs, the low-power laser beam was directed to single points of interest on the dendrites. The soma, together with the patch pipette, represents a large reservoir of unbleached molecules that may accelerate fluorescence recovery. To minimize this effect, FRAP spots were at distances of at least 4 μm from their somatic point of origin (9 ± 4 μm, means ± SD, n= 65 cells). For photobleaching a brief (1 ms), high-intensity laser pulse was applied to irreversibly bleach the fluorophores within the focal volume. The fluorescence was subsequently monitored again at low laser intensity and the recovery of the fluorescence, which reflects diffusion of unbleached FD molecules from neighbouring regions into the focal volume, was recorded (Fig. 1B).

Figure 1. Anomalous subdiffusion in granule cell dendrites.

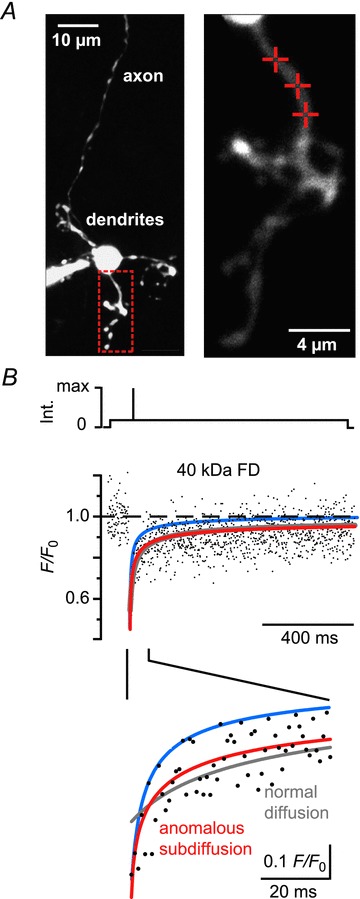
A, left: contrast-enhanced two-photon image (z-stack) of a granule cell filled with a 40 kDa FD (500 μm) via a somatic patch pipette. The red box outlines the dendritic region shown magnified on the right. Cross-hairs denote the positions on which fluorescence recovery after photobleaching recordings (shown in B) were performed. B, top: scheme of the laser intensity protocol. Middle: dendritic fluorescence recovery after photobleaching time course. The dots represent the average of three normalized recordings (F/F₀) from the spots denoted in A. The lines represent fits to the fluorescence recovery assuming free diffusion (grey line, eqn 1 in Methods) or anomalous subdiffusion (red line, eqn 2). The blue line shows the calculated recovery for free diffusion using the previously published diffusion coefficient of 40 kDa FD (Schmidt et al. 2007a). The lower panel shows the initial recovery expanded in time. Note that the subdiffusion model yields the best fit to the recovery. FD, fluorescein dextrans; Int., laser intensity.

A model of free Brownian motion [eqn (1), cf. Schmidt et al. 2007a] fitted the late recovery phase well. It failed, however, to capture the initial recovery (Fig. 1B, grey line). Moreover, the obtained D values were surprisingly small. Median values were 2 μm² s⁻¹ (IQR 0.3–6.0 μm² s⁻¹) for 10 kDa FDs (n= 69 recordings from 24 cells) and 1.5 μm² s⁻¹ (0.6–4.0 μm² s⁻¹) for 40 kDa FDs (n= 69 recordings from 23 cells). These values are approximately five times smaller than those reported for FDs in axons of Purkinje cells (Schmidt et al. 2007a). The previously published D values would lead to significantly faster recoveries (blue line in 1B) than the one determined in this study. Incorporating an immobile fraction (IF) into the diffusion model (cf. Schmidt et al. 2005) improved the fit (not shown) and yielded D values compatible with the literature. The requirement for an IF, however, is not in line with the assumption that FDs are inert markers with respect to their intracellular mobility (Luby-Phelps et al. 1985, 1995; Reits & Neefjes, 2001; Schmidt et al. 2005; Sprague & McNally, 2005).

We tested for the possibility that the rapid initial recovery was due to the presence of free dye in the FDs containing solutions. Using gel electrophoresis of these solutions we found only a single band for each FD that was clearly separated from a free dye band tested in a separate column (data not shown), indicating that dye contamination is not responsible for the initial rapid recovery phase. A further possibility is that radial diffusion contributed to recovery, a phenomenon known to affect fluorescence recovery in bounded systems (Sullivan & Brown, 2011). However, the radial (ω_r) and axial (ω_z) radii of the bleach spot at the e⁻² intensity were 0.53 and 1.95 μm, respectively in our system (Schmidt et al. 2007a). Both values are larger than the radii of the dendrites estimated from fluorescence images (≤0.5 μm) or reported in the literature (Eccles et al. 1967; Ito, 1984). The size of the focal volume is thus larger than or equal to the radial dendritic dimension, and FRAP data are unlikely to be distorted by radial diffusion.

The described discrepancies between model and data (early recovery phase) and between published and estimated D values (late recovery) are resolved if molecular movements are described by anomalous subdiffusion (Feder et al. 1996; Brown et al. 1999). Anomalous subdiffusion is a process in which free diffusion of inert molecules is hindered by the cell's geometry (Ölveczky & Verkman, 1998; Sbalzarini et al. 2005; Santamaria et al. 2006), molecular crowding or transient trapping (Bouchaud & Georges, 1990; Saxton, 1996; Weiss et al. 2004). In many cases, however, the physical mechanisms inducing anomalous subdiffusion remain ill-defined. Therefore, the model below gives just an ad hoc fit with no direct information about the diffusion-hindering processes in the compartment under study. In subdiffusion models, the mean square displacement of the diffusing particle is no longer proportional to time, but obeys a power law in time and the diffusion coefficient D becomes a function of time (Feder et al. 1996), i.e.:

(4)

where α≤ 1 is the anomalous subdiffusion exponent and Γ is a transport coefficient (Feder et al. 1996; Brown et al. 1999).

Anomalous subdiffusion models have previously been shown to improve fits to FRAP data obtained in biological systems and to eliminate the requirement of an IF (Feder et al. 1996; Brown et al. 1999; Klafter & Sokoov, 2005). Mathematically, anomalous subdiffusion was implemented by replacing terms of Dt in eqn (1) by (γt)^α, The effective diffusion coefficient at any time t (e.g. D_10ms) is then equal to γ^αt^α−1 (Brown et al. 1999). This results in a 1D anomalous subdiffusion equation (eqn (2)), which substantially improved the accuracy of the fit during the initial phase of the recovery (Fig. 1B, red trace, lower panel) and eliminated the requirement of an IF.

The values of γ are not in units of μm² s⁻¹ and can only be compared directly between groups if α values are identical. To allow comparing fitting results with different α values, the time-dependent diffusion coefficient D_(t) at t= 10 ms after bleaching was calculated. We found a median D_10ms of 12 μm² s⁻¹ (IQR 8–18 μm² s⁻¹) for 10 kDa FD (n= 69 from 24 cells) and of 10 μm² s⁻¹ (7–14 μm² s⁻¹) for 40 kDa FD (n= 69 from 23 cells). While the data showed a substantial variability, most likely due to the signal-to-noise ratio of FRAP recordings in thin dendritic structures, the D_10ms values of the dextrans were significantly different from each other (P < 0.05). The median anomality exponent α was not significantly different for 10 and 40 kDa FDs 0.64 (0.47–0.89) and 0.68 (0.60–0.87), respectively, P > 0.1]. These results point towards a size dependency of D_(t) (larger molecules diffuse more slowly), while α is independent of molecular weights between 10 kDa and 40 kDa and, thus, may reflect cellular hindrances (Saxton & Jacobson, 1997; Santamaria et al. 2006). Taken together, the molecular movement of inert traces in granule cell dendrites is not well described by free diffusion, while a model of 1D anomalous subdiffusion improved data description.

Dye-labelled calretinin diffusion in granule cell dendrites

Having established a basic framework for diffusion in granule cells, we continued with FRAP experiments on dendrites loaded with a pipette solution that contained 80 μm CR* (Fig. 2A). The cells equilibrated with CR* on timescales similar to the dextrans, i.e. cellular structures were clearly resolvable after ∼15 min loading time, indicating that CR* had access to all cellular compartments. For FRAP recordings of CR*, similar laser intensity protocols as for the FDs were used. Subsequently, data were quantified using the anomalous subdiffusion model (Fig. 2B). On average, the fits yielded an α-value of 0.68 (IQR 0.52–0.95, n= 63 from 18 cells) for CR*, a value not different from the α-values for the FDs (P > 0.7; Fig. 2E). Thus, in addition to its independence of the molecular weight, α is also independent of the nature of the diffusing particle, which is in accordance with the notion of α as a structural parameter. By contrast, the median time-dependent diffusion coefficient at t= 10 ms was remarkably low, being only 3.2 (IQR 1.6–5.9) μm² s⁻¹ (Fig. 2C and E). This value is significantly smaller than D_10ms of 10 kDa FD (P < 0.001) and even of 40 kDa FD (P < 0.001), which has a higher molecular weight than CR* (∼31.5 kDa).

Figure 2. Reduced mobility of CR in granule cells.

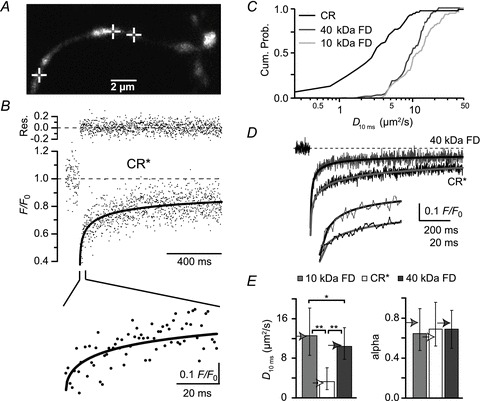
A, granule cell dendrite loaded with 80 μm of CR* via a somatic patch pipette. The cross-hairs mark the spots at which FRAP experiments were performed. B, average of three FRAP recordings from the points indicated in A. The black line represents a fit by the subdiffusion equation. In the top line, the residuals (measured values – fit values) are shown. The lower panel shows the initial recovery expanded in time. C, cumulative probability histograms of time-dependent D values at 10 ms (D_10ms). D, grand averages of FRAP recordings from different cells but with similar bleach depth (45–55%) obtained with 40 kDa FD (grey, n= 31 from 10 cells) and CR* (black, n= 25 from six cells), fitted with the anomalous subdiffusion equation (continuous lines). The lower panel shows the initial recoveries expanded in time. E, values of D_10ms and anomalous subdiffusion coefficients (alpha) for 10 and 40 kDa FD and CR*, as indicated (n= 69 FRAP measurements from 24 cells for 10 kDa FD, n= 69 from 23 cells for 40 kDa FD, and n= 63 from 18 cells for CR*). The arrowheads indicate the values obtained by fitting the grand averages for 40 kDa FD and CR* (as in D) and for 10 kDa FD (n= 39 from 10 cells). Note that the molecular weight of CR* is ∼31.5 kDa. *P < 0.05, **P < 0.001. CR, calretinin; CR*, dye-labelled CR; FD, fluorescein dextrans; FRAP, fluorescence recovery after photobleaching.

Validation of dye-labelled calretinin fluorescence recovery after photobleaching

To exclude the possibility that the observed reduction in D_10ms of CR* in comparison to the FDs is due to the labelling procedure or to agglomeration of the protein, CR* purity was tested by SDS-gel electrophoresis (Fig. 3A) and by single-photon time-correlated FRAP recordings in a cuvette (Fig. 3B).

Figure 3. CR* diffusion in vitro.

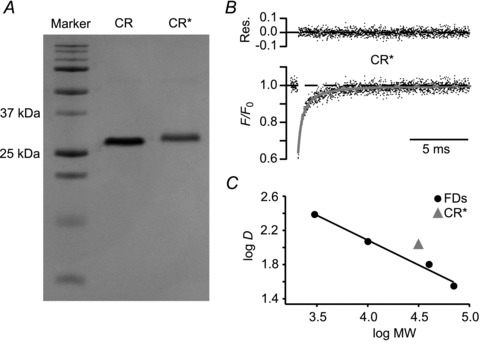
A, SDS-gel of native and CR* (CR and CR*, respectively). MW markers are shown in the left lane: 10, 15, 20, 25, 37, 50, 75, 100, 150 and 250 kDa from bottom to top. B, aqueous fluorescence recovery after photobleaching time course of CR* dissolved in pipette solution in a cuvette (average of 2500 individual recordings) and a fit to a three-dimensional, normal diffusion equation (grey line; top: residuals). C, logarithms of the mean aqueous D values of CR*, 3 kDa, 10 kDa, 40 kDa and 70 kDa FD plotted against the logarithms of their MW. Four experiments each. s.e.m. values are smaller than the markers. Linear regression to the dextran data yielded a slope of –0.55. CR, calretinin; CR*, dye-labelled CR; FD, fluorescein dextrans; MW, molecular weight; Res., residuals.

The gel electrophoresis resulted in clear, single bands for CR and CR*, showing that in each case only one diffusing species was present and that the staining increased the mass of the protein only slightly and as expected. For time-correlated FRAP recordings, FDs of various sizes or CR* (50 μm each) were dissolved in the intracellular solution and were measured independently (Fig. 3B). In cuvettes, the fluorescence recovery curves of FDs as well as of CR* were well described by a 3D free Brownian diffusion model (Brown et al. 1999). The diffusional mobility of the molecules decreased with increasing molecular weight (Fig. 3C). The means ±s.e.m. values for 3 kDa, 10 kDa, 40 kDa and 70 kDa were 250 ± 6, 141 ± 1, 71 ± 1 and 40 ± 1 μm² s⁻¹, respectively. The logarithms of these data were well fitted by a straight line with a slope of −0.55 when plotted against logarithms of their molecular weights (Fig. 3C), which is consistent with previous reports on aqueous diffusion of FDs (Arrio-Dupont et al. 1996). For CR* the aqueous D was determined as 120 ± 1 μm² s⁻¹ (means ±s.e.m.). When introduced into the above log–log plot, this value falls close to the fitting line, with a deviation towards faster diffusion. The latter may be explained by differences between the tertiary structure of FDs and of CR* but is in absolute contrast to the slowed cytoplasmic diffusion of CR* in granule cell dendrites. Thus, these data indicate that the reduced dendritic CR* mobility is neither due to impurities of CR* nor to the labelling procedure or to other technical aspects.

Dependence of dye-labelled calretinin diffusion on granule cell activity

The above data suggest that CR undergoes a specific, yet unidentified interaction in dendrites, i.e. CR could have characteristics of a Ca²⁺ sensor. For a Ca²⁺ sensor, such an interaction should depend on the intracellular Ca²⁺ concentration ([Ca²⁺]_i). To test for this sensor hypothesis, we analysed whether CR* diffusion would be affected by an elevated [Ca²⁺]_i.

Granule cells were loaded via a somatic patch pipette with 50 μm of the Ca²⁺ indicator dye Oregon Green BAPTA-1 (OGB-1) and, as OGB-1 is dim at resting Ca²⁺ levels, additionally with 50 μm of the red fluorescent, Ca²⁺ insensitive dye Atto-637. Collecting fluorescence from both dyes allowed resolving the cell morphology despite the low indicator concentration (Fig. 4A). Trains of action potentials were evoked by somatic step depolarization (Fig. 4B, upper panel) and resulted in an average firing frequency of 96 ± 20 Hz (means ± SD, n= 16 cells). During action potential firing, the dendritic fluorescence increased (Fig. 4B, lower panel) and reached a plateau value of 42 ± 7%ΔF/F₀ within ∼0.3 s (means ±s.e.m., n= 6 cells). This demonstrates that somatic APs are associated with a dendritic Ca²⁺ influx in granule cells, with amplitude and time course being consistent with previous reports from granule cells (Gall et al. 2005) as well as from pyramidal neurons (Helmchen et al. 1996). We performed numerical simulations (see Methods for details), to back-calculate the Ca²⁺ transient in the absence of OGB-1 and to estimate the corresponding fraction of Ca²⁺-bound CR during the train. This simulation indicated that saturation of CR by Ca²⁺ increased from 4.7% under resting conditions to 11.7% during the plateau of the Ca²⁺ transient (Fig. 4C).

Figure 4. Decreased mobility of CR* during neuronal activity.

A, left: a granule cell loaded with 50 μm OGB-1 and 50 μm Atto-637 via a somatic patch pipette. The box delineates the dendritic region (shown magnified on the right) from which the fluorescence signals in B were recorded. The corresponding regions of interest are denoted by solid and dashed ellipses. B, top: voltage response (V_m) to a somatic current injection (I_hold) of the granule cell shown in A. Bottom: associated relative fluorescence increases of OGB-1 (ΔF/F₀) recorded from the dendritic regions indicated by the small dashed (grey traces) and large solid ellipses (black trace) in A. C, scheme of CR (upper panel) with the EF-hands of which five bind Ca²⁺ (Schwaller et al. 1997). The N- and C-terminals as well as the numbering of the amino acids are indicated. The lower panel shows a numerical simulation of CR's Ca²⁺ saturation during the average action potential train in the absence of indicator dye. The dashed line indicates 0% saturation. The resting saturation is 4.7%. The two bottom traces illustrate the experimental approach for FRAP recordings during action potential firing. D, FRAP time course of CR* during repetitive firing (average of six recordings). The continuous line represents a fit of the recovery to the subdiffusion equation. E, cumulative probability graph of D_10ms values under control conditions (‘CR* rest’, ‘10 kDa FD rest’; data from Fig. 2C) and during action potential firing (‘CR* stim’; n= 56 recordings from 10 cells; *P < 0.05 and ‘10 kDa FD* stim’; n= 36 recordings from nine cells). F, FRAP time course of CR* in the presence of peptide resembling EF-hand 5 of CR, the putative interaction site. The continuous line represents a fit of the recovery to the subdiffusion equation. Note the accelerated recovery compared to Fig. 2B. G, cumulative probability histograms of D_10ms values under control conditions (CR*; as in 2C) or in the presence of peptide representing EF-hand 5 of CR (‘pep’; n= 92 recordings from 17 cells) or a scrambled peptide (‘scr’; n= 76/7). **P < 0.001. CR, calretinin; CR*, dye-labelled CR; FD, fluorescein dextrans.

Next, CR* FRAP recordings were performed during granule cell activation identical to the above but without the dyes necessary for Ca²⁺ imaging (Fig. 4D). The bleach pulse was applied at a time when a stable elevation in [Ca²⁺]_i and Ca²⁺-saturated CR could be expected based on the imaging experiments and the simulation. Fitting the corresponding fluorescence recovery with the 1D anomalous subdiffusion model yielded a median D_10ms of 2.2 (IQR 1.2–4.0) μm² s⁻¹ (n= 56 from 10 cells), a value significantly smaller than under resting conditions (Fig. 4E; P < 0.05). In contrast, no change in the α-value was observed (α= 0.66, IQR 0.56–0.83, not shown). Control experiments performed with 10 kDa FD showed no effect of stimulation on either D_{10 ms} (14.4 μm² s⁻¹, IQR 9.8–24.6 μm² s⁻¹; n= 36 from 9 cells) or α (0.68, IQR 0.60–0.89), indicating that the calcium-dependent decrease in mobility is specific to CR (Fig. 4E).

Identification of the binding site of calretinin

FRAP allows testing for specific binding sites by co-dialysing peptides that block the putative binding site and, thereby, accelerate the mobility of the protein (Schmidt et al. 2005). We reasoned that CR's EF-hand 5 could represent a likely candidate region for interaction with other proteins. As no structural data are currently available for CR, we compared the structures of the related hexa-EF-hand CaBPs, calbindin D-28k (Kojetin et al. 2006) and secretagogin (Bitto et al. 2009). In both proteins, EF-hand domains 1–4 form relatively compact structures insulated from EF-hand 5 by the non-functional EF-hand 6. EF-hand 5, which is highly conserved between mice, rats and humans (94% identity at the amino acid level), has a rather low Ca²⁺ affinity of ∼36 μm (Faas et al. 2007) to ∼500 μm (Schwaller et al. 1997), and is freely accessible to the aqueous environment, rendering it a likely interaction site. We synthesized a peptide embracing mouse EF-hand 5 and a small part of the 5/6 linker region (Fig. 4C). When co-dialysed with CR* into granule cells, FRAP recordings revealed a significantly increased mobility of CR with D_10ms of 7.7 μm² s⁻¹ (IQR 4.1–12.4 μm² s⁻¹; n= 92 from 17 cells) without affecting α (0.59, IQR 0.42–0.84) (Fig. 4F). This was a specific effect of the EF-hand 5 peptide as a scrambled peptide (Fig. 4G) did not affect CR's mobility (D_10ms= 2.3 μm² s⁻¹ (IQR 1.4–5.0 μm² s⁻¹; α= 0.69, IQR 0.55–0.96; n= 76 from seven cells).

Discussion

Using two-photon FRAP we analysed the mobility of CR in granule cell dendrites. We found that anomalous subdiffusion better describes the movement of macromolecules (inert tracers and CR) than free diffusion and that the movement of CR, the main Ca²⁺ buffer expressed in granule cells, is further hindered by specific interactions with yet unidentified binding partners. The interaction is most likely mediated by the EF-hand 5 region of CR and enhanced by Ca²⁺ binding of EF-hands 1–4, indicating that CR acts as a Ca²⁺ sensor in granule cells.

Despite an increasing amount of observations of anomalous subdiffusion (Klafter & Sokoov, 2005), its physical importance is not well understood and distinct mechanisms may underlay this phenomenon. Anomalous subdiffusion has been shown to occur when diffusing molecules are temporarily trapped. Trapping can be due to molecular interactions (Feder et al. 1996; Saxton, 1996, 2001; Luby-Phelps, 2000) or to morphological constraints (Santamaria et al. 2006, 2011), which delay diffusion in a time-dependent manner (cf. eqn (4)). The trapping has to operate on a timescale similar to diffusion to induce subdiffusion. Substantially longer-lasting interactions induce fixed offsets in the FRAP curves (Schmidt et al. 2005), while shorter-lasting interactions lead to slowed but otherwise normal diffusion (Sprague & McNally, 2005). However, it is often difficult to distinguish between the various diffusion regimes, in particular since IF and the subdiffusion coefficient α can have a dependency on each other (Feder et al. 1996). The use of inert tracer dyes, therefore, is of crucial importance to clarify the diffusion regime applicable for the solute of interest (Sprague & McNally, 2005).

The prevalence and the significance of anomalous diffusion are only slowly emerging (Klafter & Sokoov, 2005). For diffusion over longer stretches of spiny dendrites of Purkinje cells, spines act as molecular traps and cause diffusion to become anomalous (Santamaria et al. 2006, 2011). In the same cell type, diffusion of inert tracer dyes can be described by normal diffusion when analysed in smooth dendrites (Santamaria et al. 2006), in axons (Schmidt et al. 2007a), or between single spines and their parent dendrite (Schmidt et al. 2003a, 2005). Within the cytosol of Purkinje cells, therefore, normal diffusion prevails, arguing against other than morphological constraints to hinder diffusion in Purkinje cells (Santamaria et al. 2011). On the other hand, diffusion of green fluorescent protein in somata of rat basophilic leucemia (RBL) cells is anomalous (Brown et al. 1999) while diffusion of dextrans and parvalbumin is normal in somata of Purkinje cells (Schmidt et al. 2007a), indicating molecule- and/or cell type-specific differences in diffusional mobility. To the best of our knowledge, our dextran data (Fig. 1) represent the first example of anomalous subdiffusion occurring in aspiny dendrites. Data from aspiny dendrites of neocortical interneurons (Goldberg et al. 2003) and cerebellar stellate cells (Soler-Llavina & Sabatini, 2006) make it unlikely that morphological constraints delay diffusion. In consequence, transient trapping by interactions with large and/or immobile molecules could be responsible for anomalous diffusion (Saxton, 1996). For an inert tracer such as FD as well as for proteins, electrostatic interactions may represent a probable explanation. Further experimentation, however, will be required to identify the factors inducing anomalous diffusion in dendrites and somata.

CR diffused unexpectedly slowly in granule cells, especially when compared to dextrans of similar molecular weight (Fig. 2C and E). Typically, proteins diffuse faster than dextrans (Fig. 3C), most likely due to their different tertiary structure (Arrio-Dupont et al. 1996). In Purkinje cells, for example, the observed diffusion coefficient for parvalbumin is ∼1.4 times larger than that expected for a dextran of comparable size (Schmidt et al. 2003a). We attribute CR's low mobility to an interaction with yet unidentified intracellular binding partners.

Depending on the endogenous concentration of CR ([CR]_endo), we may have over- or underestimated the retardation of CRs mobility. If [CR]_endo would be substantially higher than our estimate of 80 μm, saturation of binding partners may occur in unperturbed cells, leading to a higher average mobility. If, on the other hand, [CR]_endo would be substantially lower (and if binding partners are already substantially saturated at 80 μm), we may have underestimated CR's mobility. However, given the quantitative data on the endogenous Ca²⁺-binding capacity of granule cells (Brenowitz & Regehr, 2007), for which CR is the only endogenous Ca²⁺ buffer expressed at a relevant concentration (Schiffmann et al. 1999), and given the Ca²⁺-binding kinetics of CR (Faas et al. 2007), we consider 80 μm to represent the most likely value, or at least an upper limit of [CR]_endo. In line with this assumption, we could recently show that this CR concentration maximizes the overlap between simulations and Ca²⁺ imaging data as well as electrophysiological recordings from wild-type and CR-deficient mice (Schmidt et al. 2013).

Irrespective of the stoichiometry, the binding partners must be of considerable size and/or they must be immobilized to explain the substantial immobilization they exert on CR. Interestingly, CR has been shown to be associated with membranes (Winsky & Kúznicki, 1995; Hack et al. 2000) and to regulate voltage-gated Ca²⁺ channels (Christel et al. 2012). However, the expected dendritic channel density is too low to convey a substantial retardation of μm amounts of CR, therefore additional targets need to be considered, such as interactions with cytoskeletal or cytoskeletal-associated elements (Marilley & Schwaller, 2000).

Independent of the identity of the target, we suggest EF-hand 5 as the likely interaction site of CR (Fig. 4F and G). EF-hand 5 has a rather low Ca²⁺ affinity (∼36 μm, Faas et al. 2007), rendering it important for buffering Ca²⁺ close to the mouth of open Ca²⁺ channels (Schmidt et al. 2013) but poorly suited to affect the low-amplitude Ca²⁺ dynamics occurring within dendrites and somata.

Characteristic for a Ca²⁺ sensor are conformational changes upon Ca²⁺ binding, which enable interaction with binding partners (da Silva & Reinach, 1991; Ikura, 1996). Such conformational changes were found for rat and for human CR upon Ca²⁺ binding in vitro (Kúznicki et al. 1995a,b; Schwaller et al. 1997). Furthermore, Winsky and Kúznicki (1995) demonstrated a Ca²⁺-dependent interaction of CR with a brain membrane fraction in vitro and Hack et al. (2000) showed for chick auditory brainstem neurons that CR gets concentrated beneath the plasma membrane during postnatal development. Our data suggest that EF-hand 5 acquired an additional function as an interacting site. As CR's mobility is reduced by submicromolar Ca²⁺ and as EF-hand 6 is non-functional (Schwaller et al. 1997), Ca²⁺ binding by EF-hands 1–4 (Faas et al. 2007) is proposed to allosterically affect the EF-hand 5 region.

It cannot be excluded that the labelling procedure affected the spatial structure of CR and, therefore, its molecular interactions, because this possibility is an inherent and at present unavoidable problem of any labelling procedure. Yet, because of the small size of the fluorescent label and because our procedure led to a preferential labelling of the α-amino group, which is at the opposite site of the proposed interaction site, we consider it unlikely that the labelling strongly affected CR's tertiary structure and, thereby, induced the specific binding via EF-hand 5.

In other Ca²⁺ sensor proteins of the EF-hand family, e.g. the neuronal Ca²⁺ sensor subfamily, Ca²⁺-dependent immobilization is caused by the ‘myristoyl switch’, where a myristoyl group attached to an amino acid in the N-terminal region is inserted in the plasma membrane caused by a Ca²⁺-dependent conformational change of the protein (Spilker & Braunewell, 2003; Burgoyne, 2004). We hypothesize that the low-affinity EF-hand 5 represents another way of transiently immobilizing a CaBP (CR) to specific targets. Thus, in light of our findings CR, initially considered as a conventional mobile Ca²⁺ buffer, has to be viewed as an immobilizable neuronal Ca²⁺ sensor. Whether the effects of immobilized CR are linked to its Ca²⁺-binding properties or to modulation of CR targets remains to be determined. Identifying CR's specific binding partners, possibly also differing in various CR-expressing subpopulations will be of importance in understanding the physiological significance behind CR's cell type-specific expression in the CNS.

Glossary

CaBP

Ca²⁺-binding protein

CR

calretinin

CR*

dye-labelled calretinin

FD

fluorescein-labelled dextran

FRAP

fluorescence recovery after photobleaching

γ

transport coefficient

IQR

interquartile range

PMTs

photomultiplier tubes

Additional information

Competing interests

None.

Author contributions

Conception and design of the experiments: H.S. and J.E.; collection, analysis and interpretation of data: O.A., B.S., E.B.B., H.S. and J.E.; drafting and revising the manuscript: O.A., B.S., E.B.B., H.S. and J.E. All authors approved the final version of the manuscript.

Funding

This work was supported by grants to J.E. and H.S. (DFG, EI 342/4), to E.B. (NIH 1DP2OD00650-01 and DoD BCRP W81XWH-09-1-0405) and to B.S. (SFN no. 130680).