The importance of geometry in mathematical models of developing systems

Abstract

Understanding the interaction between the spatial variation of extracellular signals and the interpretation of such signals in embryonic development is difficult without a mathematical model, but the inherent limitations of a model can have a profound impact on its utility. A central issue is the level of abstraction needed, and here we focus on the role of geometry in models and how the choice of the spatial dimension can influence the conclusions reached. A widely-studied system in which the proper choice of geometry is critical is embryonic development of Drosophila melanogaster, and we discuss recent work in which 3D embryo-scale modeling is used to identify key modes of transport, analyze gap gene expression, and test BMP-mediated positive feedback mechanisms.

1D models may miss important effects of transport and other processes

The role of mathematical models in science and engineering is essentially context independent – good models synthesize known observations into a coherent framework and from that framework make testable predictions as to how systems will evolve in response to perturbations. Models also serve to amplify understanding of mechanism, particularly when feedback and non-linear processes are analyzed. Modeling has reached the highest level in physics, as exemplified by the recent ‘discovery’ of the Higgs boson more than 50 years after its existence was predicted. Modeling of development in biology has played a somewhat softer role due to the fact that overarching general principles for the evolution of systems during development remain to be discovered, in large part due to the inherent complexity of biological systems. Furthermore, the utility of a model in experimental biology is very time-sensitive – if too little is known, the model may not be compelling enough to justify new experiments, whereas if most of the phenomena are understood the model simply serves to tidy up after the parade.

Since mathematical models in biology usually represent a simplification of reality, a key question is what level of complexity should be embedded in a model. A first level decision is often whether spatial variation of the quantities of interest is important, and the answer may depend on the particular molecular and transport processes involved, and on whether forces and the mechanical properties are important, etc. If spatial variations of components in the model are important, then one must determine whether the system is isotropic, and whether the detailed geometry of the system is essential or whether the system can be simplified by using a one- or two-dimensional representation of what is usually a three-dimensional system. Examples of how oversimplification of the geometry leads to dubious conclusions are given later.

An accurate geometric representation, augmented by detailed data on the signal transduction and gene control networks – such as is available to varying degree in the Drosophila gene atlas, the zebrafish nuclear dynamic data, Flyex, (Keranen et al., 2006; Fowlkes et al., 2008; Keller et al., 2008; Pisarev et al., 2009), leads to more detailed and realistic models that can drive further experimentation. Recent work in the model organism Drosophila melanogaster provides examples of the effectiveness of using 3D modeling to address both long-standing and new questions for two distinct patterning pathways -- anterior-posterior patterning by Bicoid and the downstream gap genes of the embryo, and Bone Morphogenetic Protein (BMP) patterning along the dorsal ectoderm of the embryo (Figure 1).

Figure 1. An example of how 3D geometry is used to evaluate pattern formation in Drosophila.

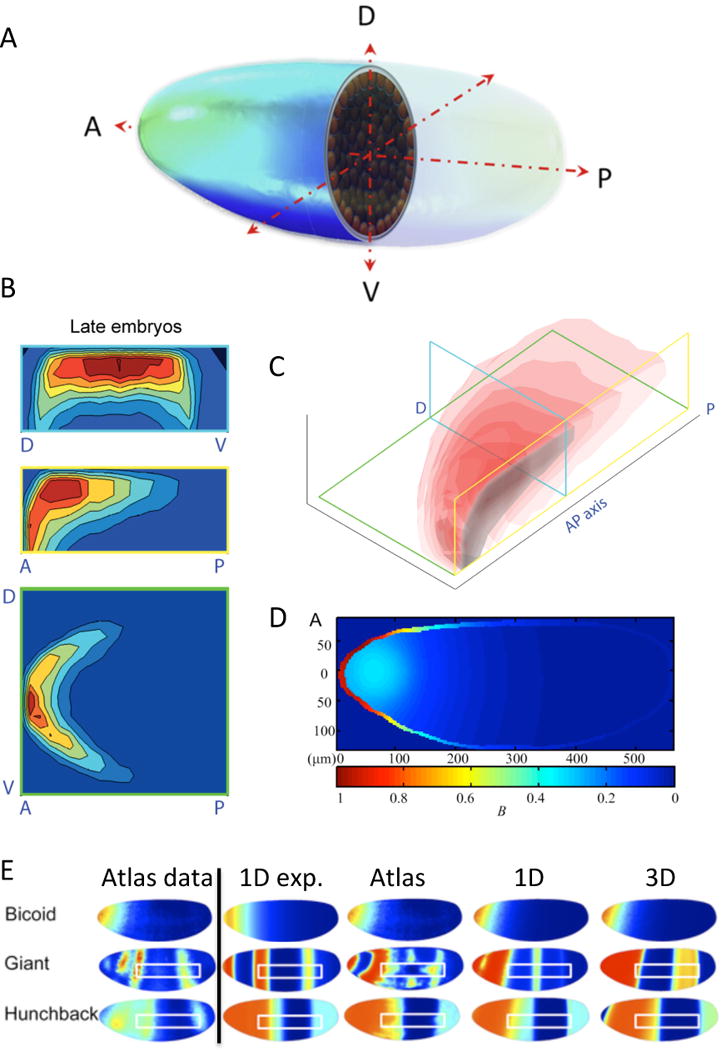
(A) Rendering of Drosophila blastoderm embryo (from Umulis et al. 2010, with permission). (B) bcd mRNA density map (from Little et al. 2011, with permission). Top: transverse; Middle: coronal; and Bottom: Midsaggital planes (planes shown at right in C). (C) isosurfaces for bcd mRNA density. (D) 3D model results for Bcd transport (from He et al., 2010). (E) 3D model results for gap gene system with different types of Bicoid input. Atlas data is shown in left column (reproduced with permission, PLoS ONE; Hengenius et al. 2011) Model results are shown at right for different types of Bcd input including exponential (1D exp.), direct data input from atlas (Atlas), and a Bcd SDD model optimized in 1D and 3D.

3D modeling of anterior-posterior patterning by Bicoid

The positional information paradigm in its simplest form postulates a spatial gradient of a morphogen along a 1D axis (for a recent review see Shvartsman et al. 2012), and while this is appropriate in some systems, it cannot represent the range of observations on AP and DV patterning in the Drosophila embryo. The genes involved show complex, graded 3D patterns that must be modeled accurately in order to develop a full quantitative understanding of the regulatory network.

The AP morphogen Bicoid is produced from maternally-deposited mRNA that is localized in a diffuse region around the dorsal-anterior embryonic pole (Fig. 1 B–C). Bicoid protein, which initiates the expression of the downstream gap genes, is monotonically-decreasing along the AP axis and varies across the cross-section of the embryo (Figure 1 D).

A basic experimental and theoretical question is: “How does the Bcd protein distribution form in the embryo?” and a recent review discusses alternative explanations and mathematical models (Grimm et al., 2010). While a 1D synthesis-diffusion-decay (SDD) model has been widely-used to answer this, conflicting evidence suggested that 1) diffusion of Bcd is too slow for patterning in the limited time of development (Gregor et al., 2007), 2) the bcd mRNA distribution pre-encodes the spatial distribution and protein is produced locally, and 3) Bcd may not degrade sufficiently on the time-scale of development. Here, 3D modeling at two scales has been utilized to overcome some of the limitations of the 1D models. First, FRAP measurements of tagged protein yielded a diffusion coefficient too small to produce a gradient in the available time, but re-analysis of the results using a 3D model of the local environment yielded a 3-fold greater estimate for Bcd diffusion (Castle et al., 2011; Mogilner and Odde, 2011). Furthermore, the quantitative distributions of Bicoid protein and the downstream gap gene proteins (Keranen et al., 2006; Luengo Hendriks et al., 2006; Fowlkes et al., 2008) point to several important aspects not captured by 1D models (Figure 1E), including the following.

1. AP expression pattern boundaries do not appear at a constant egg length but instead vary continuously from the dorsal to the ventral surface.

2. Along a given domain of expression (e.g., individual stripes of eve or ftz) the peak expression level varies significantly -- by as much as a factor of 5x – in the DV direction.

3. gap genes such as kni, gt, hb have relatively simple patterns prior to cycle 14 in the trunk region, but show a very complex pattern with rapid dynamics in the cephalic region.

4. The 3D locations of nuclei on the surface of the blastoderm are dynamically regulated (even during the hour prior to gastrulation during which there are no divisions) along the AP and DV coordinate.

5. Measurements of bicoid mRNA localization in 3D yield a cup-like distribution that is important for establishing experimentally consistent protein gradients (Little et al., 2011).

To account for some of these behaviors, early 3D modeling of AP patterning suggested that the Bicoid distributions are most consistent with simulations that placed a bolus of mRNA in the anterior dorsal region of the embryo (He et al., 2010), but later work invoked dual contributions to Bcd patterning by a distributed mRNA source and protein transport from the source (Little et al., 2011). The authors of the latter study found that an optimal fit to the data required both a spatially non-uniform source and a time-varying diffusion constant that went to zero during nc 11–12. While this provided a big step forward, problems remain that need to be addressed. For instance, there is little evidence to support the sudden change in diffusion of Bcd needed by the 3D model to reproduce experimental observations. Moreover, this directly contradicts other results that predict a diffusion coefficient D= 7 microns²/sec at nc 13 (Castle et al., 2011). Thus there is a huge disparity in the transport rates needed to explain the data, which suggests that other important processes have been neglected. A more complete 3D model could help to resolve this issue.

Successes and limitations of 3D modeling of gap gene patterning

Other models focus on the next step of AP patterning, gap gene expression, and address the question of whether optimization of a 3D model with the same number of parameters as a simpler 1D model leads to better estimates of parameters and/or the identification of the underlying network? Two recent models for gap gene patterning use more realistic 3D model geometries (Bieler et al., 2011; Hengenius et al., 2011) to address this. The model by Hengenius et al. performed well against wild type data and arrived at regulatory networks similar to those found for 1D after optimization (Figure 1E), but highlighted the hypersensitivity of the patterning system to noise in the distribution of Bcd (Figure 1E). Smoothing out the Bicoid profile led to more accurate predictions of hunchback and giant expression. The model due to Bieler et al., also yielded patterns of gap gene expression consistent with observations, and also showed some improvement over earlier models at producing the experimentally-observed phenotypes for gap gene mutants (Bieler et al., 2011). However, the networks identified by both groups did not differ significantly from those derived from the earlier 1D models, which suggest that the quality of data available does not warrant the additional complexity of a 3D model at present.

3D modeling of dorsal surface patterning by BMPs

Dorsal surface patterning by Drosophila BMPs involves the ligands Dpp and Scw, the co-factor inhibitors Sog and Tsg, BMP type I and II receptors, and the metalloprotease Tld. These interact to form a dorsal-high to lateral-low distribution of BMP signaling activity that specifies the amnioserosa, an extraembryonic tissue required for proper dorsal closure (see Figure 2 and for review see (Umulis et al., 2009)). 1D models of the pathway have been developed to 1) investigate whether there are conditions under which a proposed shuttling mechanism, where BMP ligands are moved ventro-dorsally by binding to a mobile carrier, is feasible, 2) to determine whether the system is robust to changes in the levels of components, and 3) to evaluate the dynamics of pattern formation in the presence of positive feedback (Eldar et al., 2002; Mizutani et al., 2005; Umulis et al., 2006; Iber and Gaglia, 2007; Umulis et al., 2010). 1D models based on mid-embryo cross-sections (Figure 1) proved effective at addressing these questions, yet were simple enough to characterize the system over wide regions of parameter space.

Figure 2. Model development and testing for BMP-mediated dorsal surface patterning.

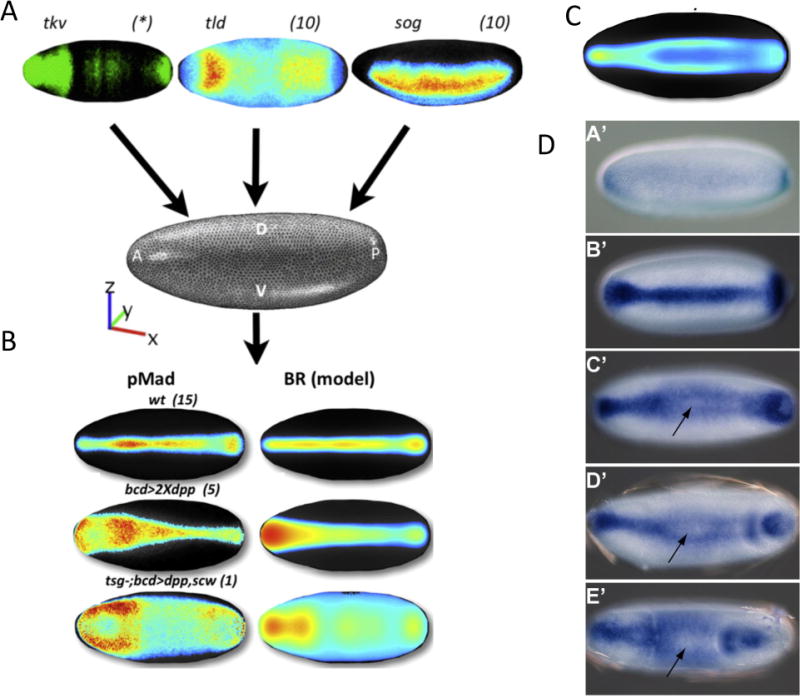
(A) A schematic of the data integration methodology. (Umulis et al., 2010; Dev. Cell, with permission.) (B) An example of model success for wild type and failure (ectopic overexpression). Notice the peak loss, or peak splitting behavior in the data. (C) An example model result that exhibits peak splitting along the dorsal surface of the embryo. (D) Dynamics of M. abdita BMP patterning (Rafiqi et al., 2012). Dynamic evolutions from early (A’) to late (E’) blastoderm embryo. Arrow indicates position of trough between peaks after the pMad distribution splits.

Despite the successes, the 1D models have several limitations. These include the lack of quantitative or semi-quantitative data integration for model testing and optimization, they cannot explain spatial patterns observed in new experiments designed to test feedback, and BMP signaling between different species of Drosophila gives rise to different quantitative and qualitative patterns (Figure 2) (Umulis et al., 2010). The latter show a high degree of anterior-posterior variations in intensity and width, various data shows that patterning along the AP and DV axes are coupled, and existing phenotypes lead to non-intuitive defects in patterning that cannot be explained by 1D models. Model identification using alternative forms of the 3D BMP patterning model took advantage of the additional data to find networks that were most consistent with the observations (Umulis et al., 2010). Three models emerged that exhibited an improvement over a model that lacked feedback, and one model with feedback on a secreted binding protein emerged as the overall “best” fit.

However, the model was not able to reproduce a number of observations from experiments that overexpress ligands in the anterior of the embryo (Umulis et al., 2010). The model predicted peak signaling near the regions where ligands are over-expressed, as expected, but the experiments consistently yielded a “splitting” of the single peak of high level signaling into two high level peaks with a valley of reduced BMP signaling between them (Figure 2 B). The discrepancy between the model and data is significant, because it stimulates both new hypotheses and new experiments. There is some concern that over-expression data represents a non-physiological condition, but it is a consistent with other model observations, including similar “peak-splitting” behavior observed whenever there is an imbalance between the transport of BMP-ligands and the rate at which they are captured by receptors (Figure 2C).

Intriguingly, the formation of two parallel peaks of BMP signaling has now been observed in a related species of diptera, the scuttle fly Megaselia abdita (Rafiqi et al., 2012). In D. melanogaster, high BMP signaling levels are needed to induce formation of amnioserosa, whereas M. abdita employs two phases of BMP signaling. M. abdita does not form a single amnioserosa tissue, but instead forms a dorsal serosa tissue that secretes cuticle below the eggshell, and the amnion, an extraembryonic tissue that closes the dorsal germband. An initial phase of signaling in the M. abdita blastoderm embryo leads to peak activity at the dorsal midline where serosa forms, later, at the beginning of gastrulation, signaling is shifted laterally and coincides with increased BMP signaling in the presumptive amnion (Figure 2D).

The dynamics of patterning of M. abdita are remarkably similar to model predictions in which an initial broad gradient splits into two. The embryonic position in the model where peak splitting is most prominent occurs around 50–60% embryo length. Both of these behaviors are seen in M. abdita, which provides indirect evidence consistent with a positive feedback mechanism that dynamically shortens the range of morphogen activity. Highly active feedback will eventually cause the peak to split and equilibrate when the distribution balances flux by transport with ligand capture and internalization.

Future directions

The focus herein has been exclusively on Drosophila patterning mechanisms, but other systems also require a better representation of their geometry in models. One example arises in vertebrate limb development. The limb bud first appears as a small protrusion from the flank of the embryo, which then elongates along the proximo-distal axis, flattens along the dorsal-ventral (top-to-bottom) axis, and develops an asymmetric pattern of cartilage condensations along the anterior-posterior (thumb-to-smallest-digit) axis during outgrowth. Signaling, mechanical forces, and changes in shape are all important during outgrowth of the limb bud, and a minimal model requires at least two spatial dimensions to capture essential features. For instance, the signaling regions at the ZPA and the AER are spatially-separated and interact via diffusible molecules. Fibroblast growth factors produced by AER cells are required for outgrowth and continued production of Sonic hedgehog, which is produced in the ZPA (Sun et al., 2000). The expression of FGFs in the AER is in turn up-regulated by Shh through Gremlin, which suppresses FGF inhibition by Bmp-2 (Litingtung et al., 2002). 2D mathematical models that treat a horizontal slice through the limb bud can capture some of the shape changes (Dillon and Othmer, 1999) and details of the morphogen distributions (Dillon et al., 2003) (Dillon et al., 2003), but a 3D model is needed to accurately describe the full system (Hopyan et al., 2011).

Other examples include early development of Xenopus and zebrafish, and wing disc development in Drosophila. Both zebrafish and Xenopus embryos form ventral-high to dorsal-low distributions of BMP signaling activity and the molecules that regulate the processes are fairly well understood (Tucker et al., 2008; Zakin and De Robertis, 2010). Early models in zebrafish have supported the proposed networks responsible for spatial patterning (Zhang et al., 2007), but there is more debate regarding the mechanisms of Xenopus patterning and the observed scale-invariance (Ben-Zvi et al., 2008; Francois et al., 2009). Modeling of BMP-mediated patterning in zebrafish is poised to make significant new contributions to our understanding of BMPs due to new imaging modalities that allow for isotropic, quantitative measurement of gene expression and signaling intensity.

Over the past 5 years there has been a significant growth in the development of imaging technologies to capture high resolution 3D images in larger specimens than was previously possible by SPIM, DLSM, and microfluidic manipulation, each of which leads to movement of the sample for isotropic 3D imaging (Chung et al., 2011; Keller et al., 2011; Swoger et al., 2011). As new image acquisition approaches generate vast amount of data, theoretical work should utilize the available data to the fullest extent possible. For this to occur, better strategies are needed to include “soft” constraints on models to improve the utilization of data that is currently available or acquirable with current technology. The seamless integration between model and data is a critical piece needed to shift current paradigms in biological analysis so that models become more widely used to discover mechanism and eventually used as a common tool alongside molecular biology, biochemistry, imaging and genetics. However mathematical models require parameters for quantitative predictions, not just responses in arbitrary units, and thus there is a dire need for more biochemical studies aimed at establishing parameters.