Improved equation for estimating single-pool Kt/V at higher dialysis frequencies

we need a standard method of calculating dialysis dose, taking all the required factors into account. This would be a dialysis-equivalent GFR

Abstract

Rationale

To measure adequacy in patients dialyzed other than three times per week, guidelines recommend the use of ‘standard’ Kt/V, which commonly is estimated from treatment Kt/V, time and frequency; however, the accuracy of equations that predict treatment Kt/V in patients being dialyzed other than three times per week has not been evaluated.

Methods

In patients enrolled in the Frequent Hemodialysis Network (FHN) Daily and Nocturnal Trials who were being dialyzed three, four or six times per week, we tested the accuracy of the following Kt/V prediction equation: Kt/V = −ln(R − GFAC × T_hours) + (4–3.5 × R) × 0.55 × weight loss/V, where R = post-dialysis/pre-dialysis blood urea nitrogen and GFAC, originally set to 0.008 for a 3/week schedule (Daugirdas, J Am Soc Nephrol 1993), is a factor that adjusts for urea generation.

Results

With the above equation, there was <0.1% mean error in predicted treatment Kt/V for 3/week patients, but mean errors were −5, −9 and −13% for the 6/week daily, 4/week nocturnal and 6/week nocturnal patients. Modeling simulations were performed to optimize the GFAC term for dialysis schedule and length of the preceding interdialysis interval (PIDI). After substituting schedule- and interval-optimized GFAC terms, the treatment Kt/V prediction errors were reduced to −0.81, +0.1 and −1.3% for the three frequent dialysis schedules tested.

Conclusion

For frequent dialysis schedules, the urea generation factor (GFAC) of one commonly used Kt/V prediction equation should be adjusted based on length in days of the PIDI and number of treatments per week.

INTRODUCTION

Current guidelines for hemodialysis adequacy are based on Kt/V, the fractional removal of urea per dialysis treatment, expressed as clearance (K) multiplied by treatment time (t) and divided by the urea distribution volume (V). For three treatments per week, the 2006 Kidney Disease Outcomes Quality Initiative (KDOQI) adequacy guidelines recommend a minimum single-pool Kt/V of 1.2 [1]. The European Best Practice Guidelines recommend a minimum equilibrated Kt/V value of 1.2, corresponding to a minimum single-pool Kt/V of 1.35–1.40 [2]. Although the KDOQI guidelines recommend that kinetic modeling be used to measure Kt/V, simple explicit formulas such as the urea reduction ratio (URR) and estimation equations for single-pool Kt/V based on the URR, the dialysis session length and fractional volume removal (weight loss divided by V or weight loss divided by body weight) are also allowed by the KDOQI guidelines [1]. In the USA, these simplified formulas continue to be widely used. One commonly used estimating equation for single-pool Kt/V (spKt/V) was developed by Daugirdas and will be referred to as the ‘D2’ equation in this report [3]:

where R is the ratio of post-dialysis blood urea nitrogen (BUN) to pre-dialysis BUN. GFAC (short for ‘g-factor’) is a urea generation term that is multiplied by the session length (in hours) and is subtracted from R to give an approximate value of what R would have been in the absence of urea generation during dialysis. The second compound term in the above equation [(4–3.5 × R) × 0.55 × weight loss/V] adjusts for urea removal that occurs as a result of volume contraction and which contributes substantially to Kt/V, but which is not reflected by a change in R. The above ‘D2’ equation, using a GFAC term of 0.008, has been widely used to estimate the dialysis adequacy both clinically, in many research publications examining the impact of delivered Kt/V on outcome, and in calibrating machine-based measures of Kt/V to measures derived from the blood measured URR. The D2 equation gives results similar to the two-blood sample method of modeling spKt/V described by Depner and Cheer [4] (Daugirdas, Depner, unpublished information) provided that the modeling day is the midweek session after a 2-day preceding interdialysis interval (PIDI). The D2 equation has not been evaluated when blood samples are drawn during the first-of-the-week dialysis after a 3-day PIDI, e.g. on a Monday or Tuesday. More importantly, the D2 equation has not been evaluated for dialysis schedules other than 3/week.

When evaluating adequacy of hemodialysis schedules other than three times per week, the treatment Kt/V is an insufficient measure of outcome, as it does not reflect the greater or lesser amount of dialysis being delivered due to more or fewer treatments per week. For such schedules, use of the so-called ‘standard Kt/V’ (stdKt/V) to ensure minimum adequacy has been recommended [1]. Standard Kt/V is defined as the modeled urea nitrogen generation rate (g) in mg/min divided by the average pre-dialysis BUN, multiplied by 10 080 and divided by V [5]. Standard Kt/V (per week) can be calculated directly using urea modeling [5] or it can be estimated from equilibrated treatment Kt/V [6–8], session length and number of treatment per week by an equation proposed by Leypoldt [9] or by an equation developed by the Frequent Hemodialysis Network (FHN) [10], which accounts for volume changes and gives values for stdKt/V that are ∼7% higher than the Leypoldt estimate. The FHN equation-estimated stdKt/V closely matches the value derived from the formal two-pool kinetic modeling [10].

For other than 3/week dialysis schedules, KDOQI proposed a minimum value of 2.0 for stdKt/V estimated using the Leypoldt equation [1], which translates into a minimum value of 2.14 for stdKt/V calculated by formal two-pool modeling or estimated using the FHN equation [10]. Before a non-modeling approach to computing stdKt/V can be accepted, the validity of the estimating equation-based approach to calculate treatment Kt/V for these novel dialysis schedules needs to be validated. This is the purpose of the present paper.

MATERIALS AND METHODS

Preliminary work showed that the D2 equation predicted spKt/V for 3/week schedules quite well but that spKt/V was substantially underestimated when dialysis was given more often than three times per week. To better understand the problem, we simulated dialysis schedules where two to seven treatments were being given per week to patients with a urea distribution volume (V) of 35 L and urea generation rates, g of 3, 5 or 7 mg/min. Session lengths ranged from 120 to 420 min, and dialyzer urea clearances ranged from 160 to 300 mL/min. For these simulations, the two-pool model used was based on two storage pools for urea, the proximal pool being one-third of the total distribution volume (V) and the distal pool being two-thirds of V [11]. All fluid removed or added to the body during the week was assumed to be added to the proximal urea pool (presumed extracellular water space). The intercompartmental transfer clearance between these two pools was assumed to vary with body size and was set so it would be equal in milliliters per minute to 16 times V measured in liters [11]. Rather than starting with values of pre- and post-dialysis BUN, we began with input values for V (35 L), g and the weekly fluid removal rate (0.1–14 L/week). We then used numerical integration methods to generate minute-by-minute weekly BUN concentration profiles over sequential weeks until the profiles stabilized. From the weekly concentration BUN profile, one could then retrieve projected values for pre- and post-dialysis BUN for every dialysis day of the week. These projected BUN values were then used to compute single-pool Kt/V (spKt/V) using the Depner and Cheer modeling approach [4]. We then compared these modeled values of spKt/V with the D2 estimate of spKt/V using both the originally proposed ‘g-factor’ or GFAC value of 0.008 and new values for GFAC optimized by number of treatments per week and length of the PIDI in days, where PIDI was calculated from the beginning of the preceding dialysis to the start time of the modeled session.

Finally, we tested the ability of both the original D2 equation and the revised equation using the schedule- and PIDI-optimized values for GFAC to predict spKt/V in subjects enrolled in the FHN Trials [12, 13] who were undergoing dialysis three, four or six times per week. The two FHN trials examined intermediate outcomes after changing from conventional 3/week dialysis to 6/week schedules. In the FHN Daily Trial [12], the average 6/week session length was 150 min, whereas in the Nocturnal Trial [13], it was 390 min. Data were also available in patients undergoing nocturnal dialysis four times per week, as not all patients randomized to 6/week nocturnal treatment were compliant with the assigned number of treatments per week. For these analyses, we excluded patients with residual renal function >2.0 mL/min and assumed residual renal function to be zero.

RESULTS

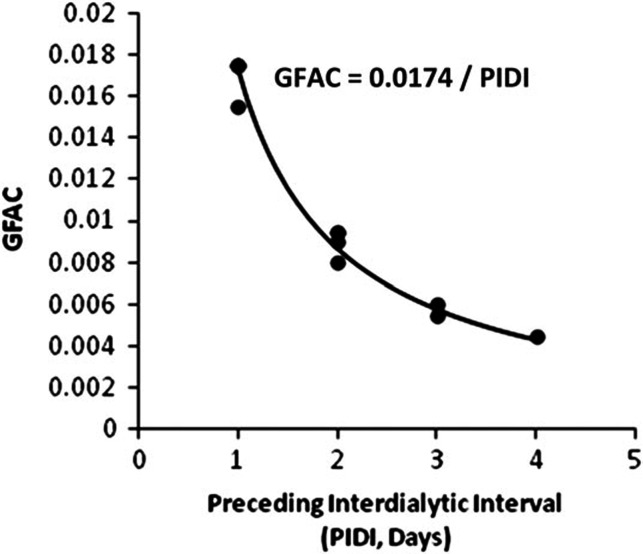
Optimized values for GFAC based on number of treatments per week for different PIDI are shown in Table 1. As shown in Figure 1, GFAC was primarily dependent on PIDI and could be roughly estimated as 0.0174 divided by PIDI in days. Dialysis frequency (F, number of treatments per week) had a lesser impact, but the optimum value for GFAC was obtained after adjusting for both PIDI and F.

Table 1.

Simulation-derived values for the GFAC term

	PIDI (days)
	1	2	3	4
2/week			0.0055	0.0045
3/week		0.0080	0.0060
4/week	0.0155	0.0090
5/weeka	0.0175	0.0095
6/weeka	0.0175	0.0095
7/weeka	0.0175	0.0175

^aWhen dialysis session length was >300 min, a slightly higher (e.g. +0.0010) GFAC value gave better results (with PIDI values of 1 or 2).

FIGURE 1:

Plot of GFAC term in the D2 equation versus length of the PIDI (in days) based on simulated modeling sessions as described in the text.

Comparison of D2-predicted treatment Kt/V with modeled Kt/V in the FHN patients studied is shown in Table 2. For 541 ‘conventional’ dialysis sessions delivered three times per week, the D2 equation using a GFAC value of 0.008 predicted the modeled spKt/V with a mean error of only 0.067 ± 1.0%. However, the unmodified D2 equation substantially underestimated spKt/V for 6/week ‘daily’ dialysis (Table 2), where the mean error was −5.0 ± 1.9%, and for 6/week long nocturnal dialysis, where the mean error was −13 ± 8.8%. In patients in the FHN Nocturnal trial dialyzed only four times per week, the unmodified D2 equation also underestimated spKt/V with a mean error of −8.9 ± 9.3%. As shown in Table 2, changing GFAC from 0.008 to the frequency and PIDI-specific coefficients shown in Table 1 markedly improved the spKt/V estimate. When using the simpler, frequency-independent PIDI-corrected value of GFAC (GFAC = 0.0174/PIDI), the errors in spKt/V were only slightly higher for the 4/week and 6/week schedules tested (Table 2).

Table 2.

Modeled versus estimated spKt/V

	3/wk_conv (nd = 541)	6/wk_day (nd = 687)	6/wk noc (nd = 120)	4/wk noc (nd = 18)
Time (min)	221 ± 33	147 ± 21	419 ± 37	430 ± 56
Kd (mL/min)	264 ± 29	274 ± 27	167 ± 20	185 ± 33
Modeled two-pool V (L)	37.3 ± 9.6	36.3 ± 9.5	41.0 ± 14	38.9 ± 15
Modeled spKt/V	1.59 ± 0.29	1.20 ± 0.22	1.87 ± 0.64	2.24 ± 0.80
Estimated spKt/V GFAC = 0.008	1.59 ± 0.29	1.14 ± 0.22	1.60 ± 0.50	2.01 ± 0.66
Estimated spKt/V GFAC adjusted for both F and PIDIa	1.58 ± 0.29	1.19 ± 0.26	1.87 ± 0.73	2.25 ± 0.82
Estimated spKt/V GFAC = 0.0174/PIDI)	1.59 ± 0.30	1.19 ± 0.22	1.85 ± 0.72	2.33 ± 0.92

^aAdjustment for F (number of treatments per week) and PIDI (days): GFAC = 0.008 (3/2); 0.006 (3/3); 0.0095 (6/2); 0.0175 (6/1); 0.009 (4/2); 0.0155 (4/1). Of the 6/week dialyses, 535 had PIDI = 1 and 272 PIDI = 2; of the 3/week dialyses, 387 had PIDI = 2 and 154 PIDI = 3; of the 4/week dialyses, 8 had PIDI = 1 and 10 had PIDI = 2; nd, no. of dialyses; conv, conventional; noc, nocturnal.

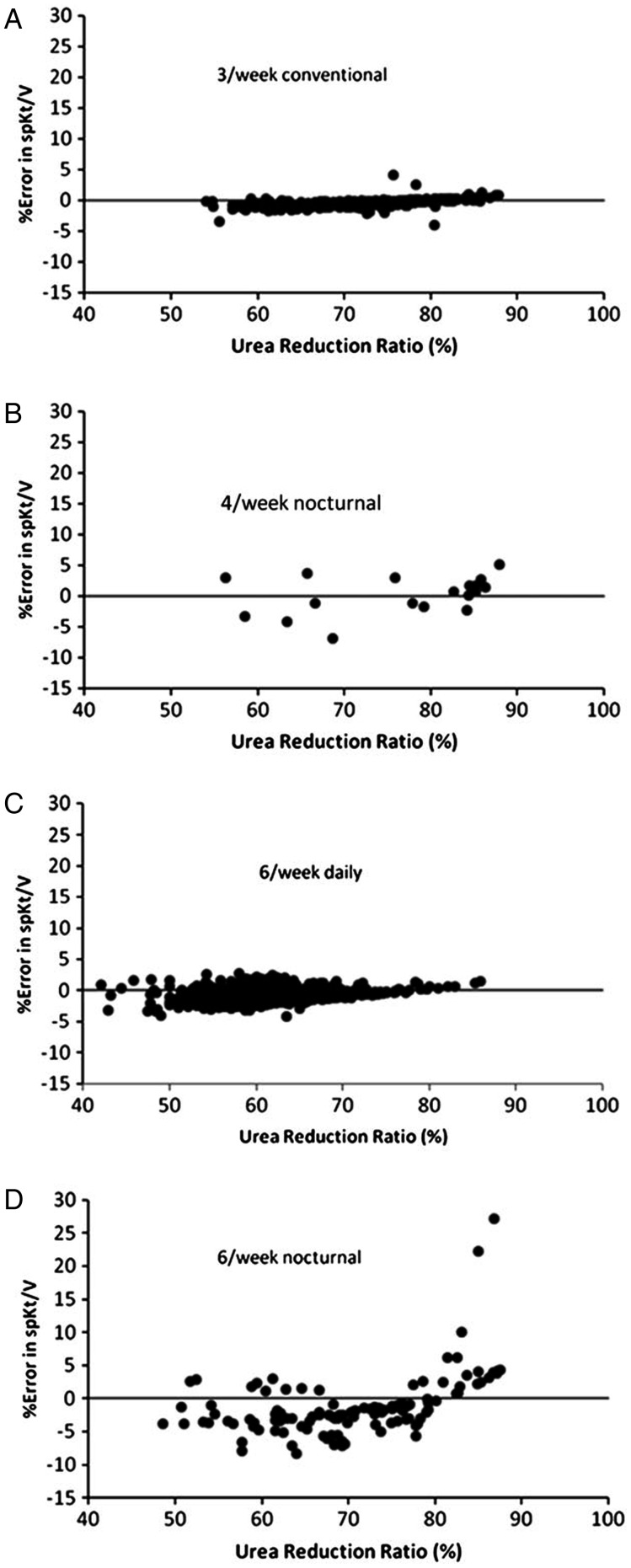
Figure 2 shows the URR plotted against the percent error in treatment spKt/V calculated according to the D2 equation using the schedule- and PIDI-optimized GFAC values shown in Table 1. The errors were under 10% except for two outliers in the 6/week nocturnal group. In these two cases, the URR values were 83 and 85%, respectively, and they had a very low ratio of modeled to anthropometric (Watson) volume, 0.32 and 0.37, respectively (normally this ratio should be ∼0.9). The modeled spKt/V values in these two outlier patients were quite high, 3.97 and 3.89, respectively. Previous modeling work showed that the D2 approach to calculating spKt/V begins to overestimate spKt/V markedly at very high values of URR, e.g. when URR >88%. These outliers suggest that for long nocturnal dialysis, D2 should not be used to estimate spKt/V when the URR is >82%.

FIGURE 2:

Percent error in estimated spKt/V using the D2 equation and the frequency and PIDI-specific GFAC values shown in Table 1. Each dialysis schedule is plotted as a separate graph.

A third level of GFAC optimization might be to take into account the dialysis session length. Modeling suggested that for 5–7/week dialysis, when dialysis session length was >300 min, the optimum GFAC values were slightly higher (by 0.0010) than those shown in Table 1. Accordingly, the optimum GFAC values for subjects undergoing 6/week long nocturnal dialysis would be 0.0185 and 0.0105 when the PIDI are 1 and 2 days, respectively.

In the Supplemental material, in Figure 3A through D, we plot the percent error in spKt/V against weight loss, while using schedule- and PIDI-optimized values for GFAC as per Table 1. These results corroborated findings from simulations that the volume contraction term of the original D2 equation would be unlikely to benefit from further adjustment based on dialysis frequency or PIDI.

DISCUSSION

Our results suggest that the accuracy of the original D2 equation can be improved for dialysis schedules other than 3/week by applying the frequency and PIDI-dependent GFAC values shown in Table 1. Acceptable accuracy can also be obtained by approximating GFAC as 0.0174/PIDI. The procedure to estimate stdKt/V would be as follows: (i) compute estimated treatment spKt/V using the D2 equation with schedule and frequency (and perhaps session length) optimized values for GFAC, (ii) compute eKt/V from spKt/V and dialysis session length using the optimized Tattersall equation [6, 1] and (iii) from eKt/V, session length and treatments per week, compute stdKt/V using the FHN equation [10]. It should be noted that these improvements to the D2 equation were determined for typical hemodialysis prescriptions during the FHN trial and the accuracy of these improvements may not apply if the prescription deviates substantially from those evaluated here. When more exact values are required, values for stdKt/V can be calculated directly using formal kinetic modeling [11].

SUPPLEMENTARY DATA

Supplementary data are available online at http://ndt.oxfordjournals.org.

CONFLICT OF INTEREST STATEMENT

JK Leypoldt and A Akonur are employees of Baxter Healthcare Corporation. (See related article by Tattersall. Do we need another Kt/V? Nephrol Dial Transplant 2013; 28: 1963–1966.)