Investigating Factorial Invariance of Latent Variables Across Populations When Manifest Variables Are Missing Completely

Abstract

Difficulties arise in multiple-group evaluations of factorial invariance if particular manifest variables are missing completely in certain groups. Ad hoc analytic alternatives can be used in such situations (e.g., deleting manifest variables), but some common approaches, such as multiple imputation, are not viable. At least 3 solutions to this problem are viable: analyzing differing sets of variables across groups, using pattern mixture approaches, and a new method using random number generation. The latter solution, proposed in this article, is to generate pseudo-random normal deviates for all observations for manifest variables that are missing completely in a given sample and then to specify multiple-group models in a way that respects the random nature of these values. An empirical example is presented in detail comparing the 3 approaches. The proposed solution can enable quantitative comparisons at the latent variable level between groups using programs that require the same number of manifest variables in each group.

Structural equation modeling (SEM) has become the method of choice to answer many important questions in psychological research. The range of models proposed thus far—including confirmatory factor analysis (CFA) models (Jöreskog, 1969, 1971), test theory models (Jöreskog, 1974), latent variable structural models (Bentler & Speckart, 1979; Jöreskog, 1974), and longitudinal models using latent growth factors or latent difference scores (McArdle, 1988, 2001; McArdle & Epstein, 1987; McArdle & Hamagami, 2001; Meredith & Tisak, 1984, 1990)—is remarkable, and new models extending the basic framework are published with regularity.

Especially useful are multiple-group models that enable investigations of similarities and differences across groups in key parameters of interest. Establishing factorial invariance of measurement model parameters across groups provides putative evidence that the same underlying constructs are present in different groups (Horn, McArdle, & Mason, 1983; Meredith, 1964a, 1964b, 1993; Widaman & Reise, 1997). Once a sufficient level of factorial invariance is achieved, researchers can concentrate on other parameters of interest, such as group differences in latent variable means, variances, or the magnitude of directed relations among latent variables. One consistent goal of science is to replicate and extend prior research findings, and multiple-group SEM is a sophisticated, state-of-the-art method for social science researchers to pursue this goal by enabling quantitative comparisons across groups.

One of the more useful, recent developments in estimation techniques for SEM is full information maximum likelihood (FIML) estimation in the presence of missing data (Arbuckle, 1996). Under FIML estimation, structural models are fit directly to the raw data matrix, rather than to summary matrices such as correlation or covariance matrices. FIML estimation uses all available data values for all observations and builds up estimates of parameters and their standard errors from all data values present in all observations. Thus, FIML estimation can achieve estimates of model parameters when some values are missing for a given observation and does not require deletion of observations with missing values (i.e., listwise deletion), as is required under traditional maximum likelihood (ML) estimation. Monte Carlo studies have verified that FIML estimation is more efficient and less biased than traditional methods—such as ML estimation of complete-data observations (i.e., data sets derived after listwise deletion of observations with missing values)—if missing values are missing at random or missing completely at random; indeed, FIML estimation might be the optimal approach even if data are missing not at random (Arbuckle, 1996; Muthén, Kaplan, & Hollis, 1987).

One circumstance that poses a problem for structural modeling, particularly under FIML estimation, is the case of multiple-group analyses in which certain manifest variables are missing completely in particular groups. Many standard programs for SEM (e.g., LISREL; Jöreskog & Sörbom, 1996) require that all groups in a multiple-group analysis have the same number of manifest variables. When collating measures for analysis across multiple samples from different studies, the manifest variables of interest for a particular group include manifest variables present (MVP) and manifest variables missing completely (MVMC) in the research protocol for that group. To move forward with analyses using such structural modeling programs, each manifest variable in each group must exhibit variability in observed scores. If one or more manifest variables were not measured in a particular group, all data values on this variable are missing completely within the group. If a manifest variable in a given group contains either constant values (i.e., no variability) or completely missing values, the manifest variable covariance matrix is singular and has no inverse, so statistical analyses under FIML estimation cannot proceed.

If certain manifest variables were assessed in some groups but not in others and one is using a program requiring the same manifest variables be present in each group, at least three analytic approaches might initially be considered for circumventing the MVMC problem: imputation, manifest variable deletion, and conceptual replication. Imputation involves replacing missing values with representative values that preserve patterns of relations among manifest variables (Dempster, Laird, & Rubin, 1977; Little & Rubin, 1987; Rubin, 1976, 1996). Typically, researchers generate between 5 and 10 data sets, each with different sets of imputed values in place of missing values. Analyses are then performed separately on each data set, and parameter estimates and their standard errors are summarized across data sets. In multiple-group data, imputations are typically performed within each group, to ensure accurate representation of relations among variables within the group (Allison, 2002; Enders & Gottschall, 2009). However, within-group imputation requires at least some information within the group regarding relations among variables for which imputed values are generated. If all values on a given manifest variable are missing for a particular group (e.g., because the manifest variable was not part of the study protocol), no information is available within the group concerning the relation of the given manifest variable with other manifest variables. An imputation algorithm would have no basis for generating representative values on any manifest variable that was missing completely in a particular group, so within-group imputation is not a viable option.

An alternative imputation option is to place all groups into a single data set and perform the imputations on this “total sample” data set (Enders & Gottschall, 2009). This analysis could “borrow strength” from the multiple groups, using information about relations among variables across all groups to guide the imputation algorithm when estimating representative values for any manifest variable that was missing completely in a given group. But, if the goal of subsequent analyses was to evaluate factorial invariance across groups, this form of imputation would generate imputed values biased in favor of exhibiting factorial invariance as relations among manifest variables from other groups would be used to generate imputed values in a group for which a manifest variable was missing completely (cf. Enders & Gottschall, 2009). To combat such potential bias, some experts recommend generating dummy variables to represent groups and including these dummy variables and products of these dummy variables with manifest variables (which function as interaction vectors) as an alternative to within-group imputation (Allison, 2002; Enders & Gottschall, 2009). For any group with at least one manifest variable missing completely, the corresponding product or interaction vector would contain no information in that group, so this form of imputation would also fail. The upshot is that neither within-group nor “total sample” imputation is a viable option.

The second approach to the MVMC problem is manifest variable deletion, or deleting those manifest variables from multiple-group analyses that were missing completely in any of the groups in the analysis. This analytic approach results in analyses that are based on a reduced set of variables, but ensures presence of the same set of manifest variables in each group. Although this approach appears to yield an acceptable solution, at least two problems could arise. First, deleting key manifest variables from analyses might lead to latent variables that do not meet common specifications for a particular latent variable. For example, if a given manifest variable (e.g., Raven’s Standard Progressive Matrices) is often used as the central indicator of a particular latent variable (e.g., fluid intelligence), but that manifest variable was not included in the protocol of one or more groups, then deleting the key manifest variable from all analyses would lead to a latent variable that was missing an important indicator. Second, cases could arise in which no single manifest variable for a particular latent variable was included in the protocol in all groups. In such situations, manifest variable deletion would result in the elimination of the associated latent variable, and this would likely be an unacceptable option.

A third approach to the MVMC problem is conceptual replication, or the performing of parallel sets of analyses across groups, using whichever manifest variables are available in each group, although the sets of manifest variables then differ across groups. Using this approach, one might collate findings across groups, arguing that similar patterns of influence hold across groups. Hofer and Piccinin (2009) recently provided a strong argument in favor of a sophisticated form of conceptual replication, proposing ways of ensuring optimal similarity, if not identity, of measurement and analysis procedures across studies. Of course, if manifest variables differ across groups, strong statements about similarities or differences across groups cannot be made, because factorial invariance across groups cannot be specified or tested. Thus, conceptual replication, although useful, is not a viable option for strict testing of differences across groups in model parameters.

The goal of this article is to compare three approaches to the MVMC problem that enable researchers to proceed with multiple-group analyses, test hypotheses related to factorial invariance, and proceed to tests of key theoretical hypotheses. In the rest of this article, we first describe an empirical research application that embodies the problem of MVMC. We then present results of analyses under three alternative approaches to dealing with the problem, comparing results under the three approaches. We close with recommendations for research and practice.

A MOTIVATING EXAMPLE

Consider the following research situation: Prior research has shown that economic pressure on the family has a number of negative influences, including associations with higher levels of depression in fathers and mothers, higher marital conflict, lower levels of positive parenting behaviors, and lower levels of child developmental outcomes (see Conger & Donnellan, 2007, for a review). However, much of the prior research on detrimental influences of family economic pressure has been conducted on European American families. Because theories regarding cultural influences on family processes and child development suggest that the patterning of relations among family process variables might differ across ethnic groups (Parke et al., 2004), researchers should not assume that research findings from European American families will generalize to families of different ethnic origins. Instead, investigators should seek to establish whether relations of similar magnitude hold across different ethnic groups.

We had access to data on participants from three ethnic groups living in the United States and wanted to test whether economic pressure was related to father and mother depression in similar ways across groups. The three groups were obtained from the following studies: (a) the Family and Community Health Study (FACHS), a study of 889 African American children and their families; (b) the California Families Project (CFP), a study of 327 Mexican-origin families and children; and (c) the Iowa Youth and Families Project (IYFP), a study of 451 European American children and families. Because we were testing the influence of economic pressure on both mothers and fathers, we focused on two-parent families, yielding 428 families from the FACHS study, 262 families from the CFP study, and 385 families from the IYFP study, for a total of 1,075 families across the three groups.

The first latent variable in our study was economic pressure. All three studies included the same three indicators of economic pressure, consisting of: (a) unmet material needs (U), the average of four items assessing unmet material needs in different domains, including “having enough money to afford the kind of home, clothing and food your family needs” (response scale 1 = strongly agree to 4 = strongly disagree); (b) can’t make ends meet (C), the average of two items measuring difficulties in having money to cover expenses, including “difficulty paying bills” and “the amount of money left at the end of the month” (response scale: 1 = no difficulty at all to 4 = a great deal of difficulty; 1 = more than enough money left over to 4 = not enough to make ends meet); and (c) financial cutbacks (F), the number of 11 areas in which the family had to make cutbacks, including “the family postponing major household purchases, changing residence, and or eliminating medical insurance” (each area scored dichotomously, 0 = no cutbacks, 1 = cutbacks). Fathers and mothers provided responses on the preceding scales. Consistent with prior research (e.g., Conger & Donnellan, 2007), average responses across fathers and mothers were used as analyzed scores. For families in which fathers did not participate, scores on economic pressure variables were treated as missing data. Scores on all three indicators were reverse-scored when necessary so that higher scores indicated greater economic pressure on the family.

The remaining two latent variables to be studied were father depression and mother depression. Across the three studies, two scales were used to assess father and mother depression. One scale was the General Distress Depression subscale from the Mini-Mood and Anxiety Symptom Questionnaire (Mini-MASQ; Clark & Watson, 1991; Casillas & Clark, 2001), consisting of five items, each answered on a scale ranging from 1 (not at all) to 4 (extremely). The second scale was a 10-item short form of the Center for Epidemiological Studies Depression scale (CES–D; Radloff, 1977), with responses falling on a scale ranging from 1 (almost never or never) to 4 (almost always or always). Two parcels (one two-item and one three-item parcel) were formed from the Mini-MASQ, and these are denoted M1F, M2F, M1M, and M2M for Mini-MASQ Parcels 1 and 2 from father and mother, respectively. Two parcels (two five-item parcels) were formed from the CES–D scale items, and these parcels are termed C1F, C2F, C1M, and C2M for CES–D Parcels 1 and 2 for father and mother, respectively. Thus, the data to be analyzed consist of 11 manifest variables: (a) three indicators of economic pressure (U, C, and F), (b) four indicators of father depression (M1F, M2F, C1F, and C2F), and (c) four indicators of mother depression (M1M, M2M, C1M, and C2M).

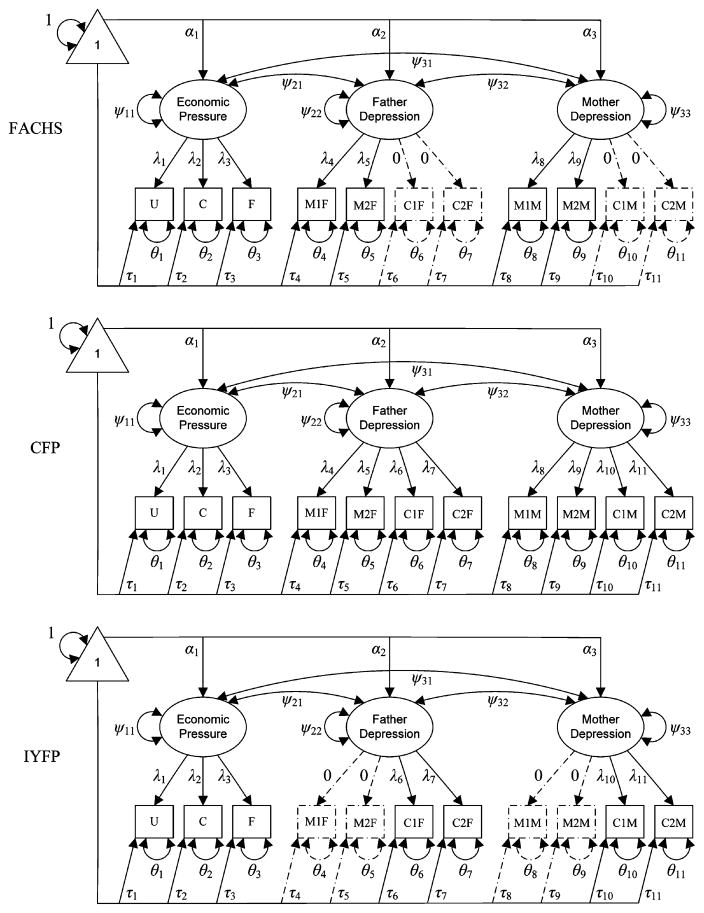
Figure 1 shows confirmatory factor models containing 11 manifest variables and three latent variables for each of the three groups. In Figure 1, standard notation is used: Triangles denote the unit constant used to estimate means or intercepts, squares or rectangles represent manifest variables, circles or ellipses stand for latent variables, single-headed arrows denote directed effects (e.g., factor loadings, regression weights), and double-headed arrows represent variances or covariances. Solid lines represent observed manifest variables and all related latent variables and parameter estimates. Dashed lines denote manifest variables that are missing completely (i.e., MVMC) in a given sample, along with related parameters for these manifest variables.

FIGURE 1.

Figural representation of three-factor confirmatory factor model in each of three groups: Family and Community Health Study (FACHS), California Families Project (CFP), and Iowa Youth and Families Project (IYFP), with dashed lines associated with manifest variables missing completely. Note. U = unmet material needs; C = can’t make ends meet; F = financial cutbacks; M1F and M2F = Mini-MASQ Parcels 1 and 2 father report, respectively; C1F and C2F = CES–D Parcels 1 and 2 father report, respectively; M1M and M2M = Mini-MASQ Parcels 1 and 2 mother report, respectively; C1M and C2M = CES–D Parcels 1 and 2 mother report, respectively.

In Figure 1, common denotations are used for parameters. Specifically, τ_j (j = 1, …, 11) represents the measurement intercept for manifest variable j, λ_j denotes the loading of variable j on its corresponding latent variable, θ_j represents unique factor variance for variable j, ψ_kk(k = 1, …, 3) represents the factor variance for latent variable k, ψ_kk′ (k ≠ k′)denotes the covariance between latent variables k and k′, and α_k represents the factor mean for latent variable k. As a result, the measurement model equation for each of the 11 manifest variables in Figure 1 can be written as:

$$Y_j={\tau }_j+{\lambda }_j\eta +{\epsilon }_j,$$ (1)

where ε_j is the unique factor for Y_j, and other symbols were defined earlier. Unique factor scores cannot be estimated directly, so only the variance of ε_j, labeled θ_j, is estimated, as shown in Figure 1.

As shown in Figure 1, the CES–D was not administered in the FACHS study, so the CES–D parcels were MVMC in this sample. In the IYFP, the Mini-MASQ was not administered, so Mini-MASQ parcels were MVMC for the IYFP sample. The CFP study protocol employed both the Mini-MASQ and the CES–D, so all 11 manifest variables were measured in the CFP study. However, we note that, within each study, data were not complete.

As noted earlier, imputation is not a viable option for the data structure represented by Figure 1 because certain variables are MVMC in one or another group, leaving two remaining analytic approaches. The manifest variable deletion approach is also not viable in this case. Because CES–D parcels were MVMC in the FACHS study and Mini-MASQ parcels were MVMC in the IYFP sample, all depression parcel scores shown in Figure 1 would be deleted if one deleted all MVMC in any sample, precluding any analyses related to depression. Finally, taking the conceptual replication approach, a researcher could compare the FACHS and CFP samples based on Mini-MASQ scores and could separately compare the CFP and IYFP samples based on CES–D scores, but the researcher would be unable to compare results quantitatively across the preceding sets of analyses, because comparability of the metrics of scores on depression latent variables defined by Mini-MASQ and CES–D parcels could not be ensured. Further, no comparisons could be made between the FACHS and IYFP samples due to the mismatching sets of manifest variables related to depression in these samples. What is needed is an approach to the MVMC problem that uses all available observations and variables in each group and can implement quantitative comparisons across all groups, thereby testing strongly the theoretical models under consideration.

Solution 1: Use a Program That Can Handle MVMC

The first solution to the MVMC problem is to use a program, such as EQS¹ (Bentler & Wu, 1996), that can handle differing numbers of manifest variables in each sample. The clear advantage of this approach is that the resulting solution yields the maximum likelihood solution when fitting a model to data, and the MVMC have no influence on the solution. However, we note that EQS is the only program of which we are aware that is able to fit multiple group models with differing numbers of manifest variables. Thus, this might not be a reasonable solution if other SEM programs are utilized (e.g., LISREL).

Solution 2: Use Pattern Mixture Procedures With Known Groups

A second solution is to use the Pattern Mixture Procedure with Known Groups available in certain programs, such as Mplus (Muthén & Muthén, 2007).² The Pattern Mixture Procedure utilizes the mixture modeling framework for specification and estimation, but treats class membership as known. Thus, the probability of class membership is treated as observed and based on the grouping variable. The logic behind this solution is that, in mixture modeling, one class of individuals might have MVMC. This approach circumvents the need to have the same variables measured in each group. This approach is not without limitations, however. Similar to Solution 1, this option is not widely available. Also, when utilizing this approach, absolute and global indexes of model fit (e.g., comparative fit index [CFI], root mean square error of approximation [RMSEA]) are not provided. Of course, these indexes could be calculated post-hoc by first estimating the saturated (e.g., means, variances, and covariances) model separately for each group, calculating the chi-square statistic, and then calculating each fit index. Additionally, the fitting of the pattern mixture model is not straightforward. The model is fit according to Figure 1; however, dotted paths are fixed to 0 in each known class, with the exception of the dotted residual variances, which were fixed at a small positive value (e.g., .01).

Solution 3: Generate Random Data for MVMC

A third solution to the MVMC problem, proposed here, is the following two-step procedure: (a) generate random normal deviates for all observations (i.e., persons) in a given sample for all MVMC in that sample, and (b) proceed with model specification and testing in a fashion that respects, or is consistent with, the random nature of the generated scores.³

The first step is the generation of random normal deviates (i.e., pseudo-random numbers from a population that is normally distributed with M = 0 and SD = 1) for all observations on MVMC in a given sample. In the population, a given random variate Y_j has a mean of 0 (μ_j = 0), standard deviation (SD) of unity (σ_j = 1), and correlations of zero (ρ_jj′ = 0) with all other variables Y_j′. In any finite sample, these population values would not be observed, as sample estimates would depart from population parameters due to sampling variability. However, as sample size increases, sample statistics should converge on population values, so the mean of Y_j should approach zero (as N → ∞, E(Y_i) → 0), the variance and, hence, the SD of Y_j should approach unity (as N → ∞, E[(Y_i − Ȳ)²] → 1), and correlations of Y_j with all other manifest variables Y_j′ should approach zero (as N → ∞, E(r_jj′ → 0)), where E is the expected value operator.

The preceding characteristics of random normal deviates have implications for proper model specification. For a manifest variable Y_j that is missing completely in a given sample and therefore has its missing values replaced by random normal deviates, the model specification should be:

1. Its intercept τ_j should be freely estimated in all structural models.

2. Its factor loading, λ_j, should be fixed at 0 in all structural models.

3. Its unique factor variance, θ_j, and the covariances of its unique factor with unique factors for all other manifest variables Y_j′, θ_jj′, should be freely estimated in all structural models.

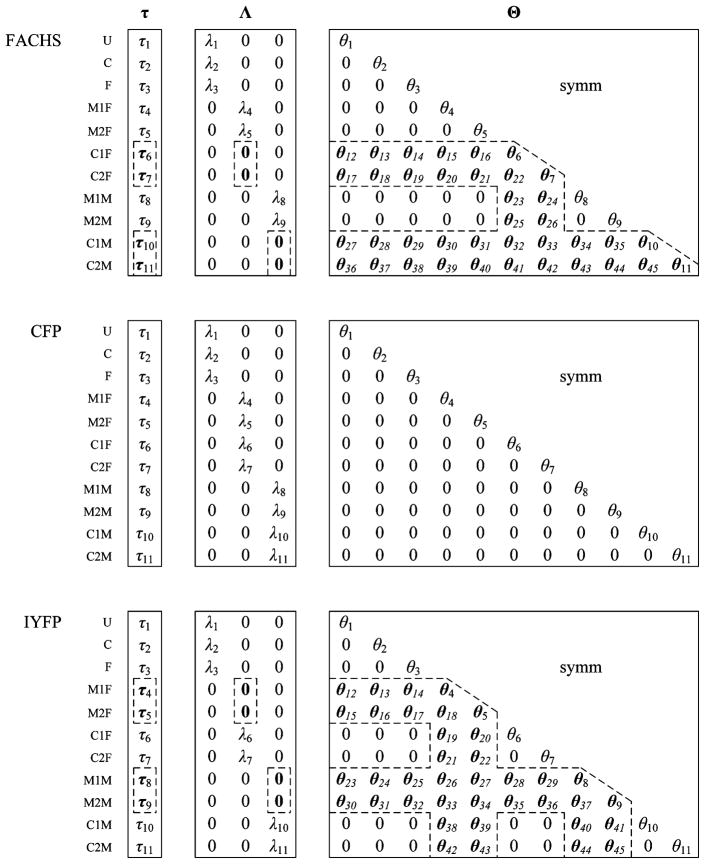
Model specifications noted here are shown for the current problem in Figure 2, where all parameters enclosed in dashed lines are associated with MVMC. In the FACHS sample, these parameters are associated with CES–D parcels and include (a) intercepts τ₆, τ₇, τ₁₀, and τ₁₁; (b) corresponding factor loadings, shown as fixed at zero; and (c) unique factor variances θ₆, θ₇, θ₁₀, and θ₁₁, and unique factor covariances θ₁₂ through θ₄₅. In the CFP, no manifest variables are MVMC, so no parameters are contained in dashed lines. In the IYFP sample, the four parcels derived from the MASQ are shown within dashed lines, and these include (a) intercepts τ₄, τ₅, τ₈, and τ₉; (b) corresponding factor loadings, shown as fixed at zero; and (c) unique factor variances θ₄, θ₅, θ₈, and θ₉, and unique factor covariances θ₁₂ through θ₄₅. All parameters associated with MVMC should be freely estimated with no constraints across groups in any models. If this is done, the number of parameter estimates associated with MVMC will be equal to the number of new sample statistics (i.e., means, variances, and covariances) associated with these variables. The degrees of freedom (df) reported by the program will be correct, based on the sample statistics and number of parameters for MVP across samples. Analyses can then proceed with cross-group constraints on parameter estimates associated with manifest variables that were assessed in common across each pair of samples. Specifics with regard to these details of specification are illustrated next.

FIGURE 2.

Schematic representation of the intercept vector τ, factor loading matrix Λ, and unique factor covariance matrix Θ for the Family and Community Health Study (FACHS), California Families Project (CFP), and Iowa Youth and Families Project (IYFP) studies. Note. U = unmet material needs; C = can’t make ends meet; F = financial cutbacks; M1F and M2F = Mini-MASQ Parcels 1 and 2 father report, respectively; C1F and C2F = CES–D Parcels 1 and 2 father report, respectively; M1M and M2M = Mini-MASQ Parcels 1 and 2 mother report, respectively; and C1M and C2M = CES–D Parcels 1 and 2 mother report, respectively.

Our proposed solution might lead to potential bias in model fit and in obtained parameter estimates when incomplete data are present within each group to the extent that the pseudo-random values generated for MVMC display sample estimates of mean and covariance with other variables that depart from population values. Assume the presence of a covariance or moment structure model for a set of manifest variables that yields model-based estimates of the population mean vector μ and covariance matrix Σ. Under FIML estimation, the function to be minimized, F, can be written

$$F=\sum _{i=1}^{N}log\mid {\mathbf{\sum }}_i\mid +\sum _{i=1}^N{({\mathbf{y}}_i-{\mathbf{\mu }}_i)}^{\prime }{\mathbf{\sum }}_i^{-1}({\mathbf{y}}_i-{\mathbf{\mu }}_i),$$ (2)

where y_i is the vector of scores observed for observation i (i.e., deleting manifest variables for observation i that contain missing values), μ_i is the corresponding population mean vector, and Σ_i is the covariance matrix among manifest variables deleting rows and columns associated with missing values for observation i. To invoke Equation 2, model-based estimates of μ and Σ based on sample data are utilized in the equation. Thus, if the means and variances of MVMC depart from 0.0 and 1.0 and the correlations of MVMC with MVP depart from zero—as would be expected under sampling, these sample values for the MVMC would affect model-based estimates of μ and Σ for all manifest variables if the MVP also contained some missing values. If this were to occur, somewhat different estimates of model fit or estimates of model parameters might be obtained when MVMC are included in an analysis compared with when MVMC were deleted from the analysis. Investigating the magnitude of these forms of potential bias is a task for this project.

RESULTS

Descriptive statistics and the correlations among manifest variables for each of the three samples are shown in Table 1. Statistics shown in Table 1 are ML estimates based on FIML estimation in the presence of missing data, and sample sizes with data on each variable are shown in the first data column of the table. The results of data analyses are presented in four major sections including a description of results from fitting separate factor models to each sample, and descriptions of testing for factorial invariance utilizing the three solutions discussed earlier.

TABLE 1.

Descriptive Statistics and Correlations Among 11 Manifest Variables for Three Samples of Participants

Manifest Variable	Participant	Descriptives			Correlations
		N	M	SD	U	C	F	M1F	M2F	C1F	C2F	M1M	M2M	C1F	C2F
FACHS study
U	Couple	310	2.08	0.54	1.00
C	Couple	310	2.16	0.62	.601	1.00
F	Couple	301	0.12	0.14	.426	.528	1.00
M1F	Father	311	1.45	0.62	.234	.336	.266	1.00
M2F	Father	311	1.14	0.45	.289	.337	.274	.763	1.00
C1F	Father	428	−0.06	1.00	−.078	.032	−.014	.009	−.014	1.00
C2F	Father	428	−0.01	0.97	.065	−.043	−.033	.055	−.014	−.041	1.00
M1M	Mother	428	1.53	0.59	.275	.340	.219	.156	.168	−.070	.026	1.00
M2M	Mother	428	1.17	0.47	.213	.331	.176	.123	.103	.021	.062	.652	1.00
C1F	Mother	428	−0.03	1.02	.158	.025	.012	.058	.038	−.027	−.001	−.099	−.120	1.00
C2F	Mother	428	0.04	1.01	.056	.013	.015	−.035	−.044	.017	−.032	−.059	−.040	−.034	1.00
CFP study
U	Couple	182	2.23	0.63	1.00
C	Couple	182	2.33	0.65	.667	1.00
F	Couple	181	0.17	0.17	.609	.663	1.00
M1F	Father	178	1.44	0.65	.226	.284	.228	1.00
M2F	Father	178	1.17	0.44	.306	.316	.306	.765	1.00
C1F	Father	177	1.59	0.41	.195	.309	.243	.492	.542	1.00
C2F	Father	178	1.67	0.44	.294	.349	.240	.562	.547	.591	1.00
M1M	Mother	249	1.58	0.71	.220	.280	.228	.286	.254	.238	.123	1.00
M2M	Mother	249	1.22	0.55	.225	.271	.147	.235	.207	.251	.178	.767	1.00
C1M	Mother	241	1.66	0.45	.212	.297	.162	.116	.041	.120	−.011	.602	.569	1.00
C2M	Mother	245	1.68	0.51	.186	.285	.084	.183	.093	.221	.107	.657	.635	.726	1.00
IYFP study
U	Couple	377	2.06	0.53	1.00
C	Couple	377	2.34	0.69	.663	1.00
F	Couple	376	0.16	0.15	.675	.706	1.00
M1F	Father	385	0.02	1.08	−.001	.040	.049	1.00
M2F	Father	385	−0.04	1.05	.054	.039	.052	−.054	1.00
C1F	Father	375	1.36	0.39	.177	.174	.163	.002	.005	1.00
C2F	Father	376	1.40	0.46	.187	.203	.196	−.004	.005	.674	1.00
M1M	Mother	385	−0.04	1.04	.049	.000	.009	−.099	.052	.019	.004	1.00
M2M	Mother	385	0.01	0.97	−.048	−.033	−.069	.017	.102	−.116	−.100	.000	1.00
C1F	Mother	385	1.43	0.43	.064	.082	.073	−.049	−.015	.023	.090	−.048	.021	1.00
C2F	Mother	384	1.46	0.52	.168	.164	.124	−.100	−.001	.099	.153	−.034	−.031	.680	1.00

Note. Tabled values are maximum likelihood estimates of means, standard deviations, and correlations produced by full information maximum likelihood estimation in the presence of missing data. Family and Community Health Study (FACHS) study N = 428 African American families, California Families Project (CFP) study N = 262 Mexican-origin families, and Iowa Youth and Families Project (IYFP) study N = 385 European American families. Boldfaced values are statistics for manifest variables missing completely (MVMC), specifically, the CES–D parcels in the FACHS study and the MASQ parcels in the IYFP study. Manifest variables: U = unmet material needs; C = can’t make ends meet; F = financial cutbacks; M1F and M2F = Mini-MASQ Parcels 1 and 2 father report; C1F and C2F = CES–D Parcels 1 and 2 father report; M1M and M2M = Mini-MASQ Parcels 1 and 2 mother report; C1M and C2M = CES–D Parcels 1 and 2 mother report.

Separate Sample Analyses Excluding MVMC

As a first step in our analyses, we performed a CFA separately in each sample, deleting any MVMC in each sample. Thus, using EQS, we performed CFA analyses on 7 manifest variables for the FACHS and IYFP samples and on 11 manifest variables for the CFP sample. Models were specified as shown in Figure 2, except that the MVMC for each sample were deleted completely from the models. That is, in the FACHS sample, because the CES–D parcels were MVMC, three manifest variables (U, M, & N) were indicators for the economic pressure factors, the two father-report parcels from the MASQ were indicators for father depression, and the two mother-report parcels from the MASQ were indicators for mother depression. In the CFP sample, no variables were MVMC, so the three variables U, M, and N loaded on economic pressure, all four father-report parcels (two from MASQ, two from CES–D) loaded on father depression, and all four mother-report parcels loaded on mother depression. Finally, in the IYFP, the MASQ parcels were MVMC, so the three variables of U, M, and N loaded on economic pressure, the two father-report parcels from the CES–D loaded on father depression, and the two mother-report parcels from the CES–D loaded on mother depression. In each sample, we identified the model by fixing the factor variance to 1.0 and factor mean to 0.0 for each of the three factors.

The resulting fit indexes are listed in the top three lines of Table 2. As can be seen in Table 2, the fit of the CFA model was very good in the FACHS and IYFP samples, with χ² values slightly less than the degrees of freedom for the models and therefore CFI and Tucker–Lewis Index (TLI) values of approximately 1.00 and RMSEA values of .000. The fit of the three-factor CFA model in the CFP sample was slightly worse, with a statistical index of fit that was rejectable at the .05 level, χ²(39, N = 262) = 58.77, p = .02. However, both the CFI and TLI were greater than or equal to 1.00, and the RMSEA was .045, so the fit of the CFA model in the CFP sample was very good. We note one modification to the model in the CFP sample: Two covariances among unique factors were estimated, one between unique factors for the two father-report MASQ parcels (M1F, M2F) and the other between unique factors for the two mother-report MASQ parcels (M1M, M2M). These covariances among unique factors indicate that MASQ parcels share content overlap beyond that reproduced by the specified latent variables, and these covariances among unique factors were estimated on an a priori basis. Comparable covariances among unique factors for CES–D parcels were nonsignificant, so were not included in the final model.

TABLE 2.

Solution 1: EQS Fit Indexes for Alternative Models Using Different Subsets of Variables per Sample

Model	χ2	df	Prob	CFI	TLI	RMSEA [CI]	Δχ2	Δdf
Separate analyses by sample
FACHS (7 manifest variables)	8.57	11	.66	1.000	1.010	.000 [.000, .041]	—	—
CFP (11 manifest variables)	58.77	39	.02	1.000	1.024	.044 [.017, .067]	—	—
IYFP (7 manifest variables)	6.96	11	.80	1.000	1.009	.000 [.000, .035]	—	—
Total	74.30	61
Three-group analyses
Configural invariance	74.32	61	.12	1.000	1.015	.025 [.000, .042]	—	—
Weak factorial invariance	95.81	69	.02	1.000	1.011	.033 [.014, .048]	21.49	8
Strong factorial invariance	139.36	77	< .001	1.000	1.006	.048 [.035, .060]	43.55	8
Strict factorial invariance	256.10	91	< .001	1.000	1.007	.071 [.061, .082]	116.74	14

Note. Family and Community Health Study (FACHS) study N = 428 African American families; California Families Project (CFP) study N = 262 Mexican-origin families; and Iowa Youth and Families Project (IYFP) study N = 385 European American families. CFI = Comparative Fit Index; TLI = Tucker-Lewis Index; RMSEA [CI] = root mean square error of approximation and its associated confidence interval.

Solution 1: Combined Estimation Using Program That Can Handle MVMC

Multiple group factor models were fit using EQS, a program that can handle MVMC, to investigate factorial invariance. Specifically, we examined the set of models of increasing factorial invariance outlined by Widaman and Reise (1997): (a) configural invariance, or the same pattern of fixed and free parameters across groups; (b) weak factorial invariance, adding to the configural invariance model the invariance of factor loadings; (c) strong factorial invariance, adding to the weak invariance model the invariance of intercepts; and (d) strict factorial invariance, adding to the strong invariance model the invariance of unique factor variances.

The configural invariance model was identified in the following fashion, and we refer to certain parameters in Figure 2 when describing model identification. In the FACHS sample, we fixed the factor mean to zero and the factor variance to 1.0 on each of the three factors, which identified all remaining parameter estimates. In the CFP sample, we constrained one factor loading on each factor and the corresponding intercept to be identical to the corresponding values from the FACHS sample. Specifically, we constrained CFP sample factor loadings λ₁, λ₄, and λ₈ and intercepts τ₁, τ₄, and τ₈ to be invariant with values from the FACHS sample, which identified all latent variables in the CFP samples and enabled the estimation of latent variable means and variances in this sample. In the IYFP sample, we again constrained one factor loading per factor and the corresponding intercept to be identical to the corresponding values from a prior sample.

As shown in the bottom half of Table 2, the configural invariance model had quite acceptable fit to the data, both statistically, χ²(61, N = 1,075) = 74.32, p = .12, and practically, with CFI and TLI values over 1.00 and an RMSEA of .025. Comparing fit of the configural model with the total (summed χ² and df) fit information from the three separate analyses, we see a high degree of similarity. Ideally, these values would be identical; however, due to incomplete data within each sample, small differences were found between fit of the three-group configural model and separate fit of the factor model to each group.

The fit of the weak factorial invariance model is shown next in Table 2. The weak invariance model retained very good practical fit indexes, but resulted in a significant increase in statistical fit of the model, Δχ²(8, N = 1,075) = 21.49, p < .005; however, indexes of global and practical fit and the nonexistent or small changes in these indexes indicate the weak factorial invariance model fit the model well. The strong factorial invariance model had a level of statistical fit that was significantly worse than the weak factorial invariance model, Δχ²(8, N = 1,075) = 43.55, p < .0001. However, as with the weak factorial invariance model, the CFI and TLI remained equal to or greater than 1.00. The RMSEA still indicated close model fit with a value of .048. Thus, the strong factorial invariance model appears to represent the observed data well. Finally, the strict factorial invariance model was fit and had much worse fit than the strong factorial invariance model, Δχ²(14, N = 1,075) = 116.74, p < .0001. The CFI and TLI values remained excellent; however, the RMSEA increased to .071. Thus, retaining the strong factorial invariance model or accepting the strict factorial invariance model can be justified. Being conservative in our model comparisons, the strong factorial invariance model was retained.

Solution 2: Combined Estimation Using Pattern Mixture Procedures With Known Groups

The pattern mixture procedure with known groups was estimated using Mplus. The model is specified similarly to a three-group model with separate model statements for each group (or class in this case) as the mixture modeling analysis type is specified. For each group, the full model of Figure 2 is specified for 11 variables; however, the dotted paths of Figure 2 were set equal to 0.0. To achieve convergence, the residual variances for MVMC were set equal to a small nonzero value (e.g., .01).

The configural invariance was fit with the pattern mixture approach and fit indexes are presented in Table 3. Fit indexes include the −2 log likelihood (−2LL), number of estimated parameters, and three information criteria. Because the mixture approach was utilized, examination of absolute fit is difficult; however, we can make fit comparisons among the different factorial invariance models. The fit of the weak factorial invariance model is shown next in Table 3. The weak invariance model fit significantly worse based on statistical fit of the model (Δ−2LL = 22.45, Δparms = 8, p < .005); however, the Bayesian Information Criterion (BIC; a conservative information criterion) decreased, indicating the weak invariance model fit better than the configural invariance model. The fit of the strong factorial invariance model is shown next in Table 3. The strong invariance model had a level of statistical fit that was significantly worse than the weak factorial invariance model (Δ−2LL = 42.63, Δparms = 8, p < .001). However, the BIC showed further reduction, suggesting the strong invariance model represented the data slightly better than the weak invariance model. Finally, the strict factorial invariance model was fit and had much worse fit than the strong factorial invariance model (Δ−2LL = 116.81, Δparms = 14, p < .001). The BIC and other information criteria all increased, suggesting the strict invariance model did not fit as well as the strong invariance model. Thus, the strong factorial invariance model was retained.

TABLE 3.

Solution 2: Mplus Fit Indexes for Alternative Models Using Pattern Mixture Approach

Model	−2LL	Parms	Δ−2LL	ΔParms	AIC	BIC	ABIC
Three-group analyses
Configural invariance	8,367.08	88	—	—	8,543.08	8,980.92	8,701.41
Weak factorial invariance	8,389.53	80	22.45	8	8,549.53	8,947.56	8,693.47
Strong factorial invariance	8,432.16	72	42.63	8	8,576.16	8,934.39	8,705.71
Strict factorial invariance	8,548.97	58	116.81	14	8,664.97	8,953.55	8,769.33

Note. Family and Community Health Study (FACHS) study N = 428 African American families; California Families Project (CFP) study N = 262 Mexican-origin families; and Iowa Youth and Families Project (IYFP) study N = 385 European American families. −2LL = −2 times the log likelihood; parms = number of parameters; Δ−2LL = change in −2 times log likelihood; Δparms = difference in number of parameters; AIC = Akaike Information Criterion; BIC = Bayesian Information Criterion; ABIC = adjusted Bayesian Information Criterion.

Solution 3: Combined Estimation With Random Data Generated for MVMC

To determine whether inclusion of the MVMC in CFA models would lead to any bias in indexes of model fit or in estimating parameters associated with MVP, we fit CFA models to 11 manifest variables in the FACHS and IYFP samples. Here, we included the MVMC in the CFAs, but specified the models as shown in Figure 2. That is, in the FACHS sample, we estimated intercepts for the four CES–D parcels (two father-report and two mother-report parcels), fixed the associated factor loadings at zero, and then estimated the unique variance for each of these four parcels as well as all covariances among unique factors for these four indicators with unique factors for all other variables in the analysis. A similar approach to model specification was undertaken in the IYFP sample, except the MASQ-derived parcels were the MVMC, so their intercepts, factor loadings, and unique factor variances and covariances were specified in the fashion shown in Figure 2.

The initial CFA model for the FACHS study that deleted the MVMC employed 7 manifest variables, resulting in a total of 35 sample statistics, consisting of 7(8)/2 = 28 variances and covariances among manifest variables and 7 manifest variable means. The CFA model included 7 intercepts, 7 factor loadings, 7 unique factor variances, and 3 correlations among factors, or 24 parameter estimates, leading to a χ² statistic with 11 df. In the current CFA model for the FACHS study that included the MVMC, the analysis was conducted on 11 manifest variables, leading to 11(12)/2 = 66 variances and covariances among manifest variables and 11 manifest variable means, for a total of 77 sample statistics. But, the model for the FACHS study shown in Figure 2 included 11 intercepts, 7 nonzero factor loadings, 45 unique factor variances and covariances, and 3 correlations among factors, for a total of 66 parameter estimates. Thus, the CFA model still has 11 df, because the increase in sample statistics was compensated equally by the additional estimates in the model.

As shown in the next section of Table 4, overall fit of the CFA model in the FACHS sample for the 11-variable analysis, with χ²(11, N = 428) = 8.56, p = .66, was virtually identical to that for the seven-variable analysis, with χ²(11, N = 428) = 8.54, p = .66. The fit of the 11-variable CFA model in the IYFP sample, with χ²(11, N = 285) = 6.16, p = .86, differed little from the fit of the seven-variable CFA, with χ²(11, N = 285) = 6.96, p = .80. Thus, use of random deviates in place of MVMC with proper compensation in model specification did not lead to notable bias in model fit.

TABLE 4.

Solution 3: Fit Indexes for Alternative Models for Random Data for Manifest Variables Missing Completely

Model	χ2	df	Prob	CFI	TLI	RMSEA [CI]
Separate analyses by sample
FACHS (7 manifest variables)	8.54	11	.66	1.000	1.006	.000 [.000, .041]
CFP (11 manifest variables)	58.77	39	.02	.983	.976	.044 [.017, .067]
IYFP (7 manifest variables)	6.69	11	.80	1.000	1.008	.000 [.000, .035]
Total	73.36	61
FACHS (11 manifest variables)	8.56	11	.66	1.000	1.015	.000 [.000, .041]
IYFP (11 manifest variables)	6.16	11	.86	1.000	1.024	.000 [.000, .029]
Three-group analyses
Configural invariance	73.49	61	.13	.996	.989	.024 [.000, .042]
FACHS	8.56
CFP	58.77
IYFP	6.16
Weak factorial invariance	95.94	69	.02	.991	.979	.033 [.014, .048]
Strong factorial invariance	139.42	77	<.001	.979	.956	.048 [.035, .060]
Strict factorial invariance	255.98	91	<.001	.945	.901	.071 [.061, .082]

Note. Family and Community Health Study (FACHS) study N = 428 African American families; California Families Project (CFP) study N = 262 Mexican-origin families; and (IYFP) study N = 385 European American families. CFI = Comparative Fit Index; TLI = Tucker–Lewis I; RMSEA [CI] = root mean square error of approximation and its associated confidence interval.

Measurement model parameter estimates from analyses excluding MVMC are shown in the left half of Table 5, and corresponding estimates from analyses including MVMC are shown in the right half of the table. In Table 5, we report the intercept τ and its standard error (SE), the raw factor loading λ and its SE, the standardized factor loading, and unique variance θ with its SE for each manifest variable in each analysis. Comparison of the left and right sides of Table 5 will show that the largest difference in an intercept was .004, the largest difference in a factor loading was .002, and the largest difference in a unique variance was .001. As with measures of overall fit, inclusion of the MVMC with random values did not appear to bias parameter estimates to any significant degree.

TABLE 5.

Measurement Model Parameter Estimates for Unconstrained Confirmatory Factor Analysis Models Fit to Three Samples, Excluding and Including MVMC

Latent Variable	Manifest Indicator	Analyses Excluding MVMC				Analyses Including MVMC
		τ (SE)	λ (SE)	std λ	θ (SE)	τ (SE)	λ (SE)	std λ	θ (SE)
FACHS study
Factor 1: Economic pressure	U	2.079 (.030)	.371 (.030)	.689	.152 (.016)	2.083 (.030)	.373 (.031)	.692	.152 (.016)
	C	2.168 (.035)	.539 (.034)	.868	.095 (.023)	2.170 (.035)	.539 (.034)	.868	.095 (.023)
	F	.118 (.008)	.085 (.008)	.611	.012 (.001)	.118 (.008)	.085 (.008)	.611	.012 (.001)
Factor 2: Father depression	M1F	1.327 (.029)	.439 (.033)	.851	.073 (.021)	1.331 (.029)	.441 (.033)	.853	.072 (.021)
	M2F	1.333 (.031)	.490 (.035)	.897	.059 (.025)	1.335 (.031)	.489 (.035)	.894	.060 (.025)
	C1F	—	—	—	—	−.063 (.048)	.000 (.000)	.000	.995 (.068)
	C2F	—	—	—	—	−.002 (.047)	.000 (.000)	.000	.939 (.064)
Factor 3: Mother depression	M1M	1.391 (.025)	.442 (.035)	.852	.074 (.026)	1.391 (.025)	.441 (.035)	.850	.075 (.026)
	M2M	1.380 (.026)	.406 (.034)	.765	.117 (.023)	1.380 (.0260	.408 (.034)	.767	.116 (.023)
	C1M	—	—	—	—	−.029 (.049)	.000 (.000)	.000	1.042 (.071)
	C2M	—	—	—	—	.035 (.049)	.000 (.000)	.000	1.018 (.070)
CFP study
Factor 1: Economic pressure	U	2.257 (.047)	.491 (.044)	.772	.164 (.024)	2.257 (.047)	.491 (.044)	.772	.164 (.024)
	C	2.345 (.047)	.564 (.043)	.874	.099 (.024)	2.345 (.047)	.564 (.043)	.874	.099 (.024)
	F	.175 (.013)	.135 (.012)	.763	.013 (.002)	.175 (.013)	.135 (.012)	.763	.013 (.002)
Factor 2: Father depression	M1F	1.355 (.044)	.398 (.044)	.681	.183 (.025)	1.355 (.044)	.398 (.044)	.681	.183 (.025)
	M2F	1.316 (.038)	.360 (.038)	.705	.131 (.019)	1.316 (.038)	.360 (.038)	.705	.131 (.019)
	C1F	1.592 (.030)	.299 (.030)	.736	.075 (.012)	1.592 (.030)	.299 (.030)	.736	.075 (.012)
	C2F	1.670 (.033)	.346 (.031)	.795	.069 (.013)	1.670 (.033)	.346 (.031)	.795	.069 (.013)
Factor 3: Mother depression	M1M	1.446 (.041)	.478 (.037)	.742	.186 (.021)	1.446 (.041)	.478 (.037)	.742	.186 (.021)
	M2M	1.413 (.038)	.423 (.035)	.712	.174 (.019)	1.413 (.038)	.423 (.035)	.712	.174 (.019)
	C1M	1.658 (.029)	.369 (.026)	.815	.069 (.009)	1.658 (.029)	.369 (.026)	.815	.069 (.009)
	C2M	1.679 (.032)	.450 (.027)	.889	.054 (.011)	1.679 (.032)	.450 (.027)	.889	.054 (.011)
IYFP study
Factor 1: Economic pressure	U	2.060 (.027)	.419 (.024)	.798	.100 (.010)	2.060 (.027)	.419 (.024)	.799	.100 (.010)
	C	2.341 (.035)	.574 (.031)	.834	.144 (.017)	2.341 (.035)	.574 (.031)	.834	.144 (.017)
	F	.164 (.008)	.129 (.007)	.844	.007 (.001)	.164 (.008)	.129 (.007)	.844	.007 (.001)
Factor 2: Father depression	M1F	—	—	—	—	.017 (.055)	.000 (.000)	.000	1.156 (.083)
	M2F	—	—	—	—	−.041 (.053)	.000 (.000)	.000	1.097 (.079)
	C1F	1.366 (.020)	.293 (.032)	.746	.068 (.017)	1.366 (.020)	.294 (.032)	.746	.068 (.017)
	C2F	1.401 (.023)	.410 (.042)	.903	.038 (.031)	1.401 (.023)	.411 (.042)	.904	.038 (.032)
Factor 3: Mother depression	M1M	—	—	—	—	−.039 (.053)	.000 (.000)	.000	1.085 (.078)
	M2M	—	—	—	—	.007 (.049)	.000 (.000)	.000	.940 (.068)
	C1M	1.427 (.022)	.253 (.052)	.585	.123 (.026)	1.427 (.022)	.253 (.052)	.585	.123 (.026)
	C2M	1.457 (.026)	.602 (.115)	1.163	−.094 (.137)	1.457 (.026)	.602 (.115)	1.163	−.095 (.137)

Note. Family and Community Health Study (FACHS) study N = 428 African American families; California Families Project (CFP) study N = 262 Mexican-origin families; and Iowa Youth and Families Project (IYFP) study N = 385 European American families. Boldfaced values are statistics for manifest variables missing completely (MVMC). U = unmet material needs; C = can’t make ends meet; F = financial cutbacks; M1F and M2F = Mini-MASQ Parcels 1 and 2 father report; C1F and C2F = CES–D Parcels 1 and 2 father report; M1M and M2M = Mini-MASQ Parcels 1 and 2 mother report; C1M and C2M = CES–D Parcels 1 and 2 mother report.

Investigations of factorial invariance

Because the analyses including MVMC led to model fit and parameter estimates that were acceptable, we next performed three-group CFAs to investigate factorial invariance. As shown in the bottom half of Table 4, the configural invariance model had quite acceptable fit to the data, both statistically, χ²(61, N = 1,075) = 73.49, p = .13, and practically, with CFI and TLI values over .98 and an RMSEA of .024. We reported the separate-sample contributions to the overall χ² for the configural invariance model to show that these values were identical to the χ² values obtained in 11-variable analyses for each group. This was our expected outcome, given the minimally constrained nature of the configural invariance model and the fact that analyses were based on the 11-variable data set for each sample.

The fit of the weak factorial invariance model is shown next in Table 4. The weak invariance model retained very good practical fit indexes, but resulted in a significant worsening in statistical fit of the model, χ²(8, N = 1,075) = 22.45, p < .005. The strong factorial invariance model had a level of statistical fit that was significantly worse than the weak factorial invariance model, χ²(8, N = 1,075) = 43.48, p < .0001, but had good practical fit. Finally, the strict factorial invariance model had much worse fit than the strong factorial invariance model, χ²(14, N = 1,075) = 116.56, p < .0001. Thus, as with previous demonstrations, we settled on the strong factorial invariance model.

Measurement model parameter estimates and their associated SEs for the strong invariance model are shown in Table 6. Estimates associated with MVMC exhibited predicted patterns, with intercepts near 0.0 and unique factor variances near 1.0. All parameter estimates associated with MVP were statistically significant, falling 5 SE or more from zero. Factor loadings had relatively high levels of communality in all samples, with standardized values ranging between .6 and .9. The CFP sample tended to exhibit somewhat higher unique factor variances ? on depression parcels, particularly on parcels derived from the Mini-MASQ, which likely led to the failure to attain adequate fit of the strict factorial invariance model. The strong factorial invariance model shown in Table 6 supports the conclusion that the same factors were identified in all three samples.

TABLE 6.

Measurement Model Parameter Estimates From the Strong Factorial Invariance Model

Latent Variable	Manifest Indicator	τ (SE)	λ (SE)	std λ	θ (SE)
FACHS sample
Factor 1: Economic pressure	U	2.022 (.025)	.357 (.022)	.669	.157 (.016)
	C	2.177 (.032)	.490 (.029)	.813	.123 (.018)
	F	.131 (.007)	.104 (.006)	.701	.011 (.001)
Factor 2: Father depression	M1F	1.337 (.029)	.468 (.026)	.899	.052 (.017)
	M2F	1.326 (.030)	.458 (.028)	.846	.083 (.018)
	C1F	−.052 (.049)	.000 (.000)	.000	.996 (.068)
	C2F	−.015 (.047)	.000 (.000)	.000	.941 (.065)
Factor 3: Mother depression	M1M	1.393 (.025)	.450 (.023)	.867	.067 (.016)
	M2M	1.376 (.024)	.399 (.022)	.751	.123 (.014)
	C1M	−.049 (.050)	.000 (.000)	.000	1.042 (.071)
	C2M	.028 (.049)	.000 (.000)	.000	1.018 (.070)
CFP sample
Factor 1: Economic pressure	U	2.022 (.025)	.357 (.022)	.704	.194 (.025)
	C	2.177 (.032)	.490 (.029)	.910	.075 (.023)
	F	.131 (.007)	.104 (.006)	.732	.014 (.002)
Factor 2: Father depression	M1F	1.337 (.029)	.468 (.026)	.655	.188 (.025)
	M2F	1.326 (.030)	.458 (.028)	.713	.131 (.019)
	C1F	1.591 (.035)	.362 (.045)	.724	.077 (.011)
	C2F	1.672 (.041)	.438 (.054)	.804	.068 (.013)
CFP sample
Factor 3: Mother depression	M1M	1.393 (.025)	.450 (.023)	.743	.186 (.021)
	M2M	1.376 (.024)	.399 (.022)	.713	.174 (.019)
	C1M	1.603 (.031)	.351 (.031)	.819	.068 (.009)
	C2M	1.646 (.035)	.420 (.036)	.884	.055 (.011)
IYFP sample
Factor 1: Economic pressure	U	2.022 (.025)	.357 (.022)	.797	.104 (.011)
	C	2.177 (.032)	.490 (.029)	.841	.141 (.017)
	F	.131 (.007)	.104 (.006)	.829	.007 (.001)
Factor 2: Father depression	M1F	.009 (.056)	.000 (.000)	.000	1.156 (.083)
	M2F	−.038 (.055)	.000 (.000)	.000	1.097 (.079)
	C1F	1.591 (.035)	.362 (.045)	.799	.056 (.010)
	C2F	1.672 (.041)	.438 (.054)	.845	.059 (.015)
Factor 3: Mother depression	M1M	−.026 (.054)	.000 (.000)	.000	1.086 (.078)
	M2M	.011 (.050)	.000 (.000)	.000	.938 (.068)
	C1M	1.603 (.031)	.351 (.031)	.818	.063 (.011)
	C2M	1.646 (.035)	.420 (.036)	.830	.082 (.016)

Note. Family and Community Health Study (FACHS) sample N = 428 African American families; California Families Project (CFP) sample N = 262 Mexican-origin families; and Iowa Youth and Families Project (IYFP) sample N = 385 European American families. Boldfaced values are statistics for manifest variables missing completely (MVMC). U = unmet material needs; C = can’t make ends meet; F = financial cutbacks; M1F and M2F = Mini-MASQ Parcels 1 and 2 father report; C1F and C2F = CES–D Parcels 1 and 2 father report; M1M and M2M = Mini-MASQ Parcels 1 and 2 mother report; C1M and C2M = CES–D Parcels 1 and 2 mother report.

With acceptance of the strong invariance model, estimates of factor means, SDs, and correlations among factors, shown in Table 7, have straightforward interpretation. Because factor means were fixed at zero and factor variances to unity on all factors in the FACHS sample, the means and variances of factors in the remaining two samples are interpretable relative to the fixed values for the FACHS sample. Participants in the CFP sample reported higher mean levels of economic pressure (M = .397, SE = .108), but about the same mean level of father and mother depression (M s = .003 and .111, SEs = .103 and .102, respectively) relative to the FACHS sample. In contrast, although participants in the IYFP reported higher levels of economic pressure (M = .357, SE = .086) that matched that for the CFP sample, they had moderately lower levels of father and mother depression (M s = −.613 and −.472, SEs = .125 and .111, respectively) relative to the FACHS sample.

TABLE 7.

Means, Standard Deviations, and Correlations Among Latent Variables, by Sample

Variable	M (SE)	SD (SE)	Correlations
			Factor 1	Factor 2
FACHS study
Factor 1: Economic pressure	.000 (.000)	1.000 (.000)
Factor 2: Father depression	.000 (.000)	1.000 (.000)	.456 (.059)
Factor 3: Mother depression	.000 (.000)	1.000 (.000)	.456 (.062)	.202 (.067)
CFP study
Factor 1: Economic pressure	.404 (.118)	1.493 (.244)
Factor 2: Father depression	−.001 (.103)	.646 (.144)	.451 (.076)
Factor 3: Mother depression	.107 (.102)	1.130 (.193)	.341 (.086)	.182 (.095)
IYFP study
Factor 1: Economic pressure	.264 (.093)	1.418 (.194)
Factor 2: Father depression	−.622 (.125)	.762 (.192)	.272 (.058)
Factor 3: Mother depression	−.475 (.111)	1.032 (.192)	.166 (.061)	.142 (.064)

Note. Factor means were fixed at zero and factor standard deviations were fixed at 1.0 for all three factors in the FACHS sample to identify the model. FACHS = Family and Community Health Study; CFP = California Families Project; IYFP = Iowa Youth and Families Project.

Correlations among factors revealed rather strong correlations of economic pressure with both father depression (r = .448, SE = .058) and mother depression (r = .457, SE = .061) for the African American participants in the FACHS sample. For Mexican-origin families in the CFP study, correlations of economic pressure were still substantial with both father depression (r = .452, SE = .076) and mother depression (r = .337, SE = .087). In the European American families in the IYFP, economic pressure was only moderately related to father depression (r = .271, SE = .058) and weakly related to mother depression (r = .165, SE = .061). Father depression and mother depression were not highly correlated in any of the samples.

DISCUSSION

The primary goal of this study was to compare three multiple-group SEM methods that allow inclusion of manifest variables that were missing completely for a particular group. This situation is common when the multiple groups arise out of different studies with different protocols. A great deal of attention has been focused on issues related to missing data during the past 15 to 20 years. Much of this work has concerned methods for imputing missing values. Multiple imputation leads to one or more complete data matrices with imputed values that preserve the patterns in data observed for the nonmissing values. Although great strides have been made in development of useful methods of imputation, these methods are not viable for within-group imputation if one or more manifest variables are missing completely in a group.

Other approaches to deal with the MVMC problem exist. One of these is deletion of any manifest variable that is missing completely in any group. But, this approach can lead to elimination of key latent variables or questionable identification of a latent variable, given the deletion of all or most indicators for the latent variable in question. The method of conceptual replication has been improved considerably due to recent work by Hofer and Piccinin (2009) and might be optimal in some contexts. However, developing ways to allow stronger, more direct quantitative tests of difference across groups are preferred to the weaker method of conceptual replication.

Yet another approach to the MVMC problem was presented recently by Curran et al. (2008), who described how to use item response theory (IRT) methods to obtain scores on a comparable metric across groups when some manifest variables are missing in one or another group. Our proposed method has some similarities to the Curran et al. approach, but can be applied in situations in which an IRT-based approach is inapplicable. Use of IRT methods, following Curran et al., requires the presence of item-level data for analyses and items with answer options viable for IRT modeling. But, data sets may contain only scale-level total scores as data values (i.e., may contain no item-level data) or the manifest variables that are missing completely in a group might be in a form that is not amenable to IRT methods (e.g., manifest variable score is time taken to solve a series of problems or number of problems solved in a set period of time). As a result, our proposed method might be a viable alternative to IRT-based methods in many research contexts like those discussed by Curran et al., but also can be applied in contexts in which their methods cannot be used. Despite similarities between the two, our proposed method and the Curran et al. approach are implemented in different analytic traditions, and each likely will have unique strengths in contexts in which the other method would be tedious or unworkable.

Prior seminal work on missing data in the SEM field employed multiple-group methods to circumvent the presence of missing data on certain variables within a single population. Allison (1987) and Muthén et al. (1987) devised interesting ways of calculating summary matrices for multiple groups, where each group shared the same pattern of missing data on particular variables. By substituting specified values for the mean and standard deviation of missing variables and nil correlations of missing variables with all other manifest variables in the analysis, application of invariance constraints on key parameters, including factor loadings and intercepts, led to less biased estimates of model parameters than other common missing data approaches, such as listwise deletion of observations that have any missing values.

The Allison (1987) and Muthén et al. (1987) approaches are innovative ways of dealing with missingness of data values. These methods are very restrictive, though, because they assume that each group (a) contains no missing values on one set of manifest variables and completely missing values on the remaining set of manifest variables, and (b) has a sufficient number of observations to have an invertible covariance matrix (i.e., each group must have a number of observations exceeding by 1 the number of manifest variables). Unfortunately, these assumptions are unlikely to be met in most empirical studies. In most large studies, some missing values will occur rather haphazardly on many manifest variables included in the protocol, due to unpredictable events such as failure by one person to complete a single item on a particular scale. The upshot would be a need to employ such a large number of groups as to make the methods unusable. In addition, Allison (1987) and Muthén et al. (1987) argued that observations defining groups too small to yield an invertible covariance matrix must be deleted from analyses, another unfortunate component of this approach.

The method proposed in this article is to generate pseudo-random normal deviates for all observations for all MVMC in a given sample and then to specify and test structural models in ways that respect the random nature of scores on these manifest variables. After generating pseudo-random deviates for the MVMC, these MVMC have complete, if random, values. In contrast, the manifest variables that were present in the study protocol (i.e., the MVP) might or might not have missing values. If the MVP have missing values, then a researcher can follow the approach outlined in our discussion of Case I analyses. On the other hand, if the MVP contain no missing values, various options are available for analysis. Interestingly, in the latter case of MVP with no missing values, the three analytic options we implemented in this article provided identical results in terms of overall model fit and all characteristics of parameter estimates, their standard errors, and their associated asymptotic z values. Thus, regardless of whether MVP do or do not have missing values, the general approach advocated here-direct FIML fitting of models to raw data matrices with pseudo-random normal variates standing for MVMC-appears to provide optimal results with little or no bias.

One significant advantage of the proposed method is that quantitative comparisons at the latent variable level are possible even when groups share no manifest variables for a given latent variable. For example, the FACHS study protocol included the Mini-MASQ as a measure of father and mother depression, but did not include the CES–D for this construct. Conversely, the IYFP study protocol included only the CES–D as a measure of father and mother depression, but did not include the Mini-MASQ. Thus, the FACHS and IYFP study protocols have no overlap in measures for father and mother depression. Given the lack of any information in the FACHS study about how CES–D scores might relate to other manifest variables, imputation methods were not viable, and the same occurred for the IYFP sample with regard to the Mini-MASQ scores. However, because the CFP study protocol included both the Mini-MASQ and the CES–D, strong factorial invariance constraints across groups on factor loadings and intercepts resulted in a model that supported the contention that the same latent variables were identified in the three samples. Given this finding, quantitative comparisons could be made between the FACHS and IYFP samples on father and mother depression that would have been impossible using methods proposed to date.

One reviewer observed that a problem for the procedures advocated in this article would arise if the MVMC in a particular group would have exhibited noninvariance if these MVMC had been observed, even though the manifest variables present in groups show clear patterns of invariance. That is, if the MVMC would have demonstrated noninvariance, but a researcher has no information on this point because the manifest variables in question were missing completely in one or more groups, then the researcher might incorrectly conclude that factorial invariance holds for the manifest and latent variables in the analysis. We note simply that this is indeed a potential problem, one that should be acknowledged. But, we also note that this problem applies equally to all three methods investigated in this article. Furthermore, the problem applies to all invariance analyses, even if all manifest variables included for study are present in all groups. That is, in any study of factorial invariance, additional indicators for latent variables being evaluated could have been located and included in the study, and these additional indicators might have exhibited noninvariance had they been observed. To proceed with scientific inquiry, we offer the current approaches, acknowledging the potential problems, and recommending that future studies replicate and extend research to evaluate the possibility of incorrect conclusions in a single study.

Given the preceding concerns, future research should be undertaken to determine whether conditions exist under which the new methods proposed in this study lead to less acceptable outcomes. Pending such research, we trust that the methods proposed here will provide a useful extension to methods currently available for handing missing values—particularly manifest variables missing completely from a study—in structural modeling of psychological data.