Abstract
Finite element (FE) analysis has been applied for the past 40 years to simulate the mechanical behavior of bone. Although several validation studies have been performed on specific anatomical sites and load cases, this study aims to review the predictability of human bone strength at the three major osteoporotic fracture sites quantified in recently completed in vitro studies at our former institute. Specifically, the performance of FE analysis based on clinical computer tomography (QCT) is compared with the ones of the current densitometric standards, bone mineral content, bone mineral density (BMD) and areal BMD (aBMD). Clinical fractures were produced in monotonic axial compression of the distal radii, vertebral sections and in side loading of the proximal femora. QCT-based FE models of the three bones were developed to simulate as closely as possible the boundary conditions of each experiment. For all sites, the FE methodology exhibited the lowest errors and the highest correlations in predicting the experimental bone strength. Likely due to the improved CT image resolution, the quality of the FE prediction in the peripheral skeleton using high-resolution peripheral CT was superior to that in the axial skeleton with whole-body QCT. Because of its projective and scalar nature, the performance of aBMD in predicting bone strength depended on loading mode and was significantly inferior to FE in axial compression of radial or vertebral sections but not significantly inferior to FE in side loading of the femur. Considering the cumulated evidence from the published validation studies, it is concluded that FE models provide the most reliable surrogates of bone strength at any of the three fracture sites.
Introduction
Application of finite element (FE) analysis to determine stresses in human bones was initiated in the early 1970s in the field of orthopedic biomechanics.
In the 1980s, FE analysis was already perceived as a highly promising tool in orthopedics and other clinical fields, but the enormous gap between the idealized biomechanical models that could be solved by FE and the clinical applications was readily recognized. The question as to whether this new computational methodology helps the patient could not be answered definitively. The communication between engineering and the medical faculty was considered a major problem that contributed to the establishment of joint educational programs.
The lack of accurate three-dimensional (3D) anatomy, bone material properties and loading conditions was also identified. In fact, the FE method was available but the necessary input data were missing.
In the 1990s, the availability of computer tomography (CT) provided a strong impulse for the generation of anatomy-specific FE models of whole bones.1 Bone heterogeneity and anisotropy were found to be important for both static and dynamic analyses.2
The elastic properties of cortical bone were assembled from those of osteons by homogenization theory.3 Trabecular bone was analyzed by FE as idealized open and/or closed cell models or from the first microCT reconstructions,4 and its apparent elastic properties were also computed by homogenization theory.5 Nonlinear 3D constitutive models for bone based on plasticity and damage appeared in the literature.6 Bone-remodeling scenarios were also intensively developed using FE.7,8
During the past Bone and Joint decade (2000–2010), awareness of osteoporosis increased and the number of publications with the string ‘FE' grew rapidly.9 The development of computer hardware and software tools allowed substantial progress in the area of model validation10 and began the era of patient-specific FE modeling.
A recent report reviewed the principles of the CT-based FE method and its application in the hip and spine.11 In this paper, we aim to synthesize three recent validation experiments performed in our laboratory for patient-specific modeling of three skeletal sites at high risk of osteoporotic fractures: the distal radius, the vertebral body and the proximal femur. In particular, we quantify the predictive power of the voxel-based FE methodology for the image resolution available in vivo and compare it with the current densitometric surrogates of bone strength, bone mineral content (BMC) and areal bone mineral density (aBMD), for each anatomical site.
Study design
The adopted study design consisted first in obtaining a substantial number of human bones from both genders and a broad age range with the approval of the local ethics commission. Custom chambers were built to scan the bones in a predefined coordinate system with CT. Before scanning, the bones were immersed in saline solution to mimic the presence of soft issues and exposed to vacuum in order to remove air bubbles that create artifacts in the local mineral density. A calibration phantom was used to calculate the calibration function between the attenuation coefficient and BMD for each bone.
Representative but maximally simplified loading scenarios were then applied to each bone to reproduce typical fractures observed in patients with osteoporosis. The number of materials and interfaces intervening in the testing set-up were minimized for proper reproduction of the loading scenario in the FE model. The bones were tested monotonically to failure in a servohydraulic testing system (MTS 858 Mini-Bionix, MTS Corp, Eden Prairie, MN, USA).
Voxel meshes of the bones and potential embedding materials were generated in a fully automated manner with an element size that saved computational resources in the perspective of large clinical studies but showed acceptable accuracy when compared with refined meshes.12 For microstructural FE (microFE) models such as those obtained from high-resolution peripheral CT (HR-pQCT), the elastic properties of bone tissue were based on nanoindentation measurements.13 For homogenized FE models generated from clinical CT (QCT), the nonlinear material properties of each element were based on the local calibrated BMD converted into bone volume fraction and morphology–mechanical property relationships for trabecular bone14 that were identified on human biopsies.15 When available, fabric information was included in the morphology–mechanical property relationships, but the cortex was not distinguished from trabecular bone.
The morphology–mechanical property relationships fitted for trabecular bone were adequately extrapolated to reach bone tissue properties for a volume fraction equal to 1. The constitutive model for bone tissue was elastic, plastic with damage, that is, coupled accumulation of plastic deformation and reduction of stiffness beyond a given yield surface in stress space.16 The FE meshes were generated with a custom script manager (MedTool, TU-Wien, Vienna, Austria) and the analyses were performed on a computing server (2 × 2 XEON 3.0 GHz processors, 32 GB RAM) with ParFE (Professor P Arbenz, ETHZ, Zurich, Switzerland) software for the linear models of the distal radius and with Abaqus (version 6.8, Simulia, Dassault Systèmes, Velizy-Villacoublay, France) software for the nonlinear models of the vertebral sections and proximal femora.
Full methodological details of the three studies on the distal radius, vertebral sections and proximal femora can be found in Varga et al.17 and Dall'Ara et al.18,19
Linear regressions were calculated between the experimental maximal force or strength and the FE or densitometric variables. The adjusted Pearson's correlation coefficients and the root mean square errors (RMSE) of the predictions were calculated for all linear regressions. The statistical comparisons of the dependent correlation coefficients were made with the T2 distribution described in Steiger.20
Ultimate load of the distal radius using HR-pQCT
Colle's fracture is considered as an early osteoporotic fracture and is characterized by an angulated compressive failure of the distal radius.21 In a recent radiographical study, the fracture line was located dorsally 7.9±2.7 mm and palmarly 11.7±3.9 mm proximal to the corresponding lunate fossa apex.22
Materials and methods
After alignment of the shaft and embedding of the proximal and distal ends in polymethyl methacrylate (PMMA), 26 formalin-fixed distal radii (11 men and 16 women, aged 61–103) were scanned using a clinical HR-pQCT (XtremeCT, Scanco Medical, Brüttisellen, Switzerland) protocol with a voxel size of 82 μ. The biomechanical testing set-up developed in Varga et al.23 and illustrated in Figure 1 consisted of an axial loading of the radial shaft with an inclined distal embedding that produced a combined compression and bending in the distal region. All bones were tested to failure with a loading rate of 1 mm s−1. Cutting of the radii in a sagittal plane after testing revealed a white, inclined compression line that corresponded rather well to the definition of Colle's fracture. Although a nonlinear homogenized FE model of this experiment was realized and allowed to reproduce the individual fracture loads and locations of this experiment, a clinically more important question was addressed in a subsequent paper24 where only the distal 9 mm section of the radius corresponding to the standard clinical protocol of the HR-pQCT manufacturer was modeled (Figure 1). As Colles' fracture was found to occur in the vicinity of this section, it was legitimate to test whether the strength of that standard section would predict the strength of the whole-distal radius. A simple linear microFE model was therefore generated for each radial section and subjected to axial compression between two rigid plates with infinite friction. The elastic modulus of bone tissue was set to 15 GPa and the Poisson ratio to 0.3, based on a previous indentation study.23,25 The fracture load was determined from the linear FE analysis using an empirical rule proposed by Pistoia et al.26
Figure 1.
On the left, experimental model of Colle's fracture.23 On the right, FE model of the standard 9 mm radius section obtained with the clinical protocol of the HR-pQCT.24 The boundary conditions correspond to a displacement-based axial compression at the distal end with fully fixed nodes at the proximal end of the section.
Results
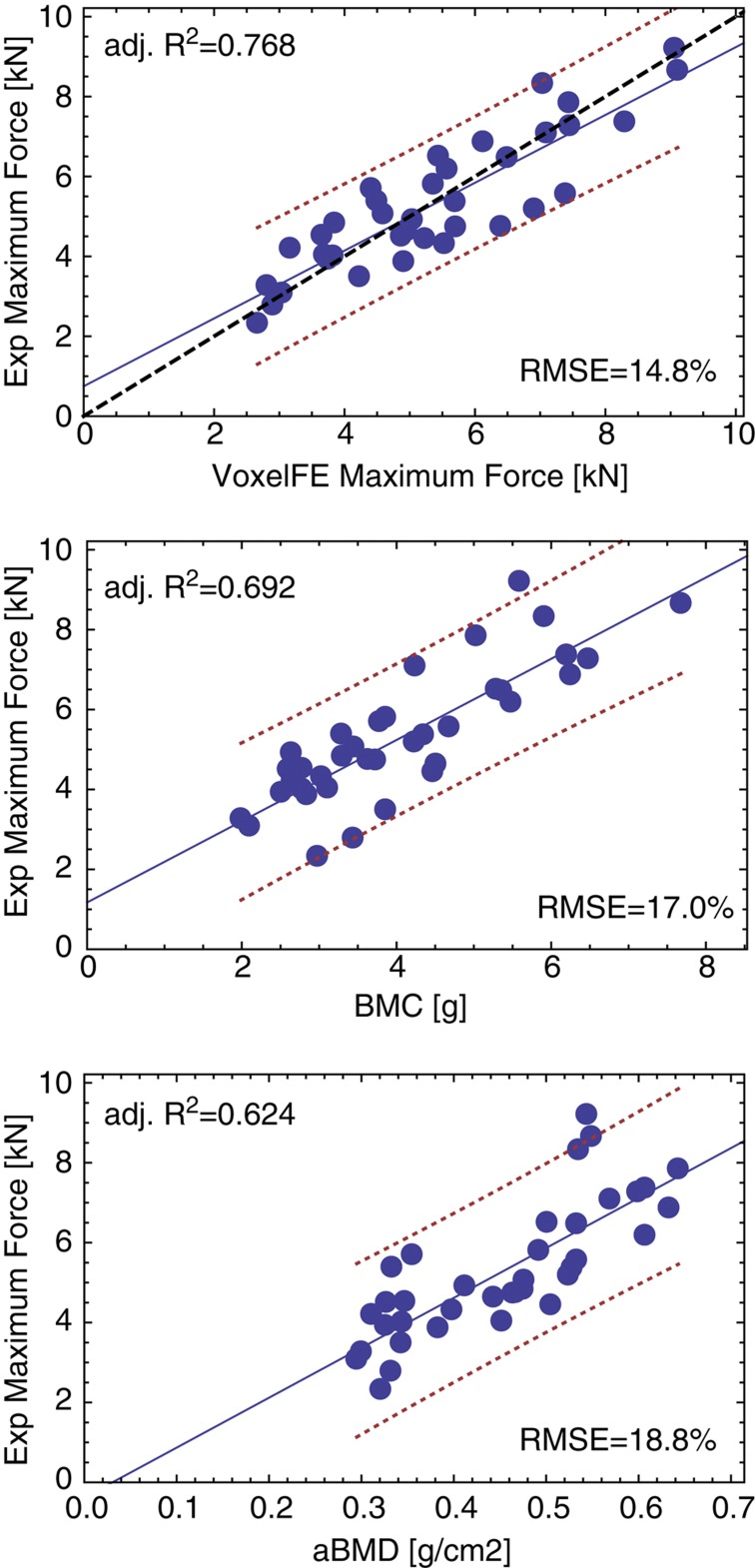
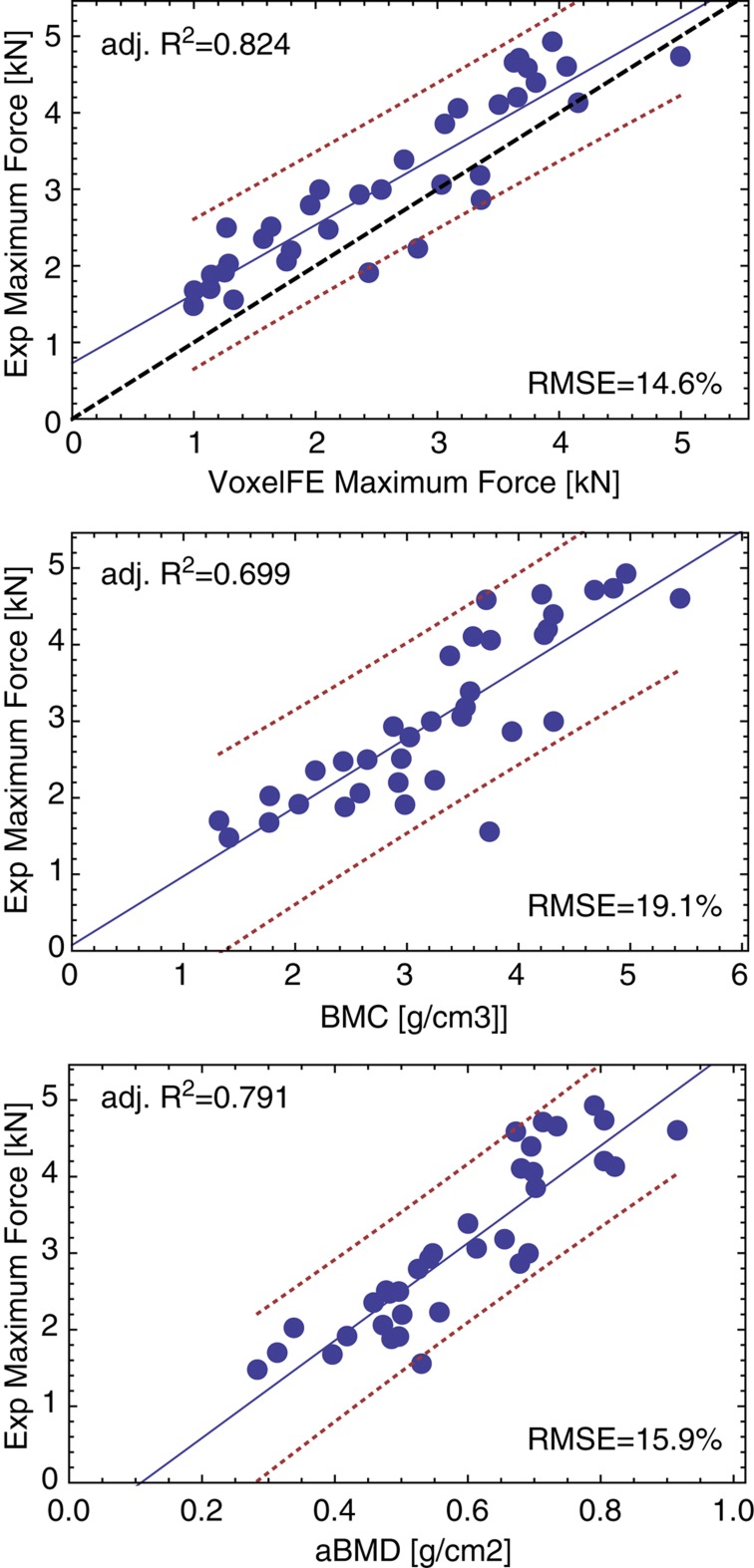
The regression plots for prediction of the experimental strength of the distal radius are shown in Figure 2 for microFE, BMC and simulated aBMD. The predictions of microFE are quantitatively correct with a slope close to 1. Although the microFE analysis delivers the highest correlation coefficient and the lowest RMSE for maximal force, the predictions of BMC and CSA*BMD (cross-sectional area times bone mineral density) are remarkable and not significantly different (Tables 1 and 2). The predictions of aBMD are significantly inferior for maximal load (P=0.003) but not for maximal apparent stress (P=0.284). The predictions of BMD are approaching those of the microFE method for maximal apparent stress (P=0.347).
Figure 2.
Linear regressions between experimental strength of the distal radii and microFE analysis (MicroFE), bone mineral content (BMC) and areal bone mineral density (aBMD). The blue solid line is the regression, the red dotted lines are the confidence intervals and the black dashed line is the 1:1 relationship. Adj. R2, the adjusted coefficient of determination; RMSE, relative root mean square error.
Table 1. Adjusted correlations coefficients for prediction of maximal force and maximal apparent stress using FE, QCT and aBMD.
|
Adj. R2 |
Maximum force |
Maximum apparent stress |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Site | Imaging | N | FE | BMD*CSA | BMC | aBMD | BMD | FE | |
| Distal radius | HR-pQCT | 21 | 0.920 | 0.893 (P=0.158) | 0.892 (P=0.151) | 0.769* (P=0.003) | 0.707 (P=0.284) | 0.751 (P=0.347) | 0.775 |
| Vertebra | QCT | 37 | 0.768 | 0.707 (P=0.179) | 0.692 (P=0.175) | 0.624* (P=0.046) | 0.467* (P=0.001) | 0.732 (P=0.283) | 0.771 |
| Hip (fall) | QCT | 36 | 0.824 | — | 0.699* (P=0.032) | 0.791 (P=0.264) | — | — | — |
Abbreviations: aBMD, areal bone mineral density; Adj. R2, adjusted coefficient of determination; BMC, bone mineral content; BMD, bone mineral density; FE, finite element; HR-pQCT, high-resolution peripheral computer tomography.
For aBMD, which is neither a structural nor a material variable, the predictions of both maximal force and apparent stress are reported.
*Designates a statistically different correlation coefficient with respect to the corresponding FE variable (P<0.05).
Table 2. Root mean square error of the prediction in percentage of the average experimental force or stress variable using FE, QCT and DXA.
|
Adj. R2 |
Maximum force |
Maximum apparent stress |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Site | Imaging | N | FE | BMD*CSA | BMC | aBMD | BMD | FE | |
| Distal radius | HR-pQCT | 21 | 13.6 | 15.8 | 15.8 | 23.1 | 18.2 | 16.8 | 16.0 |
| Vertebra | QCT | 37 | 14.8 | 16.6 | 17.0 | 18.8 | 22.0 | 15.7 | 14.5 |
| Hip (fall) | QCT | 36 | 14.6 | — | 19.1 | 15.9 | — | — | |
Abbreviations: aBMD, areal bone mineral density; Adj. R2, adjusted coefficient of determination; BMC, bone mineral content; BMD, bone mineral density; DXA, dual-energy X-ray absorptiometry; FE, finite element; HR-pQCT, high-resolution peripheral computer tomography.
For DXA, the predictions of both maximum force and apparent stress are reported.
Discussion
As shown in Table 3, the precise biomechanical testing set-up of the present study allowed achieving better microFE predictions of maximal force of the standard distal radius section than in the studies by Pistoia et al.26 (R2=0.75) and Mueller et al.27 (R2=0.73). The experimental compression of the wrist including soft tissues but neglecting muscle forces may have generated stress fields that were more difficult to reproduce in a FE model. Given the HR-pQCT images, the use of a homogenized nonlinear model in Varga et al.28 did not improve the correlations with respect to linear microFE models for radial sections but may help to reduce the necessary computational resources for clinical applications in the future.
Table 3. Overview of previous validation experiments using clinical CT-based FE models to predict strength of the distal radius, thoracolumbar vertebrae and proximal femur under typical fracture-loading conditions: axial compression on the distal radius and vertebral sections and fall on the side on the proximal femora.
| Structure–configuration condition | Age(Years) | NNo. of F+M | Loading rate(mm min−1) | Maximum force(kN) | FE model | Image resolution(μm) | R2(–) | Reference |
|---|---|---|---|---|---|---|---|---|
| Structure, element, size, w/o cortex, symmetry, linearity | ||||||||
| Wrist–potted embalmed | 82±9 | 33F+21M | 200 | 0.4–2.5 | Wrist, microFE, linear | 165 × 165 × 165 | 0.75 | Pistoia et al.76 |
| Wrist–potted embalmed | 82±9 | 33F+21M | 200 | 0.4–2.5 | Standard section 9.1 mm microFE, linear | 165 × 165 × 165 | 0.66 | Pistoia et al.26 |
| Wrist–potted formalin fixed | 81±9 | 50F+50M | 100 | ∼0.4–5.0 | Standard section 9.1 mm, microFE, linear | 82 × 82 × 82 | 0.73 | Müller et al.27 |
| Distal radius 2/3–potted embalmed | 81±10 | 12F+9M | 60 | 1.5–7.4 | Distal radius 2/3, tetrahedral 1.2 mm, w cortex, fabric, nonlinear | 82 × 82 × 82 | 0.87 | Varga et al.17 |
| Distal radius section 20 mm–plate embalmed | 81±14 | 18F+7M | 5 | 0.95–4.7 | Distal section 20 mm, tetrahedral 1.3 mm, w cortex, fabric, nonlinear | 82 × 82 × 82 | 0.94 | Varga et al.28 |
| Distal radius 2/3–potted embalmed | 81±10 | 12F+9M | 60 | 1.5–7.4 | Standard section 9.1 mm, microFE, linear | 82 × 82 × 82 | 0.92 | Varga et al.24 |
| T12-L5–plate frozen, few embalmed | 42–84 | 16 F&M | 1 | ∼1–5 | Body, hexahedra, w cortex, iso, nonlinear | 300 × 300 × 2000 | 0.79 | Martin et al.40 |
| L1-L4–potted frozen | 37–87 | 7F+6M | 9 | ∼2–8 | Body, voxel 1 × 1 × 1.5 mm, wo cortex aniso, linear | 674 × 674 × 1500 | 0.86 | Crawford et al.39 |
| T11-L1–potted frozen | 31–83 | 12M | 0.5 | ∼1–5 | Body, tetrahedral <2 mm, w cortex, iso, nonlinear | 351x351 × 1000 | 0.96 | Imai et al.37 |
| T1-L5–potted fresh frozen | 54–97 | 77 F&M | 1 | ∼1–8 | Body, voxel 1 mm, wo cortex, aniso, nonlinear | 1000 × 1000 × 1000 | 0.80* | Buckley et al.38 |
| T12-L5 section–plate fresh frozen | 44–82 | 37 F&M | 5 | ∼2–9 | Section, voxel 1.3 mm, wo cortex, aniso, nonlinear | 391 × 391 × 450 | 0.78 | Dall'Ara et al.18 |
| Proximal femur–potted fresh frozen | 52–92 | 10F+8M | 30 | 0.5–4.5 | Voxel 3 mm, wo cortex, linear | 1080 × 1080 × 3000 | 0.90 | Keyak et al.51 |
| Proximal femur–potted fresh frozen | 51–69 | 6F+3M | 6000 | 1.7–6.2 | Tetrahedral <4mm, w cortex, linear/kill | <450 × 450 × 400 | 0.86 | Dragomir-Daescu et al.55 |
| Proximal femur–potted fixed in alcohol-formalin | 55–100 | 25F+15M | 396 | 1.5–5.5 | Tetrahedral <3 mm, w cortex, nonlinear | 250 × 250 × 750 | 0.87 | Koivumäki et al.77 |
| Proximal femur–potted fresh frozen | 46–96 | 19F+17 M | 5 | 1.5–5.3 | Voxel 3 mm, wo cortex, nonlinear | 330 × 330 × 1000 | 0.85 | Dall'Ara et al.19 |
Abbreviations: F, female; FE, finite element; M, male; microFE, microstructural FE.
*designates an adjusted R2.
The remarkable predictions of maximum force by BMC may be attributed to the optimal structure of the distal radius to sustain axial compressive load. There is no superfluous tissue and mineral mass correlates significantly with stiffness, which in turn is closely related to strength. The weak performance of aBMD in predicting maximal force was also observed by Pistoia et al.26
The implications of these outstanding in vitro results of microFE analysis are reflected by its discrimination power of fragility fractures in a number of cross-sectional studies, for example, Vilayphiou et al.,29 Stein et al.,30 Vilayphiou et al.,31 Boutroy et al.32 and Melton et al.33
Ultimate load of vertebral sections using QCT
Nontraumatic vertebral fractures represent a hallmark of osteoporosis and have been thoroughly classified.34 Although numerous biomechanical tests were realized by embedding the vertebral bodies in PMMA (Table 3), an alternative consisted in resecting the endplates to produce two flat surfaces that adapt well to compression plates. A recent FE analysis study demonstrated that the strength of vertebral bodies embedded in PMMA is essentially equivalent to that of the corresponding vertebral section without the endplates.35
Materials and methods
In the second study performed in our laboratory,18 37 vertebral sections (7 men and 3 women, aged 44–82, T12-L5) were prepared and scanned in a custom chamber using a clinical CT protocol (Brilliance64, Philips, Hamburg, Germany) with a voxel size of 0.391 × 0.391 × 0.45 mm3. The sections were compressed monotonically at a rate of 5 mm min−1 up to failure between two steel plates with a ball joint above the upper plate to allow free rotation (Figure 3). The vertebral bodies were positioned carefully to bring the axis of the testing machine anterior to the center of gravity of the middle cross-section. Most often, anterior, and twice posterior, wedge fractures were produced, which can be found in radiological assessment schemes.
Figure 3.
On the left, mechanical testing set-up of a human vertebral section. The upper plate is free to rotate and its position during the test is recorded with the help of three linear variable differential transformers (LVDT). On the right, a voxel-based homogenized FE model of a vertebral section is shown. The boundary conditions correspond to a displacement-driven axial compression at the cranial end with free rotation and fully fixed nodes at the caudal end. The gray level corresponds to the calibrated bone volume fraction.
A homogenized voxel-based FE model of each section was generated with an edge size of 1.3 mm. The nonlinear material properties were transverse isotropic with the axis of symmetry along the inferior–superior direction. The motion of the upper plate measured in the experiment was imposed on the top surface of the FE model. Like in the experiment, the fracture load of the FE analysis was obtained from the maximum of the force–displacement curve.
Results
The regression graphs for prediction of the in vitro strength of the vertebral sections are shown in Figure 4 for homogenized FE (voxelFE), BMC and lateral aBMD. The linear regression of the FE analysis is close to the 1:1 relationship without fitting of the bone material properties. The FE analysis provides the highest correlations and the minimum relative errors. The difference between the FE model and BMC or CSA–BMD in predicting maximal force is more pronounced than that for the radial sections but remains insignificant (P=0.175 and P=0.179, respectively). The lowest correlations were obtained by aBMD and the differences with voxelFE did reach significance for both maximum force and maximum apparent stress (Table 1). The predictions of BMD are again comparable to those of voxelFE for maximum apparent strength (P=0.283).
Figure 4.
Linear regressions between experimental strength of the vertebral sections and homogenized FE analysis (voxelFE), bone mineral content (BMC) and areal bone mineral density (aBMD). The blue solid line is the regression, the red dotted lines are the confidence intervals and the black dashed line is the 1:1 relationship. Adj. R2, the adjusted coefficient of determination; RMSE, relative root mean square error.
Discussion
As shown in Table 3, other validation studies on vertebral bodies achieved comparable or better correlations with maximum force using QCT-based homogenized FE, for example, Chevalier et al.,36 Imai et al.,37 Buckley et al.,38 Crawford et al.39 and Martin et al.40 Size and heterogeneity of the data set are known to affect such correlations. Nevertheless, modeling of the cortex in Imai et al.37 seems to substantially improve the FE predictions in the vertebral body. This effect was also reported in an ex vivo study using HR-pQCT.41 A further issue is the absence of any fitting in the FE model by Dall'Ara et al.18 Tuning material properties for a given data set may well achieve higher correlations but disregard the universality sought for a better surrogate of bone strength. The positive results of these biomechanical studies in vitro provided solid ground for its use in cross-sectional or prospective clinical studies, for example, Imai et al.,42 Graeff et al.43 and Keaveny et al.44 Finally, nonlinear FE of the vertebral body was shown to be statistically more sensitive than densitometric variables to evaluate the biomechanical benefit of drugs against osteoporosis.45
Ultimate load of the proximal femur in a sideways fall configuration using QCT
Fractures of the hip lead to the highest mortality, morbidity and health-care costs. A very large body of research has been conducted to study the mechanical behavior of the proximal femur and specifically for the validation of FE models in terms of strain,10,46,47 fracture load48,49,50,51 and fracture location.52,53 Although very few fractures seem to occur in the standing position, both stance and side-loading configurations were investigated.
Materials and methods
In the third study conducted in our laboratory,19 36 pairs of proximal femora (17 men and 19 women, aged 46–96) were freed of soft tissues except the cartilage of the head and embedded distally in polyurethane (PU). Each bone was submerged in a custom chamber filled with saline and subjected to a standard dual-energy X-ray absorptiometry examination (Discovery QDR, Hologic Inc., Bedford, MA, USA). In the same chamber, each sample was then scanned by clinical QCT (Brilliance64, Philips) with a calibration phantom. The reconstruction voxel size was 0.33 × 0.33 × 1.0 mm3.
The left and right femora of each pair were randomly assigned to a stance and side group for assignment to the biomechanical loading protocol. The side configuration did mimic a sideways fall onto the greater trochanter. The distal embedding of each femur was fully fixed in a servohydraulic testing system, and an axial load was applied to the head through an embedding cap in PU that allowed rotations. Custom bearings eliminated transverse forces and torsional moment. Each bone was loaded quasistatically and monotonically to failure at a displacement rate of 5mm min−1. The fracture pattern of each bone was then assessed with an antero-posterior (AP) X-ray. A homogenized voxel-based FE model of each bone with the relevant embedding was created with an element size of 3 × 3 × 3 mm3 (Figure 5). The nonlinear material properties were isotropic. The distal end was fully fixed and the embedding of the greater trochanter was free to move in the horizontal plane. The axial motion of the experimental loading device was applied to the upper surface of the embedding cap taken as a rigid body where the other degrees of freedom were kept free. The fracture load of both experiment and FE analysis was again defined as the maximum of the force–displacement curve.
Figure 5.
On the left, experimental design for testing the human proximal femur in a side-loading configuration. On the right, voxel-based FE models of the human proximal femur in the same side-loading configuration. The gray level represents the bone volume fraction.
Results
In general, the experiments produced typical subcapital, neck and trochanteric fractures with a few atypical or indiscernible fractures. The agreement between X-rays and damage distribution computed by FE was 71% for the side configuration. The regression graphs of prediction of the femoral fracture load are shown in Figure 6 for homogenized FE (VoxelFE), BMC and the aBMD of the neck. There is a fair quantitative correspondence between the experiment and the FE prediction for the fall configuration. The coefficient of determination of the FE prediction of maximum force is higher than that of aBMD, but the difference did not show statistical significance (P=0.264). In contrast to the radial and vertebral sections, the predictions of maximum force by BMC in the femur were significantly lower than those of FE (P=0.032).
Figure 6.
Linear regressions between experimental strength of the proximal femora and homogenized FE analysis (voxelFE), bone mineral content (BMC) and areal bone mineral density (aBMD). The blue solid line is the regression, the red dotted lines are the confidence intervals and the black dashed line is the 1:1 relationship. Adj. R2, adjusted coefficient of determination; RMSE, relative root mean square error.
Discussion
The correlation coefficients between the FE strength predictions and the experimental strength in the fall configuration are highly consistent among the validation studies listed in Table 3. Surprisingly, the inclusion of the cortex in the proximal femur does not appear to have the same impact on the strength predictions as in the vertebral body. This may be related to the difficulty in extracting the varying thickness of the cortex and material anisotropy of the proximal femur from whole-body QCT images. It should be noted that for homogenized voxel models of the proximal femur, nonlinear analysis performs better than linear analysis.49 The predictions of maximum force by the FE method were higher but not significantly different than that by aBMD, which may reflect a lack of statistical power but also confirm the value of neck aBMD in predicting not only hip strength in a side configuration but also hip fractures, as shown in numerous epidemiological studies, for example, Johnell et al.54 Nevertheless, one study could demonstrate higher correlation coefficients for some FE strength predictions when compared with hip aBMD in the fall configuration.55
The experimental evidence supporting these QCT-based FE models of the proximal femur motivated their application in several clinical and space-flight studies.56,57,58,59,60,61,62 Finally, a recent study in White women and men showed that femoral strength assessed by homogenized FE declines much faster with age than aBMD.63
General discussion
Three biomechanical experiments were developed to reproduce the three most common osteoporotic fractures in the laboratory and to compare the performance of several surrogates of the bone strength.
A recurrent criticism of such experiments is that they are only caricatures of the load cases occurring in the real lives of real patients. However, the aim of these experiments is not the perfect match with an individual reality but the systematic validation of the QCT-based FE methodology for representative anatomies and loading modes. The FE method is founded on the universal principles of mechanics and has the potential, after proper validation, to simulate arbitrarily complex loading cases whenever these are accurately known, for instance, from musculoskeletal models of the human body.64 The particular load cases selected in these experiments should, therefore, not be seen as limitations in regard to the diversity of clinical fractures, but rather as opportunities to test the universal assumptions of the FE approach.
The highest correlations and lowest errors for prediction of the maximum force using the FE method were obtained at the distal radius site that benefits from detailed HR-pQCT images and for which microFE models can be realized. The FE models for vertebral sections and proximal femora exhibited weaker predictions, as their bone material properties were homogenized and based on QCT images with comparably coarser resolution. The proper consideration of cortical thickness and trabecular anisotropy may be the key factors to improve the current models and are investigated in several laboratories using high-resolution CT.41,65,66 Given the excellent FE predictions obtained in the trabecular bone samples using microCT,67 future improvements of CT technology are expected to lead to improved FE models alongside the development of refined image-processing tools.
In the case of axial compression, which was used for the distal radius and the vertebral sections, it is possible to define intensive (as opposed to extensive or additive) variables that normalize the bone mass by volume (BMD), the forces by the area (apparent stresses) and the displacements by height (apparent strains). In this perspective, aBMD is a hybrid variable that lies somewhere between BMC and BMD. In the case of the side loading of the proximal femur, the resulting stresses are heterogeneous and do not allow for a simple geometrical normalization.
In this context, the correlation coefficients (R2) and the relative RMSE for the prediction of maximal force and maximal apparent stress are summarized in Tables 1 and 2. Clearly, it makes sense to correlate intensive or extensive variables among themselves but not to mix them up. In the distal radius, the extensive variables provided better correlations and lower errors than the intensive variables. In the vertebral sections, they were comparable. The origin of this difference may be because of the distinct coefficients of variation in maximal force (32 versus 40%) and ultimate stress (31 versus 30%) in the vertebral body versus the distal radius. The normalized variables are attractive for moving from bone strength to a factor of risk toward bone fracture risk,68 which depends on the applied load and therefore on patient body weight. On the basis of a simple dimensional analysis, it can be argued that unlike maximal force, maximal stress is approximately independent of body size and weight,69 and therefore reflects a more objective factor of risk.
The hybrid variable aBMD has a level of strength prediction that seems to depend on the anatomical site, load configuration70 and the particular sample collection.55 These facts emphasize the main limitations of aBMD as a surrogate for bone strength. Although not all validation studies listed in Table 3 report comparisons with densitometric variables, their strength predictions are less consistent and are systematically, often significantly, inferior to those of the FE method. Nevertheless, it should be acknowledged that aBMD in the spine and hip requires substantially less radiation dose than QCT, costs less and is easier to calculate than FE models.
The presented FE models share several limitations with densitometric variables. First, the composition and mechanical properties of the bone extracellular matrix are assumed to be independent of anatomical site, gender and age. Although an indentation study indicates that matrix stiffness is independent of gender and age in the human vertebra,71 it was also shown that microdamage increases72 and the bone toughness decreases with age.73 Second, while trabecular architecture is highly heterogeneous, its relationship with volume fraction and fabric (or its optimality) is similarly assumed to be independent of anatomical site, gender and age. However, there is still little evidence that this is not the case.74,75 Third, only one validation study accounted for the high strain rates characteristic of falls on the proximal femur.55 This issue can be addressed by using rate-dependent constitutive laws in the FE models, but these need to be carefully identified for the relevant impact velocities.
To conclude, for the three most common osteoporotic fracture sites, QCT-based FE analysis is a more reliable surrogate of bone strength than densitometric variables. This implies that despite the above limitations, FE analysis represents an improved basis for fracture risk assessment when compared with densitometric variables such as aBMD when calibrated QCT images are available. This improvement may gain in clinical significance with the progress of imaging technologies and FE modeling techniques, but obviously does not address the other determinants of fracture risk such as the occurrence of falls.
Acknowledgments
This work was supported by the Vienna University of Technology and the University of Bern. We are grateful to Gerhard Schneider, Heinz Pettermann, Robert Exler and Jarunan Panyasantisuk for their contributions.
Footnotes
The authors declare no conflict of interest.
References
- Prendergast PJ. Finite element models in tissue mechanics and orthopaedic implant design. Clin Biomech 1997;12:343–366. [DOI] [PubMed] [Google Scholar]
- Hobatho MC, Darmana R, Pastor P, Barrau JJ, Laroze S, Morucci JP. Development of a three-dimensional finite element model of a human tibia using experimental modal analysis. J Biomech 1991;24:371–383. [DOI] [PubMed] [Google Scholar]
- Crolet JM, Aoubiza B, Meunier A. Compact bone: numerical simulation of mechanical characteristics. J Biomech 1993;26:677–687. [DOI] [PubMed] [Google Scholar]
- Rüegsegger P, Koller B, Müller R. A microtomographic system for the nondestructive evaluation of bone architecture. Calcif Tissue Int 1996;58:24–29. [DOI] [PubMed] [Google Scholar]
- Hollister SJ, Kikuchi N. Homogenization theory and digital imaging: a basis for studying the mechanics and design principles of bone tissue. Biotechnol Bioeng 1994;43:586–596. [DOI] [PubMed] [Google Scholar]
- Zysset PK, Curnier AA. 3D damage model for trabecular bone based on fabric tensors. J Biomech 1996;29:1549–1558. [PubMed] [Google Scholar]
- Beaupre GS, Orr TE, Carter DR. An approach for time-dependent bone modeling and remodeling--theoretical development. J Orthop Res 1990;8:651–661. [DOI] [PubMed] [Google Scholar]
- Huiskes R, Ruimerman R, van Lenthe GH, Janssen JD. Effects of mechanical forces on maintenance and adaptation of form in trabecular bone. Nature 2000;405:704–706. [DOI] [PubMed] [Google Scholar]
- Erdemir A, Guess TM, Halloran J, Tadepalli SC, Morrison TM. Considerations for reporting finite element analysis studies in biomechanics. J Biomech 2012;45:625–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schileo E, Taddei F, Malandrino A, Cristofolini L, Viceconti M. Subject-specific finite element models can accurately predict strain levels in long bones. J Biomech 2007;40:2982–2989. [DOI] [PubMed] [Google Scholar]
- Carpenter RD. Finite element analysis of the hip and spine based on quantitative computed tomography. Curr Osteop Rep 2013;11:156–162. [DOI] [PubMed] [Google Scholar]
- Keyak JH, Skinner HB. Three-dimensional finite element modelling of bone: effects of element size. J Biomed Eng 1992;14:483–489. [DOI] [PubMed] [Google Scholar]
- Zysset PK. Indentation of bone tissue: a short review. Osteop Int 2009;20:1049–1055. [DOI] [PubMed] [Google Scholar]
- Pahr DH, Zysset PK. From high-resolution CT data to finite element models: development of an integrated modular framework. Comput Methods Biomech Biomed Engin 2009;12:45–57. [DOI] [PubMed] [Google Scholar]
- Rincon-Kohli L, Zysset PK. Multi-axial mechanical properties of human trabecular bone. Biomech Model Mechanobiol 2009;8:195–208. [DOI] [PubMed] [Google Scholar]
- Garcia D, Zysset PK, Charlebois M, Curnier A. A three-dimensional elastic plastic damage constitutive law for bone tissue. Biomech Model Mechanobiol 2009;8:149–165. [DOI] [PubMed] [Google Scholar]
- Varga P, Baumbach S, Pahr D, Zysset PK. Validation of an anatomy specific finite element model of Colle's fracture. J Biomech 2009;42:1726–1731. [DOI] [PubMed] [Google Scholar]
- Dall'Ara E, Schmidt R, Pahr D, Varga P, Chevalier Y, Patsch J et al. A nonlinear finite element model validation study based on a novel experimental technique for inducing anterior wedge-shape fractures in human vertebral bodies in vitro. J Biomech 2010;43:2374–2380. [DOI] [PubMed] [Google Scholar]
- Dall'Ara E, Luisier B, Schmidt R, Kainberger F, Zysset PK, Pahr DH. A nonlinear QCT-based finite element model validation study for the human femur tested in two configurations in vitro. Bone 2013;52:27–38. [DOI] [PubMed] [Google Scholar]
- Steiger JH. Tests for comparing elements of a correlation matrix. Psychol Bull 1980;87:247–251. [Google Scholar]
- Colles A. On the fracture of the carpal extremity of the radius. Edinb Med Surg J. 1814;10:181. Clin Orthop Relat Res 2006;445:5–7. [DOI] [PubMed] [Google Scholar]
- Baumbach SF, Schmidt R, Varga P, Heinz T, Vecsei V, Zysset PK. Where is the distal fracture line location of dorsally displaced distal radius fractures? J Orthop Res 2011;29:489–494. [DOI] [PubMed] [Google Scholar]
- Varga P, Baumbach S, Pahr D, Charlebois M, Zysset P. Validation of an anatomy-specific finite element model of Colle's fracture. J Biomech 2009;42:1726–1731. [DOI] [PubMed] [Google Scholar]
- Varga P, Pahr DH, Baumbach S, Zysset PK. HR-pQCT based FE analysis of the most distal radius section provides an improved prediction of Colles' fracture load in vitro. Bone 2010;47:982–988. [DOI] [PubMed] [Google Scholar]
- Hoffler CE, Moore KE, Kozloff K, Zysset PK, Brown MB, Goldstein SA. Heterogeneity of bone lamellar-level elastic moduli. Bone 2000;26:603–609. [DOI] [PubMed] [Google Scholar]
- Pistoia W, van Rietbergen B, Lochmuller EM, Lill CA, Eckstein F, Ruegsegger P. Image-based micro-finite-element modeling for improved distal radius strength diagnosis: moving from bench to bedside. J Clin Densitom. 2004;7:153–160. [DOI] [PubMed]
- Mueller TL, Christen D, Sandercott S, Boyd SK, van Rietbergen B, Eckstein F et al. Computational finite element bone mechanics accurately predicts mechanical competence in the human radius of an elderly population. Bone 2011;48:1232–1238. [DOI] [PubMed] [Google Scholar]
- Varga P, Dall'Ara E, Pahr DH, Pretterklieber M, Zysset PK. Validation of an HR-pQCT-based homogenized finite element approach using mechanical testing of ultra-distal radius sections. Biomech Model Mechanobiol 2011;10:431–444. [DOI] [PubMed] [Google Scholar]
- Vilayphiou N, Boutroy S, Szulc P, van Rietbergen B, Munoz F, Delmas PD et al. Finite element analysis performed on radius and tibia HR-pQCT images and fragility fractures at all sites in men. J Bone Miner Res 2011;26:965–973. [DOI] [PubMed] [Google Scholar]
- Stein EM, Liu XS, Nickolas TL, Cohen A, Thomas V, McMahon DJ et al. Abnormal microarchitecture and reduced stiffness at the radius and tibia in postmenopausal women with fractures. J Bone Miner Res 2010;25:2572–2581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilayphiou N, Boutroy S, Sornay-Rendu E, Van Rietbergen B, Munoz F, Delmas PD et al. Finite element analysis performed on radius and tibia HR-pQCT images and fragility fractures at all sites in postmenopausal women. Bone 2010;46:1030–1037. [DOI] [PubMed] [Google Scholar]
- Boutroy S, Van Rietbergen B, Sornay-Rendu E, Munoz F, Bouxsein ML, Delmas PD. Finite element analysis based on in vivo HR-pQCT images of the distal radius is associated with wrist fracture in postmenopausal women. J Bone Miner Res 2008;23:392–399. [DOI] [PubMed] [Google Scholar]
- Melton LJ 3rd, Riggs BL, van Lenthe GH, Achenbach SJ, Muller R, Bouxsein ML et al. Contribution of in vivo structural measurements and load/strength ratios to the determination of forearm fracture risk in postmenopausal women. J Bone Miner Res 2007;22:1442–1448. [DOI] [PubMed] [Google Scholar]
- Genant HK, Guglielmi G, Jergas M (eds)Bone Densitometry and Osteoporosis Springer-Verlag: Berlin, Germany, 1998;. [Google Scholar]
- Maquer G, Dall'Ara E, Zysset PK. Removal of the cortical endplates has little effect on ultimate load and damage distribution in QCT-based voxel models of human lumbar vertebrae under axial compression. J Biomech 2012;45:1733–1738. [DOI] [PubMed] [Google Scholar]
- Chevalier Y, Charlebois M, Pahra D, Varga P, Heini P, Schneider E et al. A patient-specific finite element methodology to predict damage accumulation in vertebral bodies under axial compression, sagittal flexion and combined loads. Comput Methods Biomech Biomed Engin 2008;11:477–487. [DOI] [PubMed] [Google Scholar]
- Imai K, Ohnishi I, Bessho M, Nakamura K. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine 2006;31:1789–1794. [DOI] [PubMed] [Google Scholar]
- Buckley JM, Loo K, Motherway J. Comparison of quantitative computed tomography-based measures in predicting vertebral compressive strength. Bone 2007;40:767–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford RP, Cann CE, Keaveny TM. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone 2003;33:744–750. [DOI] [PubMed] [Google Scholar]
- Martin H, Werner J, Andersen R, Schober H-C, Schmitz K-P. Noninvasive assessment of stiffness and failure load of human vertebrae from CT-data. Biomed Tech 1998;43:82–88. [DOI] [PubMed] [Google Scholar]
- Chevalier Y, Pahr D, Zysset PK. The role of cortical shell and trabecular fabric in finite element analysis of the human vertebral body. J Biomech Eng 2009;131:111003. [DOI] [PubMed] [Google Scholar]
- Imai K, Ohnishi I, Matsumoto T, Yamamoto S, Nakamura K. Assessment of vertebral fracture risk and therapeutic effects of alendronate in postmenopausal women using a quantitative computed tomography-based nonlinear finite element method. Osteop Int 2009;20:801–810. [DOI] [PubMed] [Google Scholar]
- Graeff C, Chevalier Y, Charlebois M, Varga P, Pahr D, Nickelsen TN et al. Improvements in vertebral body strength under teriparatide treatment assessed in vivo by finite element analysis: results from the EUROFORS study. J Bone Miner Res 2009;24:1672–1680. [DOI] [PubMed] [Google Scholar]
- Keaveny TM, Donley DW, Hoffmann PF, Mitlak BH, Glass EV, San Martin JA. Effects of teriparatide and alendronate on vertebral strength as assessed by finite element modeling of QCT scans in women with osteoporosis. J Bone Miner Res 2007;22:149–157. [DOI] [PubMed] [Google Scholar]
- Tawara D, Sakamoto J, Murakami H, Kawahara N, Oda J, Tomita K. Mechanical evaluation by patient-specific finite element analyses demonstrates therapeutic effects for osteoporotic vertebrae. J Mech Behav Biomed Mater 2010;3:31–40. [DOI] [PubMed] [Google Scholar]
- Yosibash Z, Trabelsi N, Milgrom C. Reliable simulations of the human proximal femur by high-order finite element analysis validated by experimental observations. J Biomech 2007;40:3688–3699. [DOI] [PubMed] [Google Scholar]
- Keyak JH, Fourkas MG, Meagher JM, Skinner HB. Validation of an automated method of three-dimensional finite element modelling of bone. J Biomed Eng 1993;15:505–509. [DOI] [PubMed] [Google Scholar]
- Bessho M, Ohnishi I, Matsuyama J, Matsumoto T, Imai K, Nakamura K. Prediction of strength and strain of the proximal femur by a CT-based finite element method. J Biomech 2007;40:1745–1753. [DOI] [PubMed] [Google Scholar]
- Keyak JH. Improved prediction of proximal femoral fracture load using nonlinear finite element models. Med Eng Phys 2001;23:165–173. [DOI] [PubMed] [Google Scholar]
- Cody DD, Gross GJ, Hou FJ, Spencer HJ, Goldstein SA, Fyhrie DP. Femoral strength is better predicted by finite element models than QCT and DXA. J Biomech 1999;32:1013–1020. [DOI] [PubMed] [Google Scholar]
- Keyak JH, Rossi SA, Jones KA, Skinner HB. Prediction of femoral fracture load using automated finite element modeling. J Biomech 1998;31:125–133. [DOI] [PubMed] [Google Scholar]
- Ota T, Yamamoto I, Morita R. Fracture simulation of the femoral bone using the finite-element method: how a fracture initiates and proceeds. J Bone Miner Metab 1999;17:108–112. [DOI] [PubMed] [Google Scholar]
- Keyak JH, Rossi SA, Jones KA, Les CM, Skinner HB. Prediction of fracture location in the proximal femur using finite element models. Med Eng Phys 2001;23:657–664. [DOI] [PubMed] [Google Scholar]
- Johnell O, Kanis JA, Oden A, Johansson H, De Laet C, Delmas P et al. Predictive value of BMD for hip and other fractures. J Bone Miner Res 2005;20:1185–1194. [DOI] [PubMed] [Google Scholar]
- Dragomir-Daescu D, Op Den Buijs J, McEligot S, Dai Y, Entwistle RC, Salas C et al. Robust QCT/FEA models of proximal femur stiffness and fracture load during a sideways fall on the hip. Ann Biomed Eng 2011;39:742–755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keaveny TM, Hoffmann PF, Singh M, Palermo L, Bilezikian JP, Greenspan SL et al. Femoral bone strength and its relation to cortical and trabecular changes after treatment with PTH, alendronate, and their combination as assessed by finite element analysis of quantitative CT scans. J Bone Miner Res 2008;23:1974–1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orwoll ES, Marshall LM, Nielson CM, Cummings SR, Lapidus J, Cauley JA et al. Finite element analysis of the proximal femur and hip fracture risk in older men. J Bone Miner Res 2009;24:475–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keyak JH, Koyama AK, LeBlanc A, Lu Y, Lang TF. Reduction in proximal femoral strength due to long-duration spaceflight. Bone 2009;44:449–453. [DOI] [PubMed] [Google Scholar]
- Lewiecki EM, Keaveny TM, Kopperdahl DL, Genant HK, Engelke K, Fuerst T et al. Once-monthly oral ibandronate improves biomechanical determinants of bone strength in women with postmenopausal osteoporosis. J Clin Endocrinol Metab 2009;94:171–180. [DOI] [PubMed] [Google Scholar]
- Amin S, Kopperdhal DL, Melton LJ 3rd, Achenbach SJ, Therneau TM, Riggs BL et al. Association of hip strength estimates by finite-element analysis with fractures in women and men. J Bone Miner Res 2011;26:1593–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keyak JH, Sigurdsson S, Karlsdottir G, Oskarsdottir D, Sigmarsdottir A, Zhao S et al. Male-female differences in the association between incident hip fracture and proximal femoral strength: a finite element analysis study. Bone 2011;48:1239–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keaveny TM, McClung MR, Wan X, Kopperdahl DL, Mitlak BH, Krohn K. Femoral strength in osteoporotic women treated with teriparatide or alendronate. Bone 2012;50:165–170. [DOI] [PubMed] [Google Scholar]
- Keaveny TM, Kopperdahl DL, Melton LJ 3rd, Hoffmann PF, Amin S, Riggs BL et al. Age-dependence of femoral strength in white women and men. J Bone Miner Res 2010;25:994–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damsgaard M, Rasmussen J, Christensen ST, Surma E, de Zee M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul Model Pract Th 2006;14:1100–1111. [Google Scholar]
- Eswaran SK, Gupta A, Adams MF, Keaveny TM. Cortical and trabecular load sharing in the human vertebral body. J Bone Miner Res 2006;21:307–314. [DOI] [PubMed] [Google Scholar]
- Fields AJ, Eswaran SK, Jekir MG, Keaveny TM. Role of trabecular microarchitecture in whole-vertebral body biomechanical behavior. J Bone Miner Res 2009;24:1523–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfram U, Wilke HJ, Zysset PK. Valid micro finite element models of vertebral trabecular bone can be obtained using tissue properties measured with nanoindentation under wet conditions. J Biomech 2010;43:1731–1737. [DOI] [PubMed] [Google Scholar]
- Hayes WC, Piazza SJ, Zysset PK. Biomechanics of fracture risk prediction of the hip and spine by quantitative computed tomography. Radiol Clin N Am 1991;29:1–18. [PubMed] [Google Scholar]
- Biewener AA. Musculoskeletal design in relation to body size. J Biomech 1991;24(Suppl 1): 19–29. [DOI] [PubMed] [Google Scholar]
- Dall'ara E, Luisier B, Schmidt R, Pretterklieber M, Kainberger F, Zysset P et al. DXA predictions of human femoral mechanical properties depend on the load configuration. Med Eng Phys 2013;S1350-4533:00101–0010. [DOI] [PubMed] [Google Scholar]
- Wolfram U, Wilke HJ, Zysset PK. Rehydration of vertebral trabecular bone: influences on its anisotropy, its stiffness and the indentation work with a view to age, gender and vertebral level. Bone 2010;46:348–354. [DOI] [PubMed] [Google Scholar]
- Schaffler MB, Choi K, Milgrom C. Aging and matrix microdamage accumulation in human compact bone. Bone 1995;17:521–525. [DOI] [PubMed] [Google Scholar]
- Nyman JS, Makowski AJ. The contribution of the extracellular matrix to the fracture resistance of bone. Curr Osteop Rep 2012;10:169–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homminga J, McCreadie BR, Weinans H, Huiskes R. The dependence of the elastic properties of osteoporotic cancellous bone on volume fraction and fabric. J Biomech 2003;36:1461–1467. [DOI] [PubMed] [Google Scholar]
- Gross T, Pahr DH, Zysset PK. Morphology-elasticity relationships using decreasing fabric information of human trabecular bone from three major anatomical locations. Biomech Model Mechanobiol 2013;12:793–800. [DOI] [PubMed] [Google Scholar]
- Pistoia W, VanRietbergen B, Lochmüller EM, Lill CA, Eckstein F, Rüegsegger P. Estimation of distal radius failure load with micro- finite element analysis models based on three-dimensional peripheral quantitative computed tomography images. Bone 2002;30:842–848. [DOI] [PubMed] [Google Scholar]
- Koivumaki JE, Thevenot J, Pulkkinen P, Kuhn V, Link TM, Eckstein F et al. CT-based finite element models can be used to estimate experimentally measured failure loads in the proximal femur. Bone 2012;50:824–829. [DOI] [PubMed] [Google Scholar]