Aris-Taylor dispersion with drift and diffusion of particles on the tube wall

Abstract

A laminar stationary flow of viscous fluid in a cylindrical tube enhances the rate of diffusion of Brownian particles along the tube axis. This so-called Aris-Taylor dispersion is due to the fact that cumulative times, spent by a diffusing particle in layers of the fluid moving with different velocities, are random variables which depend on the realization of the particle stochastic trajectory in the radial direction. Conceptually similar increase of the diffusivity occurs when the particle randomly jumps between two states with different drift velocities. Here we develop a theory that contains both phenomena as special limiting cases. It is assumed (i) that the particle in the flow can reversibly bind to the tube wall, where it moves with a given drift velocity and diffusivity, and (ii) that the radial and longitudinal diffusivities of the particle in the flow may be different. We derive analytical expressions for the effective drift velocity and diffusivity of the particle, which show how these quantities depend on the geometric and kinetic parameters of the model.

INTRODUCTION

The increase of the diffusivity of Brownian particles due to a radial gradient of advection velocity (often referred to as the Aris-Taylor or shear dispersion^{1, 2, 3}) is of a significant importance in a number of fields of science and technology covering many practical applications. Examples include chemical engineering (microfluidics,⁴ chromatography,^{5, 6} heterogeneous catalysis²), biophysics (vascular flow,⁷ airflow in lungs,⁸ targeted drug delivery⁹), and transport processes in geophysical systems (capillary flows in fractures,¹⁰ colloid filtration,¹¹ mixing in rivers¹²). Starting with the seminal works of Taylor,^{13, 14} who calculated the diffusivity of a passive tracer in the Poiseuille flow (laminar flow in a cylindrical tube), followed by a more rigorous derivation of Aris,¹⁵ this problem has been in the focus of both theoretical and experimental studies for the last six decades. There is a vast amount of literature devoted to this subject (see Refs. ^{1, 2, 3, 16, 17} and references therein). Although the Aris-Taylor dispersion is nowadays discussed in textbooks,^{1, 2, 16, 17} it is still the area of active research.^{18, 19, 20, 21, 22, 23}

The celebrated result obtained by Taylor^{13, 14} can be summarized as follows. Consider a laminar stationary flow of viscous fluid in a cylindrical tube of radius a (Fig. 1). The velocity profile of the Poiseuille flow is given by the well-known expression

$$v_{\mathit{f}}\left(r\right)=2{\overline{v}}_{\mathit{f}}\left(1-\frac{r^2}{a^2}\right),$$ (1.1)

where ${\overline{v}}_{\mathit{f}}$ is the velocity averaged over the tube cross-section, ${\overline{v}}_{\mathit{f}}=(2/a^2){\int }_0^a{v}_{\mathit{f}}\left(r\right)rdr$. Taylor showed that the effective diffusivity of a point Brownian particle along the tube axis is given by

$$D_{\mathit{eff}}=D_{\mathit{f}}+\frac{{\overline{v}}_{\mathit{f}}^2{a}^2}{48D_{\mathit{f}}},$$ (1.2)

where D_f is the particle diffusivity in the absence of the flow.

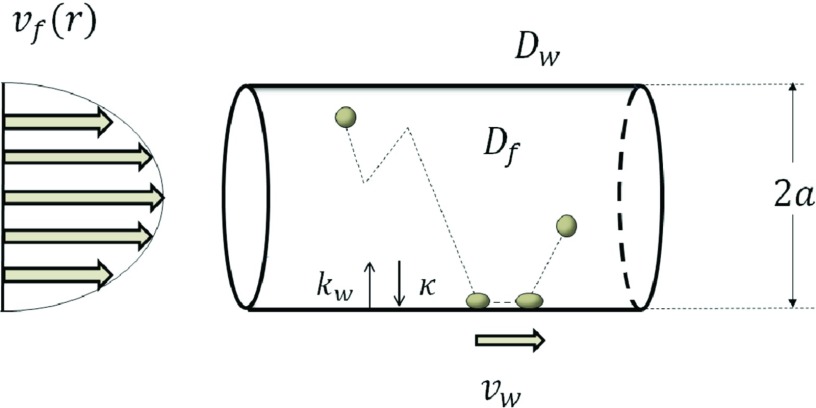
Figure 1.

The Aris-Taylor dispersion of a Brownian particle with reversible binding to the tube walls: a is the tube radius, v_f(r) is the velocity profile of the Poiseuille flow, v_w is the particle velocity on the wall, D_f and D_w are the particle diffusivities in the fluid and on the wall, κ and k_w are the intrinsic rate constants (see Eq. 1.3).

Since the pioneering work of Taylor this problem has been extended to cover more complicated settings including various geometrical complexities,^{24, 25} oscillating flows,^{7, 26} transient phenomena,¹⁹ effects of chemical reactions,^{27, 28, 29} and many others (see, for instance, books^{1, 2} and recent papers^{19, 21}). An important generalization of the problem is to account for the “effect of wall” (absorption and desorption, as well as diffusion of the particle on the wall). The “wall effect” is especially important for the design of microfluidic devices (so-called “Lab-on-a-Chip”^{17, 30}). It has been studied theoretically in a number of recent publications (see Refs. ^{20, 22, 27, 31, 32} and references therein).

When a Brownian particle is advected by a laminar flow, its reversible binding to the tube wall can be described by the kinetic scheme

$$\mathrm{flow}\underset{k_w}{\stackrel{\kappa }{\rightleftarrows }}\mathrm{wall},$$ (1.3)

where κ and k_w are the intrinsic rate constants (see Fig. 1). Let $P_w^{eq}$ and $P_f^{eq}$ be the equilibrium probabilities of funding the particle on the wall and in the flow, $P_w^{eq}+P_f^{eq}=1$. As follows from the principle of detailed balance the ratio of these probabilities is

$$\frac{P_w^{eq}}{P_f^{eq}}=\frac{2\kappa }{a{k}_{\mathit{w}}}=K,$$ (1.4)

where K is the equilibrium constant. This allows us to write $P_w^{eq},P_f^{eq}$ in terms of the equilibrium constant

$$P_f^{eq}=\frac{1}{1+K},P_w^{eq}=\frac{K}{1+K}.$$ (1.5)

If the particle on the wall diffuses with the diffusivity D_w and has no drift velocity, the effective drift velocity and diffusivity are given by^{1, 5, 20, 27}

$$v_{\mathit{eff}}={\overline{v}}_{\mathit{f}}{P}_f^{eq},$$ (1.6)

$$D_{\mathit{eff}}=D_{\mathit{f}}{P}_{\mathit{f}}^{eq}+D_{\mathit{w}}{P}_{\mathit{w}}^{eq}+▵D,$$ (1.7)

where

$$▵D={\left(P_f^{eq}\right)}^3{\overline{v}}_{\mathit{f}}^2\left[\frac{K}{k_w}+\frac{a^2}{48D_{\mathit{f}}}(1+6K+11K^2)\right].$$ (1.8)

An interesting result was obtained by Dorfman and Brenner,³³ who pointed out that the increase of the particle diffusivity, which is conceptually identical to the Aris-Taylor dispersion, occurs when the particle randomly jumps between two states with different drift velocities. To formulate the Dorfman–Brenner results using the kinetic scheme in Eq. 1.3, we assume that the particle diffusion in the flow is anisotropic, namely, its radial diffusivity is infinite, while its diffusivity along the tube axis is finite and equal to D_f. Then, when the particle enters the flow from the wall, it instantly equilibrates over the tube cross section. As a result, (i) the particle drift velocity in the flow does not fluctuate and is equal to ${\overline{v}}_{\mathit{f}}$, and (ii) its survival probability in the flow decays as a single exponential with the rate constant k_f = 2κ/a. In addition, we assume that the particle on the wall has drift velocity v_w and diffusivity D_w. In this case the Dorfman–Brenner theory leads to (see also Ref. 34)

$$v_{\mathit{eff}}={\overline{v}}_{\mathit{f}}{P}_{\mathit{f}}^{eq}+v_{\mathit{w}}{P}_{\mathit{w}}^{eq},$$ (1.9)

and the effective diffusivity given by Eq. 1.7, in which △D is

$$\begin{array}{c}\hfill ▵D={\left(P_f^{eq}\right)}^3{({\overline{v}}_{\mathit{f}}-v_{\mathit{w}})}^{2}K/k_{\mathit{w}}.\end{array}$$ (1.10)

In the present paper, we extend the results in Eqs. 1.6, 1.7, 1.8, 1.9, 1.10. More specifically, we developed a general theory assuming (i) that the radial diffusivity D_r of the particle in the flow can be arbitrary, and (ii) that the particle on the wall has a finite drift velocity v_w. We will see that the effective drift velocity is given by Eq. 1.9, and the effective diffusivity has the form of Eq. 1.7 with △D given by

$$\begin{array}{ccc}\hfill ▵D& =& {\left(P_{\mathit{f}}^{eq}\right)}^3\{{({\overline{v}}_{\mathit{f}}-v_{\mathit{w}})}^2\frac{K}{k_{\mathit{w}}}\hfill \\ & & +\frac{a^2}{48D_r}[(1+6K+11K^2){\overline{v}}_{\mathit{f}}^2-4K(K+1){\overline{v}}_{\mathit{f}}{v}_{\mathit{w}}\hfill \\ & & +6K^2{v}_{\mathit{w}}^2\left]\right\}.\hfill \end{array}$$ (1.11)

This is a modification of the expression for △D in Eq. 1.8 due to a finite particle drift velocity on the wall and its anisotropic diffusivity in the flow. Note that the product ${\left(P_{\mathit{f}}^{eq}\right)}^3$ and the first term in the curly brackets is identical to the Dorfman–Brenner formula for △D, Eq. 1.10. At $v_{\mathit{w}}={\overline{v}}_{\mathit{f}}$ Eq. 1.11 simplifies and takes the form

$$▵D={\left(P_{\mathit{f}}^{eq}\right)}^3{\overline{v}}_{\mathit{f}}^2\left[\frac{a^2}{48D_r}(1+2K+13K^2)\right].$$ (1.12)

The expressions in Eqs. 1.7, 1.9, 1.11 are the main results of the present paper. When v_w = 0 and D_x = D_r = D_f they reduce to Eqs. 1.6, 1.7, 1.8. In the other limiting case of D_r → ∞, we recover the Dorfman–Brenner formulas 1.7, 1.9, 1.10.

A number of methods have been developed for analytical treatment of the Aris-Taylor dispersion including the method of statistical moments (originally proposed by Aris¹⁵), the method of matched asymptotic expansions,²⁷ the center manifold approach^{3, 35} and some others (see Refs. ^{19, 32} and references therein). In the present study, we apply the approach proposed in Ref. 18, which is based on consideration of the axial displacement of a single particle that moves in the plane perpendicular to the tube axis along a given trajectory ${\left\{\mathbf{r}\right\}}_t$. The approach exploits the fact that the radial motion of the particle is independent of its axial coordinate. Averaging the displacement and its square over realizations of ${\left\{\mathbf{r}\right\}}_t$, we find the first two moments of the particle displacement along the tube axis, which in turn are used to calculate v_eff and D_eff.

The outline of the paper is as follows. The expressions for the effectively velocity, Eq. 1.9, and the effective diffusivity, Eqs. 1.7, 1.11, are derived in Secs. 2, 3, respectively. Some concluding remarks are made in Sec. 4.

EFFECTIVE DRIFT VELOCITY

Let $\mathbf{r}\left(t\right)$ be the particle position in the plane normal to the tube axis at time t; r = a corresponds to the particle on the tube wall, while r < a corresponds to the particle in the bulk flow. The particle velocity along the tube axis at time t is given by

$$\dot{x}\left(t\right|\mathbf{r}\left(t\right))=v\left(r\left(t\right)\right)+f\left(t\right|r\left(t\right)),$$ (2.1)

where the velocity v(r) is

$$\begin{array}{c}\hfill v\left(r\right)=\left\{\begin{array}{cc}{v}_f\left(r\right),\hfill & r<a,\hfill \\ v_w,\hfill & r=a,\hfill \end{array}\right.\end{array}$$ (2.2)

and f(t|r) is the Gaussian δ-correlated random force

$$\begin{array}{c}\hfill f\left(t\right|r)=\left\{\begin{array}{cc}{f}_f\left(t\right),\hfill & r<a,\hfill \\ f_w\left(t\right),\hfill & r=a,\hfill \end{array}\right.\end{array}$$ (2.3)

with zero mean ⟨f_f(t)⟩ = ⟨f_w(t)⟩ = 0. The correlation functions of the two components of the random force are ⟨f_f(t)f_w(t′)⟩ = 0, and

$$\frac{1}{D_f}⟨f_f\left(t\right)f_f\left(t^{\prime }\right)⟩=\frac{1}{D_w}⟨f_w\left(t\right)f_w\left(t^{\prime }\right)⟩=2\delta (t-t^{\prime }),$$ (2.4)

where the angular brackets ⟨…⟩ denote averaging over realizations of the random force.

Let ${\left\{\mathbf{r}\right\}}_t$ be a particle trajectory observed for time t: ${\left\{\mathbf{r}\right\}}_t=\{\mathbf{r}\left(t^{\prime }\right),0\le t^{\prime }\le t\}$. We can formally integrate Eq. 2.1. Taking x(0) = 0, we find that

$$x\left(t\right|{\left\{\mathbf{r}\right\}}_t)={\int }_0^{t}v\left(r\left(t^{\prime }\right)\right|{\left\{\mathbf{r}\right\}}_t)d{t}^{\prime }+{\int }_0^{t}f(t,r\left(t^{\prime }\right)|{\left\{\mathbf{r}\right\}}_t)d{t}^{\prime }.$$ (2.5)

Averaging this over realizations of the random force and taking that the particle starts from ${\mathbf{r}}_0=\mathbf{r}\left(0\right)$, we obtain

$${⟨x\left(t\right)⟩}_{{\mathbf{r}}_0}={\int }_0^t{⟨v\left(r\left(t^{\prime }\right)\right|{\left\{\mathbf{r}\right\}}_t)⟩}_{{\mathbf{r}}_0}d{t}^{\prime },$$ (2.6)

where the subscript ${\mathbf{r}}_0$ indicates the particle initial position in the plane perpendicular to the tube axis. Using the identity

$$\int \delta (\mathbf{r}-\mathbf{r}(t\left)\right)d\mathbf{r}=1,$$ (2.7)

Eq. 2.6 can be written as

$${⟨x\left(t\right)⟩}_{{\mathbf{r}}_0}=\int v\left(r\right)\left({\int }_0^t⟨\delta {(\mathbf{r}-\mathbf{r}\left(t^{\prime }\right)⟩}_{{\mathbf{r}}_0}d{t}^{\prime }\right)d\mathbf{r},$$ (2.8)

where v(r) is given by Eq. 2.2.

The averaged δ-function is the particle propagator (the Green function) in the plane perpendicular to the tube axis

$${⟨\delta (\mathbf{r}-\mathbf{r}\left(t\right))⟩}_{{\mathbf{r}}_0}=G(\mathbf{r},t|{\mathbf{r}}_0).$$ (2.9)

Therefore,

$${⟨x\left(t\right)⟩}_{{\mathbf{r}}_0}=\int v\left(r\right)\left({\int }_0^{t}G(\mathbf{r},t^{\prime }|{\mathbf{r}}_0)d{t}^{\prime }\right)d\mathbf{r}.$$ (2.10)

This formula has a transparent interpretation.¹⁸ Since ${\int }_0^{t}G(\mathbf{r},t^{\prime }|{\mathbf{r}}_0)d{t}^{\prime }d\mathbf{r}$ is the mean cumulative time spent by the Brownian particle observed for the time t in the small vicinity of point r, the integrand in Eq. 2.10 is the particle displacement during this cumulative time. Thus, Eq. 2.10 gives ${⟨x\left(t\right)⟩}_{{\mathbf{r}}_0}$ as the sum of such displacements.

Next, we average ${⟨x\left(t\right)⟩}_{{\mathbf{r}}_0}$, Eq. 2.10, over the equilibrium initial distribution $p_{eq}\left({\mathbf{r}}_0\right)$, where

$$p_{eq}\left(\mathbf{r}\right)=\frac{1}{\pi a^2}{P}_f^{eq}H(a-r)+\frac{1}{2\pi a}{P}_w^{eq}\delta (r-a)$$ (2.11)

with H(z) denoting the Heaviside step function. Hereafter, we assume that H(0) = 0 and ${\int }_0^a\delta (r-a)dr=1$. The averaging leads to

$$\begin{array}{ccc}\hfill {⟨x\left(t\right)⟩}_{eq}& =& \int {⟨x\left(t\right)⟩}_{{\mathbf{r}}_0}{p}_{eq}\left({\mathbf{r}}_0\right)d{\mathbf{r}}_0\hfill \\ & =& {\int }_0^{t}d{t}^{\prime }\int v\left(r\right)G(\mathbf{r},t^{\prime }|{\mathbf{r}}_0)p_{eq}\left({\mathbf{r}}_0\right)d\mathbf{r}d{\mathbf{r}}_0.\hfill \end{array}$$ (2.12)

Finally, invoking the relation

$${⟨G(\mathbf{r},t|{\mathbf{r}}_0)⟩}_{eq}=\int G(\mathbf{r},t|{\mathbf{r}}_0)p_{eq}\left({\mathbf{r}}_0\right)d{\mathbf{r}}_0=p_{eq}\left(\mathbf{r}\right),$$ (2.13)

we arrive at

$${⟨x\left(t\right)⟩}_{eq}=v_{\mathit{eff}}t,$$ (2.14)

where the effective drift velocity of the particle is given by

$$v_{\mathit{eff}}=\int v\left(r\right)p_{eq}\left(\mathbf{r}\right)d\mathbf{r}={\overline{v}}_{\mathit{f}}{P}_f^{eq}+v_{\mathit{w}}{P}_w^{eq}.$$ (2.15)

This is the main result of this section.

EFFECTIVE DIFFUSIVITY

In this section, we derive the expression for the effective diffusivity D_eff given in Eqs. 1.7, 1.11. We begin with the definition of D_eff,

$$D_{\mathit{eff}}=\frac{1}{2}\underset{t\to \infty }{lim}\frac{1}{t}\left[{⟨x^2\left(t\right)⟩}_{eq}-{⟨x\left(t\right)⟩}_{eq}^2\right],$$ (3.1)

where ⟨x²(t)⟩_eq is the second moment of the particle displacement $x\left(t\right|{\left\{\mathbf{r}\right\}}_t)$, Eq. 2.5, averaged over the realizations of the random trajectory ${\left\{\mathbf{r}\right\}}_t$ and the equilibrium radial distribution of the starting point, Eq. 2.11,

$${⟨x^2\left(t\right)⟩}_{eq}=\int {⟨x^2\left(t\right)⟩}_{{\mathbf{r}}_0}{p}_{eq}\left({\mathbf{r}}_0\right)d{\mathbf{r}}_0.$$ (3.2)

The expression for ${⟨x\left(t\right)⟩}_{eq}^2$ immediately follows from Eq. 2.14:

$${⟨x\left(t\right)⟩}_{eq}^2=v_{\mathit{eff}}^2{t}^2.$$ (3.3)

Averaging the square of the displacement in Eq. 2.5 over the trajectories that start from ${\mathbf{r}}_0$, we can present ${⟨x^2\left(t\right)⟩}_{{\mathbf{r}}_0}$ as a sum of two terms

$${⟨x^2\left(t\right)⟩}_{{\mathbf{r}}_0}={⟨{\left[x\left(t\right|{\left\{\mathbf{r}\right\}}_t)\right]}^2⟩}_{{\mathbf{r}}_0}=T_1\left(t\right|{\mathbf{r}}_0)+T_2\left(t\right|{\mathbf{r}}_0),$$ (3.4)

where

$$\begin{array}{c}\hfill T_1\left(t\right|{\mathbf{r}}_0)={\int }_0^t{\int }_0^t{⟨v\left(r\left(t_1\right)\right|{\left\{\mathbf{r}\right\}}_t)v\left(r\left(t_2\right)\right|{\left\{\mathbf{r}\right\}}_t)⟩}_{{\mathbf{r}}_0}d{t}_{1}d{t}_2\end{array}$$ (3.5)

and

$$\begin{array}{ccc}\hfill T_2\left(t\right|{\mathbf{r}}_0)& =& {\int }_0^t{\int }_0^t{⟨f(t_1,r\left(t_1\right)|{\left\{\mathbf{r}\right\}}_t)f(t_2,r\left(t_2\right)|{\left\{\mathbf{r}\right\}}_t)⟩}_{{\mathbf{r}}_0}d{t}_{1}d{t}_2.\hfill \end{array}$$ (3.6)

Then we can write ⟨x²(t)⟩_eq as

$${⟨x^2\left(t\right)⟩}_{eq}=T_1^{eq}\left(t\right)+T_2^{eq}\left(t\right),$$ (3.7)

where

$$T_{1,2}^{eq}\left(t\right)={⟨T_{1,2}\left(t\right|{\mathbf{r}}_0)⟩}_{eq}=\int T_{1,2}\left(t\right|{\mathbf{r}}_0)p_{eq}\left({\mathbf{r}}_0\right)d{\mathbf{r}}_0.$$ (3.8)

We begin with $T_2\left(t\right|{\mathbf{r}}_0)$, Eq. 3.6. Using Eqs. 2.3, 2.4, one can check that the correlation function of the random force is

$$\begin{array}{ccc}& & {⟨f(t_1,r\left(t_1\right)|{\left\{\mathbf{r}\right\}}_t)f(t_2,r\left(t_2\right)|{\left\{\mathbf{r}\right\}}_t)⟩}_{{\mathbf{r}}_0}\hfill \\ & & =2[D_f{P}_f\left(t\right|{\mathbf{r}}_0)+D_w{P}_w\left(t\right|{\mathbf{r}}_0)]\delta (t_1-t_2),\hfill \end{array}$$ (3.9)

where $P_f\left(t\right|{\mathbf{r}}_0)$ and $P_w\left(t\right|{\mathbf{r}}_0)$ are the probabilities of finding the particle in the flow and on the wall at time t, conditional on that it starts from ${\mathbf{r}}_0$ at t = 0. Substituting the correlation function, Eq. 3.9, into Eq. 3.6 we obtain

$$T_2\left(t\right|{\mathbf{r}}_0)=2{\int }_0^t[D_f{P}_f\left(t_1\right|{\mathbf{r}}_0)+D_w{P}_w\left(t_1\right|{\mathbf{r}}_0)]d{t}_1.$$

Averaging this over the particle initial position and using the relationship

$${⟨P_{f,w}\left(t\right|{\mathbf{r}}_0)⟩}_{eq}=\int P_{f,w}\left(t\right|{\mathbf{r}}_0)p_{eq}\left({\mathbf{r}}_0\right)d{\mathbf{r}}_0=P_{f,w}^{eq},$$ (3.10)

we arrive at a simple formula for $T_2^{eq}\left(t\right)$,

$$T_2^{eq}\left(t\right)=2\left(D_f{P}_f^{eq}+D_w{P}_w^{eq}\right)t,$$ (3.11)

where $P_{f,w}^{eq}$ are given by Eq. 1.5.

Next we proceed to the evaluation of $T_1\left(t\right|{\mathbf{r}}_0)$, Eq. 3.5. Using the relationships in Eqs. 2.7, 2.9, $T_1\left(t\right|{\mathbf{r}}_0)$ can be written as

$$\begin{array}{ccc}\hfill T_1\left(t\right|{\mathbf{r}}_0)& =& 2\int v\left(r_1\right)d{\mathbf{r}}_1\int v\left(r_2\right)d{\mathbf{r}}_2{\int }_0^{t}d{t}_2\hfill \\ & & \times {\int }_0^{t_2}G({\mathbf{r}}_2,t_2-t_1|{\mathbf{r}}_1)G({\mathbf{r}}_1,t_1|{\mathbf{r}}_0)d{t}_1.\hfill \end{array}$$ (3.12)

Averaging this over ${\mathbf{r}}_0$ and using Eq. 2.13, we obtain

$$\begin{array}{ccc}\hfill T_1^{eq}\left(t\right)& =& 2\int v\left(r_1\right)d{\mathbf{r}}_1\int v\left(r_2\right)d{\mathbf{r}}_2{\int }_0^{t}d{t}^{″}\hfill \\ & & \times {\int }_0^{t^{″}}G({\mathbf{r}}_2,t^{\prime }|{\mathbf{r}}_1)p_{eq}\left({\mathbf{r}}_1\right)d{t}^{\prime }.\hfill \end{array}$$ (3.13)

As t → ∞ the propagator $G(\mathbf{r},t|{\mathbf{r}}_0)$ tends to $p_{eq}\left(\mathbf{r}\right)$, Eq. 2.11. Denoting the difference between the propagator and $p_{eq}\left(\mathbf{r}\right)$ by $u(\mathbf{r},t|{\mathbf{r}}_0)$, we can write

$$G(\mathbf{r},t|{\mathbf{r}}_0)=p_{eq}\left(\mathbf{r}\right)+u(\mathbf{r},t|{\mathbf{r}}_0),$$ (3.14)

where $u(\mathbf{r},t|{\mathbf{r}}_0)\to 0$ as t → ∞. In addition, $u(\mathbf{r},t|{\mathbf{r}}_0)$ satisfies

$$\begin{array}{c}\hfill {⟨u(\mathbf{r},t|{\mathbf{r}}_0)⟩}_{eq}=\int u(\mathbf{r},t|{\mathbf{r}}_0)p_{eq}\left({\mathbf{r}}_0\right)d{\mathbf{r}}_0=\int u(\mathbf{r},t|{\mathbf{r}}_0)d\mathbf{r}=0.\end{array}$$ (3.15)

Substituting the propagator in Eq. 3.14 into Eq. 3.13, we can find the large-t asymptotic behavior of $T_1^{eq}\left(t\right)$,

$$\begin{array}{c}\hfill T_1^{eq}\left(t\right)=v_{\mathit{eff}}^2{t}^2+2t\int v\left(r_2\right)d{\mathbf{r}}_2\int v\left(r_1\right)\theta ({\mathbf{r}}_2,{\mathbf{r}}_1)p_{eq}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1,\end{array}$$ (3.16)

where

$$\theta ({\mathbf{r}}_2,{\mathbf{r}}_1)={\int }_0^{\infty }u({\mathbf{r}}_2,t|{\mathbf{r}}_1)dt.$$ (3.17)

This integral is the Laplace transform of $u({\mathbf{r}}_2,t|{\mathbf{r}}_1)$ at the zero value of the Laplace parameter

$$\theta ({\mathbf{r}}_2,{\mathbf{r}}_1)=\left.\widehat{u}({\mathbf{r}}_2,s|{\mathbf{r}}_1\right){|}_{s=0},$$ (3.18)

where $\widehat{F}\left(s\right)$ denotes the Laplace transform of function F(t), $\widehat{F}\left(s\right)={\int }_0^{\infty }F\left(t\right)\exp (-st)dt$.

Eventually using the relationships in Eqs. 3.7, 3.11, 3.16, we find that the definition in Eq. 3.1 leads to the expression for D_eff in Eq. 1.7, in which △D is

$$▵D=\int v\left(r_2\right)d{\mathbf{r}}_2\int v\left(r_1\right)\theta ({\mathbf{r}}_2,{\mathbf{r}}_1)p_{eq}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1.$$ (3.19)

Thus, to finish the calculation of the effective diffusivity, we have to evaluate the double integral in Eq. 3.19.

Since the particle can be in two states (in the flow and on the wall), the angle-averaged particle propagator has two components, g_f(r, t|σ) and P_w(t|σ), which are the probability density of finding the particle in the flow and the probability of finding the particle on the wall at time t, conditional on that it starts from state σ at t = 0. Initially, the particle can also be either in the flow or on the wall. Therefore, σ = r₀, if the particle starts in the flow at distance r₀ from the tube axis, and σ = w, if the particle is on the wall at t = 0. The four functions, g_f(r, t|σ) and P_w(t|σ), satisfy

$$\frac{\partial g_f}{\partial t}=\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial g_f}{\partial r}\right),{\left.\frac{\partial g_f}{\partial r}\right|}_{r=0}=0,$$ (3.20)

$$\frac{d{P}_w}{dt}=2\pi a\kappa g_f{\mid }_{r=a}-k_w{P}_w=-2\pi a{D}_r{\left.\frac{\partial g_f}{\partial r}\right|}_{r=a},$$ (3.21)

with the initial conditions

$$P_w\left(0\right|w)=1,g_f(r,0|w)=0$$ (3.22)

and

$$P_w\left(0\right|r_0)=0,g_f(r,0|r_0)=\frac{1}{2\pi r}\delta (r-r_0),$$ (3.23)

where g_f ≡ g_f(r, t|σ) and P_w ≡ P_w(t|σ).

It is convenient to introduce notations for the deviations of the two components of the propagator from their large-t asymptotic values (cf. Eq. 3.14),

$$U_w\left(t\right|\mathit{\sigma })=P_w\left(t\right|\mathit{\sigma })-P_w^{eq},$$ (3.24)

$$u_f(r,t|\mathit{\sigma })=g_f(r,t|\mathit{\sigma })-P_f^{eq}/\pi a^2.$$ (3.25)

Denoting the Laplace transforms of these functions at s = 0 by ${\widehat{U}}_w\left(\mathit{\sigma }\right)\equiv {\widehat{U}}_w{\left(s\right|\mathit{\sigma })|}_{s=0}$ and ${\widehat{u}}_f\left(r\right|\mathit{\sigma })\equiv {\widehat{u}}_f{(r,s|\mathit{\sigma })|}_{s=0}$, we can write Eq. 3.19 as

$$▵D=({\Theta }_{ff}+{\Theta }_{wf})P_f^{eq}/\left(\pi a^2\right)+({\Theta }_{fw}+{\Theta }_{ww})v_w{P}_w^{eq},$$ (3.26)

where

$$\begin{array}{ccc}\hfill {\Theta }_{ff}& =& {\left(2\pi \right)}^2{\int }_0^a{\int }_0^a{\widehat{u}}_f\left(r_2\right|r_1)v_{\mathit{f}}\left(r_2\right)v_{\mathit{f}}\left(r_1\right)r_2{r}_{1}d{r}_{2}d{r}_1,\hfill \end{array}$$ (3.27)

$$\begin{array}{ccc}\hfill {\Theta }_{wf}& =& 2\pi v_w{\int }_0^a{\widehat{U}}_w\left(r\right)v_{\mathit{f}}\left(r\right)rdr,\hfill \end{array}$$ (3.28)

$$\begin{array}{ccc}\hfill {\Theta }_{fw}& =& 2\pi {\int }_0^a{\widehat{u}}_f\left(r\right|w)v_{\mathit{f}}\left(r\right)rdr,\hfill \end{array}$$ (3.29)

$$\begin{array}{ccc}\hfill {\Theta }_{ww}& =& v_{\mathit{w}}{\widehat{U}}_w\left(w\right).\hfill \end{array}$$ (3.30)

These four constants correspond to particular sets of realizations of the particle trajectory that is reflected in their indices. Terms Θ_ff and Θ_wf are due to realizations that start in the flow and end in the flow (Θ_ff) or on the wall (Θ_wf) at time t. Analogously, terms Θ_fw and Θ_ww take into account those realizations in which the particle is initially on the wall and is still on the wall (Θ_ww) or in the flow (Θ_fw) at the time t.

Explicit expressions for the four constants, in terms of the geometrical and kinetic parameters of the system are (see derivations in the Appendixes):

$$\begin{array}{ccc}\hfill {\Theta }_{ff}& =& \frac{\pi a^2{\overline{v}}_f^2}{k_w}{\left(P_f^{eq}\right)}^2\left[K+\frac{k_w{a}^2}{48D_r}(1+6K+11K^2)\right],\hfill \end{array}$$ (3.31)

$$\begin{array}{ccc}\hfill {\Theta }_{wf}& =& -\frac{\pi a^2{v}_w{\overline{v}}_f}{k_w}{\left(P_f^{eq}\right)}^2\left[\frac{\kappa a}{12D_r}+\left(1+\frac{\kappa a}{3D_r}\right)K\right],\hfill \end{array}$$ (3.32)

$$\begin{array}{ccc}\hfill {\Theta }_{fw}& =& -\frac{{\overline{v}}_f}{k_w}{\left(P_f^{eq}\right)}^2\left(1+\frac{\kappa a}{3D_r}+\frac{k_w{a}^2}{24D_r}\right),\hfill \end{array}$$ (3.33)

$$\begin{array}{ccc}\hfill {\Theta }_{ww}& =& \frac{v_w}{k_w}{\left(P_f^{eq}\right)}^2\left(1+\frac{\kappa a}{4D_r}\right).\hfill \end{array}$$ (3.34)

Substituting these expressions into Eq. 3.26 we arrive at △D in Eq. 1.11. Thus, we have derived the formula for the effective diffusivity given by Eqs. 1.7, 1.11, starting from the definition in Eq. 3.1.

CONCLUDING REMARKS

Main results of the present paper are the expressions for the effective velocity, Eq. 1.9, and diffusivity, Eqs. 1.7, 1.11, derived in Secs. 2, 3, respectively. The expressions show how these quantities depend on the parameters of the model, ${\overline{v}}_f,v_w$, D_f, D_r, D_w, κ, k_w, and a. In this section, we briefly discuss the dependence of the effective diffusivity on the velocities ${\overline{v}}_f$ and v_w, as well its dependence on the equilibrium constant K = 2κ/(ak_w), Eq. 1.4. It is worth mentioning that the non-monotonic dependence of D_eff on K has been reported earlier.^{1, 5, 20, 27, 33, 34}

The velocity dependence of the effective diffusivity is completely determined by the term △D, Eq. 1.11, which is a quadratic form in ${\overline{v}}_f$ and v_w. One can see that △D (and hence D_eff) being considered as function of v_w at a given value of ${\overline{v}}_f$ has a minimum at some $v_w=v_w^{*}$, which is proportional to ${\overline{v}}_f$, i.e., $v_w^{*}=A{\overline{v}}_f$, where the pre-factor A is a function of D_r, κ, k_w and a. As D_r → ∞, Eq. 1.11 reduces to Eq. 1.10, so that $v_w^{*}$ tends to ${\overline{v}}_f$, and A approaches unity.

Next we consider the D_eff dependence on K at fixed values of all other parameters, assuming that diffusion in the flow is isotropic, i.e., D_r = D_f. As K increases from zero to infinity, D_eff changes from D_eff(0) given by the Taylor formula, Eq. 1.2, to D_eff(∞) = D_w. It can be seen that the large-K asymptotic behavior of D_eff is given by

$$D_{\mathit{eff}}\left(K\right)\simeq D_{\mathit{w}}+\frac{B}{K},K\to \infty ,$$ (4.1)

where $B=D_f+[a^2/\left(48D_f\right)](11{\overline{v}}_{\mathit{f}}^2-4{\overline{v}}_{\mathit{f}}{v}_{\mathit{w}}+6v_{\mathit{w}}^2)$. Since B > 0, D_eff(K) always approaches its asymptotic value D_w from above. As K tends to zero, D_eff takes the form

$$D_{\mathit{eff}}\left(K\right)\simeq D_f+\frac{a^2{\overline{v}}_{\mathit{f}}^2}{48D_f}+QK,K\to 0,$$ (4.2)

where

$$Q=D_w-D_f+\frac{1}{k_{\mathit{w}}}{({\overline{v}}_{\mathit{f}}-v_{\mathit{w}})}^2+\frac{a^2}{48D_f}{\overline{v}}_{\mathit{f}}(3{\overline{v}}_{\mathit{f}}-4v_{\mathit{w}}).$$ (4.3)

One can see that Q can be both positive and negative. Therefore, D_eff(K) may both increase and decrease with K at small K.

Now we employ the asymptotic expressions, Eqs. 4.1, 4.2, to discuss the K-dependence of the effective diffusivity over the entire range of K. When Q > 0, D_eff increases with K at small K, reaches a maximum and then decreases approaching the limiting value D_eff(∞) = D_w from above. If Q < 0 and D_eff initially decreases, the behavior of D_eff can be qualitative different depending on whether D_eff(0) is smaller or lager than D_eff(∞). If D_eff(0) < D_eff(∞), D_eff(K) first decreases, reaches a minimum, then increases and reaches a maximum, and then it decreases again finally approaching its limiting value D_w from above. When the opposite inequality holds, i.e., D_eff(0) > D_eff(∞), in addition to the “wavy” profile of D_eff(K) discussed above (decrease-increase-decrease), the effective diffusivity can be a monotonically decreasing function of K.

To summarize, the effective diffusivity is a complex function of the model parameters. Therefore, its profiles in the multidimensional parameter space may have very different shapes, as can be seen from the above discussion.

APPENDIX A: EVALUATION OF CONSTANTS Θ_fw, Θ_ww FROM EQS. 3.29, 3.30

Consider a particle that is bound to the wall at t = 0. According to Eqs. 3.20, 3.21, 3.22, functions U_w(t|w), u_f(r, t|w), Eqs. 3.24, 3.25, satisfy

$$\frac{\partial u_f}{\partial t}=\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_f}{\partial r}\right),{\left.\frac{\partial u_f}{\partial r}\right|}_{r=0}=0,$$ (A1)

$$\frac{d{U}_w}{dt}=2\pi a\kappa u_f{\mid }_{r=a}-k_w{U}_w=-2\pi a{D}_r{\left.\frac{\partial u_f}{\partial r}\right|}_{r=a},$$ (A2)

with the initial conditions

$$U_w\left(0\right|w)=P_f^{eq},u_f(r,0|w)=-P_f^{eq}/\left(\pi a^2\right),$$ (A3)

and an additional relationship

$$U_w\left(t\right|w)+2\pi {\int }_0^a{u}_f(r,t|w)rdr=0,$$ (A4)

which follows from Eq. 3.15.

Laplace transforming Eqs. A1, A2, A3, A4, we arrive at

$$s{\widehat{u}}_f+\frac{1}{\pi a^2}{P}_f^{eq}=\frac{D_r}{r}\frac{d}{dr}\left(r\frac{d{\widehat{u}}_f}{dr}\right),{\left.\frac{d{\widehat{u}}_f}{dr}\right|}_{r=0}=0,$$ (A5)

$$\begin{array}{ccc}\hfill s{\widehat{U}}_w-P_f^{eq}& =& 2\pi a\kappa {\widehat{u}}_f{\mid }_{r=a}-k_w{\widehat{U}}_w=-2\pi a{D}_r{\left.\frac{\partial {\widehat{u}}_f}{\partial r}\right|}_{r=a},\hfill \end{array}$$ (A6)

$${\widehat{U}}_w\left(s\right|w)+2\pi {\int }_0^a{\widehat{u}}_f(r,s|w)rdr=0,$$ (A7)

where ${\widehat{U}}_w\left(s\right|w)$ and ${\widehat{u}}_f(r,s|w)$ are the Laplace transforms of U_w(t|w) and u_f(r, t|w), respectively.

Solving these equations at s = 0, we find that

$${\widehat{U}}_w\left(w\right)=\frac{1}{k_w}{\left(P_f^{eq}\right)}^2\left(1+\frac{\kappa a}{4D_r}\right),$$ (A8)

$$\begin{array}{ccc}\hfill {\widehat{u}}_f\left(r\right|w)& =& -\frac{1}{\pi a^2{k}_w}{\left(P_f^{eq}\right)}^2\left(1+\frac{\kappa a}{2D_r}+\frac{k_w{a}^2}{8D_r}\right)\hfill \\ & & +\frac{r^2}{4\pi a^2{D}_r}{P}_f^{eq}.\hfill \end{array}$$ (A9)

Substituting the solution for ${\widehat{u}}_f\left(r\right|w)$ into Eq. 3.29 and carrying out the integration, we obtain the expression for Θ_fw in Eq. 3.33.

The term Θ_ww, Eq. 3.34, is simply the product of v_w and the solution for ${\widehat{U}}_w\left(w\right)$ in Eq. A8.

APPENDIX B: EVALUATION OF CONSTANTS Θ_wf, Θ_ff FROM EQS. 3.27, 3.28

For the evaluation of Θ_ff and Θ_wf consider the particle in the flow that at t = 0 is separated by distance r₀, 0 ⩽ r₀ < a from the tube axis. As follows from Eqs. 3.20, 3.21, 3.23 functions U_w(t|r₀) and u_f(r, t|r₀), Eqs. 3.24, 3.25, satisfy Eqs. A1, A2 with the initial conditions

$$U_w\left(0\right|r_0)=-P_w^{eq},u_f(r,0|r_0)=\frac{1}{2\pi r}\delta (r-r_0)-\frac{1}{\pi a^2}{P}_f^{eq},$$ (B1)

and an additional relationship

$$U_w\left(t\right|r_0)+2\pi {\int }_0^a{u}_f(r,t|r_0)rdr=0,$$ (B2)

which follows from Eq. 3.15.

Functions ${\widehat{U}}_w\left(r_0\right)$ and ${\widehat{u}}_f\left(r\right|r_0)$ entering into Eqs. 3.27, 3.28 are evaluated from the Laplace transforms of Eqs. A1, A2, B2 at s = 0. They obey the following system of equations:

$$\begin{array}{ccc}\hfill \frac{D_r}{r}\frac{d}{dr}\left(r\frac{d{\widehat{u}}_f\left(r\right|r_0)}{dr}\right)& =& \frac{1}{\pi a^2}{P}_f^{eq}-\frac{1}{2\pi r}\delta (r-r_0),\hfill \\ \\ & & {\left.\frac{d{\widehat{u}}_f\left(r\right|r_0)}{dr}\right|}_{r=0}=0,\hfill \end{array}$$ (B3)

$$\begin{array}{ccc}\hfill P_w^{eq}& =& 2\pi a\kappa {\widehat{u}}_f\left(r\right|r_0){\mid }_{r=a}-k_w{\widehat{U}}_w\left(r_0\right)\hfill \\ & =& -2\pi a{D}_r{\left.\frac{d{\widehat{u}}_f\left(r\right|r_0)}{dr}\right|}_{r=a},\hfill \end{array}$$ (B4)

$${\widehat{U}}_w\left(r_0\right)+2\pi {\int }_0^a{\widehat{u}}_f\left(r\right|r_0)rdr=0.$$ (B5)

In order to simplify calculations, it is convenient to introduce new auxiliary functions

$$W=2\pi {\int }_0^a{\widehat{U}}_w\left(r_0\right)v_f\left(r_0\right)r_{0}d{r}_0,$$ (B6)

$$w\left(r\right)=2\pi {\int }_0^a{\widehat{u}}_f\left(r\right|r_0)v_f\left(r_0\right)r_{0}d{r}_0.$$ (B7)

As follows from Eqs. B3 to B5, W and w(r) satisfy

$$\frac{D_r}{r}\frac{d}{dr}\left(r\frac{dw}{dr}\right)={\overline{v}}_f{P}_f^{eq}-v_f\left(r\right),{\left.\frac{dw}{dr}\right|}_{r=0}=0,$$ (B8)

$$-\pi a^2{\overline{v}}_f{P}_w^{eq}=k_{w}W-2\pi \kappa w\left(a\right)=2\pi a{D}_r{\left.\frac{dw}{dr}\right|}_{r=a},$$ (B9)

$$W+2\pi {\int }_0^{a}w\left(r\right)rdr=0.$$ (B10)

Solving Eqs. B8, B9, B10, we obtain

$$W=-\frac{\pi a^2{\overline{v}}_f}{k_w}{\left(P_f^{eq}\right)}^2\left[\frac{\kappa a}{12D_r}+\left(1+\frac{\kappa a}{3D_r}\right)K\right],$$ (B11)

$$w\left(r\right)=w\left(0\right)+\frac{{\overline{v}}_f}{8a^2{D}_r}\left[r^4-2P_f^{eq}(1+2K)a^2{r}^2\right],$$ (B12)

$$\begin{array}{c}\hfill w\left(0\right)=\frac{{\overline{v}}_f}{k_w}{\left(P_f^{eq}\right)}^2\left[\frac{k_w{a}^2}{12D_r}+\frac{2\kappa a}{3D_r}+\left(1+\frac{3\kappa a}{4D_r}\right)K\right].\end{array}$$ (B13)

We can write Θ_ff, Eq. 3.27, in terms of w(r),

$$\begin{array}{ccc}\hfill {\Theta }_{ff}& =& {\left(2\pi \right)}^2{\int }_0^a{\int }_0^a{v}_f\left(r_1\right){\widehat{u}}_f\left(r\right|r_0)v_f\left(r_2\right)r_{2}d{r}_{1}d{r}_2\hfill \\ & =& 2\pi {\int }_0^a{v}_f\left(r\right)w\left(r\right)rdr.\hfill \end{array}$$ (B14)

Finally, using Eqs. B12, B13 and performing the integration we arrive at the expression in Eq. 3.31.

The constant Θ_wf, Eq. 3.33, is simply the product of v_w and the solution for W in Eq. B11.