Abstract
Oscillating microbubbles within microvessels could induce stresses that lead to bioeffects or vascular damage. Previous work has attributed vascular damage to the vessel expansion or bubble jet. However, ultra-high speed images of recent studies suggest that it could happen due to the vascular invagination. Numerical simulations of confined bubbles could provide insight into understanding the mechanism behind bubble–vessel interactions. In this study, a finite element model of a coupled bubble/fluid/vessel system was developed and validated with experimental data. Also, for a more realistic study viscoelastic properties of microvessels were assessed and incorporated into this comprehensive numerical model. The wall shear stress (WSS) and circumferential stress (CS), metrics of vascular damage, were calculated from these simulations. Resultant amplitudes of oscillation were within 15% of those measured in experiments (four cases). Among the experimental cases, it was numerically found that maximum WSS values were between 1.1–18.3 kPa during bubble expansion and 1.5–74 kPa during bubble collapse. CS was between 0.43–2.2 MPa during expansion and 0.44–6 MPa while invaginated. This finding confirmed that vascular damage could occur during vascular invaginations. Predicted thresholds in which these stresses are higher during vessel invagination were calculated from simulations.
INTRODUCTION
Ultrasound contrast agent microbubbles have gained a lot of attention due to their application in ultrasound imaging and therapy.1, 2, 3 Microbubbles, when injected into the blood stream, remain intravascular and undergo a volumetric oscillation when activated by an ultrasound pulse. Different studies have shown that microbubbles could induce mechanical bioeffects on their confining vasculature.4, 5, 6 The bioeffects could be therapeutically beneficial and might range from increasing the vascular permeability for intravascular drug and gene delivery, opening the blood–brain barrier locally and transiently to vessel rupture and occlusion.1, 2, 4, 7, 8, 9 One major challenge in using microbubbles for medical ultrasound application is the lack of knowledge about the behavior of confined bubbles and the impact bubbles might have on the surrounding tissue.
It is important to investigate bubble mediated mechanical effects on the vessel wall and to understand the mechanism involved. Previously, the vascular damage was attributed to either the vessel distension or direct impact of a bubble jet on a vessel wall.10, 11, 12 However, recent high speed photographs of ex vivo vessels showed that the bubble collapse within a vessel generates a distinct invagination of the vessel wall (i.e., toward the lumen of the vessel).13, 14 This bubble–vessel coupling may be responsible for some vascular damage. The fluid shear stress and circumferential stress are the two important metrics in quantifying the mechanical bioeffects. Vessels in the microstreaming field, generated by pulsating bubbles, experience fluid shear stress. If this stress is high enough it may have an impact on the cell membrane integrity or even detachment of the endothelial cells.15 Circumferential stress, the other important stress, might be responsible for vessel rupture. Previously, vascular rupture due to bubble activity was observed and reported in different studies.4, 5, 16, 17, 18
A numerical simulation of the experimental data could shed light on understanding bubble–vessel interactions. In particular, such a theoretical model could predict encapsulated bubble oscillations inside a vessel. Also it could provide fluid flow information as well as stress levels exerted on the vessel wall during the vessel distension and invagination, thus providing a means to predict which mechanism is responsible for cavitation-induced bioeffects.
A confined microbubble behaves differently than unbound bubbles surrounded by infinite fluid. A number of confined bubble models have been developed over the years.19, 20, 21 However, these models either neglected shell effects, assumed a spherical bubble, or they lacked the usage of appropriate vessel properties. While these models are suitable for low acoustic pressures and bubble spherical oscillations, at relatively high acoustic pressures (∼1 MPa) the bubble in a small blood vessel deviates from its spherical shape and forms an ellipsoid. Realistic vessel parameters are critical for bubble/fluid/vessel simulation as well.
In this study, numerical simulations were compared with experimental observations of bubbles within rat mesenteric microvessels ex vivo. Chen et al. speculated that the tissue viscosity could be significant due to vessel wall invagination.22 It was also reported elsewhere that mesenteric tissue behaves in a viscoelastic manner.23 Also, Swayne et al. observed a nonlinear behavior from mesenteric microvessels when increasing the pressure in increments. They suggested that the basement membrane has the appropriate properties to explain this behavior.24 Skalak et al. suggested that the vessel wall could be modeled using a standard viscoelastic solid.25 Because it is crucial to have proper viscoelastic parameters for the numerical work, in the first part of this study the viscoelastic properties of ex vivo rat mesentery microvessels were assessed. This assessment was done using a standard linear solid (SLS) viscoelastic model. Then, these viscoelastic parameters were used in our first numerical model. In the first part of the simulations, bubble oscillations were dictated to mimic the experimental data sets and vessel wall stresses were calculated. Then, in the second numerical part, we developed a comprehensive encapsulated confined bubble model while accounting the effects of surface tension within a viscoelastic vessel. Four experimental data sets (cases 1–4) of micron size bubbles inside different rat mesentery microvessels are considered for the comparison with the numerical work. The second numerical part was done with the intention to predict the confined bubble behavior as well as the associated wall stresses. From both numerical parts, the vessel wall shear stress (WSS) and circumferential stress (CS) are calculated during bubble expansion or collapse and the threshold at which the stresses are higher during vascular invagination are predicted.
METHODS
Experimental data
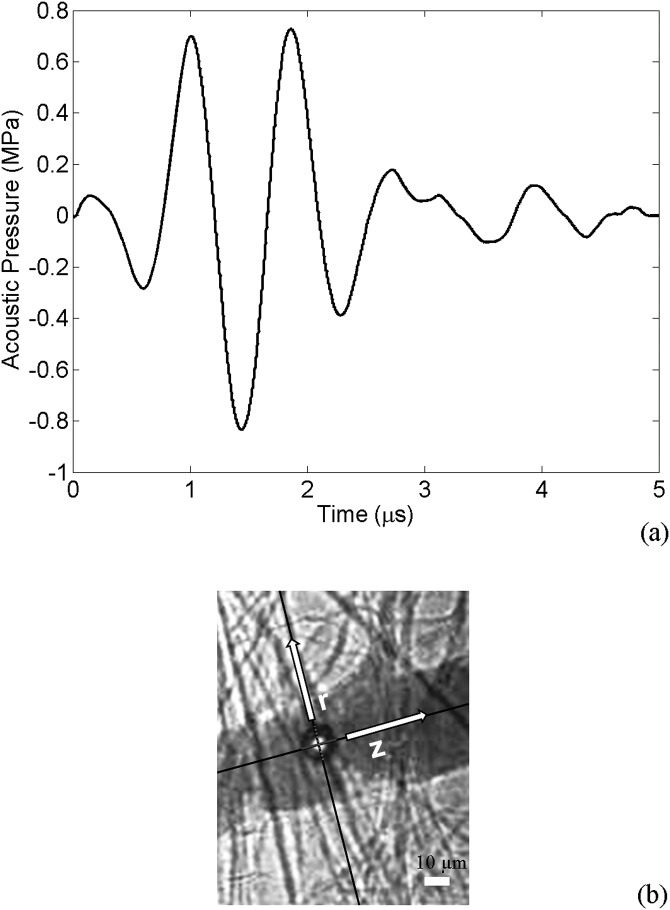
High speed photomicrography was used to visualize the direct transient interactions between ultrasound-activated microbubbles and blood vessels within ex vivo tissue. The microscope was aligned confocally with a focused annular ultrasound transducer. Rat mesenteries were used as the animal model. After the mesentery was flushed clear of blood, the animal was sacrificed and the mesentery with intestine was dissected away from the rat body. Then Definity® (Lantheus Medical Imaging, North Billerica, Massachusetts) microbubbles were mixed with saline and injected into the mesentery segment. The transducer was driven by a single cycle sine wave produced by a function generator (33120A; Hewlett Packard, Palo Alto, CA) and amplified by a power amplifier (A150; ENI, Rochester, NY). The acoustic pressure at the focus of the transducer was measured with a fiber optic probe hydrophone (FOPH 2000; RP Acoustics, Leutenbach, Germany). Figure 1a displays the pressure waveform used in this study. The ultrasound pulse had a peak negative pressure of 0.8 MPa at 1 MHz and lasted for about 2 μs. During each insonation, images were captured by a camera (Imacon 200; DRS Hadland, Cupertino, CA) using an exposure time of 50 ns. Full details of the experimental setup and image analysis method were reported earlier.26
Figure 1.
(Color online) (a) The applied ultrasound pulse with 1 MHz frequency and peak negative pressure of 0.8 MPa. (b) A confined bubble within a microvessel with semi-minor and major axes along r (radial) and z (axial) directions, respectively; the scale bar represents 10 μm.
From the recorded images the bubble and vessel radii were evaluated using ImageJ software (ImageJ 1.41o; National Institutes of Health, Bethesda, MD). Assuming that the confined bubbles are ellipsoidal (in the image plane), the bubbles' semi-minor and -major axes were along r (radial) and z (axial) direction, respectively [Fig. 1b]. From the experiments, four data sets were examined in this work. Table TABLE I. presents the bubble and vessel radii of the four experimental cases. These cases were chosen because of their known initial bubble sizes prior to the ultrasound exposure. The bubble behavior and accurate numerical simulations highly depended on the bubble's initial size.
TABLE I.
Experimental cases of single confined bubble within a microvessel.
| Case number | Bubble initial radius (μm) | Vessel initial radius (μm) | Frame interval (ns) |
|---|---|---|---|
| 1 | 1.2 | 5.6 | 150 |
| 2 | 1.3 | 16 | 300 |
| 3 | 4.7 | 21 | 300 |
| 4 | 3 | 16 | 300 |
Viscoelastic properties of microvessels
In order to perform a numerical simulation of a bubble within a viscoelastic vessel, viscoelastic properties of vessels were assessed. Previously, a number of rat mesentery ex vivo experiments was performed in which collapsing microbubbles inside mesenteric venules caused the vessels to invaginate to their maximum extent. Then, the recovery process of the invaginated vessel wall was photographed with the intention of estimating the viscoelastic properties of the vessel.27
Microvessels in this study were venules (diameters larger than 8 μm) and they were distinguished from other microvessels by the flow direction as well as vessel branching and collecting. The experimental setup in this part was the same as that used to photograph the confined bubble activity (Sec. 2C of this work) except that longer times were captured to observe the vessel wall recovery.27 The vessel properties were characteristic and reported recently27 using a Voigt solid model. In this work, the experimental data were fitted with a SLS model as it predicts both creep and stress relaxation. Also, Skalak et al. suggested that SLS can be used to describe the vessel wall.25 The SLS model is made up of two branches— one with a single spring and the other with a spring and a dashpot. The creep function of a SLS model can be written as28
σ is the applied stress on the structure, is the strain, μ0 is the spring constant on the first branch, and on the second branch, μ1 and η1 are the spring constant and the coefficient of viscosity of the dashpot, respectively.
Since the collected experimental data corresponded to the recovery phase of the vessel wall, the vessel initial position was set to vessel's maximum invagination (), the maximum vessel displacement during invagination. Therefore, , where is the vessel displacement. Now, the governing equation for the recovery phase would be
| (1) |
where μ0, μ1, and η1 are the three parameters of this model.
μ0(the long term elastic modulus) was set to 50 kPa. This selection was based on Smaje's work, in which they reported the elasticity of capillaries and venules in cat mesentery in vivo.29 The experimental invaginated vessel data were fitted with Eq. 1 while fixing the long term elastic modulus to 50 kPa), in order to evaluate the other unknown parameters, μ1 and η1. The fittings were done using MATLAB (version 7.11, The MathWorks, Natick, MA) and its lsqcurvefit function (which solves nonlinear data-fitting problems in least-squares sense) in the optimization toolbox.
The fitted data sets are shown in Figs. 2a, 2b. The first data set belonged to a small microvessel with a maximum displacement of [Fig. 2a]. The second data set, which represented a larger microvessel [Fig. 2b], had a maximum displacement of . The best results for the fit between Eq. 1 and data set 1 gave the values of μ1 = 5 MPa and η1 = 1.02 Pa s. The best values for the fit between Eq. 1 and data set 2 resulted in μ1 = 5 MPa and η1 = 0.78 Pa s.
Figure 2.
Fitted standard linear solid model with experimental results. (a) First invaginated vessel data with the best fit of parameters μ0 = 50 kPa, μ1 = 5 MPa, and η1 = 1.02 Pa s. (b) Second data with the best fit of parameters μ0 = 50 kPa, μ1 = 5 MPa, and η1 = 0.78 Pa s.
The viscoelastic parameter for the two data sets above were within 26% of each other. In order to implement these findings into Sec. 2C and to model a bubble within a viscoelastic vessel, the parameters obtained from data sets 1 and 2 were averaged. The average parameters of μ1 = 5 MPa and η1 = 0.9 Pa s (= 0.1817 μs) along with μ0 = 50 kPa were used as inputs into the vessel properties for bubble/fluid/vessel simulation in Sec. 2C. It is worth noting that the viscosity values found here were in the same order of magnitude as that found by Girnyk et al. (i.e., 0.15 Pa s) in liver using ultrasound measurements at 1 MHz.30 Also, the elasticity values are within those reported earlier (i.e., 1–10 MPa).29, 31
Numerical simulation
In our numerical model a microbubble was placed at the center (both axially and radially) of a microvessel (vessels were 2 μm in thickness and 100 μm in length). A two-dimensional model with axisymmetrical assumption was used as it was less computationally expensive. Furthermore, in the experimental data, the bubble was nearly in the middle of the vessel.
Subsections here are organized as follows. In Sec. 2C1, the bubble within the vessel was forced to oscillate mimicking the experimental cases 1–4. The WSS and CS induced by the forced bubble oscillation on the vessel wall were calculated. In Sec. 2C2, a comprehensive bubble model was developed. This model enabled us to elaborate on the bubble's behavior within the vessel and to understand the physics behind the coupled bubble/fluid/vessel system. A threshold at which stresses were higher during vascular invagination was also predicted. In this numerical work, the fluid and solid domains were fully coupled (two-way coupling). In Sec. 2C3, the details of the fluid/solid coupling and fluid properties are described. Other boundary conditions and method of solution are explained in Sec. 2C4. Table TABLE II. provides a list of notations used in this work. Figure 3 shows a schematic illustration of the numerical model.
TABLE II.
Notations.
| Symbol | Definition of symbol |
|---|---|
| r | Radial direction in cylindrical coordinate system (m) |
| z | Axial direction in cylindrical coordinate system (m) |
| Creep function (Pa−1) | |
| Vascular strain | |
| Relaxation time for constant stress (s) | |
| Relaxation time for constant strain (s) | |
| σ | Applied stress on the vessel (Pa) |
| μ0 | Spring constant on first branch (Pa) |
| μ1 | Spring constant on second branch (Pa) |
| η1 | Viscosity of dashpot (Pa s) |
| Maximum vessel displacement (m) | |
| Vessel displacement (m) | |
| Fluid velocity (m/s) | |
| ρ | Fluid density (kg/m3) |
| μ | Dynamic viscosity of the fluid (Pa s) |
| P | Pressure in the fluid (Pa) |
| Bubble pressure at the wall (Pa) | |
| Gas pressure (Pa) | |
| Gas pressure at resting state (Pa) | |
| Ambient pressure in microvessels (Pa) | |
| Initial bubble radius (m) | |
| R | Bubble radius (m) |
| κ | Total curvature (m−1) |
| γ | Surface tension as a function of bubble area (N/m) |
| Laplace pressure (Pa) | |
| k | Polytropic index |
| Intravascular pressure (Pa) | |
| Pressure on the outer diameter of vessel wall (Pa) | |
| Inner vessel diameter (m) | |
| Outer vessel diameter (m) | |
| χ | Shell elastic modulus (N/m) |
| Shell viscosity (kg/s) | |
| Surface tension of water (N/m) | |
| A | Bubble area (m2) |
| Bubble area at shell buckling regime (m2) | |
| Bubble radius at break-up regime (m) | |
| Bubble area at break-up regime (m2) | |
| Spherical bubble's equivalent radius (m) | |
| Maximum bubble radius (m) | |
| Maximum vessel radius (m) | |
| Circumferential (hoop) stress (Pa) |
Figure 3.
(Color online) Schematic illustration of the numerical model. (a) Forced bubble oscillation in numerical section part I, and (b) microbubble model in numerical section part II.
Forced bubble oscillation and stresses: Numerical section part I
In this section, an ellipsoidal bubble was forced to oscillate mimicking the bubble in the experimental cases 1–4 [Fig. 3a]. The bubble wall was coupled to the surrounding fluid within a viscoelastic vessel. A velocity boundary condition was used at the bubble wall. The fluid velocity was set equal to the forced bubble velocity while the bubble wall velocity itself was derived from experimental bubble wall displacements. The vessel wall movements, WSS and CS, were calculated as a result of this numerical section.
Microbubble model: Numerical section part II
The focus of this section was on the microbubbles' behavior in a confined geometry. Therefore, a bubble model was developed considering the effects of surface tension and encapsulating shell. In this section, contrary to Sec. 2C1, the bubble oscillation was not dictated anymore. Instead, the bubble oscillated due to the ideal gas law inside the bubble and fluid force surrounding the bubble.
Since the acoustic pressure in this study was relatively high (∼1 MPa range) and the blood vessels were relatively small (the bubble wall could get very close to the blood vessel wall), the bubble oscillated in an ellipsoidal fashion. Therefore a non-spherical bubble model was developed.
Typically, bubble models (e.g., Rayleigh–Plesset equation) consist of a pressure function and an inertia function. In this confined bubble model, the pressure function was applied on the bubble wall while the inertia function due to the surrounding fluid and vessel was numerically solved. A pressure boundary condition at the bubble wall was used (the stress in the tangential direction is assumed to be zero)
| (2) |
where is the pressure function at the bubble wall, n is the outward unit normal, is the Laplace pressure, and μ is the fluid viscosity. In this equation, the bubble pressure () was greater than the normal stress in the fluid (left hand side) due to the surface tension pressure (). The following equation was applied for the bubble pressure, using the polytropic gas law along with encapsulating shell properties:
| (3) |
where is the gas pressure, is the gas pressure at the resting state, and k, the polytropic index, was set to 1.07.32 and V are the initial bubble volume and bubble volume at any other time points, respectively. The bubble volume was calculated at each time step and then it was updated in Eq. 3. is the ambient pressure in microvessels, which was set to 104.6 kPa. is the ultrasound pressure pulse. In our simulations, bubbles were driven with the ultrasonic pulse shown in Fig. 1a. Due to the large acoustic wavelength (i.e., a few millimeters) compared to the bubble size, it was assumed that the ultrasonic pulse pressure is uniform around the bubble. The second term on the right hand side in Eq. 3 represented the fluid viscosity effects and the third term accounted for the encapsulating shell viscosity. μ, the fluid viscosity of saline, was set to 0.001 Pa s. The shell viscosity, , was set to 1.2 × 10−8 kg s−1. The fluid viscosity and shell viscosity terms were developed assuming a radial symmetry on the bubble wall.33 Therefore, in order to implement these terms, we calculated the bubble equivalent radius, . The equivalent radius was calculated by equating the bubble volume with a sphere volume of radius, . Basically, Eq. 3 calculates the bubble pressure with the ideal gas law while accounting for fluid and shell viscosity and also assuming that the acoustic pulse is acting on the bubble wall.
In order to investigate the effects of surface tension on bubbles, a weak form of the boundary condition in Eq. 2 was applied. In this equation, , where γ is the surface tension and κ is the total curvature (κ was twice the mean curvature, where the surface mean curvature was ). After applying the weak form on this boundary condition, the right hand side of Eq. 2 becomes , where Γ is the surface boundary and is the test function. Using the surface divergence theorem,34 the term on the right hand side above becomes
| (4) |
where c is the contour bounding the surface, and m is the outward unit normal to c and while on c, it is perpendicular to n (). The second term on the right hand side in Eq. 4 (i.e., a contour integral) is equal to zero. represents the surface gradient operator.
In this model, for encapsulating shell surface tension, we followed the model proposed by Marmottant et al.35 The Marmottant surface tension has three regimes: buckling, elastic, and ruptured state. The surface tension of the three regimes can be described as follows:
| (5) |
where A is the bubble area and χ is the shell elastic modulus. Tu et al.36 measured the shell elasticity of Definity microbubbles and, based on their work, it was set χ = 0.7 Nm−1. is the bubble area at which the shell buckles. The surface tension varies in an elastic regime until the shell breaks at . The surface tension of water, , was set to 0.072 N/m (assuming it is similar to saline).
Assuming that the bubble radius at rest is equal to the radius below which it buckles (), the Laplace pressure term () vanishes. Thus, in this work reduces to . , the radius at which the bubble shell breaks, is set to , based on the bubble radial threshold for inertial cavitation ()37 and as well = . At each time step, the bubble area was calculated along with its corresponding surface tension. Then, the surface tension from Eq. 5 was implemented in Eq. 4 for γ. In this work and in all of the experimental cases, the bubble passed the early in its expansion phase. Exceeding this point, the shell had no influence on the bubble oscillations and the surface tension of water was applied on bubble wall.
Fluid structure interaction
The fluid and vessel were coupled in a two-way manner. The Navier–Stokes equations for a viscid incompressible Newtonian liquid and equations for a viscoelastic solid were solved simultaneously. In the fluid domain, the following equation was solved:
| (6) |
where ρ is the fluid density, is the fluid velocity field, P is the pressure in the fluid, and σ is the stress tensor. The continuity equation was also satisfied: . The load from the fluid exerted on the vessel boundary is , where n was the normal vector to the boundary. This load represented a sum of the pressure and viscous forces.
In the solid domain, the following equation for a viscoelastic vessel, analogous to the standard linear solid model, was solved
| (7) |
where P is the fluid pressure at the vessel wall and is its time derivative.
The fluid pressure at the vessel wall caused the vessel to undergo displacements. Also, at the vessel wall boundary, the normal fluid velocity was set equal to the vessel wall velocity. This latter condition ensures the coupling between the fluid and the structure.
Method of solution
In the numerical study (both Secs. 2C1 and 2C2), the pressure on vessel ends and initial conditions of the whole fluid were set to the ambient pressure in the capillaries, . The numerical part was solved with a finite element method (FEM) using Comsol Multiphysics 4.2 (COMSOL AB, Burlington, MA). In the numerical part, the vessel length was set to 100 μm which was long enough to make the results independent of the vessel length. A moving mesh method (arbitrary Lagrangian–Eulerian, ALE) was used since the bubble and vessel wall boundaries of our computational domain were moving. As a boundary condition in the moving mesh, the mesh normal velocity at the bubble wall was set equal to the fluid normal velocity. This boundary condition was applied for both Secs. 2C1 and 2C2.
Triangular meshes for this two-dimensional model were used with 4000–10 000 elements for cases 1–4. Since this numerical model was time dependent, the time resolution was set to 0.005 μs for case 1 and 0.01 μs for the rest.
Two of the important stresses were calculated on the vessel wall. WSS was calculated using in cylindrical coordinates, where u and w are the fluid velocity components in r and z directions, respectively. The CS was calculated using a thick wall cylinder equation,38 where and are inner and outer vessel diameters. was the fluid pressure on the vessel wall and was the pressure on the outer diameter of the vessel, which was assumed20 to be .
NUMERICAL RESULTS
Numerical section part I
The numerical viscoelastic vessel displacement as well as the experimental measurement of the vessel wall for cases 1–4 are shown in Figs. 4a, 4b, 4c, 4d, respectively. An ellipsoidally oscillating bubble within a viscoelastic vessel caused these vessel displacements. Generally, there is good agreement between the numerical wall movements and experimental measurements, except for case 3 wherein, during the bubble collapse, the numerical results deviate from the experimental data. Histology data of case 3 shows that endothelium has been torn away and this may explain the discrepancy.
Figure 4.
Radial displacement of the vessel wall. The numerical viscoelastic vessel compared to the experimental of (a) case 1, (b) case 2, (c) case 3, and (d) case 4.
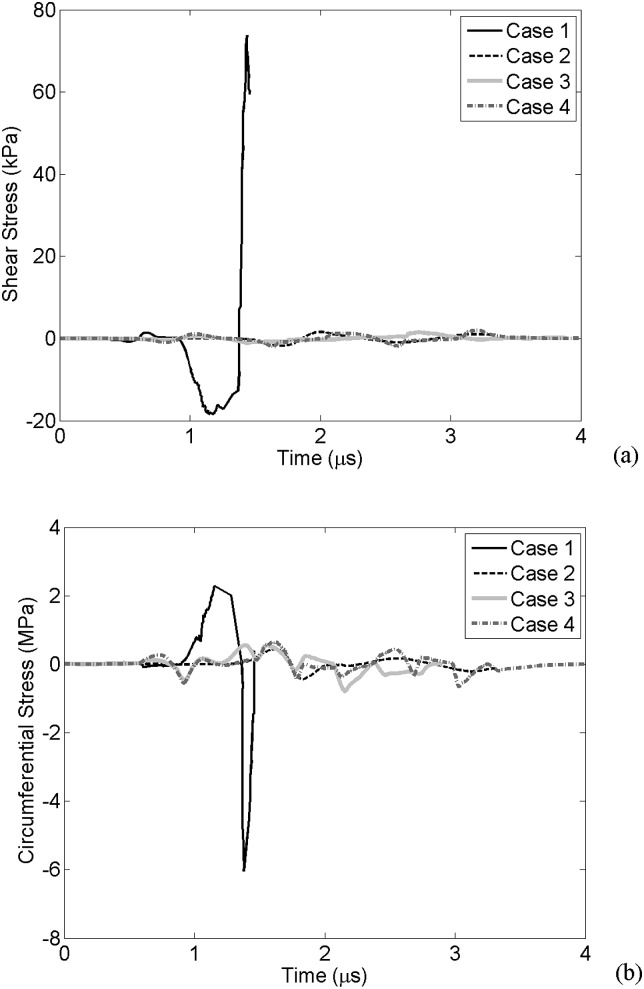
Figure 5a presents the WSS at the vessel wall for cases 1–4 obtained from the first numerical simulations. The negative WSS values correspond to the bubble expansion and the positive stress values correlate with the bubble collapse. For case 1, the maximum positive and negative WSS values are 73.8 kPa and 18.3 kPa, respectively. As in cases 2–4, the bubble wall does not approach the vessel wall, and the stress values are lower. WSS for cases 2, 3, and 4 are +1.6/−1.7 kPa, +1.5/-1.1 kPa and +2/−2.3 kPa, respectively. These results are summarized in Table TABLE III..
Figure 5.
Wall stresses. (a) Wall shear stress calculated at r = rv and an axial distance of z = 3 μm (case 1), z = 11 μm (case 2), z = 13 μm (case 3), and z = 9 μm (case 4). (b) The circumferential stress for case 1, case 2, case 3, and case 4 at r = rv and z = 0.
TABLE III.
Ratio of maximum WSS and CS during vascular invagination to expansion. (Stresses are larger during vascular invagination if boldface values are larger than 1.)
| Case number | WSSinv (kPa) / WSSexp (kPa) | CSinv (MPa) / CSexp (MPa) |
|---|---|---|
| 1 | 73.8/18.3 = 4 | 6/2.2 = 2.7 |
| 2 | 1.6/1.7 = 0.94 | 0.44/0.43 = 1 |
| 3 | 1.5/1.1 = 1.36 | 0.8/0.6 = 1.3 |
| 4 | 2/2.2 = 0.87 | 0.74/0.7 = 1.1 |
Figure 5b shows the CS on the vessel wall in all cases. This stress has its maximum value right above the bubble (r = rv, z = 0). Here, the positive and negative circumferential stresses correspond to bubble expansion and collapse phases, respectively. In case 1, the maximum positive circumferential stress is 2.2 MPa during the bubble expansion phase and the maximum negative CS is 6 MPa during the bubble collapse. In case 2, the maximum CS during expansion and collapse phases reached 0.43 and 0.44 MPa, respectively. These stress values were 0.6 and 0.93 MPa for case 3, and 0.7 and 0.74 MPa for case 4 (Table TABLE III.). Depending on the bubble's initial size and the extent the bubble wall reaches the vessel wall, the wall stress values change. A predicted threshold at which stresses are higher during bubble collapse is calculated and shown in Sec. 3B.
Numerical section part II
In Figs. 67, the results of the second numerical simulations for all cases are plotted.
Figure 6.
Comparison of the numerical simulations with experiments. Bubble radial displacements for cases 1 (a), 2 (b), 3 (c), and 4 (d). From the experimental data in case 1, the bubble was not apparent in a couple of middle time points.
Figure 7.
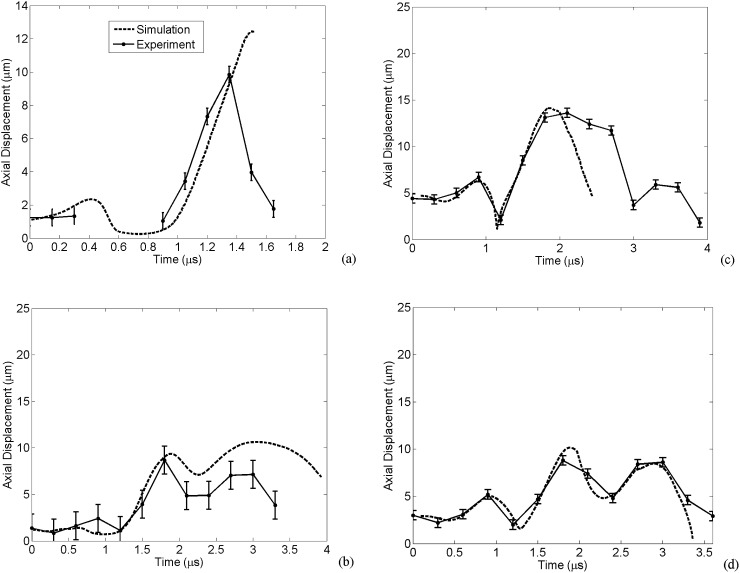
Comparison of the numerical simulations with experiments. Bubble axial displacements for cases 1 (a), 2 (b), 3 (c), and 4 (d).
Figures 6a, 6b, 6c, 6d show the bubbles' semi-minor axis and vessel wall for case 1–4, respectively, and the bubble's axial displacements (bubbles' semi-major) are plotted in Figs. 7a, 7b, 7c, 7d. The bubble semi-minor radius and vessel displacement in Fig. 6a (case 1) are within 4% of the experimental data. The bubble's axial wall in case 1 peaks at a value 25% more than that measured in the experiments [Fig. 7a]. The numerical bubble amplitude of oscillation for cases 2, 3, and 4 were within 13%, 15%, and 11% of those measured in experiments [Figs. 6b–6d, 7b–7d], respectively. In case 3 [Figs. 6c, 7c], the numerical simulation stopped during the bubble collapse and therefore the last cycle of oscillation is not simulated.
The WSS and CS were calculated from the second numerical part as well. The maximum variations of these stresses are compared to the results of the first numerical part. Stresses had the same trends similar to those reported in Fig. 5. WSS and CS calculated from the second numerical part for case 1 were 13% and 7% higher than that calculated in the first numerical part, respectively. These stresses were higher by 17% (WSS) and 19% (CS) for case 2, 33% (WSS) and 5% (CS) for case 3, and 38% (WSS) and 32% (CS) for case 4.
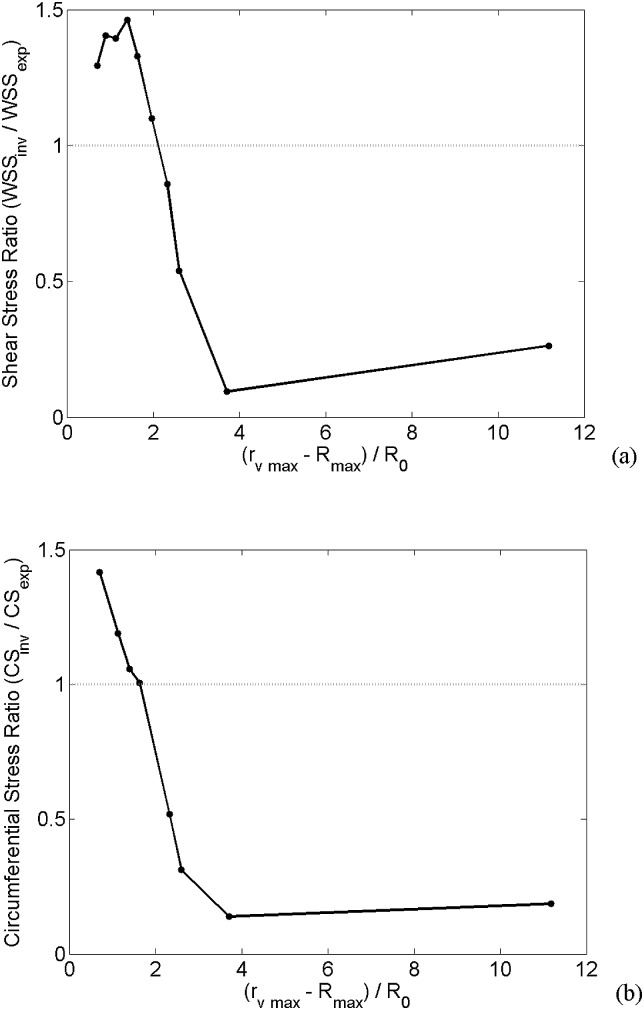
The stress values obtained for the four experimental cases used here suggest that there is a threshold where the stresses are higher during the bubble collapse, and this threshold depends on the distance the bubble wall gets to the vessel wall. Numerical simulations (part II) of a 1 μm bubble within various vessel sizes (3–20 μm) were performed to predict this threshold. Figure 8 shows the ratio of stresses (invagination over expansion phase) versus a dimensionless metric, , where is the maximum vessel radius and is the maximum bubble radius. This metric calculates the bubble wall to the vessel wall distance (at bubble's maximum expansion) normalized to the bubble initial radius. Figures 8a, 8b show the WSS and CS ratios, respectively. In this case, where the bubble size was fixed at 1 μm, d increased with the vessel radius. The shear stress was higher during the bubble collapse when the vessel size was 8 μm or smaller. For 7 μm vessels or smaller, the CS passed the threshold value as it was higher during the bubble collapse. In other words, the results in Fig. 8 represent that stresses during the bubble collapse phase are stronger when the bubble/vessel interactions are strong.
Figure 8.
Relative stress values versus relative bubble to vessel distance normalized to bubble initial size. (a) Wall shear stress ratio, (b) circumferential stress ratio. The dotted line represents the invagination stress threshold.
DISCUSSION
The experimental results had two sources of measurement uncertainties: (i) user variability in measuring the bubble and vessel radii, which was less than 1 μm; (ii) frame-to-frame alignment jitter of the camera's optics; the added uncertainty was about 1 μm. The overall estimated uncertainties in displacement measurements ranged from 1–3 μm.26
Due to some variability in tissue sample positions, some uncertainties in the timing of image frames relative to the ultrasound pulse arrival were introduced. In most of the observations, the first bubble collapse occurred about 1 μs after the arrival of the ultrasound pulse. To reduce the uncertainty, a common temporal axis was adopted to all photographic observations. In addition, cases 2, 3, and 4 had a lower temporal resolution of 0.3 μs. The numerical results in part II (bubble/vessel wall displacements in Figs. 67) were shifted by less than 0.2 μs to align with the experimental measurements.
In Sec. 2C1, wall stresses due to a bubble responding to an acoustic wave passing through the surrounding media could be different from those produced by the forced oscillating bubble. However, in the experimental data, the vessel wall underwent displacements only at the bubble site. In fact, in locations where the acoustic pressure was acting on the vessel with no bubble present (e.g., a few microns away from the bubble site), the vessel wall did not have any displacements due to the acoustic force itself compared to time zero when ultrasound was off. Therefore, it was assumed that stresses leading to vessel wall expansion and invagination were only due to the oscillating bubble.
In Sec. 2C2, it was assumed that the acoustic pressure was acting on the bubble wall directly to save computational time. The resultant wall stresses produced due to this assumption could be different from those when an acoustic wave was passing through the surrounding media. In this work, the experimental mesentery network was relatively thin and the vessels were soft. Therefore, the impedance mismatch between the vessels and fluid as well as the attenuation is low. Furthermore, according to the numerical work by Qin et al. in which the transmitted ultrasound pressure was assessed within different microvessels at various frequencies, ultrasound pressure was disturbed the most in the lumen of rigid vessels and at higher frequencies.39 In this study, the vessel wall was soft and the frequency was relatively low. Therefore, it was safe to assume that the acoustic pressure within the lumen acting on the bubble wall was not distorted compared to the transmitted pulse.
The numerical simulation was performed using an axisymmetrical assumption. The bubble was in the vessel center for cases 1 and 3. In cases 2 and 4, the bubble was slightly off from the vessel center. However, there was no bubble deformation due to this asymmetry. Also in this case, the bubble distance to the vessel wall was large enough that the wall impact on the bubble oscillation was small. Therefore, the axisymmetrical assumption in our numerical work could be valid.
The microbubble model used in this study (Sec. 2C2) was different from the model we previously developed.40 Our previous model was suitable for relatively low acoustic pressures, but in this study the acoustic pressure was ∼1 MPa. However, the bubble oscillations in our current bubble model at low acoustic pressures (in kPa range) converge to the results of our previous model. To further validate this work for the extreme case of an unbound bubble within an infinite fluid, the bubble model was compared with the solution of the Rayleigh–Plesset equation. The numerical solution of our unbound bubble converged to that of the Rayleigh–Plesset.
In case 1, stresses were significantly higher during bubble collapse and, in fact, the WSS was 4 folds and CS was 2.7 folds higher than those during the bubble expansion phase. High velocity gradients and stress values of case 1 were generated due to the fact that the bubble expanded to the size of the vessel and its wall nearly came into contact with the vessel wall.
This model was solved assuming an ellipsoidal bubble; however, we also tested this model with spherical symmetry in order to reveal the importance of asymmetries. Case 1 was chosen for this comparison (Sec. 2C1) and the equivalent bubble radius was used for the spherical bubble. The WSS and CS during bubble collapse from the spherical bubble symmetry were 69 kPa and 3.45 MPa, respectively. These values were 6% and 43% lower than those obtained from the ellipsoidal model, respectively. Based on theses simulations, using a spherical symmetric model for confined bubbles could result in an underestimation of the stresses.
The WSS and CS calculated from the second numerical part (Sec. 2C2) was higher than those calculated from the first numerical part (Sec. 2C1; Fig. 5). This could be due to the fact that the bubble oscillated to a higher extent in the second numerical part compared with the experimental observations (13% in case 2, 15% in case 3, and 11% in case 4). A reason for this might be that bubbles in reality had experienced lower acoustic pressures. Other than that, the encapsulating shell or the vessel wall might have been stiffer than those we used in this study.
The values of the vascular strength reported in the literature vary between 0.46 MPa and 3.6 MPa.41, 42, 43 The maximum CS calculated for cases 1, 3, and 4 exceeded the minimum reported vascular strength, and in case 2 it was on the border of the vascular strength. This suggests that the bubble might have ruptured the vessel wall to some extent or if more experiments were to be conducted some vessels would rupture. It is important to note that the physiological shear induced on the vessel wall by the flowing blood in the cardiovascular system is about 1 Pa,44 and shear stresses in the range of a few kilopascals might induce cell lysis or cell detachment.15
The endothelial cell damage (due to bubble–vessel interactions) was reported by performing histology and transmission electron microscopy.45 The cell damage was attributed to the vessel's invagination-dominated response. In this work, we found that during the vessel invagination the stresses were higher than those during the expansion phase when the bubble gets close to the vessel wall (clearly shown in case 1) indicating that the vascular damage is most likely to occur in this phase.
Parametric studies of the vascular damage along with using a high speed photomicrography system are required in the future. As a result of such experiments, the stress values found numerically could be correlated to and calibrated with the vascular damage thresholds.
SUMMARY
Numerical simulations of confined ultrasound contrast agents within vessels were performed in this work and results were compared with experimental observations. Simulations agreed reasonably well with the experimental observations indicating that this comprehensive model can be used to gain new understanding about physical forces associated with bubble oscillations in small blood vessels. These simulations were used to calculate the WSS and CS (as two vascular damage metrics). In the first numerical part, the bubble was forced to mimic the experimental bubble oscillations. As a result, vessel wall movements and stresses were calculated. In the second numerical part, the confined bubble oscillated due to the ideal gas law and surrounding pressure on the bubble's wall considering the effect of surface tension. Using the numerical model, a predicted threshold was calculated beyond which the stresses were higher during the bubble collapse. These simulations could provide some insight into the mechanism behind the bubble and vessel interaction, as well as the extent of vascular damage microbubbles could induce on the vessel wall.
ACKNOWLEDGMENTS
The authors would like to Dr. David Steinman for helpful discussions. Support for this work was provided by the Terry Fox Foundation, National Institutes of Health under Grant No. EB003268, and the Canada Research Chair Program as well as Ontario Graduate Scholarships in Science and Technology (OGSST).
References
- Miller D. L., Williams A. R., Morris J. E., and Chrisler W. B., “ Sonoporation of erythrocytes by lithotripter shockwaves in vitro,” Ultrasonics 36, 947–952 (1998). 10.1016/S0041-624X(98)00017-1 [DOI] [PubMed] [Google Scholar]
- Hynynen K., McDannold N., Vykhodtseva N., and Jolesz F., “ Noninvasive MR imaging-guided focal opening of the blood-brain barrier in rabbits,” Radiology 220, 640–646 (2001). 10.1148/radiol.2202001804 [DOI] [PubMed] [Google Scholar]
- Unger E. C., Matsunaga T. O., McCreery T., Schumann P., Sweitzer R., and Quigley R., “ Therapeutic applications of microbubbles,” Eur. J. Radiol. 42, 160–168 (2002). 10.1016/S0720-048X(01)00455-7 [DOI] [PubMed] [Google Scholar]
- Skyba D. M., Price R. J., Linka A. Z., Skalak T. C., and Kaul S., “ Direct in vivo visualization of intravascular destruction of microbubbles by ultrasound and its local effects on tissue,” Circulation 98, 290–293 (1998). 10.1161/01.CIR.98.4.290 [DOI] [PubMed] [Google Scholar]
- Miller D. L. and Quddus J., “ Diagnostic ultrasound activation of contrast agent gas bodies induces capillary rupture in mice,” Proc. Natl. Acad. Sci. U.S.A. 18, 10179–10184 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller D. L. and Gies R. A., “ Gas-body-based contrast agent enhances vascular bioeffects of 1.09 MHz ultrasound on mouse intestine,” Ultrasound Med. Biol. 24, 1201–1208 (1998). 10.1016/S0301-5629(98)00063-5 [DOI] [PubMed] [Google Scholar]
- Bao S., Thrall B. D., Gies R. A., and Miller D. L., “ In vivo transfection of melanoma cells by lithotripter shock waves,” Cancer Res. 58, 219–221 (1998). [PubMed] [Google Scholar]
- Kooiman K., Harteveld M., de Jong N., and van Wamel A., “ Transiently increased endothelial layer permeability by ultrasound-activated microbubbles,” Proc.-IEEE Ultrason. Symp. 2006, 529–531 (2006). [Google Scholar]
- Hwang J. H., Brayman A. A., Reidy M. A., Matula T. J., Kimmey M. B., and Crum L. A., “ Vascular effects induced by combined 1-MHz ultrasound and microbubble contrast agent treatments in vivo,” Ultrasound Med. Biol. 31, 553–564 (2005). 10.1016/j.ultrasmedbio.2004.12.014 [DOI] [PubMed] [Google Scholar]
- Caskey C. F., Stieger S. M., Qin S., Dayton P. A., and Ferrara K. W., “ Direct observations of ultrasound microbubble contrast agent interaction with the microvessel wall,” J. Acoust. Soc. Am. 122, 1191–1200 (2007). 10.1121/1.2747204 [DOI] [PubMed] [Google Scholar]
- Zhong P., Zhou Y., and Zhu S., “ Dynamics of bubble oscillation in constrained media and mechanisms of vessel rupture in SWL,” Ultrasound Med. Biol. 27, 119–134 (2001). 10.1016/S0301-5629(00)00322-7 [DOI] [PubMed] [Google Scholar]
- Qin S. and Ferrara K. W., “ Acoustic response of compliable microvessels containing ultrasound contrast agents,” Phys. Med. Biol. 51, 5065–5088 (2006). 10.1088/0031-9155/51/20/001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., Brayman A. A., Bailey M. R., and Matula T. J., “ Direct observation of microbubble interactions with ex vivo microvessels,” J. Acoust. Soc. Am. 125, 2680 (2009). [Google Scholar]
- Chen H., Brayman A. A., and Matula T. J., “ Microbubble dynamics in microvessels: Observations of microvessel dilation, invagination and rupture,” Proc.-IEEE Ultrason. Symp. 2008, 1163–1166 (2008). [Google Scholar]
- VanBavel E., “ Effects of shear stress on endothelial cells: Possible relevance for ultrasound applications,” Prog. Biophys. Mol. Biol. 93, 374–383 (2007). 10.1016/j.pbiomolbio.2006.07.017 [DOI] [PubMed] [Google Scholar]
- Song J., Chappell J. C., Qi M., VanGieson E. J., Kaul S., and Price R. J., “ Influence of injection site, microvascular pressure and ultrasound variables on microbubble-mediated delivery of microspheres to muscle,” J. Am. Coll. Cardiol. 39, 726–731 (2002). 10.1016/S0735-1097(01)01793-4 [DOI] [PubMed] [Google Scholar]
- Hynynen K., McDannold N., Martin H., Jolesz F. A., and Vykhodtseva N., “ The threshold for brain damage in rabbits induced by bursts of ultrasound in the presence of an ultrasound contrast agent (Optison®),” Ultrasound Med. Biol. 29, 473–481 (2003). 10.1016/S0301-5629(02)00741-X [DOI] [PubMed] [Google Scholar]
- Stieger S. M., Caskey C. F., Adamson R. H., Qin S., Curry F. E., Wisner E. R., and Ferrara K. W., “ Enhancement of vascular permeability with low frequency contrast-enhanced ultrasound in the chorioallantoic membrane model,” Radiology 243, 112–121 (2007). 10.1148/radiol.2431060167 [DOI] [PubMed] [Google Scholar]
- Ogũz H. N. and Prosperetti A., “ The natural frequency of oscillation of gas bubbles in tubes,” J. Acoust. Soc. Am. 103, 3301–3308 (1998). 10.1121/1.423043 [DOI] [Google Scholar]
- Miao H., Gracewski S. M., and Dalecki D., “ Ultrasonic excitation of a bubble inside a deformable tube: Implications for ultrasonically induced hemorrhage,” J. Acoust. Soc. Am. 124, 2374–2384 (2008). 10.1121/1.2967488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin S. and Ferrara K. W., “ The natural frequency of nonlinear oscillation of ultrasound contrast agents in microvessels,” Ultrasound Med. Biol. 33, 1140–1148 (2007). 10.1016/j.ultrasmedbio.2006.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., Brayman A. A., Bailey M. R., and Matula T. J., “ Blood vessel rupture by cavitation,” Urol. Res. 38, 321–326 (2010). 10.1007/s00240-010-0302-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung Y. C., “ Structure and stress-strain relationship of soft tissues,” Am. Zool. 24, 13–22 (1984). [Google Scholar]
- Swayne G. T., Smaje L. H., and Bergel D. H., “ Distensibility of single capillaries and venules in the rat and frog mesentery,” Int. J. Microcirc.: Clin. Exp. 8, 25–42 (1989). [PubMed] [Google Scholar]
- Skalak R., Ozkaya N., and Skalak T. C., “ Biofluid mechanics,” Annu. Rev. Fluid Mech. 21, 167–204 (1989). 10.1146/annurev.fl.21.010189.001123 [DOI] [Google Scholar]
- Chen H., Kreider W., Brayman A. A., Bailey M. R., and Matula T. J., “ Blood vessel deformations on microsecond time scales by ultrasonic cavitation,” Phys. Rev. Lett. 106, 034301 (2011), supplementary material. 10.1103/PhysRevLett.106.034301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., Brayman A. A., and Matula T. J., “ Characteristic microvessel relaxation timescales associated with ultrasound-activated microbubbles,” Appl. Phys. Lett. 101, 163704 (2012). 10.1063/1.4761937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung Y. C., Biomechanics: Mechanical Properties of Living Tissues (Springer, New York, 1993), Chap. 2, pp. 23–65. [Google Scholar]
- Smaje L. H., Fraser P. A., and Clough G., “ The distensibility of single capillaries and venules in the cat mesentery,” Microvasc. Res. 20, 358–370 (1980). 10.1016/0026-2862(80)90064-3 [DOI] [PubMed] [Google Scholar]
- Girnyk S., Barannik A., Barannik E., Tovstiak V., Marusenko A., and Volokhov V., “ The estimation of elasticity and viscosity of soft tissues in vitro using the data of remote acoustic palpation,” Ultrasound Med. Biol. 32, 211–219 (2006). 10.1016/j.ultrasmedbio.2005.11.015 [DOI] [PubMed] [Google Scholar]
- Duck F. A., Physical Properties of Tissue: A Comprehensive Reference Book (Academic, London, 1990), pp. 1–336. [Google Scholar]
- van der Meer S., Dollet B., Voormolen M. M., Chin C. T., Bouakaz A., de Jong N., Versluis M., and Lohse D., “ Microbubble spectroscopy of ultrasound contrast agents,” J. Acoust. Soc. Am. 121, 648–656 (2007). 10.1121/1.2390673 [DOI] [PubMed] [Google Scholar]
- de Jong N., Cornet R., and Lancée C. T., “ Higher harmonics of vibrating gas filled microspheres. Part one: Simulations,” Ultrasonics 32, 447–453 (1994). 10.1016/0041-624X(94)90064-7 [DOI] [Google Scholar]
- Walkley M. A., Gaskell P. H., Jimack P. K., Kelmanson M. A., and Summers J. L., “ Finite element simulation of three-dimensional free-surface flow problems,” J. Sci. Comput. 24, 147–162 (2005). 10.1007/s10915-004-4611-0 [DOI] [Google Scholar]
- Marmottant P., van der Meer S., Emmer E., Versluis M., de Jong N., Hilgenfeldt S., and Lohse D., “ A model for large amplitude oscillations of coated bubbles accounting for buckling and rupture,” J. Acoust. Soc. Am. 118, 3499–3505 (2005). 10.1121/1.2109427 [DOI] [Google Scholar]
- Tu J., Swalwell J. E., Giraud D., Cui W., Chen W., and Matula T. J., “ Microbubble sizing and shell characterization using flow cytometry,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 58, 955–963 (2011). 10.1109/TUFFC.2011.1896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flynn H. G., “ Cavitation dynamics. I. A mathematical formulation,” J. Acoust. Soc. Am. 57, 1379–1396 (1975). 10.1121/1.380624 [DOI] [Google Scholar]
- Srivastava A. K. and Gope P. C., Strength of Materials (Prentice-Hall of India Private Limited, New Delhi, 2007), pp. 127–148. [Google Scholar]
- Qin S., Kruse D. E., and Ferrara K. W., “ Transmitted ultrasound pressure variation in micro blood vessel phantoms,” Ultrasound Med. Biol. 34, 1014–1020 (2008). 10.1016/j.ultrasmedbio.2007.11.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosseinkhah N. and Hynynen K., “ A three-dimensional model of an ultrasound contrast agent gas bubble and its mechanical effects on microvessels,” Phys. Med. Biol. 57, 785–808 (2012). 10.1088/0031-9155/57/3/785 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada H. and Evans F. G., Strength of Biological Materials (Williams and Wilkins, Baltimore, MD, 1970), pp. 1–297. [Google Scholar]
- Rowe A. J., Finlay H. M., and Canham P. B., “ Collagen biomechanics in cerebral arteries and bifurcations assessed by polarizing microscopy,” J. Vasc. Res. 40, 406–415 (2003). 10.1159/000072831 [DOI] [PubMed] [Google Scholar]
- Snowhill P. B. and Silver F. H., “ A mechanical model of porcine vascular tissues: Part II. Stress–strain and mechanical properties of juvenile porcine blood vessels,” Cardiovasc. Eng. 5, 157–169 (2005). [Google Scholar]
- Rooney J. A., “ Hemolysis near an ultrasonically pulsating gas bubble,” Science 169, 869–871 (1970). 10.1126/science.169.3948.869 [DOI] [PubMed] [Google Scholar]
- Chen H., Brayman A. A., Evan A. P., and Matula T. J., “ Preliminary observations on the spatial correlation between short-burst microbubble oscillations and vascular bioeffects,” Ultrasound Med. Biol. 38, 2151–2162 (2012). 10.1016/j.ultrasmedbio.2012.08.014 [DOI] [PMC free article] [PubMed] [Google Scholar]