Modeling the biological response of normal human cells, including repair processes, to fractionated carbon beam irradiation

Abstract

To understand the biological response of normal cells to fractionated carbon beam irradiation, the effects of potentially lethal damage repair (PLDR) and sublethal damage repair (SLDR) were both taken into account in a linear-quadratic (LQ) model. The model was verified by the results of a fractionated cell survival experiment with normal human fibroblast cells. Cells were irradiated with 200-kV X-rays and monoenergetic carbon ion beams (290 MeV/u) at two irradiation depths, corresponding to linear energy transfers (LETs) of approximately 13 keV/μm and 75 keV/μm, respectively, at the Heavy Ion Medical Accelerator in Chiba of the National Institute of Radiological Sciences. When we only took into account the repair factor of PLDR, γ, which was derived from the delayed assay, the cell survival response to fractionated carbon ion irradiation was not fully explained in some cases. When both the effects of SLDR and PLDR were taken into account in the LQ model, the cell survival response was well reproduced. The model analysis suggested that PLDR occurs in any type of radiation. The γ factors ranged from 0.36–0.93. In addition, SLD was perfectly repaired during the fraction interval for the lower LET irradiations but remained at about 30% for the high-LET irradiation.

INTRODUCTION

Radiotherapy is in some cases a primary medical treatment for cancer because it is less somatically invasive than surgery. Compared to conventional radiation, including X-rays, irradiation by heavy charged particles such as carbon ions is more suitable for cancer therapy, because carbon ions realize good absorbed dose localization for deep-seated tumors, which is known as the Bragg peak [1]. The extent of the localization is biologically enhanced in accordance with the increased stopping power toward the beam range [2, 3].

Following the pioneering study at Lawrence Berkeley National Laboratory in the USA [4], the Heavy Ion Medical Accelerator in Chiba (HIMAC) was established in 1994 at the National Institute of Radiological Sciences (NIRS), and carbon ion radiotherapy was begun there [5, 6]. So far, about 7000 patients have been treated for various solid tumors, and excellent outcomes have been achieved [7, 8].

Radiation therapy is usually carried out on a fractionated irradiation basis. In fractionated therapeutic irradiations, repair is thought to be completed before the subsequent irradiations; in other words, the dose response is considered identical among irradiations. Then, in fractionated radiotherapy, the side effects in normal tissues are generally mitigated by repair mechanisms, while the tumor control level is, ideally, maintained due to deficient repair capacity of the tumor. The ideal dose localization of carbon ions mentioned above has made hypofractionated irradiation feasible.

However, in some experiments a difference in response has been observed between single and fractionated irradiations with a high linear energy transfer (LET) heavy-ion beam.

From the experiment with fractionated irradiation (1–6 fractions) with carbon ions applied to mouse skin, a non-linear relationship on the Fe plot appeared in the case of carbon 100 keV/μm irradiation (Fig. 4 in ref. [9]). This suggests that the linear-quadratic (LQ) model alone cannot explain the entire response of fractionated irradiations.

Fig. 4.

Fit to the cell survival data by eq. (11) where θ equals 0 with α and β values of single irradiation. Black solid line: single fraction, gray solid line: twice repeated irradiations, black dashed line: three times repeated irradiations, gray dashed line: four times repeated irradiations. Experimental data: closed circles for single fraction, closed squares for twice repeated irradiations, closed diamonds for three times repeated irradiations, and closed triangles for four times repeated irradiation.

In order to understand the result, we carried out an in vitro biological response study of fractionated irradiations and developed a dose-response model for fractionated irradiations by incorporating the repair effects into the conventional LQ model. To date, few fundamental in vitro studies have examined the repair characteristics under fractionated carbon-ion irradiation, especially in human cells. Suzuki et al. reported the recovery ratio by potentially lethal damage repair (PLDR) in various cell lines for different fractionated irradiation schedules, including carbon ions [10]. The study estimated the extent of PLDR in normal cells when cells were kept under the stationary phase. The result showed that PLDR depended on the cell lines and the radiation quality. However, the characteristic of PLDR was obtained only for a fixed fraction size. The overall biological dose under therapeutic carbon-ion irradiation has not been reported. So, we performed a fractionated irradiation experiment with carbon beams that mimicked the clinical schedule with human cells. A delayed-assay experiment was also conducted with the cells in order to reveal the extent of PLDR. By combining both PLDR and sublethal damage repair (SLDR) a new LQ was developed that aptly modeled the cellular response to fractionated irradiation.

MATERIALS AND METHODS

Cell survival response for fractionated irradiation

The LQ model has been widely used as a cell survival model. In the LQ model, the cell survival probability S_n for n fractionated irradiations with a single dose d is given by implicitly assuming the full recovery between the fractionations as:

(1)

Here we take into account the repair effects in this study. It is regarded that radiation causes two types of DNA damage [11]. One is potentially lethal damage (PLD). In principle, PLD is considered fatal as is, and the initial yield is estimated by the LQ formalism. However, some part of the PLD can be repaired depending on the environment after the irradiation [12]. The other is sublethal damage (SLD), which can be repaired in hours unless additional sublethal damage occurs. Lethal damage originates from unrepaired PLD and SLD. Each repair mode is explained in detail below.

Repair modes

PLDR-like repair

PLDR is considered possible if cell cycles are suspended for >6 h after irradiation [13, 14]. Marchese et al. [15] considered that, by PLDR, the original LQ survival curve is scaled to the repaired one by a single factor γ where γ = 1 for immediate plating.

(2)

In fractionated irradiation, this behavior of PLDR is assumed to be repeated in multiple irradiations by following Marchese's formalism as below:

(3)

In the fractionated irradiation for normal cells, this PLDR is expected to occur if the cells are kept in a confluent condition and are suspended from cell division. In parallel, PLDR can be also evaluated by a delayed assay by keeping the cells in confluence for 24 h after irradiation.

SLDR-like repair

The incomplete repair (IR) model [16, 17] was proposed for SLDR as an extension to the LQ model. In the case of two fractionated irradiations, the survival level, S_2, after two doses of size d irradiations with interval Δt under SLDR, is given as follows:

(4)

(5)

The extent of unrepaired SLDs is indicated by an index, θ. To represent the repair kinetics, θ takes an exponential form as a function of time, as follows:

(6)

where T_SLDR corresponds to the repair time constant of SLD. If the SLDR is completed, i.e. Δt is long enough, θ = 0. In this case, the initial LQ response is expected to be repeated in the fractionated irradiations. If the SLDR is uncompleted, the dose response of the second irradiation does not coincide with the first one.

When generalizing eq. (4) to n fractions under the assumption that cell proliferation is negligible (this is the case for normal cells, as the cells were kept in a confluent state and unable to proliferate), then survival, S_n, is given with the formula h_n (θ), as follows:

(7)

(8)

Again, if the SLDs are repaired completely (θ = 0), the survival curve agrees to the LQ formalism, i.e.

Overall response in fractionated irradiations

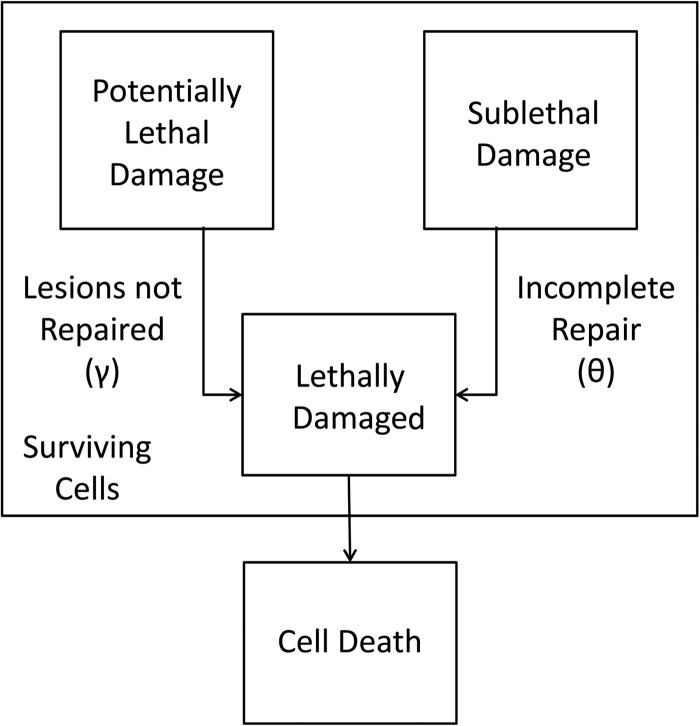
The repair processes of SLD and PLD have been found to occur in vitro [18] as well as in vivo [19]. In this study, we consider the simultaneous action of both repair processes in the fractionated irradiation. Figure 1 shows a simplified schematic of processes leading to cell death. Some PLD (γ) and some SLD (θ) causes lethal damage and results in cell death.

Fig. 1.

Simplified schematic of processes leading to cell death. Some of the potentially lethal damage (PLD) and some of the sublethal damage (SLD) causes lethal damage (LD) and results in cell death.

For the sake of simplicity, we start with the two fractionated irradiations with SLDR only (eqs. (7) and (8)). In this case, the survival, S₂, can be considered as:

(9)

For the last term,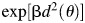, which is regarded as the SLD repair term, the original β value was used throughout the irradiation. In case of PLDR, the first term in eq. (9) is replaced by 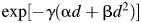. When the effect of PLDR is added, this equation (9) can be rewritten as

(10)

The first term corresponds to the lesions remaining after the PLDR process: for the second irradiation the γ is not given because the cells were immediately assayed after the irradiation. The last term corresponds to the SLDR to be expected between the irradiations.

On the other hand, the response of the delayed-assay experiment is regarded to be affected only by PLDR, and is simply given as eq. (2), which makes it possible to estimate the γ value in isolation. When generalizing eq. (10) to n fractions, the survival, S_n, is given as:

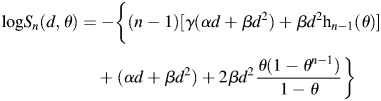(11)

Again, in this fractionated experiment, the irradiated cells are immediately assayed after the final irradiation. Then the PLDR after the final irradiation does not take place; i.e. PLDR is repeated (n − 1) times for n fractionated irradiations.

Here we assume that for X-rays the time constant of both repair processes are on the same order, or ∼6 h [20–22]. Then, even if the cross term exists, the effect is considered to be limited in the first order. From the reason we assume that both the PLDR and SLDR take place independently; i.e. the cross term between the PLDR and SLDR is not taken into consideration.

In the fractionated irradiation experiment it is not possible to derive γ and θ separately, because the observed cell survival response is affected by both processes. On the other hand, PLDR can be evaluated separately, by comparing immediate plating (normal single fraction) and delayed plating (delayed assay) survival. Thus, at first we tried to evaluate the parameter γ by the delayed-assay experiment with α and β values of the immediate assay. Then, in order to reproduce the response in fractionated irradiations, we searched for the θ which gave the best fit (in the least squares sense) to the experimental data with the derived γ. This approach is based on the assumption that PLDR is prior to SLDR.

Fractionated cell survival experiment to verify the model

Cell lines

The cells of two human normal cell lines were used in this study. NB1RGB is a normal human skin fibroblast cell line (Cell No. RCB0222), and HFL-I is a normal embryonic lung fibroblast cell line (Cell No. RCB0521), distributed by the RIKEN BRC Cell Bank of Japan. These cell lines were chosen for this study to better understand the previously mentioned in vivo mouse skin cell response, considering the significance of the response in radiotherapy. [23]. NB1RGB and HFL-I were first cultured in a 75-cm² plastic flask (BD Falcon^TM 353084) in Eagle's minimum essential medium (MEM: Nissui Pharmaceutical) with 10% fetal bovine serum. The plating efficiency of these cells was 20–30% in a 10-cm diameter plastic dish (BD Falcon^TM, 353003). These cells were held in a 5% CO₂ incubator at 37°C.

The phase of the normal cell cycle was synchronized and stopped at G₁/G₀ in this experiment by keeping the cells at the 100% confluent condition to exclude the extra variation in response due to the cell-cycle dependence of the radiosensitivity [24, 25].

Irradiation

Biological experiments with carbon ion beams were carried out at the biology experiments port of HIMAC. The initial energy of the carbon beam was 290 MeV/u, and the dose rate at the point of irradiation was controlled in the range of 0.1–7.0 Gy/min in order to maintain dosimetric precision. Incident beams were broadened uniformly to 10 cm in diameter at the isocenter. Cells were irradiated at two different irradiation depths to investigate the LET dependence of the responses. One depth was at the entrance of the beam, where the dose-averaged LET was approximately 13 keV/μm, and the other was at the ascending slope to the Bragg peak, where the LET was approximately 75 keV/μm, adjusted by inserting an energy absorber made of polymethyl methacrylate (PMMA) upstream from the cells. The cell lines were inoculated into 25-cm² plastic flasks 3 days prior to the irradiation at various cell concentrations. The cells were almost 100% confluent by the first day of irradiation.

For the fractionations, doses of 0.15–5.5 Gy were delivered to each cell flask placed at the isocenter in the single-, two-, three-, or four-dose fractionated irradiation over a 24-h interval. Within an hour after the final irradiation, the cells were re-plated onto a dish, then held in a 5% CO₂ incubator at 37°C for 2 weeks to form colonies. For the delayed assay, the cells were incubated for 24 h post-irradiation to determine cell survival as a function of delayed plating time.

A similar experiment was carried out with X-rays as a reference to the carbon beam experiment just described. In this experiment, 200-kV X-rays (20 mA) with 0.5-mm Al and 0.5-mm Cu filters were used at a dose rate of 0.85 Gy/min, and doses of 0.15–6.0 Gy were delivered. All of the irradiations were carried out at room temperature.

Clonogenic survival assay

Cell survival estimated by colony-forming assay as a result of cell death was chosen as the endpoint of this study. After irradiation, the cells were rinsed twice with phosphate-buffered saline and trypsinized, and different numbers of each sample were immediately plated in a 10-cm-diameter plastic dish, with the expectation that 50–70 colonies would grow in the dish. The produced colonies were fixed and stained with crystal violet solution after 14 days of incubation. The experiment was repeated at least three times for each condition to establish reproducibility. To detect PLDR (delayed assay), irradiated cells were incubated for 24 h in a 5% CO₂ incubator at 37°C and plated in the same way for immediate assay.

RESULTS

Cell survival curves in fractionated irradiation

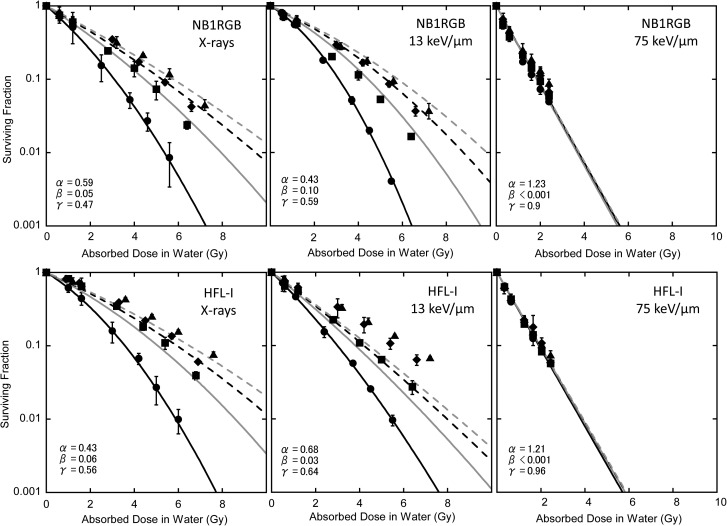
Figure 2 shows the surviving fraction of each cell line. Lines in the figure correspond to the survival curve with eq. (1) based on the α and β values of single irradiation. It is obvious from the figure that the cell survival response in fractionated irradiation was not a simple repeat of a single irradiation. The α, β and α/β value of the single fraction, and the D₁₀ values of single, two, three and four fractions derived from experimental data are summarized in Table 1.

Fig. 2.

Fit to the cell survival data by eq. (1) with α and β values for single irradiation. Black solid line: single fraction, gray solid line: twice repeated irradiations, black dashed line: three times repeated irradiations, gray dashed line: four times repeated irradiations. Experimental data: closed circles for single fraction, closed squares for twice repeated irradiations, closed diamonds for three times repeated irradiations, and closed triangles for four times repeated irradiation.

Table 1:

α, β, α/β, and D₁₀ values of single fractionation derived by the LQ fit to the data, and D₁₀ values of two, three and four fractions

		α (Gy−1)	β (Gy−2)	α/β (Gy)	1F D10 (Gy)	2F D10 (Gy)	3F D10 (Gy)	4F D10 (Gy)
NB1RGB	X-rays	0.59 ± 0.17	0.05 ± 0.02	12.0 ± 8.23	3.1 ± 0.4	4.4 ± 0.3	5.2 ± 0.1	5.8 ± 0.3
	13 keV/μm	0.43 ± 0.05	0.10 ± 0.01	4.25 ± 0.08	3.1 ± 0.1	4.1 ± 0.2	5.1 ± 0.2	5.5 ± 0.3
	75 keV/μm	1.32 ± 0.04	<0.001	∞	1.7 ± 0.1	1.9 ± 0.1	2.0 ± 0.2	2.2 ± 0.2
HFL-I	X-rays	0.43 ± 0.14	0.06 ± 0.02	7.31 ± 4.12	3.6 ± 0.4	5.5 ± 0.1	6.1 ± 0.1	7.0 ± 0.1
	13 keV/μm	0.68 ± 0.07	0.03 ± 0.02	23.6 ± 21.4	3.0 ± 0.1	4.2 ± 0.1	5.4 ± 0.7	6.3 ± 0.1
	75 keV/μm	1.21 ± 0.04	<0.001	∞	1.9 ± 0.1	1.9 ± 0.0	2.0 ± 0.1	2.1 ± 0.1

Estimation of PLDR-like repair from the delayed assay

The surviving fractions of the delayed assay are shown in Fig. 3. The α, β, α/β and D₁₀ values of the delayed assay of the cell lines are summarized in Table 2. Cell survival probability was increased in the delayed plating. We used a least-square method to fit the PLDR factor, γ, in eq. (2) to the experimental data as shown in Table 3.

Fig. 3.

Cell survival of delayed assay. The value of γ was derived from eq. (2). Closed symbols: immediate assay (single fraction), open symbols: delayed assay. Solid line: fit to immediate assay with eq. (1), dashed fit to the cell survival data by eq. (2) with α and β values for immediate assay.

Table 2:

α, β, α/β, and D₁₀ values of delayed assay derived by the LQ fit to the data

		α (Gy−1)	β (Gy−2)	α/β (Gy)	D10 (Gy)
NB1RGB	X-rays	0.06 ± 0.02	0.06 ± 0.01	0.89 ± 0.08	5.6 ± 0.4
	13 keV/μm	0.25 ± 0.18	0.05 ± 0.03	5.26 ± 9.09	4.9 ± 0.8
	75 keV/μm	1.19 ± 0.02	<0.001	∞	1.9 ± 0.0
HFL-I	X-rays	0.05 ± 0.04	0.07 ± 0.01	0.81 ± 0.67	5.6 ± 0.2
	13 keV/μm	0.48 ± 0.04	<0.001	∞	4.5 ± 0.1
	75 keV/μm	1.17 ± 0.06	<0.001	∞	2.0 ± 0.1

Table 3:

The α, β and γ parameters from the delayed assay experiment

		α (Gy−1)	β (Gy−2)	γ
NB1RGB	X-rays	0.59 ± 0.17	0.05 ± 0.02	0.47 ± 0.08
	13 keV/μm	0.43 ± 0.05	0.10 ± 0.01	0.59 ± 0.08
	75 keV/μm	1.32 ± 0.04	<0.001	0.90 ± 0.03
HFL-I	X-rays	0.43 ± 0.14	0.06 ± 0.02	0.56 ± 0.08
	13 keV/μm	0.68 ± 0.07	0.03 ± 0.02	0.64 ± 0.01
	75 keV/μm	1.21 ± 0.04	<0.001	0.96 ± 0.02

The values of α and β were derived from the immediate assay (single fraction) and γ was determined by fitting with eq. (2).

Verification of the cell survival model

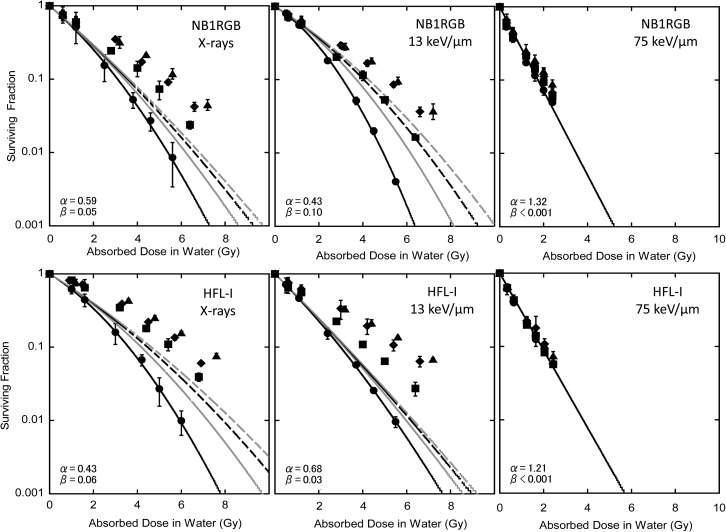
At first, we considered whether the fractionated irradiation response could be explained only with PLDR derived from the delayed assay. Figure 4 shows the result with the eq. (11) where θ = 0, i.e. neglecting the SLDR term. As shown in the figure, it was possible to reproduce the cell response by considering PLDR alone on X-rays; however, a discrepancy was found, especially with HFL-I, for carbon 13 keV/μm. Then, we derived the parameter θ for the SLDR effect with fixed γ from the delayed assay. The results are summarized in Table 4. As shown in the table, θ was not determined under the fixed γ.

Table 4:

The α, β, and γ parameters from the delayed assay experiment

		α (Gy−1)	β (Gy−2)	γ	θ
NB1RGB	X-rays	0.59 ± 0.17	0.05 ± 0.02	0.47 ± 0.08	0.09 ± 0.07
	13 keV/μm	0.43 ± 0.05	0.01 ± 0.01	0.59 ± 0.08	0.11 ± 0.04
	75 keV/μm	1.32 ± 0.04	<0.001	0.90 ± 0.03	a
HFL-I	X-rays	0.43 ± 0.14	0.06 ± 0.02	0.56 ± 0.08	<0.001
	13 keV/μm	0.68 ± 0.07	0.03 ± 0.02	0.64 ± 0.01	a
	75 keV/μm	1.21 ± 0.04	<0.001	0.96 ± 0.02	a

The values of α and β were derived from the immediate assay (single fraction) and γ was determined by fitting with eq. (2). θ was determined simultaneously by fitting eq. (11) to the experimental survival curves (Fig. 2). ^aunsettled.

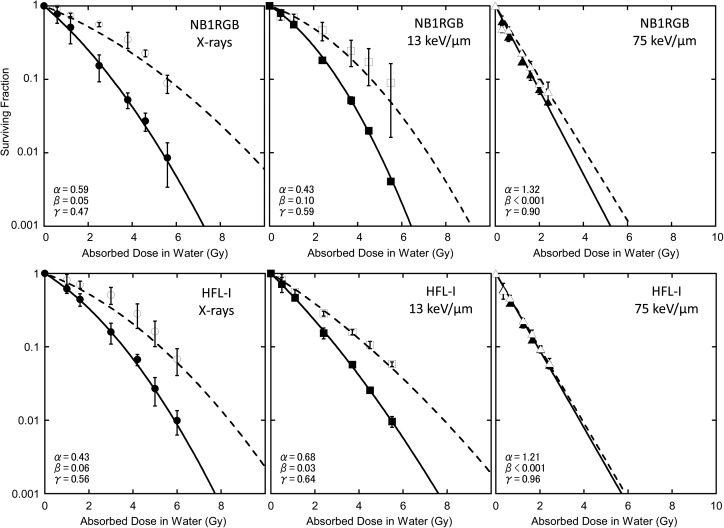
Table 5 shows the summary of SLDR and PLDR parameters as a result of fitting the experimental data by the new model (eq. (11)).

Table 5:

Summary of the PLDR and SLDR factors γ and θ

		α (Gy−1)	β (Gy−2)	γ	θ
NB1RGB	X-rays	0.59 ± 0.17	0.05 ± 0.02	0.46 ± 0.00	0.09 ± 0.06
	13 keV/μm	0.43 ± 0.05	0.01 ± 0.01	0.67 ± 0.05	0.00 ± 0.00
	75 keV/μm	1.32 ± 0.04	<0.001	0.79 ± 0.06	0.30 ± 0.02
HFL-I	X-rays	0.43 ± 0.14	0.06 ± 0.02	0.47 ± 0.04	<0.001
	13 keV/μm	0.68 ± 0.07	0.03 ± 0.02	0.36 ± 0.09	0.12 ± 0.14
	75 keV/μm	1.21 ± 0.04	<0.001	0.93 ± 0.06	0.34 ± 0.13

The values of γ and θ were determined simultaneously by fitting eq. (11) to the experimental survival curves (Fig. 2).

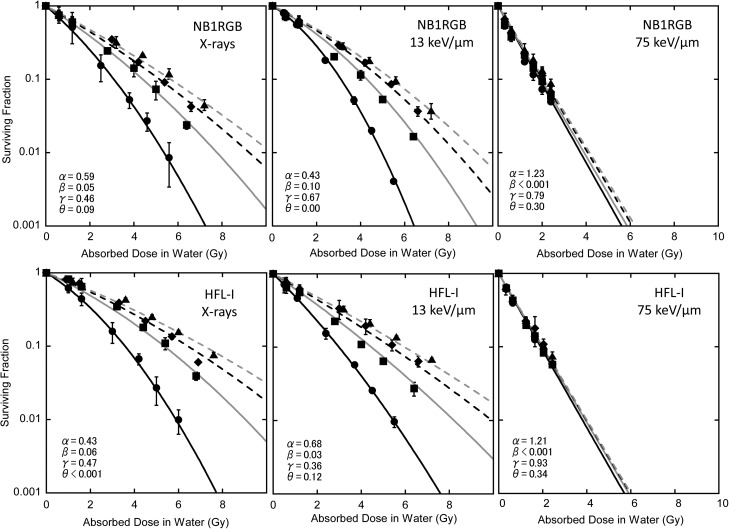
Concerning the SLDR, θ was almost zero for X-rays. This means that SLD was completely repaired. On the other hand, ∼30% of the 75 keV/μm SLDs were left unrepaired for both cell lines. Here, γ values derived by best fits were almost identical with those derived from delayed assay (Table 3) except HFL-I for 13 keV/μm. Figure 5 shows the cell survival fitting by the parameters in Table 5. As shown in the figure, the model in this study can reproduce the normal tissue cell response.

Fig. 5.

Fit to the cell survival data by eq. (11). The α and β values of single irradiation were used. Black solid line: single fraction, gray solid line: two fractions, black dashed line: three fractions, gray dashed line: four fractions. Experimental data: closed circles for single fraction, closed squares for two fractions, closed diamonds for three fractions, and closed triangles for four fractions.

DISCUSSION

As shown in Fig. 2 and Fig. 5, the cell survival response in fractionated irradiation was not reproduced by the LQ model alone but by the combination of the LQ model with two types of repairs, as proposed in this study. This difference was found in each cell line used in this study; i.e. the initial dose response by single irradiation was not repeated in the case of multiple irradiations regardless of radiation quality. This suggests that the repair process plays an important role in the fractionated irradiations.

Concerning the PLDR repair, the delayed assay after 24 h revealed that PLDR repair occurs in normal cells as shown in Fig. 3. As the fractionated irradiations were also performed in 24-h intervals, and it was observed that the cell cycle of the NB1RGB and HFL-1І cells was suspended at the G₀/G₁-phase (Suzuki, personal communication), the same extent of PLDR was expected in the fractionated irradiations.

Marchese et al. [15] reported that the PLDR factor, γ, of normal lung fibroblast cells was around 0.7 for ¹³⁷Cs γ-ray irradiation. Our data (0.47 and 0.56), derived from delayed assay by X-rays, were lower than their result. This suggests that the capacity for PLDR is dependent on the cell line.

The PLDR factor, γ, showed LET dependence (Table 3). The γ value increased with increasing LET. This means that PLDR is less likely to occur in high LET. The LET dependency of PLDR has already been reported in studies of mouse embryos and Ehrlich ascites tumor cells, in which PLDR was less prominent for higher LET beams [26]. In addition, the suppression of PLD repair was reported in high LET with a 90 keV/μm carbon beam [27]. PLDR was also observed in experiments using mouse embryo cells with other beam species such as silicon and neon beams [28].

Figure 4 shows the cell survival response in fractionated irradiation fitted by eq. (11), without the effect of SLDR being taken into account. The cell survival response of HFL-l under 13 keV/μm irradiation was especially not reproduced in this condition. This suggested that consideration of SLDR is necessary, at least in some cases.

Figure 5 shows the fit of experimental results by taking into account both the SLDR and PLDR (eq. (11)). The summary of θ and γ are shown in Table 5. SLDR repair was found to be related to LET. SLD was almost fully repaired in low-LET beams such as X-rays or 13 keV/μm carbon-ions. Travis et al. reported that in vivo SLDR in mouse lung after ¹³⁷Cs γ-ray irradiation is completed perfectly if the time interval is >8 h, but is not complete if the interval is <2 h [20, 21]. This suggests that SLD has repair kinetics.

In our experiment, despite 24-h intervals between irradiations, a certain amount of SLDR was not perfectly repaired, especially in the case of a high-LET 75 keV/μm carbon beam. In our study, as the irradiation interval was fixed, it is not possible to estimate SLDR kinetics for carbon beams. The time-course requires further investigation.

When comparing Tables 3 and 5, γ values are almost identical except for 13 keV/μm with HFL-I cells. Concerning the SLDR, θ was almost zero for both the X-rays and 13 keV/μm carbon beams. This means that SLD was completely repaired. On the other hand, about 30% of the 75 keV/μm SLDs are left unrepaired in normal cell lines. By choosing the optimal values for parameters θ and γ, the new model can reproduce the experimental results fairly well.

Here, γ values of HFL-I cells under 13 keV/μm irradiation derived by best fits were different from those derived from delayed assay. There are several possible reasons why, one of which is the modeling. As explained, in this study the cross term between PLDR and SLDR was not taken into consideration. The other is, as reported in some studies, the repair capacity could change over time during fractionated irradiation [29], while we assumed a fixed repair capacity. These factors, i.e. the repair kinetics of PLD and SLD and their crossing effect, are worth studying to enable more accurate modeling in the future.

The results of SLDR and PLDR clearly suggest that both types of damages by high-LET radiation are less repaired than those caused by low-LET radiation. High-LET radiation is likely to form cluster-like damage in the cell nucleus, and such damage is in general not repaired by nonhomologous end joining (NHEJ) [30], which is the major repair mechanism for human cells. Thus, chromatin damage, as a consequence of clustered DNA damage, cannot be repaired perfectly, and cell division is consequently suppressed. Finally, the damaged cells are likely to cause reproductive death. In this sequence, the structural deformation of chromatin could also cause a loss of function for DNA repair, the control of gene expression, and the replication of DNA [31, 32].

In this study, we focused on the response of normal cells. Marchese reported that PLDR works even in tumor cells [15]. They estimated the PLDR factor γ in six malignant cell lines as ranging from 0.62–0.93. As their experimental data was derived from 6-h-interval experiments, the effect of repopulation was negligible there. With a 24-h interval, however, repopulation is requisite, together with PLDR for modeling the response in fractionated irradiations.

In conclusion, a new model, combining LQ cell survival and two repair modes, was developed to assess fractionated cell survival response. The model successfully explained the cell survival response of normal cells. Our analysis with this model suggested that PLDR-like repair was observed in both types of radiation, and that SLDR-like repair was nearly complete for only the lower-LET irradiation and partly unrepaired for the higher-LET irradiation.

The simultaneous action of the SLDR and the PLDR we have modeled has been suggested experimentally in vitro [18] and in vivo [19], and its importance in radiotherapy has been asserted [33]. This proposed model is appropriate and useful for understanding clinical responses to carbon ion radiotherapy.

In this study we assumed constant PLDR and SLDR as a function of time; however, in the future it would be worthwhile to study their time-course in order to understand the repair mechanisms further.

FUNDING

This study was supported by the Research Project with Heavy Ions at the Heavy Ion Medical Accelerator in Chiba of the National Institute of Radiological Sciences (NIRS-HIMAC), and the International Open Laboratory.