Abstract
Microwave breast imaging (using electromagnetic waves of frequencies around 1 GHz) has mostly remained at the research level for the past decade, gaining little clinical acceptance. The major hurdles limiting patient use are both at the hardware level (challenges in collecting accurate and noncorrupted data) and software level (often plagued by unrealistic reconstruction times in the tens of hours). In this paper we report improvements that address both issues. First, the hardware is able to measure signals down to levels compatible with sub-centimeter image resolution while keeping an exam time under 2 min. Second, the software overcomes the enormous time burden and produces similarly accurate images in less than 20 min. The combination of the new hardware and software allows us to produce and report here the first clinical 3-D microwave tomographic images of the breast. Two clinical examples are selected out of 400+ exams conducted at the Dartmouth Hitchcock Medical Center (Lebanon, NH). The first example demonstrates the potential usefulness of our system for breast cancer screening while the second example focuses on therapy monitoring.
Keywords: Breast cancer, breast cancer diagnostic, discrete dipole approximation, Gauss–Newton algorithm, therapy monitoring, tomographic imaging, 3-D microwave imaging
I. Introduction
Biomedical imaging is experiencing an increased interest among research institutions, pharmaceutical companies, and hospitals due to unique properties such as noninvasiveness, wide applicability range, and potential high sensitivity and high specificity. Most clinical imaging modalities are currently based on the interaction of either electromagnetic or acoustic waves with body tissues and fluids [1]. In the realm of electromagnetic waves, a large portion of the spectrum has already been exploited, from very high frequencies (positron emission tomography, X-ray/computed tomography), to lower and nonionizing frequencies such as infrared, near-infrared, terahertz, and low megahertz regions where magnetic resonance (MR) operates. A portion of the spectrummuch less investigated is that of microwave frequencies, from a few hundreds of megahertz to several gigahertz. Electromagnetic waves, the means by which microwaves transport power and information, are well understood and their propagation can be accurately simulated in a large variety of environments. The interaction of electromagnetic waves and matter depends on dielectric properties which can be directly related to various types of biological constituents due to their varying degree of water content: bone, fat, muscle, etc. This specificity can be exploited in different tissue types and even offers the rationale for detecting tumors: ex vivo studies have revealed varying degrees of contrast in the dielectric properties between normal and malignant tissue [2]–[5]. The permittivity is normally high at lower frequencies due to the insulating effect of cell membranes, and decreases over higher frequencies due to dispersion and relaxation. Low water content tissues include for example fat, bone, and lung, whereas high water content tissues include muscles, brain, blood, internal organs, and tumors. For low water-content tissues such as the breast, studies indicate that tumor versus normal tissues property contrast can range from 10% to 400%, sufficiently large to be captured by microwave imaging.
Among various possible applications, breast cancer imaging remains a high research priority because of its vast incidence. Roughly 200 000 new cases of breast cancer are typically diagnosed in the U.S. every year, with an estimated 25%–30% of women dying from the disease making it the second largest cause of female cancer deaths in the U.S. [6]. There have been numerous reports demonstrating that early detection is the single most significant predictor of long term survival [7], [8]; therefore, improvements in detection may help reduce the current high mortality rates. Mammography is the front line screening modality but its weaknesses in terms of sensitivity and specificity are well documented [7]. Largely because of cost, magnetic resonance is limited primarily to screening for high risk patients and staging for treatment. Ultrasound provides very good resolution but is especially operator dependent and time consuming, generally limiting its role to the diagnostic setting. Notwithstanding, the morphology of breast tissue is ideal for microwave imaging: fibroglandular tissue has been shown to have higher dielectric properties than fat but with properties that are still lower than tumors in most cases. Furthermore, studies have shown that the amount of fibroglandular tissue can vary widely from fattier breasts (very little) to denser breasts (much larger proportions with highly heterogeneous tissue mixture) suggesting that the baseline electrical properties of the normal breast may be highly variable [9].
The microwave imaging techniques presently being pursued are generally either radar or tomography. With respect to radar technology, the most advanced concepts appear to be confocal microwave imaging [10]–[13] and near field synthetic focusing [14]. Studies of microwave tomography also exist and include reports by Bolomey et al. [15], [16], Liewei et al. [17], Souvorov et al. [18], Bulyshev et al. [19], Meaney et al. [20], [21], Ciocan et al. [22], among others. Most of these efforts are occurring at the simulation and prototype stages where the goal is to identify and optimize the design rather than report on electrical characteristics of breast tissues per se. In addition, most of the microwave breast cancer detection algorithms currently used in conjunction with actual hardware are burdened with significant computational times which currently limit their clinical utility. For example, it is not uncommon to wait tens of hours or even days for a single 3-D microwave tomographic image [23].
In contrast to these limitations, we present our new microwave imaging system which achieves an exam time of under 2 min and produces 3-D tomographic images in minutes. Our new ultra-fast system is based on a unique synergy between hardware and software where both have been jointly optimized to yield near real-time imaging without sacrificing accuracy. The hardware has been designed for state-of-the art performance, incorporating features such as cross-plane data acquisition and patient comfort, while the surrounding tank can be customized for special applications such as integration within an MR chamber for simultaneous MR and microwave exams. The software takes advantage of the weak field disturbances introduced by the antennas, due to both their low profile and the lossy liquid within which they are immersed. The scattering effects, therefore, arise dominantly from the biological tissues which can be efficiently modeled as lossy dielectric scatterers by the discrete dipole approximation (DDA). The system thus created is capable of taking patient data and producing 3-D microwave tomographic images in minutes, and is already in use at the Dartmouth Hitchcock Medical Center (DHMC). Our validation campaign has included studies using simulated data and measured phantom configurations, as well as measured clinical data on patients taking part in our preclinical studies. Initial results from a pilot diagnostic study showed that our microwave technique could distinguish at a statistically significant level between malignant and benign for lesions 1 cm in diameter or greater [24]. In subsequent sections, we concentrate exclusively on clinical cases and focus in particular on two examples, one relating to a cancer screening case along with a second to track tumor progression over the course of neoadjuvant chemotherapy. These results represent the first clinical 3-D microwave tomographic images of the breast.
II. Microwave Imaging: Principle and Hardware
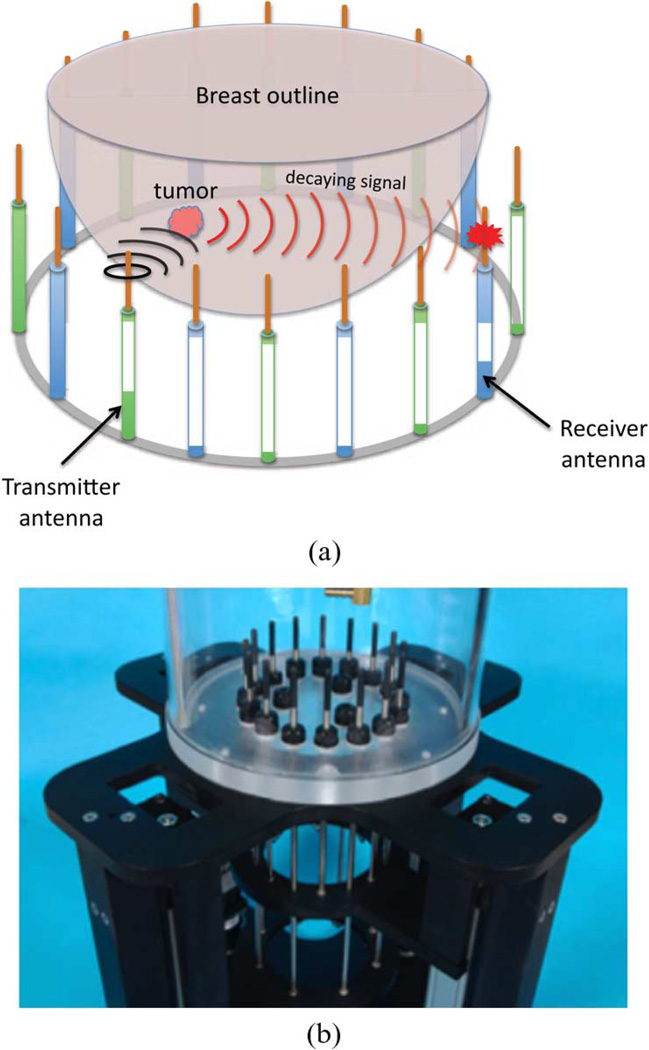
The data acquisition platform takes advantage of the most recent hardware advancements to achieve state of the art data acquisition speed in a clinical setup, thus representing a major improvement over our past system [25]. A photograph as well as a schematic representation of the illuminating chamber are presented in Fig. 1: an array of 16 monopole antennas is organized in a circular fashion, each antenna sequentially transmitting an electromagnetic wave which propagates through the breast within the imaging region. Measurements are collected at the remaining 15 antennas so that those close to the radiator mainly measure waves reflected off tissue surfaces whereas those opposite to the transmitter mainly measure transmitted waves. The multi-view scattered intensity and phase distributions provide information about the local dielectric properties of the transilluminated tissues.
Fig. 1.
Schematic representation and actual photograph of our newest data acquisition platform for breast cancer exam. (a) Schematic 3-D representation of our tomographic microwave imaging setup. (b) Assembled antenna hardware.
Our prototype allows for cross-plane measurements by having the antennas divided into two interleaved sets of eight antennas controlled by separate motors for their vertical positioning. The hydraulic seals in the tank base have been designed to allow free vertical antenna motion over the full tank span, ensuring proper data acquisition for all breast sizes from the chest wall to the nipple region. The tank itself has been optimized for smaller packaging, with current dimensions of 28 cm and 30.5 cm inner and outer plexiglass cylinder diameters, respectively. We have also designed an even smaller tank with specialized antennas operating in MR chambers where we can perform microwave exams simultaneously with MR exams, facilitating the use of specialized imaging algorithms and improved validation.
In order to limit reflections off the tank boundaries, we chose a lossy liquid comprised of a mixture of Glycerin and water which provides a biologically sterile medium into which the patient’s breast can be safely immersed. The two liquids are completely missible and their mixture ratios can be adjusted to match breast tissue properties as close as possible without prior information. We often use a 80:20 glycerin to water ratio for dense breast but a 86:14 ratio for fattier breasts. Losses ensure that signals collected by the receivers are dominated by waves propagating through the imaging region, and that all other reflections and various multi-path signals remain negligible. A secondary effect of these losses is to significantly weaken the received signals, requiring reception channels to accurately capture very low power signals. To this end, our newest hardware system reliably measures down to −140 dBm, which effectively translates into higher operating frequencies and, therefore, improved resolution. Such a low noise floor requires a channel-to-channel isolation of 150 dB. We have also implemented a technique to suppress surface waves along the antenna feedlines and tank structures to minimize unwanted multi-path signal corruption [26]. The antennas are simple monopoles which, when submerged in a lossy liquid, provide the necessary radiation characteristics: omni-directional pattern for full target coverage and good, broadband, impedance matching. Although other types of antennas have been investigated, most often motivated by the availability of optimized designs for free-space operation, we have found that the monopole antennas are one of the most versatile and efficient geometries with respect to our configuration. As will be discussed later, we can accurately use the DDA as a forward solver because the disruption of the field by the array of monopoles in the lossy glycerin bath is minimal.
Our newest system collects 240 data points (16 transmitters with 15 receivers) in roughly 1 s. Typically eleven frequencies are collected across seven coronal planes of the breast, amounting to a total exam time under 2 min per breast. In order to achieve sub-centimeter resolution, we found that an operating frequency of 1.3 GHz is often optimal, although this depends somewhat on breast composition (fat, dense, scattered, or heterogeneous) which justifies ourmulti-frequency data collection. We should emphasize that although resolution improves with increasing frequency, thus intuitively prompting for higher operating frequencies, signal losses and channel isolation can become limiting factors for certain breast types at higher frequencies. Improvements in this direction are currently being pursued.
III. Microwave Imaging Algorithm
A major limitation of current microwave imaging algorithms, in addition to being mostly applied to simulated data, is their heavy computational burden, typically reaching tens of hours or even days for single 3-D images [23]. Conversely, our newest implementation produces images from measurement data in typically less than 10 min on a dual 2.8 GHz Intel Xeon processor, with further speed improvement expected. This ultra-fast processing is possible because of our low profile antenna geometry and the lossy background within which they are embedded. This particular configuration has two consequences. First, scatterers such as tank boundaries and antenna supports produce negligible electric fields at the receivers and do not need to be modeled. Second, the field radiated by the antennas can be assumed to propagate in a homogeneous medium with properties equal to those of the liquid bath, hence lending itself to an analytical solution, only to be perturbed by the scattering from tissues which is accounted for by the DDA discretization (in practise the discretization includes portions of the background medium since we do not have a precise knowledge on the breast boundary). This forward solver is then combined with the Gauss–Newton solution of the normal equation which we have previously documented [27]. Adopting a single and double bar notation for vectors and matrices, respectively, the minimization problem is written as
| (1) |
where Δκ2 denotes the increment in κ2 with κ2 = ω2∊μ0 + iωμ0σ being the complex wavenumber squared which gathers the two unknowns ∊ (dielectric permittivity) and σ (electric conductivity),ω = 2πf where f is the frequency in Hz, J̿ and J̿T are the Jacobian matrix and its transpose, respectively, I̿ is the identity matrix, λ is a regularization parameter, and ΔE is the difference between the measured and computed electric fields (we only measure the vertical component of the electric field in our case, aligned with the monopole antennas). The algorithm, therefore, iteratively updates the values of ∊ and σ across the imaging region in order to minimize ΔĒ. An important novelty of our algorithm is the analytical computation of the Jacobian matrix J̿ which improves accuracy over the more widely used adjoint method [28]. In addition, a logarithmic version of (1) is used, whereby the amplitude and phase differences of the electric field are minimized rather than its real and imaginary parts [27]. The advantages of this method are to linearize the problem and retain phase information, necessary for the recovery of ∊ and σ. A comparison between the two algorithms reveals important advantages of the logarithmic implementation: fast convergence, insensitivity to initial guess (a crucial property in medical imaging where prior information is rarely available), robust even for increasing frequencies (thus lending itself to improved resolution), all of which contribute to produce significantly more accurate images in cases of large and/or strong scatterers [29].
The DDA is used as the forward solver, required at each iteration and representing an important portion of the overall computation burden of the algorithm. The discretization of scatterers such as biological tissues into dipoles [30]–[32] is well suited for modeling heterogeneous structures and is ideal for our configuration since each dipole, with its polarizability, represents a pixel in our images. In addition, all the interaction matrices necessary for the implementation of the DDA are computed offline, resulting in a considerable saving in computational time and memory compared to a numerical approach such as the finite-difference time-domain which we used in the past (typical forward solutions are obtained in seconds instead of minutes). Within the DDA, the electric field is computed from the collective sum of interacting dipoles whose elementary field at position r̄i due to a dipole at r̄j is governed by [33]
| (2) |
where P̄i is the polarization vector, with ∊b being the background permittivity, and r̂ij=(r̄j–r̄i)/| r̄j–r̄i| is the normalized vector between point i and point j separated by a distance rij=|r̄j– r̄i|. Equation (2) can be cast as a matrix operation Ē(r̄ij) = Āij · P̄j and the collective response of all dipoles in response to the incident field is written as
| (3a) |
where
| (3b) |
to which the incident field Ēinc (r̄i) needs to be added in order to obtain the total field. The self-term i = j is given by Ē(r̄i)=P̄i/αi where the polarizability αi of dipole i, whose effective volume is vi, is related to the unknowns by
| (4) |
It should be mentioned that other expressions of αi are possible depending on which definition of the dipole polarizability is adopted [32]. The unknowns P̄j are solved from the DDA master equation
| (5) |
The computation of the Jacobian matrix remains analytical if we realize that the total field at receiver ℓ can be written in a similar way to (5). We denote the interaction matrix by B̿ij and write the total field at receiver ℓ
| (6) |
Hence, B̿ has the exact form as A̿ [obtained from (3b)] but is computed between all the dipole locations and all the receiver locations, whereas A̿ is the interaction matrix between all the dipole locations themselves. In particular, these interaction matrices are only functions of frequency and dipole/receiver locations, but independent of αi. Omitting the indices for simplicity, the Jacobian matrix with respect to ξ where ξ = {∊, σ} is computed as
| (7a) |
From (5)
| (7b) |
so that
| (7c) |
and
| (7d) |
Introducing back into (7a), the Jacobian is obtain as
| (7e) |
The computation therefore only requires the derivative of the polarizability α with respect to ∊ and σ, which is straightforward in view of (4)
| (8a) |
| (8b) |
Again, these expressions could take different forms depending on the definition of the polarizabilities α [32].
These equations can be cast in a series of matrix multiplications, where the matrices themselves can be precomputed and reused at each iteration of the Gauss–Newton iterative approach, yielding a considerable time saving. The basic system of equation can be written as
| (9) |
where ℜ(·) and ℑ(·) denote the real and imaginary part operators, respectively, and
| (10) |
Equation (9) can be directly transformed into the logarithmic version of the algorithm following the procedure outlined in [34], with all the previously documented advantages [27], [29].
Although not shown here, we have extensively validated the forward solver by comparing the 240 electric field points (15 receivers for each 16 transmitters) computed by our DDA method and the 2-D finite-difference time-domain (FDTD) method proposed in [35]. Due to the necessary 2-D nature of the problem, we limited ourselves to the scattering from a cylinder of radius 4 cm and various permittivities and conductivities sampling randomly in the intervals 10 < ∊ < 60 and 0 < σ < 1 [S/m] for a background of parameters (∊,σ) = (15,1.07 [S/m]) which corresponds to a bath of 86% glycerin at 1.5 GHz. The 240 field data points were used to compute the root mean square error (rms) of both the amplitude and phase, with the following results:
Amplitude: the maximum amplitude difference between 2-D FDTD and 3-D DDA was 0.3 dB for overall variations within ±2 dB, with a cumulative average error of 7.3 × 10−4 dB per data point.
Phase: the maximum difference between 2-D FDTD and 3-D DDA was 1.9 for overall variations between −10° and +30°, with an average cumulative error of 6.8 × 10−2 degrees per point.
This study was extended to 3-D by comparing field values obtained with DDA and a 3-D FDTD method of reference. The configuration was that of a sphere of radius 2 cm (hence a large scatterer prone to produce nontrivial scattered fields with peak-to-peak variations of amplitude and phase amounting to about 25 dB and 700° at the frequencies of interest in this paper) with electric parameters equivalent to those of a 50:50 glycerin:water bath in a 90:10 glycerin:water background. The 240 electric fields were samples at 10 planes every centimeter within ±4.5 cm, and at frequencies of 1100, 1300, and 1500 MHz. The mean and standard deviations errors were computed over the 2400 measurement points at each frequencies and resulted in the values summarized in Table I. These errors were obtained with the DDA discretization subsequently used in this paper to analyze clinical data, and are well within acceptable ranges compared to our method of reference. The errors are seen to increase with frequency due to the smaller wavelengths which require finer discretization for both methods. We further confirmed that these errors are indeed reduced with finer DDA and FDTD discretizations, as expected, yielding credibility to our DDA implementation. In the next section, we apply this algorithm to invert clinical data.
TABLE I.
Mean and Standard Deviation (Std) of the Error Between the Scattered Field Computed by DDA and A 3-D FDTD Reference Method for a Sphere (Radius 2 cm, Composition 50:50 Mixture of Glycerin and Water) Within a 90:10 Glycerin and Water Liquid Bath. The Field Values Were Sampled at 240 Points Per Plane, Across 10 Planes Between ± 4.5 cm, and at the Frequencies Shown
| Amplitude [dB] | Phase [degrees] | |||
|---|---|---|---|---|
| mean | std | mean | std | |
| 1100 MHz | 0.04 | 0.17 | 1.1 | 3.7 |
| 1300 MHz | 0.04 | 0.2 | 1.3 | 4.3 |
| 1500 MHz | 0.07 | 0.22 | 1.4 | 4.9 |
IV. Clinical Results
We chose two representative clinical examples out of over 400 cases collected at the DHMC under a Dartmouth College, IRB-approved protocol with associated patient informed consent. The first case demonstrates the potential usefulness of our system for breast cancer screening, showing good sensitivity to regions of higher water content, indicative of potentially malignant tissues. The second case focuses on the therapy monitoring setting, whereby data gathered several weeks apart on a patient undergoing chemotherapy produced images clearly indicating a regressing tumor.
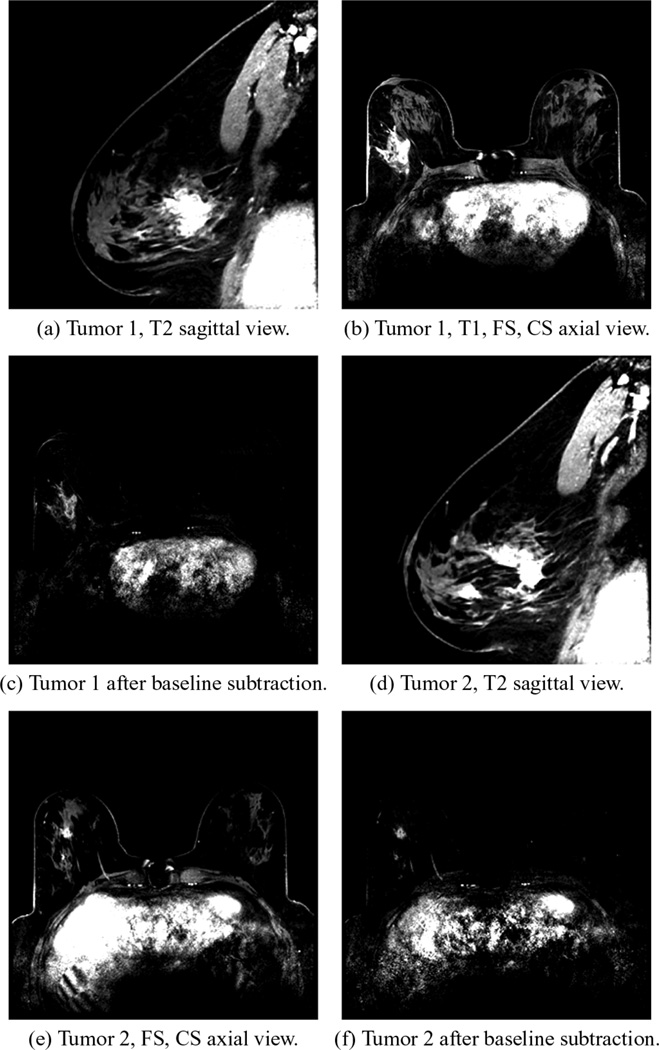
The first example is that of an invasive ductal carcinoma detection in a 55-year-old patient, who had radiographically scattered density breasts. Two malignant lesions in the right breast were confirmed in pathology after a full mastectomy. The first, rated as an BI-RADS 6 before surgery, was 4.2 × 3.2 × 3.1 [cm] located 8.3 cm from the nipple and oriented at 9:00 in terms of the clockface view and was 16 mm from the skin surface. Given an anterior/posterior (AP) diameter of 10 cm, this lesion was quite close to the chest wall. The second was rated as an BI-RADS 5 from mammography and was considerably smaller, 1.2 × 1.3 × 1.0 [cm]. It was located 4.3 cm from the nipple, oriented at 6:30 from the clockface view and was 26 mm from the skin. Fig. 2 shows the corresponding 1) T2 images, 2) T1, fat-suppressed, contrast-enhanced images, and 3) the latter with subtracted baseline prior to gadolinium injection, respectively.
Fig. 2.
MR images: (a)–(c) are for Tumor 1 and (d)–(f) are for Tumor 2. (a) and (d) are frequency selected fat suppression T2 images, (b) and (e) are T1 fat-suppressed (FS), contrast-enhanced (CS) images, while (c) and (f) are T1, FS, CS subtraction images, respectively.
Microwave data were collected in seven anatomically coronal planes spanning a distance of 3.0 cm from the nipple towards the chest wall. As a consequence, only the small tumor is expected to be visible, the larger one being beyond the current illumination zone. The liquid bath consisted of a mixture of about 82% glycerin and water, yielding a relative permittivity and conductivity of ∊b = 23.25 and σb = 1.30 S/m, respectively, for an operating frequency of 1300 MHz at which results are reported. These values are typically closer to those for normal than malignant tissue properties, reducing the bath/normal tissue contrast while accentuating the tumor visibility.
The reconstruction algorithm operated with slightly under 4500 dipoles organized in a cylindrical fashion: spanning 5 cm in height with a radius of 7.0 cm, i.e. located just within the radiating antennas. Note that a generic cylindrical domain was used due to a lack of information on the breast location and volume. Applying more dipoles than necessary ensures that all dielectric and conductivity discontinuities are properly captured. In future versions of our system, a breast surface scanning will be incorporated, confining the reconstruction region to customized smaller volume, subsequently lowering the number of dipoles required and further reducing the computation time.
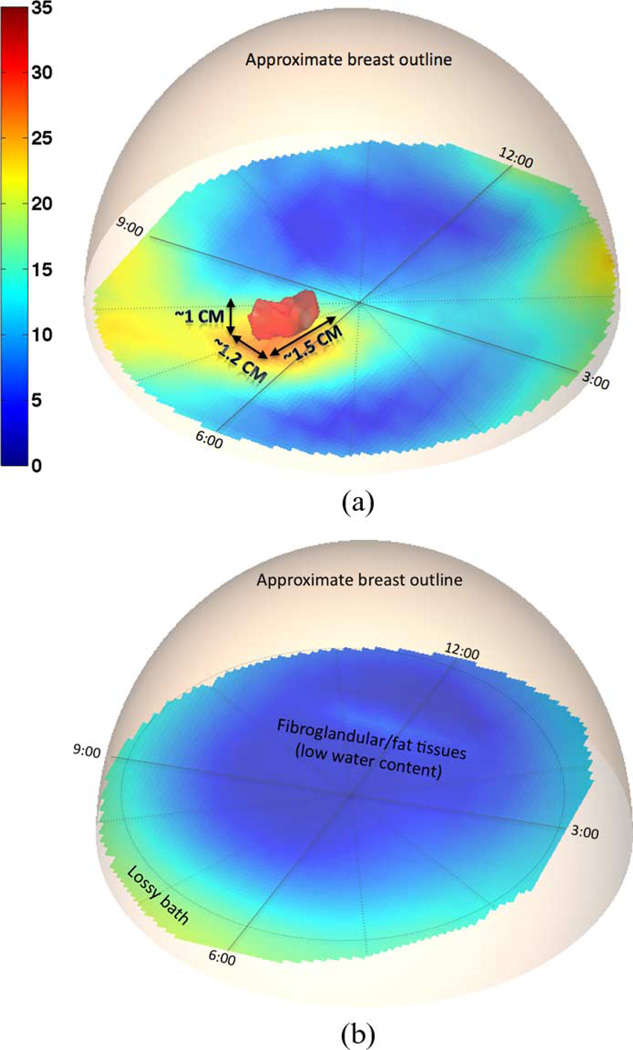
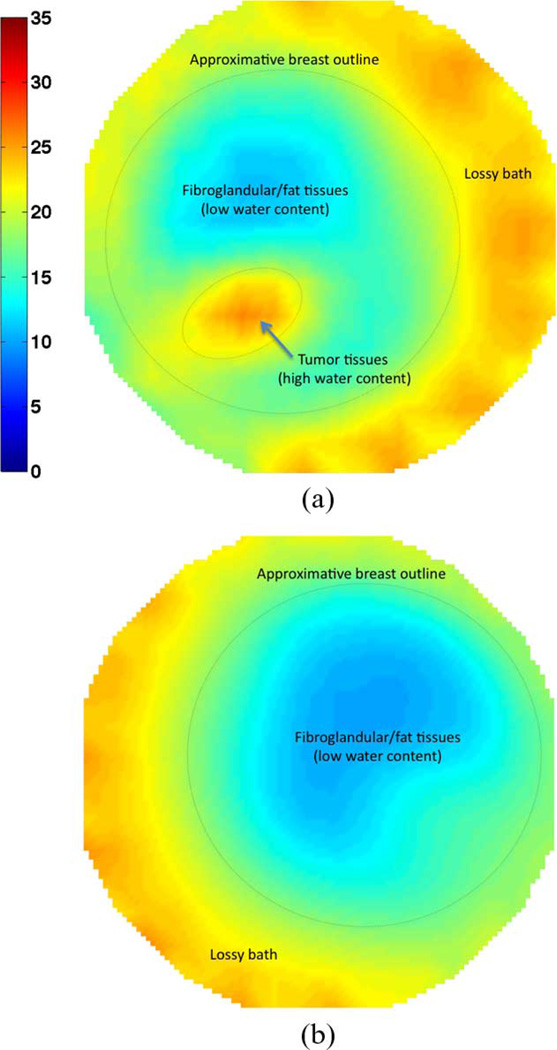
Permittivity results are reported in Fig. 3 for both the right and the left breast, with the outlines only approximately indicative of the boundaries since exact surface rendering was not available for this patient. The red iso-surface shown corresponds to a relative permittivity of ∊ = 30. Fig. 3(a) clearly reveals the presence of a tumor in the right breast at roughly 6:30 from an en face view, about 3 cm from the skin surface and close to the chest wall, in good agreement with the MR images. From the microwave image, the tumor size is estimated at 1.5 cm × 1.2 cm × 1 cm. Incontrast, the 3-D image for the left breast in Fig. 3(b) shows a relatively homogeneous breast with quite low properties situated within the higher property surrounding bath. Only slight perturbations in the breast distribution are visible and are most likely related to the limited amount of associated fibroglandular tissue. Fig. 4 shows a directional averaging of the 3-D permittivity images for each breast compressed into a single coronal image (similar in concept to that observed in standard mammograms). Consistent with the previous images and discussions, the tumor is readily visible in the right breast image as an elevated permittivity zone, with no discerning features visible for the left breast.
Fig. 3.
3-D microwave tomographic permittivity images at 1300 MHz. Higher value iso-surfaces reveal the 3-D structure of a tumor in the right breast while none for the left breast. Results have been confirmed by magnetic resonance images. (a) Right breast. (b) Left breast.
Fig. 4.
Directionally averaged 2-D coronal permittivity images at 1300 MHz. The region of high permittivity in the right breast indicates the presence of a tumor which is noticeably absent in the left breast (used as control). (a) Right breast. (b) Left breast.
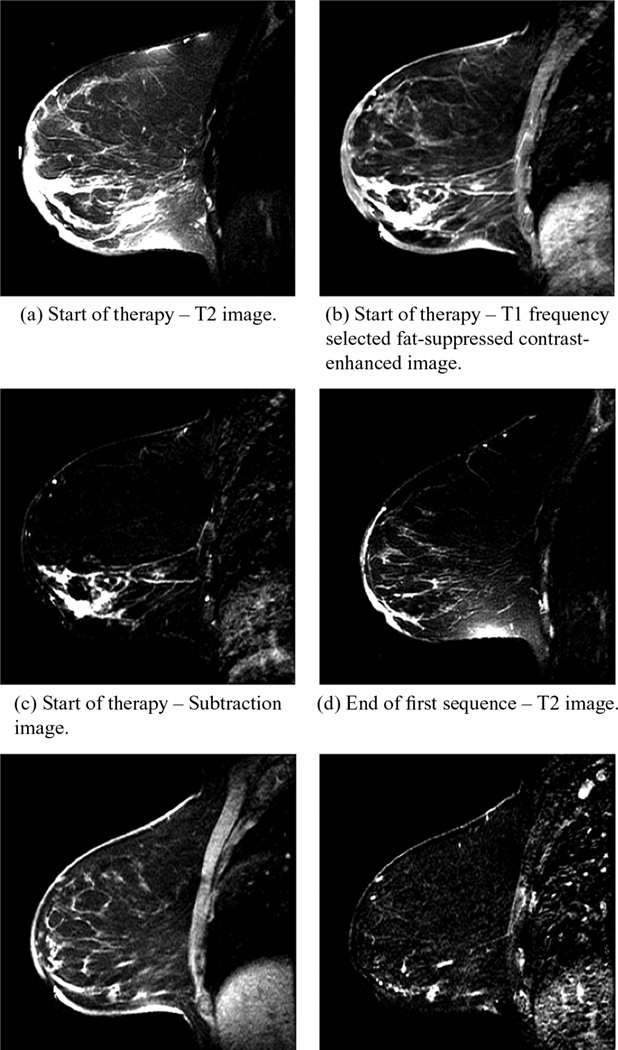
As a second example, we studied a 36-year-old woman also with heterogeneously dense breasts. From the MR exams, an invasive ductal carcinoma measured 6.5 × 3.7 × 7.1 [cm] and was located in the lower right quadrant (en face view) of the right breast and extended from just under the areola region to nearly the chestwall. The patient received neoadjuvant chemotherapy, specifically a widely used regimen consisting of AC (doxorubicin [adriamycin] and cyclophosphamide) X 4 cycles followed by paclitaxel (Taxol) and trastuzumab (Herceptin) X 4 cycles (each cycle was three weeks). She subsequently underwent a modified right mastectomy, and was found pathologically to have had a complete response, with no residual cancer in the breast. Contrast enhanced MR was performed at the start of the treatment (Doxorubicin and Cy-clophosphamide protocol) and at the end of the first set of four cycles of therapy, reported in Fig. 5. For each date, we show the frequency selected fat suppression T2 images, T1 fat-suppressed and contrast-enhanced images, and the latter with a subtracted baseline before contrast injection. For the first date, the images reveal a large, dispersed tumor extending from just under the nipple all the way to the chestwall. The image also shows an extensive skin thickening effect and associated oedema around most of the breast—the skin thickening is not visible in the subtraction image as expected. It was inconclusive as to whether there was any tumor involvement of the skin at the time of the first MR exam. For the purposes of the microwave image, the more important feature of the skin was the increased surface water content. The skin was tested in Pathology after the mastectomy and there was no evidence of tumor there or anywhere else in the breast. In the second set of images there is a marked decrease in the degree of segmental enhancement in the inferior right breast with a change in kinetics from washout/plateau to more benign progressive enhancement. There was also a decrease in degree of skin thickening and axillary nodal involvement.
Fig. 5.
Sagittal MR images of the right breast of the test patient prior to therapy (top row) and after the first set of four cycles of treatment (bottom row). (a) and (d) show the T2 images, (b) and (e) show the T1, FS, CE images, and (c) and (f) are the same as (b) and (e) with a subtracted baseline before contrast injection.
Microwave data were collected at six time points during the treatment: (a) just before the treatment started (day 1), at (b) 23 days, (c) 44 days, (d) 114 days, (e) 163 days, and (f) 229 days. Data were collected for a coupling bath composed of a mixture of 85% glycerin and water, yielding a relative permittivity of 19.1 and a conductivity of 1.23 S/m at 1300 MHz. Other conditions were kept as constant as possible between each exam: exam bath, temperature, power levels, frequency and set of measurement planes. The reconstruction domain is similar to the one used for the previous case, defined by just under 4500 dipoles within a cylindrical region of radius 7.0 cm and height 8 cm.
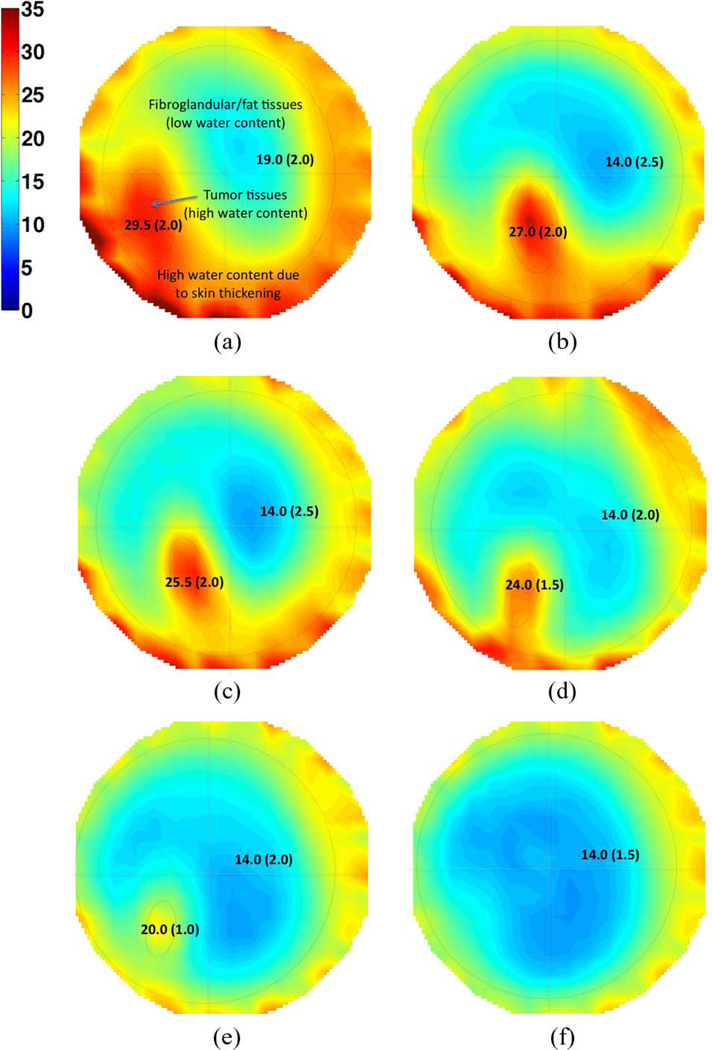
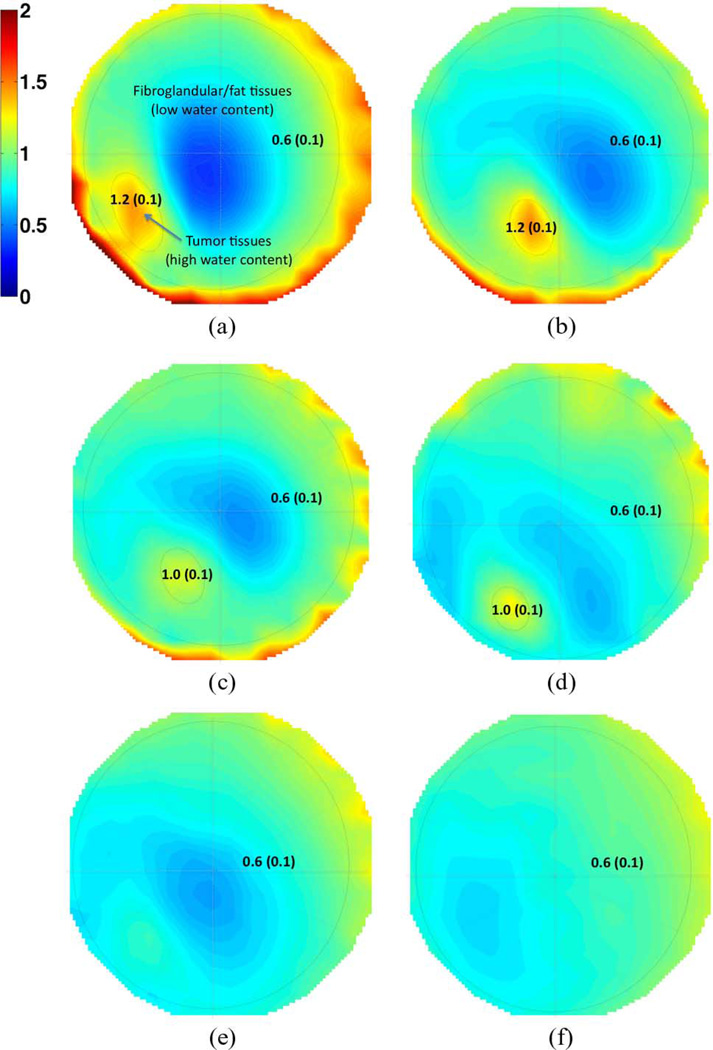
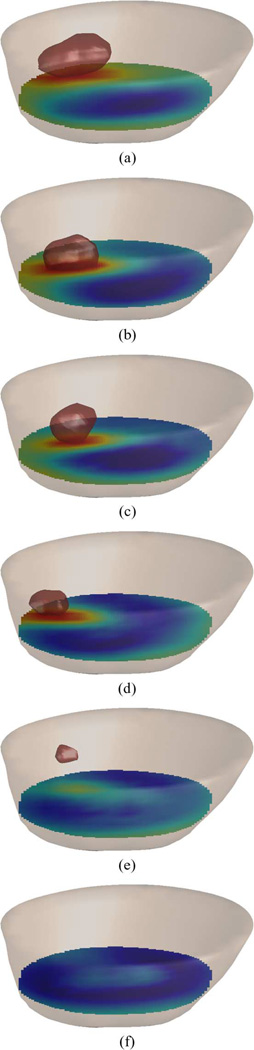
Anatomically coronal permittivity and conductivity image planes for 1300 MHz are presented in Figs. 6 and 7, respectively, where the 3-D images have been projected into a single 2-D image through the coronal direction for the purpose of display. The location of the tumor is obvious, and compares well with MR image interpretations. The sequence of microwave images clearly shows the regression of the tumor throughout the treatment. Statistical specificity information is indicated in the figures directly, providing both the mean and standard deviation of the dielectric property values within the regions of interest. Differentiation between tumor and healthy tissues for both the permittivity and conductivity is clear, with standard deviations decreasing as the tumor shrinks. Isolevels at a relative permittivity of ∊ = 44 are shown in Fig. 8 and again illustrate the shrinking size of the tumor with time.
Fig. 6.
Permittivity images at 1300 MHz at six dates as the patient underwent chemotherapy. The 2-D images are obtained by performing a coronal averaging of the 3-D images shown in Fig. 8. Numerical values show the mean and standard deviation (in parenthesis) of dielectric properties. (a) Day 1. (b) 23 Days. (c) 44 Days. (d) 114 Days. (e) 163 Days. (f) 229 Days.
Fig. 7.
Same as Fig. 6 but for conductivity images. Numerical values show the mean and standard deviation (in parenthesis) of dielectric properties. (a) Day 1. (b) 23 Days. (c) 44 Days. (d) 114 Days. (e) 163 Days. (f) 229 Days.
Fig. 8.
3-D permittivity images at 1300 MHz for six dates as the patient underwent chemotherapy. The contour of the breast is shown in which the isolevel relative permittivity ∊ = 44 has been isolated. The evolution of the contour with time illustrates the shrinking tumor during the chemotherapy treatment. (a) Day 1. (b) 23 Days. (c) 44 Days. (d) 114 Days. (e) 163 Days. (f) 229 Days.
V. Conclusion
The results presented in this paper are the first clinical 3-D microwave tomographic images of the breast and demonstrate the level of maturity recently achieved by our microwave imaging system: the optimized synergy between our novel data acquisition hardware and our fast data processing software yields a system able to image patients in several minutes. The system is currently deployed at the Dartmouth Hitchcock Medical Center where our pre-clinical patient study is ongoing.
On a broader scope, our technology presents important advantages that could complement other imaging modalities: it is safe (power level are about 1/1000th of those used by cell phones are applied over much shorter time periods), fast (data acquisition is less than 2 min—image processing is currently under 20 min with further speed improvement expected), low cost, does not require reagents, and is noninvasive. These advantages may make microwave imaging ideally suited for clinical applications such as breast cancer screening in low and medium income countries where lower incidences of the disease suggest screening programs to be undertaken at earlier ages [36]. Alternatively, our technology is also well suited for therapy monitoring whereby patients need to be imaged frequently. This repetition of exams currently cannot be performed by mammography due to the use of ionizing radiation or by MR due to their elevated costs.
The greatest strength of microwave tomography is its specificity driven by the wide range of dielectric properties which readily allow for differentiation between tissue types and abnormalities. The resolution is still limited to roughly 0.5 cm and 1.0 cm in fatty and denser breasts, respectively. Although comparable to other emerging modalities, in particular elastography, these figures can be improved by operating at higher frequencies and/or using a multi-frequency approach over an ultra-wide band. The hardware used in this work has the capability of gathering data up to 3 GHz, where dielectric contrasts between benign and malignant tissues are still sufficient to be captured. Algorithmic improvements under current investigation are expected to allow us to report on higher resolution images in the near future.
Acknowledgments
This work was sponsored in part by the National Institutes of Health/National Cancer Institute (NIH/NCI) under Grant PO1-CA080139 and in part by Delpsi discretionary funds
Contributor Information
Tomasz M. Grzegorczyk, Delpsi, Newton, MA 02458 USA.
Paul M. Meaney, The Thayer School of Engineering, Dartmouth College, Hanover, NH 03755 USA.
Peter A. Kaufman, Dartmouth-Hitchcock Medical Center, Lebanon, NH 03766 USA
Roberta M. diFlorio-Alexander, Dartmouth-Hitchcock Medical Center, Lebanon, NH 03766 USA
Keith D. Paulsen, The Thayer School of Engineering, Dartmouth College, Hanover, NH 03755 USA.
References
- 1.Fass L. Imaging and cancer: A review. Molecular Oncol. 2008;vol. 2:115–152. doi: 10.1016/j.molonc.2008.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lazebnik M, Popovic D, McCartney L, Watkins CB, Lind-strom MJ, Harter J, Sewall S, Ogilvie T, Magliocco A, Breslin TM, Temple W, Mew D, Booske JH, Okoniewski M. A large-scale study of the ultrawideband microwave dielectric properties of normal, benign and malignant breast tissues obtained from cancer surgeries. Phys. Med. Biol. 2007 Oct;vol. 52(no. 20):6093–6115. doi: 10.1088/0031-9155/52/20/002. [DOI] [PubMed] [Google Scholar]
- 3.Chaudhary SS, Mishra RK, Swarup A, Thomas JM. Dielectric-properties of normal and malignant human-breast tissues at radiowave and microwave-frequencies. Indian J. Biochem. Biophys. 1984;vol. 21(no. 1):76–79. [PubMed] [Google Scholar]
- 4.Joines WT, Zhang Y, Li CX, Jirtle RL. The measured electrical-properties of normal and malignant human tissues from 50 to 900 MHz. Med. Phys. 1994 Apr;vol. 21(no. 4):547–555. doi: 10.1118/1.597312. [DOI] [PubMed] [Google Scholar]
- 5.Duck FA. Physical Properties of Tissue: A Comprehensive Reference Book. London, U.K: Academic; 1090. [Google Scholar]
- 6.Society AC. Breast cancer facts and figures 2007–2008. Atlanta, GA: 2008. [Google Scholar]
- 7.Joy JE, Penhoet EE, Petitti DD. Saving Women’s Lives: Strategies for Improving Breast Cancer Detection and Diagnosis. Washington, DC: Nat. Acad. Press; 2005. [PubMed] [Google Scholar]
- 8.Tabar L, Yen MF, Vitak B, Chen HHT, Smith RA, Duffy SW. Mammography service screening and mortality in breast cancer patients. Lancet Carcinoma Mortality. 2003 Apr;vol. 361(no. 9367):1405–1410. doi: 10.1016/S0140-6736(03)13143-1. [DOI] [PubMed] [Google Scholar]
- 9.Wei J, Chan HP, Helvie MA, Roubidoux MA, Sahiner B, Hadjiiski LM, Paquerault CAZS, Chenevert T, Goodsitt MM. Correlation between mammographic density and volumetric fibroglandular tissue estimated on breast MR images. Med. Phys. Screen.-Program. 2004 Apr;vol. 31(no. 4):933–942. doi: 10.1118/1.1668512. [DOI] [PubMed] [Google Scholar]
- 10.Li X, Bond EJ, Veen BDV, Hagness SC. An overview of ultra-wideband microwave imaging via space-time beamforming for early-stage breast-cancer detection. IEEE Antennas Propag. Mag. 2005 Feb;vol. 47(no. 1):19–34. [Google Scholar]
- 11.Davis SK, Tandradinata H, Hagness SC, Veen BDV. Ultrawideband microwave breast cancer detection: A detection-theoretic approach using the generalized likelihood ratio test. IEEE Trans. Biomed. Eng. 2005 Jul;vol. 52(no. 7):1237–1250. doi: 10.1109/TBME.2005.847528. [DOI] [PubMed] [Google Scholar]
- 12.Fear EC, Li X, Hagness SC, Stuchly MA. Confocal microwave imaging for breast cancer detection: Localization of tumors in three dimensions. IEEE Trans. Biomed. Eng. 2002 Aug;vol. 49(no. 8):812–822. doi: 10.1109/TBME.2002.800759. [DOI] [PubMed] [Google Scholar]
- 13.Yun X, Fear EC, Johnston RH. Compact antenna for radar-based breast cancer detection. IEEE Trans. Antennas Propag. 2005 Aug;vol. 53(no. 8):2374–2380. [Google Scholar]
- 14.Benjamin R, Craddock IJ, Hilton GS, Litobarski S, Mc-Cutcheon E, Nilavalan R, Crisp G. Microwave detection of buried mines using non-contact, synthetic near-field focusing. IEE-Proc., Radar, Sonar Navigat. 2010;vol. 148:233–240. [Google Scholar]
- 15.Bolomey JC, Izadnegahdar A, Jofre L, Pichot C, Peronnet G, Solaimani M. Microwave diffraction tomography for biomedical applications. IEEE Trans. Microwave Theory Tech. 1982 Nov;vol. 30(no. 11):1998–2000. [Google Scholar]
- 16.Bolomey JC, Jofre L, Peronnet G. On the possible use of microwave-active imaging for remote thermal sensing. IEEE Trans. Microwave Theory Tech. 1983 Sep;vol. 31(no. 9):777–781. [Google Scholar]
- 17.Sha LW, Nolte LW, Zhang ZQ, Liu QH. Performance analysis for Bayesian microwave imaging in decision aided breast tumor diagnosis. Proc. 2002 IEEE Int. Symp. Biomed. Imag. 2002:1039–1042. [Google Scholar]
- 18.Souvorov AE, Bulyshev AE, Semenov SY, Svenson RH, Tatsis GP. Two-dimensional computer analysis of a microwave flat antenna array for breast cancer tomography. IEEE Trans. Microwave Theory Tech. 2000 Aug;vol. 48(no. 8):1413–1415. [Google Scholar]
- 19.Bulyshev AE, Semenov SY, Souvorov AE, Svenson RH, Nazarov AG, Sizov YE, Tatsis GP. Computational modeling of three-dimensional microwave tomography of breast cancer. IEEE Trans. Biomed. Eng. 2001 Sep;vol. 48(no. 9):1053–1056. doi: 10.1109/10.942596. [DOI] [PubMed] [Google Scholar]
- 20.Meaney PM, Fanning MW, Li D, Poplack SP, Paulsen KD. A clinical prototype for active microwave imaging of the breast. IEEE Trans. Microwave Theory Tech. 2000 Nov;vol. 48(no. 11):1841–1853. [Google Scholar]
- 21.Meaney PM, Pendergrass SA, Fanning MW, Li D, Paulsen KD. Importance of using a reduced contrast coupling medium in 2-D microwave breast imaging. J. Electromagn. Waves Appl. 2003;vol. 17(no. 2):333–335. [Google Scholar]
- 22.Ciocan R, Jiang HB. Model-based microwave image reconstruction: Simulations and experiments. Med. Phys. 2004 Dec;vol. 31 doi: 10.1118/1.1812871. [DOI] [PubMed] [Google Scholar]
- 23.Semenov SY, Bulyshev AE, Abubakar A, Posukh VG, Sizov YE, Souvorov AE, van den Berg PM, Williams TC. Microwave-tomographic imaging of the high dielectric-contrast objects using different image-reconstruction approaches. IEEE Trans. Microwave Theory Tech. 2005 Jul;vol. 53(no. 7):2284–2294. [Google Scholar]
- 24.Poplack SP, Paulsen KD, Hartov A, Meaney PM, Pogue B, Tosteson T, Grove M, Soho S, Wells W. Electromagnetic breast imaging: Pilot results in women with abnormal mammography. Radiology. 2007;vol. 243:350–359. doi: 10.1148/radiol.2432060286. [DOI] [PubMed] [Google Scholar]
- 25.Paulsen KD, Meaney PM. Nonactive antenna compensation for fixed array microwave imaging: Part I—Model development. IEEE Trans. Med. Imag. 1999 Jun;vol. 18(no. 6):496–507. doi: 10.1109/42.781015. [DOI] [PubMed] [Google Scholar]
- 26.Meaney PM, Shubitidze F, Fanning MW, Kmiec M, Epstein NR, Paulsen KD. Surface wave multipath signals in near-field microwave imaging. Int. J. Biomed. Imag. 2012;vol. 2012 doi: 10.1155/2012/697253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Meaney PM, Fang Q, Rubaek T, Demidenko E, Paulsen KD. Log transformation benefits parameter estimation in microwave tomographic imaging. Med. Phys. 2007 Jun;vol. 34(no. 6):2014–2023. doi: 10.1118/1.2737264. [DOI] [PubMed] [Google Scholar]
- 28.Fang Q, Meaney PM, Paulsen KD. Microwave image reconstruction of tissue property dispersion characteristics utilizing multiple-frequency information. IEEE Trans. Microwave Theory Tech. 2004 Aug;vol. 52(no. 8):1866–1875. [Google Scholar]
- 29.Grzegorczyk TM, Meaney PM, Jeon SI, Paulsen KD. Importance of phase unwrapping for the reconstruction of microwave tomographic images. Biomed. Opt. Exp. 2011 Feb.vol. 2(no. 2):315–330. doi: 10.1364/BOE.1.000315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Draine BT. The discrete-dipole approximation and its application to interstellar graphite grains. Astrophys. J. 1988 Oct 15;vol. 333:848–872. [Google Scholar]
- 31.Goodman JJ, Draine BT, Flatau PJ. Application of fast-Fourier-transform techniques to the discrete dipole approximation. Opt. Lett. 1991 Aug 1;vol. 16(no. 15):1198–1200. doi: 10.1364/ol.16.001198. [DOI] [PubMed] [Google Scholar]
- 32.Yurkin MA, Hoekstra AG. The discrete-dipole approximation: An overview and recent developments. J. Quantitative Spectroscopy Radiative Transfer. 2007;vol. 106:558–589. [Google Scholar]
- 33.Kong JA. Electromagnetic Wave Theory. Cambridge, MA: EMW; 2000. [Google Scholar]
- 34.Meaney PM, Paulsen KD, Pogue BW, Miga MI. Microwave image reconstruction utilizing log-magnitude and unwrapped phase to improve high-contrast object recovery. IEEE Trans. Med. Imag. 2001 Feb;vol. 20(no. 2):104–116. doi: 10.1109/42.913177. [DOI] [PubMed] [Google Scholar]
- 35.Fang Q, Meaney PM, Paulsen KD. Viable three-dimensional medical microwave tomography: Theory and numerical experiments. IEEE Trans. Antennas Propag. 2010 Feb;vol. 58(no. 2):449–458. doi: 10.1109/TAP.2009.2037691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Harford JB. Breast-cancer early detection in low-income and middle-income countries: Do what you can versus one size fits all. Lancet Oncol. 2011;vol. 12:306–312. doi: 10.1016/S1470-2045(10)70273-4. [DOI] [PubMed] [Google Scholar]