Percent Body Fat Prediction Equations for 8 to 17 year old American Children

Abstract

Background

Percent body fat equations are usually developed in specific populations and have low generalizability.

Objectives

To use a nationally representative sample of the American youth population (8–17 years old) from the 1999–2004 NHANES data to develop gender-specific percent body fat equations.

Methods

Percent body fat equations were developed for girls and boys using information on weight, height, waist circumference, triceps skinfolds, age, race/ethnicity, and menses status compared to dual-emission X-ray absorptiometry (DXA). Terms were selected using forward and backward selection in regression models and in a 2/3 development sample and were cross-validated in the remaining sample. Final coefficients were estimated in the full sample.

Results

Final equations included 10 terms in girls and 8 terms in boys including interactions with age and race/ethnicity. In the cross-validation sample the adjusted R² was 0.818 and the root mean squared error (RMSE) was 2.758 in girls. Comparable estimates in boys were 0.893 and 2.525. Systematic bias was not detected in the estimates by race/ethnicity or by BMI categories.

Conclusion

Gender-specific percent body fat equations were developed in youth with a strong potential for generalizability and utilization by other investigators studying adiposity-related issues in youth.

Introduction

Obesity is a condition in which excess adipose tissue has accumulated to the extent that it has adverse effects on health¹. Although the classic definition of obesity emphasizes adiposity, in practice body mass index (BMI) is the measure most often used to characterize obesity. BMI was constructed with the intention to provide an index of weight independent of height, but it is sometimes viewed as a simple prediction equation for percentage body fat. Nevertheless, since BMI does not distinguish fat from lean tissue, some misdiagnosis of obesity is inevitable. Factors that influence body composition in ways not detected by BMI include gender, puberty, age, race/ethnicity, and physical activity^2–3.

As an alternative to methods that require relatively expensive equipment, trained technicians and high subject burden and cooperation, investigators often measure percent body fat using equations that are derived from more field-friendly assessments such as height, weight, skinfold thickness, bioelectric impedance and/or circumferences. Nevertheless, identifying an age, gender and race/ethnicity appropriate equation is often challenging^4–34. Most body composition equations to date have been derived from a convenience or purposive sample with investigators intentionally recruiting such that a range of body sizes was studied. Internal validity (an equation that performed well in those subjects being studied) is the focus rather than external validity (an equation with high generalizability), which impedes researchers from using these equations for other study populations. We know of only one study that has developed an equation using a sample representative of the United States³⁵. That study concentrated on testing mathematical functions of height, weight and BMI (such as the square root) and did not use either circumferences or skinfolds.

The objective of this study was to use extant data from a nationally representative sample to derive and validate gender-specific percent body fat equations that are composed of demographic and anthropometric variables and can be applied to youth (8–17 years old). This age range was selected in order to develop equations for use in the Childhood Obesity Prevention and Treatment Research (COPTR) Consortium field centers at Case Western Reserve University and Stanford University. Our goal was to produce precise, accurate and unbiased percent body fat equations that use the variables collected by the COPTR investigators (gender, age, height, weight, triceps skinfold, waist circumference and menses in girls).

METHODS

The NHANES uses a complex multistage probability design to provide a representative sample of US non-institutionalized children and adults³⁶. NHANES oversampled African Americans, Mexican Americans, low income Whites (beginning in 2000), adolescents aged 12–19 and adults aged 60+ years. Data for this study were from the 1999- 2004 NHANES.

Race and ethnicity were self-reported and categorized as non-Hispanic Whites, non-Hispanic Blacks, Mexican Americans, other Hispanics and other race/ethnicities. The other race/ethnicities group includes other non-Hispanic race groups and non-Hispanic multiracial groups. Maturation status (e.g. Tanner stages) was not collected in the 1999–2004 NHANES. Girls over 12 years of age were asked the age when their first menstrual period occurred. Using this information, we created a dichotomous variable indicating presence or absence of menarche.

Weight, height, waist circumference and triceps skinfolds were measured using standardized procedures in the mobile examination centers³⁶. For all anthropometrics, two trained and certified staff members performed and recorded the measurements. Weight was measured to the nearest 0.1 kilogram in an examination gown without shoes. Standing height (without shoes) was measured to the nearest 0.1 centimeter using a stadiometer with a fixed vertical backboard and adjustable head piece. Waist was measured just above the iliac crest to the nearest 0.1 centimeter and triceps skinfolds were measured to the nearest 0.1 millimeter using Holtain skinfold calipers.

DXA measurements were obtained on participants 8 years of age or older using a Hologic QDR-4500A fan-beam densitometer (Hologic, Inc., Bedford, Massachusetts). Details of the DXA procedures are described in technical documents³⁷. The DXA data were adjusted as described by Schoeller et al.³⁸. Participants were excluded from DXA measurement if pregnant, had a self-reported history of radiographic contrast material use in past 7 days or participation in nuclear medicine studies in the past 3 days, had amputations other than fingers and toes, weighted over 300 pounds or had a height over 6’5”. Pregnancy tests were performed for all females 12 to 59 years of age and menstruating 8 to 11 year olds. Unresolved IRB issues concerning the reporting of pregnancy test results to minors resulted in no DXA data in females 8 to 17 years of age in 1999. Since NHANES data were weighted by two-year increments, there are no DXA data available for girls 8–17 years from the 1999–2000 survey. We used the 4-year (2001–2004) and 6-year (1999–2004) sampling weights in females and males, respectively.

Analytic sample

There are 7,730 children 8 –17 years old in the 1999–2004 NHANES datasets. We excluded children who had missing height, weight, waist circumference or triceps skinfolds (n=614), had an anthropometric flag (e.g. non-standard clothing, not standing straight) (n=28), had biologically implausible values for height, weight or BMI (n=49), were missing all measured DXA data (n=1,599), had given birth in the last year or were breastfeeding (n=13), and were missing menarche status (girls only) (n=53). The full analytic sample included 5,374 children (3,334 boys and 2,040 girls)

Analysis plan

Our goal was to produce equations that maximized the percent of variance explained (R² and adjusted R²) while minimizing the root mean squared error (RMSE) and the bias (mean signed difference, MSD). Age, race/ethnicity, menarche status (girls only), weight, waist, height, and triceps were our base variables. These variables were selected because they were measured by the COPTR investigators and are correlated with percent body fat. Here we distinguish variables (e.g. race/ethnicity, weight) from terms (e.g. squared terms, interaction terms). We selected the terms to study based on our review of terms used in published equations^4–33 and our own exploratory analyses. We tested a total of 76 terms in girls and 65 terms in boys. These terms included squared terms, height as a reciprocal and 2-way interactions of age, age squared, race/ethnicity and menses with the anthropometric variables.

The following steps outline our approach:

Step 1. Create a development and cross-validation dataset

We used the PROC SURVEYSELECT Procedure in SAS (SAS/STAT® 9.2 User’s Guide, 2011) to create the development dataset containing a random sample of 2/3 of the children. The remaining 1/3 of the children constituted the cross-validation dataset. All analyses were stratified by gender and all continuous variables were centered on the mean prior to analysis to improve the interpretability and decrease multi-colinearity^39–40. Race/ethnicity was a categorical variable with non-Hispanic Whites as the referent.

Step 2. Generate models in development dataset

We started with a base model (age, race/ethnicity, menarche status (girls only), weight, waist, height, and triceps), and then used PROC SURVEYREG with the appropriate sample weights to determine which additional terms to add to the model using forward selection to best estimate percent body fat measured by DXA. Because of the large sample size several terms were significant (p<0.05) even though their addition to the model only changed the adjusted R² negligibly. We did not use p-values to determine which variables to select, but instead we used a criterion that an equation must increase the adjusted R² over a simpler equation by at least 0.005 or decrease RMSE by at least 0.025 in order for the change to be judged non-trivial. We used the same criteria to confirm the models using backward selection. This created our models including the base terms plus selected terms. We also tested three additional models: 1) BMI only; 2) BMI z-score only and 3) base terms only.

Step 3. Evaluate models in the cross-validation datasets

The intercept and coefficients for all of the terms in each model from the development dataset were used to calculate the predicted percent body fat in the cross-validation dataset. Gender-specific univariate regression models were run using the estimated percent body fat as the only independent variable and DXA as the dependent variable. R², RMSE and MSD were calculated. Since there was only one independent term in these models adjusted R² was not calculated. MSD were calculated overall and by race/ethnicity and weight status groups. as the predicted percent body fat from an equation minus the percent body fat measured by DXA.

Step 4. Obtain and examine final equations in full dataset

To estimate the coefficients with greater precision, we ran the models by gender in the full dataset and calculated the same parameters shown in step 3. As a final check, an independent programmer calculated percent body fat for 200 randomly chosen girls and boys in a Microsoft Excel spreadsheet using our final formula and compared results to those predicted by our SAS program and the observed DXA values.

RESULTS

Table 1 shows descriptive information on the girls and boys included in the analytic sample. The majority of the sample was non-Hispanic White. Girls had a lower mean weight and height, and higher percent body fat from DXA compared to boys. Over half of the girls had reached menarche.

Table 1.

Descriptive information on analysis sample from the 1999– 2004 NHANES

	Girls (n=2,040)		Boys (n=3,334)
	Mean or %	SE	Mean or %	SE
Age (years)	12.4	0.09	12.4	0.08
Ethnicity (%)
Non-Hispanic White	63.3		61.1
Non-Hispanic Black	14.0		14.8
Mexican American	10.4		11.6
Other Hispanic	6.7		6.6
Other	5.7		5.9
Height (cm)	152.9	0.35	157.1	0.51
Weight (kg)	50.5	0.50	53.5	0.53
Triceps skinfold (mm)	17.5	0.25	13.6	0.23
Waist (cm)	74.1	0.50	74.3	0.36
Menstruating (%)	56.7		----	----
DXA % body fat	32.27	0.24	25.66	0.27
BMI (kg/m2)	21.18	0.16	20.97	0.13
BMI z-score	0.49	0.04	0.49	0.03
BMI percentile categories (%)
< 5th %tile	2.9		3.5
≥5th to < 85th %tile	64.6		62.6
≥85th to < 95th %tile	17.5		16.7
≥95th %tile	15.0		17.2

The forward and backward selection procedures added 3 terms for girls and 2 terms for boys. In girls, the base plus selected terms model included triceps squared, menses * triceps interaction and menses * triceps square interaction in addition to age, race/ethnicity, weight, height, waist, triceps and menses. In boys, the base plus selected terms model also included triceps squared and an age * weight interaction. In both genders, triceps skinfold explained more variance than any other anthropometric variable. Table 2 shows evidence that the adjusted R² and RMSE for BMI and BMI Z-score were inferior to the other models tested for the prediction of percent body fat. Although the difference was not substantial, the addition of selected terms to the base model improved performance. The overall MSD was not different from zero in all the models tested, and the base plus selected terms model had the tightest confidence intervals around the MSD.

Table 2.

Adjusted R², RMSE and mean signed mean difference (MSD) from percent body fat prediction models in the development and cross-validation datasets¹

		Girls (n = 2,040)				Boys (n = 3,334)
	BMI2	BMI z-score3	Base terms4	Base + selected terms5	BMI2	BMI z-score3	Base terms6	Base + selected terms7
Development dataset
R2	0.615	0.628	0.805	0.832	0.346	0.522	0.865	0.884
Adjusted R2	0.615	0.628	0.804	0.831	0.346	0.522	0.865	0.884
RMSE	4.114	4.041	2.940	2.732	6.368	5.442	2.894	2.678
Mean Signed Difference (95% Confidence Interval)	0.000 (−0.335, 0.335)	0.000 (−0.330, 0.330)	0.000 (−0.233, 0.233)	−0.015 (−0.239, 0.209)	0.000 (−0.481, 0.481)	0.000 (−0.398, 0.398)	0.000 (−0.246, 0.246)	0.000 (−0.239, 0.209)
Cross-validation dataset
R2	0.622	0.608	0.786	0.818	0.348	0.506	0.874	0.893
RMSE	3.978	4.055	2.991	2.758	6.233	5.428	2.746	2.525
Mean Signed Difference (95% Confidence Interval)	0.000 (−0.521, 0.521)	0.000 (−0.434, 0.434)	−0.063 (−0.430, 0.304)	−0.078 (−0.394, 0.239)	0.000 (−0.561, 0.561)	0.000 (−0.468, 0.468)	−0.055 (−0.320, 0.210)	−0.078 (−0.315, 0.160)

¹– Intercept and coefficient values were calculated using the development dataset.

²– BMI model included only BMI (wt/ht²)

³– BMI z-score model included only BMI z-score

⁴– Base terms model for girls included age, race/ethnicity (5 categories), weight, height, waist, triceps and menses

⁵– Base plus selected terms model for girls included all terms in the base model plus triceps squared, menses-triceps interaction and menses-triceps squared interaction.

⁶– Base terms model for boys included age, race/ethnicity (5 categories), weight, height, waist, and triceps

⁷– Base plus selected terms model for boys included all terms in the base model plus triceps squared and age-weight interaction

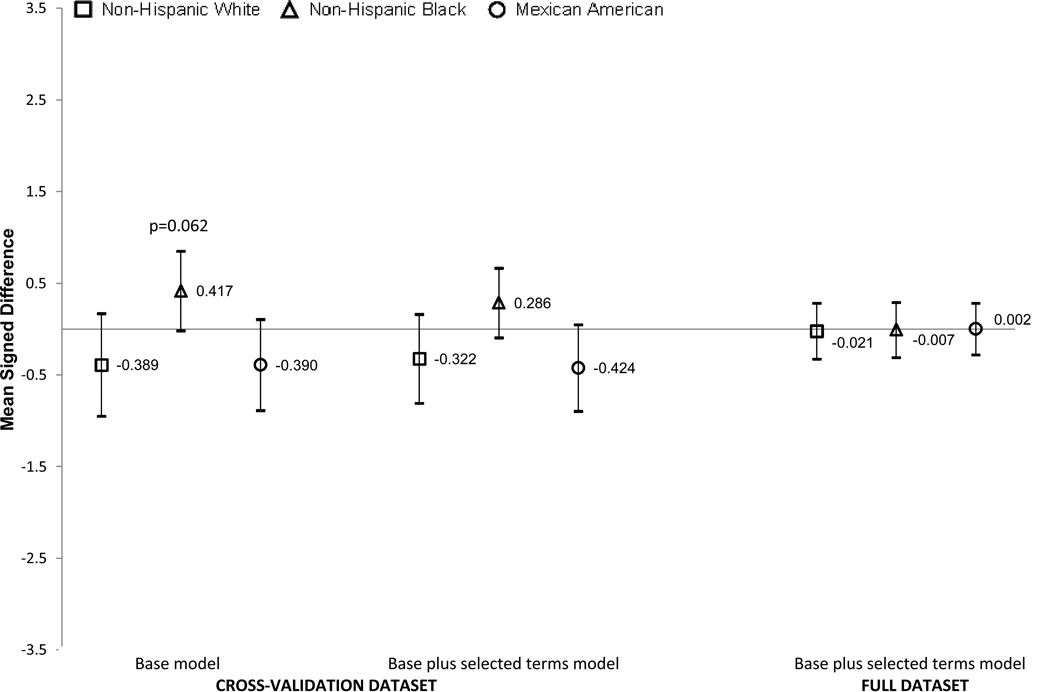
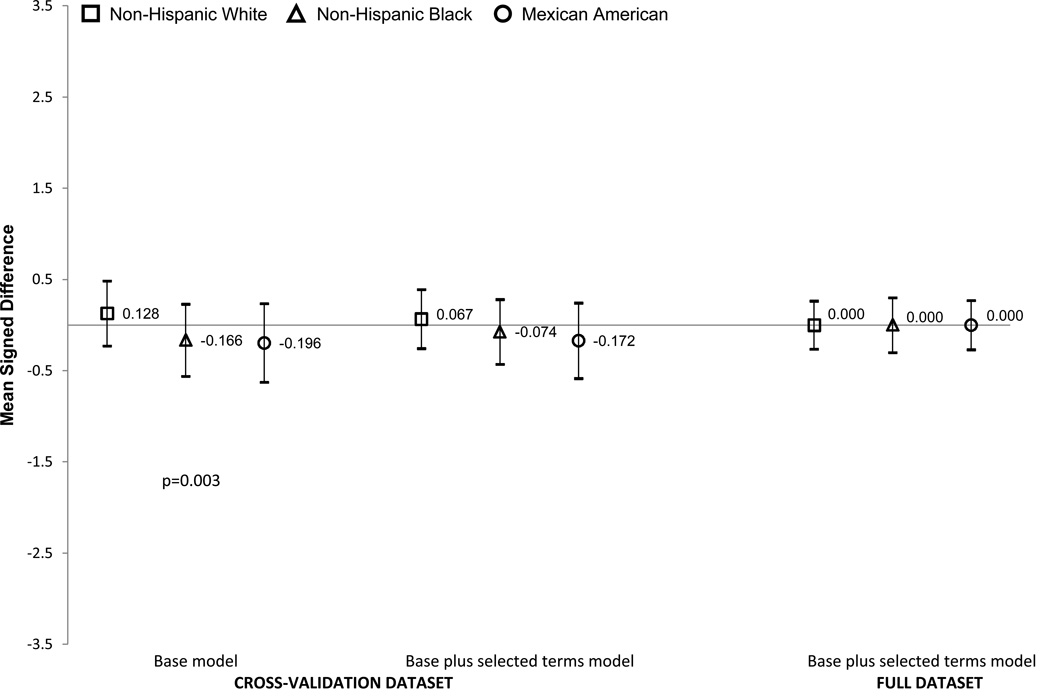
Figures 1 and 2 show the MSDs by race/ethnicity for the base terms model and the base plus selected terms model in the cross-validation. Results for the base plus selected terms are also shown in the full dataset using coefficients calculated using the full dataset rather than the development data set (final equation). We elected not to show the results for the other Hispanic and other race/ethnic groups due small sample sizes and wide confidence intervals. In girls (Figure 1), the MSDs were small (all less than half a body fat percentage point) and not statistically significant, indicating little systematic bias by race/ethnicity. Similar results were seen for non-Hispanic White, non-Hispanic Black and Mexican American boys (Figure 2). None of the prediction equation results were significantly different from zero. As expected, confidence intervals were narrower when the full dataset was used.

Figure 1. GIRLS.

Signed mean difference (SMD) and 95% Confidence Intervals for the base model and base plus selected terms model in the cross validation dataset and base plus selected terms model in the full dataset by race/ethnicity in girls. The base model included age, race/ethnicity (5 categories), weight, height, waist, triceps and menses. The selected terms are triceps squared, menses-triceps interaction and menses-triceps squared interaction. The y-axis is the SMD difference (prediction equation percent body fat minus DXA percent body fat). Positive values mean that the percent body fat equation overestimated the DXA percent body fat and negative values indicated that the estimation equation underestimated the DXA body fat percentage.

Figure 2. BOYS.

Signed mean difference (SMD) and 95% Confidence Intervals for the base model and base plus selected terms model in the cross validation dataset and base plus selected terms model in the full dataset by race/ethnicity in boys. The base model included age, race/ethnicity (5 categories), weight, height, waist, and triceps. The selected terms are triceps squared, age-weight interaction. The y-axis is the SMD difference (prediction equation percent body fat minus DXA percent body fat). Positive values mean that the percent body fat equation overestimated the DXA percent body fat and negative values indicated that the estimation equation underestimated the DXA body fat percentage.

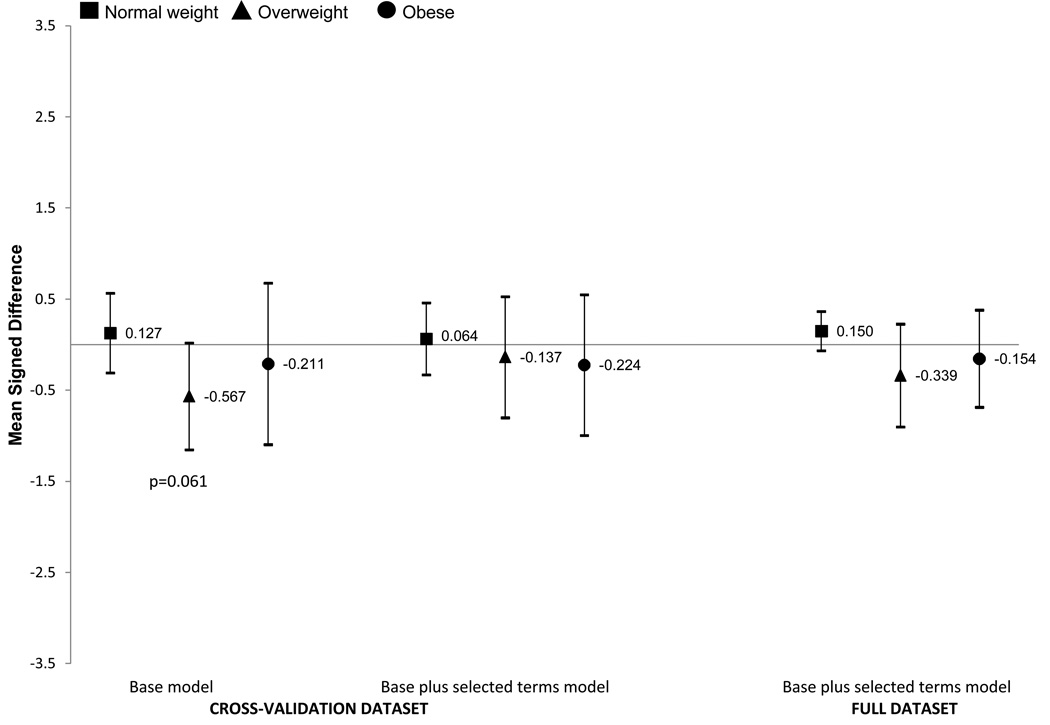
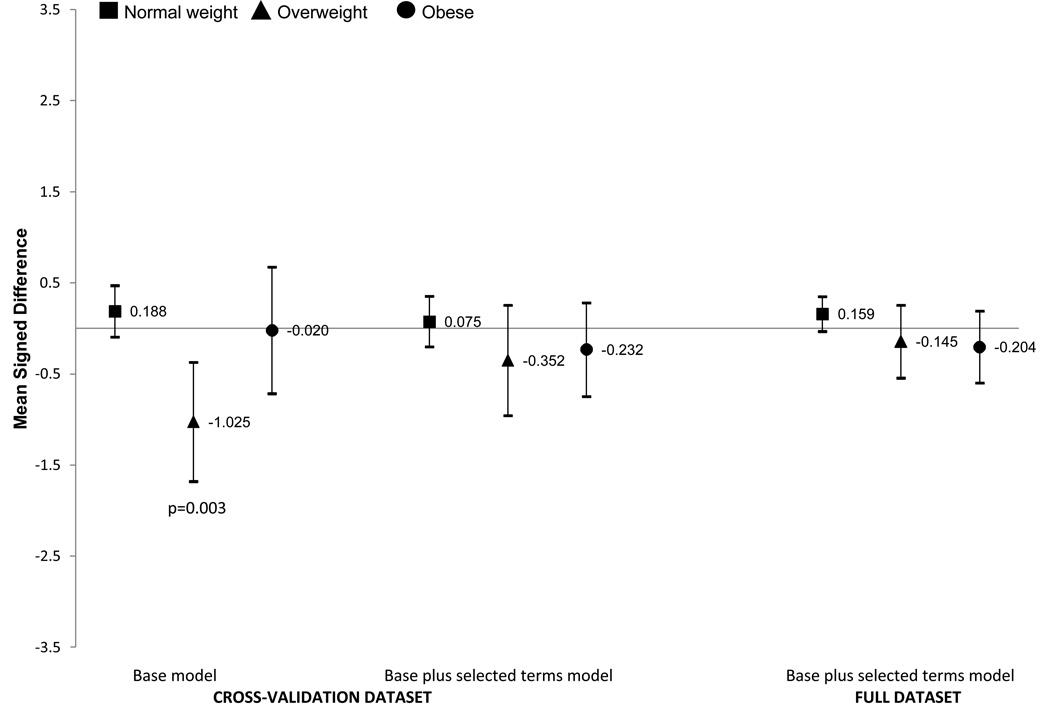
Across weight status groups (Figures 3 and 4) the prediction equations tended to slightly overestimate percent body fat in normal weight girls and boys and underestimate in overweight and obese girls and boys. These differences were small and not statistically significant for the base plus selected terms model. The base model underestimated percent body fat by −0.567 percentage points in overweight girls (p=0.061) and −1.025 in overweight boys (p=0.003). We do not show the underweight group as the confidence intervals were very wide, likely due to small sample sizes (n = 16 in girls and 42 in boys in the cross-validation dataset). The large confidence intervals for MSD did include zero for underweight boys but not underweight girls.

Figure 3. GIRLS.

Signed mean difference (SMD) and 95% Confidence Intervals for the base model and base plus selected terms model in the cross validation dataset and base plus selected terms model in the full dataset by weight status in girls. The base model included age, race/ethnicity (5 categories), weight, height, waist, triceps and menses. The selected terms are triceps squared, menses-triceps interaction and menses-triceps squared interaction. The y-axis is the SMD difference (prediction equation percent body fat minus DXA percent body fat). Positive values mean that the percent body fat equation overestimated the DXA percent body fat and negative values indicated that the estimation equation underestimated the DXA body fat percentage.

Figure 4. BOYS.

Signed mean difference (SMD) and 95% Confidence Intervals for the base model and base plus selected terms model in the cross validation dataset and base plus selected terms model in the full dataset by weight status groups in boys. The base model included age, race/ethnicity (5 categories), weight, height, waist, and triceps. The selected terms are triceps squared, age-weight interaction. The y-axis is the SMD difference (prediction equation percent body fat minus DXA percent body fat). Positive values mean that the percent body fat equation overestimated the DXA percent body fat and negative values indicated that the estimation equation underestimated the DXA body fat percentage.

Table 3 shows the final (base plus selected terms from the full dataset) percent body fat equations and the corresponding R², adjusted R², and RMSE in girls and boys in the full dataset. Overall, the final equations performed better in boys than girls. In girls, the base plus selected terms had a R² of 0.829 and slightly underestimated percent body fat overall, although not significantly (MSD: −0.013, 95% CI: −0.227, 0.201). In boys, the R² was 0.888 and the MSD was 0.000 (95% CI: −0.187, 0.187).

Table 3.

Base plus selected terms percent body fat prediction equation for girls and boys and corresponding model fit values in the full dataset¹

Gender	Equation2	R2	Adj R2	RMSE
Girls	%BF = 31.836841 - 0.609018 * (menses) + 0.003317 * (age - 161) - 0.975391 * (Race1) + 0.499227 * (Race2) + 0.602171 * (Race3) + 0.173877 * (Race4) + 0.053756 * (weight - 56) - 18.641446 * (height – 1.58) + 0.218830 * (waist - 76) + 0.744310 * (triceps - 15) - 0.018648 * (triceps -15)2 – 0.194114 * (menses) * (triceps-15) + 0.005748 * (menses)*(triceps)2	0.829	0.828	2.744
Boys	%BF = 28.009373 - 0.038460 * (age - 161) - 0.425327 * (Race1) + 0.350376 * (Race2) - 0.238080 * (Race3) - 0.106154 * (Race4) - 0.113560 * (weight - 56) - 10.010607 * (height – 1.58) + 0.353623 * (waist - 76) + 0.690984 * (triceps - 15) - 0.016657 * (triceps - 15)2 - 0.000852 * (age - 161) * (weight - 56)	0.888	0.888	2.624

¹Intercept and coefficient values were calculated using the full dataset.

²Menses = menarche status (girls) is 0 if have not started period and 1 if started periods; Race1 = 1 if non-Hispanic Black and 0 if not non-Hispanic Black; Race2 = 1 if Mexican American and 0 if not Mexican American; Race3 = 1 if Other Hispanic and 0 if not Other Hispanic; Race4 = 1 if Other non-Hispanic race group including non-Hispanic multiracial and 0 if not other non-Hispanic race group; weight = weight in kilograms; height = height in meters; waist = waist circumference in centimeters; triceps = triceps skinfolds in millimeters.

In additional work (data not shown) we used forward and backward selection to choose terms without forcing the base variables. Those models included only 5 terms in both girls (triceps, triceps squared, waist, race/ethnicity, and height) and boys (triceps, triceps squared, waist, age and weight). In the cross-validation dataset the adjusted R² and RMSE estimates were comparable to those of the base plus selected terms model shown in Table 2, but the bias associated with race/ethnicity was larger and for some points statistically significant. We also explored the use of lower limits for term selection into models (R² > 0.001 instead of 0.005 or RMSE > 0.01 instead of 0.025). This resulted in many more terms in the prediction equations (28 in girls and 29 in boys), but only trivial effects on the R², RMSE and MSD compared to the base plus selected terms models.

DISCUSSION

We successfully created equations for the prediction of percent body fat that produced an adjusted R² > 0.83 and used variables that are feasible to measure in the field. The final equations performed better in boys than in girls, despite the inclusion of a puberty-related variable in girls, but not boys. We have no ready explanation for this difference. Both equations far outperformed BMI as an indicator of percent body fat for which the R² was only 0.62 in girls and 0.35 in boys. The addition of terms using pre-determined criteria of R² and RMSE resulted in an equation that provided a less biased estimate in overweight boys (and to a lesser degree, also in overweight girls) compared to the base model.

Our analyses showed that triceps skinfold added more to the predictive ability of the equations than the more commonly measured variables weight and height. Triceps skinfold alone, with no other variables in the model, resulted in an R² for percent body fat of 0.73 for boys (RMSE= 4.06) and 0.71 for girls (RMSE=3.58). Thus, this skinfold measurement alone performed better than BMI alone (see Table 2), even though skinfold measurements are known to be prone to larger measurement errors than height and weight⁴¹. For comparison, waist alone only reached an R² of 0.34 (RMSE= 6.39) in boys and an R² of 0.58 (RMSE= 4.31) in girls. Other studies in children have also shown that skinfolds make an important contribution to the prediction of percent body fat^{3, 16, 42–44}. Freedman et al. showed that the addition of triceps skinfolds to a model that included BMI z-score increased the R² value by 0.07 or more and decreased prediction errors by 20–30% in 5–18 year old children compared to DXA measurements¹⁶. Given the large number of participants and the resources of NHANES, it is likely that anthropometrics were obtained by technicians who were more experienced than those used in many other studies. However, the Pathways⁴² and Trial of Activity in Adolescent Girls (TAAG)³ studies cited above used local, trained and certified staff^43–44 temporarily assigned to the study to obtain skinfold measurements (communication from Coordinating Center Principal Investigator, coauthor JS). Thus, in community research settings it is feasible to train technicians to collect skinfolds that add importantly to the prediction of percent body fat, and their contribution to validity appears to more than compensate for lower levels of repeatability⁴¹. In some clinical settings obtaining reliable measurements may be more problematic as periodic training and certification of data collectors and on-going quality control may be needed to insure high quality.

A judgment that is fundamental to the selection of an appropriate prediction equation is the level of accuracy and precision needed in order for it to successfully substitute for measurements obtained using more direct, but more difficult methods. Results from observational studies in children indicate that physical activity is associated with percent body fat calculated from prediction equations, but not with BMI. In the Pathways trial⁴⁴, higher levels of accelerometry-measured physical activity in 2^nd grade normal weight American Indian elementary school children were associated with lower levels of calculated percent body fat in 5^th grade, but there was no association with BMI⁴². In children who were overweight and obese in 2^nd grade, physical activity was positively associated with BMI (the opposite of the expected direction). In TAAG⁴³ accelerometry-measured minutes of moderate to vigorous physical activity in 6^th grade girls was associated with lower percent body fat in 8^th grade, but again there was no association with BMI. In the Pathways study investigators measured percent body fat using prediction equations that included demographic and anthropometric variables and BIA¹⁹. The TAAG prediction equation did not include BIA²⁵. R² values when compared to a criterion measure of percent body fat were 0.843 in Pathways and 0.88 in TAAG; levels similar to those found here (0.829 in girls and 0.888 in boys).

The randomized controlled trial literature in children has shown that some interventions aiming at increasing physical activity had no effect on BMI, but showed a meaningful impact on percent body fat⁴⁵. A study by Pudar et al.⁴⁶ examined the impact of a school-based multidimensional lifestyle intervention in predominantly migrant preschool children living in Switzerland. They found no difference in BMI between the control and intervention groups (−0.07 kg/m², −0.19 to 0.06; p=0.31), but the intervention group had a lower percent body fat (−1.1%, −2.0 to −0.2; p=0.02). In this research percent body fat was measured using a prediction equation that included BIA measurements²⁹. Given these consistent findings across observational studies and randomized trials, a calculated percent body fat may prove useful for detection of effects associated with physical activity.

To our knowledge, only one other published paper has used DXA percent body fat measures from the NHANES to explore associations with anthropometric variables. Dugas et al.³⁵ examined non-Hispanic White, non-Hispanic Black and Mexican American adolescents 12 to 20 years of age in the 1999–2004 NHANES. Their primary goal was to investigate whether percent body fat was equivalent at comparable BMI’s across three race/ethnic groups of adolescents in the United States. Their main analysis compared the mean percent fat levels as measured by DXA within the normal weight, overweight and obese BMI categories³⁵ in gender-stratified analyses in the 3 ethnic groups studied and found several ethnic differences. Relevant to the work presented here, they also examined prediction equations for percent body fat. These analyses were not stratified by gender, but gender was included as a variable in all models in addition to ethnicity and age. BMI with exponents of ½, −1, and −2 and body weight were explored in selected combinations. The authors indicated that the model with gender, ethnicity, age, weight and BMI^1/2 explained the most variance (R² = 0.786). No evidence of potential systematic differences between the observed and the predicted values from their equation was shown for race/ethnic groups or for weight status groups.

Differences in body composition between White and African American populations have been noted for decades^47–48. It is well known that at the same BMI African Americans tend to have more lean mass and skeletal mass than Whites. African Americans with the same subscapular skinfold as White children have a smaller triceps skinfold. Researchers have shown that published equations have either underestimated or overestimated percent body fat in different ethnic groups^{6, 8, 19, 25–27, 34–35, 48}. Our final equations included race/ethnicity and did not systematically under or over-estimate percent body fat in African Americans, Mexican Americans or Whites. We tested numerous interactions between race/ethnicity and our candidate anthropometric variables, but none contributed substantially to the prediction equations, and, therefore, they were not retained.

Investigators have used several approaches to determine optimal models for the prediction of percent body fat in children, but details on the criteria used for variable selection are not always given. As was done here, other investigators have formed models around a base of preselected variables and then tested the contribution of adding additional terms^{17, 24}. Many authors use regression analyses (often stepwise) with terms selected either according to p values^{5, 9, 11–12, 20, 23, 26, 29, 33} or R² (or adjusted R² or r)^{8, 18}. The criterion p value used is usually provided, but criterion levels for R² are not stated. Similarly, investigators seek to minimize RMSE (or SEE) but do not state limits. It is a strength of this work that the steps used in equation development are clearly articulated and a priori criteria for model selection are presented.

Our final equations are not very convenient for hand calculations. Nevertheless, they are simple to implement using a computerized spreadsheet or statistical software. The equations developed met our goals of providing a means for the COPTR investigators to calculate percent body fat from a limited number of relatively easily obtained measurements using a valid equation with relatively low error and bias. Given that the equations were developed in a sample of boys and girls assembled to be representative of the United States population, the potential generalizability is strong and we anticipate that these equations will be of use to other investigators studying adiposity in youth.

What is already known about the subject

1. It is often not feasible to measure percent body fat using precise methods such as dual-emission X-ray absorptiometry (DXA).

2. Equations developed to estimate percent body fat in youth using measures that are feasible to collect in a variety of settings usually have been developed in focused samples and therefore have low generalizability.

What this study adds

1. First equations developed in a representative sample of American youth that estimate percent body fat using self-reported demographic variables as well as measured skinfolds and other anthropometric variables that are feasible to collect in a variety of settings.

2. Equations were demonstrated to have low levels of bias by BMI category and by race/ethnicity in non-Hispanic Whites, Mexican Americans and African Americans.