Spectral Library Generating Function for Assessing Spectrum-Spectrum Match Significance

Abstract

Tandem mass spectrometry (MS/MS) continues to be the technology of choice for high-throughput analysis of complex proteomics samples. While MS/MS spectra are commonly identified by matching against a database of known protein sequences, the complementary approach of spectral library searching against collections of reference spectra consistently outperforms sequence-based searches by resulting in significantly more identified spectra. But while spectral library searches benefit from the advance knowledge of the expected peptide fragmentation patterns recorded in library spectra, estimation of the statistical significance of Spectrum-Spectrum Matches (SSMs) continues to be hindered by difficulties in finding an appropriate definition of ‘random’ SSMs to use as a null model when estimating the significance of true SSMs. We propose to avoid this problem by changing the null hypothesis - instead of determining the probability of observing a high SSM score between randomly matched spectra, we estimate the probability of observing a low SSM score between replicate spectra of the same molecule. To this end, we explicitly model the variation in instrument measurements of MS/MS peak intensities and show how these models can be used to determine a theoretical distribution of SSM scores between reference and query spectra of the same molecule. While the proposed Spectral Library Generating Function (SLGF) approach can be used to calculate theoretical distributions for any additive SSM score (e.g., any dot product), we further show how it can be used to calculate the distribution of expected cosines between reference and query spectra. We developed a spectral library search tool, Tremolo, and demonstrate that this SLGF-based search tool significantly outperform current state-of-the-art spectral library search tools and provide a detailed discussion of the multiple reasons behind the observed differences in the sets of identified MS/MS spectra.

Introduction

High throughput identification of peptides and proteins in complex samples is enabled by tandem mass (MS/MS) spectrometry generation of hundreds of thousands to millions of spectra, from which many thousands of proteins are typically identified by matching the resulting MS/MS spectra against genome-derived databases of known protein sequences.¹ In difference from such database search algorithms,^2–4 spectral library search approaches^5–12 identify experimental MS/MS spectra by matching against collections of previously identified reference spectra (spectral libraries) and have been consistently found to identify more spectra than database search whenever the corresponding peptides have reference spectra in the library. But despite this demonstrated superior sensitivity, the development of methods to determine the statistical significance of Spectrum-Spectrum Matches (SSMs) in peptide spectral library searches is still in its early stages.

The most common approach to controlling the False Discovery Rate (FDR) in both database search¹³ and spectral library search¹⁴ is the Target-Decoy approach where one extends the database/library of true peptides with a complement of sequences/spectra from ‘random’ peptides and uses matches to the latter to estimate the number of false matches to true sequences/spectra. But while these FDR approaches continue to be very valuable in correcting for multiple hypothesis testing in large-scale experiments, they provide little to no insight on the statistical significance of individual SSMs or Peptide Spectrum Matches (PSMs). In addition, it has been shown^4,15,16 that rigorous modeling of random PSM scores allows one to determine accurate p-values for true PSMs and thus substantially improve the performance of database search tools. In this MS-GF¹⁵ approach, dynamic programming is used to exhaustively determine the distribution of PSM scores for all possible peptides matched to a given spectrum and then this distribution is used to determine the probability (p-value) of observing a random PSM score at least as high as the score of an observed PSM derived from the database of known peptide sequences. Unfortunately this approach does not have a direct analog in the realm of spectral library searches - while it is straightforward to traverse the space of all possible random peptide sequences (as in MS-GF), it remains unclear how to generate and/or traverse a space of ‘random’ spectra that would be representative of false matches to a true spectral library. First, truly random spectra^* are easy to generate and could be traversed in a manner similar to MS-GF but such spectra would be mostly very different from the spectra that tend to be generated by mass spectrometry instruments and thus p-values obtained using this background distribution of random spectra would not accurately reflect the probability of false matches for experimental MS/MS spectra. Second, the approach used for the generation of decoy spectra¹⁴ in FDR calculations continues to work well in practice for the generation of small collections of ‘semi-random’ peptide spectra but it is not sufficient to explore the space of all ‘random’ spectra because it only considers limited changes to peak masses, allows for no variations in peak intensities and is completely peptide-specific in that it is based on sequence permutations (and thus not applicable to spectra from other types of molecules). Third, SSM scoring and p-value approaches have been proposed based on statistical models of random SSMs but these assume uniform distributions of peak masses and either ignore (e.g., hypergeometric models^11,12) or make limited use (e.g., peak ranks in Kendall-Tau statistic¹²) of MS/MS peak intensities. As a result, even though these approaches use a probabilistic model and calculate p-values, the underlying assumptions and their results on real MS/MS data suggest that these don’t represent the statistics of SSMs well enough to increase the overall number identified SSMs (more details in Results).

Given the difficulty of modeling random spectra, we propose changing the null hypothesis used to assess the significance of SSMs – instead of determining the probability of a random match with a score ≥T, our approach determines the probability that a true match has a score ≤T. While modeling true matches remains a open problem in database search due to the difficulty of predicting theoretical MS/MS spectra from peptide sequences, we show that these can be efficiently modeled in the case of spectral library searches using i) advance knowledge of expected fragmentation patterns as recorded in reference library spectra and ii) estimated models of instrument variation in measurements of MS/MS peak intensities. Our Spectral Library Generating Function (SLGF) approach combines these with an efficient dynamic programming exploration of all possible replicate spectra of the same molecules as each reference spectrum in the library to output a spectrum-specific theoretical distribution of scores for true SSMs. In addition to defining a new approach for the assessment of the statistical significance of SSMs, our comparison of SLGF with current state-of-the-art spectral library search tools shows that SLGF significantly increases the number of identified MS/MS spectra without requiring any peptide-specific assumptions or multi-feature corrections to observed cosine scores (e.g., DeltaD/DotBias).

Methods

A spectrum is defined as a set of (mass, intensity) pairs called peaks which are assigned into uniformly sized mass bins (e.g. 1 Th bins⁸). After transformation ^† a spectrum becomes a vector S with n bins, where each bin S_i contains the summed intensity of all peaks with masses in that bin; all subsequent references to “spectrum” refer to the respective spectrum’s vector. Given a library spectrum L and a query spectrum S, the projection spectrum Pro j(S, L) is defined as:

$$\mathit{Proj}(S,L)=\{S_i:(L_i>0),0\mathit{otherwise}\}$$

All library spectra L are normalized to euclidean norm ||L||= 1.0, as are all projected spectra:

$$S^L=\mathit{NormProj}(S,L)=\left\{\frac{\mathit{Proj}{(S,L)}_i}{\Vert \mathit{Proj}(S,L)\Vert }\right\},\mathit{where}\Vert \mathit{Proj}(S,L)\Vert =\sqrt{\sum _i\mathit{Proj}{(S,L)}_i^2}$$

The most common spectral similarity function used for spectral matching is cosine (also known as normalized dot product), defined as follows for vectors of Euclidian norm 1.0:

$$\mathit{cos}(L,S^L)=\sum _i{L}_i\times S_i^L$$

We define a replicate spectrum R (relative to a library spectrum L) to be a spectrum of the same molecule as L and acquired under the same or similar experimental conditions (i.e., charge state, instrument, collision energy, abundance, etc.). Due to stochastic factors in mass spectrometry fragmentation and instrument measurement error,¹⁷ some level of variation is expected between the intensities of peaks in R relative to the intensities of peaks in L. We model this variability with a log ratio of ion intensities, $\mathit{log}(R_i^L/L_i)$ where R^L = NormPro j(R, L); this ratio is calculated across all bins in R and L where L_i is not zero.

For all library spectra with replicate spectra in our training datasets, all observed log ratios were collected into an ion variation histogram. We use this histogram (scaled to total area under the curve 1.0) as the empirical probability mass function, RatioFreq(r), of variation in ion intensities for all L_i ≠ 0 (Figure 1A). In difference from varying intensities, the special cases of ion deletion (i.e., $R_i^L=0$) are modeled separately with $\mathit{DelFreq}=\frac{\#\mathit{Deletions}}{{\sum }_{L\in \mathit{Library}}\#\mathit{Peak}{s}_L\times \#{\mathit{Replicates}}_L}$, where #Deletions is the total number of peak deletions in all replicate spectra, #Replicates_L is the number of replicate spectra in our training set of a Library spectrum L, and #Peaks_L is the number of peaks in a given library spectrum L. Combining our model of ion variance, RatioFreq(r), and our model for ion deletion events DelFreq, the probability Prob(R_i|L_i) of observing a replicate ion intensity R_i given a library ion intensity L_i is:

$$\mathit{Prob}(R_i\mid L_i)=\{\begin{array}{ll}\mathit{DelFreq}\hfill & \text{if}{R}_i=0\hfill \\ (1-\mathit{DelFreq})\times \mathit{RatioFreq}({log}_2(\frac{R_i}{L_i}))\hfill & \text{if}{R}_i\ne 0\hfill \end{array}$$

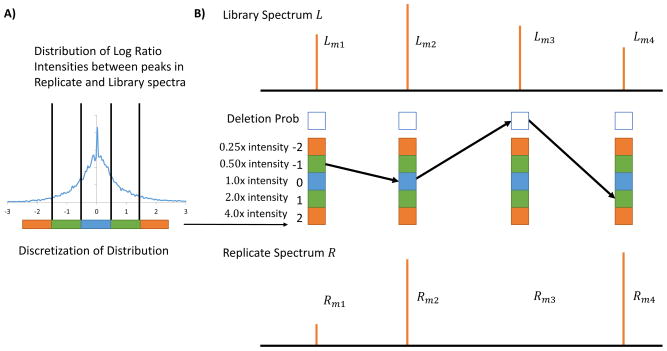
Figure 1.

Spectral Library Generating Function (SLGF) calculation of Spectrum-Spectrum Match (SSM) significance by modeling instrument variation in peak intensity measurements in replicate spectra of the same compound. In (A) the empirical distribution of variations in intensity measurements is assessed and discretized. (B) Every possible replicate spectrum R is represented by a path through each library peak’s possible intensity variations, thus representing every possible combination of variations of peaks in library spectrum L. Note that some replicate spectra (paths) are invalid, i.e. replicate spectra that do not have Euclidean norm 1; intermediate paths with norm < 1.0 are allowed during the calculation but paths resulting in euclidean norm ≠ 1.0 must be discarded when calculating the distribution of cosine scores.

Our goal is to calculate the distribution of cosines scores over all possible replicate spectra within instrument variability of a given library spectrum. To compute the generating function for each library spectrum, we use RatioFreq and DelFreq. We consider every possible replicate spectrum R (Figure 1B) by exploring all possible intensity variations of every peak L_i to R_i and calculate their aggregate probability and cosine similarity cos(R^L, L).

A three dimensional dynamic programming table, LibDP(i, c, p), is used to explore all possible ion variations, where i is the spectrum vector index, c is the cosine score, and p is the intermediate euclidean norm value. The value in each cell LibDP(i, c, p) is the probability of a replicate spectrum obtaining cosine c, having p euclidean norm, and up to and including ion index i. The recurrence for LibDP(i, c, p) is thus defined as follows for i = 1..n:

$$\mathit{LibDP}(i,c,p)=\sum _{y=0\to p}\mathit{LibDP}(i-1,c-\sqrt{y}\times L_i,p-y)\times \mathit{Prob}(\sqrt{y}\mid L_i)$$

At (i = 0), before considering any ions from the library spectrum L, every cell LibDP(0,> 0,> 0) = 0, and when no intensity is used and the cosine score is zero, it is LibDP(0,0,0) = 1. (See Supplementary Figure S1 for an illustration of the recursion).

Since each step i only depends on the values from step i − 1, one only needs to use two two-dimensional matrices of constant size to calculate all LibDP values. The size of each 2D matrix is n_c × n_p, where n_c is the number of cosine bins and n_p is the number of intensity bins, each set accordingly to the desired granularity. The time complexity of computing the entire dynamic programming table is $O(n_c\times n_p^2\times n)$. The final SLGF distribution of cosines between a library spectrum and its replicates is extracted from LibDP(n,*,1) and normalized to sum to 1. It is necessary to normalize at the end because of probability mass in discarded replicate spectra of Euclidean norm ≠ 1.

The probability that a replicate spectrum R and corresponding library spectrum L exhibit a cosine less than a threshold is expressed as the following p-value:

$${\mathit{Prob}}_L(\mathit{cos}(L,R^L)<T)$$

where T can be set according to observed cosines between query and library spectra to determine the probability of a query spectrum S being a replicate spectrum of L.

We developed a spectral library search tool called Tremolo in order to assess SLGF’s utility in library search. Since SLGF assesses the quality of a single SSM but does not correct for multiple hypothesis testing when searching many spectra in a dataset, in Tremolo, FDR is estimated by the TDA.¹⁴ In brief, decoy spectral libraries were generated using the peptide shuffle and reposition method to obtain a set of decoy spectra. For all Target and Decoy library spectra, SLGF distributions were calculated and used in the subsequent scoring function.

The scoring function of an SSM in the spectral library search between a library spectrum L identified as Peptide(L) and a query S is:

$${\mathit{SSM}}_{\mathit{score}}={\mathit{SLGF}}_e={\mathit{Prob}}_L(\mathit{cos}(L,R^L)<\mathit{cos}(L,S^L))\times \mathit{ExplainedIntensity}(S,\mathit{Peptide}(L))$$

where we define S^e|Peptide(L) to be the subset of peaks from S which are annotated by peptide of L and

$$\mathit{ExplainedIntensity}(S,\mathit{Peptide}(L))=\frac{{\sum }_i(S_i^{e\mid \mathit{Peptide}(L)})}{{\sum }_i(S_i)}$$

The score SLGF_e is also considered in addition to SLGF = Prob_L(cos(L, RL) < cos(L, SL)) because it is a closer comparison to SpectraST,⁹ which does not consider co-eluting peptides. In cases of co-eluting peptides, SLGF is able to consider these spectra because it only uses peaks at m/z values L_i ≠ 0. Yet since SpectraST penalizes for co-elution, SLGF_e is similarity penalized by the explained intensity term, and thus SLGF_e is used as the scoring function in Tremolo. While SLGF may be useful towards identification of co-eluting peptides, additional considerations are required to correctly address co-eluting peptide identification¹⁰ (e.g., addressing multiple molecules per spectrum and FDR on mixture identifications).

Datasets

The Training dataset was composed of 236 CPTAC^18,19 Study 6 Orbitrap files (2,766,504 spectra) and was used to train the distributions of variation in ion intensities. All spectra were searched with SpectraST v4.0 with a 2 Th m/z tolerance against the NIST Yeast Ion Trap peptide library (May 2011 build). The decoy spectral library was created using SpectraST’s own decoy generation feature and the resulting SSMs were filtered to 1% FDR, yielding 396,526 identified spectra from 18,440 unique precursors. Replicate spectra in this filtered dataset were matched with their respective library spectra in the library and ion variance distributions were calculated from these replicates and library spectra.

Yeast and Human Ion Trap peptide spectral libraries, containing 78,825 and 310,688 spectra repectively, were acquired from NIST (May 2011 Build) and were used in evaluating spectral library search performance. The shuffle and reposition method proposed by Lam et al¹⁴ was used to create the decoy spectral libraries for use in Tremolo’s, SpectraST’s, and Pepitome’s search. SpectraST, Pepitome, and Tremolo searched the NIST library using a 2 Th precursor tolerance; Tremolo and Pepitome used a 0.5 Th tolerance to annotate MS/MS peaks.

The Yeast Test dataset from CPTAC was composed of an arbitrarily selected file from CPTAC Study 6 that was not included in the Training dataset and contained 9,809 MS/MS spectra used for evaluating SLGF’s search of the NIST Yeast Ion Trap peptide library. A second test dataset, Hela S3 Test dataset, was also used to evaluate spectral search performance in addition to the CPTAC Yeast Test dataset described above. This dataset ²⁰ was generated from human HeLa S3 cells, by tryptic digestion, and MS acquisition was performed by an LTQ Orbitrap Classic yielding high accuracy MS1 and low mass accuracy MS2 spectra. Hela S3 Test contained 11,723 MS/MS spectra and was searched against the NIST Human Ion Trap peptide library.

For Tremolo peptide spectra library search we find that it is best to perform library preprocessing. Peaks in library spectra were annotated with the respective peptide sequence considering b, y, b++, y++ ions,²¹ their respective single ¹³C isotope peaks (+1 Da mass shift), single H₂O losses (−18 Da mass shift), single NH₃ (−17 Da mass shift) losses and a ions; all non-annotated peaks and precursor peaks were removed. Additionally, all peak intensities were transformed by square root in both library and query spectra.

Results and Discussion

SLGF distribution Evaluation

In calculating the SLGF distributions for each peptide library spectrum, it was observed that it was more accurate to have 10 different distributions of variation in ion intensity based on the relative intensity of an ion peak in the library spectrum (instead of a single distribution for all ion peaks). Figure 2 illustrates the significant differences in the distributions of log-ratio ion variations for the top 10% most intense peaks and bottom 10% least intense ion peaks (other deciles also shown). Additionally, the ion variance is also substantially different between replicate spectra from high (≥ 12,000 ions) and low total ion current (< 12,000 ions) precursors. The total ion current (TIC) of a spectrum is calculated as the total ion current of that MS/MS spectrum. As expected, low intensity replicates exhibit more variation in ion intensities (i.e., wider ion variation distributions) than high intensity replicates. Using these two separate models for high and low TIC precursors, two SLGF distributions are pre-calculated for each library spectrum. Low and high TIC query spectra are then partitioned and searched separately, with SLGF p-values calculated from the corresponding SLGF distribution.

Figure 2.

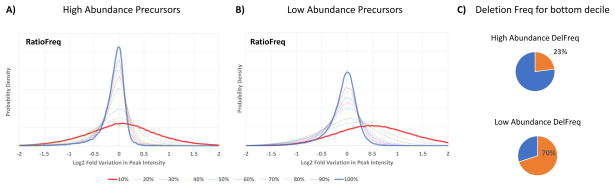
Distributions of variation in ion intensity for (A) high and (B) low TIC precursors. As illustrated by the differences between (A) and (B), the ion variation distributions for low TIC precursors tend to be wider than those of the high TIC precursors. In both cases it is shown in bold blue, the distribution of variation in ion intensities for the 10% most intense peaks in library spectra and in bold red, the distribution of variation in ion intensities for the 10% least intense peaks in library spectra, with other deciles shown in between. Note that the width of the distributions for the top decile distribution is markedly narrower than the bottom decile distribution suggesting the need to model the variation of ion intensity differently depending upon a peak’s intensity in the library spectrum. It should also be noted that the lowest decile distribution shown in (B) in red is not centered at 0 log fold variation due to the significantly higher deletion percentage (C) of the lowest decile library peaks in low TIC precursors. The deletion of these peaks caused all other peaks in the spectrum to increase in normalized intensity, for the entire spectrum is normalized to Euclidean Norm 1, thus causing a shift in the specific ion variation distribution.

The SLGF distributions were visually assessed by comparing against empirical score distributions using replicates from the Training dataset, and it was found that SLGF distributions approximated the empirical distributions (See Figure 3), but further work is necessary to enable a more accurate p-value calculation. Thus, we use SLGF p-value as a score and evaluate its performance in the context of spectral library search.

Figure 3.

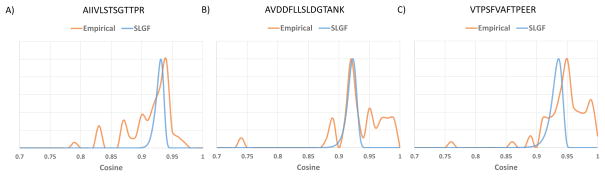
Empirical vs calculated (SLGF) distributions of cosines between library and replicate spectra. Empirical cosine distributions are histograms of cosine scores between a library spectrum and replicate experimental spectra (cos(L, R^L) for all available R^L). Examples were selected from NIST Yeast library spectra with sufficient replicates from the Training dataset to derive an empirical distribution. The probability mass in the empirical distributions to the left of the theoretical SLGF distribution is mostly caused by cases of co-elution, leading to lower cosines. The discrepancies of higher cosines result from SLGF using an average model of ion variation derived from data acquired in many experiments and laboratories. As such, our average model of ion intensity variation for certain peptides has variance higher than that of the best calibrated instruments, thus causing SLGF distributions to expect lower average cosines than some empirical distributions.

Peptide Spectral Library Search

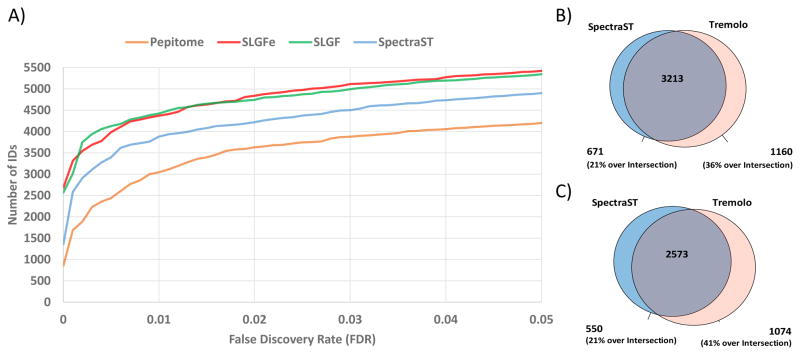
To systematically assess the performance of Tremolo as a search tool, we compared it against SpectraST and Pepitome at fixed FDR. SpectraST’s performance exceeded that of Pepitome, and thus we focus our detailed analysis on the comparison with SpectraST results. Comparing the sensitivity of Tremolo to that of SpectraST on the Yeast Test dataset we find that at 1% spectrum-level FDR (as determined by TDA), Tremolo was able to identify 4,373 spectra versus 3,884 spectra by SpectraST (12.5% more, see Figure 4).

Figure 4.

Peptide spectral library search sensitivity and specificity comparison between Tremolo, SpectraST, and Pepitome. In (A) the performance of the scoring function SLGF is shown to be comparable to that of SLGF_e, where one explicitly attempts to not consider mixture spectra (see textb for details). This contrasts to the performance of SpectraST in blue, and Pepitome in orange. (B) Number of spectra identified exclusively by SpectraST, Tremolo, and by both tools at 1% spectrum level FDR. On this Test dataset, SLGF_e was also found to be more sensitive than SpectraST across the whole range of FDR thresholds (> 12% increase in IDs at 1% FDR). (C) Number of peptide IDs at 1% FDR by SpectraST and Tremolo. Tremolo identified 16% more peptides than SpectraST.

The gain in Tremolo sensitivity can be explained by analyzing the different components in SpectraST’s SSM scores. SpectraST’s score is SSM_{spectrastscore} = 0.6D + 0.4DeltaD − b, where D is the cosine score between library and query. $\mathit{DeltaD}=\frac{D_1-D_2}{D_1}$ where D₁ and D₂ are the top and second cosine scores respectively from a set of library spectra to a query spectrum. It is argued that the larger this DeltaD term, the more the top candidate stands out from the alternatives, thus implying a greater chance the top candidate is correct. b is the penalty applied to the score for DotBias scores that are not preferable. DotBias is defined as $\mathit{DotBias}=\frac{\sqrt{{\sum }_{i=1\to n}{L}_i^2\ast {(S_i^L)}^2}}{D}$ and intuitively can be thought of a measure of how much a cosine score is dominated by a few peaks. A score of DotBias = 1.0 signifies one peak dominates the score and a score of DotBias ≈ 0.0, the cosine contribution is evenly distributed over all peaks. Thus, high DotBias scores possibly imply dubious matches as there are only a few peaks leading to a high cosine score. Low DotBias scores also are not preferable as this means many equal intensity peaks are matching, which most likely would imply noise. SpectraST’s penalty b is tuned to cause larger penalties for larger and very small DotBias values. In figure 5A it is shown the DeltaD versus the DotBias of all IDs at 1% FDR identified by SpectraST over the test dataset (orange dots). As expected SpectraST IDs tend to avoid high DotBias as well as exceedingly low DeltaD. In difference from these, Tremolo-only IDs are shown in gray dots. These tended towards lower DeltaD and higher DotBias and thus were missed by SpectraST, because of either low DeltaD (lacking the ability to distinguish between the top two SSMs) or because of high DotBias (cosine score dominated by only a few peaks). Tremolo, however, is able to identify these low DeltaD spectra because each possible library match to the query spectrum has a different expected score distribution, and even though from an absolute cosine perspective there is little difference from the top and second hit, once the cosine p-value is calculated for each respective library spectrum, then the scores separate substantially. It is clearly show in figure 5B that even though the DeltaD for these spectra that SpectraST failed to identify was very low (x-axis), the Tremolo’s delta score ( ${\mathit{SLGF}}_{\mathit{delta}}=\frac{{\mathit{SLGF}}_1-{\mathit{SLGF}}_2}{{\mathit{SLGF}}_1}$ where SLGF₁ and SLGF₂ are the top and second SLGF_e scores respectively) is considerably higher because of the separation obtained from SLGF p-values.

Figure 5.

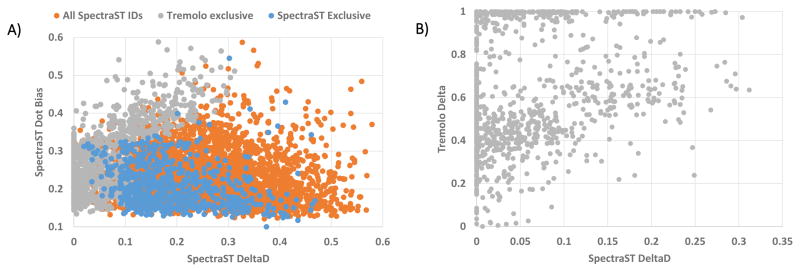
Gains of identification by Tremolo over SpectraST through analyzing SpectraST’s score’s DotBias and DeltaD. Each dot in (A) represents an identified spectra plotted with DeltaD versus DotBias as calculated by SpectraST. In orange are all the IDs by SpectraST; in blue are the identifications by SpectraST at 1% FDR that were missed by Tremolo’s search at 1% FDR; in gray are the identifications by Tremolo at 1% FDR that were missed by SpectraST at 1% FDR. For this third category of spectra, there is a clear bias towards high DotBias and low DeltaD. It is shown in (B) that while SpectraST was unable to obtain a large DeltaD for these spectra, Tremolo’s delta score was high and, since this delta score is not used anywhere in Tremolo scores, it thus reinforces the assertion that these Tremolo identifications are correct. Tremolo’s exclusive identifications show that there are classes of spectra that remained unidentified (low DeltaD and high DotBias) that Tremolo is now able to identify. Note the change of scale for the DeltaD axis (x-axis) in B as opposed to A; since there were no spectra with SpectraST DeltaD > 0.35 we opted to omit those regions in the figure.

The identification of spectra with high DotBias is also enabled by the calculated cosine distribution. For spectra whose intensities are dominated by very few peaks, cosines alone are not enough to distinguish between good SSMs and bad SSMs. Since these spectra are dominated by few peaks, the less intense peaks become especially informative in how their slight cosine changes (because of matching or not matching these small peaks) distinguish good and bad SSMs. SLGF’s distributions are able to capture these slight changes in cosine (i.e. higher SLGF distributions with lower variance) to correctly identify spectra dominated by few peaks whereas SpectraST penalizes all spectra that are dominated by a few peaks. In general we observe that the effect of DeltaD is captured by SLGF’s determination of the appropriate mean cosine per library spectrum and the effect of DotBias is captured by the variance of the SLGF distributions.

An additional source of IDs that Tremolo was able to recover were spectra that SpectraST did not consider in its search: spectra that have “negligible” intensity above 500 m/z. These spectra generally came from shorter (6-8mer) charge 2 precursors and moderate length (8-12mer) charge 3 precursors. While these spectra may be easier to match to decoys with SpectraST’s scoring scheme, Tremolo is again able to use its calculated distributions to identify 198 spectra that SpectraST discarded.

The 671 spectra that were identified by SpectraST and not by Tremolo are shown in Figure 5A as blue dots and exhibit no clear bias for or against DeltaD or DotBias. Upon closer examination we found that many of the spectra from low TIC precursors that Tremolo scored poorly seemed to exhibit relatively high cosine scores (~ 0.85) yet the SLGF distribution would expect a score significantly higher. However, these cases are mostly skewed towards very low TIC (< 5000 ions) and our training set of spectra for the low TIC ion variance models skewed toward higher TIC (Figure 6A), thus suggesting that a larger training set may be required to train ion variance models for precursors of TIC < 5000 ions.

Figure 6.

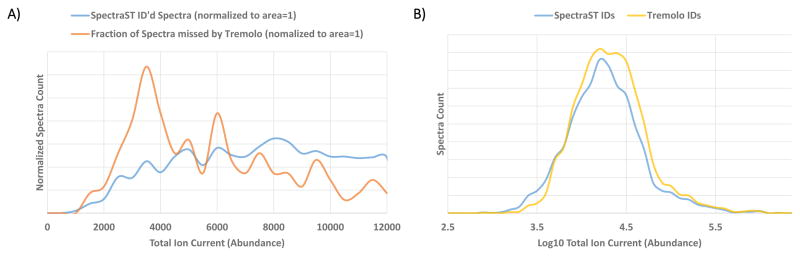
Distribution of total ion current for unidentified low TIC spectra and spectra identified at 1% FDR on the Training dataset. A) Low TIC spectra that were not identified by Tremolo but were identified by SpectraST (in orange) on the Test dataset at 1% FDR. In blue is the distribution of TICs for SpectraST identifications in the Training dataset and subsequently used to train SLGF. (B) Distribution of peptide TICs for IDs at 1% FDR on the Test dataset, with Tremolo shown in yellow and SpectraST in blue. Tremolo is found to be more sensitive in regions of high TIC (> 12000 ions) but loses some sensitivity in the very low TIC region. The loss of these identifications is caused in part by the low TIC ion variation model being trained on spectra mostly in the 5000–12000 ions range and thus not optimally modeling variation in spectra in the < 5000 ions range.

Missed identifications by Tremolo on spectra from high TIC precursors separated into several categories as shown in Table 1. Many examples of deamidation (a post translational modification that increases the mass of amino acids N or Q by 1 Da) were seen throughout our analysis for SpectraST is unable to distinguish between the two variants of the peptide because of the peak smoothing in SpectraST’s spectrum preprocessing. However, we were able to distinguish these cases and correctly not identify them because deamidated versions of spectra were not present in the library. While identifying modified peptides from unmodified spectra is a worthy goal,²² we argue that such searches should explicitly identify query spectra as modified variants of library spectra instead of just reporting them as the same unmodified peptide identification.

Table 1.

SpectraST identifications missed by Tremolo at 1% FDR. There were a total of 334 high TIC and 337 low TIC spectra that were missed by Tremolo at 1% FDR. While the numbers are comparable, the proportion of low TIC IDs missed was much higher as there were only ~ 1400 low TIC spectra identified by Tremolo at 1% FDR. This higher percentage of missed low TIC spectra can be attributed to suboptimal ion variation models for very low TIC spectra as described in the text and in Figure 6.

Reason	Number of spectra
Low TIC Deamidation or 1 13C	105
Low TIC precursor m/z with > 2 13C	36
Low TIC Other	193
High TIC Deamidation or 1 13C	60
High TIC precursor m/z with > 2 13C	63
High TIC Other	214
Total	671

Additionally, 63 spectra contained a high number (> 2) of ¹³C isotope atoms. In these cases ¹³C replaced the more common ¹²C in the peptide, causing an increase in precursor mass because of the additional neutrons. The presence of these ¹³C also affects the prefix and suffix ions in the MS/MS spectra as they skew a portion of the intensity of the b, y, b++, y++, etc. ions into peaks of 1 Da higher mass. This distorts the shape of the spectrum and exaggerates the variance in ion intensities of the query spectrum beyond what is expected by the SLGF distributions.

Of the remaining 214 other spectra that were not identified by Tremolo at 1% FDR, we manually examined a representative subset of these cases and determined that ~ 30% of spectra contained a mixture of two or more peptides. Another ~ 23% were matched to library spectra of questionable quality, exhibiting low signal to noise ratio and a high proportion of un-annotated peaks in the reference spectrum. While we have a low TIC ion variation model that accounts for low TIC query spectra matched to high quality library spectra, we could not account for lower quality library spectra since this information is not readily available. Several of these cases of lower quality library spectra were replaced in the subsequent release of the NIST yeast IT library indicating that NIST revisions also concluded that these library spectra were of lower quality. ~ 28% of the spectra were matched to high quality library spectra and exhibited high SSM cosine scores (~ 0.85) but SLGF distributions were too strict (e.g., expected mean cosine was too high), which may indicate that our average model of variation of ion intensities across all library spectra may not be the most appropriate for specific library peptides resulting in less reproducible spectra.

Despite marked gains over Pepitome¹² and SpectraST,⁹ our results suggest that 3 levels of precursor intensity models (< 5000 ions, 5000 – 12000 ions, > 12000 ions) may be better suited to model peak intensity variations across the range of precursor TICs in our sample and could thus further improve Tremolo’s performance (Figure 6A). In addition, while our models take into consideration the precursor TIC for query spectra, it would also be informative to know the precursor TIC of library spectra since fragmentation patterns in these are also very dependent on precursor TIC. Further studies will be able to determine the effect of both of these factors through the use of larger training and reference datasets.

In addition to comparing search performance on the Yeast test dataset, the Hela S3 Test dataset was searched against the NIST Human Ion Trap spectral library using both Tremolo and SpectraST. Filtering to 1% FDR, Tremolo was able to identify 7,332 MS/MS spectra compared to SpectraST’s 6,723 MS/MS spectra, yielding a 9% increase in IDs. In this search, Tremolo further imposed a threshold of a minimum explained intensity of 0.55. Note that since we calculated the SLGF theoretical distributions for the NIST human library using the ion variance models trained on the CPTAC training dataset, the amount of ion variation seemed to exceed what was estimated in the Yeast training dataset. SLGF theoretical distributions were shifted slightly lower to adjust for this higher variability in ion intensities, resulting in an additional gain in IDs, bringing the total gain to 10.5% more. This indicates that some amount of retraining may be beneficial when using different spectral libraries and experimental conditions.

Even though we did not explicitly aim to identify mixture spectra (and did not evaluate it), we note that the proposed SLGF approach is based on matching reference library spectra to subsets of peaks in query spectra (i.e., normalized projections) and thus appears to be well suited to determining containment of compounds in mixture spectra. While a detailed assessment of SLGF’s performance on mixture spectra would require a more comprehensive evaluation,¹⁰ our preliminary results illustrated in Figure 4A show that SLGF’s performance was essentially indistinguishable from that of SLGF_e and thus strongly suggests that SLGF should be suitable for identification of peptides in mixture spectra.

Despite SLGF’s utility in spectral library search, SLGF theoretical score distributions are currently unable to capture the multi-modality in empirical score distributions that are shown in figure 3 because SLGF is limited to modeling only one source of variation, i.e. instrument variability in intensity measurements. Other sources of variation, such as co-elution and alternate fragmentation pathways, would also need to be considered in order to obtain more accurate SLGF theoretical score distributions. Another limitation of SLGF p-values is that these are not usable to directly estimate false discovery rates in the absence of TDA. Unlike MS-GF’s p-values for the distribution of false matches, SLGF models the distribution of true matches. Thus, SLGF p-values could possibly enable the calculation of false negative rates and thus allow one to estimate sensitivity (proportional to area under the curve for true matches) but not accuracy (proportional to area under the curve for false matches).

Conclusion

Having been repeatedly found^9,11,12,23 that spectral library searching performs consistently better than database search of the same peptide identification search space in high-throughput pro-teomics, there is now renewed interest in establishing statistical methods to further assess the quality of Spectrum-Spectrum Matches (SSMs) and increase the total number of reported SSM-based identifications. Here we propose a new Spectral Library Generating Function (SLGF) approach to assessing the significance of SSMs, show how to rigorously calculate SLGF distributions for any spectrum from any type of molecule and demonstrate that SLGF-based peptide spectral library searching identifies significantly more spectra than state-of-the-art alternative search tools. In difference from database search (and other fields) where statistical significance is estimated by calculating the p-value of observing a high match score when matching a random sequence, we circumvent the open problem of defining realistic ‘random’ MS/MS spectra by instead calculating the p-value of observing a low match score when matching a true (replicate) spectrum to a known reference spectrum. To achieve this goal, we explicitly model instrument variation in measurement of MS/MS peak intensities and show how these can be used to derive theoretical distributions of SSM cosines between replicate and reference library spectra.

The Tremolo library search tool can be accessed at http://proteomics.ucsd.edu/.