High Sensitivity Micro-Elastometry: Applications in Blood Coagulopathy

Abstract

Highly sensitive methods for the assessment of clot structure can aid in our understanding of coagulation disorders and their risk factors. Rapid and simple clot diagnostic systems are also needed for directing treatment in a broad spectrum of cardiovascular diseases. Here we demonstrate a method for micro-elastometry, named Resonant Acoustic Spectroscopy with Optical Vibrometry (RASOV), which measures the clot elastic modulus (CEM) from the intrinsic resonant frequency of a clot inside a microwell. We observed a high correlation between the CEM of human blood measured by RASOV and a commercial Thromboelastograph (TEG), (R=0.966). Unlike TEG, RASOV requires only 150 μL of sample and offers improved repeatability. Since CEM is known to primarily depend upon fibrin content and network structure, we investigated the CEM of purified clots formed with varying amounts of fibrinogen and thrombin. We found that RASOV was sensitive to changes of fibrinogen content (0.5–6 mg/mL), as well as to the amount of fibrinogen converted to fibrin during clot formation. We then simulated plasma hypercoagulability via hyperfibrinogenemia by spiking whole blood to 150% and 200% of normal fibrinogen levels, and subsequently found that RASOV could detect hyperfibrinogenemia-induced changes in CEM and distinguish these conditions from normal blood.

Introduction

Blood coagulation is a vital physiological process for preventing hemorrhage via formation of an insoluble clot. However, inappropriate coagulation can lead to intravascular thrombosis and occlusion of blood flow; this presentation is responsible for most cardiovascular disease-related deaths and complicates many pathological conditions. Abnormal mechanical properties of clots are associated with the risk of thrombosis and the response to clinical treatments, including angioplasty and thrombolytic therapy. Demonstrated correlations between abnormally high clot stiffness and disease, including myocardial infarction at a young age⁸ and diabetes in patients with chest pain,³ also highlight the clinical significance of the clot elastic modulus (CEM).

Although the elastic modulus of individual fibers within a fibrin clot have successfully been measured by instruments such as optical tweezers,⁶ reliable and repeatable clinical tools for elastometry of blood clot samples are still lacking. Thromboelastography (TEG) has been widely used in a clinical setting for monitoring coagulation during procedures including hepatic and cardiac surgeries, which are associated with high risk of massive bleeding.¹² However, TEG is not an ideal modality for assessing clot mechanical properties due to its poor sensitivity, repeatability, and lack of standardization.²³ While the poor standardization of TEG may be due to the absence of standard clinical protocols, it may also be related to the physical method of measurement which requires accurate measurement of stress and strain, involves applying high strains to the clots that induce nonlinearity, and depends upon binding of the clot fibers to the apparatus surfaces.

Recently we developed a new method for elastometry called resonant acoustic spectroscopy with optical vibrometry (RASOV) which offers several advantages over traditional stress-strain elastometry including high measurement sensitivity and small sample volume.^16,18,27 In RASOV, the elastic modulus can be directly computed from the intrinsic resonant frequency of a sample in a well-defined geometry. Clot samples are vibrated via a downward pointing magnetic force applied to a microbead that rests on the sample surface, and the use of small strains ensures that samples remain within the linear viscoelastic regime. Samples are vibrated using a frequency sweep to detect the fundamental resonant frequency of the sample. Displacement is recorded by optical interferometry with high sensitivity (~6 nm) and speed (~ 2 second scan time). The fundamental resonant frequency is then obtained by fitting the peak in the acoustic spectrum.¹⁶ This resonance technique offers high signal-to-noise resulting in high precision elastometry. RASOV was first demonstrated on agarose gel cylinders with open boundaries where gel elastic modulus was computed according to a model solution.¹⁶ Thereafter, RASOV was employed to study fibrin clots formed inside rigid microwells where the clot resonant frequency was shown to be increasing with fibrinogen content.¹⁸ However, exact computation of elastic modulus in the microwells has thus far been elusive due to the lack of accurate models for the closed-wall boundary condition and shifts in resonant frequency observed when using actuators with various masses.²⁷

In this work we report for the first time, RASOV-based measurements of the CEM of human blood and calibration of CEM using a commercial texture analyzer as a standard. We also compare the performance of RASOV against TEG in matched human blood samples and show quantitatively how the CEM of fibrin clot samples varies with fibrinogen and thrombin concentration. Finally, we apply RASOV to measure CEM in human blood clots formed with added fibrinogen to simulate a state of hypercoagulability. This constitutes a significant advance toward the characterization and standardization of RASOV for clinical blood CEM measurement.

Materials and Methods

RASOV Experimental Setup

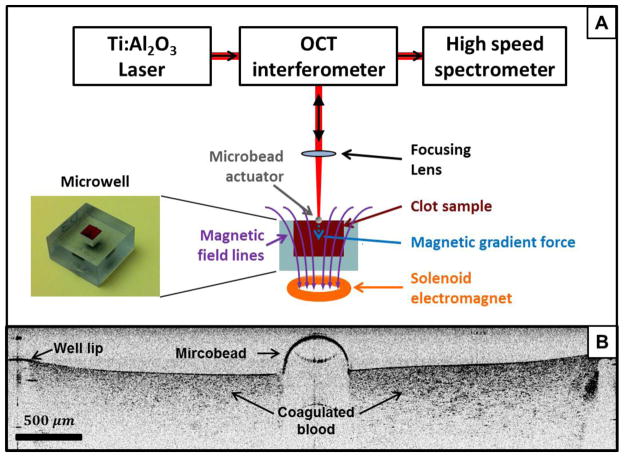
The main components of the RASOV system are an optical displacement sensor, a low inertia mechanical actuator, and a microwell to provide defined boundary conditions for the blood clot (Figure 1A). Plastic microwells were produced by 3D stereolithography printing and are rectangular with dimensions of 5 mm (l) × 5 mm (w) × 6 mm (h) requiring a blood volume of only 150 μL for testing.

FIGURE 1.

(a) Schematic diagram of RASOV integrated with an optical coherence tomography (OCT) system. The electromagnet used in conjunction with the microbead provides a modulated, frequency-swept force on the clot sample. The sample response (bead displacement) is captured by the OCT system to measure the resonant frequency of the sample. (b) Cross-sectional OCT image of a whole blood clot with a microbead placed at the center. While the blood clot surface is not visible underneath the microbead due to its high optical attenuation, it was found that the surface locally deforms to accommodate the weight (~0.7 mg) of the microbead.

Nanoscale displacement sensing was performed by a spectral-domain optical coherence tomography (SD-OCT) system, previously described in detail,¹⁷ which has the advantage of providing B-mode imaging of the micro-actuator placement on the clot samples.^18,27 We note that it is also feasible to construct a RASOV with a simpler, single point optical vibrometer. Briefly, the SD-OCT system provides a broadband 800nm laser beam focused onto the center of a chrome steel microbead (grade 25, 0.5 mm diameter, Salem ball company) gently placed on top of the clot sample using tweezers. The microbead acts as a mechanical actuator, has low inertia (~0.7 mg mass) so as to minimize the perturbation on the native resonance of the clot, and provides a high reflectivity surface for motion tracking by OCT. An example B-mode (x-z) OCT image of a blood clot is shown in Figure 1B. For rapid displacement sensing, the OCT interferogram was recorded in M-mode (z versus time t while transverse position x was fixed) during mechanical excitation. The phase angle of the complex-analytic OCT signal was unwrapped in time to obtain the optical phase φ(z,t). The displacement Δz was obtained from the optical path delay according to Δz (z, t) = φ(z, t) · λ/4π, where λ is the wavelength. The displacement resolution (i.e., the standard deviation of a stationary object) was found to be ~6 nm at a 2 kHz sampling rate for this system, as limited by the phase noise inherent to the OCT system. The acoustic spectrum was then computed by Ĩ (z,ω)=F (Δz (z, t))/ F (F (t)) for a linear, time-invariant system where F(t) is the driving force waveform comprised of a frequency-swept sinusoid and F is the Fourier transform.¹⁶ Ĩ(z, ω) is subsequently averaged in z for pixels above a minimum threshold intensity. The amplitude and phase of the acoustic spectra were then computed (e.g., Figs. 2C and 2D, respectively). The acoustic phase spectrum represents the phase difference between the sample motion, Ĩ(ω), and the driving force, F(ω), which undergoes a characteristic shift from 0 to π at resonance.

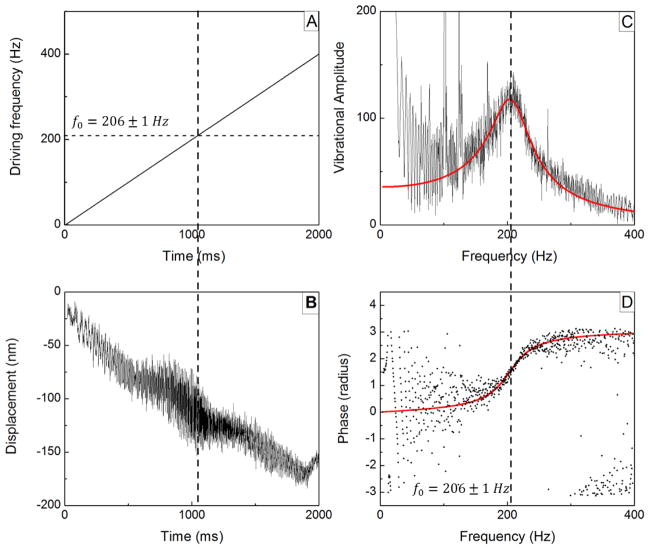
FIGURE 2.

An example of signal processing on RASOV data from a whole blood clot. (a) Timing of the frequency sweep of the driving force (0–400 Hz) generated by the magnet. (b) Corresponding measurement of average bead displacement showing increased vibration amplitude at the time when the driving frequency nears 206 Hz (Q≈2.2). (c) Computed acoustic vibration amplitude spectrum and fitting to a linear viscoelastic model, displaying a peak at 206 Hz. (d) Computed acoustic phase spectrum and model fitting. The phase exhibits a telltale shift from 0 to π at the resonance according to the Lorentzian solution to the linear viscoelastic model.

The driving force F(t) acting on the microbead actuator was supplied by a water-jacketed, solenoid electromagnet with a linearly increasing frequency (chirped frequency) spanning 0–200 Hz, 0–400 Hz and 0–1 kHz, and sampled at linerates of 1 kHz, 2 kHz, and 5 kHz, respectively, where the scan displaying the best fundamental resonance signal was chosen for subsequent analysis. (Example frequency versus time and resultant displacement waveforms are shown in Figs. 2A and 2B, respectively). We find that these frequency ranges appropriately cover the fundamental resonant frequencies of our samples. Slow drift (a downward slope in the displacement plot of Fig. 2B) is apparent but has little effect on the resulting acoustic spectrum. To ensure the clot samples remained in the linear viscoelastic regime, the peak-to-peak displacement was typically < 300 nm corresponding to a maximum strain and strain rate of 5 × 10⁻⁵ and 0.05 s⁻¹, respectively.

To compute sample elastic modulus (also known as Young’s modulus), we measured the resonant frequency f₀ from a least-squares fitting of the acoustic spectrum to a linear viscoelastic model which has the solution of a complex Lorentzian, as previously.¹⁶ An example of the fitting for a blood clot is shown in Figures 2C and 2D. Assuming a homogeneous and elastically isotropic sample, we used:

$$E=a_0\rho f_0^2,$$ Equation 1

where E is the CEM, ρ is mass density, and a₀ is a constant that depends upon Poisson’s ratio, the sample geometry, and boundary conditions.¹⁶ While the RASOV microwell controls the geometry and boundary condition of the sample, the Poisson’s ratio for blood clots has been shown to be constant in low strain conditions (and close to that of water).² For this study, we set ρ for blood to a value of 1060 g/L,¹¹ while recognizing that intra- and inter-individual variability is on the order of ~5 g/L.¹⁰ As ρ of gels and purified fibrin clots is expected to deviate from that of water in these experiments by <0.1%, ρ was set to equal to the density of water for measurements of gels and purified fibrin clots. We then calibrated RASOV as detailed below by determining the characteristic a₀ value for our microwell using controlled gels with similar mechanical properties as blood clots. Using inexpensive agarose gels allowed us to prepare larger samples needed to gain sufficient accuracy with the commercial mechanical analyzer.

RASOV Calibration

Agarose gel was chosen for calibration because its density and Poisson’s ratio are close to that of water. In addition, the elastic modulus of the agarose gel can be easily manipulated by changing the agarose concentration. Aqueous gels with 3–10 mg/mL agarose (Type I-A, Low EEO, Sigma) were prepared into the microwell for RASOV measurements and into 62 mm diameter and 38 mm height cylindrical dishes for texture analyzer measurements. Gels were sealed and refrigerated for 12 hours (4 °C before being warmed to room temperature for 60 mins at which point the seals were removed and measurements obtained.

To calibrate the elastic moduli of the gel samples, a texture analyzer (TA.XT Plus, Texture technologies) was used. The texture analyzer was used in quasi-static compression with a flat plate probe while measuring the reaction force from the sample. Compression was performed at 0.5 mm/s up to 2% engineering strain where gels remained in the linear elastic regime. The elastic modulus was calculated from the ratio of the true stress to true strain over a range of 0.1%–1.7% strain. Three samples were prepared at each concentration and measurements were repeated on separate days. The average elastic modulus at each concentration is plotted in Figure 3A. Resonant frequencies were subsequently measured on concentration-matched gels using RASOV, where quality factors typically between 2 and 5 were observed. This frequency data is shown in Figure 3B.

FIGURE 3.

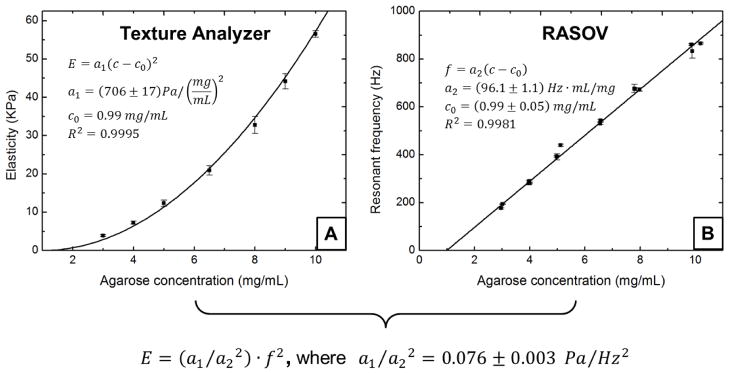
RASOV calibration using agarose gels of varying concentration. (a) Elastic modulus measured using a texture analyzer. (b) Resonant frequency measured using RASOV. Model fitting provides the proportionality constant characteristic of our RASOV system. In this way, a RASOV measurement of f₀ provides the CEM of an unknown sample.

The concentration-dependent elastic modulus of agarose was observed to follow a phenomenological power-law model with a power of 2, similar to previously reported results^1,16. Thus, we performed a weighted least-squares fit to the texture analyzer data according to E=a₁(c−c₀)², where c is the agarose concentration. At the same time, the fundamental resonant frequency f₀ measured by RASOV was found to be linearly proportional to c. We therefore performed a weighted least-squares fit to the RASOV data according to f₀ =a₂(c−c₀), where a₁ and a₂ are constants of proportionality and c₀ effectively corresponds to the threshold concentration below which agarose will not gel. Note that these equations are collectively consistent with the elastic theory equation E = a₀ρ f₀² if a₀ = a₁/(a₂²ρ), lending credence to our observation of the linearity of f₀ with c. We first fit the RASOV data to find the values of a₂ and c₀, and then we fit the texture analyzer data using the c₀ value to find the value of a₁. Using the agarose sample density ρ as that of water, a₀ was then calibrated and used with E = a₀ρf₀² to compute E for any material with the same Poisson’s ratio measured in a microwell with the same geometry. As shown in Fig. 3, we measured a₀ = (7.6 ± 0.3)×10⁻⁵ m² over the range from 4–60 kPa using the agarose gels. This a₀ value was then used to compute CEM for all subsequent clot samples.

Materials

Human alpha-thrombin was from Haematologic Technologies Inc. Purified human fibrinogen (depleted of plasminogen, fibronectin, and von Willebrand factor) was from Enzyme Research Laboratories. Bovine serum albumin (BSA) was from Fisher Scientific. Innovin (tissue factor, TF) from Dade Behring was diluted 1/30000 for use in clotting experiments.

Clot Preparation

Three types of clot samples were investigated. First, purified fibrin clot samples with varying fibrinogen and thrombin content were prepared to investigate the sensitivity of RASOV to concentration changes of these blood constituents. Second, blood samples collected from 4 healthy volunteers were used to compare CEM measured by RASOV and TEG. Third, simulated hyperfibrinogenemic blood clot samples were prepared from blood collected from 3 healthy volunteers for measurement by RASOV.

For purified clot samples, the sample buffer was made by combining 20 mM N-2-hydroxyethylpiperazine-N′-2-ethanesulfonic acid (pH 7.4), 150 mM NaCl (HBS) with 1 mg/mL bovine serum albumin, and 5 mM CaCl₂. Human purified fibrinogen (0.5 – 6 mg/mL final) was thawed at 37 °C and vigorously mixed by pipetting with the buffer and human alpha-thrombin (5 or 20 nM final) into the RASOV microwells (150 μL) at room temperature. Samples were sealed inside a humidified container immediately after mixing and were measured between 3 and 4 hours after clotting to ensure the clot was fully solidified.

Whole blood was collected via venipuncture into evacuated tubes containing 0.105 M/3.2% sodium citrate (pH 6.5), according to a protocol approved by the University of North Carolina Institutional Review Board. Coagulation was triggered in freshly-collected blood within 15 minutes of the blood draw. For RASOV measurements, each microwell was loaded with 142 μL blood mixed with 8 μL TF solution by pipetting.

Simulated hyperfibrinogenemic blood clots were made by spiking whole blood with human purified fibrinogen to 4.5 and 6 mg/mL (quantities that mimic a final percentage of 150% and 200% of normal, respectively). The fibrinogen concentration in human normal pooled plasma was previously measured to be 3 mg/mL by enzyme-linked immunosorbent assay.¹³ Fibrinogen-spiked blood (142 μL) was mixed with 8 μL TF solution for each RASOV microwell (87.2% whole blood, final) by pipetting. Both normal and fibrinogen-spiked blood clot samples were sealed inside a humidified container immediately after mixing and measured within 2 hours. This shorter time (2 hours) than that used for the purified samples (4 hours) was chosen to better match that of the TEG measurements (~1 hour).

Thromboelastography Assay

Thromboelastography (TEG) was performed according to the manufacturer’s instructions (Model 5000, Haemoscope Corp.), as follows: 340 μL of citrated blood was vigorously mixed with 20 μL TF solution in the reaction cup by pipetting. TEG measurements were performed at 37 °C within 15 minutes after phlebotomy. The shear modulus, G, of each blood clot sample was calculated in Kdyn/cm² using the equation in the product manual: G = 5·MA/(100 − MA), where MA is the maximum amplitude of the TEG graph in mm (i.e., the maximum induced pin movement in response to oscillation of the cup). Under the assumption that the blood clot formed inside the cup is homogenous and isotropic, the blood CEM was obtained from G according to E=2G(1+ν), where ν is Poisson’s ratio. We set ν = 0.5 based on previous measurements of blood clots at small strains² and therefore calculated E using E = 15·MA/(100 − MA).

Results

Comparison between RASOV and TEG of Whole Blood

First, we calibrated the resonant frequency obtained by RASOV with the elastic modulus of the sample using a commercial texture analyzer as a standard. The concentration-dependent resonant frequency of agarose gel measured by RASOV was highly linear (R² = 0.9954), and when combined with texture analyzer measurements of the same gels, is consistent with a phenomenological power-law model relating elastic modulus to the square of agarose concentration.^1,5,16 Overall, calibration of the RASOV instrument constant a₀ of Eq. 1 was possible with only 4% uncertainty over the range from 4–60 kPa. We note that this calibration curve is expected to be valid for any resonant acoustic measurement that employs a microwell of the same dimensions and a micro-actuator of the same mass.

Next, to compare the performance of RASOV with a commercially-available clot mechanical analyzer, human whole blood clot CEM was measured by both RASOV and TEG. Four healthy individuals were enrolled in this study and blood was obtained from two of the donors on two separate days for a total of six blood samples. Four samples of each blood draw were measured by RASOV and TEG (Figure 4) showing a high correlation (R = 0.966) over the range of CEM from ~1.5–5kPa. Interestingly, while the slope (0.83 ± 0.12) of the fitting line was less than 1, the RASOV measurements are typically larger than TEG except at very high CEM (>5 kPa). Additionally, we found that the CEM for blood from subject B changed considerably between different days, an effect which was detected by both RASOV and TEG. Importantly, the intra-sample variability of RASOV was only 0.17 ± 0.05 kPa in comparison to 0.3 ± 0.1 kPa for TEG. We also explored the discrepancy between TEG and RASOV measurements using a Bland-Altman plot to investigate the possible relationship between the measurement difference and mean CEM value. While the discrepancy between the two measurements was not statistically significant (p-value=0.25 by a paired t-test), there is no strong evidence showing that a larger difference appears at greater values of CEM.

FIGURE 4.

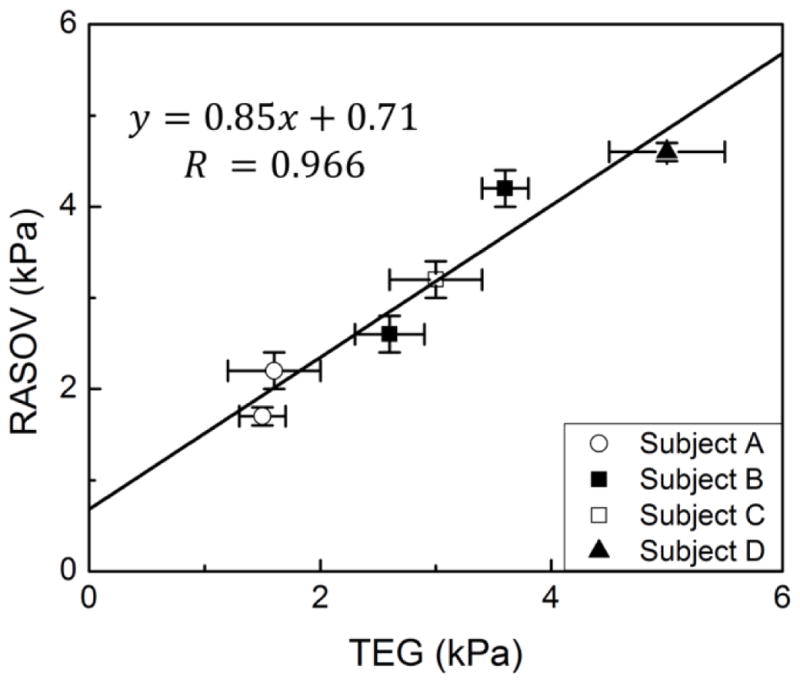
CEM of human blood measured by RASOV and TEG. Blood from two of the four donors (Subjects A and B) was measured twice on different days to highlight the intra-individual variability. Error bars indicate standard deviation over 4 identical samples.

CEM of Purified Fibrin Clots

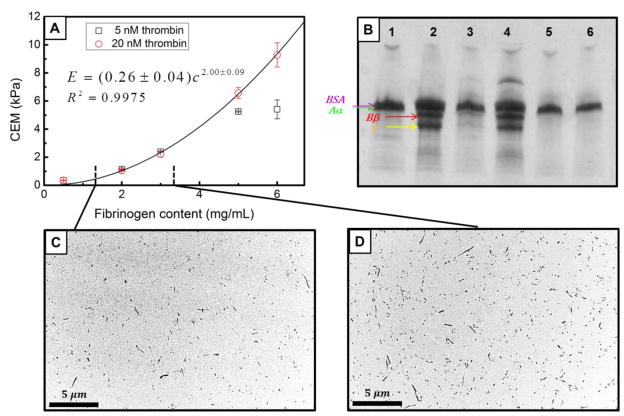
During clot formation, fibrinogen chains are cleaved by thrombin converting fibrinogen to fibrin monomer. Fibrin monomers are then polymerized into a network of fibrin that comprises the main structural component of a blood clot.²⁵ In our study, purified fibrin clots with various fibrinogen and thrombin concentrations were prepared to study the sensitivity of RASOV for detecting clot structural changes. Fibrinogen concentrations (0.5–6 mg/mL) were chosen to range across hypofibrinogenemia, normal blood, and hyperfibrinogenemia. Four fibrin clot samples were prepared and measured by RASOV at each fibrinogen and thrombin concentration and repeated on a different day. The quality factor for the fundamental resonances of the fibrin clots was typically found to be between 2 and 3. The mean and standard deviation of the CEM that were obtained are shown in Figure 5A. TEM images of clots formed from 1.2 mg/mL and 3.2 mg/mL fibrinogen (20 nM thrombin, final) confirmed that the fibrin fibers were homogeneously distributed inside the clot and increased fibrinogen content resulted in an increased fiber density (Figure 5C and D).

FIGURE 5.

Properties of purified fibrin clots with varying fibrinogen and thrombin content. (a) CEM measured by RASOV exhibits a power-law dependence at 20 nM thrombin, but a reduction of CEM at 5 nM thrombin when the fibrinogen content is high. (b) SDS-PAGE showing: 1. Sample buffer as negative control (20 nM HBS, 5 mM Ca and 1 mg/mL BSA). 2. Sample buffer with 1 mg/mL purified fibrinogen as positive control. 3. Unclotted supernatant from low fibrinogen, low thrombin clot (5 mg/mL fibrinogen and 5 nM thrombin). 4. Unclotted supernatant from high fibrinogen, low thrombin clot (6 mg/mL fibrinogen and 5 nM thrombin). 5. Unclotted supernatant from low fibrinogen, high thrombin clot (5 mg/mL fibrinogen and 20 nM thrombin). 6. Unclotted supernatant from high fibrinogen, high thrombin clot (6 mg/mL fibrinogen and 20 nM thrombin). (c) and (d) TEM images corresponding to fibrinogen levels of 1.2 mg/mL and 3.2 mg/mL (with 20 nM thrombin) show that fiber density increases with fibrinogen concentration.

As expected, CEM increased with increasing fibrinogen content exhibiting an apparent power-law dependence at 20 nM thrombin (Figure 5A). Interestingly, at high fibrinogen concentrations (5 and 6 mg/mL), the CEM was lower for clots with 5 nM thrombin compared to clots with 20 nM thrombin, where the 5 nM curve appeared to level off at the high fibrinogen concentrations. We hypothesized that these effects were due to incomplete conversion of fibrinogen into fibrin fibers. To test this hypothesis we performed SDS-PAGE on supernatant taken from clots prepared with 5 and 6 mg/mL fibrinogen final, each at 5 and 20 nM thrombin final. Contents of the supernatants included material not incorporated into the fibrin gel. Figure 5B shows a loading control band in every condition corresponding to BSA protein present in the buffer. The three bands underneath the BSA line show the Aα, Bβ, and γ chains of the fibrinogen protein, respectively, and indicate the presence of free (unclotted) fibrinogen in the sample supernatant. These bands were present in clots produced by 5 nM thrombin incubated with 5 and 6 mg/mL fibrinogen, but not in clots produced by 20 nM thrombin. This result is consistent with the theory that thrombin is trapped in the fibrin network during the conversion of fibrinogen to fibrin, resulting in an insufficient quantity of active remaining thrombin.^22,25 Thus, at sufficiently low thrombin concentration and sufficiently high fibrinogen concentration, active thrombin will be “sequestered,” leaving some fibrinogen un-converted. This scenario would result in incomplete conversion of fibrinogen to fibrin, even in a closed sample, and may explain the reduction in CEM observed in clots produced with low thrombin and high fibrinogen concentrations. Indeed, CEM is expected to be dictated by the amount of fibrin in the structural clot network, which highlights the sensitivity of RASOV specifically to fibrin rather than free fibrinogen.

For clot samples with 20 nM thrombin where no free fibrinogen was detected, CEM displayed a power law dependence on fibrinogen concentration with an exponent of 2.00 ± 0.09, which agreed with several models and measurements on clot mechanical behavior as discussed in detail below.^14,15,24

Hyperfibrinogenemic Blood

The ability to directly measure CEM in whole blood samples could have several advantages, including minimal sample manipulation and rapid characterization of CEM in patients at risk for thromboembolic disease. Thus, a direct test was performed to assess the ability of RASOV to measure CEM of human whole blood clots both with and without additional fibrinogen to simulate a state of hyperfibrinogenemia. Blood from 3 healthy subjects was either measured directly or spiked with purified human fibrinogen to levels that were 150% and 200% of normal, while each condition was split into two wells for measurement by RASOV (Figure 6). The CEM responses were statistically different in 3 groups of blood types (p-value<0.001). The fibrinogen-spiked blood samples exhibited significantly higher mean CEM (p-value=0.007 for 150% fibrinogen spiked and p-value<0.001 for 200% fibrinogen spiked) than normal blood.

Figure 6.

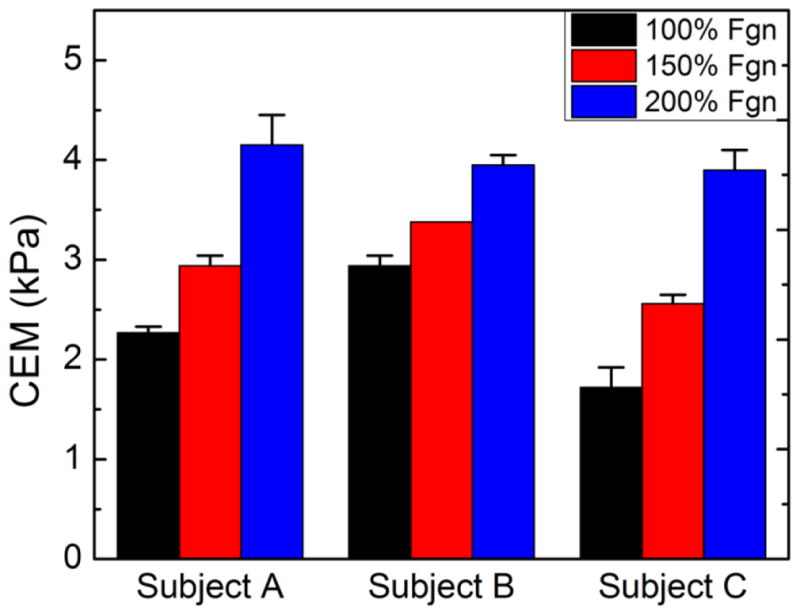
CEM of blood with varying elevated fibrinogen levels as measured by RASOV.

Discussion

Comparison Between Clot Elastometry Methods

First developed in 1948, TEG has gained wide clinical acceptance and has become a gold standard for monitoring blood coagulation. However, its use in a clinical coagulation laboratory has been limited by poor repeatability and lack of standardization.^12,23 The current method of TEG involves incubating freshly drawn blood in a 360 μL cup with a pin at the center. The TEG cup is oscillated at a fixed angle of 4.75° during blood coagulation, which defines the shear strain. The cup motion is increasingly transmitted by the forming blood clot to the center pin, where the maximum amplitude (MA) of the pin motion is recorded when the blood clot is stabilized. MA is directly related to the sample stress, which can then be used with the known strain to compute the shear modulus and subsequently the CEM. Thus, TEG requires high accuracy in both stress and strain to obtain an accurate measurement of CEM. Interestingly, due to the nonlinear relationship between CEM and MA, TEG is less sensitive to CEM when the clot has a higher CEM.

In contrast to TEG, RASOV is not yet capable of measuring dynamic changes such as clotting time during blood coagulation. However, RASOV offers several advantages over TEG: 1) Smaller sample volumes (150 μL vs. 360 μL) may enable longitudinal studies on small animals. 2) Smaller strains may avoid nonlinearity in the stress-strain curve which may result in better accuracy to CEM. 3) The ability to rapidly repeat measurements on a single sample provides better statistics. 4) Greater repeatability in CEM was found when comparing multiple samples from the same blood draw. (The standard deviation was 0.17 kPa for RASOV compared to that of 0.30 kPa for TEG). These features make RASOV an attractive developing technology for measuring blood clot properties.

It is important to recognize possible sources of systematic error in RASOV, which mainly arise from three sources: calibration, inter-individual variability of blood density, and changes in sample geometry. With respect to calibration, there is 4% uncertainty by fitting the calibration data to our model over a span from 4–60 kPa. It is important to note that the minimum elastic modulus possible to calibrate using agarose was 4 kPa, compared to a minimum of 1.7 kPa for blood clots. Thus, the confidence of RASOV measurements below 4 kPa arises from extrapolation of the agarose data, which is linear in a range spanning over an order of magnitude, as well as the consistency of the purified clot results below 4 kPa with prevailing models. In terms of variability, each individual’s blood may have a different mass density, which we expect will contribute on the order of 0.5% variability to CEM measurements.¹⁰ Finally, the sample clot slowly loses volume due to dehydration during analysis, which can shift the resonant frequency. Our comparison study between RASOV and TEG showed that, while the techniques were highly correlated (R=0.966), RASOV offered significantly better precision (by nearly half). It is important to note that TEG depends on the ability of the clot fibers to attach to the cup and pin during excitation. As a result, the CEM measured by TEG could be lower than the actual value if not all fibers transfer stress from the cup to the center pin or if some fibers break in the middle of the measurement. We suggest that this feature is one of the major reasons why RASOV generally exhibited a higher measurement value than TEG in matched samples. Future hardware improvements will include extending RASOV to provide data during coagulation such as the clotting and lysis time. We also expect that enclosing the system in a temperature- and humidity-controlled chamber will further reduce systematic error.

CEM of Purified Clots

At low strains, elastic modulus and protein concentration are expected to have a power law relationship. A current model for semiflexible biopolymers predicts the exponent to be approximately 2.5 for densely cross-linked gels and 2.2 for physically entangled gels.¹⁴ Several attempts were previously made to measure the fibrin concentration dependence experimentally. Weigandt, et al measured this exponent to be 2.22 using rheology,²⁴ while Nelb, et al showed a measured exponent of 1.9 for fine, unligated human fibrin clots using the Plazek apparatus.¹⁵ In RASOV, the power law exponent was least-squares fitted to be 2.00 ± 0.09, which is consistent with these previous measurements. Importantly, this shows that the performance of RASOV is comparable to more conventional, non-clinical rheology techniques.

Importantly, we detected free fibrinogen in fibrin clots with low thrombin content (5 nM final) and high fibrinogen content (5 and 6 mg/mL), suggesting that thrombin did not successfully convert all fibrinogen to fibrin. This experimental observation is consistent with the premise that fibrin(ogen) has “antithrombin” properties, whereby thrombin bound to fibrin becomes sequestered within the fibrin network during clot formation, and therefore, functionally inhibited.²⁶ The fact that RASOV detected lower CEM in these samples highlights its sensitivity to the polymerized fibrin contained within the network as opposed to free (unincorporated) fibrinogen. Future studies with RASOV may enable the establishment of quantitative relationships between clot composition and CEM.

CEM of Fibrinogen-Spiked Whole Blood Clots

Elevated fibrinogen is associated with increased risk of certain cardiovascular diseases.^4,21 Results from previous studies may suggest that this association stems from fibrinogen concentration-dependent effects on the resulting blood clot structure (greater fiber and branchpoint densities).^13,19,25 Here we apply RASOV for the first time to quantify the effects of added fibrinogen on CEM in human whole blood clots. Our data indicate that the CEM of fibrinogen-spiked blood increased significantly in conditions of simulated hyperfibrinogenemia, consistent with previous studies.⁷ The lower sample volumes and high repeatability of RASOV provides a new platform to study hyperfibrinogenemia and to foster insight into the pathologic role of blood hypercoagulability in many diseases, including juvenile idiopathic arthritis,⁹ myocardial infarction,²⁰ and coronary heart disease.²¹

Conclusion

In summary, we have developed novel, high-sensitivity micro-elastometry via resonant acoustic spectroscopy (RASOV) that measures blood clot elastic modulus. Our results indicate that CEM is strongly influenced by fibrinogen concentration and may provide important information on the mechanistic role of fibrinogen and other coagulation proteins in blood clot functionality. RASOV can also be employed to study the effects of other blood components and functions such as red blood cells and platelet contractile force, which have been shown to contribute to clot stiffness.⁴ In the future, a portable RASOV instrument with multiple sample inputs could greatly reduce the measurement time and cost per sample in clinical application. With utility for both fundamental animal model research and clinical medicine, RASOV has the potential to promote understanding of the relationships between a clot’s structure, composition, and its functional mechanical properties, and may provide critical diagnostic data for post-surgical monitoring and in patients undergoing prophylactic hemostatic and antithrombotic treatment regimens.