Abstract
Background/Objectives
Bio-electrical impedance analysis (BIA) is used in population and clinical studies as a technique for estimating body composition. Because of significant underrepresentation in existing literature, we sought to develop and validate predictive equation(s) for BIA for studies in populations of African origin.
Subjects/Methods
Among five cohorts of the Modeling the Epidemiologic Transition Study (METS), height, weight, waist circumference and body composition, using isotope dilution, were measured in 362 adults, ages 25 to 45 with mean BMIs ranging from 24 to 32. BIA measures of resistance and reactance were measured using tetrapolar placement of electrodes and the same model of analyzer across sites (BIA 101Q, RJL Systems). Multiple linear regression analysis was used to develop equations for predicting FFM, as measured by isotope dilution; covariates included sex, age, waist, reactance and height2/resistance, along with dummy variables for each site. Developed equations were then tested in a validation sample; FFM predicted by previously published equations were tested in the total sample.
Results
A site-combined equation and site-specific equations were developed. The mean differences between FFM (reference) and FFM predicted by the study-derived equations were between 0.4–0.6 kg (i.e. 1% difference between actual and predicted FFM) and the measured and predicted values were highly correlated. The site-combined equation performed slightly better than the site-specific equations and the previously published equations.
Conclusions
Relatively small differences exist between BIA equations to estimate FFM, whether study-derived or published equations, although the site-combined equation performed slightly better than other. The study-derived equations provide an important tool for research in these understudied populations.
Keywords: predictive equation, body composition, epidemiology
Introduction
Increases in the prevalences of overweight and obesity, often found coexisting with undernutrition, are occurring worldwide, prompting researchers to test methods for determining body composition in relatively resource-poor settings. Body mass index (BMI) is a universally accepted metric for the comparison of body sizes across individuals and populations. It correlates fairly well with adiposity and is simple to perform (1), however, it may not provide adequate detail regarding body composition for a range of epidemiologic inquiries such as assessing the association between physical activity and adiposity.
The gold standard techniques, i.e. isotope dilution or dual X-ray absorptiometry (DXA), provide accurate measures of body composition (2), however, the cost and expertise required are often unrealistic when conducting large population-based field studies, particularly in resource-poor environments. Bioelectrical impedance analysis (BIA) has been used as a less expensive alternative for estimating body composition in both adults and children (3). The accuracy of BIA is affected by several physiologic variables such as extra- and intracellular electrolyte concentrations, limb length, and body water distribution which can vary by age, gender and ethnicity (4). The potential for these physiologic variables to differ across populations has led investigators to propose that population-specific equations be developed when using BIA to estimate body composition.
There are relatively few BIA equations developed specifically for use among healthy African-origin populations (5, 6), although the BIA method has been utilized for a number of nutritional studies among children (7–11), in pregnancy and lactation (12), as well as in disease states such as sickle cell disease (13, 14) and HIV (12, 15–17).
The aim of the present study was to develop and validate an equation for the estimation of fat-free mass (FFM) by BIA, using isotope dilution as the reference method, in adults of African descent enrolled in the Modeling the Epidemiologic Transition Study (METS) (18). METS is a longitudinal examination of the relationships between physical activity, diet and other lifestyle factors and the development of obesity and cardiovascular and diabetes risk factors among African-origin cohorts of young adults from five countries at differing stages of social and economic development.
Methods
Sampling and other methods used in METS have been described in detail previously (18). Briefly, 500 adults, 25 to 45 years (~50% women), were enrolled in each of five study sites between January 2010 and December 2011: rural Nkwantakese, Ghana; urban Khayelitsha, Cape Town, South Africa; urban Kingston, Jamaica; the island of Mahé, Seychelles; and suburban Maywood, Illinois, United States. All of the participants were of predominantly African descent in the five countries. The study sites were selected to represent a broad range of social and economic development as defined by the UN Human Development Index (HDI) 2011: i.e., Ghana as a low middle HDI country [HDI rank 135], South Africa as middle [123], Jamaica [80] and the Seychelles as high [52], and the US as a very high HDI country [4] (19). The samples are not meant to be representative of the countries as a whole but are, however, characteristic of broad lifestyle patterns common to each site. Individuals with infectious diseases, including HIV-positive individuals, and pregnant or lactating women, as well as persons with conditions preventing normal physical activities, e.g. lower extremity disability were excluded from participation in METS. The protocol for METS was approved by the institutional review boards or ethics committees of all participating institutions and written, informed consent was obtained from all participants by local investigators in the local language or dialect (18)
All procedures conducted in METS followed protocols standardized across all sites with centralized training completed prior to the start of participant recruitment (18). The sample size for these analyses was determined by the requisite sample needed for the comparison of total energy expenditure across the METS cohorts, as assessed by the doubly labeled water method. Weight was measured to the nearest 0.1 kg using the same model balance at all sites (Seca 770, Hamburg, Germany); height was measured to the nearest 0.1 cm (e.g. Invicta Stadiometer, Invicta, London, UK). A single-frequency (50 kHz) impedance analyzer (model BIA 101Q; RJL Systems, Clinton Township, MI) was used to obtain measures of resistance; a tetrapolar placement of electrodes on the right hand and foot was employed with the participant in the supine position (20). Total body water was measured as a constituent of the measurement of total energy expenditure by doubly labeled water, using dilution with stable isotopes, i.e., the average of total body water spaces as measured by deuterium and 18oxygen was used as the reference method (21). Fat-free mass was calculated from total body water using a hydration constant (0.73) (22).
The participants were randomly divided into an equation development sample (66.7% of total) and a validation sample (remaining 33.3% of total) using a random sample generator (StataSE, version 12; College Station, TX). Descriptive statistics including means and distributions of all variables were calculated. In the equation development sample, multiple linear regression analysis was used to develop equations for predicting FFM as measured using isotope dilution, from resistance measured by BIA. Because of documented differences in anthropometric variables across the five cohorts, e.g., height and adiposity, three sets of equations were developed: equation 1 incorporated relevant covariates from all sites combined; equation 2 included dummy variables for each site along with covariates; equation set 3 resulted from equations being developed with covariates for each site individually. Covariates included sex (male = 0 and female = 1), age in years, waist circumference in cm, reactance in ohm and, following well-established convention, height2/resistance (cm2/ohm) measured by bioimpedance, as well as dummy variables created to characterize each site. To determine whether or not site-by-weight interactions terms were significant, a partial F test was conducted.
The equations which were derived were tested for predictive ability in the validation sample. Three parameters were computed, the coefficient of determination (R2), the mean squared error (MSE), and the concordance correlation coefficient (23). Performance of developed equations for the prediction of FFM was also tested using all available data (n=362) against previously published equations derived using participant samples which were assumed by Dioum et al. to consist of at least some ethnically black participants (5, 24–32). Like the current study, all of the previously published equations were developed using isotope dilution as the reference method (either deuterium dilution alone, the average of deuterium and 18O dilution, or tritium dilution) and all but one (Segal; Daninger Medical Technology, Columbus, OH) used bioimpedance analyzers from the same manufacturer (RJL Systems). The comparison was carried out using four parameters, namely, the average bias (average differences between predicted and measured FFM), concordance correlation coefficient (measures linear association between predicted and measured FFM, as well as shifts in the predicted compared to the measured FFM values), total error (bias standard deviation), and pure error (the average squared bias). Furthermore, Bland-Altman plots were used to assess the graphical agreement between predicted and measured FFM values.
Results
A total of 362 participants completed the stable isotope protocol, approximately 72 individuals per site. The participants were randomized to either the equation development sample (n=244) or validation sample (n=118). Participant characteristics by site, sex and sample group are presented in Table 1. There were no significant differences in characteristics between the development sample and the validation sample by site or between the total samples (all p>0.10). However, as a result of the design, mean BMI in both the development and validation samples varied widely across sites, ranging from a combined-gender mean of 24 in Ghana to greater than 30 in the United States (p<0.01 for trend). Other anthropometric measures were consistent with the trends in BMI, e.g., the Ghanaians were about 8 cm shorter than the United States groups and had much lower body weight as well as smaller abdominal circumferences.
Table 1.
Participant characteristics by site, sex and sample group
| Ghana | South Africa | Jamaica | Seychelles | United States |
Total | |
|---|---|---|---|---|---|---|
| Equation Development Sample | ||||||
| N | 44 | 50 | 47 | 54 | 49 | 244 |
| % Female | 54.5 | 56.0 | 51.1 | 50.0 | 46.9 | 51.7 |
| Age (y) | 37.3 (5.8) | 33.6 (6.5) | 33.9 (5.9) | 33.3 (6.0) | 33.9 (5.7) | 34.3 (6.1) |
| Weight (kg) | 63.0 (12.7) | 75.4 (24.1) | 72.6 (18.9) | 72.0 (13.8) | 92.8 (22.9) | 75.5 (21.4) |
| Height (cm) | 162.9 (8.3) | 165.2 (5.6) | 169.5 (9.2) | 165.9 (7.4) | 171.5 (9.2) | 167.1 (8.5) |
| Body Mass Index (kg/m2) | 23.9 (5.8) | 27.8 (9.1) | 25.2 (6.0) | 26.2 (4.6) | 31.7 (8.5) | 27.0 (7.5) |
| Waist (cm) | 83.2 (11.7) | 90.4 (20.2) | 83.5 (14.0) | 85.6 (9.1) | 98.5 (19.4) | 88.3 (16.5) |
| TBW* (kg) | 34.6 (6.5) | 34.1 (5.1) | 35.9 (7.9) | 35.5 (6.4) | 42.8 (8.9) | 36.6 (7.7) |
| FFM (kg) | 47.5 (6.9) | 46.8 (9.0) | 49.2 (10.8) | 48.6 (8.7) | 58.6 (12.2) | 50.1 (10.5) |
| Body Fat (%) | 23.6 (11.6) | 34.4 (13.5) | 30.7 (11.6) | 31.4 (11.9) | 35.5 (12.3) | 31.3 (12.8) |
| Resistance (Ω) | 560.0 (94.7) | 576.3 (90.7) | 548.5 (92.6) | 553.9 (101.5) | 540.3 (78.7) | 555.8 (92.0) |
| Reactance (Ω) | 63.0 (8.6) | 60.4 (10.9) | 59.1 (9.9) | 71.3 (10.3) | 68.4 (11.6) | 64.6 (11.3) |
| Equation Validation Sample | ||||||
| N | 26 | 22 | 27 | 21 | 22 | 118 |
| % Female | 57.6 | 72.7 | 51.9 | 67.7 | 54.5 | 60.9 |
| Age (y) | 35.5 (6.3) | 33.9 (5.1) | 33.4 (5.2) | 32.3 (6.4) | 33.2 (6.2) | 33.7 (5.9) |
| Weight (kg) | 63.2 (12.9) | 76.2 (25.4) | 74.5 (12.7) | 79.5 (18.3) | 85.0 (16.3) | 75.2 (18.6) |
| Height (cm) | 162.2 (7.3) | 163.5 (8.3) | 169.8 (8.3) | 167.1 (6.1) | 170.5 (10.1) | 166.6 (8.7) |
| Body Mass Index (kg/m2) | 24.2 (5.7) | 28.6 (9.8) | 26.1 (5.6) | 28.5 (6.7) | 29.4 (5.9) | 27.2 (7.0) |
| Waist (cm) | 81.5 (11.2) | 93.9 (20.2) | 86.0 (14.2) | 92.3 (14.3) | 95.1 (17.2) | 89.3 (16.1) |
| TBW* (kg) | 33.5 (6.1) | 33.0 (7.4) | 37.3 (5.2) | 35.5 (5.8) | 38.8 (7.2) | 35.6 (6.6) |
| FFM (kg) | 45.9 (8.3) | 45.2 (10.1) | 51.1 (7.1) | 48.7 (7.9) | 53.2 (9.9) | 48.8 (9.0) |
| Body Fat (%) | 26.1 (13.2) | 38.0 (12.2) | 29.8 (13.5) | 37.0 (10.9) | 36.4 (11.4) | 33.0 (13.1) |
| Resistance (Ω) | 557.3 (91.8) | 602.1 (112.9) | 528.3 (61.5) | 568.4 (78.0) | 547.8 (60.4) | 559.2 (85.1) |
| Reactance (Ω) | 64.0 (10.2) | 63.8 (10.1) | 60.7 (8.2) | 73.4 (10.7) | 72.5 (10.3) | 66.5 (11.0) |
Measured using stable isotope dilution (mean of deuterium and 18oxygen dilution spaces).
Considering the marked anthropometric differences across the five sites and the potential for body geometry to influence measurements of resistance and reactance, site-specific equations were derived and tested. Three sets of equations were developed for predicting FFM from resistance as measured using BIA (Table 2). Age, waist circumference, reactance and site-by-weight interactions were found to be not significant and were omitted from final models. Equation 1 resulted when all participants regardless of study site were included in the modeling; the proportion of variance in FFM explained by these variables (R2) was 89%. The second set of equations, 2a – 2e, included all data plus dummy variables for site, resulting in site-specific equations; inclusion of the dummy site variables improved the R2 and MSE modestly (R2: 91%). Each equation in the third set, 3a – 3e, was developed using only those data generated in each site; (R2 varied from 86% to 95%, with a range of associated mean square errors).
Table 2.
Equations for predicting FFM in different populations of predominantly African descent derived from resistance measured by bioelectrical impedance analysis in the development sample (N=244) and performance of equations tested in the validation sample (N=118)
| Equation | Equation* | Site | R2 | MSE* (kg) |
Concordance Correlation Coefficient** |
Bias*** | Error† | Pure Error∫ |
|---|---|---|---|---|---|---|---|---|
| METS 1 | FFM = 12.6 + 0.22(Wt) + 0.46(Ht2/R) − 5.7(Sex) | All combined | 0.89 | 3.5 | 0.94 | 0.4 | 3.1 | 3.1 |
| METS 2a | FFM = 15.5 + 0.20(Wt) + 0.48(Ht2/R) − 5.2(Sex) − 1.2 | Ghana | 0.91 | 3.2 | 0.93 | 0.6 | 3.3 | 3.3 |
| METS 2b | FFM = 15.5 + 0.20(Wt) + 0.48(Ht2/R) − 5.2(Sex) − 4.0 | South Africa | 0.91 | 3.2 | ||||
| METS 2c | FFM = 15.5 + 0.20(Wt) + 0.48(Ht2/R) − 5.2(Sex) − 4.2 | Jamaica | 0.91 | 3.2 | ||||
| METS 2d | FFM = 15.5 + 0.20(Wt) + 0.48(Ht2/R) − 5.2(Sex) − 3.2 | Seychelles | 0.91 | 3.2 | ||||
| METS 2e | FFM = 15.5 + 0.20(Wt) + 0.48(Ht2/R) − 5.2(Sex) | United States | 0.91 | 3.2 | ||||
| METS 3a | FFM = 10.4 + 0.22(Wt) + 0.52(Ht2/R) − 4.2(Sex) | Ghana | 0.86 | 3.4 | 0.93 | 0.6 | 3.3 | 3.3 |
| METS 3b | FFM = 12.2 + 0.16(Wt) + 0.51(Ht2/R) − 3.1(Sex) | South Africa | 0.89 | 2.4 | ||||
| METS 3c | FFM = 13.7 + 0.25(Wt) + 0.38(Ht2/R) − 6.2(Sex) | Jamaica | 0.95 | 2.4 | ||||
| METS 3d | FFM = 17.7 + 0.21(Wt) + 0.37(Ht2/R) − 7.1(Sex) | Seychelles | 0.87 | 3.2 | ||||
| METS 3e | FFM = 11.9 + 0.18(Wt) + 0.58(Ht2/R) − 5.3(Sex) | United States | 0.90 | 4.0 |
Wt is weight in kg, Ht is height in cm; R is resistance in ohm; Sex 0=male, 1=female; MSE is root mean square error
Concordance correlation between reference value for FFM and FFM predicted from the specified equation(s)
Bias is within-subject difference in kg (predicted FFM – measured FFM) using cited equations
SD of the bias
√∑ bias2/n, where n is number of subjects in sample
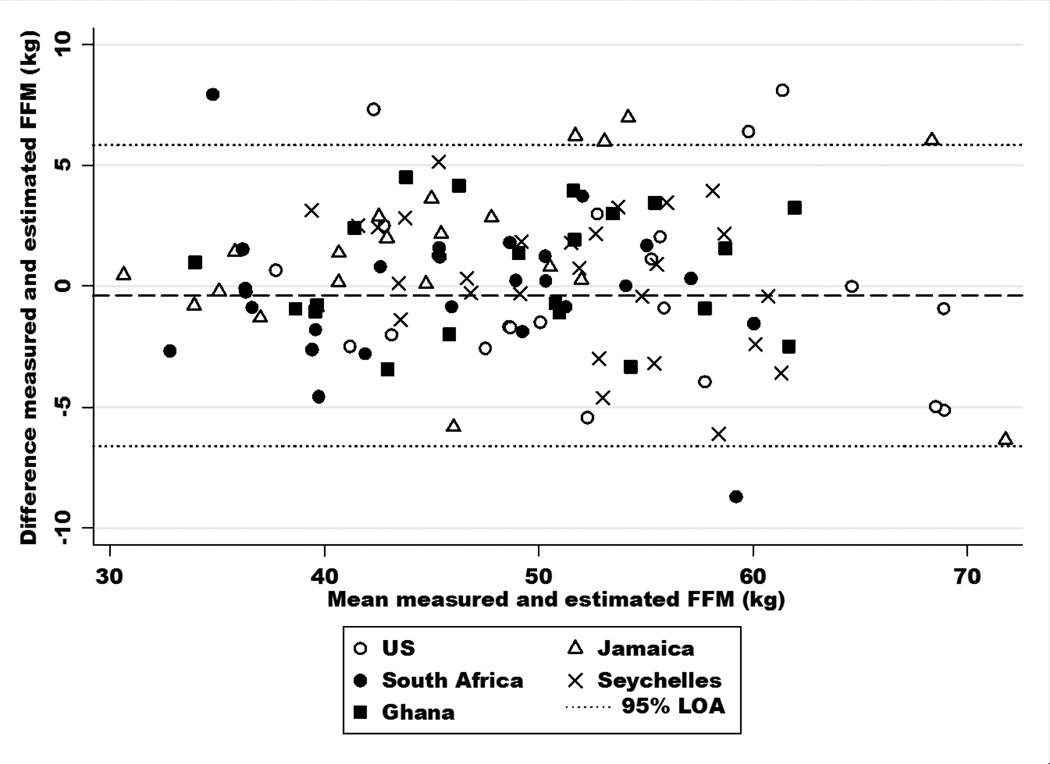
Mean FFM (reference method) in the validation samples was 48.8 kg, whereas the mean FFM estimated by the METS equations were larger by 1%, i.e. mean differences of only 0.4–0.6 kg (Table 2). Overall, all three study-derived equations exhibited high agreement with the reference values determined by isotope dilution (concordance correlation=0.93–0.94). In the combined sample (Table 3), previously published equations yielded differences in mean FFM of 0.6–0.9 kg compared to the reference values. The concordance correlation coefficient was largest for our equation (0.94) compared to any of the other equations previously reported (range 0.86–0.92). Similarly, the average bias and error was smallest for the newly developed equation (average bias = −0.1, error = 3.4 and pure error = 3.4). The Bland-Altman plot (Figure 1) confirms the high level of concordance and small bias associated with the new equation.
Table 3.
Performance of published equations for predicting FFM in different populations of predominantly African descent derived from resistance measured by bioelectrical impedance analysis in the combined sample (N=362)
| First Author (Cit.) |
Equation* | Mean FFM** (± SD) |
Concordance Correlation Coefficient |
Bias*** | Error#x02020; | Pure Error∫ |
|
|---|---|---|---|---|---|---|---|
| Reference FFM | 49.7 ± 10.1 | ||||||
| Development in all black samples | |||||||
| METS 1 | FFM = 12.6 + 0.22(Wt) + 0.46(Ht2/R) − 5.7(Sex) | 49.8 ± 9.6 | 0.94 | −0.1 | 3.4 | 3.4 | |
| Leman (5) | FFM = (1.93 + 0.13(Wt) + 0.47(Ht2/R) −1.2(Sex))/0.73 | 48.5 ± 9.8 | 0.92 | 1.4 | 3.7 | 3.9 | |
| Luke (26) | FFM = (1.3 + 0.097(Wt) + 0.518(Ht2/R))/0.73 | 49.8 ± 9.8 | 0.92 | −0.1 | 3.9 | 3.9 | |
| Zillikens (28) | FFM = (4.563 + 0.621(Ht2/R))/0/73 | 50.1 ± 9.3 | 0.89 | −0.4 | 4.5 | 4.5 | |
| Developed in ethnically mixed samples | |||||||
| Sun (31) | FFM = (3.747 + 0.113(Wt) + | 0.45(Ht2/R))/0.73 | 48.7 ± 8.8 | 0.91 | 1.1 | 3.9 | 4.1 |
| Developed in samples of unknown ethnic composition | |||||||
| Kushner (24) | FFM = (0.04 + 0.065(Wt) + 0.593(Ht2/R))/0.73 | 48.8 ± 10.0 | 0.92 | 1.0 | 4.0 | 4.1 | |
| Kushner (25) | FFM = (0.83 + 0.714(Ht2/R))/0.73 | 51.7 ± 10.8 | 0.88 | −2.0 | 4.8 | 5.2 | |
| Wang (27) | FFM = 0.282(Ht2/R) − 0.034(Age) + 0.16(Wt) + 0.135(Ht) − 9.53)/0.73 | 52.6 ± 8.5 | 0.86 | −2.9 | 4.1 | 5.0 | |
| Lukaski (29) | FFM = (2.03 + 0.63(Ht2/R))/0.73 | 47.3 ± 9.5 | 0.87 | 2.5 | 4.5 | 5.1 | |
| Van Loan (32) | FFM = (9.9868 +0.000724(Ht2) + 0.2822(Wt) − 0.0153(R) − 2.3313(Sex) − 0.1319(Age))/0.73 | 50.8 ± 10.6 | 0.88 | −1.1 | 5.0 | 5.1 | |
| Segal (30) | FFM = (3.432026 + 0.454796(Ht2/R) + 0.139523(Wt))/0.73 | 51.2 ± 9.4 | 0.91 | −1.5 | 4.0 | 4.3 | |
Wt is weight in kg, Ht is height in cm, R is resistance in ohm, Age in years, Sex 0=male 1=female
Reference FFM value is mean (± SD) of FFM measured using isotope dilution in combined Development and Validation samples (n = 362); remaining values mean (± SD) FFM predicted by cited equation
Bias is within-subject difference in kg (predicted FFM – measured FFM) using cited equations
SD of the bias
√Σ bias2/n, where n is number of subjects in sample
Figure 1.
Bland-Altman plot of the estimation of fat-free mass (FFM) by the site-combined equation (METS 1) compared to FFM measured using isotope dilution in the five cohorts participating in the Modeling the Epidemiologic Transition Study (Ghana, South Africa, Jamaica, Seychelles, United States).
Discussion
Three sets of equations were developed to estimate FFM from resistance as measured by BIA and validated for use among young adults from five populations of African origin. Two of the three sets (2.a–2.e and 3.a–3.e) provide equations specific to each of the cohorts, however, the equation developed using the data from all sites combined yielded the smallest bias as well as the highest concordance correlation with the reference values, although the differences resulting from the different equations were minor. The single, site-combined equation is thus recommended for use in these five populations and may be relevant for other African-origin groups, as anthropometric measurements varied widely across sites and the site-combined equation captures this variability.
There has been a multitude of equations for the prediction or estimation of total body water or FFM using BIA published over the last 25 or so years. Relatively few have been derived using data from African-origin or ethnically black populations; it is not clear, however, whether or not biomedical research has been hindered by this under-representation. A 2005 review by Dioum et al. examined the validity of a wide variety of published BIA equations for the prediction of total body water in Senegalese women, some derived from all white or all black samples, some from ethnically mixed samples and some from samples of unknown ethnic composition (33). The authors concluded that there was little difference in the accuracy of existing equations based on the ethnic origins of the development sample i.e., equations developed from wholly or largely African-origin or black participants did not predict total body water better than those from non-African participants (33). In agreement with the conclusions of Dioum et al., most of the published equations that were tested against FFM measured using isotope dilution in the present study gave comparable estimates of concordance, bias and error; our own equations were better at estimating FFM, although not dramatically. The equations developed for use in METS have the advantage of being derived from wholly black community-based samples of healthy young adults, which may be better accepted for use in black populations by biomedical researchers and physicians.
In conclusion, bioelectrical impedance analysis, although fraught with imprecision relative to gold standard methods such as isotope dilution or DXA, has the potential to be an important tool for assessing nutritional status and chronic disease risk, particularly for epidemiologic research in resource-poor settings. There has, however, historically been a dearth of equations developed specifically for use in healthy African populations, although a few do exist (5, 6) and others have been created with African Americans included in the development samples (6, 24). The validated equations presented here performed better than a sampling of existing equations and provide a viable option for the estimation of body composition by BIA among African-origin populations.
Acknowledgements
The authors would like to acknowledge the site-specific clinic staff members as well as the 2,500 participants. METS is funded in part by the National Institutes of Health (1R01DK80763).
Footnotes
Conflict of interest No authors declare any competing financial interests in relation to the work described.
References
- 1.NHLBI Obesity Education Initiative. Practical Guide to the Identification, Evaluation and Treatment of Overweight and Obesity in Adults. In: U.S. Department of Health and Human Services, editor. National Heart LaBI. Washington: 2000. DC; NIH Publication Number 02-4084. [Google Scholar]
- 2.Roche AF, Heymsfield SB, Lohman TG. Human Body Composition. Champaign, IL: Human Kinetics; 1996. pp. 25–78. [Google Scholar]
- 3.Lukaski HC, Bolonchuk WW, Hall CB, Siders WA. Validation of tetrapolar bioelectrical impedance method to assess human body composition. J Appl Physiol. 1986 Apr;60(4):1327–1332. doi: 10.1152/jappl.1986.60.4.1327. [DOI] [PubMed] [Google Scholar]
- 4.Snijder MB, Kuyf BE, Deurenberg P. Effect of body build on the validity of predicted body fat from body mass index and bioelectrical impedance. Ann Nutr Metab. 1999;43(5):277–285. doi: 10.1159/000012795. [DOI] [PubMed] [Google Scholar]
- 5.Leman CR, Adeyemo AA, Schoeller DA, Cooper RS, Luke A. Body composition of children in south-western Nigeria: validation of bio-electrical impedance analysis. Ann Trop Paediatr. 2003 Mar;23(1):61–67. doi: 10.1179/000349803125002887. [DOI] [PubMed] [Google Scholar]
- 6.Schoeller DA, Luke A. Bioelectrical impedance analysis prediction equations differ between African Americans and Caucasians, but it is not clear why. Ann N Y Acad Sci. 2000 May;904:225–226. doi: 10.1111/j.1749-6632.2000.tb06456.x. [DOI] [PubMed] [Google Scholar]
- 7.Wells JC, Hawton K, Darch T, Lunn PG. Body composition by 2H dilution in Gambian infants: comparison with UK infants and evaluation of simple prediction methods. Br J Nutr. 2009 Dec;102(12):1776–1782. doi: 10.1017/S0007114509991255. [DOI] [PubMed] [Google Scholar]
- 8.Buffa R, Floris G, Marini E. Assessment of nutritional status in free-living elderly individuals by bioelectrical impedance vector analysis. Nutrition. 2009 Jan;25(1):3–5. doi: 10.1016/j.nut.2008.07.014. [DOI] [PubMed] [Google Scholar]
- 9.Hawkesworth S, Prentice AM, Fulford AJ, Moore SE. Dietary supplementation of rural Gambian women during pregnancy does not affect body composition in offspring at 11–17 years of age. J Nutr. 2008 Dec;138(12):2468–2473. doi: 10.3945/jn.108.098665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Prins M, Hawkesworth S, Wright A, Fulford AJ, Jarjou LM, Prentice AM, et al. Use of bioelectrical impedance analysis to assess body composition in rural Gambian children. Eur J Clin Nutr. 2008 Sep;62(9):1065–1074. doi: 10.1038/sj.ejcn.1602830. [DOI] [PubMed] [Google Scholar]
- 11.VanderJagt DJ, Morales M, Thacher TD, Diaz M, Glew RH. Bioelectrical impedance analysis of the body composition of Nigerian children with calcium-deficiency rickets. J Trop Pediatr. 2001 Apr;47(2):92–97. doi: 10.1093/tropej/47.2.92. [DOI] [PubMed] [Google Scholar]
- 12.Medoua GN, Nana ES, Essa'a VJ, Ntsama PM, Matchawe C, Rikong HA, et al. Body composition of Cameroonian lactating women determined by anthropometry, bioelectrical impedance, and deuterium dilution. Nutrition. 2011 Apr;27(4):414–419. doi: 10.1016/j.nut.2010.09.008. [DOI] [PubMed] [Google Scholar]
- 13.VanderJagt DJ, Trujillo MR, Jalo I, Bode-Thomas F, Glew RH, Agaba P. Pulmonary function correlates with body composition in Nigerian children and young adults with sickle cell disease. J Trop Pediatr. 2008 Apr;54(2):87–93. doi: 10.1093/tropej/fmm070. [DOI] [PubMed] [Google Scholar]
- 14.VanderJagt DJ, Okolo SN, Rabasa AI, Glew RH. Bioelectrical impedance analysis of the body composition of Nigerian children with sickle cell disease. J Trop Pediatr. 2000 Apr;46(2):67–72. doi: 10.1093/tropej/46.2.67. [DOI] [PubMed] [Google Scholar]
- 15.Mutimura E, Anastos K, Zheng L, Cohen M, Binagwaho A, Kotler DP. Effect of HIV infection on body composition and fat distribution in Rwandan women. J Int Assoc Physicians AIDS Care (Chic) 2011 May-Jun;9(3):173–178. doi: 10.1177/1545109710366472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Villamor E, Saathoff E, Mugusi F, Bosch RJ, Urassa W, Fawzi WW. Wasting and body composition of adults with pulmonary tuberculosis in relation to HIV-1 coinfection, socioeconomic status, and severity of tuberculosis. Eur J Clin Nutr. 2006 Feb;60(2):163–171. doi: 10.1038/sj.ejcn.1602281. [DOI] [PubMed] [Google Scholar]
- 17.Papathakis PC, Rollins NC, Brown KH, Bennish ML, Van Loan MD. Comparison of isotope dilution with bioimpedance spectroscopy and anthropometry for assessment of body composition in asymptomatic HIV-infected and HIV-uninfected breastfeeding mothers. Am J Clin Nutr. 2005 Sep;82(3):538–546. doi: 10.1093/ajcn.82.3.538. [DOI] [PubMed] [Google Scholar]
- 18.Luke A, Bovet P, Forrester TE, Lambert EV, Plange-Rhule J, Schoeller DA, et al. Protocol for the modeling the epidemiologic transition study: a longitudinal observational study of energy balance and change in body weight, diabetes and cardiovascular disease risk. BMC Public Health. 2012;11:927. doi: 10.1186/1471-2458-11-927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Barro RJ, Lee JW. A New Data Set of Educational Attainment in the World, 1950–2010. The National Bureau of Economic Research. 2011 [Google Scholar]
- 20.Lukaski HC, Bolonchuk WW. Estimation of body fluid volumes using tetrapolar bioelectrical impedance measurements. Aviat Space Environ Med. 1988 Dec;59(12):1163–1169. [PubMed] [Google Scholar]
- 21.Schoeller DA, van Santen E, Peterson DW, Dietz W, Jaspan J, Klein PD. Total body water measurement in humans with 18O and 2H labeled water. Am J Clin Nutr. 1980 Dec;33(12):2686–2693. doi: 10.1093/ajcn/33.12.2686. [DOI] [PubMed] [Google Scholar]
- 22.Wang Z, Deurenberg P, Wang W, Pietrobelli A, Baumgartner RN, Heymsfield SB. Hydration of fat-free body mass: new physiological modeling approach. Am J Physiol. 1999 Jun;276(6 Pt 1):E995–E1003. doi: 10.1152/ajpendo.1999.276.6.E995. [DOI] [PubMed] [Google Scholar]
- 23.Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989 Mar;45(1):255–268. [PubMed] [Google Scholar]
- 24.Kushner RF, Schoeller DA, Fjeld CR, Danford L. Is the impedance index (ht2/R) significant in predicting total body water? Am J Clin Nutr. 1992 Nov;56(5):835–839. doi: 10.1093/ajcn/56.5.835. [DOI] [PubMed] [Google Scholar]
- 25.Kushner RF, Schoeller DA. Estimation of total body water by bioelectrical impedance analysis. Am J Clin Nutr. 1986 Sep;44(3):417–424. doi: 10.1093/ajcn/44.3.417. [DOI] [PubMed] [Google Scholar]
- 26.Luke A, Durazo-Arvizu R, Rotimi C, Prewitt TE, Forrester T, Wilks R, et al. Relation between body mass index and body fat in black population samples from Nigeria, Jamaica, and the United States. Am J Epidemiol. 1997 Apr 1;145(7):620–628. doi: 10.1093/oxfordjournals.aje.a009159. [DOI] [PubMed] [Google Scholar]
- 27.Wang J, Thornton JC, Burastero S, Heymsfield SB, Pierson RN., Jr Bio-Impendance Analysis for Estimation of Total Body Potassium, Total Body Water, and Fat-Free Mass in White, Black and Asian Adults. Am J Hum Biol. 1995;7:33–40. doi: 10.1002/ajhb.1310070105. [DOI] [PubMed] [Google Scholar]
- 28.Zillikens MC, Conway JM. Estimation of Total Body Water by Biolectrical Impedance Analysis in Blacks. Am J Hum Biol. 1991;3:25–32. doi: 10.1002/ajhb.1310030106. [DOI] [PubMed] [Google Scholar]
- 29.Lukaski HC, Johnson PE, Bolonchuk WW, Lykken GI. Assessment of fat-free mass using bioelectrical impedance measurements of the human body. Am J Clin Nutr. 1985 Apr;41(4):810–817. doi: 10.1093/ajcn/41.4.810. [DOI] [PubMed] [Google Scholar]
- 30.Segal KR, Burastero S, Chun A, Coronel P, Pierson RN, Jr, Wang J. Estimation of extracellular and total body water by multiple-frequency bioelectrical-impedance measurement. Am J Clin Nutr. 1991 Jul;54(1):26–29. doi: 10.1093/ajcn/54.1.26. [DOI] [PubMed] [Google Scholar]
- 31.Sun SS, Chumlea WC, Heymsfield SB, Lukaski HC, Schoeller D, Friedl K, et al. Development of bioelectrical impedance analysis prediction equations for body composition with the use of a multicomponent model for use in epidemiologic surveys. Am J Clin Nutr. 2003 Feb;77(2):331–340. doi: 10.1093/ajcn/77.2.331. [DOI] [PubMed] [Google Scholar]
- 32.Van Loan MD, Mayclin P. Bioelectrical impedance analysis: is it a reliable estimator of lean body mass and total body water? Hum Biol. 1987;1987(59):299–309. [PubMed] [Google Scholar]
- 33.Dioum A, Gartner A, Cisse AS, Delpeuch F, Maire B, Wade S, et al. Validity of impedance-based equations for the prediction of total body water as measured by deuterium dilution in African women. Am J Clin Nutr. 2005 Mar;81(3):597–604. doi: 10.1093/ajcn/81.3.597. [DOI] [PubMed] [Google Scholar]