The role of the circadian system in fractal neurophysiological control

Abstract

Many neurophysiological variables such as heart rate, motor activity, and neural activity are known to exhibit intrinsic fractal fluctuations - similar temporal fluctuation patterns at different time scales. These fractal patterns contain information about health, as many pathological conditions are accompanied by their alteration or absence. In physical systems, such fluctuations are characteristic of critical states on the border between randomness and order, frequently arising from nonlinear feedback interactions between mechanisms operating on multiple scales. Thus, the existence of fractal fluctuations in physiology challenges traditional conceptions of health and disease, suggesting that high levels of integrity and adaptability are marked by complex variability, not constancy, and are properties of a neurophysiological network, not individual components. Despite the subject's theoretical and clinical interest, the neurophysiological mechanisms underlying fractal regulation remain largely unknown. The recent discovery that the circadian pacemaker (suprachiasmatic nucleus) plays a crucial role in generating fractal patterns in motor activity and heart rate sheds an entirely new light on both fractal control networks and the function of this master circadian clock, and builds a bridge between the fields of circadian biology and fractal physiology. In this review, we sketch the emerging picture of the developing interdisciplinary field of fractal neurophysiology by examining the circadian system’s role in fractal regulation.

I. INTRODUCTION

The human heart beats about once a second, but the actual time between beats varies from beat to beat, by fractions of a second. It has been known for more than twenty years that changes in the intervals between beats are not independent (Peng et al, 1995b; Stanley et al, 1992). Specifically, if the interval decreases from one pair of beats to the next, it is likely to increase with the next pair of beats. The sizes of these incremental changes are also organized, so a large change in either direction is likely to be followed by another large change (Ashkenazy et al, 2001). Moreover, the dependence between intervals described above holds beyond successive intervals, extending far forward and backward in time. In fact, a healthy cardiovascular system seems to remember every adjustment it’s made for at least the past 24 hours, combining that information with current conditions to make minute, instant-to-instant adjustments in its rate of beating.

The result of these calculations is a scale-invariant or fractal pattern of increases and decreases in heart rate – one exhibiting similar temporal fluctuation structures at different timescales. Such patterns are a signature of complex, nonlinear dynamics. Their discovery in heart-rate regulation is one example of the diverse translational efforts of researchers in the life sciences, who have turned to concepts and techniques from modern statistical physics to illuminate the intricacies of neurophysiological function and biological systems (Bassingthwaighte, Liebovitch & West, 1994; Paraschiv-Ionescu & Aminian, 2009; West, 1990). Fractal patterns have been discovered in a wide variety of physiological variables including gait (Hausdorff et al, 2001; Scafetta, Marchi & West, 2009), respiration (Fadel et al, 2004; Peng et al, 2002; Suki, 2002), heart rate (Meyer & Stiedl, 2003; Peng et al, 1993) and neural activity (Beggs & Plenz, 2003; He et al, 2010; Stam & de Bruin, 2004).

The fractal patterns present in physiological fluctuations are intrinsic, existing independently of external driving forces (Hu et al, 2004b; Nunes Amaral et al, 2001). The classical theory of homeostasis (Cannon, 1929) predicts that such intrinsic physiological fluctuations should be dominated by random (Gaussian) noise, fluctuating around a homeostatic set point. But the intrinsic fractal fluctuations seen in physiological systems are not completely random, and they are more than just noise; while unpredictable, they have a complex temporal organization that extends over multiple time scales.

Furthermore, the temporal structure of fractal fluctuations contains hidden information about the health of the regulatory system producing them. Numerous studies in the last two decades have provided evidence that fractal patterns are reliable and sensitive biomarkers of healthy physiological function and of the alterations in function that accompany age and pathology. In many cases, fractal analyses are better predictors of morbidity and mortality than more classical biomarkers, suggesting that changes in fractal patterns may occur far in advance of the changes in average measures which now define disease. For example, a breakdown of fractal fluctuations in human heart rate occurs about ninety minutes before the onset of atrial fibrillation (Vikman et al, 1999); is the best predictor of vulnerability to ventricular tachycardia post myocardial infarction (Makikallio et al, 1997); and is the best predictor of sudden cardiac death in elderly patients (Makikallio et al, 2001b), post-stroke (Makikallio et al, 2004), and in heart failure (Huikuri et al, 2000; Makikallio et al, 2001a).

Given the association of fractal fluctuations and healthy physiological function, it is natural to ask for the source of fractal fluctuations in physiology. Mathematical simulations show that it is highly improbable that fractal patterns in physiology could result from something as simple as the summation of regulatory mechanisms operating at different timescales (Ashkenazy et al., 2001; Hausdorff & Peng, 1996; Ivanov et al, 2009). Rather, it is likely that nonlinear feedback interactions between regulatory mechanisms are required to explain the presence of fractal fluctuations. Thus, fractal fluctuations may be a representation of the degree of coupling between different components of a physiological system, and it has been hypothesized that fractal patterns in physiologic outputs may reflect system adaptability and integrity (Chiesa et al, 2010; Hu et al., 2004b; Hu et al, 2008; Peng et al, 1995b). However, detailed and physiologically-relevant mechanisms for the production of fractal fluctuations have yet to be uncovered.

A powerful analogy for fractals in physiology comes from modern statistical physics, where fractal fluctuations have been explained in the context of so-called critical systems – systems undergoing a transition from one stable state to another. As we will explain below, critical systems are highly sensitive to perturbations, reacting with organized patterns of activity spanning many scales. It has been suggested that the central nervous system might have evolved to utilize something like criticality as an organizing principle, in order to maintain a flexible repertoire of behavioral responses to an environment which is itself critical, complex, and unpredictable (Chialvo, 2010). Similarly, physiological systems may employ something similar to criticality as a control mechanism, thus avoiding responses to environmental stimuli that are either too random to be relevant, or too rigidly ordered to be appropriate.

A key feature of critical systems is that they are made up of a population of many simple interacting units. The richness of the collective behavior of this population, exemplified by the presence of fractality, cannot be derived from the properties of the individual units. Rather, it emerges from system-wide interactions. It is unclear whether fractal fluctuations are indicative of such collective behavior, of the cross-scale interactions between a handful of distinct regulatory mechanisms, or of some mixture of the two. What is clear is that the understanding of fractal patterns in physiology cannot be obtained with traditional reductive approaches that focus on individual physiological processes operating at a single timescale. Elucidating the principles governing fractal fluctuations in physiology will require an integrative, holistic (systems-level) approach, based on a network view of multiple component processes and their interactions. The mechanisms producing fractal patterns are not the simple homeostatic control mechanisms of Bernard and Cannon (Cannon, 1929), designed to maintain constant conditions through negative feedback regulation, but new kinds of fractal control and fractal regulatory mechanisms.

In exploring fractal physiological control, we should be prepared for seemingly distant physiological processes, operating at seemingly different temporal scales, to play a surprising role in each other’s fractal regulation. In this review, we bring together recent findings that have begun to provide a mechanistic understanding of the role of the circadian system – a system known to be composed of a large number of relatively simple interacting units, organized into sub-components which communicate with each other at a variety of spatial scales – in fractal physiological control. These findings point to a central role for the circadian system in fractal regulatory networks responsible for the time organization of both heart rate and motor activity. They open the door to transferring the existing knowledge of the circadian system to the domain of fractal physiology, while at the same time posing entirely new questions to researchers in the field of circadian biology. We believe this represents a turning point in the search for mechanistic and physiological explanations of fractals in neurophysiology.

It is our hope that this paper will serve as an invitation to the rapidly growing field known as fractal physiology, and in particular to its emerging interactions with circadian biology. In addition to providing a brief overview of recent evidence regarding the fractal regulatory function of the circadian system, we include a selective introduction to certain basic topics and concepts related to circadian control and fractal regulation. Our emphasis is not on technical issues, and those interested in a more in depth look at fractals, criticality, and their relation to biology will find a number of helpful papers in the references; Gisiger’s review (Gisiger, 2001) is especially recommended. Nor have we attempted to provide an exhaustive review of fractal physiology, a field that is over 20 years old, encompasses a variety of physiological systems, methodologies, scales of organization, and conceptual approaches (Gupta, Suryanarayanan & Reddy, 1997; Masters, 2004; McNamee, 1991; Ruttimann, Webber & Hazelrig, 1992; Smith, Jr., Lange & Marks, 1996; West et al, 2003; Yan & Guo, 2012), and now has its own journal (West, 2010b). West’s recent review provides a valuable overview of the subject (West, 2010a). Neither do we even gesture at a comprehensive review of circadian biology. Intensive investigations of circadian rhythms in the past 100 years have provided great insights into the molecular and systems-level mechanisms underlying the generation and orchestration of circadian rhythms in different physiological systems, as well as the synchronization of these rhythms with external stimuli, and the physiological consequences of their alteration with aging and disease. These aspects of circadian research have been well summarized in previous review articles (Albrecht & Eichele, 2003; Moore, 1996; Reppert & Weaver, 2002; Weaver, 1998).

The rest of the paper is organized as follows. We first define fractals, describe how the fluctuations of variables in time can exhibit fractality, introduce quantitative measures of these fractal patterns, and describe the significance of a few key types of fractal patterns. We then discuss fractal patterns in physiology, with a focus on heart rate and behavioral activity. We briefly cover the appearance of different fractal patterns at different timescales, the presence of cross-scale nonlinear interactions in physiological fractals, the selective stability and dynamical nature of these patterns, and these patterns’ alterations with changing physiological states, aging, and disease. We then review theoretical work on fractal fluctuations, introducing the theory of critical systems, and discussing the hypothesis that fractality in physiological regulation is an emergent property of a multiscale network of control nodes with nonlinear feedback interactions. We then highlight recent findings from human and animal studies, which indicate the mechanistic links between the circadian system and fractal regulation. In the last section, we present open questions suggested by these findings.

II. SAME PATTERN, DIFFERENT SCALE

(1) Fractals in space and time

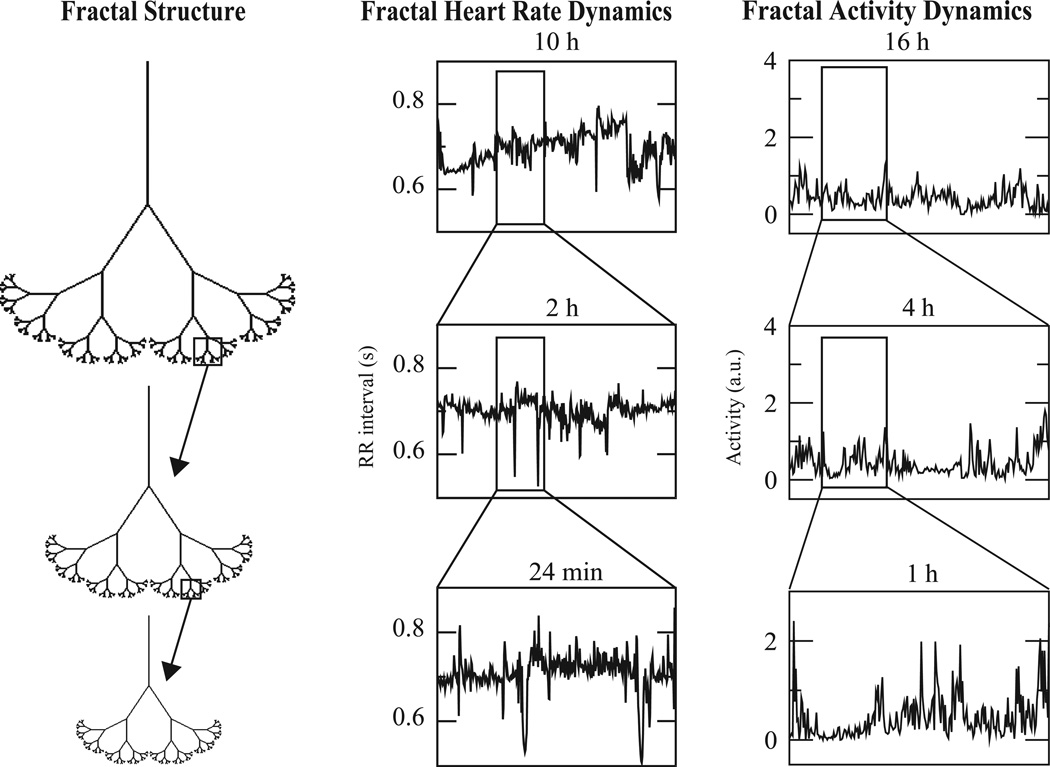
For our purposes, a fractal structure is one that exhibits similar complex patterns on many different scales. Nested within the overall fractal structure are sub-regions which mimic that structure. These sub-regions in turn contain sub-sub-regions reminiscent of the large-scale structure, and so on. This self-similarity may occur in different ways: the sub-regions may be exact or distorted copies of the overall structure, or they may simply share quantitative, qualitative, or statistical properties with it. At one extreme, certain carefully chosen pieces of the structure are identical to the whole after enlargement and possibly rotation (Figure 1, left panel). At the other extreme, sub-regions of all sizes may share certain statistical regularities (Figure 1, middle and right panels). Regardless, structures shared across scales make it hard to discern how large a part of a fractal you are looking at, a property formally expressed in the concept of scale invariance. Fractal structures are ubiquitous in biology and the physical world, existing in the branching structures of trees and vascular systems, and the irregular profiles of coastlines and mountains (Kamiya & Takahashi, 2007; Mandelbrot, 1982; Masters, 2004; Zamir, 2001).

Figure 1.

Schematic representations of fractal structures and fluctuations. The tree-like spatial structure (left panel) has fractal branching, such that the small-scale structure resembles the large-scale form. Fractal temporal processes, such as healthy heart rate (middle panel) and behavioral activity (right panel), may generate fluctuations that are statistically fractal. (Adapted with permission from Goldberger 1996.)

A time series can also be fractal, if its temporal fluctuations are statistically similar at different time scales (Figure 1). Rather than regularly spaced occurrences of large and small values, fractal signals exhibit bursts of large values, which display their own sub-bursts of large and small values. These subbursts in turn contain sub-sub-bursts, and so on. These nested patterns are typical of fractal signals, with the result that it is often hard to distinguish between recordings of different lengths, provided that the vertical axis is scaled appropriately to match the horizontal axis (Figure 1).

The fluctuations of a wide variety of physical, biological, and social signals exhibit fractal properties. Examples include light emission in quasars, noise and conductance in electronic devices, velocities of underwater sea currents (Gisiger, 2001), the flow of sand in an hourglass (Schick & Verveen, 74), voltage changes across neuronal membranes (Verveen, Derksen & Schick, 67), the sizes of insect populations (Rohani, Miramontes & Keeling, 2004), stock prices (Clauset, Shalizi & Newman, 2009), and even volume changes in music (Jennings et al, 2004). Neurophysiological signals exhibiting fractality include spontaneous motor activity (Hu et al, 2004a; Hu et al, 2007a), fluctuations in heart rate (Peng et al., 1993), errors in rhythmic finger-tapping (Torre & Wagenmakers, 2009), variations in stride length (Hausdorff et al., 2001), spontaneous cortical activity (Beggs & Plenz, 2003), and synchronicity in multi-channel EEG recordings (Stam & de Bruin, 2004). A comprehensive bibliography of the enormous volume of reports of fractal patterns in various signals can be found at http://www.nslij-genetics.org/wli/1fnoise/. Within neurophysiology, fractal signals are, themselves, found across multiple scales of organization – from cellular to tissue to organ to entire organism levels – mirroring the nested fractal organization present at each scale (Kello et al, 2007; Liebovitch et al, 2001; Teich et al, 1997; Varanda et al, 2000).

(2) Measuring fractality

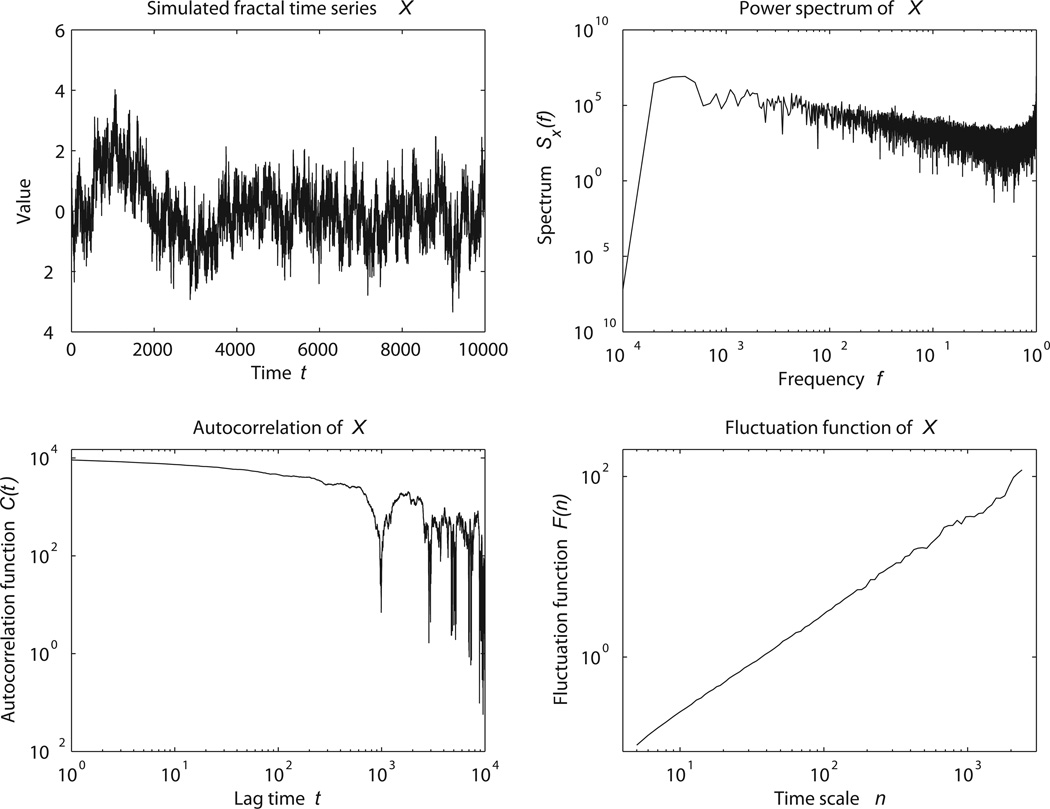
The functions describing the statistical properties of fractal processes at different scales (such as the probability distribution, rescaled range, power spectrum, auto-correlation, and nonlinearity) have a power-law form (Figure 2). Roughly speaking, this means that if we change the timescale over which we compute these statistics, and normalize the statistics appropriately, we obtain identical values. On a log-log scale, such a power-law function appears as a straight line, and the slope of this line – the exponent of the power-law – characterizes the fractal fluctuations. In contrast, the absence of a power-law form in these functions indicates a lack of fractality.

Figure 2.

Power-law functional properties of a simulated fractal signal. Notice that while some power-law behavior is evident in the power spectrum, autocorrelation function, and fluctuation function of the signal, the last exhibits the clearest power-law behavior.

A variety of methods take advantage of these power laws to test for and characterize fractal fluctuations. Perhaps the oldest is the Hurst exponent (Hurst, 51), which quantifies how the rescaled range – the range of signal values divided by their standard deviation – changes with timescale. The Hurst exponent is related to the exponent of the power spectrum, which quantifies how the power of the signal’s oscillatory components changes with their frequency. Briefly, the exponent of the power spectrum describes the relative contributions of oscillations with different characteristic time scales to the signal – the lower the frequency, the longer the timescale. An exponent of zero indicates that oscillations of all periods contribute equally to the signal. A negative exponent indicates that oscillations at long time scales – having low frequencies – dominate the signal, while a positive exponent indicates that high frequency oscillations dominate the signal.

The exponent of the power spectrum is also related to the correlation properties of the signal – how its value at one time depends on previous values. Another way to measure this is through the exponent of the autocorrelation function, which quantifies how the correlation between different segments of the signal decays as the time separation between those segments increases. The relationship between the exponents of the power spectrum and the autocorrelation function is intuitive, since the correlation between values at different times depends on whether fluctuations at short or long time scales dominate. A power spectral exponent of zero indicates an uncorrelated signal, in which the values at different times are statistically independent. Positive power spectral exponents indicate an anticorrelated signal, in which the preponderance of high frequency oscillations means that positive values are likely to be followed by negative values, and vice versa. Negative values of the power spectral exponent indicate a correlated signal, in which positive values are likely to be followed by positive values, and the values of the signal are likely to stay positive far into the future. Such correlated signals are said to have long memory, since the state of the system at one time affects the state of the system at far later times. In contexts where interest is restricted to correlated signals, the sign of the power spectral exponent is often dropped to make it positive, and we will follow this convention in the rest of the paper.

Many of the results we will mention employ a fractal analysis known as detrended fluctuation analysis (DFA; Peng et al, 1994), which can be robustly applied to the kinds of highly variable signals encountered in physiology. For a signal whose mean and standard deviation are constant in time, DFA, Hurst, autocorrelation, and power spectral analyses yield equivalent results. However, unlike the other techniques, DFA can be applied even to signals that do not meet these criteria, a class which includes most physical and biological signals. Furthermore, power spectral and autocorrelation analyses often give less reliable results at short time scales compared to DFA, especially for signals of short duration (Figure 2).

In DFA, a signal is fit repeatedly with piecewise polynomial trends. As the size or scale of the “pieces” composing the fit varies, so does the sum of squares of the residuals. Plotting the sum of the squared residuals against the scale used to fit trends to the data yields a fluctuation function (Peng et al, 1992). For a fractal signal, this fluctuation function has a power law form (Figure 2). The exponent of the fluctuation function describes how the changes in the signal at different time scales relate to each other. A signal having a DFA exponent of 0.5 is random and uncorrelated. A signal having a DFA exponent above 0.5 is correlated – so that positive values are likely to follow each other – and the higher the DFA exponent, the further back in time such correlations exist. A signal having a DFA exponent less than 0.5 is anticorrelated, so that a positive value is likely to be followed by a negative value, and vice-versa.

(3) Fractality and complexity

Fractality in a signal is often interpreted as an indication of the complexity of the processes producing that signal. One way to think of this complexity is as the amount of information required to describe the signal. Not all fractals are equally complex, and the presence of long memory in a signal is no guarantee of complexity.

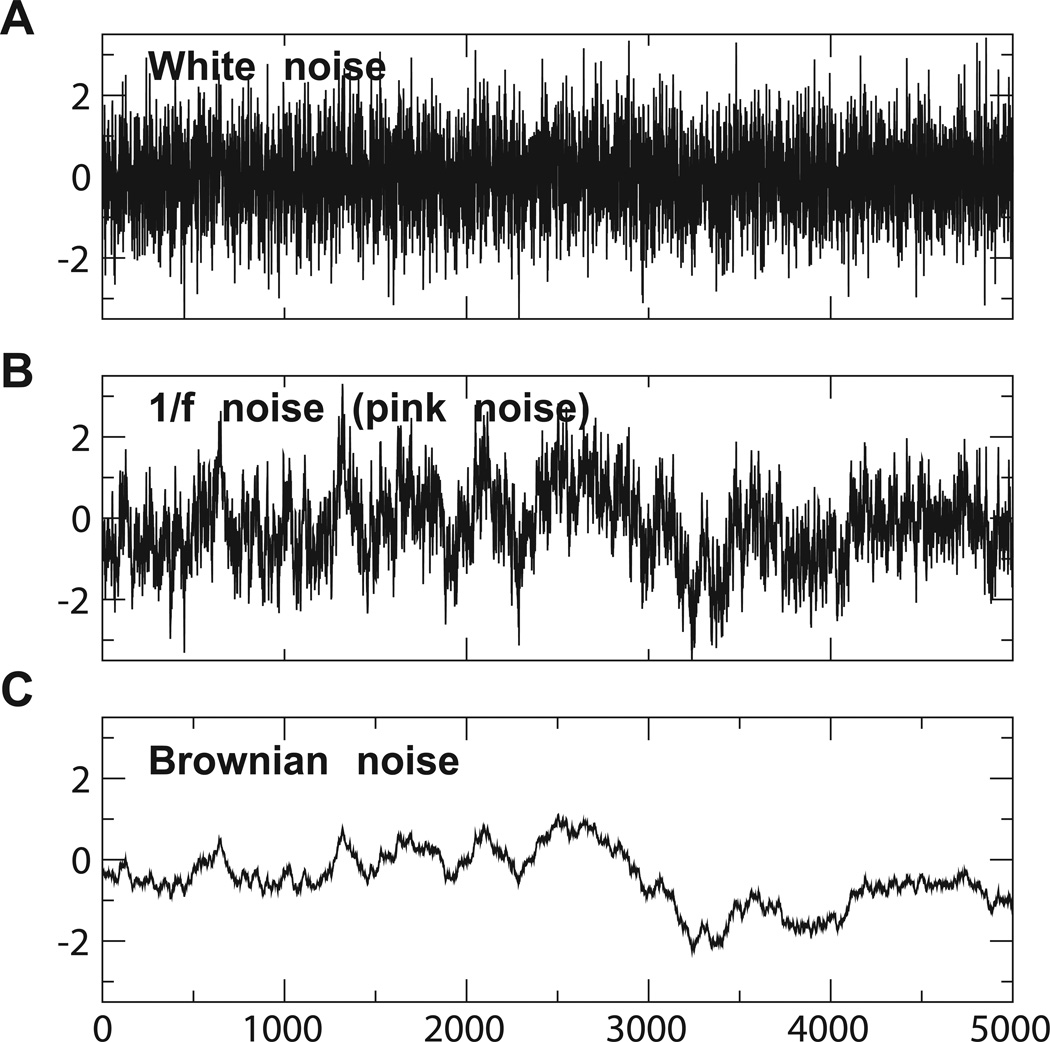
We illustrate this point with three canonical signals. First, consider the signal known as white noise, whose values are chosen at random from a normal distribution (Figure 3A). The power spectrum, autocorrelation, and fluctuation functions of this signal are power-law in form, indicating that it is fractal. However, the ease with which we can describe the signal – each value is just a random number – indicates that it is not complex.

Figure 3.

Three canonical fractal signals. White noise (A) exhibits short-scale fluctuations and is uncorrelated. Red or Brownian noise (C) exhibits long-scale fluctuations and correlated regularity. Pink noise (B) exhibits both the unpredictability associated with small-scale fluctuations and the long memory associated with large-scale fluctuations, and high complexity. (The colors used to describe white and pink noise signals are due to analogy with light: white noise contains component oscillations of all frequencies; Brownian noise is also called red noise, and is dominated by low-frequency (slow) oscillations; pink noise is intermediate between the two.)

As we might guess from the uncorrelated nature of white noise, its power spectral exponent is zero, indicating that it does not contain long range correlations. Long memory by itself, however, is not enough to guarantee complexity. Cumulatively summing the values of a white noise signal results in a signal known as red or Brownian noise (Figure 3C). The summation introduces regularity and eliminates short-scale fluctuations, and Brownian noise has a power spectrum with exponent of 2, indicating that it is highly correlated. However, this signal can be described almost as easily as white noise can, as we have just done, and is not generally considered complex.

In contrast, the statistical properties of signals with a power spectral exponent close to 1 cannot be described as simply. These signals, known as pink noise, exhibit a fine balance between the uncorrelated randomness of white noise and the correlated regularity of Brownian noise (Figure 3B). For such signals, the relative magnitudes of fluctuations at short and long time scales are similar (the power in each octave is the same), resulting in both unpredictability and long memory. It is findings of pink noise which are cataloged in the online bibliography mentioned above.

While such simple examples can provide intuition about time series exhibiting a given scaling exponent, there are many aspects to complexity, and they are not all consistent with fractal scaling. For example, the human cortical EEG – which many would argue is one of the most complex signals known to science – has a scaling exponent close to that of Brownian motion (He et al., 2010). Alternatively, by adding together oscillatory signals with amplitudes inversely proportional to the square root of their frequency, one obtains so-called spectral pink noise, which has a scaling exponent of 1 but debatable complexity. In practice the complexity of a time series must be decided on a case by case basis, with reference to the context of the investigation, as well as the source and the structural and statistical characteristics of the signal. For these reasons, it is important to differentiate between fractal signals using other measures of complexity besides scaling exponents. A number of techniques for directly measuring the complexity of time series have been developed – including multifractal analyses, approximate entropy, Lyapunov exponents, correlation dimension, and so on. Other techniques of particular relevance to fractal physiology will be discussed in Section 3.2.

Certainly, pink noise is produced by a number of interesting physical systems, and may be generated by very complex mechanisms (see the discussion in Section 4). The combination of long memory and unpredictability exhibited by pink noise are evocative of the types of complex behavior seen in many biological systems. Most importantly, however, scaling exponents around 1 are observed in most healthy physiological systems (Stanley et al., 1992; Stanley, 1995), while exponents deviating from 1 are associated with disease and aging (see Section 3.4). For this reason more than any other, signals exhibiting fractal fluctuations with power spectral and DFA exponents around 1 are the fractals we are primarily concerned with in this paper.

III. FRACTALS IN PHYSIOLOGY

(1) Fractal signals in the real world

It is possible for theoretical models of fractals to exhibit self-similarity or a single scaling relationship at all scales, from infinitesimal to infinite. However, in the real world, such fractal properties can only exist over a limited range of scales, due to limits on the sizes of the system and its smallest elements. For example, the lung vasculature and the arborizations of trees are widely held to be fractal, but their scale invariance stops abruptly at the cellular scale, and again at the scale of the entire structure; it cannot continue down or up past these limits to encompass all possible scales.

Similarly, sample length and sampling frequency place limits on the range of time scales over which fractal patterns can be quantified in physiological variables. (DFA can be safely used to quantify fractal fluctuations at time scales which, on the low end, contain sufficiently many data points to confidently fit a polynomial trend, and on the high end, break the sample into sufficiently many subintervals to confidently estimate the fluctuation function; five is a reasonable benchmark for both numbers. Of course, the number of time scales at which the fluctuation function is determined must also be sufficient to allow confident estimation of the scaling exponent.) For example, human behavioral activity as measured by wrist accelerometry has been shown to exhibit fractality (with a DFA exponent of ~0.9) over a range of time scales from 4 minutes up to 24 hours (Hu et al, 2007a), while longer and shorter time scales have not been investigated.

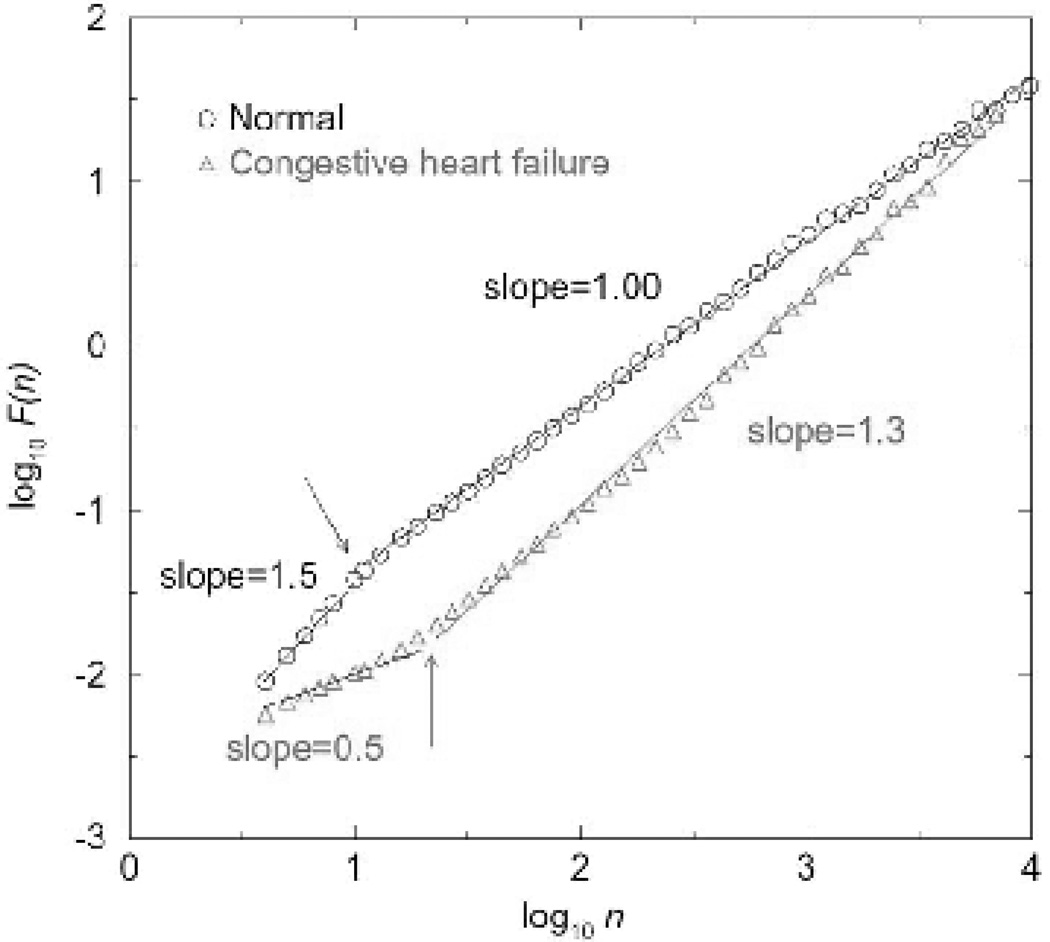
In physiological systems, signals may exhibit different scaling exponents over different scale ranges, perhaps due to different underlying control mechanisms. Thus, it is especially important to report the time scales at which fractal fluctuations are observed. For instance, healthy human heart-rate exhibits two scaling regimes (Figure 4; Peng et al., 1993; Peng et al., 1995b). For very short timescales, less than 10 beats, healthy heart rate exhibits a DFA scaling exponent of 1.5, indicating that heartbeat is relatively regular at these scales. For longer time scales, from 10 beats up to ~3 hours, healthy heart-rate exhibits a scaling exponent around 1. Such a change in the pattern of fractality at a specific scale has been termed a crossover.

Figure 4.

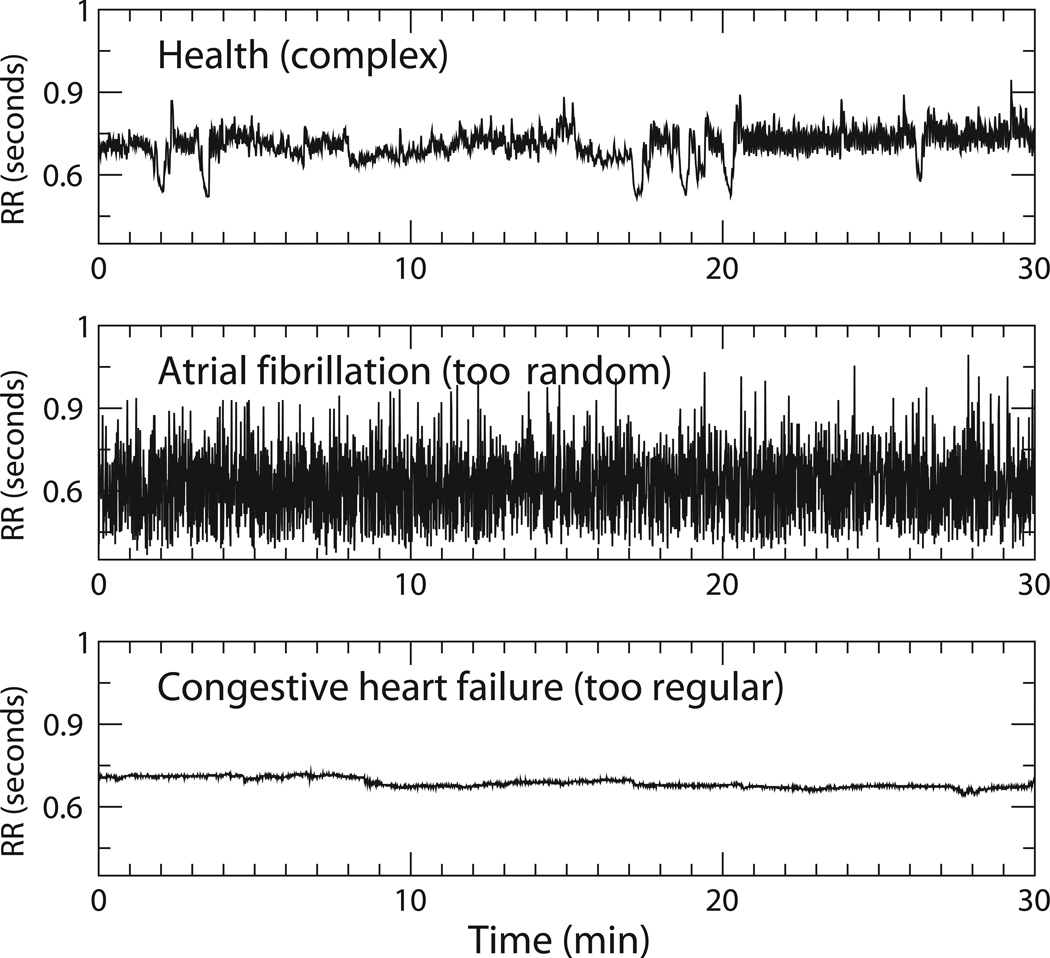
Physiological signals can exhibit different fractal patterns at different time scales, and disease can have different effects at each of these scales. Healthy heart rate is regular at scales <10 beats, but exhibits complex fractal fluctuations at scales between 10 beats and ~3 hours. Congestive heart failure has different effects on the fractal patterns in heart rate at small and large time scales. Here n refers to timescale (i.e., number of heart beats), and F(n) is the fluctuation function. (Taken with permission from Peng et al. 1995a.)

(2) Physiological fractals are manifestations of multiscale interactions

Simulations have shown that fractal fluctuations in heart rate and activity are highly unlikely to be generated by simply adding multiple influences at different time scales (Ashkenazy et al., 2001; Hausdorff & Peng, 1996; Ivanov et al., 2009). Thus, it is probably a general misunderstanding to believe that complex physiological fluctuations are always caused by the superposition of numerous intrinsic and external inputs, or that fractal fluctuations can be modeled by simply summing established pathways.

Nonlinear relationships between oscillatory components at different frequencies are what differentiate complex physiological time series from spectrally generated time series having the same fractal scaling exponents. Multiple techniques are available for assessing such relationships between scales. Nonlinear relationships between the phases of oscillations at different frequencies can manifest in the correlation properties of the magnitude and sign series derived from the increments of the time series. The magnitude series indicates the size of changes in time series values from one time step to another, while the sign series indicates the directions of these changes. These magnitude series lack correlation structures in spectrally generated noise, but they exhibit strong correlation structures in physiological time series. For example, for interbeat interval time series, the magnitude series is correlated, while the sign series is anticorrelated (Ashkenazy et al., 2001; Ivanov et al., 2009). Thus, a large change in interbeat intervals induces a bias towards large changes that lasts for hours, with decrements and increments alternating far into the future, hinting at underlying nonlinear interactions between scales.

More direct measures of cross-frequency coupling have emerged in neuroscience. For example, nested oscillations – oscillations at a high frequency which occur preferentially during certain phases of a lower frequency oscillation – may be an indication of dynamics on a slow scale influencing dynamics on a fast scale. Such cross-frequency coupling is both common and functionally significant in EEG data (Axmacher et al, 2010; Canolty & Knight, 2010; Darvas et al, 2009; He et al., 2010; Jensen & Colgin, 2007; Sauseng et al, 2008; Scheffzuk et al, 2011; Tort et al, 2008), and has also been found in geological and financial time series (He et al., 2010; Rennert & Wallace, 2009), but has yet to be assessed in physiological time series.

(3) Fractals reflect intrinsic physiological dynamics, not simply environmental influences

The fractal fluctuations present in physiological systems persist even in the absence of external stimuli. For instance, the fractal properties of heartbeat fluctuations in healthy adults remain unchanged when subjects’ physical activity and postural changes are kept to a minimum (Ivanov, 2006; Nunes Amaral et al., 2001). Similarly, fractal activity fluctuations are virtually identical from one healthy subject to another, and are unaffected either by the changes in mean behavioral activity level that occur on different days of the week, or by laboratory experiments in which behavior is highly restricted and controlled (Hu et al., 2004a).

Fractal patterns do, however, change with physiological states, such as sleep (Bunde et al, 2000; Ivanov et al, 1999b; Kantelhardt et al, 2002) and exercise (Karasik et al, 2002). For example, heart rate becomes increasingly regular (exhibiting higher DFA exponents) with deeper stages of non-REM sleep (Bunde et al., 2000), and also becomes more correlated at long time scales with exercise (Karasik et al., 2002). It has been suggested that the increased long-range correlations during sleep reflect the influence of the higher cortical regions on the autonomic nervous system (Bunde et al., 2000), but this hypothesis has yet to be tested.

One way to understand the selective stability of fractal patterns is to see fractals in physiology as a signature of the default dynamics of a physiological system. In contrast to the homeostatic view of physiology, which emphasizes what aspects of physiology are constant over time, the dynamical, fractal view of physiology puts an emphasis on how the physiological system changes over time, seeing the pattern of changes as an indication of the underlying mechanisms – the pushes and pulls – that constitute the physiological system. Fractal fluctuations are thus “the sound of the engine” of a healthy person. When the physiological system “switches gears” dramatically – entering an entirely different control regime such as sleep or exercise – we can expect the pattern of fluctuations to change as well, as a different linkage of neurophysiological systems is put into play.

It is widely believed the rumble of the human engine represented by fractal fluctuations does not correspond to a single gear, but rather a characteristic pattern of “gear shifts”. The gears in question are often referred to as modes or dynamical regimes. Each mode has its own patterns of change and characteristic timescale. Fractal fluctuations may be the signature of a system in which a number of modes maintain a loose allegiance, with particular modes or mixtures of modes transiently dominating the dynamics of the system. From this perspective, the multiscale interactions present in physiological fractals may be a manifestation of the competition between modes (Ivanov et al, 1998; Karasik et al., 2002), or of the characteristic timing of jumps between modes (Allegrini et al, 2009; Allegrini et al, 2010). New methods for teasing apart the multiple dynamical modes present in physiological time series may help clarify this picture.

This perspective also links fractal fluctuations to an important signature of biological systems: namely, their ability to switch quickly between very different behaviors. The mature brain, for example, shifts effortlessly between – and sometimes manages simultaneously – different sensory modalities, tasks at different levels of cognitive difficulty, and planning and action. This switching between multiple capabilities doesn’t require large changes in system configuration or parameters, as would be the case for example if neuromodulatory or hormonal signals were required to move from the planning to the execution of motor sequences. Rather, these multiple operating regimes coexist stably within one configuration. This coexistence of multiple behaviors or modes is known as multistability.

(4) When good fractals go bad

Just as some fractals are more complex than others, and perhaps for the same reason, not all fractal patterns are equally “healthy”. Numerous studies show that alterations of fractal patterns and loss of complexity in physiological fluctuations are associated with aging, pathological conditions and disease (Goldberger et al, 2002). For instance, fractal correlations in gait are degraded (exhibiting lower DFA exponents) with aging and in Huntington’s disease (Hausdorff et al, 1996; Hausdorff et al, 1997), in a way related linearly to the severity of impairment; inter-breath interval time series become closer to white noise in elderly men (Peng et al., 2002); reduced fractal correlations of heartbeat intervals occur with cardiovascular diseases (Goldberger et al., 2002; Huikuri & Makikallio, 2001; Ivanov et al, 1999a; Peng et al, 1995a) and are associated with reduced survival (Huikuri et al., 2000; Makikallio et al., 2004; Perkiomaki et al, 2001; Stein et al, 2005); and fractal fluctuations in behavioral activity are progressively diminished with aging and more disturbed in patients with Alzheimer's disease (Hu et al, 2009a). Similarly, there are indications that the complexity of a physiological system reflects its ability to cope with challenges: the baseline complexity of postural control dynamics in both healthy and impaired elderly adults is correlated with the amount of postural sway observed during a dual-tasking challenge condition (Manor et al, 2010).

There are two types of alterations or breakdown of fractal regulation: fluctuations either become too random (exhibiting DFA exponents closer to 0.5) or become too regular (either exhibiting DFA exponents closer to 1.5 or losing their fractal character; Figure 5). Too much randomness reduces the system’s ability to orchestrate its subsystems appropriately in response to external stimuli, while too much regularity restricts the functional responsiveness of the system, making it vulnerable to catastrophic events. Both may occur in physiological dysfunction. Gait becomes more random with aging and in Huntington’s disease (Hausdorff et al., 1996; Hausdorff et al., 1997), and the time series of peak expiratory flow is more random in asthmatics than controls (Frey et al, 2005). Regularity can occur in two ways. As large scale fluctuations begin to dominate, if these large-scale fluctuations are periodic, then the behavior of the system becomes dominated by a single frequency, and the power spectrum of the signal loses its power law form. This can be seen in the heart rate of patients with obstructive sleep apnea. On the other hand, if the large-scale fluctuations are not periodic, the signal begins to exhibit a DFA exponent close to 1.5, becoming similar to Brownian noise. An example occurs in congestive heart failure, where the DFA exponent of beat-to-beat intervals at scales from 100 beats (about a minute and a half) to 10,000 beats (~3 hours) averages 1.24, as compared to 0.9 in controls (Peng et al., 1995b). A similar increase in the heart beat scaling exponent at large scales (11 to 8,000 beats) was found in healthy middle-aged and elderly adults (Pikkujamsa et al, 1999), suggesting that the physiological changes leading to heart failure may be similar to age-related regulatory changes.

Figure 5.

The breakdown of fractal fluctuations can result in increased regularity or increased randomness.

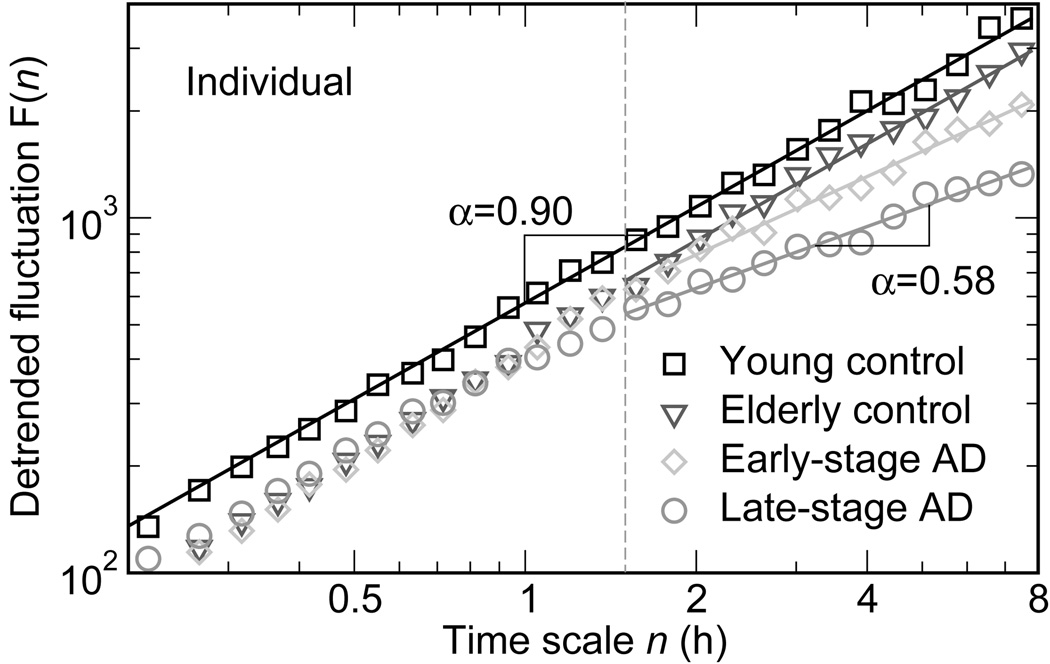
Aging and disease may have different influences on fractal scaling over different ranges of time scales, resulting in the appearance of crossovers absent in healthy young individuals. For example, in elderly subjects and those with Alzheimer’s, the fractal pattern in behavioral activity breaks down into two scaling regimes – one for scales less than ~1.5 hours, and another at scales from ~1.5 hours to 8 hours. The large scale regime exhibits exponents smaller than 0.9, and behavioral activity fluctuations are significantly more random than in healthy young adults (Figure 6). Similarly, multiple changes in the fractal scaling of heart beat fluctuations are observed in congestive heart failure. As discussed above, the heart rate of patients with severe heart failure is more regular than that of controls at scales from 20 beats to around 3 hours. However, it is more random than that of controls at scales smaller than 20 beats, exhibiting scaling exponents closer to 0.5 (Figure 4); (Peng et al., 1995b).

Figure 6.

Age and AD induce crossovers in fractal activity fluctuations at ~90 minutes. (Taken with permission from Hu et al. 2009.)

A universal mechanism behind the appearance of crossovers in physiological fractals, if there is one, has yet to be elucidated. Experiments have shown that the fractality of small-scale fluctuations in heart rate is altered by changing the sympathovagal balance (Tulppo et al, 2005). These experiments are in accord with a statistical model, called stochastic feedback, proposed to account for the crossover observed in the scaling of healthy heart rate, and its alteration with congestive heart failure and during exercise (Ivanov et al., 1998; Karasik et al., 2002). In this model, the fractal fluctuations in heart rate result from the competing influences of the sinoatrial node and the sympathetic and parasympathetic branches of the autonomic nervous system, and the changes observed during heart failure and exercise are the result of the dominance of one of these physiological components. Intuitively, the stochastic feedback model agrees with the interpretation of fractal fluctuations as resulting from the competition between dynamical modes operating at different scales. However, it is physiologically simplistic, not yet well understood mathematically, and cannot account for crossovers appearing in heart rate under other conditions, or crossovers in behavioral activity fluctuations. Addressing these issues will require significant further work.

A different approach to explaining the presence of crossovers in fractal time series lies in a general model composed of a network of units which can be switched on or off (Amaral et al, 2004). Each unit is coupled to its neighbors, and also to a number of units further away. The state of each unit depends on its past states and the states of its coupled units, according to simple rules which can be interpreted as approximating “integrate-and-fire” neurons (Amaral et al., 2004). These rules are implemented with a certain amount of noisiness. When the number of non-nearest-neighbor couplings and the noisiness of the units are tuned to appropriate levels, the time series of the sum of their states exhibits fractal fluctuations. In a paper on this model, Diaz-Guilera and colleagues observed in the caption of a figure that as the number of distant units to which each unit is coupled increases, not only does the scaling change from Brownian to white, but crossovers appear (Diaz-Guilera et al, 2007). This tantalizing relationship between network connectivity and crossovers bears further investigation, but at present all that can be said in general is that the appearance of crossovers in aging and disease hints at an imbalance in the multiscale network of mechanisms giving rise to fractal fluctuations, and a possible decoupling of control mechanisms at different scales.

(5) Change is integral to healthy physiological function

Unaffected by external conditions, but altered in sleep, pathological conditions, and aging, fractal fluctuations are not a reflection of extrinsic environmental influences. Rather, they reflect important dynamical properties of the neurophysiological systems that produce them. The intrinsic nature of fractal patterns in physiology, and their importance to healthy physiological function, challenge the traditional theory of homeostasis (Cannon, 1929). They suggest that rather than acting solely to minimize or reduce change, physiological regulatory mechanisms actually incorporate some level of variability and fluctuation into their healthy function.

In addition to changing our picture of health, the presence of fractals in physiology also suggests a change in our understanding of disease (West, 2010). The changes in fractal fluctuations that occur with disease reflect changes in the dynamics of the underlying regulatory mechanisms. The loss or reduction of fractal fluctuations indicates a physiological control system which is less complex, less adaptive to perturbations, and more vulnerable to catastrophic events. The fact that these changes may precede changes in average measures indicates that these dynamical changes are more important to the definition of disease states than average measures.

Sleep, aging, and disease have in common diminished system integrity – a decline in communication and coordination between different physiological mechanisms (Bashan et al, 2012). It has been hypothesized that fractal patterns in physiological fluctuations are a measure of system integrity and adaptability (Chiesa et al., 2010; Hu et al., 2004b; Hu et al., 2008; Peng et al., 1995b), and that interactions between the various components of the autonomic nervous system (Ivanov et al., 1998; Karasik et al., 2002) and higher cortical regions (Bunde et al., 2000) are important for their production. However, meaningful and detailed neurophysiological models of the mechanisms producing fractal patterns are still lacking, and the underlying neural substrates of fractal physiological regulation are largely unknown (see more discussion in Section 5.3).

IV. MODELS OF FRACTAL FLUCTUATIONS

There are many theoretical models capable of producing fractal fluctuations, ranging from simple to complex, and each has its own implications for the physiological significance of fractality. The pressing question in fractal physiology is to find theories with biological and empirical relevance. Among the phenomena that any theoretical account of fractal physiological fluctuations must explain are the selective stability of fractal fluctuations – the fact that these fluctuations change with physiological states but not external stimuli – their alteration and the appearance of crossovers with disease and aging, and their complex fine-scale structure. Finally, any model of fractal fluctuations must make contact with the known structural and functional realities of physiological systems.

Explaining the widespread presence of complex fractal fluctuations in physical systems has been one of the most pressing open problems in physics. The search for universal principles has led to a well-studied class of physical systems exhibiting complex fractal patterns in both time and space, so-called critical systems (Stanley, 71). Criticality occurs in a system composed of a large number of coupled units when the system undergoes a phase transition, changing, for instance, from a stable state with random behavior, in which the units act completely independently, to another stable state with ordered behavior, in which the units exhibit fully correlated behavior. Examples of phase transitions are the change from liquid water to ice, and from an iron bar to a magnet.

At the exact point of transition, the so-called critical point, the system achieves a balance between randomness and order. Water can be brought to the critical point by tuning its pressure and temperature precisely, obtaining a mixture of liquid water and ice crystals. A magnet is critical when held at the critical or Curie temperature, the temperature above which it loses its magnetization. Fractality emerges only at the critical point, with the appearance of strongly correlated clusters of units, of sizes ranging from small to large to the system size, having a highly organized fractal structure. Figure 7 shows the emergence of multiscale, fractal structures in the spin dispositions of a model of magnetization at the critical temperature. These fractal structures are a manifestation of the long-range interactions that emerge at the critical point, when local interactions are strong enough to link the states of distant units, but before a global ordering renders those interactions insignificant (Stanley et al, 2000). The activity of these systems is organized into a scale-free network of functional coalitions (Turalska et al, 2012) and may exhibit fractal fluctuations (Matsumoto, Saito & Ohmine, 2002). Overall, the system at the critical point exhibits a high degree of heterogeneity – with structure and function varying from one location to another – as well as self-similarity, and functional and structural relationships on all scales. Balanced as it is between randomness and order, the state of the system at the critical point can change dramatically as a result of even small shifts in the controlling parameters, for instance temperature. These properties emerge from the collective behavior of a population of interacting units, and cannot be predicted from those units’ individual properties.

Figure 7.

Snapshots of the spin states (black or white) of the two-dimensional Ising model of magnetization below, at, and above the critical temperature T_c At subcritical temperatures, all spins are aligned, and magnetization is high. At supercritical temperatures, spins are random, and magnetization is zero. Only at critical temperatures do fractal correlated structures arise. (Taken with permission from Chialvo 2010.)

The appeal of criticality to provide a unifying theoretical framework for the observation of fractal fluctuations in biological and human systems is undeniable, especially in social and neural systems, where the relevance of theories describing the collective behavior of large numbers of similar, interacting units is plain. As such systems are not easily cast into the framework of statistical physics, a number of alternative “routes to criticality” have been proposed. One notion is that criticality might emerge in a system with many degrees of freedom that is perched on the edge of chaos, just before the parameters describing the system plunge it into turbulent, irregular, and unpredictable dynamics (Gisiger, 2001). Another is that criticality might emerge spontaneously in a system that is dominated by internal interactions, and slowly driven by its environment (Bak, Tang & Wiesenfeld, 1987; Dickman et al, 2000; Turcotte, 1999; Turcotte, 2001). Such a system evolves to the edge of stability as its energy is continually built up by interactions with the environment and then released unpredictably, at all timescales and in all quantities.

Regardless of how they are instantiated, it has been suggested that the properties of critical systems – existence on the edge of stability, large-scale correlations or long memory, and responses at all scales – might serve an adaptive role in biological systems (Chialvo, 2010). This hypothesis has been paid special attention to in neuroscience, where it has a long history (Hopfield, 82). Models incorporating various degrees of neurophysiological realism have been shown to exhibit various features of criticality (Rubinov et al, 2011), and models in which features of criticality are incorporated or arise have been shown to be biologically adaptive in various ways. For example, model networks of sensory neurons have been shown to exhibit maximum dynamic range when the interactions between neurons have been tuned to a critical level, so that the interactions are strong enough for small stimuli to elicit measurable responses, yet weak enough to avoid explosive, self-sustaining responses to large stimuli (Kinouchi & Copelli, 2006). A model of learning based on negative feedback illustrates how a system poised on the edge of stability, in which one behavioral response is just barely preferred over another in a given context, allows for rapid switching between behaviors to meet the demands of a changing environment and for easy recall of behaviors that were adaptive in the past (Bak & Chialvo, 2001; Chialvo & Bak, 1999). It has been suggested that the global instability of criticality may allow neurophysiological systems to reshape themselves dramatically and rapidly, entering different dynamical states with slight changes in neurophysiological parameters – for example, concentrations of neuromodulators (Chialvo, 2010). The long memory of critical systems may provide the mechanism by which similar stimuli elicit very different responses from a neurophysiological system at different times. Dynamic range and long memory together might allow critical neurophysiological systems to persist through disturbances which are large in magnitude but small in significance, while responding dramatically to small but significant details – a property which hints at multistability. Thus many simulations and models suggest that criticality may play an important role in neurophysiological systems. At the very least, parameters describing the connectivity or interaction strength between components in a system must be tuned precisely, by one mechanism or another, in order for the system to both produce power laws and function optimally with regard to a number of performance measures.

However, all that is known for sure is that the fractal fluctuations in physiological systems arise from nonlinear interactions between physiological processes at multiple timescales. It is unknown whether these multiscale interactions reflect the coordination of a handful of dissimilar processes, each operating at their own characteristic scale, or, as the theory of criticality suggests, whether they arise from the coordinated behavior of large numbers of similar units, as they come together to produce functionally coherent ensembles operating on all time and space scales.

While alternatives to criticality, emphasizing built-in functional and structural heterogeneity across scales, rather than self-similarity, have been proposed in the systems biology community (Carlson & Doyle, 1999; Carlson & Doyle, 2000), the boundary between these two perspectives is rapidly eroding. Researchers are investigating the effects of heterogeneity in systems of interacting units (Laing et al, 2012; Pikovsky & Rosenblum, 2008; Pikovsky & Rosenblum, 2011; Rajendran & Kevrekidis, 2011), as well as how multiple networks of similar units might interact with each other (Brummitt, D'Souza & Leicht, 2012; Buldryev et al, 2010). Indeed, such investigations have already shed light on the physiological importance of pink noise, by showing that the optimal information transfer between two networks occurs when both operate at a critical regime and produce pink noise outputs (Aquino et al, 2011; Turalska et al., 2009). Such models might be particularly important for physiology, insofar as individual organs are often composed of many identical or similar interacting units (e.g., the heart and the brain) and exhibit self-similar structures (the lungs and the brain again), while the physiological system as a whole is made up of multiple distinct and diverse organs which exchange information and material with each other (Bashan et al., 2012). In the same way, biological organization at different levels – such as cells, organs, organisms, and ecosystems – may exhibit features of criticality, while interactions across levels may be characterized by some other mechanisms.

What is clear is that fractal dynamics pose a major challenge to contemporary efforts aimed at developing realistic models of physiological control. Mathematical and statistical concepts, such as infinitely autoregressive processes, fractional Brownian motion, and the fractional calculus (West, 2010), can replicate the kinds of fractal signals found in physiology (Anteneodo & Chialvo, 2009; Torre & Wagenmakers, 2009), but there is as yet no mapping between these concepts and the known structure and function of physiological systems. No precedent exists in physiology to account for dynamics with multi-scale complexity. Traditional models focus on one physiological process operating at a particular time scale, and cannot explain control processes operating at multiple time scales. To account for fractal control in physiology, new systems-based approaches are needed to obtain holistic views of the component systems and their interactions. Ideas from complexity theory – which led to the discovery of fractal patterns in physiology (Peng et al., 1993) – and network theory (Newman, 2003) will probably be useful in understanding the mechanisms behind, and the meaning of, these patterns. We believe that extending existing network models to make them more specifically relevant to fractal physiological regulation will be an important direction for future theoretical research.

V. THE ROLE OF THE CIRCADIAN SYSTEM

Based on a variety of empirical and theoretical results (see Sections 2, 3, and 4), it has been hypothesized that fractal physiological fluctuations reflect the integrative function of a complex network of regulatory processes interacting nonlinearly across a range of temporal and spatial scales (Ashkenazy et al, 2002; Ivanov et al., 1998). This control network can be contrasted with homeostatic mechanisms of control operating at specific scales. West has proposed that the process giving rise to fractal fluctuations be termed allometric control (West, 2010). For conceptual simplicity, we will refer to a control network responsible for fractal fluctuations as a fractal control network or fractal regulatory network, without insisting that its components or its organization exhibit fractal properties themselves. The crucial first step in building a meaningful physiological model of the network responsible for fractal regulation is to identify the control nodes of that network. In this section, we will review recent findings that provide insights into the involvement of the circadian system in the fractal control network.

(1) The mammalian circadian system

The circadian system generates and coordinates circadian rhythms in a wide range of neurophysiologic functions in synchrony with sleep/wake cycles (Reppert & Weaver, 2002; Schwartz, 2002), an example of optimizing physiology and behavior to the anticipated environmental alterations that occur across each day and night. The endogenous control of these circadian rhythms involves a complex network of coupled central neural nodes that interact with peripheral organs and systems through numerous neural and humoral feedback loops (Sakamoto et al, 1998; Yamazaki et al, 2000). The mammalian circadian pacemaker is located in the suprachiasmatic nucleus (SCN), containing tens of thousands of neurons that can act as cell-autonomous oscillators (Welsh et al, 1995). In animal studies, lesioning the SCN results in a cessation of circadian rhythmicity in core physiological variables such as heart rate, body temperature and motor activity (Moore & Eichler, 72; Scheer et al, 2005; Scheer et al, 2001; Stephan & Zucker, 72). SCN-lesioned mice receiving SCN transplants from conspecifics having an altered circadian period (of 20 rather than 24 hours) exhibit circadian rhythmicity in behavioral activity with the period of the donor, proving the SCN’s role as a circadian pacemaker (Ralph et al, 1990).

Recent studies have shown that cells in peripheral organs such as heart and liver have their own circadian clockwork (Balsalobre, Damiola & Schibler, 1998; Damiola et al, 2000; Hara et al, 2001; Yamazaki et al., 2000; Yoo et al, 2004). These peripheral circadian clocks can operate independently of the oscillators in the SCN and generate oscillations of ~24 h in the function of the peripheral organs. Nevertheless, the SCN is still the master clock that in healthy individuals synchronizes all peripheral clocks. Such synchronization is clearly important for optimally integrated function of the body because disruption of the synchronization, as occurs for example in humans during shift work, is associated with an increased incidence of cardiovascular diseases (Kawachi et al, 1995; Knutsson et al, 1986; Tuchsen, Hannerz & Burr, 2006), gastrointestinal complaints (Caruso, Lusk & Gillespie, 2004; Vener, Szabo & Moore, 1989), sleep disorders (Schwartz & Roth, 2006), and increased risk for obesity (Karlsson, Knutsson & Lindahl, 2001) and diabetes (Kroenke et al, 2007).

(2) A circadian rhythm in fractal cardiac dynamics

Hints of the possible link between the circadian system and fractal regulation can be traced back to early studies that show a difference in fractal cardiac dynamics between the biological day and the biological night (Ivanov et al., 1999b; Otsuka, Cornelissen & Halberg, 1997; Yum et al, 1999). Heartbeat fluctuations in healthy adults were found to be less regular during the night time than during the day time (showing a change in DFA exponent of ≈ 0.2; Ivanov et al., 1999b). The same study also reported a similar difference between the day and night time in subjects with severe heart disease and between sleep and wake periods in cosmonauts during orbital flight (Ivanov et al., 1999b). Though the authors attributed the alterations in fractal patterns to differences between sleep and wake, circadian influences may also have contributed to these alterations, because the sleep-wake and circadian cycles are normally synchronized.

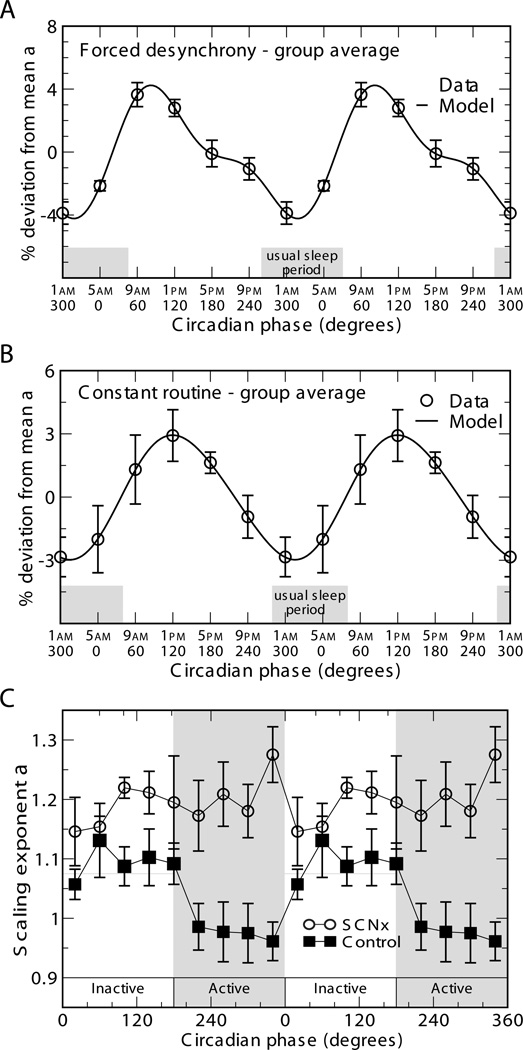
To separate endogenous circadian influences from the influences of the behavioral (sleep-wake) cycle, our group previously investigated fractal cardiac dynamics in humans using a forced desynchrony (FD) protocol (Hu et al., 2004b). In this protocol, the sleep-wake cycle was adjusted to recurring 28 hour “days” during which subjects were kept in dim light conditions, allowing their circadian pacemakers to “run free” at the inherent period of ~24.2 hours, and thus dissociating the imposed sleep-wake cycle from the intrinsic circadian cycle. Under these conditions, we found an endogenous circadian rhythm in fractal heartbeat fluctuations at short time scales (between ~4 and ~60 minutes) with a sharp peak in the DFA exponent at the circadian phase corresponding to ~10AM (Figure 8), top panel). This finding provided the first indication that the circadian system is involved in fractal cardiac dynamics.

Figure 8.

Circadian influences on the fractal scaling of heart rate. A–B. Results from complementary protocols in humans: (A) a 10-day forced desynchrony protocol in which subjects’ sleep-wake cycles were adjusted to 28 hours (~340 hours of data from 9 subjects); (B) a constant routine protocol in which subjects remained awake for a prolonged period of 38 hours (~600 hours of data from 6 subjects). C. Results from intact (black squares) and SCN-lesioned (red circles) rats in constant dark conditions. Core body temperature was used to determine circadian period. Circadian phase zero was assigned to the time of minimal core body temperature in humans, and to the onset of the light period in the preceding light-dark protocol in rats. The average circadian period of the control rats was used for assignment of extrapolated circadian phase bins in SCN-lesioned rats. Humans and intact rats showed significant circadian rhythms in the scaling exponent characterizing fractal cardiac control. There was no significant rhythm for SCN-lesioned rats (p>0.2). (Taken with permission from Hu et al., 2004b, Hu et al., 2008, and Ivanov, 2006.)

The circadian rhythm of fractal cardiac dynamics in humans at these small scales was later confirmed using a complementary experimental protocol, the constant routine (CR), in which subjects remained awake in dim light, maintaining constant posture and consuming equispaced isocaloric snacks, for a prolonged period of 38 hours (Figure 8), middle panel; Ivanov, 2006). Rhythms in fractal scaling of heart rate were also found in rats during constant dark conditions, suggesting that there may be a common mechanistic link between the circadian clock and fractal cardiac control mechanism in mammals (Hu et al., 2008). Moreover, lesioning the SCN in rats completely abolished the circadian rhythm (Figure 8), bottom panel), demonstrating that the circadian pacemaker is crucial for the circadian rhythm in fractal cardiac control.

These findings are also important from the perspective of cardiovascular pathology. The degree of circadian change in the DFA exponent (a peak increase of 5% from the average value) is reminiscent of the increase in this exponent seen in pathological conditions such as congestive heart failure. Furthermore, the time of the peak in the DFA exponent coincides with the morning peak in occurrences of cardiovascular events (Muller et al, 1985; Willich et al, 1987). Thus, the circadian rhythm in fractal heart rate scaling provides indirect evidence for an endogenous circadian influence on daily patterns of cardiovascular risk. It is important to determine whether the circadian rhythm of fractal cardiac control persists with aging and under pathological conditions such as congestive heart failure. These results will provide further useful information about the relevance of circadian control to the peak in cardiac risk during the morning (Muller et al., 1985).

While these results provide strong and consistent evidence that the circadian pacemaker generates an endogenous ~24 hour rhythm in fractal cardiac control, there are also intriguing differences to be observed. For instance, note that the circadian rhythm in the fractal scaling of heartbeat fluctuations in these two species (diurnal vs. nocturnal) has the same phase relative to their common circadian rhythms in SCN neural activity or melatonin secretion (Buijs et al, 2006; Meijer, Rusak & Ganshirt, 1992; Scheer, Kalsbeek & Buijs, 2003), while having the opposite phase relative to their activity-inactivity cycles, which are themselves in phase opposition between (diurnal) humans and (nocturnal) rats. Also, the circadian profile of the heartbeat scaling exponent is slightly different between the FD and CR protocols. The peak of the exponent was at a circadian phase between 60°–90° (corresponding to circadian time 9–11AM) during the forced desynchrony (FD) protocol and at ~120° (circadian time ~1PM) during the constant routine (CR) protocol; and the circadian rhythm in the CR is close to a simple sinusoidal waveform while a better description of the rhythm in the FD requires additional harmonics. These differences may be caused by individual variations in the circadian influence on fractal cardiac control (9 subjects participated in the CR, while only 6 participated in the FD), or by differences in the two protocols themselves. There is accumulating evidence that the circadian and behavioral influences on physiological functions may be not simply additive (Scheer et al, 2009) and that endogenous circadian rhythms are not necessarily unchangeable (Scheer et al, 2007; Wehr, 1991). Thus, it is possible that the desynchronization introduced in the FD and the sleep deprivation introduced in the CR could have modulated the circadian rhythmicity of physiological functions, including fractal cardiac control. How circadian influences on physiological functions change under different environmental conditions is an area of considerable research activity in circadian biology, and the interactions between such changes and fractal regulation is an important topic for further study.

(3) The central circadian pacemaker is a major node in the fractal control network

It is well known that the circadian system generates and coordinates rhythms of ~24 hours in numerous physiological functions (see Section 6.1). From this point of view, the circadian rhythm in fractal scaling of cardiac output at time scales smaller than ~60 minutes might not be very surprising. Neither does it have much direct impact on the mechanistic understanding of the fractal control network, because fractal regulation at these time scales persists even without the central circadian pacemaker, indicating that the SCN is not essential for fractal regulation at these scales (Hu et al., 2008).

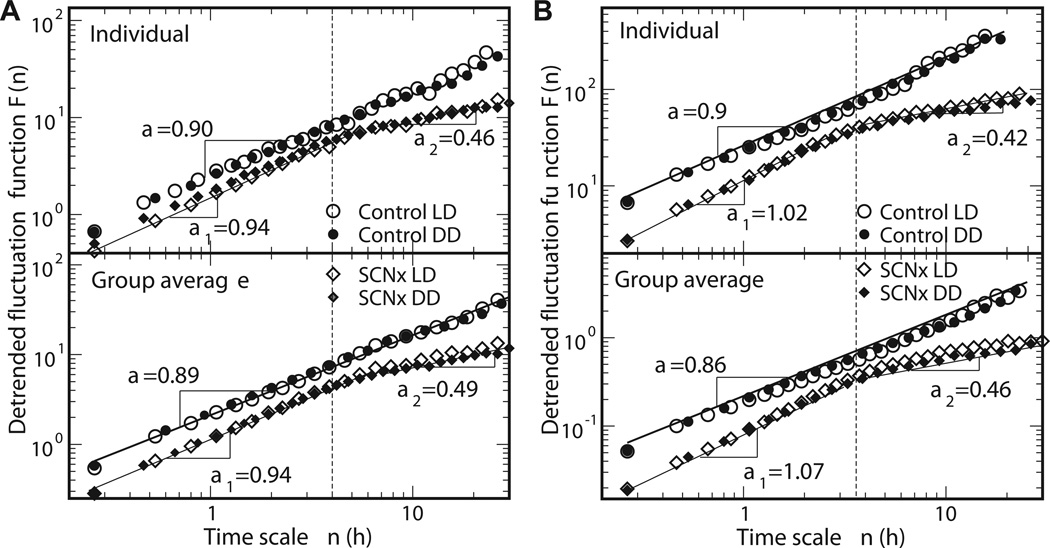
More surprising are recent studies exploring fractal patterns in activity and heart rate at longer time scales. In rats, we found that lesioning the SCN led to the disappearance of fractality in motor activity fluctuations at time scales between ~4 and 24 hours (Hu et al., 2007a). Specifically, activity fluctuations at large time scales resembled white noise after the SCN lesion (showing DFA exponents of ~0.5, Figure 9). In other words, SCN ablation introduced a crossover in the scaling behavior, indicating a decoupling of the control of activity over short and long time scales. Similar effects of SCN lesions were also observed in heart rate fluctuations in rats (Hu et al., 2008). These findings provided the first evidence that the SCN is a major node in the network of fractal regulation, playing an essential role in generating fractal heart rate and behavioral activity patterns at large time scales. For researchers in circadian biology, these findings are surprising, suggesting the SCN has regulatory functions at multiple time scales, and not only at the circadian time scale of ~24 hours. These findings pose a challenge to current statistical models of fractal fluctuations and crossovers in heart rate, which do not yet incorporate the SCN or account for crossovers around 4 hours (Ivanov et al., 1998).

Figure 9.

Lesioning the SCN in rats induces crossovers in fractal scaling of behavioral activity (left) and heart rate (right) at ~4 hours. Above this crossover, fractal control disappears, and DFA exponents approach those of white noise. Below this crossover, behavioral activity becomes slightly more regular.

Additionally, lesioning the SCN affected fractal regulation at time scales less than ~4 hours, introducing more regularity in activity and heart rate fluctuations, as indicated by slight but significant increases in the respective DFA exponents (a change of 0.17 for heart rate and 0.09 for behavioral activity). Thus, the SCN lesion also perturbs the fractal control network responsible for fractal regulation at small scales. It remains to be seen whether this altered fractal regulation has any adverse consequences for health.

Possible evidence for a similar role of the SCN in humans comes from our recent study showing that fractal activity regulation at large time scales (between ~2 hours and ~8 hours) was reduced (DFA exponent closer to 0.5) in elderly subjects, and further reduced in elderly subjects with Alzheimer’s disease (AD, Figure 6; Hu et al, 2009a). The alteration resembles the change observed in SCN-lesioned animals, and both aging and AD are accompanied by SCN dysfunction, suggesting that the SCN may play the same role in fractal regulation in both humans and rats. Of course, AD is accompanied by decreased neuronal function at many sites. Determining the extent to which AD-associated alterations in fractal activity patterns specifically reflect dysfunction or neuroanatomical change in the SCN will require further study. Furthermore, long-term treatment of AD with bright light and melatonin was recently shown to help restore disrupted circadian control (Riemersma-van der Lek RF et al, 2008), possibly by restoring SCN function. Thus, it would be interesting to test whether light and melatonin can also improve fractal regulation in AD patients.

(4) The SCN carries out multiple independent roles, and does not act alone

A related question is whether the role of the SCN in fractal control can be dissociated from its role as a circadian pacemaker. Evidence that the two functions are independent comes from a recent study (Chiesa et al., 2010) in which constant bright light was used to render rats arrhythmic – that is, to eliminate circadian rhythms in their activity. This light condition did not abolish fractal patterns in their activity. Instead animals showed stronger fractal correlations in motor activity fluctuations over the time scales from ~4 hours to 24 hours. More interestingly, Chiesa et al. reported that the condition of constant darkness led to a decrease in fractal correlations, bringing motor activity fluctuations towards white noise (more random). Since arrhythmicity induced by constant bright light is associated with the desynchronization of SCN oscillators (Ohta, Yamazaki & McMahon, 2005), Chiesa et al. hypothesized that the increase in long memory under bright light conditions reflects the increased predictability of individual SCN oscillators in this uncoupled condition. The authors also drew the conclusion that the presence of fractal regulation does not require circadian rhythmicity. This is consistent with our previous finding in humans that fractal activity patterns remained unchanged while the circadian rhythm of mean activity level was abolished during a constant routine protocol (Ivanov et al, 2007).

If the circadian rhythmicity of activity and heart-rate can indeed be dissociated from their fractal control, it may shed some light on the puzzling ability of the SCN to generate and coordinate ~24 hour rhythms while simultaneously contributing to fractal regulation at a wide range of shorter time scales. Specifically, the SCN is responsible not only for synchronizing circadian rhythmicity in a variety of physiological systems, but also for adjusting that circadian rhythmicity to maintain optimal functionality in the face of constantly changing environmental conditions. For instance, even a single 1–2h exposure to light at a specific time can lead to a significant phase shift of the human circadian clock (Canton et al, 2009; St Hilaire et al, 2012); scheduled food availability and intake in animals can accelerate the re-entrainment of the circadian clock with shifted light-dark cycles (Angeles-Castellanos et al, 2011); and the neural connectivity of the SCN can re-organize when the period of the light-dark cycle, or the duration of light exposure, is altered (de la Iglesia et al, 2004; Gorman, Yellon & Lee, 2001; Naito et al, 2008; Yan, Silver & Gorman, 2010). In a healthy circadian network, these dynamic responses and changes should persist even when external conditions abolish or desynchronize circadian rhythms in neurophysiological functions. It may be the integrity of these circadian dynamics, rather than merely the circadian system’s current state of synchrony or desynchrony, that underlies the contribution of the SCN to fractal activity regulation.

Another important question is what the relationship is—if any—between the SCN’s roles in the fractal regulation of activity and that of heart rate. A recent study addressed this issue by investigating circadian rhythmicity in the fractal scaling of heart rate and activity, in the context of forced-desynchrony and constant-routine protocols (Ivanov, 2006). In both protocols, fractal scaling of activity exhibited significant 12-hour rhythmicity, but not circadian rhythmicity. Contrasting this result with the (~24-hour) circadian rhythmicity in heart rate scaling, the authors suggested that the fractal regulation of activity and heart rate are not coupled in a simple way.

Precisely how the SCN generates fractal fluctuations in activity and heart rate at long time scales, and modulates fractal fluctuations at short time scales, is unknown. To investigate whether the neuronal network within the SCN generates fractal patterns, or whether feedback interactions between the SCN and other control nodes are required for fractal regulation, we recently performed fluctuation analyses of the multi-unit neural activity (MUA) of the in vitro and in vivo SCN in mice and rats (unpublished observations). MUA was measured from the SCN using tripolar stainless steel electrodes, and the number of action potentials crossing a preset threshold (~5SV) was counted by a computer in 10 second bins. In vivo SCN-neural activity exhibited fractal patterns similar to motor activity at time scales from minutes up to 10 hours. The DFA scaling exponent α characterizing the fractal pattern of in vivo MUA was virtually identical in mice and rats, and remained the same during light-dark cycles (LD, 12h:12h) and during constant darkness (DD): α =1.04±0.03 (SE) for mice in LD; 1.04±0.01 for rats in LD; 1.04±0.03 for mice in DD; 1.11±0.04 for rats in DD. In vitro, however, the MUA of the SCN does not exhibit power-law fluctuations at all, indicating a complete lack of fractality. Instead, in vitro SCN activity shows fluctuations that grow super-exponentially at large scales and decay superexponentially at small scales. These results indicate that it is not the activity of the SCN in isolation, but the activity of the SCN in concert with other physiological mechanisms that leads to fractal fluctuations in physiological output.

VI. SUMMARY AND OUTLOOK

The studies that we have reviewed show that the SCN is a crucial control node in the network responsible for fractal physiological control of heart rate and behavioral activity. The SCN is critical for fractal fluctuations in behavioral activity and heart rate at long time scales, and modulates fluctuations in these variables at short time scales. The SCN does not produce these patterns on its own, but rather through interactions with an unknown network of physiological regulatory agents. It appears that the SCN’s role in fractal regulation is independent from its role as a circadian pacemaker, and that its influences on fluctuations in behavioral activity and heart rate are likewise independent.

These facts challenge our current understanding of the SCN, but they also provide an opportunity to translate knowledge from circadian biology into fractal physiology. They provide a first step towards a fully mechanistic understanding of fractal patterns in physiology, and represent the beginning of the journey to identify the circuitry and ultimately build meaningful network models of fractal physiological regulation. Below, we outline important questions to be addressed, hopefully helping to establish a roadmap for future study in the new interdisciplinary field of fractal physiology.

(1) Methodological Challenges

As we have tried to demonstrate, the careful quantification of fractal patterns in physiological systems – including the use of robust analyses such as DFA, the specification of the specific scales over which fractal patterns appear, and alertness to the presence of crossovers and their significance – are crucial to continued investigations into fractal physiology. In addition, given the variety of mathematical models of fractal fluctuations, from the fractional calculus (West, 2010) to stochastic feedback (Ivanov et al., 1998; Karasik et al., 2002) to network models (Amaral et al., 2004), we echo the call of He et al. for the use of other data analysis techniques to further characterize and discriminate between the fractal fluctuations associated with different systems. Data analysis techniques which simply give a measure of the fractality, complexity, or nonlinearity of a time series may be inadequate for this purpose. Instead, methods which illuminate the fine temporal structures and multiscale interactions underlying fractal fluctuations – such as cross-frequency coupling analyses (Onslow, Bogacz & Jones, 2011; Ozkurt & Schnitzler, 2011; Tort et al, 2010) – those which explore the transitions between dynamical modes and the nature of those modes – such as analyses of rapid transition processes (Allegrini et al., 2009; Allegrini et al., 2010) or modeling with switching linear dynamical systems (Nemati et al., 2012) – and those providing insight into the flow of information between fractal processes in different systems and at different scales – such as transfer entropy (Schreiber, 2000) and related measures – will prove particularly useful.

(2) Physiological Challenges at Multiple Scales

Our findings raise many questions about the SCN itself, which has until now been understood mainly as a circadian pacemaker. How does the SCN mediate fractal control at ultradian scales? Can we treat the SCN as a single node in the fractal control network, or is it more appropriately viewed as a collection of multiple subcomponents (Butler & Silver, 2009)? The neurons of the SCN exhibit autonomous rhythmicity at a variety of frequencies and phases, and with different temporal profiles. There is evidence that the nucleus can be divided into finer subpopulations than the traditional weakly oscillatory, light-receiving core and oscillatory shell (Butler & Silver, 2009; Foley et al, 2011; Morin et al, 2006). SCN neurons interact both locally (through gap junctions and electrical synapses; Long et al, 2005) and globally (e.g., through the release of VIP). While most models of the circadian system focus on how this distributed network of oscillators produces coherent circadian rhythmicity, there is growing interest in this network’s role in generating rhythms at other time scales (Bonnefont, 2010; Brown et al, 2008). Given that the SCN does not produce fractal fluctuations in isolation, does it communicate with other control nodes through neuronal or humoral mechanisms? Transplant studies could shed light on this question. How does the SCN couple small and large scale fractal regulation of behavioral activity, and how does it uncouple its roles as a circadian pacemaker and a generator of fractal control? Further studies of fractal regulation under conditions known to induce desynchrony amongst circadian oscillators are necessary to answer these questions.

We have identified only a single node (the SCN) in the network responsible for the fractal control of heart rate and behavioral activity. It is still unknown which of the many neuronal sites and pathways interacting with the SCN might cooperate in the fractal regulatory network. There are a variety of candidates for the other control nodes (Abrahamson & Moore, 2001). Given the suggestion by multiple investigators that higher cortical activity may play a role in the fractal fluctuations seen in heart rate, and the fact that higher cortical activity (as measured in a number of different ways) has been shown to exhibit fractal patterns, it may be worth investigating possible couplings between the fractal patterns observed in cortical and physiological variables. For circadian researchers, a particularly intriguing question regards the role that peripheral oscillators in other body tissues play in fractal control. How do alterations to other potential nodes, including peripheral oscillators, affect fractal regulation? The systems that control short-scale regulation of behavioral activity and heart-rate are not well understood, and physiological conditions that alter short-term scaling should be sought.

While it is known that multiple physiological variables are under fractal control, it is also clear that there are different levels of complexity in fractal control. For example, the fractal control of heart rate is more complex than that of gait (Ivanov et al., 2009), and there are indications that fractal heart rate regulation is independent of fractal respiratory control (West et al, 2005). Is fractal control monolithic, or – as seems likely – are different fractal control networks responsible for different processes, different levels of complexity, and different scale ranges? The SCN is important to fractal control in at least two different physiological modalities – heart rate and behavioral activity. How does the SCN function distinctly in these two different processes? What kinds of coordination, if any, exist between the two processes?

Most broadly, we can ask about the extent of fractal control in physiology. What other physiological variables exhibit complex fractal patterns? It is known that fractal control occurs to some degree in the cardiovascular, respiratory, and motor systems. Does fractal control operate in the metabolic, endocrine, sensory, or affective systems? Are there fractal fluctuations in body temperature, glucose tolerance, vigilance, inter-saccade intervals, mood, or neuroendocrine secretion? Do the fractal patterns in other physiological fluctuations exhibit circadian rhythmicity? Does fractal control extend to infradian scales?

(3) Theoretical Challenges

As discussed in Section 4, fractal control in physiology poses many theoretical challenges. The principles underlying fractal control will be systems-level and network-based. Physiological investigations of fractal control must proceed alongside physiologically-relevant theoretical investigations. What kinds of networks of oscillators – or other physiologically relevant functional units – are capable of producing fractal fluctuations? Fractal physiological regulation might be modeled through the coupling of a handful of distinct control mechanisms, as the collective behavior of a large system of similar units, or as some hybrid of the two. What kinds of physiologically realistic network models are capable of producing crossovers, and what roles do coupling and competition between dynamical modes play in their appearance? How do other signatures of complexity – including magnitude and sign correlations, nested frequencies, and the presence of “crucial events” and switching dynamics – constrain these models?

The discovery that the circadian system is involved in the fractal regulation of activity and heart rate also opens the door to using existing mathematical and computational models of the SCN (Antle et al, 2003; Antle et al, 2007; Bernard et al, 2007; Indic et al, 2006; Indic et al, 2007; Kunz & Achermann, 2003; Wang & Doyle, III, 2011) as a springboard to the development of computational and mathematical models of fractal physiology. The burgeoning literature on heterogeneous coupled oscillator networks also provides an important stepping stone. But new techniques and perspectives will surely be required if the focus of these investigations is to transition from oscillatory synchrony to the broader perspective of scaling behavior and multiscale interactions. These investigations may be guided by work on the theoretical basis of fractal patterns in cortical networks, which have a long history.

(4) Clinical Significance

We believe fractal fluctuations have the potential to be more than just tools for diagnosis and prognosis. Already, the perspective of fractal physiology has led to a rethinking of the principles of mechanical ventilation (Mutch et al, 2000). By illuminating new aspects of physiological function in health and disease, a deeper and more complete understanding of fractal phenomena can provide new targets for behavioral, pharmacological, and surgical interventions. By harnessing the power of ideas from physics and nonlinear dynamics, and applying them to the physiological domain, we hope for a greater understanding of human health, and concomitantly greater power to do good for those in the grip of disease.

VII. CONCLUSIONS

(1) Fractal physiological fluctuations reflect the integrative function of a complex network of regulatory processes interacting nonlinearly across a range of temporal and spatial scales. This control network can be contrasted with homeostatic mechanisms of control operating at specific scales. The crucial first step in building a meaningful physiological model of the network responsible for fractal regulation is to identify the control nodes of that network.

(2) The SCN is a major node in the fractal control network. It is critical for fractal fluctuations in behavioral activity and heart rate at long time scales, and modulates fluctuations in these variables at short time scales. The SCN does not produce these patterns on its own, but rather through interactions with an unknown network of physiological regulatory agents. It appears that the SCN’s role in fractal regulation is independent from its role as a circadian pacemaker, and that its influences on fluctuations in behavioral activity and heart rate are likewise independent.

(3) The translation of theoretical and empirical knowledge from circadian biology to fractal physiology, the continuing empirical identification of nodes in fractal physiological regulatory networks, the use of data analysis methods to further characterize the fractal fluctuations present in physiological systems, and the development of physiologically relevant mathematical models reproducing these empirical observations provide a multifaceted approach to the development of a mechanistic, physiological understanding of fractal fluctuations. Employing this strategy will allow fractal physiological fluctuations to serve as important model phenomena for the study of fractal fluctuations in other neurophysiological and biological systems.