Rare Genetic Variants and Treatment Response: Sample Size and Analysis Issues

Abstract

Incorporating information about common genetic variants may help improve the design and analysis of clinical trials. For example, if genes impact response to treatment, one can pre-genotype potential participants to screen out genetically determined non-responders and substantially reduce the sample size and duration of a trial. Genetic associations with response to treatment are generally much larger than those observed for development of common diseases, as highlighted here by findings from genome-wide association studies. With the development and decreasing cost of next generation sequencing, more extensive genetic information—including rare variants—is becoming available on individuals treated with drugs and other therapies. We can use this information to evaluate whether rare variants impact treatment response. The sparseness of rare variants, however, raises issues of how the resulting data should be best analyzed. As shown here, simply evaluating the association between each rare variant and treatment response one-at-a-time will require enormous sample sizes. Combining the rare variants together can substantially reduce the required sample sizes, but require a number of assumptions about the similarity among the rare variants’ effects on treatment response. We have developed an empirical approach for aggregating and analyzing rare variants that limit such assumptions and work well under a range of scenarios. Such analyses provide a valuable opportunity to more fully decipher the genomic basis of response to treatment.

1. Introduction

An individual’s response to treatment in clinical trials may in part depend on their genetic sequence. For example, when testing a novel drug some people may be more or less likely to respond—or have toxicity issues—based on whether they carry particular variants in genes that code for drug metabolizing enzymes [1]. One can also incorporate into a trial an individual’s genetic susceptibility to the outcome of interest [2]. Integrating such genetic information into the design of trials can reduce their size and duration [2]. Moreover, incorporating genetic information into the analysis of clinical trial data can help clarify the treatment’s effectiveness [3].

The genetic information available on individuals in ongoing or previous clinical trials is rapidly expanding with the development of low-cost, high-throughput genotyping and sequencing technologies [4–8]. Genome-wide association studies (GWAS) have successfully detected associations between thousands of common single nucleotide polymorphisms (SNPs) and various traits, including treatment response [4]. The value of GWAS results is a topic of much debate. Some argue that while any given GWAS SNP may have a very modest association, combining known and future findings together will help explain a substantial proportion of trait heritability [4]. Others suggest that studying rare variants will help much more heritability [9–11].

The recent rapid growth in sequencing technology allows for detecting such rare genetic variants across the human genome [12]. Leveraging this technology, focused sequencing studies, the 1,000 Genomes Project (1KGP), and higher density SNP chips are making studies of rare variants increasingly feasible [6, 13]. These studies will undoubtedly help explain more heritability of traits—including the genetic basis underlying response to treatment.

We focus here on how genetic information may impact treatment response and how to best analyze such data, especially for rare variants. We first show that the treatment response GWAS have substantially larger effect sizes than conventional GWAS of common traits. This suggests that rare genetic variants may have even stronger effects on treatment response. As we highlight second, however, even with large effects conventional one-at-a-time analyses of rare variants require very large sample sizes that may be infeasible for clinical trials. This issue can in part be addressed by aggregating together rare variants for analysis. We provide an overview of such approaches, distinguishing between those that aggregate based on a priori hypothesis versus those that use empirical evidence for combining rare variants. The former should work well if the hypotheses are relevant to the mechanism underlying treatment response; otherwise one should consider empirically determining the optimal aggregation scheme for rare variants.

2. Comparison of GWAS: Treatment Response versus other Traits

The NIH catalog of published GWAS gives details on 14 studies that had binary disease traits listed as ‘Response to …’, ‘Adverse response to…’, or ‘Drug induced liver injury…’ [14]. From these studies, 18 SNPs were associated with treatment response (p-values ≤ 10⁻⁶). Table 1 provides specific details from these studies. Interestingly, the GWAS of treatment response have detected relatively large effects [15]. In particular, the 14 GWAS of treatment response reported a median odds ratio = 2.70 (interquartile range = 2.01 to 4.35) (Table 1).

Table 1.

Results from genome-wide association studies of treatment and adverse responses. Details for common genetic variants with association p-values ≤ 10⁻⁶. From NIH catalog of GWAS; included here if trait was ‘Response to…’, ‘Adverse response to…’, or Drug-induced liver injury’ [14]

Trait	Locus			Sample Size	Association			Citation PMID
	Region	Gene	Variant (SNP rs#)		Odds Ratio	95% CI	P-value
Response to cerivastatin	1q43	RYR2	rs2819742	917	2.08	[1.59–2.78]	2×10−7	21386754
Response to treatment for acute lymphoblastic leukemia	2q33.1	Intergenic	rs1569175	487	2.73	[1.52–4.93]	9×10−7	19176441
Response to treatment for acute lymphoblastic leukemia	4q31.21	Intergenic	rs17007695	487	2.67	[1.53–4.68]	9×10−7	19176441
Drug-induced liver injury (amoxicillin-clavulanate)	6p21.32	HLA	rs9274407	733	3.10	[2.30–4.20]	5×10−14	21570397
Drug-induced liver injury (amoxicillin-clavulanate)	6p21.33	HLA-A	rs2523822	733	2.30	[1.80–2.90]	2×10−10	21570397
Adverse response to carbamapezine	6p21.33	HLA-A	HLA-A*3101	996	9.50	[5.6–16.3]	1×10−16	21149285
Drug-induced liver injury (flucloxacillin)	6p21.33	HCP5	rs2395029	340	45.0	[19.4–105]	9×10−33	19483685
Adverse response to carbamapezine	6p22.1	HLA	rs1061235	4,389	9.12	[4.03–20.7]	1×10−7	21428769
Response to citalopram treatment	7q36.3	Intergenic	rs6966038	1,491	1.64	[1.35–1.99]	5×10−7	19846067
Response to treatment for acute lymphoblastic leukemia	10p12.33	ST8SIA6	rs359312	487	3.91	[1.52–10.1]	9×10−8	19176441
Response to metformin	11q22.3	ATM	rs11212617	3,920	1.35	[1.22–1.49]	3×10−9	21186350
Response to statin therapy	12p12.1	SLCO1B1	rs4149056	20,031	4.50	[2.60–7.70]	2×10−9	18650507
Response to platinum-based chemotherapy in non- small-cell lung cancer	12q23.3	CMKLR1	rs1878022	914	1.33	[1.19–1.48]	5×10−7	21483023
Adverse response to aromatase inhibitors	14q32.13	Intergenic	rs7158782	878	2.13	[1.58–2.87]	8×10−7	20876420
Response to hepatitis C treatment	19q13.2	Intergenic	rs8099917	2,383	3.00	[2.40–3.80]	1×10−20	21228123
Response to hepatitis C treatment	19q13.2	Intergenic	rs8099917	848	1.98	[1.57–2.52]	9×10−9	19749758
Response to hepatitis C treatment	19q13.2	Intergenic 23	rs8099917	326	27.1	[14.6–50.3]	3×10−32	19749757
Response to citalopram treatment	20q13.31	Intergenic	rs6127921	1,491	1.75	[1.39–2.17]	1×10−6	19846067

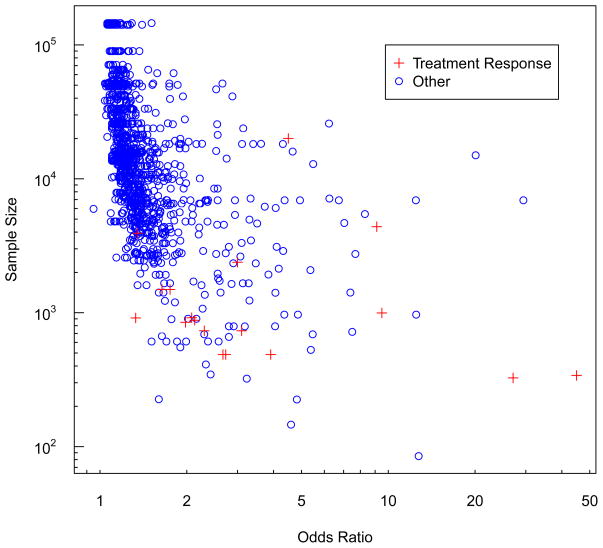
In contrast, GWAS of common diseases have generally only detected very modest single-SNP associations [16]. From the NIH catalog (accessed 6/11/11), non-treatment GWAS report a total of 1,173 SNPs as being associated with binary outcomes (p-values ≤ 10⁻⁶, not checked for independence) [14]. These SNPs have a median odds ratio of only 1.26 (interquartile range = 1.16 to 1.46). This striking difference in effect sizes is highlighted in Figure 1, which plots the odds ratios by sample size for the 1,192 (= 18 + 1,173) GWAS SNPs. The odds ratios from the treatment response GWAS are statistically significantly larger than those observed for the other GWAS (P-value = 2.2 × 10⁻⁹, non-parametric rank sum test).

Figure 1.

Odds ratios and sample sizes for genetic variants association with binary traits from genome-wide association studies (P≤10⁻⁶). Red crosses are results from studies of treatment response (details given in Table 1). Blue circles are the 1,173 findings from all other binary traits reported in the NIH catalog of GWAS [14].

From Figure 1 we can also see that the studies of treatment response have substantially smaller sample sizes than the other GWAS. The median total sample size for GWAS of treatment response = 916 (interquartile range = 762 to 2,160) whereas for other common binary phenotypes the median sample size = 14,175 (interquartile range = 6,693 to 33,355) (discovery and replication phases combined, not checked for independence). As with the odds ratios, these striking differences in sample size are highly statistically significant (P-value = 2 × 10⁻¹⁰). The smaller sample sizes for treatment response GWAS may reflect limitations in the number of subjects that can be recruited into such studies. These reduced sample sizes and the limited number of studies may in part explain the larger odds ratios. That is, the treatment response studies may suffer from the ‘winners curse’ and overestimate the true associations [17–19].

Another possibility is that these larger associations could reflect differences in the biology underlying treatment response compared to other common variation. Genetic variants that impact treatment response may have little effect on ill-health outcomes; moreover, since humans have only recently been exposed to most drugs and treatments, genes impacting their efficacy or toxicity may not have experienced much selective pressure [15]. Even if there is limited selection, one might surmise that rare variants also play a role in treatment response. In light of the large odds ratios from GWAS of common variants, we might also expect rare variants to have relatively large effects on treatment response. However, undertaking studies of rare variants raises a number of challenges, some of which we consider below.

3. Rare Variants: Analysis Approaches and Power

3.1 One-at-a-time Analysis

As noted above, one of the key issues in studying rare variants is reduced power due to sparse data. This is highlighted with the following example. Assume that we undertake a study to assess whether genetic variants impact the response to a particular treatment. For example, that we have sequenced a group of individual’s exomes to see if certain genetic variants affect response. At each genetic variant we can model this potential relation as

$$\mathit{logit}Pr(\mathit{response}\mid x)=\alpha +{\beta }_{x}x$$ (1)

where treatment response is a binary (yes/no) outcome, and x is the genetic variant. For simplicity’s sake we assume that the x is coded to reflect the number of minor alleles at a particular base-pair location in the human genome. That is, x = 0 if the corresponding genotype is homozygous wildtype, x = 1 if heterozygous, x = 2 if homozygous variant. Note that in general the ‘variant’ is assumed to be the less common allele (i.e., with the smaller minor allele frequency).

A conventional analysis—and what is generally undertaken for GWAS—fits model (1) for each variant to test its association with the outcome. The estimated logistic regression coefficient β_x gives the logs odds ratio for the association between that variant and response. As is well known, our ability to detect such associations will be driven by the magnitude of the odds ratios, the genetic variant’s minor allele frequency (MAF), and the number of variant’s tested. We have shown that increasing the number of common variants tested to hundreds of thousands has a relatively limited impact on the sample size required to detect association [20]. In particular, for a given MAF the sample size increases only linearly as the number of variants increases logarithmically [3, 20].

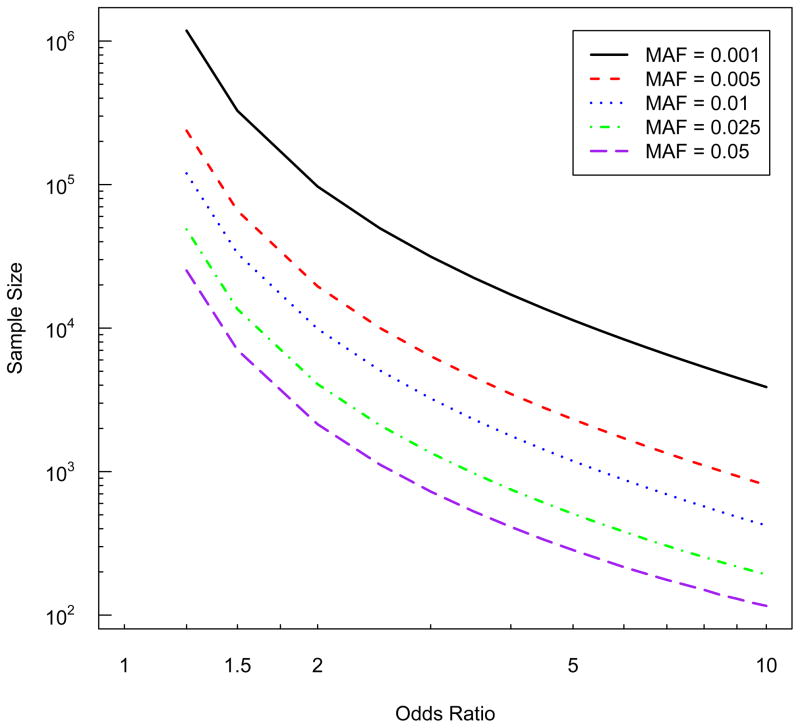
However, as the variants’ MAF decreases into the ‘less common’ or ‘rare’ range, the required sample size quickly becomes quite large unless the associations are strong. Figure 1 highlights this increase with power calculations for testing the log odds ratio β_x for treatment response when evaluating genetic variants that are less common (i.e., MAF = 0.01 to 0.05) or rare (i.e., MAF < 0.01). For less common genetic variants, the number of subjects required is large by not untenable, especially if the odds ratios are not too small. For example, when the MAF=0.025 and the odds ratio for treatment response = 3.0, 1,352 subjects are required to maintain 80% power for detecting association at an α-level = 10⁻⁶ (Figure 1). The number of subjects required for sufficient power rapidly increases with decreasing MAF. When a genetic variant with MAF = 0.01 triples the treatment response, 3,236 subjects are required for 80% power. If the causal variant’s MAF = 0.001, an enormous 31,510 individuals total are required to detect an OR=3.0.

There are situations in which one can collect enough subjects to individually analyze each rare variant. For example, Nejentsev et al. [21] studied almost 18,000 subjects to detect an association between a rare variant (MAF ~0.005) and Type I Diabetes. This approach, however, may not work for studies of treatment response since the number of potential study subjects may be limited, prompting some to argue that rare variants not even be considered in studies of treatment response [Cardon]. In general, due to sparse data, single SNP analyses may be uninformative due to low power and result in unstable estimates of rare variant effects on treatment.

3.2 A Priori Aggregation of Rare Variants

Instead of testing each rare variant independently, they can be collapsed into a single variable for analysis. For example, we can calculate a new genetic variable, x′ that is a weighted combination of the original rare variants. Assume that our exome sequencing detected m rare variants in a given candidate gene. Then we can write x′ as

$$x^{\prime }={\sum }_{i=1}^m{w}_i{x}_i$$ (2)

where w_i is a weight that defines how to combine the rare variants. Determining w_i is a crucial aspect of aggregation-based rare variant techniques and can reflect a priori or empirical weighting approaches.

The weights can be defined a priori in a number of different ways. The most basic approach assumes that w_i = 1 for some set of m rare variants (e.g., all exonic variants within a particular gene that have a MAF < 0.01). With this weighting, the j^th element of x′ is the total number of rare variants observed for individual j. In other words, this approach assumes that having an additional rare variant in any of the m possibilities has an identical impact on treatment response.

One can simplify this weighting further by coding x′_j to reflect whether any of the m rare variants are observed for individual j. That is,

$${x_j}^{\prime }=\{\begin{array}{cc}0,& {\sum }_{i=1}^m{x}_{ij}=0\\ 1,& {\sum }_{i=1}^m{x}_{ij}\ge 1\end{array}$$

In other words, regardless of whether an individual has one or more rare variants—including being homozygous for a variant—the genetic effect is assumed equivalent to having a single variant. Of course, since the variants are rare it is unlikely that many individuals will have multiple copies. Contrasting case-control differences for rare variants aggregated in this manner has been termed the Cohort Allelic Sums Test (CAST) [22].

This aggregation approach can be refined further by restricting which rare variants are given a weight w_i = 1 to those having particular properties. One might use other MAF cutoffs besides < 0.01; for example, first combine together variants with 0.005 < MAF < 0.01, and then those with MAF < 0.005. The w_i can also be set to values that reflect their potential impact on treatment response. For example, we could set w_i =1 if aggregating rare variants that result in non-synonymous amino acid changes and/or are putatively functional [22, 23]. We can even use a non-scalar value for w_i here, such as the probability that a particular variant leads to a deleterious mutation from functional prediction algorithms such as Polyphen [24, 25] or SIFT [26]. Another possibility is to set the w_i to positive or negative values depending on the corresponding variant’s known mechanisms (i.e., whether the variant is expected to improve or worsen treatment response). A combination of these weights can be assigned to rare variants by simply multiplying them together.

The major benefit of weighted aggregation of rare variants is that the new ‘combined’ variable x′ will have a larger MAF than any single variant, and in turn higher power. This is easily seen in Figure 2 as an increasing MAF requires fewer samples to detect the same association. For example, if we combine 10 rare variants that each have MAF = 0.005, x′ will have a MAF=0.05 (this assume w_i = 1 and that the variants are observed in unique individuals). Then the sample size required to detect an odds ratio for treatment response due to x′ is almost one tenth what it would have been for any of the individual variants (Figure 2). Note that this reduction is a best-case scenario because it assumes that all 10 rare variants are causal for treatment response. If instead only a subset of the 10 were causal, collapsing them together will result in substantially less reduction in the required sample size.

Figure 2.

Sample size required to detect associations between less common and rare variants and a binary outcome (e.g., treatment response). All results are for power =0.80 and alpha-level = 10⁻⁶, assuming the population risk of the outcome = 0.0001.

This point about collapsing together causal and non-causal variants highlights a key issue with aggregation approaches: they can make fairly strong assumptions about the exchangeability of the genetic variant’s effects (e.g., on treatment response). For example, if a set of rare variants are combined using w_i = 1, this assumes that they all have identical impacts on the outcome. For most traits it remains unclear whether a given set of rare variants will have similar effects on disease, both with regard to their magnitude of and direction (i.e., making treatment response better or worse). Even with very specific weighting schemes, the broad range of possible groupings emphasizes the numerous assumptions required when aggregating rare variants.

3.3 Empirical Aggregation

Instead of a priori defining the set of m rare variants to aggregate and their weights, the observed data can help guide empirical groupings and weights. Higher weights can be assigned to variants seen very rarely in those who do not have the outcome of interest (e.g., non-responders to a treatment, or controls in a case-control study). For example, for a given rare variant one can calculate the standard deviation of the number of variants observed among controls, and then let w_i equal the inverse of this value [27]. The data can also be used to determine the optimal MAF cutpoint at which rare variants should be combined together [28]. Here one cycles through different potential MAF thresholds to determine that which provides the optimal grouping of rare variants [28, 29].

The issue of directionality can be addressed empirically by letting the w_i take positive or negative values reflecting differing potential effects of the variant on outcome. If a variant is more common among responders, w_i could be left positive; but if more common among non-responders one could make the corresponding w_i negative [29]. Similarly, if the regression coefficient for the genetic or gene-treatment effect from (1) is positive the allele coding would remain the same, but if the coefficient was negative the coding could be reversed so the ensuing regression coefficient was positive (i.e., so all effects were in the same direction) [30].

We have recently developed a comprehensive empirical approach that searches across multiple possible groupings of rare variants, and selects the optimal set based on statistical criteria [29]. For example, when determining which variants to aggregate, one can consider external information about the potential functionality of variants, all possible minor allele frequency cutoffs, and different directionality of effects [29]. Instead of evaluating all possible combinations—which may be computationally infeasible—this work proposes a “step-up” approach that adds variants to an overall set if it improves the aggregated association signal, and uses permutation procedures to determine the resulting test statistic’s correct value [29]. This approach is akin to variable selection, albeit building the most parsimonious set of rare variants for grouping together. Ultimately, the ‘step-up’ approach considers multiple possible weights for each variant in a recursive manner—initially setting the w_i = 0, which excludes the ith variant—and selects the “best” set and their weights based on statistical criteria.

In comparison with a number of other weighted aggregation approaches, we found that the agnostic ‘step-up’ approach exhibited the best, or almost the best performance across a range of simulation scenarios [29]. This reflects the following observations, which highlight the sensitivity of results to a priori assumptions about weighting rare variants. First, if there are protective and deleterious rare variants, ignoring this directionality in the analysis gives poor results. Furthermore, in this situation, weighting based on the number of variants observed among one outcome group does not perform well; if all variants are deleterious, however, this approach does work well [27]. Third, using a single MAF cutoff to decide which rare variants to aggregate did not exhibit good properties—unless of course it truly reflected the disease model; instead testing all possible MAFs worked reasonably well, as did incorporating information from protein coding function algorithms [29]. In general, unless one knows with high certainty which rare variants should be aggregated, the ‘agnostic’ empirical approaches such as step-up may be best.

There have also been other empirical approaches for combining rare variants that do not fit directly clearly within the weighted framework presented here, such as tests that test the distribution of variants in cases versus control. For example, the C-alpha approach tests for differences in the proportions of rare variants in cases and controls (deviations from a random split) [31]. Another approach that might be useful when there are interactions amongst the rare variants is the kernel-based adaptive cluster (KBAC) method that uses an adaptive weighting procedure to compare the distributions of multi-site genotype counts between cases and controls [32].

3.4 Combining Common and Rare Variants

Since response to treatment is most likely due to both rare and common variants one might consider simultaneously analyzing variants across the entire spectrum of MAFs. For example, we can extend equation (1) to also include terms for common variants, as proposed in the Combined Multivariate and Collapsing (CMC) approach [33]. Here, the rare variants could be aggregated using any of the above approaches (e.g., using ‘step-up’), followed by selecting common variants for inclusion using a technique such as the lasso [34]. One can also incorporate penalties on the grouping of variants by gene or pathway [35].

In a similar fashion, one can use a Bayesian framework and place priors on the rare variant effects, which may work well in sparse data situations [36]. There are also other multi-marker approaches that have been developed to combine common and rare variants (which can of course work for just rare variants). The multivariate distance matrix regression (MDMR) approach uses genetic similarity scores [37] for small genomic regions [38]. There are also flexible non-parametric kernel-based methods, which also recommend using similarity scores and allow for interactions [39, 40]. For example, the sequence kernel association test (SKAT) is a regression approach that tests for association between common and rare variants within a particular genomic region; this approach performs well for both binary and continuous phenotypes, and is computationally efficient whereby it can be scaled genome-wide in a straightforward manner [40].

Finally, we can statistically determine what subset m of variants should even be considered for aggregation. We previously developed an algorithm that defines ‘mutational spectra’ within which one might consider aggregating rare and common variants [41]. This approach uses recursive segmentation and nested likelihood ratio tests to partition chromosomal regions into those containing ‘clusters’ of variants with similar properties (e.g., MAFs, case-control differences, disrupting the same functionally important region of a gene). In an application to colorectal tumors, we found that this approach worked well in identifying clusters of variants corresponding to biologically important regions of p53 [41]. Such clustering can be used across numerous different genes or chromosomal regions to distinguish variants for potential aggregation. Once defined, one could simply combine these, or apply the above a priori or empirical approaches to determine the final set of collapsed variants.

The rapidly increasing number of rare variant approaches are compared in [42] Scenarios when the different approaches worked best are exactly as one might expect based on the assumptions underlying these approaches. For example, if there are few rare variants in a region of interest and they all have the same direction of association, then simply aggregating them together works well; in contrast, when there are numerous rare variants with differing directions of association, the sequential model selection approached such as ‘step-up’ are preferred [42].

4. Discussion

There is growing evidence that the potential response to therapy in clinical trials depends in part on genetic variants. These effects appear relatively strong based on GWAS findings to date. This may also hold for studies of rare genetic variants, which are of growing interest due to advances in our ability to sequence subjects in an efficient manner and the catalogue of rare variants being developed by the 1000 Genomes Project [43]. Studying rare variants using conventional analytic approaches, however, requires enormous sample sizes that may not be feasible in studies of treatment response. This issue is being addressed in part by the development of methods that aggregate rare variants for analysis; these range from a priori weighting schemes to empirical algorithms.

A key benefit of the empirical aggregation approaches is that they do not require strong assumptions about what variants should be grouped together. Our simulation results and findings of others suggest that these approaches work quite well for the analysis of rare variants [27–29]. The step-up approach was one of the best rare variants procedures across a range of scenarios. Of course, with empirical approaches one needs to use permutation testing since the data are used both to determine what should be aggregated and to test the association with treatment response. If there is clear external information about which rare variants should be grouped together, using a priori aggregation approaches to expressly incorporate this knowledge into the analysis should give good results. A priori aggregation can also be used on downstream prediction models when novel variants are found for treatment.

For the sake of focus we have assumed here that a limited number of rare variants are under consideration. The approaches highlighted here can be extended to larger sets of variants (e.g., genes in pathways), although they may require modification for computational feasibility when evaluating large numbers of rare variants (e.g., exome- or genome-wide) [29].

At present, one limitation for rare variant studies of treatment response is the cost of undertaking sequencing on large numbers of subjects. This is rapidly decreasing, and nowadays an entire genome can be sequenced for under $5,000 and an entire exome for a substantially smaller amount. Much less expensive genotyping can also be used for rare variant studies, leveraging information from existing genome- or exome sequencing data (e.g., the ‘exome array’). The 1,000 Genomes Project is compiling an extensive collection of less common and rare variants that are being incorporated onto genome-wide SNP arrays [6, 13]. The 1,000 Genomes Project data also allow for imputing information about less common genetic variants even if these are not directly genotyped. However, if individuals with particular outcomes (e.g., treatment response) are thought to have unique rare variants, discovering these may still require directly sequencing some individuals. In this situation one could use a multistage sequencing / genotyping hybrid design that first sequences a subset of the study population and then genotypes the observed variants on the remaining population. The percentage of subjects included in each stage will depend in part on the minimum MAF desired for the rare variants. Moreover, the best approach may entail sequencing individuals with extreme phenotypes or strong family histories. For example, here we might be interested in those people that exhibit a large response even at low treatment levels contrast with those with no response regardless of treatment level.

In summary, the strong associations observed for common genetic variants suggest that rare variants may also play an important role in treatment response. Analyzing rare variants, however, is complicated by sparse data issues that may be magnified in studies of treatment response due to limited sample sizes. A number of approaches have recently been developed to more efficiently analyze rare variants. Many of these leverage existing information about the human genome and the nature of putatively causal variants. If one does not know—or is not prepared to assume—how rare variants impact treatment response, our agnostic ‘step-up’ approach to combining rare variants exhibits good properties across a range of scenarios. Such methods provide an avenue for appropriately analyzing the increasing genomic information available to help us dissect the genetic basis of treatment response.