AERODYNAMIC SOUND OF A BODY IN ARBITRARY, DEFORMABLE MOTION, WITH APPLICATION TO PHONATION

Abstract

The method of tailored Green’s functions advocated by Doak (Proceedings of the Royal Society A254 (1960) 129 – 145.) for the solution of aeroacoustic problems is used to analyse the contribution of the mucosal wave to self-sustained modulation of air flow through the glottis during the production of voiced speech. The amplitude and phase of the aerodynamic surface force that maintains vocal fold vibration are governed by flow separation from the region of minimum cross-sectional area of the glottis, which moves back and forth along its effective length accompanying the mucosal wave peak. The correct phasing is achieved by asymmetric motion of this peak during the opening and closing phases of the glottis. Limit cycle calculations using experimental data of Berry et al. (Journal of the Acoustical Society of America 110 (2001) 2539 – 2547.) obtained using an excised canine hemilarynx indicate that the mechanism is robust enough to sustain oscillations over a wide range of voicing conditions.

1. Introduction

Philip Doak [1] was one of the first to propose the use of ‘tailored’ Green’s functions in applications of Lighthill’s [2] theory of aerodynamic sound to problems involving flow sources near solid boundaries. It is now well understood how structural elements comparable or smaller in size than the characteristic wavelength of the sound can significantly increase the efficiency of sound production, and that this gain is most usefully expressed in terms of a Green’s function that incorporates both the geometrical and mechanical properties of the structure.

Doak later advocated the adoption of the total enthalpy B as the fundamental acoustic variable, instead of Lighthill’s perturbation density (see, e.g. [3]). When this is done a principal source of aerodynamic sound is identified as the vorticity [4 – 6]. More generally, the sources are then confined to those regions where the vorticity ω ≠ 0 and ∇_s ≠ 0, where s is the entropy. In the important approximation where the source flow is effectively homentropic (an homogeneous medium with no combustion) Lighthill’s equation becomes

$$\left(\rho \frac{D}{Dt}\left(\frac{1}{c^2}\frac{D}{Dt}\right)-\nabla ·(\rho \nabla )\right)B=\text{div}(\rho \mathit{\omega }\wedge \mathbf{v}),$$ (1)

where ρ, c, v are the fluid density, sound speed and velocity (with ω = curl v), and where ρ ≡ ρ(p) can be expressed as a function of the pressure p and

$$B=\int \frac{dp}{\rho }+\frac{1}{2}{v}^2.$$ (2)

Bernoulli’s equation implies in the absence of vorticity and moving boundaries that B = constant throughout the flow; and B may therefore be assumed to vanish in the absence of sound. When the Mach number M ~ v/c is small local mean values of ρ and c differ from their uniform respective values ρ_o and c_o by terms of relative order M² ≪ 1. Equation (2) then takes the simplified form

$$\left(\frac{1}{c_o^2}\frac{{\partial }^2}{\partial t^2}-{\nabla }^2\right)B=\text{div}(\mathit{\omega }\wedge \mathbf{v}).$$ (3)

Outside the source flow the unsteady motion is entirely irrotational. It can be represented by a velocity potential ϕ(x, t) that satisfies B = −∂ϕ/∂t. In the far field the acoustic pressure p is given by

$$\frac{1}{\rho }\frac{\partial p}{\partial t}=\frac{DB}{Dt}.$$ (4)

If the mean flow is stationary at infinity p = ρ_oB, where ρ_o is the corresponding mean density.

The solutions of aeroacoustic problems in the presence of high speed moving boundaries are frequently obtained numerically by means of an appropriate extension of Kirchhoff’s surface integral representation [7], in particular high-speed fan and rotor noise can be expressed in terms of surface terms derived by Ffowcs Williams and Hawkings [8 – 10]. These solutions usually involve the free space Green’s function [6, 9, 11]. However, radiation from surfaces and sources at lower Mach numbers (M ~ 0.4 or less) are often treated more effectively in terms of the vortex sound equation (1), and it is then that the great utility of Doak’s recommended use of a tailored Green’s function becomes apparent.

Equation (1) is self-adjoint [12, 13] and Green’s function G(x, y, t, τ) is an ‘advanced potential’ that satisfies

$$\left(\rho \frac{D}{D\tau }\left(\frac{1}{c^2}\frac{D}{D\tau }\right)-\frac{\partial }{\partial y_j}\left(\rho \frac{\partial }{\partial y_j}\right)\right)G=\rho \delta (\mathbf{x}-\mathbf{y})\delta (t-\tau ),G=0\text{for}\tau >t.$$ (5)

G(x, y, t, τ) is a disturbance that propagates as an ‘incoming’ wave as a function of (y, τ) towards the singularity at y = x on the right of the equation, arriving at τ = t and vanishing thereafter. It turns out to be convenient to require that ∂G(x, y, t, τ)/∂y_n = 0 on any stationary or moving boundary S(τ) of the flow, where y_n is a local normal coordinate on S directed into the fluid. The usual application of Green’s theorem using equations (1) and (5) then yields [7, 12, 13]

$$\rho B(\mathbf{x},t)={\int }_{-\infty }^{\infty }{\oint }_{S(\tau )}\left[\rho G\frac{\partial \mathbf{v}}{\partial \tau }-\eta \frac{\partial G}{\partial \mathbf{y}}\wedge \mathit{\omega }\right]·\text{d}\mathbf{S}(\mathbf{y})\text{d}\tau -{\int }_{-\infty }^{\infty }{\int }_{V(\tau )}\rho \frac{\partial G}{\partial \mathbf{y}}·\mathit{\omega }\wedge \mathbf{v}{\text{d}}^3\mathbf{y}\text{d}\tau ,$$ (6)

where η is the shear coefficient of viscosity, V (τ) is the time dependent domain occupied by the fluid, and where Green’s function and source terms vanish respectively at τ = ±∞. In deriving this result the momentum equation has been used in the form

$$\partial \mathbf{v}/\partial t+\nabla B=-\mathit{\omega }\wedge \mathbf{v}-(\eta /\rho )\text{curl}\mathit{\omega },$$

where only the shear component of viscosity is important close to S.

This equation is applied in this paper to discuss a ‘reduced complexity’ analysis of voiced speech. This is traditionally based on Fant’s equation governing the unsteady flow of air through the glottis [14 – 16]. During voicing a steady flow from the lungs is interrupted by the periodic opening and closing of the glottis by aerodynamically driven vibrations of the vocal folds. The air emerges in a succession of ‘puffs’ of volume velocity Q(t), which determines an equivalent monopole sound source radiating into the supraglottal vocal tract and thence from the mouth to listeners in free space.

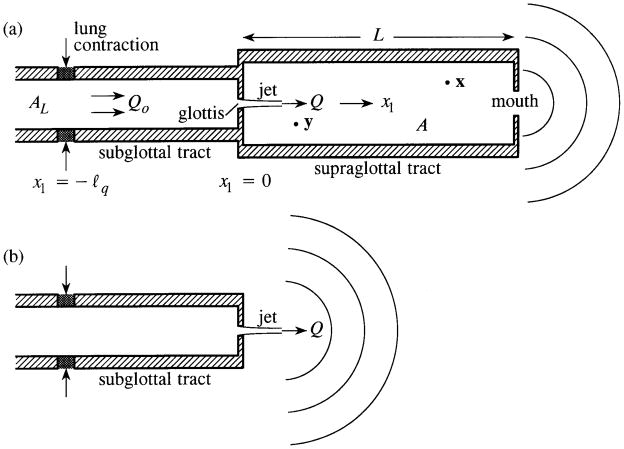
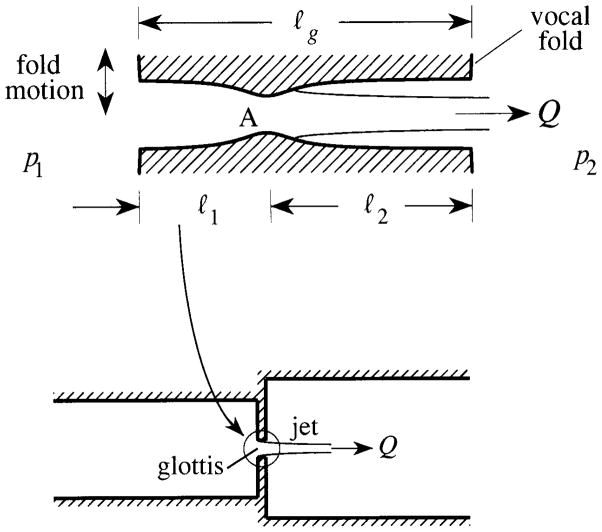
The wavelengths of voiced speech mostly exceed the vocal tract diameter, and it is usual to model the supraglottal tract by a uniform, hard walled, circular cylindrical duct of length L and cross-sectional area A in which sound propagates back and forth as plane waves, and radiates from an open ‘mouth’ (Figure 1a). The subglottal tract is also regarded here as rigid and uniform with cross-section A_L < A and terminating in the lung complex, where wave energy is absorbed without reflection, or reflected in accordance with a suitable impedance condition [17 – 21]. Similarly, the glottis is modelled by a ‘necked’ duct of v rectangular cross-section and streamwise length ${\ell }_{\text{g}}\ll \sqrt{A}$, which opens and closes at a nominal ‘free’ vocal fold frequency f_o (~ 125 Hz for an adult male) [22, 23]. This is indicated in the upper part of Figure 2, which shows the sagittal section parallel to the mean flow, where the cross-hatched upper and lower glottis walls correspond to the medial surfaces of the vocal folds. The glottis has constant span ℓ_s ≫ ℓ_g (out of the plane of the paper in the figure) and a blade-like jet is formed (according to experiment [24]) by separation a short distance downstream of the point labelled A in Figure 2, where the glottis cross-sectional area takes its minimum value A_g(t). The Strouhal number f_oℓ_g/V ~ 0.05 at typical flow speeds V ~ 10 m/s. This is small enough for it to be assumed that the glottal flow passes through a continuous sequence of quasi-static states during a cycle of oscillation.

Figure 1.

Idealized configurations of the subglottal and supraglottal sections of the vocal tract. (a) Damping of sound within the lung complex is modelled by permitting sound from the glottis to radiate without reflection into the lungs, as if the subglottal tract were semi-infinite in length; (b) ‘exposed’ glottis with the supraglottal tract removed.

Figure 2.

Simplified representation of the subglottal and supraglottal sections of the vocal tract. The upper part of the figure illustrates the idealised glottis, which is treated as a ‘necked’ rectangular duct within which flow separation occurs just downstream of the point A of narrowest cross-section.

Basic reduced order equations for A_g(t) are derived from a ‘one’ or ‘two-mass’ approximation of a vocal fold [25 – 27]. The original single mass model cannot self-excite, however, except in the absence of damping or with acoustic feedback. The two-mass approximation represents the fold as two lumped masses connected by springs and dampers which are adjusted to provide the necessary asymmetry in surface pressure force to promote self-excited oscillations. Avanzini [28] has developed a quasi-one-mass model by assuming that the displacement of the ‘upper’ mass of the conventional two-mass model is proportional to that of the lower mass after a suitable time delay. This permits the two-mass model to be described by a single equation of motion for the lower mass.

The two-mass model is effective because it provides a rudimentary approximation to the influence on the surface force of the mucosal wave. This force depends on the pressure produced by lung contraction, and its modification by flow separation from the vocal folds and jet formation in the glottis outflow. Separation depends on the position within the glottis of its cross-sectional minimum A_g, which is governed by the mucosal wave propagating over the medial surfaces of the folds [29 – 37]. The separation point is sometimes expressed in terms of a ‘flow separation coefficient’ A_s/A_g, where A_s is the cross-sectional area downstream of the minimum glottis cross section at which separation occurs. Sidlof et al. [24] concluded from measurements of a model vocal fold that this point remains close to the narrowest cross-section during most of the vibration cycle, but that it can move significantly further downstream just before and after glottal closure. Because of the asymmetry provided by separation, a knowledge of A_s/A_g constitutes an essential input to numerical models. Thus, Deverge et al. [38] assume A_s/A_g = 1.2, and values of A_s/A_g ranging from 1.08 to 1.6 are used in [28, 39 – 42].

In this paper the time-dependent position of the separation point is obtained from measurements of Berry et al. [32] of mucosal waves on an excised canine hemilarynx. These are incorporated into the single mass-spring model of the glottis illustrated in Figure 2. The experiment involved imaging of the vocal fold medial surface along a coronal cross-section of the left vocal fold. Excised fold tissue responds passively to an applied subglottal pressure rise, but it was claimed that many aspects of the intact voice are duplicated in the experiment (chest like, falsettolike, frylike vibrations) including abnormalities observed in voice disorders. Previous measurements on an hemilarynx [43] also indicate that observations over a wide range of driving pressures yield results comparable to the full larynx.

The aeroacoustic theory of voicing for this simple model is discussed in Section 2. The Berry et al. [32] data are sufficiently precise for the time-dependent position of the glottal minimum area A_g to be determined as a two-valued function of the fractional open area A_g/A_max, respectively applicable during the opening and closing phases of the glottis, where A_max is the maximum open area attained during a cycle. This is discussed in Section 3. The result is used in Section 4 to calculate the unsteady normal driving force for use in the single-spring-mass equation of motion of the vocal folds. This equation must be solved simultaneously with the Fant equation governing the glottis volume velocity Q(t). Limit cycle solutions of the equations are then investigated (Section 5), for which the moving separation point provides the necessary phase variation to overcome system damping and maintain vocal fold vibration. The influence on the glottis of the back-reaction of standing waves in the supraglottal tract is discussed in Section 5.

2. Green’s function and the Fant equation

In the vocal tract the Mach number is small and variations in the mean air density can be neglected. We can therefore set ρ = ρ_o in equation (6), so that

$$B(\mathbf{x},t)={\int }_{-\infty }^{\infty }{\oint }_{S(\tau )}\left[G\frac{\partial \mathbf{v}}{\partial \tau }-v\frac{\partial G}{\partial \mathbf{y}}\wedge \mathit{\omega }\right]·\text{d}\mathbf{S}(\mathbf{y})\text{d}\tau -{\int }_{-\infty }^{\infty }{\int }_{V(\tau )}\frac{\partial G}{\partial \mathbf{y}}·\mathit{\omega }\wedge \mathbf{v}{\text{d}}^3\mathbf{y}\text{d}\tau ,$$ (7)

where ν = η/ρ_o is the kinematic viscosity.

2.1 Green’s function

Consider the evaluation of this integral formula at x in Figure 1a, in the supraglottal v tract where $x_1>\sqrt{\mathcal{A}}$. Green’s function will be determined in the compact approximation (for characteristic wavelengths $~O(L)\gg \sqrt{\mathcal{A}}$), when only plane waves can propagate. To avoid unnecessary complications let us assume that the upper and lower tracts have the same cross-sectional area A = A_L. Use rectangular coordinates x = (x₁, x₂, x₃) with the origin at the centroid of the glottis and with x₁ directed along the axis of symmetry. Within and close to the acoustically compact glottis Green’s function reduces to a solution of Laplace’s equation, which can be written

$$G(\mathbf{x},\mathbf{y},t,\tau )=\alpha (\tau ,x_1,t)+\beta (\tau ,x_1,t)Y(\mathbf{y},\tau )$$ (8)

where α(τ, x₁, t), β(τ, x₁, t) do not depend on y and ∇²Y (y, τ) = 0. Y (y, t) can be regarded as a velocity potential of an ideal flow from y₁ < 0 to y₁ > 0 through the glottis normalised to have unit speed in the positive y₁ direction in the upper and lower tracts. In particular it is required that ∂Y/∂y_n = 0 on all surfaces, including the instantaneous surface of the glottis, and Y can be normalised such that

$$Y(\mathbf{y},\tau )~\{\begin{array}{cc}{y}_1,& y_1>\sqrt{A}\text{in}\text{the}\text{upper}\text{tract},\\ y_1-\overline{\ell },& y_1<-\sqrt{A}\text{in}\text{the}\text{lower}\text{tract},\end{array}$$ (9)

where ℓ̄= ℓ̄(τ) is a characteristic length ~ (A/A_g)ℓ_g.

It follows that the functional forms of G ≡ G(x₁, y₁, t, τ) when y lies within the upper and lower tracts must satisfy

$$\begin{array}{lll}G=\alpha -\overline{\ell },\hfill & \partial G/\partial y_1=\beta ,\hfill & y_1\to -0\hfill \\ G=\alpha ,\hfill & \partial G/\partial y_1=\beta ,\hfill & y_1\to +0\hfill \end{array}\}.$$ (10)

In these regions we have (see [44] for further details)

$$G(x_1,y_1,t,\tau )=f(\tau -y_1/c_o)\text{in}\text{the}\text{lower}\text{tract},$$ (11a)

$$G(x_1,y_1,t,\tau )=G_o(x_1,y_1,t,\tau )+\frac{1}{2\pi }\int {\int }_{-\infty }^{\infty }\frac{\beta (\xi ,x_1,t)sin[k_o(y_1-\widehat{L})]}{k_{o}cos(k_o\widehat{L})}{\text{e}}^{i\omega (\tau -\xi )}\text{d}\omega \text{d}\xi ,\text{in}\text{the}\text{upper}\text{tract},$$ (11b)

where f(τ − y₁/c_o) is an incoming plane wave from the lungs, k_o = ω/c_o, and

$$G_o(x_1,y_1,t,\tau )=-\frac{1}{2\pi A}{\int }_{-\infty }^{\infty }\{\text{H}(x_1-y_1)cos(k_o{y}_1)sin[k_o(x_1-\widehat{L})]+\text{H}(y_1-x_1)cos(k_o{x}_1)sin[k_o(y_1-\widehat{L})]\}\frac{{\text{e}}^{-i\omega (t-\tau )}\text{d}\omega }{k_{o}cos(k_o\widehat{L})},$$ (12)

in which H(·) is the Heaviside step function. The integrations with respect to ω pass above singularities on the real axis. G_o(x₁, y₁, t, τ) is just the compact Green’s function for x, y in the upper tract when ∂G_o/∂y₁ = 0 at y₁ = 0 (i.e. when flow through the glottis is blocked).

The representation (11b) satisfies ∂G/y₁ → β as y₁ → +0, and G = 0 at the ‘mouth’ y₁ = L̂, where L̂ is the internal duct length L increased by an appropriate ‘open-end correction’ [45]. The conditions that G → α − ℓ̄, α respectively as y₁ → ∓0, and ∂G/∂y₁ → β as y₁ → −0 supply the following consistency relations:

$$f(\tau )=\alpha (\tau ,x_1,t)-\overline{\ell }\beta (\tau ,x_1,t);f^{\prime }(\tau )=-c_o\beta (\tau ,x_1,t);\frac{\partial }{\partial \tau }(\overline{\ell }\beta ))-c_o\beta =\frac{\partial \alpha }{\partial \tau }$$ (13)

$$\alpha (\tau ,x_1,t)-\frac{1}{2\pi }\int {\int }_{-\infty }^{\infty }\beta (\xi ,x_1,t)\frac{sin(k_{o}L)}{k_{o}cos(k_{o}L)}{\text{e}}^{-i\omega (\xi -\tau )}\text{d}\omega \text{d}\xi =G_o(x_1,0,t,\tau )\equiv -\frac{1}{2\pi A}{\int }_{-\infty }^{\infty }\frac{sin[k_o(x_1-L)]}{k_{o}cos(k_{o}L)}{\text{e}}^{-i\omega (t-\tau )}\text{d}\omega .$$ (14)

2.2 The Fant equation

It is not possible to simplify further the above equations to obtain an explicit representation of G, which depends implicitly on the time-dependent geometry of the glottis, and therefore on the solution of the acoustic problem! However, this coupling leads to the Fant equation in the guise of a further consistency condition that must be satisfied by the glottis volume velocity Q(t). This is derived by equating the results of two different calculations of the acoustic pressure: (i) in terms of the monopole source Q(t), and (ii) via the aerodynamic sound integral representation (7).

2.2.1 Prediction (i) via the monopole source

To do this we consider the sound field at an arbitrary point x in the upper vocal tract. We first regard the glottis opening into the tract as a monopole source distribution in the wall at x₁ = 0, and then apply a special case of (7) using the Green’s function G_o of equation (12) for a duct closed at x₁ = 0. Only the surface integral on the right hand side of (7) is retained (with the viscous term discarded) to yield for case (i)

$$B(\mathbf{x},t)={\int }_{-\infty }^{\infty }\frac{\partial Q}{\partial \tau }(\tau )G_o(x_1,0,t,\tau )\text{d}\tau ,x_1>\sqrt{A}.$$ (15)

This result is now expressed in terms of the coefficient β(τ, x₁, t) by use of the consistency relation (14) and the third of equations (13):

$$\begin{array}{c}B(\mathbf{x},t)={\int }_{\infty }^{\infty }\beta (\tau ,x_1,t)\left[\overline{\ell }(\tau )\frac{\partial Q}{\partial \tau }(\tau )+c_{o}Q(\tau )-\frac{{ic}_o}{2\pi }\int {\int }_{-\infty }^{\infty }Q(\xi )\frac{sin(k_{o}L)}{cos(k_{o}L)}{\text{e}}^{i\omega (\xi -\tau )}\text{d}\omega \text{d}\xi \right]\text{d}\tau .\\ x_1>\sqrt{A}\text{in}\text{the}\text{upper}\text{tract}.\end{array}$$ (16)

2.2.2 Prediction (ii) via the aerodynamic sound formula

Turning now to the full aeroacoustic representation (7), there are two principal sources corresponding to the two integrals on the right hand side, and we write

$$B=B_o+B_{\sigma },$$ (17)

where B_o and B_σ are the respective contributions from the surface and volume integrals.

Surface motions are significant in two regions. One of these is the wall region within and close to the glottis. The overall monopole contribution from this motion is small, because of tissue incompressibility, and is ignored. Other surface integral contributions from within the glottis can also be ignored [46]; in particular the viscous drag within the glottis is significant only near closure – the Reynolds number typically exceeds 10³ during most of the open phase and detailed calculation [46] indicates that the net contribution of surface friction is uniformly small over a complete cycle of oscillation.

The remaining contribution is furnished by steady contraction of the lungs, which will be assumed to give a net volume flux Q_o towards the glottis. The contraction is necessarily equivalent to a compact source centred on x₁ ~ −ℓ_q, say, (Figure 1) so that

$$B_o=-{\int }_{-\infty }^{\infty }{Q}_o\frac{\partial }{\partial \tau }f(\tau +{\ell }_q/c_o)\text{d}\tau ={\int }_{-\infty }^{\infty }{c}_o{Q}_o\beta (\tau ,x_1,t)\text{d}\tau ,$$ (18)

where use has been made of the second of equations (13).

Next, Green’s function is given by equation (8) when y is in the compact region adjacent to the glottis, and therefore

$$B_{\sigma }(\mathbf{x},t)=-{\int }_{-\infty }^{\infty }{\int }_V\beta (\tau ,x_1,t)\nabla Y(\mathbf{y},\tau )·(\mathit{\omega }\wedge \mathbf{v})(\mathbf{y},\tau ){\text{d}}^3\mathbf{y}\text{d}\tau ,$$ (19)

where the volume integral may be regarded as confined to the jet just downstream of the glottis (or just upstream if reverse flow should occur). Although turbulence (vortex) sources exist elsewhere in the vocal tract, they are essentially weak quadrupoles and contribute negligibly to the sound.

Combining the results (18), (19) we conclude that the aggregate aeroacoustic prediction (ii) within the upper tract is simply

$$\begin{array}{c}B(\mathbf{x},t)={\int }_{-\infty }^{\infty }\beta (\tau ,x_1,t)\left[c_o{Q}_o-{\int }_V\nabla Y(\mathbf{y},\tau )·(\mathit{\omega }\wedge \mathbf{v})(\mathbf{y},\tau ){\text{d}}^3\mathbf{y}\right]\text{d}\tau \\ x_1>\sqrt{A}\text{in}\text{the}\text{upper}\text{tract}.\end{array}$$ (20)

2.2.3 Fant equation

Predictions (16) and (20) for the sound in the upper tract are evidently equivalent provided

$$\overline{\ell }\frac{\partial Q}{\partial t}+c_{o}Q-\frac{{ic}_o}{2\pi }\int {\int }_{-\infty }^{\infty }Q(\tau )\frac{sin(k_{o}L)}{cos(k_{o}L)}{\text{e}}^{-i\omega (t-\tau )}\text{d}\omega \text{d}\tau =c_o{Q}_o-{\int }_V\nabla Y(\mathbf{y},t)·(\mathit{\omega }\wedge \mathbf{v})(\mathbf{y},t){\text{d}}^3\mathbf{y}$$ (21)

This is the Fant equation for the volume velocity Q(t). Its more conventional form is [14 – 16]

$${\rho }_o\ell \frac{\partial Q}{\partial t}+\frac{{\rho }_o{A}_g}{A}{\int }_V\nabla Y(\mathbf{y},t)·(\mathit{\omega }\wedge \mathbf{v})(\mathbf{y},t){\text{d}}^3\mathbf{y}=A_{\text{g}}\{p_1(t)-p_2(t)\}$$ (22)

where ℓ = ℓ(t) ≡ (A_g/A)ℓ̄(t) is the effective length of the slug of fluid within and near the glottis that contributes to the inertia of the unsteady glottal flow [45]. The integrated term on the left represents the influence of the unsteady jet on the glottal flow, and can be evaluated when information is available about the jet vorticity and velocity distributions. The terms in the curly brackets on the right hand side are respectively the overall unsteady pressures just upstream and downstream of the glottis, which force the glottal volume flow over its effective cross-section A_g:

$$\begin{array}{l}{p}_1=\frac{{\rho }_o{c}_o}{A}\left(Q_o-Q(t)\right)\hfill \\ p_2=\frac{-i{\rho }_o{c}_o}{2\pi A}\int {\int }_{-\infty }^{\infty }Q(\tau )\frac{sin(k_{o}L)}{cos(k_{o}L)}{\text{e}}^{-i\omega (t-\tau )}\text{d}\omega \text{d}\tau \hfill \end{array}\}.$$ (23)

An investigation based on equation (22) is often more convenient than full numerical treatments of the structural and compressible motions [41, 47 – 51], which are computationally intensive and frequently cannot be run for more than one or two voicing cycles. They have mostly neglected the back-reaction on the glottal flow of standing acoustic waves in the supra and subglottal tracts, by permitting sound to radiate towards the mouth and lungs without reflections. Back-reactions of this kind are easily incorporated into equation (22) [17, 18, 20, 21, 25, 44, 52 – 55], in our case via the second of equations (23).

2.2.4 Vocal fold equation

Equation (22) must be solved in conjunction with equations governing A_g(t) and ℓ(t). The simplest reduced order equation for A_g(t) is based on the single mass-spring system of the vocal folds indicated in Figure 2 [25]. With the origin at the centroid of the glottis, and x₁ parallel to the vocal tract, the x₂ and x₃ axes may be taken respectively vertically upwards and out of the plane of the paper in Figure 2. The folds are assumed to vibrate symmetrically in the x₂ direction, and the displacement ζ(t) of the upper fold (Figure 3) is taken to satisfy the damped-oscillator equation

Figure 3.

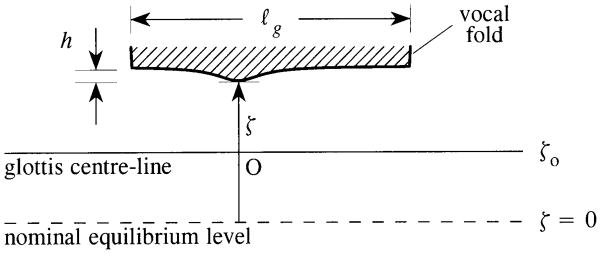
The vocal folds are assumed to oscillate symmetrically relative to the centre-line ζ = ζ_o of the glottis; ζ − ζ_o is the distance from the centre-line to the point of maximum amplitude h of the mucosal wave, so that A_g = 2ℓ_s(ζ− ζ_o).

$$\frac{{\text{d}}^2\zeta }{\text{d}{t}^2}+2\alpha \mathrm{\Omega }\frac{\text{d}\zeta }{\text{d}t}+{\mathrm{\Omega }}^2\zeta =\frac{F(t)}{m},$$ (24)

where m is the effective mass of the fold, α ≃ 0.1 is the structural damping ratio, Ω = 2πf_o is the radian natural frequency determined by muscular adjustment of the folds, and F(t) is the normal force exerted by the air on the medial surface of the fold. The two folds touch and ‘close’ the glottis when ζ = ζ_o, say, which corresponds to the centre-line of the glottis, so that ζ > ζ_o during free motion. If ζ_o > 0 (as in Figure 3) and the folds are in their undisturbed rest positions, they are pressed tightly together with equal and opposite forces of magnitude mΩ²ζ_o. When ζ_o < 0 the glottis remains open in the rest position, and the folds are then separated by a distance 2|ζ_o|.

The driving force F(t) is governed by the pressure produced by lung contraction, modified by flow separation from the vocal folds and jet formation in the outflow. These events depend on the position within the glottis of the cross-sectional minimum A_g, which is influenced by the mucosal waves propagating over the medial surfaces of the folds [29 – 37]. In the case of the single mass-spring system of Figure 2, the position of A_g coincides with that of the maximum mucosal wave amplitude. Interactions with the opposite fold during collision also affect the volume velocity Q(t), and certain voice disorders have been identified with vocal fold abnormalities (nodules, polyps, etc) that can disrupt normal mucosal wave propagation [56].

3. Mucosal wave data

Berry et al. [32] measured fleshpoint motions on an excised canine hemilarynx using nine microsutures placed along the medial surface of a mid-coronal section of the left vocal fold, spaced approximately one mm apart. Fleshpoint motions were primarily confined to the static mid-coronal plane, the observed out-of-plane vibrations (parallel to the flow direction in Figure 2) were observed to be an order of magnitude smaller. The experiments were performed in the absence of a supraglottal tract over a range of subglottal pressures p_I, up to a maximum of about 1600 Pa.

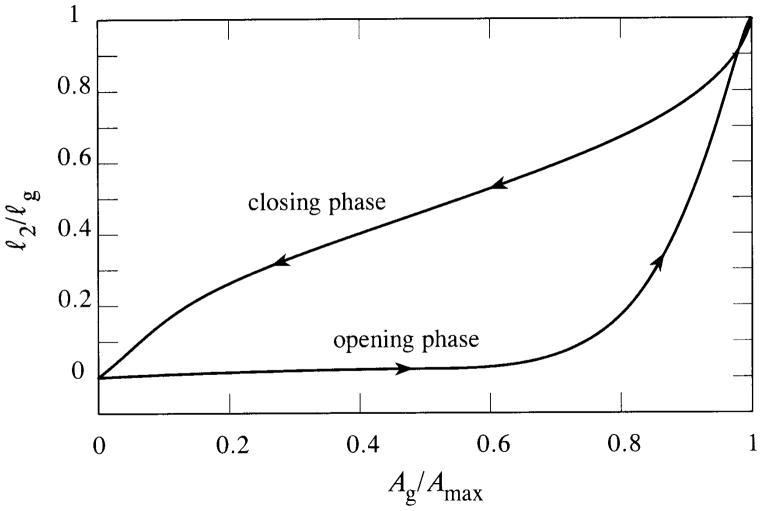
A periodic, chest-like vibration pattern was observed at p_I ~ 800 Pa with fundamental frequency ~102 Hz. Data for this case displayed in Figure 8(a) of [32] has been digitised to provide an empirical relation between the glottis fractional minimum cross-section A_g/A_max and its distance ℓ₂ from the downstream end of the glottis. For the simplified glottis of Figure 2, the overall glottal length ℓ_g is defined to be the observed value of ℓ₂ at which A_g attains its maximum A_max.

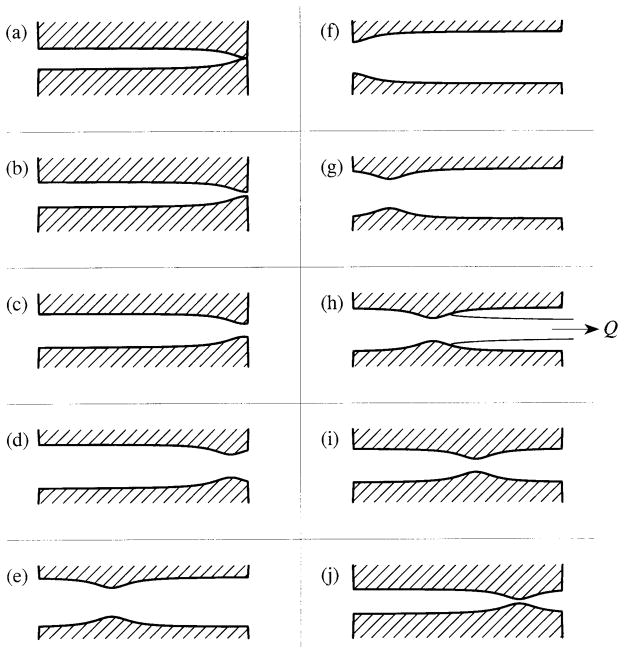
The digitised data have been smoothed and ℓ₂/ℓ_g plotted in Figure 4 as a two-valued function of A_g/A_max over a complete cycle, the dependence on A_g being different during the opening and closing phases. In the opening phase ℓ₂ remains at or very close to the downstream end of the glottis until A_g exceeds about 80% of A_max, after which it recedes rapidly to the subglottal end. The variation when closing is relatively uniform and the folds exhibit a sharp, whip-like motion reminiscent of the chest or modal register [32]. The corresponding changes in glottal geometry at equal time intervals over a cycle are illustrated in Figure 5. The profiles are drawn by assuming that the nominally flat medial surface is displaced a distance y inwards, towards the glottal axis, according to the formula

Figure 4.

Empirical relation between the minimum glottal cross-sectional area A_g and its distance ℓ₂ from the supraglottal end expressed in terms of the idealised glottis of Figure 2. The curves are constructed using digitised data from Figure 8(a) of Berry et al. [32] for measurements on an excised canine hemilarynx at p_I ~ 800 Pa.

Figure 5.

Illustrating the changes in glottal geometry for equally spaced instants in a complete cycle of oscillation calculated from the data of Figure 4: (a) – (e), opening phase; (f) –(j) closing phase.

$$y=\frac{h{\ell }_{\text{w}}^2}{({\ell }_{\text{w}}^2+x_{\text{w}}^2)},$$ (25)

where x_w = (distance/ℓ_g) along the x₁ axis from the position ℓ₂ of minimum glottis cross-section, h is the nominal peak amplitude of the mucosal wave (see Figure 3) and ℓ_w = 0.1. Thus, 2h is the mean glottis width in the upstream section in the fully closed state of Figure 5a. Although this width is arbitrary, its actual value has little or no significance for the calculations to be discussed below. The sequence of profiles in Figure 5 is similar to Figure 2.1 of Stevens [16], except that in Stevens’s closed state, corresponding to our Figure 5a, the region of contact of the vocal folds extends a distance of about 0.2ℓ_g from the supraglottal end of the glottis.

4. Equations of motion in the quasi-static approximation

4.1 The Q-equation

The Berry et al. [32] data are applied to the simplified case of Figure 1 where the subglottal and supraglottal tracts are hard-walled and have equal uniform cross-sectional areas A ≫ A_max. Steady contraction of the lung cavity is assumed to be equivalent to a uniform driving pressure p_I = ρ_oc_oQ_o/A in the subglottal region, resulting in a volume flux Q(t) through the glottis and the propagation of plane sound waves into x ≷ 0 on either side of the glottis.

The unsteady pressure p₁ just upstream of the glottis (where f_o|x₁|/c_o ≪ 1) is

$$p_1=p_I-\frac{{\rho }_o{c}_{o}Q(t)}{A}.$$ (26)

When the Strouhal number f_oℓ_g/V ≪ 1, the flow within and near the glottis is quasi-static and the steady form of Bernoulli’s equation is applicable in local regions of irrotational flow. It is assumed that flow separation just downstream of the minimum glottis section (A in Figure 2) produces a well defined jet of volume velocity Q(t) bounded by idealised free streamlines (the Reynolds number based on jet thickness ~ 10³ typically). The unsteady pressure within the jet and in the glottis to the left of A is therefore given by

$$p=p_I-\frac{{\rho }_o{c}_{o}Q(t)}{A}-\frac{1}{2}{\rho }_o{V}^2,$$ (27)

where V (x, t) is the local flow speed. In the downstream region, outside the jet, the pressure is equal to p₂.

The overall internal duct length L (~ 17 cm for an adult male) will be increased to L̄ = 20 cm (Table 1) to account for the acoustic end-correction at the mouth [45]. In the absence of dissipation in the duct and when radiation losses from the mouth are ignored, the pressure p₂ is given in terms of Q by the second of equations (23). The integration path along the real ω axis passes above simple poles of the integrand at ${\omega }_n=(n-\frac{1}{2})\pi c_o/\overline{L}$, (−∞ < n < ∞).

Table 1.

Vocal tract parameters

Parameter	Value
glottal length ℓg	3 mm
glottal span ℓs	10 mm
mucosal wave amplitude h	1 mm
mass of one vocal fold m	0.5 × 10−4 kg
nominal vibration frequency fo = Ω/2π	125 Hz
subglottal and supraglottal cross-sections A	100π mm2
perimeter of the supraglottal tract ℓp	20π mm
effective length of the supraglottal tract L̄	20 cm
density of air ρo	1.23 kg/m3
speed of sound co	359 m/s

In practice, however, dissipation at the walls of the supraglottal tract and radiation losses from the mouth can be important. For the hard-wall, mechanical model of Figure 1a thermo-viscous damping occurs in the duct wall boundary layers, and usually exceeds the radiation damping at lower frequencies. When these effects are taken into account the resonance frequencies become complex and are given to a first approximation by [57]

$$\begin{array}{ll}\hfill & \omega ={\omega }_n-i{\epsilon }_n\hfill \\ \text{where}\hfill & {\omega }_n=\left(n-\frac{1}{2}\right)\frac{\pi c_o}{\overline{L}},{\epsilon }_n=\frac{{\ell }_{\text{p}}\mid {\omega }_n{\mid }^{\frac{1}{2}}}{2^{\frac{3}{2}}A}\left(\sqrt{\nu }+(\gamma -1)\sqrt{\chi }\right)+\frac{{\omega }_n^{2}A}{4\pi c_o\overline{L}},\hfill \end{array}\}$$ (28)

in which ℓ_p is the perimeter of the upper tract, and ν ≃ 1.5 ×10⁻⁵ m²/s, χ ≃ 2 × 10⁻⁵ m²/s are respectively the kinematic viscosity and thermometric conductivity of the air in the upper tract. Dissipation produced by flexing of wall-tissue by standing waves in the upper tract is actually much larger [16], but the simple model (28) will suffice to illustrate the influence of dissipation on standing waves in the upper tract.

When this correction is incorporated into the second of equations (23) we find

$$\begin{array}{l}{p}_2=\frac{-i{\rho }_o{c}_o}{2\pi A}\int {\int }_{-\infty }^{\infty }\frac{Q(\tau )sin[k_o\overline{L}(1+i{\epsilon }_n/{\omega }_n)]}{cos[k_o\overline{L}(1+i{\epsilon }_n/{\omega }_n)]}{\text{e}}^{-i\omega (t-\tau )}\text{d}\omega \text{d}\tau \\ ={\rho }_o{c}_o^2\sum _{n=1}^{\infty }{Z}_n(t),\end{array}$$ (29a)

$$\text{where}{Z}_n=\frac{2}{A\overline{L}}{\int }_{-\infty }^{t}Q(\tau )cos{\omega }_n(t-\tau ){\text{e}}^{-{\epsilon }_n(t-\tau )}\text{d}\tau .$$ (29b)

The results (26) and (29) may now be substituted into the Fant equation (22).

In the quasi-static approximation the vorticity integral in equation (22) is given to first order by [44, 58]

$${\int }_V\nabla Y(\mathbf{y},t)·(\mathit{\omega }\wedge \mathbf{v})(\mathbf{y},t){\text{d}}^3\mathbf{y}=\frac{A}{A_{\text{g}}^2}\frac{Q\mid Q}{2{\sigma }^2},$$ (30)

which is applicable also in the case of reversed flow (towards the lungs) through the glottis. This quadratic term represents the influence of the unsteady jet on the glottal motion, and this quasi-static representation is applicable provided $f_o\sqrt{A_g}/U_{\sigma }$ is small, where U_σ = Q/_σA_g is the free jet speed and s is the jet contraction ratio. Jet instability in the downstream region can be ignored because the integrand is only significantly different from zero close to the glottis. The contraction ratio σ ≃ 0.61 for a simple circular or rectangular aperture in thin wall, where the streamlines turn through about 90° at the aperture edge [13], but it will be much larger for a confined jet where separation takes place just downstream of the narrowest section A_g. Experiment [59] and ideal analytical modelling [23] suggest that a value closer to σ ≃ 1 is probably more appropriate, and we shall use this in what follows.

Finally, because the glottal region is compact, we can neglect ℓ̄∂Q/t in (22) compared to c_oQ.

Thus, collecting together the results (26), (29a) and (30), the Fant equation (22) is reduced to quasi-static form

$$\frac{{\rho }_{o}Q(t)\mid Q(t)\mid }{2{\sigma }^2{A}_{\text{g}}^2}=p_I-\frac{{\rho }_o{c}_{o}Q(t)}{A}-{\rho }_o{c}_o^2\sum _{n=1}^{\infty }{Z}_n(t).$$ (31)

4.2 The surface force F(t)

The net normal force F(t) applied by the airflow to the vocal fold of Figure 3 (in the direction of increasing ζ) consists of two components produced by the air pressure acting on the sections of the glottis wall upstream and downstream of the separation point, approximately of respective lengths ℓ₁ and ℓ₂. The pressure on the downstream section is equal to p₂. Except in the immediate vicinity of the mucosal wave peak, Bernoulli’s equation (27) gives for p_u, the upstream wall pressure,

$$p_{\text{u}}=p_I-\frac{{\rho }_o{c}_{o}Q}{A}-\frac{{\rho }_o{Q}^2}{2A_c^2},A_c=2{\ell }_{\text{s}}(\zeta -{\zeta }_o+h),$$ (32)

where A_c ≡ A_g + 2ℓ_sh is the uniform cross-sectional area of the glottis upstream of the minimum cross-sectional area. These approximations neglect small edge-transitional modifications of the pressure discussed by McGowan & Howe [60].

Using equations (26), (29a) and (32), and eliminating Q|Q| by means of the Fant equation (31), we find

$$\begin{array}{l}F(t)\simeq {\ell }_{\text{s}}\{{\ell }_1{p}_{\text{u}}+{\ell }_2{p}_2\}\\ ={\ell }_{\text{s}}{\ell }_{\text{g}}\left\{{\rho }_o{c}_o^2\sum _{n=1}^{\infty }{Z}_n(t)+\frac{{\ell }_1}{{\ell }_{\text{g}}}\left(p_I-\frac{{\rho }_o{c}_{o}Q}{A}-{\rho }_o{c}_o^2\sum _{n=1}^{\infty }{Z}_n(t)\right)\left(1-\frac{{\sigma }^2{A}_{\text{g}}^2}{A_{\text{c}}^2}\right)\right\},Q>0,\\ ={\ell }_{\text{s}}{\ell }_{\text{g}}\left\{p_I-\frac{{\rho }_o{c}_{o}Q}{A}-\frac{{\ell }_2}{{\ell }_{\text{g}}}\left(p_I-\frac{{\rho }_o{c}_{o}Q}{A}-{\rho }_o{c}_o^2\sum _{n=1}^{\infty }{Z}_n(t)\right)\left(1-\frac{{\sigma }^2{A}_{\text{g}}^2}{A_{\text{c}}^2}\right)\right\},Q<0.\end{array}$$ (33)

4.3 The vocal fold equation of motion

The substitution

$$A_{\text{g}}=2{\ell }_{\text{s}}(\zeta -{\zeta }_o),$$ (34)

permits the vocal fold equation (24) to be cast in the form

$$\frac{{\text{d}}^2{A}_{\text{g}}}{{\text{d}t}^2}+2\alpha \mathrm{\Omega }\frac{{\text{d}A}_{\text{g}}}{\text{d}t}+{\mathrm{\Omega }}^2{A}_{\text{g}}=2{\ell }_{\text{s}}\left(\frac{F(t)}{m}-{\mathrm{\Omega }}^2{\zeta }_o\right),A_{\text{g}}\ge 0.$$ (35)

The net force on the right hand side must be positive to open the glottis during a period of closure. Solutions of the simultaneous equations (31) and (35) are obtained below for the standard set of parameter values in Table 1. The damping ratio α is believed to be about 0.1 [25, 61], although no precise data is available.

The vocal fold motion starts at t = 0 by application of a sufficiently large and constant lung overpressure p_I, with the initial conditions A_g = 0, dA_g/dt = 0. Two simple alternative procedures can be applied to model inelastic and elastic vocal fold collisions [25]. In the inelastic case each fold is reduced to rest on contact, and the motion is re-started with the initial values A_g = 0, dA_g/dt = 0 by the pressure force p_I. During elastic impact A_g remains zero for a finite time dependant on tissue resilience. This is modelled by formally permitting A_g to become negative subject to the modified equation of motion

$$\frac{{\text{d}}^2{A}_{\text{g}}}{{\text{d}t}^2}+2\overline{\alpha }\mathrm{\Omega }\frac{{\text{d}A}_{\text{g}}}{\text{d}t}+{\mathrm{\Omega }}^2{A}_{\text{g}}=2{\ell }_{\text{s}}\left(\frac{p_I{\ell }_{\text{g}}}{m}-{\mathrm{\Omega }}^2{\zeta }_o\right),A_{\text{g}}<0.$$ (36)

The contact motion will be assumed to be critically damped by taking the damping ratio ᾱ = 1. When predictions are plotted, however, the glottis area A_g(t) is set to zero during those time intervals where the equations imply that A_g < 0, i.e. we plot A_g = 0 for times when the vocal folds are in contact.

To determine Q(t) and A_g equations (31), (33), (35), (36) are augmented by equations for Z_n(t), n = 1, 2, ···. These are obtained from equation (29b), which implies that Z_n is also given in terms of Q(t) by the equations

$$\begin{array}{l}\frac{{\text{d}Z}_n}{\text{d}t}=\frac{2Q(t)}{A\overline{L}}-{\epsilon }_n{Z}_n-{\omega }_n{Z}_n^{\prime }\hfill \\ \frac{{\text{d}Z}_n^{\prime }}{\text{d}t}={\omega }_n{Z}_n-{\epsilon }_n{Z}_n^{\prime }\hfill \end{array}\}n=1,2,\cdots ,$$ (37)

where $Z_n^{\prime }=(2/A\overline{L}){\int }_{-\infty }^{t}Q(\tau )sin{\omega }_n(t-\tau ){\text{e}}^{-{\epsilon }_n(t-\tau )}\text{d}\tau$. In practice the component of the back-pressure p₂ determined by the modal coefficient Z_n(t) will be small when the glottal radian frequency Ω ≪ ω_n. This is satisfied when n > 2 for normal voicing, which indicates that the infinite system (37) can safely be truncated at, say, n = 5. The validity of this approximation has been verified by numerical tests. The whole set of governing equations can then be solved by Runge-Kutta integration, subject to the additional initial conditions Z_n = 0, $Z_n^{\prime }=0$ at t = 0.

5. Numerical results

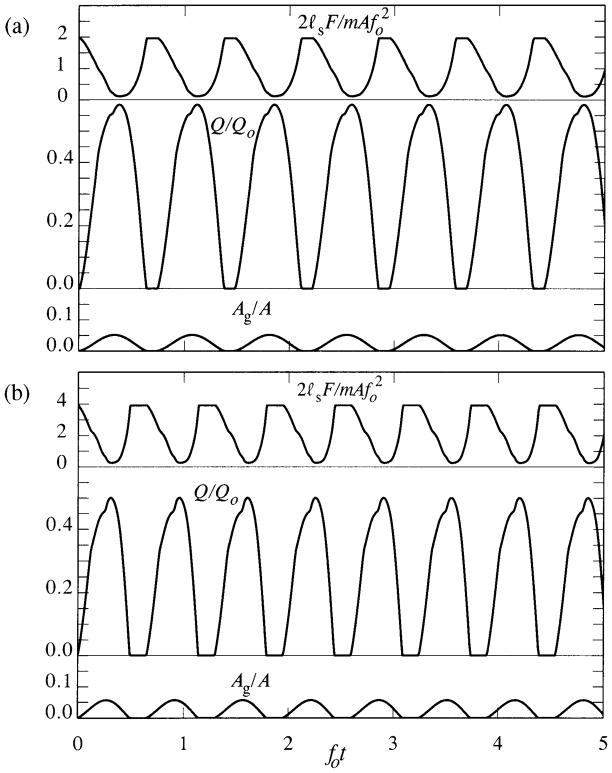
Typical numerical predictions when the separation point moves in accordance with the Berry et al. [32] measurements are depicted in Figure 6. The variations of A_g(t)/A, Q(t)/Q_o, $2{\ell }_{\text{s}}F(t)/{\mathit{mAf}}_o^2$ are plotted during the initial time period 0 < f_ot < 5, where Q_o = p_I A/ρ_oc_o is mean volume velocity from the lungs, corresponding to a subglottal pressure of amplitude p_I. The variation of Q(t) determines the acoustic pressure radiated towards the mouth (prior to reflection and transmission). The motion is started at t = 0 with A_g = 0, dA_g/dt = 0 with the folds just touching (ζ_o = 0) by a constant applied subglottal pressure p_I. The damping ratio α = 0.1, and critical damping ᾱ = 1 is assumed in equation (36) during vocal fold impact. Other parameter values are given in Table 1.

Figure 6.

Limit cycle variations of A_g(t)/A, Q(t)/Q_o, $2{\ell }_{\text{s}}F(t)/{\mathit{mAf}}_o^2$ when separation occurs just downstream of the minimum of the glottis cross-sectional area which moves according to the data of Berry et al. [32], for the conditions of Table 1 when α = 0.1, ᾱ = 1, L̄ = 20 cm. (a) p_I = 800 Pa; (b) p_I = 1600 Pa, ζ_o = 0.5 mm.

The surface force F(t) falls almost to zero when the glottis is fully open, when the separation point is at the upstream end of the glottis, because the whole of this force is then furnished by the back pressure p₂ (equation (29a)), which is very small when f_o ≪ f₁ = ω₁/2π ~ 450 Hz. This is favourable to the maintenance of limit cycle oscillations. According to Figure 6 the asymmetry of F(t) relative to the instant at which A_g = A_max (produced by the corresponding asymmetric motion of the separation point) ensures that the surface force is always larger during opening than at the corresponding point during the closing phase of the glottis, conducive to the supply of energy to overcome vocal fold damping. The waveforms plotted in Figure 6a are for a mean subglottal pressure p_I = 800 Pa, for which the peak of the limit cycle volume velocity wave profile is skewed slightly to the latter half of the cycle. The effective limit cycle fundamental frequency is about 40% larger than f₀.

Figure 6b indicates how these conclusions are changed when the subglottal pressure is increased to 1600 Pa accompanied by the application of an adduction force F_a, say, to the vocal folds, causing them to be tightly pressed together in the rest position. This force corresponds to the second term (Ω²ζ_o) in the braces on the right of equation (35), where the parameter ζ_o is taken to be 0.5 mm. Because in ‘pressed voicing’ the folds are unable to execute a full cycle of the ‘free’ equation of motion (35), the effective frequency of the limit cycle is increased, in the present case by about 60% of f₀.

5.1 The ‘exposed’ glottis

Insight into the influence on the glottal flow of standing acoustic waves in the upper tract is obtained by consideration of the configuration of Figure 1b, where the glottis radiates directly into free space. The pressure p₂ downstream of the glottis now vanishes to a good approximation.

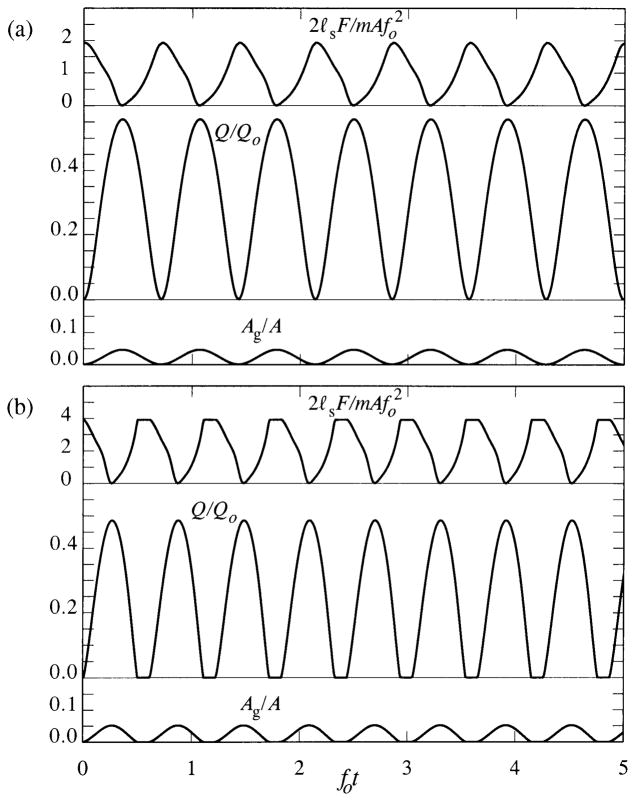
The calculations of Figure 6 have been repeated for an exposed glottis (with A_L = A of Table 1) and the results displayed in Figure 7. The force and volume velocity waveforms are now much smoother, F(t) vanishing when the glottis is fully open. The predicted volume velocity profiles Q/Q_o are perfectly symmetric, and exhibit marginally increased oscillation frequencies and reduced maximum amplitudes relative to the corresponding predictions in Figure 6 in the presence of the upper tract. Upper tract back-reaction therefore appears to be responsible for the asymmetry in the volume velocity waveforms.

Figure 7.

Predictions of A_g(t)/A, Q(t)/Q_o, $2{\ell }_{\text{s}}F(t)/{\mathit{mAf}}_o^2$ for an ‘exposed’ glottis (Figure 1b) when separation occurs just downstream of the minimum of the glottis cross-sectional area which moves according to the data of Berry et al. [32], for the conditions of Table 1 when α = 0.1, ᾱ = 1. (a) p_I = 800 Pa; (b) p_I = 1600 Pa, ζ_o = 0.5 mm.

5.2 Resonant back-reaction

The broadly similar predictions for corresponding cases in Figures 6, 7 suggest that the experimental data of [32] in Figure 4 measured using an excised canine hemilarynx (with the supraglottal tract removed) probably provides a good model also in the presence of the upper tract, at least when the back-reaction of standing waves is weak (when f_o ≪ f₁). But the data can also be used to investigate the back-reaction when f_o is close to an upper tract resonance frequency, when the motion in the glottis could be strongly influenced by standing acoustic waves. This is known to be important for an exposed glottis when f_o is close to a subglottal resonance [17 – 21]. According to Joliveau et al. [62] tuning of the first upper tract resonance frequency f₁ to f_o can be used by singers to attain increased radiated power, and Titze [30] has argued that vocal fold vibrations are enhanced when f_o just exceeds f₁.

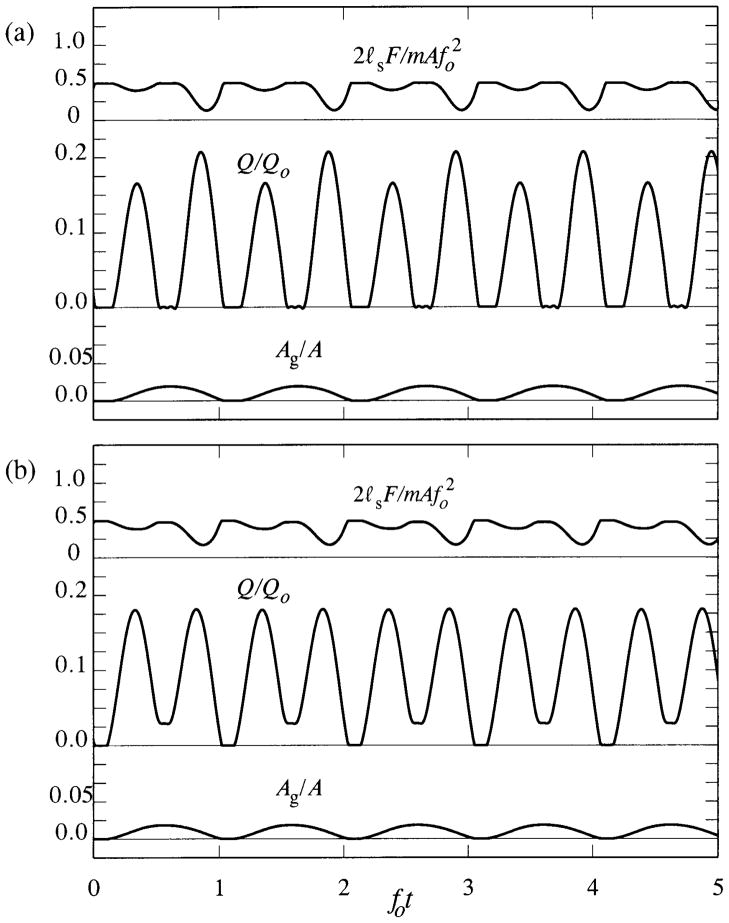
To examine this effect in terms of the mechanical vocal tract of Figure 1a, the length L̄ of the upper tract must be artificially changed. Figure 8 depicts typical predictions when the unforced vocal fold resonance frequency f_o = 250 Hz and the upper tract is adjusted to make f₁ = 246.6 Hz (L̄ = 36.4 cm), and when the subglottal driving pressure p_I = 800 Pa. No allowance is made for a possible corresponding reduction in the effective dynamic mass of the vocal folds. Equations (37) are truncated at n = 8 to ensure proper convergence.

Figure 8.

Resonant acoustic back-reaction from the supraglottal tract when separation occurs just downstream of the minimum of the glottis cross-sectional area which moves according to the observations of Berry et al. [32], for the conditions of Table 1 when α = 0.1, ᾱ = 1, p_I = 800 Pa, f_o = 250 Hz, f₁ = 246.6 Hz. (a) no upper tract damping; (b) upper tract damping defined as in (28).

In Figure 8 the limit cycle oscillations of the vocal folds are at frequency ~ f₁. The glottis ejects two distinct puffs per cycle into the upper tract separated by a short interval of ‘silence’, during which the surface force F(t) rises to its maximum value ℓ_sℓ_gp_I normally attained only when the glottis is closed. When boundary layer damping in the upper tract is ignored (Figure 8a), Q/Q_o rises to a maximum of 0.165 when A_g has opened to about 0.5A_max, after which it falls to zero, and remains zero until A_g starts to decrease. During this time the supraglottal back pressure p₂ ~ p_I is large enough to completely block the flow, even though the glottis is fully open (cf. Lighthill [63], Section 2.5; [44]). A second larger volume velocity peak of Q/Q_o ~ 0.207 occurs when A_g decreases to about 0.55A_max, at which time the surface force F(t) falls to a positive minimum. The overall profile of the volume velocity is therefore periodic with frequency f_o, but with a substantial second harmonic component. The principal effect of upper tract damping (Figure 8b) is to replace the flow blockage near A_g ~ A_max with a deep, positive minimum of the volume velocity Q. The depth of this minimum will in practice be further reduced when more realistic damping associated with vocal tract wall flexing is taken into account.

For the simple mechanical model of Figure 1a, these ‘double puff’ volume velocity profiles are evident in numerical predictions only when the glottis frequency f_o is close to an upper tract resonance frequency. However, effects of this kind are believed to occur in the human vocal tract over much wider frequency bands centred on upper tract resonance frequencies [64], because of the diffusive influence of the relatively large contribution to overall damping produced by tissue-flexure in the tract walls.

6. Conclusion

The acoustic source responsible for voiced speech involves the periodic release of high pressure air from the lungs by the opening and closing of the glottis. Air emerges in a rapid succession of puffs of unsteady volume velocity that is usually identified as a monopole source radiating into the supraglottal tract. But this is really a nonlinear aeroacoustic problem whose solution by the tailored Green’s function method propounded by Doak [1] is formally intractable, because the time history of Green’s function depends on the solution of the direct acoustic problem. Green’s function and the glottis volume velocity Q(t) are coupled by a consistency equation, i.e. by the Fant equation, usually derived by heuristic argument, but shown here to be a rigorous consequence of Lighthill’s theory of aerodynamic sound.

The mucosal wave propagates back and forth over the medial surfaces of the separated vocal folds, and is responsible for the amplitude and phase modulation of the surface force. The state of the wave determines the position within the glottis of the minimum of the glottis cross-sectional area (A_g). Flow separation from the wall near this moving minimum is responsible for the desired phasing of the force, achieved principally because of asymmetric motion of A_g during opening and closing of the glottis. This is the significance of the experimental data in Figure 4, obtained from measurements on an excised canine hemilarynx [32]. Our calculations using this data for a simplified vocal tract model indicate that the mechanism is robust enough to maintain limit cycle oscillations over a wide range of voicing conditions. The characteristic locus of A_g displayed in Figure 4 is likely to be typical of most voicing cycles involving an interval of closure of the glottis, but confirmation of this awaits the availability of in vivo data.