MATCHING IN INFORMAL FINANCIAL INSTITUTIONS

Abstract

This paper analyzes an informal financial institution that brings heterogeneous agents together in groups. We analyze decentralized matching into these groups, and the equilibrium composition of participants that consequently arises. We find that participants sort remarkably well across the competing groups, and that they re-sort immediately following an unexpected exogenous regulatory change. These findings suggest that the competitive matching model might have applicability and bite in other settings where matching is an important equilibrium phenomenon. (JEL: O12, O17, G20, D40)

1. Introduction

This paper studies an informal financial institution that brings heterogeneous agents together in groups to exploit gains from trade. We develop a framework for analyzing decentralized matching into these groups, and the equilibrium composition of participants that consequently arises. The payoff from choosing a particular group is typically not observed ex ante and will in general depend on the choices made by other participants. Nevertheless, we find that participants sort remarkably well across the competing groups, and that they re-sort immediately following an unexpected regulatory change as predicted by the theory. This indicates that despite the absence of a posted price, sorting effectively allocates resources across groups in this institution. The competitive matching mechanism we propose may also shed light on other economic environments where sorting is important for equilibrating the market.

The point of departure for our application is the nationalization of the Indian banking system in 1970. This policy had the predictable effect of lowering interest rates on deposits and rationing credit, adversely affecting large numbers of small depositors and firms. In response to this market incompleteness, a particular institution—the commercial chit fund—emerged in South Indian towns and cities and rapidly grew in importance. By 1993, the amount of credit made available by registered chit funds in some parts of South India was up to 25% of bank credit, and over one million people were enrolled in this institution in the state of Tamil Nadu alone (Vaidyanathan and Sriram 2000).¹ This paper studies how the chit funds brought borrowers and lenders together and generated competition among their participants, capturing the gains from trade that remained untapped due to regulation. In addition, we analyze how this institution maintained these competitive pressures in the face of a subsequent attempt to regulate the financial market.

The rotating savings and credit association (Rosca), or chit fund as it is known in India, is an informal community-based financial arrangement found throughout the developing world.² While the traditional Rosca is a savings mechanism, the commercial chit fund is essentially a financial intermediary. Commercial chit funds emerged after nationalization, taking advantage of a legal loophole that allowed them to compete with the government banks as long as their organizational form matched the basic structure of the traditional Roscas. Commercial chit funds are most active in urban areas, with organizing companies bringing thousands of borrowers and lenders together in small groups. All participants in a group contribute a fixed amount each month, and the pot of money thus collected is subsequently auctioned within the group to more efficiently capture gains from trade. The winning bidder keeps the pot minus the bid amount, which is distributed equally within the group as a “dividend”. This process continues for as many months as there are participants, with a fresh auction each month, until all participants have received the pot once. Participants who win the pot early are effectively borrowers and those who wait until the end are effectively lenders—the participant who wins last receives his principal in return for all the dividends generated over the course of the group. The dividends generated competitively within each group thus act as an interest payment. Although participants are locked into a group for its entire duration once they have joined, they are free to choose ex ante from a menu of pot sizes and durations, which allows for competition across groups as well.

By bringing borrowers and lenders together and by stimulating competition, the chit funds effectively created an informal credit market, subject to the organizational constraints that they faced.³ Although the auctions would clearly have generated ex post competition within groups, we do not have direct evidence that similar competitive pressures were generated ex ante across groups. The model that we develop in this paper to analyze the chit fund does, however, provide predictions that allow us to identify ex ante competition, which is an important feature of this institution. In our model, participants choose a group type based on the proportion of borrowers and lenders that they expect to encounter in different types of groups, which in turn determines the payoffs that they will receive. Intuitively, an increase in the proportion of borrowers increases ex post competition for the pot, lowering the payoff for the borrowers and increasing it for the lenders. Without a participation price for each group to guide them, the (anticipated) composition of borrowers and lenders in each type of group adjusts so that agents are indifferent between the various types of groups in equilibrium. This no-arbitrage condition is shown to imply in turn that a systematic relationship between the correctly anticipated proportion of borrowers in a group and its duration (measured by the number of participants) should be obtained.

The unique data set that we utilize for the empirical analysis is obtained from the internal records of a single chit fund company, one of the largest in the country, with branches in multiple South Indian states. The data set includes the value of the winning bid in each period in each group that commenced in the city of Chennai (formerly known as Madras) between September 1992 and September 1994; nearly 80,000 subscribers were enrolled in roughly 2,000 groups over this period. The company’s records also allow us to distinguish between ex ante borrowers and lenders. Based on this classification of participants we find that the proportion of borrowers is systematically declining in the duration of the group, across the entire range of group types, consistent with the no-arbitrage condition.

The competition in this non-market institution resulted in an implicit interest rate that was substantially higher than the rate offered by the monopolistic banking system; calculations reported later indicate that the chit funds generated an implicit interest rate of 19% at a time when the rate on bank deposits was around 9%. Not surprisingly, the chit funds captured a substantial share of the credit market in a short period of time.⁴ Starting with almost no registered companies in the 1970s, deposits in registered chit funds were estimated to be roughly 10% of the volume of bank deposits in the South Indian state of Tamil Nadu by 1993 (Bouman 1995), and 15% of the deposits in the neighboring state of Kerala (where chit funds play a more prominent role in the local economy) in 1987 (Shah and Johnson 1989). The same sources report that the amount of credit made available by the chit fund companies was 12.5% of bank credit in Tamil Nadu and 25% of the credit in Kerala.⁵ Chit funds clearly provided serious competition to the banking system, at least in South India where they were most prevalent.

Government regulators and the Reserve Bank of India (RBI) were quick to notice the increasing popularity of this alternative non-market institution. RBI reports from as early as the 1970s explicitly identify chit funds as direct competitors to the banking system and take note of the higher interest rates that these institutions could provide. The response to this challenge was predictably to regulate the chit funds. Efforts by the RBI ultimately led to the imposition of a ceiling on the bids, capping them at 30% of the pot amount, in September 1993. This restriction effectively capped the interest rate that the chit funds could generate, narrowing their comparative advantage over the banks.⁶

Whereas ex post competition within the groupswas now legally restricted, the composition of the participants across different types of groups could still adjust to increase ex ante competitiveness and help complete the market. Although the 30% bid cap directly affected bids in the long duration groups alone, our model suggests that the exogenous regulatory shock should have affected the composition of borrowers and lenders in all groups. A cap on the bids reduces competition within the group, making borrowers better off, and so the no-arbitrage condition implies that the share of borrowers should have increased disproportionately in the long duration groups to equalize payoffs across different types of groups. In addition, our model predicts that the proportion of short duration groups should have increased following the bid cap. Using data one year before and one year after the regulatory shock we find that the mix of borrowers and lenders within the group, as well as the mix of different types of groups, adjusted immediately in response to the bid cap, exactly as predicted by the theory, highlighting once again the competitive response of this institution to the new regulation. We find that the bid cap predictably lowered the implicit interest rate in the chit funds, from 19% to 14%, and that there was an overall decline in participation of 20%. Nonetheless, because of the swift re-sorting among the participants that is observed—the entire transition was completed by 1995—this institution continued to provide serious competition to the formal banking sector, even after the bid cap.

The chit fund is well suited to testing the theory of decentralized matching that we develop in this paper. The rules of the game and the payoffs that participants obtain in this financial institution are well defined, and participants can choose freely between competing groups. This analytical framework may also be suitable for studying other environments in which heterogeneous agents match together. Sorensen (2007), for example, models the allocation of venture capital to startups as a matching process. Similarly in the equities market, traders with high discount rates, such as hedge funds, and traders with low discount rates, such a retail investors, could be seen to match to assets of differing liquidity. The strong empirical results that we obtain indicate that the competitive matching model might have applicability and bite in these settings and other settings where matching is an important equilibrium phenomenon.

The paper is organized in five sections. Section 2 describes the commercial chit fund institution in South India in greater detail and the events leading up to the bid cap in 1993. Section 3 presents a simple model of the chit fund, which generates predictions for the sorting of borrowers and lenders across groups, as well as the mix of groups, before and after the bid cap. Section 4 successfully tests the predictions of the competitive model, and Section 5 concludes.

2. The Institutional Setting

Although traditional chit funds have been widely prevalent in South Indian villages for centuries, the commercial chit fund is a relatively recent phenomenon. Ardener (1964) places the emergence of commercially organized ‘Chit Fund Groups’ at the beginning of the 20th century, mostly in Chennai (then known as Madras), and to some extent in Travancore and Cochin. But these exclusive commercial chit funds, which were used for the most part by businessmen to raise working capital, appear to have been quite rare even as late as the 1970s. Anderson (1962) tells us that the first registered chit fund company in Hyderabad, the capital of Andhra Pradesh and another important center for chit fund activity today (the S.N. Chit Fund Co.), was founded in 1951. Similarly, the company that provided us with the data (Shriram Chits and Investments Pvt. Ltd.), one of the oldest and most established companies in Chennai, was founded in 1974. From our discussions with the founders of the company, there were only a handful of commercial chit fund companies in Chennai prior to that date. It was only with nationalization of the banking system that commercial chit funds in their current form emerged, bringing thousands of borrowers and lenders together from across the income distribution.

The Indian financial system was nationalized in the early 1970s, after which only specially designated Non-Bank Financial Companies (NBFCs) were permitted to function as financial intermediaries, in competition with the government banks. One such NBFC was the commercial chit fund.⁷ Companies that operate as registered chit funds have to satisfy a number of specific criteria. These criteria were first laid out in Section 2(2) of the Madras Chit Funds Act (1961), which regulated the institution in the state of Tamil Nadu. Subsequently they were adopted in their entirety in the Miscellaneous Non-Banking Companies Directions, an interim regulatory document issued by the Reserve Bank of India in 1973, and ultimately in Section 2(b) of the central Chit Fund Act (1982) which applies to the entire country:

“Chit” means a transaction whether called chit fund, chit, kuri, or by any other name, by which its foreman [the company] enters into an agreement with a number of subscribers that every one of them shall subscribe a certain sum or a certain quantity of grain by installments for a definite period and that each subscriber in his turn as determined by lot or by auction or by tender or in such other manner as may be provided for in the agreement shall be entitled to a prize amount.

As long as the chit fund is organized precisely along the lines laid out here, the company can operate as a financial intermediary, regulated by the Registrar of Chit Funds in each state, rather than by the Reserve Bank of India. As discussed in the previous section, the chit funds were able to generate an implicit interest rate that was substantially higher than the rate offered by the government banks to depositors. Businesses, and borrowers in general, also benefitted from this institution, because credit was severely rationed by the banks. Government regulators, and particularly the Reserve Bank of India, were quick to take note of the growth of the chit funds and other NBFCs, following the nationalization of the banking system. Several committees were appointed to study the working of these companies. These committees felt that although many NBFCs frequently resorted to unfair methods, and therefore needed to be regulated, prohibiting them entirely would adversely affect certain sectors of the economy that had limited access to bank credit, or chose not to deposit their money with the banks. For the particular case of the commercial chit fund companies, these study groups recommended a Model Bill, to be enacted as a Central Act of Parliament, to ensure uniform regulation throughout the country. They also recommended that the administration of the legislation be left to the state governments.

The Government of India acted on these recommendations and passed the Chit Fund Act in 1982, with implementation of the Act left to the Registrar of Chit Funds in each state. The 1982 Act departed most notably from the 1961 Madras Chit Fund Act, which it replaced, by imposing a 30% ceiling on the bids. The stated reason for the ceiling was to protect the depositors from defaults that would occur when the bids were pushed too high—this would be the standard story with adverse selection or moral hazard, in which only risky investors participate or only risky projects are chosen when interest rates are high. But it is very likely that the interest rates were also capped to restrict competition from the chit fund companies, since it was well understood that the higher interest rates that these companies could provide was perhaps their principal comparative advantage over the banks.⁸

Not surprisingly the chit fund companies went to court over the imposition of the ceiling. They were initially successful, and the Madras High Court granted a stay order in 1984 on a number of provisions of the 1982 Chit Funds Act, including the 30% bid cap.⁹ However, the case did ultimately work its way through the courts, and after numerous appeals the stay order was vacated by the Supreme Court in September 1993. Given the enormous legal backlog, it is always difficult to predict when a case will come up for hearing in the Indian judicial system, and the numerous appeals that were filed in this case would only have added to the uncertainty surrounding the timing of its completion. We will thus find it reasonable to treat the 30% bid cap imposed in September 1993, a full 11 years after the passing of the 1982 Chit Funds Act, as an unanticipated regulatory shock. Groups that commenced prior to September 1993 continued in the old regime even if they extended beyond that date. The analysis of the institutional response to the bid cap will thus compare the sorting into groups that commenced one year before and one year after September 1993.

3. A Simple Model of the Chit Fund Institution

Participants in the chit fund choose from a menu of group types, generating ex ante competition across groups. Once a group forms, the pot is auctioned in each period, resulting in ex post competition within the group. We now proceed to formalize the matching into groups and the pattern of bids that subsequently unfolds. In this simple model, there are two types of participants: high types and low types. High types have superior investment opportunities, and because in equilibrium they collect the pot earlier on average than the low types, we will often refer to them as the borrowers. The low types are the lenders. We solve the model in two stages. The first stage is the matching stage. Fixing the monthly contribution (or the pot size), each agent chooses to participate in a group of a certain duration, based on the expected future payoff from that group. The second stage determines the payoff from the sequence of auctions in the group.

Given a menu of groups, the agent chooses the group that maximizes her expected future payoff. We will see that the proportion of high types adjusts to leave each agent indifferent between the various types of groups in equilibrium. For example, if an exogenous shock increases the payoffs that the high types receive in one type of group, relative to the other groups that are available, then this will generate an inflowof high types into that group (which lowers the payoffs that they receive) until indifference is restored once again.

Section 3.1 describes the population and preferences, the matching technology and the auction technology. We solve the model backwards, starting in Section 3.2 with the pattern of bids in the second stage auction, and the payoffs that the participants receive. Subsequently, Section 3.3 derives the first stage matching equilibrium. The no-arbitrage (indifference) condition described earlier is shown to imply that a systematic relationship between the proportion of borrowers and group duration should be obtained in equilibrium. Sections 3.4 and 3.5 extend the model to derive predictions for the effect of the 30% bid cap on the sorting across groups and the mix of groups. These implications of the model will be successfully tested in Section 4, emphasizing the competitive nature of this institution.

3.1. Population, Preferences, Matching Technology, and Auction Technology

3.1.1. Population and Preferences

There is a continuum of infinitely lived chit fund participants. Each participant in this economy disposes of a fixed amount v each period that she can contribute to the chit fund. We could imagine, for example, that the participant saves a fixed fraction of her income each period. Every participant is indexed by an observable type $\gamma \in \{\overline{\gamma },\underset{¯}{\gamma }\}$, where $\overline{\gamma }$ > $\underset{¯}{\gamma }$ and where the proportion of high types in the population is μ and the proportion of low types is 1 − μ. Participants of type γ who manage to find finance have access to a deterministic investment opportunity with a return 1 + γ. The heterogeneity among agents derives from the return on the investment opportunity. Though both types can derive positive returns from investment, we will often refer to the high types $\overline{\gamma }$ as borrowers and the low types $\underset{¯}{\gamma }$ as lenders. This follows from the fact that the high types will have a higher willingness to pay for funding, and are therefore willing to bid higher in early auctions within the group. Time is discrete and all participants are risk neutral utility maximizers who discount the future at a common and constant discount factor δ ∈ [0, 1).

3.1.2. The Matching Technology

The organizer of the chit fund announces a menu of groups for potential participants to choose from. Each group is characterized by the number of participants in the group N, the contribution that each participant must make each period v, and the proportion of high types in the group p.¹⁰

Matching is instantaneous and without frictions. Participants with a given savings of v must decide on a group duration. All agents simultaneously decide which type of group to participate in and therefore choose N to maximize their normalized expected payoff from participation W(γ, N, p, v). This payoff will depend on the agent’s type γ, the per period contribution v, the group duration N, and the proportion of high types in the group p. The proportion p is determined by the choice of other participants. In equilibrium, p will act as a balancing force, adjusting endogenously through the matching process to leave agents indifferent between different group durations. The discussion that follows will describe how p varies across groups with different durations N, for a given v.¹¹

3.1.3. The Auction Technology

The proportion of high types in groups of different durations N is determined endogenously through the first stage matching, as described previously. Given p, in a group of duration N, the auction technology determines the (normalized) expected payoff for each type W(γ, N, p, v) in the second stage. In each period t = 1, …, N, all participants in a group contribute an amount v to the fund, and at the same time, at each t a second price auction is conducted in which the highest bid wins, and pays the second highest price. In the case of a tie, each of the tying bids is selected to win with equal probability. Each chit fund member can win the auction only once, so that participants in the auction are all those N − t + 1 chit fund members who have not won the auction yet. The winner receives the period’s contribution of all N participants Nv minus her bid, which is distributed as a “dividend”. The dividend is distributed equally among the remaining N − t participants, that is, those who have not won the auction yet.

The set up of the model is consistent with the actual organization of the chit fund auction in that there are no restrictions on the information concerning past bids or the identity of past winners. However, the model departs from the actual chit fund auction in two respects. First, the auction executed in reality is an English auction, namely, an ascending bid auction. Because participants bid up to their reservation value and the winner pays the loser’s reservation value, the English auction is strategically equivalent to the second price auction. Second, all N participants in the group, including the most recent winner, share the winning bid equally each period in practice. Although the assumption in the model does not change the nature of the auction, the advantage of the setup we have chosen is that it simplifies the expression for the payoff that we derive for each type.¹²

3.2. The Second Stage: Strategic Bidding

An agent who joins an N-period group obtains an expected payoff denoted by V₁(γ, N, v, p) in the first period from participation in that group. When this group terminates after N periods, the infinitely lived agent will join a new group with the same characteristics, receiving a payoff V₁(γ, N, v, p), N + 1 periods in the future, which is equivalent to a discounted payoff δ^NV₁(γ, N, v, p). This process continues indefinitely in the future so that the normalized expected payoff W(γ, N, v, p) that agents use to compare groups of different characteristics at the matching stage can be expressed as

$$W(\gamma ,N,v,p)=V_1(\gamma ,N,v,p)(1+{\delta }^N+{\delta }^{2N}+\dots )=\frac{V_1(\gamma ,N,v,p)}{1-{\delta }^N}.$$

As noted, p will adjust so that W(γ, N, v, p) is the same across different durations N for a given type γ in equilibrium. Let $\overline{W}(N,v,p)$ and $\underset{¯}{W}(N,v,p)$ be the payoffs for high and low types respectively. The equilibrium condition in the first stage will later be expressed in terms of the difference between the payoff to the borrower and the lender, denoted by $\Delta W(N,v,p)\equiv \overline{W}(N,v,p)-\underset{¯}{W}(N,v,p)$, where

$$\Delta W(N,v,p)=\frac{{\overline{V}}_1(N,v,p)-{\underset{¯}{V}}_1(N,v,p)}{1-{\delta }^N}=\frac{\Delta V_1(N,v,p)}{1-{\delta }^N},$$

and so we will begin by deriving an expression for ΔV₁(N, v, p) in the second stage of the model, taking p and N as given. The comparative statics with respect to p and N, dΔW(N, v, p)/dp and dΔW(N, v, p)/dN that we subsequently compute will be used to derive the equilibrium relationship between p and N in the first (matching) stage of the model.

Consider a group of duration N, with a proportion p of high types. In Proposition C.1 in Appendix A, the equilibrium bids are derived in greater detail, and we find that bids by high types always dominate bids by low types in equilibrium, so high types end up winning the pot in the first pN periods. Any high type’s expected payoff in period t ≤ pN, conditional on her not having won before that date, can be written as

$${\overline{V}}_t=\frac{1}{pN-t+1}({\overline{V}}_N-{\overline{b}}_t)+\left(1-\frac{1}{pN-t+1}\right)\left(\delta {\overline{V}}_{t+1}+\frac{1}{N-t}{\overline{b}}_t\right),$$

where ${\overline{V}}_N=Nv(1+\overline{\gamma })$ is the payoff in the last period, which is also equal to the return from investing.¹³ The probability of winning for a high type is 1/(pN−t+1), where pN−t+1 is the number of high types remaining in period t. When the individual wins, the payoff is the return on investment ${\overline{V}}_N$ less the bid ${\overline{b}}_t$. With complementary probability, the high type loses and gets the discounted expected payoff in the next period plus her share of the bid ${\overline{b}}_t$ that is distributed equally among the N − t remaining players who have not won yet.

We also show in Appendix A that for t = 1, …, pN − 1, the equilibrium strategy of the high types is to bid ${\overline{b}}_t=\left(\right(N-t)∕(N-t+1\left)\right)({\overline{V}}_N-\delta {\overline{V}}_{t+1})$. The intuition behind this is that in all those periods, high types are competing with high types. This bidding strategy makes a player indifferent between winning the auction today, and losing and getting the discounted continuation payoff plus the dividend: ${\overline{V}}_N-{\overline{b}}_t=\delta {\overline{V}}_{t+1}+(1∕(N-t\left)\right){\overline{b}}_t$. For t = 1, …, pN−1, the expected payoff is thus given by

$${\overline{V}}_t={\overline{V}}_N-{\overline{b}}_t=\delta {\overline{V}}_{t+1}+\frac{1}{N-t}{\overline{b}}_t.$$

For the low types, who lose for sure in the early periods, the corresponding payoff is expressed as

$${\underset{¯}{V}}_t=\delta {\underset{¯}{V}}_{t+1}+\frac{1}{N-t}{\overline{b}}_t.$$

We can now calculate ΔV_t immediately from the equilibrium payoffs above: ΔV_t = δΔV_t+1. Solving recursively, ΔV₁ = δ^pN−1ΔV_pN.

In period t = pN, there is only one high type left, and she now competes with all the low types. In this case, we show in Appendix A that the high type wins for sure, and pays the low type’s bid, which leaves low types indifferent between winning and losing in equilibrium, ${\underset{¯}{b}}_t=\left(\right(N-t)∕(N-t+1\left)\right)({\underset{¯}{V}}_N-\delta {\underset{¯}{V}}_{t+1})$. This implies that

$${\overline{V}}_t={\overline{V}}_N-{\underset{¯}{b}}_t,$$

$${\underset{¯}{V}}_t=\delta {\underset{¯}{V}}_{t+1}+\frac{1}{N-t}{\underset{¯}{b}}_t={\underset{¯}{V}}_N-{\underset{¯}{b}}_t.$$

Differencing these equations at t = pN, we find that ΔV_pN = ΔV_N. Substituting this expression for ΔV_pN in the expression for ΔV₁,

$$\Delta V_1={\delta }^{pN-1}\Delta V_N,$$

where ΔV_N = NvΔγ.

From the expression for ΔW, it immediately follows that

$$\Delta W(N,p,v)=\frac{{\delta }^{pN-1}Nv\Delta \gamma }{1-{\delta }^N}.$$ (1)

We now derive two important properties of ΔW in any group, which indicate howthe difference between the payoff to the borrowers and the lenders responds to changes in p and N. Differentiating ΔW with respect to p, it follows immediately that ΔW is decreasing in p.¹⁴ As p increases, competition between the high types increases, pushing up the bids in the early periods. Higher early bids imply higher payoffs for the low types since the bid amounts are distributed among the losers, with an accompanying decline in the payoff for the high types.

Lemma 1. Fixing the group duration N, the difference in the (normalized) expected payoff between borrowers and lenders ΔW is decreasing in the proportion of borrowers p.

Proof. Differentiating ΔW(N, p) with respect to p, we get

$$\frac{d\Delta W}{dp}=\Delta WN\ln \delta <0,$$

since ln δ < 0.

Next, we turn to the effect on ΔW of an increase in N. Consider a simple example with 10 borrowers and 10 lenders in the group (p = 0.5, N = 20). Borrowers win on average in the fifth period, and lenders win on average in the fifteenth period. Now increase the group size to 24 participants, with the same proportion p = 0.5 of borrowers and lenders as before. Borrowers win on average in the sixth period in this case, and lenders expect to win in the eighteenth period. An increase in N, holding p fixed, evidently shifts back the winning time more for lenders than for borrowers (the delay effect). Note, however, that borrowers are more impatient than lenders (this is why they bid more and win early), and so even a single-period delay can be costly for them. This delay, together with the fact that there are now more borrowers (pN), increases the competition for the pot in the early periods, lowering the payoff for the borrowers and increasing it for the lenders (the competition effect). The delay effect and the competition effect work in opposite directions: When participants (particularly borrowers) are sufficiently impatient (δ is low), the competition effect dominates and an increase in N will lower ΔW. When borrowers and lenders are both very patient (δ tends to one), the delay effect dominates and ΔW will be increasing in N.

Lemma 2. Fixing the proportion of high types p, the difference in the (normalized) expected payoff between borrowers and lenders ΔW is decreasing (increasing) in the duration of the chit fund N, for sufficiently impatient (patient) participants.

Proof. Again, from equation (1) it follows that

$$\frac{d\Delta W}{dN}=v\Delta \gamma \frac{{\delta }^{pN-1}}{{(1-{\delta }^N)}^2}\left[\right(\ln \delta \cdot pN+1\left)\right(1-{\delta }^N)+N{\delta }^N\ln \delta ].$$

Observe that as δ approaches 1, dΔW/dN = 0 and as δ approaches 0, dΔW/dN goes to −∞. Thus, even if dΔW/dN is positive for some values of δ, it must be negative for δ sufficiently small (close to zero). A sufficient condition for dΔW/dN < 0 is that ln δ · pN + 1 < 0, since ln δ < 0, which implies δ < e^−1/pN ∈ [0, 1]. As a result, there exists a δ* ≥ e^−1/pN such that for all δ < δ*, dΔW/dN < 0.

3.3. The First Stage: Endogenous Matching

We now proceed to describe the process by which participants sort themselves into chit fund groups. Each group is characterized by the number of participants N and the (correctly) anticipated belief about the proportion of high types that will decide to join that group p(N). A potential participant choosing between alternative chit fund groups will compare the normalized payoff W from each group.

Suppose that a menu of groups is offered to potential participants. Then for each group N_i there will be associated an equilibrium belief p(N_i) denoted by p_i. A matching equilibrium requires every participant to choose the group duration N that maximizes the normalized value function W(γ, N_i, p_i). Note that we suppress the fixed per period contribution v in the W function, and in all the discussion that follows, to simplify the exposition. If chit funds of different durations are to coexist, then utility maximization requires a participant of a given type to be indifferent between participating in any of the groups:

$$W(\gamma ,N_i,p_i)=W(\gamma ,N_j,p_j)\forall \gamma ,\forall i\ne j.$$ (2)

It follows immediately that if condition (2) is satisfied for both $\underset{¯}{\gamma }$ and $\overline{\gamma }$, then the difference in the normalized value δW(N, p) will also be equalized across the groups:

$$\Delta W(N_i,p_i)=\Delta W(N_j,p_j)\forall i\ne j.$$ (3)

In addition, the proportion of high types p_i in each group must be consistent with the proportion μ of high types in the entire market. Consider the case of two types $\overline{\gamma }$, $\underset{¯}{\gamma }$ with fractions μ, 1 −μ out of a total of n participants. Let the measure of groups of type i in equilibrium be n_i. Then the consistency condition requires

$$\sum _i{n}_{i}p\left(N_i\right)N_i=\mu \sum _i{n}_i{N}_i,$$ (4)

where the total measure of participants is ${\sum }_i{n}_i{N}_i=n$

We can now derive the main property of a matching equilibrium. Consider any two groups i, j with N_i < N_j. From Lemma 2, it follows that, for sufficiently impatient participants,

$$\Delta W(N_i,p)>\Delta W(N_j,p)\forall p.$$

Evaluated at p = p_i, this implies ΔW(N_i, p_i) > ΔW(N_j, p_i). In equilibrium, ΔW(N_i, p_i) = ΔW(N_j, p_j) from equation (3), so that

$$\Delta W(N_j,p_j)>\Delta W(N_j,p_i).$$

This implies, from Lemma 1, that p_i > p_j. Conversely, for sufficiently patient participants, it is easily verified that p_i < p_j.

The intuition for this result is very simple. When participants are sufficiently impatient, we know from Lemma 2 that ΔW is greater in short duration groups, for a given p. Thus p must be larger in the short duration groups, from Lemma 1, to equalize ΔW across groups of different durations. The converse is true when agents are patient. Thus we have proved Proposition 1.

Proposition 1. The proportion of high types is systematically related to the duration of the group in the matching equilibrium: This proportion is decreasing (increasing) in group duration for sufficiently impatient (patient) participants.

Proposition 1 holds for any equilibrium with multiple group durations. The Proposition does not formally establish that chit fund groups with different durations coexist, but we will later verify empirically that this is the case. Of course, the coexistence of different duration groups can be due to other reasons. For example, one could imagine that participants have an idiosyncratic taste for particular group durations. This dimension of participant heterogeneity, different from the one proposed in our model, could explain the presence of multiple group durations. However, as long as this preference for duration is independent of a participant’s type (borrower or lender), it would not explain the systematic relationship between the proportion of high types p_i and group duration N_i, as implied by Proposition 1. If the preference for duration does depend on the type, then the correlation between p_i and N_i has an alternative interpretation. But this preference for duration, even if it varies by type, will not explain the change in the correlation between p_i and N_i as a consequence of the bid cap that we derive in Proposition 2 subsequently.

As noted, competition across groups in the chit fund, which we believe is an important feature of this institution, cannot be observed directly. The systematic relationship between the proportion of borrowers in the group and its duration, which follows from the no-arbitrage condition in equation (3), allows us to empirically identify the presence of such competitive pressures in this institution.

3.4. The Bid Cap and the Change in Endogenous Matching

The law that came into force in September 1993 caps the bids at 30% of the auction value N_v. We now proceed to study the effect of this restriction on the matching equilibrium. We begin by showing that for a given p and N, the effect of capping the bids in 1993 is to increase $\overline{W}$ and decrease $\underset{¯}{W}$. Intuitively, capping reduces competition among the high types, increasing their payoffs at the expense of the low types. This change in payoffs in the capped groups leads to a re-sorting of low types and high types across the matching market, with the proportion of high types increasing disproportionately in the capped groups, to bring the market back into equilibrium.

Let ${\overline{W}}^c$ and ${\underset{¯}{W}}^c$ be the payoffs for high and low types when the group is capped, $\Delta W^c={\overline{W}}^c-{\underset{¯}{W}}^c$. Prior to the capping, the payoff to the high types is

$$\overline{W}=\frac{{\overline{V}}_1}{1-{\delta }^N}=\frac{{\overline{V}}_N-{\overline{b}}_1}{1-{\delta }^N}$$

and to the low types is

$$\underset{¯}{W}=\frac{{\underset{¯}{V}}_1}{1-{\delta }^N}=\frac{1}{1-{\delta }^N}\left(\delta {\underset{¯}{V}}_2+\frac{1}{N-1}{\overline{b}}_1\right).$$

Consider now the case in which the high bid in the first period is constrained, while the low bid is not (let b^c denote the constraint on the bid): ${\underset{¯}{b}}_1\le b^c\le {\overline{b}}_1$.¹⁵ Then it immediately follows that

$${\overline{W}}^c>\frac{{\overline{V}}_N-{\stackrel{‒}{b}}_1}{1-{\delta }^N}=\overline{W}.$$

Likewise,

$${\underset{¯}{W}}^c<\frac{1}{1-{\delta }^N}\left(\delta {\underset{¯}{V}}_2+\frac{1}{N-1}{\overline{b}}_1\right)=\underset{¯}{W}.$$

because the lowtypes are not constrained and ${\underset{¯}{V}}_2$ is not affected by the constraint in the first period. It then also follows that $\Delta W^c\ge \Delta W$. We have thereby established Lemma 3.

Lemma 3. Consider the case in which high bids are constrained, while low bids are not. Then the difference in (normalized) payoffs between high types and low types ΔW increases under the constraint, for a fixed p and N.

The increase in ΔW in the capped groups shifts the matching market out of equilibrium and we next proceed to study how the proportion of high types adjusts in both capped and uncapped groups to bring the market to its new equilibrium configuration. We will assume that there are only two types of groups, N_i and N_j, where group N_j is capped while N_i is unconstrained. Let ΔW′ denote the difference in the payoffs for high and low types in the new equilibrium, and let $p_i^{\prime }$, $p_j^{\prime }$ be the new equilibrium proportions of high types.

Because N_i is unconstrained, ΔW′(p_i) = ΔW(p_i). On the other hand, N_j is constrained, which implies from Lemma 3 that ΔW′(p_j) > ΔW(p_j). Equilibrium prior to the capping requires that

$$\Delta W\left(p_i\right)=\Delta W\left(p_j\right),$$

which in turn implies, from the earlier equations, that

$$\Delta W^{\prime }\left(p_i\right)<\Delta W^{\prime }\left(p_j\right).$$

Now equilibrium after the capping requires

$$\Delta W^{\prime }\left(p_i^{\prime }\right)=\Delta W^{\prime }\left(p_j^{\prime }\right),$$

so p_i and p_j must adjust to $p_i^{\prime }$ and $p_j^{\prime }$ in order to restore this equilibrium condition. Assuming that the proportion of high types in the market μ, and the mix of groups n_i/n_j are fixed, and because there are only two types of groups, the consistency condition, equation (4), tells us that p_i and p_j must shift in opposite directions. This follows immediately from the observation that μ is a weighted average of p_i and p_j before the capping and $p_i^{\prime }$ and $p_j^{\prime }$ after the capping.

From Lemma 1, ΔW is decreasing in p. As a result, p_i must decrease and p_j must increase to restore equilibrium after the capping:

$$p_i^{\prime }-p_i<0<p_j^{\prime }-p_j,$$

thereby proving the following proposition.

Proposition 2. The proportion of high types will increase more in the constrained groups than in the unconstrained groups.

The preceding result was derived under the condition that the proportion of high types in the market μ and the mix of groups n_i/n_j were fixed. In practice, μ not surprisingly increases after the capping. This “entry” effect shifts both $p_i^{\prime }$ and $p_j^{\prime }$ upward, but as long as the sorting across groups described here is strong enough, we would still expect the proportion of high types to increase more in the constrained groups.

3.5. The Bid Cap and the Change in the Mix of Groups

The cap on the bids was seen to increase the proportion of high types more in the capped groups than in the unconstrained groups to bring the matching market back into equilibrium. We next proceed to study how the mix of groups adjusts to the regulatory change.

Continuing with the simple case with two types of groups, of duration N_i, N_j, where N_j is capped and N_i is unconstrained, the consistency condition, equation (4), requires that

$$p_i{n}_i{N}_i+p_j{n}_j{N}_j=\mu (n_i{N}_i+n_j{N}_j),$$

where n_i and n_j denote the measure (number) of groups of each type. Then

$$\frac{n_i}{n_j}=\frac{N_j}{N_i}\frac{\mu -p_j}{p_i-\mu }.$$

Although the regulation placed a 30% cap on all groups, we will see subsequently that long duration groups ended up being capped in practice, while short duration groups remained essentially unconstrained: N_j > N_i. We will also see, consistent with Proposition 1, that the proportion of high types is decreasing in the duration of the group. With two types of groups, this implies that p_i > μ > p_j.

Treating p_i and p_j as fixed,¹⁶ it is easy to verify from the last equation that the increase in μ that will be seen to accompany the capping must lead in turn to an increase in n_i/n_j, as summarized in Proposition 3.

Proposition 3. Capping the bids in the long duration groups results in an increase in the proportion of short duration groups in the matching market.

Propositions 2 and 3 will allow us to identify the endogenous response by chit fund participants to the restrictions on ex post competition within the group that occurred as a consequence of the bid cap, further highlighting the competitive nature of this decentralized institution.

4. Testing the Theory

We now proceed to test the implications of the competitive matching model. Section 4.1 describes the various data sources used in the empirical analysis. Section 4.2 discusses the empirical specification used for testing the theory. Section 4.3 classifies groups for the empirical analysis and Section 4.4 studies the characteristics of the participants in the chit fund auctions. Section 4.5 tests Propositions 1 and 2 and Section 4.6 tests Proposition 3. Section 4.7 concludes with implicit interest rate calculations.

4.1. The Data

We use three sources of data in this paper. First, we obtained a complete record of all winning bids in all the groups operated by Shriram Chits and Investments Pvt. Ltd. that commenced between 1 October 1992 and 30 September 1994 in the city of Chennai. Recall that the bid cap applied to groups that commenced after 30 September 1993. Thus, the sample period covers exactly one year before and one year after the imposition of the 30% cap. When we refer to the years 1993 and 1994 henceforth in the paper, we will actually be referring to the 1 October to 30 September period just before and just after the capping. Chennai is the largest commercial city in South India, and Shriram Chits, which is the largest chit fund company in the state of Tamil Nadu, has its headquarters, and 20 neighborhood branches, in the city. In total, 78,000 individuals participated in the 2,000 chit fund groups that commenced in the city during the sample period.

Our second source of data provides income information for a limited number of subscribers in the sample. Although the winning bids and the group characteristics are computerized and readily available, this additional subscriber information can only be obtained from the application forms which are filled in at the time of entry. These application forms are subsequently stacked in back rooms in each branch office, located all over the city. We picked a random sample of groups and then attempted to obtain income information on all their participants, from the respective branches. Ultimately, this information was collected for 21,906 subscribers (roughly 25% of the full sample).We appear to have been more successful in collecting this additional information for individuals belonging to groups that commenced in 1994, and thus there is some concern that this restricted sample may not be randomly selected. We should emphasize, however, that income data will only be used in a few exploratory regressions and to report some basic statistics; in particular, it is not required to test Propositions 1–3.

And finally, our third source of data is an aggregate breakdown of groups, based on the size of the pot auctioned in each month and the duration, in each year over the 1992–2001 period. Extensions to the analysis that we report later in Section 4.6 will use these aggregate data to study long-term changes in the mix of groups.

4.2. The Empirical Specification

Proposition 1 describes the relationship between the proportion of borrowers and group duration in the unconstrained competitive equilibrium prior to the capping. To test this Proposition we estimate regressions of the form,

$$p_i=\alpha +\beta N_i+{\epsilon }_i,$$ (5)

where p_i is the proportion of borrowers in group i, N_i is the duration of group i, and ε_i is a mean-zero disturbance term. β < 0 for sufficiently impatient borrowers and β > 0 otherwise, from Proposition 1.

A particularly convenient feature of this institution is that we can identify ex ante borrowers, who are listed as “finance companies” in the records. These corporate subscribers account for approximately 20% of all the observations in our data. The proprietors of these select companies appear to be trusted by the chit fund organizers, and most likely have social ties to them. Whereas the private subscribers must provide information on their income, assets, and occupation to the chit fund organizers, and also furnish the names and addresses of three guarantors, the corporate subscribers face none of these requirements. The money collected from the auction is invested elsewhere by these companies, who clearly have access to superior investment opportunities than the private subscribers who are for the most part salaried employees. p_i is thus computed as the proportion of corporate subscribers in each group, and the regression above is estimated at the group level using data from 1993 only (prior to the bid cap).

We use two measures of group duration in the empirical analysis. The first measure treats duration N_i as a continuous variable, and the second measure divides the sample into long and short duration groups. For the second measure, we construct a long duration dummy that takes a value one if the group runs for 40 months or longer, zero otherwise.¹⁷ Equation (5) will be estimated using both measures of group duration.

Proposition 2 predicts that the proportion of borrowers will increase more in groups that are capped. We will see later that the long duration groups are capped severely, whereas the short duration groups remain essentially unconstrained. Equation (5) can be augmented to test these predicted changes using data from 1993 and 1994:

$$p_i=\alpha +\beta N_i+\lambda {1994}_i+\theta N_i\cdot {1994}_i+{\xi }_i,$$ (6)

where 1994_i is a binary variable that takes the value one if the group commenced after the cap in 1994, zero if it commenced in 1993. ξ_i is a mean-zero disturbance term, and the remaining variables were defined earlier. As earlier, α, β continue to measure the p_i, N_i correlation in 1993, and so have the same interpretation. The theory has no prediction for the secular change in p_i following the capping, and hence for λ. But Proposition 2 tells us that p_i should increase more in long duration groups, which are capped, than in short duration groups: θ > 0. As before, equation (6) will be estimated at the group level, treating duration N_i either as a continuous variable or as a binary variable (the long duration dummy).

The 1990s were a period of rapid economic change in India, with market liberalization opening up new opportunities and alternative sources of capital. The mix of borrowers and lenders in the chit funds might well have changed in this new environment. Given the uncertainty associated with the legal process in India, we previously found it reasonable to treat the imposition of the bid cap in September 1993, 11 years after the passing of the Chit Fund Act, as an unanticipated policy shock. Suppose instead that some potential participants had prior information and adjusted their time of entry at the margin to join groups that commenced just before or just after September 1993. Such adjustments might also have changed the overall proportion of borrowers if access to information varied by type. It is important to note, however, that compositional change of this sort would not undermine our test of the competitive response to the bid cap—Proposition 2—which is based on the differential change in the proportion of borrowers across groups of different durations.

4.3. Classification of Groups

All the results in Section 3 were derived for a given monthly contribution v. Appendix B derives the matching results under an alternative interpretation, where participants save for a target, namely, a given chit value Nv. Because both interpretations predict the same results, equations (5) and (6) will be estimated for a specific v or Nv. Chit values range from Rs.10,000 to over Rs.100,000, and monthly contributions range from Rs.200 to over Rs.1000. There are thus many values of v and Nv reported in the data, making estimation of these equations for each value infeasible. What we do instead in the empirical analysis is to partition the sample of groups into aggregate categories, along the v or the Nv dimension.

By treating v as parametric in Section 3, we implicitly assume that subscribers save a fixed fraction of their income to invest in the chit fund each period. When treating Nv as parametric in Appendix B we assume instead that subscribers save for a fixed target, which we would expect depends once more on their income. Low (high)v or Nv groups will tend to be chosen by low (high) income subscribers. We thus proceed to classify groups based on how their choice (exogenously) depends on subscribers’ incomes.

To implement this classification scheme we regress the choice of chit value or monthly contribution on subscribers’ incomes. Table C.1 in Appendix C reports multinomial logit and linear probability estimates of these regressions. The chit value regressions restrict attention to six values that together account for over 90% of all the observations in the sample. The monthly contribution regressions restrict attention to four contribution levels that account for nearly 85% of the sample. The variation in the income coefficient across these chit values or contributions then allows us to partition the full sample of groups into aggregate categories. We classify low (high)Nv or v groups as those groups whose choice is decreasing (increasing) in subscriber income. Medium value groups are defined to be those intermediate groups whose choice is unrelated to income. Based on this classification scheme, Rs.10,000 and Rs.50,000 are designated as the cut-offs separating low, medium, and high chit values. The corresponding cut-offs for low, medium, and high monthly contributions are Rs.500 and Rs.1000.¹⁸

By partitioning groups along the Nv or the v dimension we are essentially studying the relationship between p_i and N_i, and the change in this relationship within each aggregate chit value or monthly contribution category. While group durations N_i range from 20 months to 100 months in the data, Table 1 verifies that there is sufficient variation in the duration variable within each category as well, particularly when groups are partitioned by chit value.

Table 1.

Classification of groups.

		chit value			monthly contribution
Groups divided by:		Low	Medium	High	Low	Medium	High
Chit value/contribution:		(1)	(2)	(3)	(4)	(5)	(6)
Duration
20 months		17.42	3.35	5.79	–	23.29	7.02
25 months	SHORT	8.51	8.77	17.38	10. 25	–	27.41
30 months		–	49.29	5.79	–	40.85	14.47
40 months		73.87	24.77	18.90	88.93	23.41	13.60
50 months	LONG	0.20	0.90	38.11	0.82	0.24	27.41
60 months		–	12.90	10.67	–	12.20	7.68
100 months		–	–	3.35	–	–	2.41
Total		100.00	100.00	100.00	100.00	100.00	100.00
Total no. of groups		1,022	775	328	849	820	456

Note: Chit value is the product of the monthly contribution and the group duration (in months).Chit value: Low if chit value = 10,000; Medium if chit value 10,000–50,000; High if chit value ≥ 50,000.Contribution: Low if contribution < 500/month; Medium if contribution 500–1,000, High if contribution > 1,000.Duration: Long ≥ 40 months.

4.4. Description of the Participants

Each neighborhood branch of the chit fund company posts a menu of available groups, characterized by duration and chit value, at each point in time. Prospective participants choose a group from this menu and once a group is filled, it is allowed to commence after the necessary permission from the Registrar of Chit Funds has been obtained. Although new groups form throughout the year, the company helps coordinate the formation of these groups by organizing two major subscription campaigns, in April and in October, each year.

The change in the proportion of borrowers across groups of different durations, as predicted in Proposition 2, is based on the assumption that the pool of participants in the matching market is fixed over time. We test Proposition 2 using data on groups that commenced one year before and one year after the imposition of the bid cap in September 1993. Groups run for at least 20 months, and so individuals who joined groups in the year prior to the bid cap are clearly distinct from individuals who joined in the following year. Even if we observed the same individuals making repeated participation decisions, incomes could well have changed over a two-year period in this growing economy. To rule out compositional change in the pool of participants over time, we proceed to verify that the income distribution among the subscribers was roughly unchanged from 1993 to 1994.

Table 2, Panel (A) compares the income distribution in 1993 and 1994, separately for low, medium, and high chit values and monthly contributions. Incomes are similar at all quantile levels in the two years, within each chit value and monthly contribution category, indicating that the underlying income distribution among the participants was relatively stable.

Table 2.

Description of participants.

Groups partitioned by:	chit value						monthly contribution
Chit value/contribution:	Low		Medium		High		Low		Medium		High
Year:	1993	1994	1993	1994	1993	1994	1993	1994	1993	1994	1993	1994
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
A. Income Distribution (private subscribers)
Mean	2.90	2.98	3.66	3.66	4.84	7.59	2.88	2.96	3.60	3.53	4.76	7.05
(standard deviation)	(2.70)	(3.06)	(4.79)	(3.00)	(9.12)	(35.94)	(2.75)	(2.98)	(4.70)	(2.54)	(8.80)	(32.92)
0.10 quantile	1.14	1.12	1.52	1.55	1.86	1.94	1.15	1.10	1.50	1.50	1.87	1.90
0.25 quantile	1.63	1.70	2.23	2.24	2.58	2.71	1.62	1.66	2.20	2.16	2.52	2.66
0.50 quantile	2.47	2.50	3.00	3.03	3.55	3.83	2.44	2.48	3.00	3.00	3.52	3.74
0.75 quantile	3.50	3.50	4.10	4.33	5.00	5.25	3.47	3.46	4.05	4.21	5.00	5.14
0.90 quantile	4.90	5.00	5.79	6.00	7.35	8.00	4.85	5.00	5.68	5.93	7.05	7.90
B. Proportion of corporate subscribers
	0.17	0.23	0.15	0.20	0.12	0.24	0.17	0.23	0.15	0.20	0.13	0.23

Note: Chit value is the product of the monthly contribution and group duration (in months).Income is measured in thousands of Rs. per month.Statistics in Panel (A) are computed for private subscribers only.

Chit value: Low if chit value = 10,000; Medium if chit value 10,000–50,000; High if chit value ≥ 50,000.Contribution: Low if contribution < 500/month; Medium if contribution 500–1,000, High if contribution > 1000.

As noted, participants in the chit fund can be classified as private subscribers and corporate subscribers. Private subscribers reveal their income to the organizing company and supply the names of three guarantors, whereas the corporate subscribers provide no such information. The income statistics described herein are thus based on the private subscribers alone. The corporate subscribers play an important role in the chit fund institution, accounting for roughly 20% of all participants in Table 2, Panel (B). But whereas the increase in the proportion of corporate subscribers from 1993 to 1994, following the bid cap, is consistent with the view that they are effectively borrowers, we have not up to this point provided direct evidence supporting the ex ante classification of borrowers and lenders.

Table 3 verifies the classification of types by comparing the time period in which private subscribers and corporate subscribers win the auction within the group. The timing variable is defined as the month in which the subscriber wins the auction divided by the total duration of the group, and so is bounded between zero and one. The corporate subscriber variable equals one for the finance companies, zero otherwise. The constant term in the (linear) timing regression thus measures the average timing for the private subscribers, and the coefficient on the corporate subscriber dummy measures how much earlier on average the corporate subscribers win. High types win early, and as expected, the coefficient on the corporate subscriber dummy is negative, large in absolute magnitude, and very precisely estimated. The same result is obtained, without exception, in 1993 and 1994, for low, medium, and high chit values and monthly contributions.

Table 3.

Timing of winning bids by type of participant.

Dependent variable:	Timing
Chit value/contribution:	Low		Medium		High
Year:	1993	1994	1993	1994	1993	1994
	(1)	(2)	(3)	(4)	(5)	(6)
A. Groups partitioned by chit value
Corporate subscriber	−0.124	−0.124	−0.105	−0.144	−0.151	−0.118
	(0.005)	(0.006)	(0.007)	(0.006)	(0.010)	(0.008)
Constant	0.535	0.543	0.530	0.543	0.529	0.541
	(0.002)	(0.003)	(0.003)	(0.003)	(0.003)	(0.004)
Number of observations	21,400	14,635	14,300	13,411	7,555	6,750
B. Groups partitioned by contribution
Corporate subscriber	−0.122	−0.117	−0.114	−0.147	−0.134	−0.126
	(0.005)	(0.006)	(0.007)	(0.006)	(0.009)	(0.007)
Constant	0.534	0.540	0.532	0.544	0.529	0.543
	(0.002)	(0.003)	(0.003)	(0.003)	(0.003)	(0.003)
Number of observations	19,910	12,815	14,330	13,321	9,015	8,660

Note: Timing is measured as the winning month divided by the total duration of the group.Corporate subscriber equals one if finance company, zero otherwise.

Chit value: Low if chit value = 10,000; Medium if chit value 10,000–50,000; High if chit value ≥ 50,000.Contribution: Low if contribution < 500/month; Medium if contribution 500–1,000; High if contribution > 1,000.The individual subscriber is the unit of observation.Standard errors in parentheses.

4.5. Sorting across Groups

The analysis of endogenous sorting begins by testing Proposition 1, which states that the proportion of borrowers should be systematically related to the duration of the group. Restricting attention to groups that commenced in the unregulated regime, one year prior to September 1993, equation (5) is estimated within each of the aggregate chit value and monthly contribution categories in Table 4. Panel (A) of Table 4 measures duration as a binary variable (the long duration dummy), and Panel (B) measures duration as a continuous variable (in years). Consistent with ex ante competitive sorting, the coefficient on the duration variable is significant (with a few exceptions) across the entire range of pot sizes and monthly contributions, and across all the specifications that we experiment with in Table 4.¹⁹ The point estimates in Panel (A) indicate that the proportion of borrowers in the short duration groups is on average 0.17, with a corresponding proportion of 0.14 in the long duration groups. Given that the duration coefficient is negative, this implies from Proposition 1 that the participants are sufficiently impatient.

Table 4.

Matching into groups (1993).

Dependent variable:	Proportion of corporate subscribers
Groups partitioned by:	chit value			monthly contribution
Chit value/contribution:	Low	Medium	High	Low	Medium	High
	(1)	(2)	(3)	(4)	(5)	(6)
A. Duration measured by a binary variable
Long duration dummy	−0.007	−0.014	−0.098	−0.018	−0.024	−0.063
	(0.008)	(0.009)	(0.014)	(0.012)	(0.010)	(0.011)
Constant	0.179	0.141	0.208	0.190	0.150	0.173
	(0.007)	(0.005)	(0.013)	(0.012)	(0.006)	(0.009)
Number of observations	594	391	161	512	417	217
B. Duration measured as a continuous variable (in years)
Group duration	−0.004	−0.014	−0.015	−0.016	−0.026	−0.014
	(0.005)	(0.009)	(0.004)	(0.010)	(0.008)	(0.004)
Constant	0.185	0.173	0.191	0.227	0.210	0.185
	(0.017)	(0.024)	(0.018)	(0.031)	(0.020)	(0.014)
Number of observations	594	391	161	512	417	217

Note: Long duration dummy equals one if the group runs for at least 40 months, zero otherwise.Chit value: Low if chit value = 10,000; Medium if chit value 10,000–50,000; High if chit value ≥ 50,000.Contribution: Low if contribution < 500/month; Medium if contribution 500–1,000; High if contribution > 1,000.Regressions use 1993 data only and the group is the unit of observation.Standard errors in parentheses.

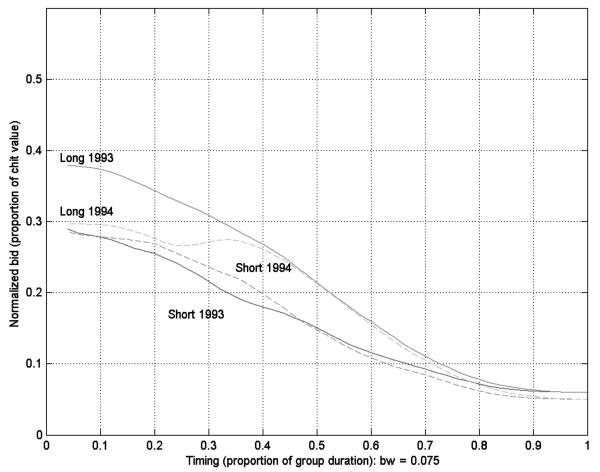
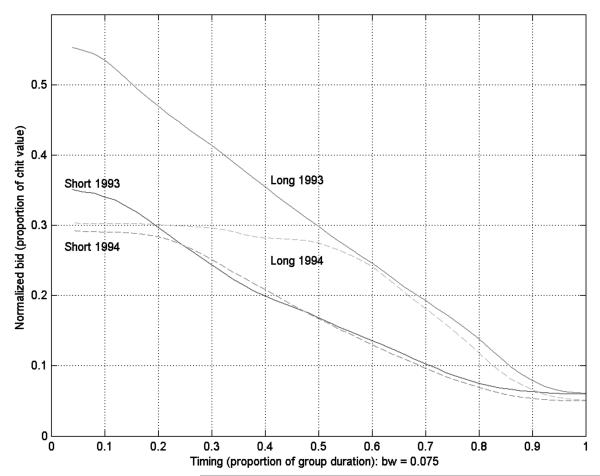
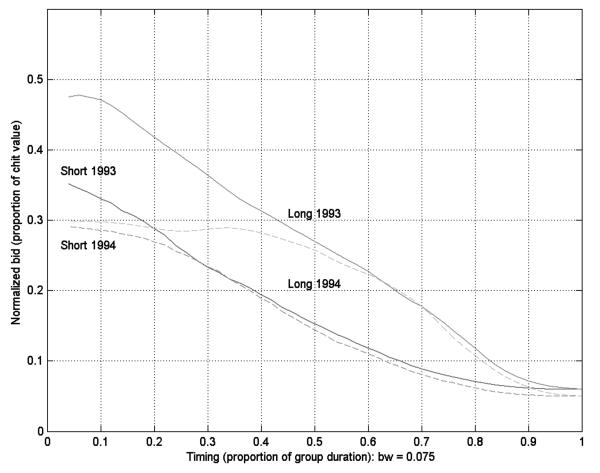
Next, we study the change in endogenous matching following the policy experiment. Proposition 2 tells us that the proportion of borrowers should increase more in capped groups, and we mentioned earlier that long duration groups were capped more severely than short duration groups. Figures 1-3 present nonparametric plots of the pattern of bids over the course of the group, in 1993 and 1994, for long and short duration groups. The bid amount is divided by the chit value to provide a normalized bid value on the y-axis that was exogenously capped at 0.3 in 1994. Because we are presenting groups with different durations on the same graph, the time period on the x-axis is measured as the fraction of the group duration, running from zero to one. Bids for long and short duration groups are not directly comparable with this normalization; for example, the average of the bids in the first and second month of a 20-month group would now be aligned vertically with the first bid in a 10-month group. But the effect of the capping on groups with the same duration is easy to visualize. Groups are partitioned into low, medium, and high monthly contributions in Figures 1-3.²⁰

Figure 1.

Bids—low monthly contribution.

Figure 3.

Bids—high monthly contribution.

The normalized bid declines over the course of the group, without exception, in Figures 1-3, bottoming out at 0.06 in 1993 and 0.05 in 1994 (this is the organizing company’s legally determined commission in each period, which is paid out of the winning bid). Normalized bids are also increasing in the monthly contribution across the figures, for both short and long duration groups. And, finally, the cap constrains 1994 bids in the early periods only. This cap is clearly more severe in the long duration groups, across all three monthly contribution categories, simply because the unconstrained 1993 bids are much higher than 0.3 in the early periods in those groups.²¹

Having established that bids in the long duration groups are capped more severely, we can now estimate equation (6). The prediction from Proposition 2 is that the coefficient on the group duration interacted with the 1994 dummy should be positive. Table 5 reports the results of this regression, with groups partitioned as usual by chit value and monthly contribution. Table 5 Panel (A) measures group duration with a long duration dummy, whereas duration is measured as a continuous variable (in years) in Panel (B).

Table 5.

Matching into groups (from 1993 to 1994)

Dependent variable:	Proportion of corporate subscribers
Groups partitioned by:	chit value			monthly contribution
Chit value/contribution:	Low	Medium	High	Low	Medium	High
	(1)	(2)	(3)	(4)	(5)	(6)
A. Duration measured by a binary variable
Long duration dummy - 1994 dummy	0.059	0.030	0.088	0.073	0.039	0.086
	(0.013)	(0.016)	(0.024)	(0.019)	(0.016)	(0.019)
Long duration dummy	−0.007	−0.014	−0.098	−0.018	−0.024	−0.063
	(0.009)	(0.011)	(0.018)	(0.013)	(0.011)	(0.014)
1994 dummy	0.004	0.031	0.040	−0.009	0.022	0.042
	(0.011)	(0.009)	(0.020)	(0.018)	(0.009)	(0.014)
Constant	0.179	0.141	0.208	0.190	0.150	0.173
	(0.008)	(0.006)	(0.016)	(0.013)	(0.006)	(0.010)
Number of observations	1,022	775	328	849	820	456
B. Duration measured as a continuous variable (in years)
Group duration - 1994 dummy	0.038	0.007	0.019	0.063	0.021	0.028
	(0.008)	(0.015)	(0.009)	(0.015)	(0.012)	(0.008)
Group duration	−0.004	−0.014	−0.015	−0.016	−0.026	−0.014
	(0.006)	(0.010)	(0.005)	(0.010)	(0.008)	(0.005)
1994 dummy	−0.063	0.020	0.037	−0.147	−0.020	−0.002
	(0.024)	(0.041)	(0.033)	(0.047)	(0.031)	(0.026)
Constant	0.185	0.173	0.191	0.227	0.210	0.185
	(0.017)	(0.028)	(0.022)	(0.033)	(0.021)	(0.017)
Number of observations	1,022	775	328	849	820	456

Note: Long duration dummy equals one if the group runs for at least 40 months, zero otherwise.1994 dummy equals one if the group commenced in 1994, zero otherwise.

Chit value: Low if chit value = 10,000; Medium if chit value 10,000–50,000; High if chit value ≥ 50,000.Contribution: Low if contribution lt; 500/month; Medium if contribution 500–1,000; High if contribution > 1,000.The group is the unit of observation.Standard errors in parentheses.

The coefficient on the duration-1994 interaction term is positive and significant (with a couple of exceptions) across all the specifications that we experiment with in Table 5.²² Thus the proportion of borrowers increases more in groups that are more severely capped, immediately following the regulatory shock, exactly as predicted by the competitive matching model. The coefficient on the 1994 dummy in Panel (A) measures the change in the proportion of borrowers in the short duration groups following the capping. The coefficient on the duration-1994 interaction term measures the additional change in the long duration groups. Looking across columns in Panel (A), group compositions clearly change dramatically from one year to the next, particularly in the long duration groups. The proportion of high types in long duration groups increases from 0.18 to 0.24 in the low chit value groups, from 0.13 to 0.19 in the medium chit value groups and from 0.11 to 0.24 in the high chit value groups.²³ Overall, the proportion of borrowers increased by 51% in the long duration groups versus 12% in the short duration groups. Adding the duration and the duration-1994 coefficients, which gives us the duration coefficient in 1994, it is apparent that the decline in the proportion of borrowers with group duration that we observed in 1993 is reversed by 1994.

4.6. Change in the Mix of Groups

The bid cap restricted competition within the group, favoring borrowers at the expense of the lenders. We see in Table 6 Panel (A) that the number of private subscribers (lenders) declines from 1993 to 1994 within all chit value and monthly contribution categories. In contrast, participation by the corporate subscribers (borrowers) increases across all categories except for the low chit values and monthly contributions. This explains the increase in the proportion of borrowers across all categories that we observed previously in Table 2 Panel (B); the overall proportion of borrowers (μ) increases from 16% to 22%. Participation levels also decline across all categories, and the total number of subscribers declines from 43,267 in 1993 to 34,797 in 1994 (a 20% decline).

Table 6.

Change in the mix of groups.

Groups partitioned by:		chit value						monthly contribution
Chit value/contribution:		Low		Medium		High		Low		Medium		High
Year:		1993	1994	1993	1994	1993	1994	1993	1994	1993	1994	1993	1994
		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
A. Subscriber participation
Private subscribers		17,688	11,331	12,133	10,772	6,637	5,108	16,468	9,848	12,113	10,700	7,877	6,663
Corporate subscribers		3,713	3,304	2,167	2,639	929	1,643	3,443	2,967	2,217	2,621	1,149	1,998
B. Proportion of short duration groups
		0.217	0.318	0.573	0.656	0.217	0.359	0.082	0.134	0.612	0.672	0.419	0.552
		(0.017)	(0.023)	(0.025)	(0.024)	(0.033)	(0.037)	(0.012)	(0.019)	(0.024)	(0.023)	(0.034)	(0.032)
C. Distribution of group durations
Duration:
20 months		14.65	21.26	2.05	4.69	6.83	4.79	–	–	21.58	25.06	7.37	6.69
25 months	SHORT	7.07	10.51	8.70	8.85	11.80	22.75	8.20	13.35	–	–	24.42	30.13
30 months		–	–	46.55	52.08	3.11	8.38	–	–	39.57	42.18	10.14	18.41
40 months		78.11	67.99	27.11	22.40	16.77	20.96	90.63	86.35	25.42	21.34	12.44	14.64
50 months	LONG	0.17	0.23	1.79	–	44.10	32.34	1.17	0.30	0.48	–	32.72	22.59
60 months		–	–	13.81	11.98	11.18	10.18	–	–	12.95	11.41	8.29	7.11
100 months		–	–	–	–	6.21	0.60	–	–	–	–	4.61	0.42
Total (%)		100	100	100	100	100	100	100	100	100	100	100	100

Note: Short duration groups run for less than 40 months.Chit value: Low if chit value = 10,000; Medium if chit value 10,000–50,000; High if chit value ≥ 50,000.Contribution: Low if contribution < 500/month; Medium if contribution 500–1,000; High if contribution ≥ 1,000.

Proportion of short duration groups in 1994 is significantly higher at the 5% level than in 1993, within each category in Pane (B) except for columns (9)–(10).Standard errors in parentheses.

Proposition 3 tells us that the increase in the proportion of borrowers in the matching market following the bid cap should result in an increase in the proportion of short duration groups. This is precisely what we see in Table 6 Panel (B) where the increase is significant at the 5% level in all cases except for columns (9)–(10). To verify the robustness of this result, group durations are disaggregated in Table 6 Panel (C). We see an increase in the popularity of groups running for less than 40 months, almost without exception, whereas this pattern is reversed for groups running 40 months or longer. It is apparent that the increase in the proportion of short duration groups in Panel (B) is driven by underlying changes across the entire range of group durations.

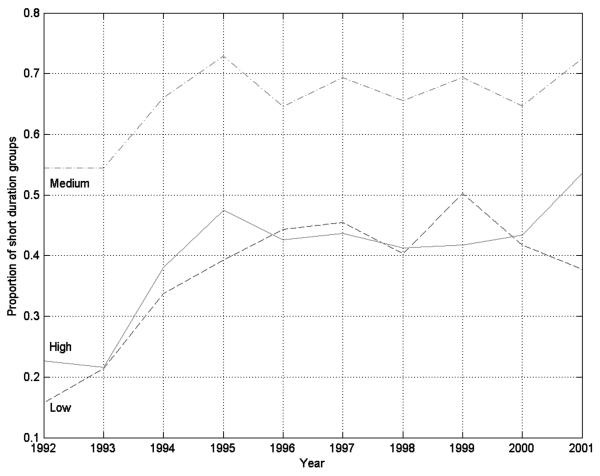
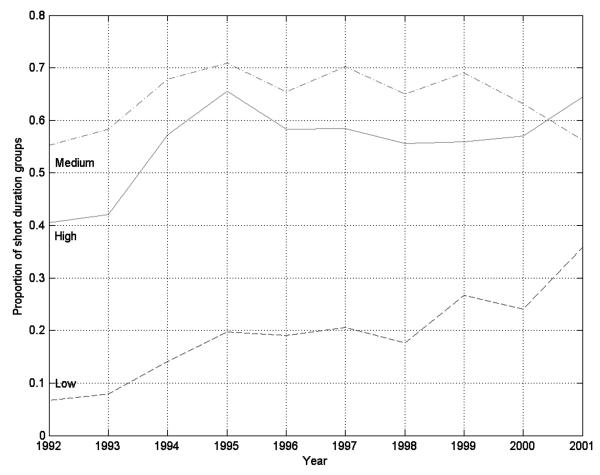
While the change in the proportion of borrowers within groups and the change in the mix of groups suggest that this decentralized institution is making its way to a new equilibrium, we cannot tell by studying behavior at two points in time whether this change is complete. The equilibrium conditions are derived in terms of the normalized payoff W, which is unobserved. But we can gain a rough sense of how quickly this institution settled into its new equilibrium by using aggregate group level data to study changes in the mix of groups over a longer ten-year period 1992–2001. The proportion of short duration groups that commenced in each year over this period is computed, separately for low, medium, and high chit values and monthly contributions. These proportions are plotted, without smoothing, in Figures 4 and 5.

Figure 4.

Proportion of short duration groups—partitioning groups by chit value.

Figure 5.

Proportion of short duration groups—partitioning groups by monthly contribution.

The proportion of short duration groups increases sharply from 1993 to 1994, for low, medium, and high chit values and monthly contributions, just as we saw in Table 6. But this increase continues for one more year, 1994–1995, after which the proportion of short duration groups flattens out. The proportion of short duration groups in low and high chit values in Figure 4 increases from about 0.2 in 1993 to over 0.4 by 1995. The medium chit values begin with a much higher proportion of short duration groups, above 0.5 in 1993, yet this proportion increases even further to 0.7 by 1995. The term structure in this market clearly responds quite dramatically to the regulatory change.

There seems to be some overshooting in 1995, and some shaking out thereafter, judging from the minor oscillations in the figures, but the basic shift from the pre-cap to the post-cap equilibrium is completed in two years.²⁴ The response to this exogenous shock is extremely rapid, given that this is a decentralized equilibrium. A fresh set of individuals enters this institution each year, which makes the rapid response even more remarkable.

4.7. Implicit Interest Rates

There is no explicit price for money (interest rate) in this non-market institution. But based on the actual bids we can still calculate the interest rate implicit in a given group. Let D ≡ 1/1+r_m ∈ [0, 1] be the monthly interest factor (where r_m is the monthly interest rate) and let c_t denote the funds received in period t. The participant contributes an amount v each month over a period of N months (the duration of the group). Hence, the internal rate of return for any participant must satisfy the condition

$$\sum _{t=1}^N{D}^{t-1}(c_t-v)=0.$$ (7)

The net present value of monthly contributions must equal the net present value of funds received. The inflow of funds in any period t in which a participant does not win the auction is given by c_t = 1/Nb_t: she gets her equal share of the bid. In one period, say τ, the participant wins the pot, in which case she collects c_τ = Nv−b_τ + 1/Nb_τ, that is, the total pot minus her bid Nv − b_τ in addition to her share of the bid. We can now rewrite the internal rate of return in equation (7) for a participant who wins the auction in period τ as

$$D^{\tau -1}(Nv-b_{\tau })+\sum _{t=1}^N{D}^{t-1}\left(\frac{1}{N}{b}_t-v\right)=0.$$

It follows immediately that the expressions for different agents only differ in the first term. Therefore, we can calculate the interest factor D from any two agents’ rate of return equations, namely, agents who win the bids in two different periods τ and τ′, as

$$D={\left(\frac{Nv-b_{\tau }}{Nv-b_{{\tau }^{\prime }}}\right)}^{1∕({\tau }^{\prime }-\tau )}$$

Using the relationship between D and the monthly interest rate r_m provided earlier, and converting r_m to the corresponding annual rate, we obtain

$$r={\left(\frac{Nv-b_{{\tau }^{\prime }}}{Nv-b_{\tau }}\right)}^{12∕({\tau }^{\prime }-\tau )}-1.$$ (8)

Table 7 reports the within-group interest rates in each chit value and monthly contribution category, for short and long duration groups, in 1993 and 1994. The interest rate is computed for τ = 2 and τ′ = N in Panel (A) and for τ = 0.2N and τ′ = N in Panel (B).²⁵

Table 7.

Implicit interest rates.

Groups partitioned by:	chit value						contribution
Chit value/contribution:	Low		Medium		High		Low		Medium		High
Duration:	Short	Long	Short	Long	Short	Long	Short	Long	Short	Long	Short	Long
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
A. Interest rate computed using first and last month
1993	16.48	14.15	18.92	18.17	24.18	20.88	15.76	14.20	18.33	18.15	20.60	20.88
	(0.36)	(0.12)	(0.32)	(0.63)	(1.02)	(0.56)	(0.38)	(0.12)	(0.28)	(0.64)	(0.69)	(0.56)
1994	17.00	9.95	14.52	8.77	16.58	8.38	16.09	9.95	15.30	8.77	15.88	8.38
	(0.42)	(0.04)	(0.15)	(0.16)	(0.37)	(0.13)	(0.36)	(0.04)	(0.24)	(0.16)	(0.25)	(0.13)
B. Interest rate computed using 0.20*duration and last month
1993	15.53	14.01	17.71	16.40	20.50	17.94	15.04	14.11	17.04	16.18	18.81	17.94
	(0.44)	(0.12)	(0.32)	(0.56)	(0.97)	(0.49)	(0.72)	(0.12)	(0.32)	(0.57)	(0.53)	(0.49)
1994	16.88	10.80	16.39	9.98	18.98	10.00	17.36	10.80	16.28	9.98	17.97	10.00
	(0.55)	(0.11)	(0.20)	(0.18)	(0.39)	(0.15)	(0.58)	(0.11)	(0.29)	−(0.18)	(0.32)	(0.15)

Note: Short duration groups run for less than 40 months, Long duration groups run for at least 40 month Chit value: Low if chit value = 10,000; Medium if chit value 10,000–50,000; High if chit value ≥ 50,000. Contribution: Low if contribution < 500/month; Medium if contribution 500–1,000; High if contribution ≥ 1,000.Mean interest rate (in percentage) with standard errors in parentheses.Interest rates are computed at the group level.

The 1989 report on Urban Informal Credit Markets in India (Dasgupta et al. 1989) tells us that the interest rate paid by non-banking finance companies, which include chit funds, was 18%. The unconstrained interest rates that we compute for 1993 match very well with this statistic, ranging from 14% to 24%. The same report tells us that the interest rate paid by nationalized banks on term deposits was 9%, so the popularity of the chit funds is easy to understand. The bid cap would have lowered the ability of the chit funds to capture gains from trade, and interest rates did decline dramatically in 1994, ranging from 8% to 19%, which is much closer to the bank rate. The sharp decline in participation by the private subscribers that we saw in Table 6 Panel (A) is consequently easy to understand.

Our model does not provide predictions for the relationship between the implicit interest rate and group duration. In practice, we see from Table 7 that interest rates within a chit value or monthly contribution category are slightly lower for long duration groups in 1993. In contrast, we see that the interest rates on the long duration groups are substantially lower than the corresponding rates in the short duration groups, within the same category, in 1994. While we cannot map the computed interest rates directly into normalized payoffs W, the much wider discrepancy in interest rates between long and short duration groups in 1994 suggests that the market was yet to reach its post-cap equilibrium, consistent with the long-term changes in the mix of groups reported earlier in Figures 4 and 5.

5. Conclusion

This paper studies a successful informal financial institution—the commercial chit fund—that brings heterogeneous agents together in groups to exploit gains from trade. We develop a framework for analyzing decentralized matching into these groups, and the equilibrium composition of participants that consequently arises. This framework predicts a systematic relationship between the composition of a group and its size, which we verify empirically. The change in the composition of groups of different sizes and the change in the mix of groups, following an unexpected regulatory change, also matches precisely with the predictions from the theory.

The chit fund is a complex institution, and unlike a standard financial market, the payoff a participant receives is not directly summarized in an ex ante price. Rather, it depends on the endogenous composition of participants in each group. It is therefore all the more striking that participants sort themselves so well across competing groups in the application that we consider. These findings suggest that the competitive matching model we develop might have applicability and bite in other settings where matching is an important equilibrium phenomenon.

Figure 2.

Bids—medium monthly contribution.

Appendix A: Equilibrium Bids and Proofs

Proposition A.1. For any group, the equilibrium bids for each type are

$${\overline{b}}_t=\frac{N-t}{N-t+1}({\overline{V}}_N-\delta {\overline{V}}_{t+1}),$$

$${\underset{¯}{b}}_t=\frac{N-t}{N-t+1}({\underset{¯}{V}}_N-\delta {\underset{¯}{V}}_{t+1}),$$

and the difference between the expected equilibrium payoffs for borrowers and lenders satisfies

$$\Delta V_1(N,p,v)={\delta }^{pN-1}\Delta V_N,$$

where $\Delta V_N(N,p,v)=Nv[\overline{\gamma }-\underset{¯}{\gamma }]=Nv\Delta \gamma$.

Proof. V_t denotes the expected payoff in period t for a participant who has not won the auction yet. Because p is assumed known to all players, this is effectively an auction of public information. There are pN high types in the group, so first consider periods in which more than one high type remains among the bidders, t = 1, …, pN − 1. The payoff to the high type i can be written as

$${\overline{V}}_t=\mathrm{Pr}\{{\overline{b}}_t^i>\max \{{\overline{b}}_t^{-i}\left\}\right\}({\overline{V}}_N-\max \{{\overline{b}}_t^{-i}\left\}\right)+(1-\mathrm{Pr}\{{\overline{b}}_t^i>\max \left\{{\overline{b}}_t^{-i}\right\}\left\}\right)\left(\delta {\overline{V}}_{t+1}+\frac{1}{N-t}\underset{{\overline{b}}_t\backslash \max \left\{{\overline{b}}_t\right\}}{\max }\left\{{\overline{b}}_t\right\}\right),$$

where ${\overline{b}}_t^i$ denotes the bid by a high type player i (as usual, the notation −i refers to any other player different from i, so ${\overline{b}}_t=\{{\overline{b}}_t^i,{\overline{b}}_t^{-i}\}$). Consider (type-contingent) symmetric bidding functions

$${\overline{b}}_t^i=\frac{N-t}{N-t+1}({\overline{V}}_N-\delta {\overline{V}}_{t+1}),$$

$${\underset{¯}{b}}_t^i=\frac{N-t}{N-t+1}({\underset{¯}{V}}_N-\delta {\underset{¯}{V}}_{t+1}),$$

and verify that bidding ${\overline{b}}_t^i$ is an equilibrium strategy. We assume that in the case of a tie in the bids, the winner is allocated at random, with uniform probability. Given the symmetric bid function for the high types, there will always be ties for t ≤ pN − 1, and as a result, the second price is equal to the winning bid. The expected payoff V_t is then

$$\begin{array}{cc}\hfill {\overline{V}}_t& =\mathrm{Pr}\{{\overline{b}}_t^i>\max \{{\overline{b}}_t^{-i}\left\}\right\}\left({\overline{V}}_N-\frac{N-t}{N-t+1}({\overline{V}}_N-\delta {\overline{V}}_{t+1})\right)+(1-\mathrm{Pr}\{{\overline{b}}_t^i>\max \left\{{\overline{b}}_t^{-i}\right\}\left\}\right)\left(\delta {\overline{V}}_{t+1}+\frac{1}{N-t}\frac{N-t}{N-t+1}({\overline{V}}_N-\delta {\overline{V}}_{t+1})\right)\hfill \\ \hfill & =\frac{1}{pN-t+1}\left(\frac{1}{N-t+1}({\overline{V}}_N+(N-t\left)\delta {\overline{V}}_{t+1}\right)\right)+\left(1-\frac{1}{pN-t+1}\right)\left(\frac{1}{N-t+1}({\overline{V}}_N+(N-t\left)\delta {\overline{V}}_{t+1}\right)\right)\hfill \\ \hfill & =\frac{1}{N-t+1}({\overline{V}}_N+(N-t\left)\delta {\overline{V}}_{t+1}\right),\hfill \end{array}$$

where Pr{${\overline{b}}_t^i$ > $\max \left\{{\overline{b}}_t^{-i}\right\}$} = 1/(pN−t+1). Note that there is no incentive to deviate either way. Overbidding, say ${\overline{b}}_t^i+d$, implies winning the auction with certainty; however the expected utility is strictly lower,

$${\overline{V}}_N-\frac{N-t}{N-t+1}({\overline{V}}_N-\delta {\overline{V}}_{t+1})-d<\frac{1}{N-t+1}({\overline{V}}_N+(N-t\left)\delta {\overline{V}}_{t+1}\right),$$

and underbidding is weakly dominated. It is easy to verify that this bidding strategy leaves the high types indifferent between winning and losing the current auction:

$$\overline{V}={\overline{V}}_N-{\overline{b}}_t=\delta {\overline{V}}_{t+1}+(1∕(N-t\left)\right){\overline{b}}_t.$$

Similarly, there is no incentive to deviate for the low type, whose payoff is

$$\begin{array}{cc}\hfill {\underset{¯}{V}}_t& =\delta {\underset{¯}{V}}_{t+1}+\frac{1}{N-t}{\overline{b}}_t\hfill \\ \hfill & =\delta {\underset{¯}{V}}_{t+1}+\frac{1}{N-t+1}({\underset{¯}{V}}_N-\delta {\underset{¯}{V}}_{t+1}).\hfill \end{array}$$

Now calculating $\Delta V_t={\overline{V}}_t-{\underset{¯}{V}}_t$ is straightforward: ΔV_t = δΔV_t+1. Solving recursively, ΔV₁ = δ^pN−1ΔV_pN.

In period t = pN, only one high type is left. Now consider the following bids:

$${\underset{¯}{b}}_{pN}=\frac{N-pN}{N-pN+1}({\underset{¯}{V}}_N-\delta {\underset{¯}{V}}_{pN+1}),$$

$${\overline{b}}_{pN}=\frac{N-pN}{N-pN+1}({\underset{¯}{V}}_N-\delta {\underset{¯}{V}}_{pN+1})+\epsilon >{\underset{¯}{b}}_{pN}.$$

(Well-known existence problems arise with discrete types and public information, which can be resolved with the introduction of trembles or by assuming that the strategy space is a fine discrete grid; assume therefore that ε is one unit in the grid, say a penny.) The low type bids lower than the high type, and as a result, the high type always wins the auction for sure, paying the low type’s bid. The high type has therefore no incentive to deviate. The low type has no incentive to deviate either. Bidding lower than ${\underset{¯}{b}}_{pN}$ is weakly dominated, and bidding higher than ${\overline{b}}_{pN}$, say ${\overline{b}}_{pN}+d$, implies a payoff

$$\begin{array}{cc}\hfill {\underset{¯}{V}}_{pN}& ={\underset{¯}{V}}_N-{\overline{b}}_{pN}\hfill \\ \hfill & =\frac{1}{N-pN+1}({\underset{¯}{V}}_N+(N-pN\left)\delta {\underset{¯}{V}}_{pN+1}\right)-\epsilon .\hfill \end{array}$$

On the other hand, bidding the equilibrium bid ${\underset{¯}{b}}_{pN}$ assures a payoff

$$\begin{array}{cc}\hfill {\underset{¯}{V}}_{pN}& =\delta {\underset{¯}{V}}_{pN+1}+\frac{1}{N-pN}{\underset{¯}{b}}_{pN}\hfill \\ \hfill & =\frac{1}{N-pN+1}({\underset{¯}{V}}_N+(N-pN\left)\delta {\underset{¯}{V}}_{pN+1}\right),\hfill \end{array}$$

which is strictly larger. It is easy to verify that the equilibrium bidding strategy leaves the low type indifferent between winning and losing the current auction,

$${\overline{V}}_{pN}={\overline{V}}_N-{\underset{¯}{b}}_{pN}$$

$${\underset{¯}{V}}_{pN}=\delta {\underset{¯}{V}}_{pN+1}+\frac{1}{N-pN}{\underset{¯}{b}}_{pN}={\underset{¯}{V}}_N-{\underset{¯}{b}}_{pN}.$$

As a result, ΔV_pN = ΔV_N. From the fact that ΔV₁ = δ^pN−1ΔV_pN, it now follows that ΔV₁ = δ^pN−1ΔV_N = δ^pN−1NΔγ.

Note that for any subsequent period t = pN + 1, …, N, the bids are ${\underset{¯}{b}}_t=\left(\right(N-t)∕(N-t+1\left)\right)({\underset{¯}{V}}_N-\delta {\underset{¯}{V}}_{t+1})$. All the high types have already won and no longer bid, and as a result

$$\begin{array}{cc}\hfill {\underset{¯}{V}}_t& =\delta {\underset{¯}{V}}_{t+1}+\frac{1}{N-t}{\underset{¯}{b}}_t={\underset{¯}{V}}_N-{\underset{¯}{b}}_t\hfill \\ \hfill & =\frac{1}{N-t+1}({\underset{¯}{V}}_N+(N-t\left)\delta {\underset{¯}{V}}_{t+1}\right).\hfill \end{array}$$

Appendix B: Normalization of Expected Chit Fund Values

We calculate the normalized expected payoff of a class of chit funds 〈kv, N/k〉 with k > 1 that are equivalent to an N period fund left〈v, N〉. By construction, each of these groups has a constant pot of vN. To make these choices comparable for an infinitely lived agent, the 〈kv, N/k〉 chit fund will be joined not every N/k periods but every period N, and the savings pattern will be to save kv for the first N/k periods and zero between N/k and N. That is, the savings pattern is kv for periods 1, …, N/k and N+1, …, N+N/k and 2N+1, …, 2N+N/k, etc., and zero in all other period. The 〈kv, N/k〉 group is joined in periods 1, N, 2N, …, each time with an expected value of V₁(kv, N/k) and therefore with life time expected value W^T of V₁(kv, N/k) · (1 + δ^N + δ^2N + …) = V₁(kv, N/k)/(1 − δ^N), where the superscript T stands for target. It therefore immediately follows from Proposition 1 that

$$\Delta W^T\left(kv,\frac{N}{k},p\right)=\frac{{\delta }^{p\frac{N}{k}-1}vN\Delta \gamma }{1-{\delta }^N}.$$

This normalization differs from the normalization in Section 3 only by a constant factor k in the power of δ, and therefore both Lemma 1 and Lemma 2 go through as before. The main matching results, Proposition 1 and Proposition 2, then follow immediately.

Appendix C: Tables

Table C.1.

Group choice–income relationship.

Panel A:
Dependent variable:	chit value
Chit value (thousands of Rs.):	10	15	25	30	50	100
A. Linear probability model Income
Income	−0.003	−0.0001	0.00006	−0.0003	0.001	0.003
	(0.0003)	(0.0002)	(0.0003)	(0.0002)	(0.0003)	(0.0001)
Constant	0.409	0.083	0.175	0.137	0.158	0.038
	(0.004)	(0.002)	(0.003)	(0.003)	(0.003)	(0.002)
B. Multinomial logit model
Income	−0.156	0.009	3.030	–	0.058	0.071
	(0.010)	(0.012)	(0.009)	–	(0.008)	(0.009)
Constant	1.574	−0.528	0.147	–	−0.040	−1.345
	(0.041)	(0.051)	(0.041)	–	(0.040)	(0.050)
Panel B:
Dependent variable:	monthly contribution
Contribution (Rs.):	250	500		625		1000
A. Linear probability model
Income	−0.011	−0.001		0.002		0.010
	(0.001)	(0.001)		(0.001)		(0.001)
Constant	0.419	0.266		0.155		0.160
	(0.005)	(0.004)		(0.003)		(0.004)
B. Multinomial logit model
Income	−0.139	–		0.036		0.058
	(0.010)			(0.008)		(0.007)
Constant	0.803	–		−0.608		−0.518
	(0.036)			(0.036)		(0.034)

Note: Chit value is the product of the monthly contribution and the group duration (in months).Chit value and income are measured in thousands of Rs.

Monthly contribution is measured in Rs.

Multinomial logit model estimated with chit value = 30 as base value in Panel (A) and contribution = 500 in Panel (1B).Linear probability model is estimated independently for each chit value or monthly contribution.

Number of observations in all regressions is 20,885 in Panel (A) and and 18,877 in Panel (B).Standard errors in parentheses.

Table C.2.

Distribution of groups by chit value and contribution.

Breakdown of groups by:		chit value						monthly contribution
Chit value/contribution:		10	15	25	30	50	100	250	500	625	1000
		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
Duration
		LOW		MEDIUM		HIGH		LOW	MEDIUM		HIGH
20 months		18.88	3.74	2.02	4.85	3.31	12.04	–	28.53	–	–
25 months	SHORT	9.23	–	27.42	–	24.86	11.11	–	–	–	28.81
30 months		–	96.26	–	28.48	–	12.04	–	53.69	–	19.92
40 months		71.69	–	69.76	6.06	11.05	38.89	100.00	1.44	100.00	–
50 months	LONG	0.21	–	0.81	–	60.77	13.89	–	0.32	–	46.61
60 months		–	–	–	60.61	–	1.85	–	16.03	–	–
100 months		–	–	–	–	–	10.19	–	–	–	4.66
Total (%)		100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00
Total no. of groups		943	348	248	165	181	108	676	624	173	236

Note: Chit value is the product of the monthly contribution and the group duration (in months). Chit value is measured in thousands of Rs., monthly contribution is measured in Rs.

The six chit values in the table account for over 90% of all observations, the four monthly contributions account for nearly 85% of the observations.

Table C.3.

Bids within the group.

Dependent variable:	Normalized bid
Contribution:	Low		Medium		High
Duration:	Short	Long	Short	Long	Short	Long
	(1)	(2)	(3)	(4)	(5)	(6)
Period 1	0.275	0.370	0.328	0.464	0.337	0.527
	(0.004)	(0.001)	(0.002)	(0.002)	(0.003)	(0.002)
Period 2	0.223	0.312	0.246	0.368	0.254	0.418
	(0.003)	(0.001)	(0.001)	(0.002)	(0.002)	(0.002)
Period 3	0.156	0.221	0.161	0.275	0.174	0.304
	(0.003)	(0.001)	(0.001)	(0.002)	(0.002)	(0.002)
Period 4	0.097	0.118	0.095	0.181	0.110	0.197
	(0.003)	(0.001)	(0.001)	(0.002)	(0.002)	(0.002)
Period 5	0.063	0.065	0.063	0.077	0.065	0.085
	(0.003)	(0.001)	(0.001)	(0.002)	(0.002)	(0.002)
Period 1 * 1994 dummy	0.003	−0.077	−0.043	−0.167	−0.046	−0.224
	(0.005)	(0.001)	(0.002)	(0.003)	(0.003)	(0.003)
Period 2 * 1994 dummy	0.020	−0.041	−0.005	−0.081	0.003	−0.123
	(0.004)	(0.001)	(0.002)	(0.003)	(0.003)	(0.003)
Period 3 * 1994 dummy	0.003	−0.002	−0.008	−0.016	0.002	−0.031
	(0.004)	(0.001)	(0.002)	(0.003)	(0.003)	(0.003)
Period 4 * 1994 dummy	−0.009	0.006	−0.008	−0.002	−0.007	−0.009
	(0.004)	(0.001)	(0.002)	(0.003)	(0.003)	(0.003)
Period 5 * 1994 dummy	−0.010	−0.009	−0.010	−0.009	−0.009	−0.014
	(0.004)	(0.001)	(0.002)	(0.002)	(0.002)	(0.003)
Number of observations	2,088	29,788	13,344	13,487	5,522	11,697

Note: Normalized bid is measured as the bid amount divided by the chit value. Short duration groups last for less than 40 months, Long duration groups last for 40 months or more. Each group is divided into five equal periods: Period 1–Period 5, covering its entire duration in sequence. Contribution: Low if contribution < 500/month; Medium if contribution 500–1,000; High if contribution ≥ 1,000.

Boldface coefficients highlight bids greater than 0.3 in Rows 1–5 and the change in those bids in Row 6–10. Standard errors in parentheses.