Skip to main content
PMC home page
Howard Hughes Medical Institute Author Manuscripts logoLink to Howard Hughes Medical Institute Author Manuscripts
. Author manuscript; available in PMC: 2014 Jan 18.
Published in final edited form as: Cell. 2013 Jul 18;154(2):285–296. doi: 10.1016/j.cell.2013.06.031

Stacked endoplasmic reticulum sheets are connected by helicoidal membrane motifs

Mark Terasaki 1,10,*, Tom Shemesh 2,10, Narayanan Kasthuri 3, Robin W Klemm 4, Richard Schalek 3, Kenneth J Hayworth 3,9, Arthur R Hand 5, Maya Yankova 6, Greg Huber 1,7, Jeff W Lichtman 3, Tom A Rapoport 4,*, Michael M Kozlov 8,10
PMCID: PMC3767119  NIHMSID: NIHMS508416  PMID: 23870120

Abstract

The endoplasmic reticulum (ER) often forms stacked membrane sheets, an arrangement that is likely required to accommodate a maximum of membrane-bound polysomes for secretory protein synthesis. How sheets are stacked is unknown. Here, we used novel staining and automated ultra-thin sectioning electron microscopy methods to analyze stacked ER sheets in neuronal cells and secretory salivary gland cells of mice. Our results show that stacked ER sheets form a continuous membrane system in which the sheets are connected by twisted membrane surfaces with helical edges of left- or right-handedness. The three-dimensional structure of tightly stacked ER sheets resembles a parking garage, in which the different levels are connected by helicoidal ramps. A theoretical model explains the experimental observations and indicates that the structure corresponds to a minimum of elastic energy of sheet edges and surfaces. The structure allows the dense packing of ER sheets in the restricted space of a cell.

Introduction

How the morphology of cellular organelles is generated and maintained is a fundamental question in cell biology, which is still largely unresolved. Organelles have characteristic shapes, with the endoplasmic reticulum (ER) being one of the most striking examples. The ER is a continuous membrane system, composed of the nuclear envelope and the peripheral ER, consisting of sheets and a polygonal network of tubules (Baumann and Walz, 2001; Friedman and Voeltz, 2011; Hu et al., 2011; Shibata et al., 2009). The relative abundance of tubules and sheets in the peripheral ER varies between different tissues and relates to the amount of membrane-bound ribosomes engaged in the synthesis of secretory proteins (Shibata et al., 2006). For example, smooth tubules lacking membrane-bound ribosomes are prominent in adrenal cortex cells, which secrete only few proteins, whereas ribosome-studded, rough ER sheets are abundant in cells that secrete most of their synthesized proteins (“professional” secretory cells), such as pancreatic and salivary gland cells (Fawcett, 1981). In these cells, the ER sheets are stacked on top of each other in a regular manner, with a constant luminal and cytoplasmic spacing. The discovery of stacked ER sheets goes back more than 60 years, when Keith Porter first used thin-sectioning electron microscopy (EM) on tissues (Porter and Blum, 1953). Subsequently, George Palade (Palade and Siekevitz, 1956a, b), Don Fawcett (Fawcett, 1981), and others obtained the amazing pictures of stacked rough ER membranes that have made it into every textbook of cell biology. Stacking of ER sheets also occurs to a lesser extent in cells that do not specialize in secretion, including tissue culture cells, indicating that it is a general phenomenon. However, how ER sheets form stacks is entirely unknown.

Initial work on the mechanisms by which ER morphology is generated concentrated on how the reticular ER network is formed. The ER tubules themselves appear to be shaped by members of two evolutionarily conserved protein families, the reticulons and DP1/Yop1p (De Craene et al., 2006; Hu et al., 2008; Shibata et al., 2008; Voeltz et al., 2006). These highly abundant membrane proteins stabilize the high curvature of tubules seen in cross-section. Although the reticulons and DP1/Yop1p proteins do not share sequence homology, they all have a conserved domain containing two long hydrophobic segments that sit in the membrane as hairpins (Voeltz et al., 2006). These hairpins may stabilize the high membrane curvature of tubules in cross section by forming a wedge in the cytoplasmic leaflet of the lipid bilayer (Shibata et al., 2009). In addition, oligomers of these proteins could form arc-like scaffolds around the tubules. Recent work has clarified that the tubules are connected into a network by a fusion process that is mediated by membrane-bound, dynamin-like GTPases (Bian et al., 2011; Byrnes and Sondermann, 2011; Hu et al., 2009; Orso et al., 2009).

There is also some insight into the mechanisms by which ER sheets are generated. ER sheets consist of two lipid bilayers that maintain a narrow spacing over a long distance. The sheet edges have high curvature, similar to that seen with tubules in cross-section. Based on the observation that the reticulons and DP1/Yop1p localize not only to tubules, but also to sheet edges, it has been proposed that these proteins stabilize the curvature of the edges, keeping the two flat membranes of a sheet closely apposed (Shibata et al., 2010). Experiments in S. cerevisiae indicate that the relative ratio of phospholipids and curvature-stabilizing proteins determines the relative abundance of tubules and sheets; the more curvature-stabilizing proteins are present, the more tubules are generated (Shibata et al., 2010). A theoretical model confirms that an increase in the concentration of the curvature-stabilizing proteins would favor the conversion of sheets into tubules (Shibata et al., 2010). In vertebrates, sheet formation may also involve several coiled-coil membrane proteins, including Climp-63, p180, and kinectin, which are found enriched in this ER domain. Climp-63 molecules may serve as luminal spacers by sitting in the apposing membranes of a sheet and interacting through coiled-coil domains (Shibata et al., 2010). Both the stabilization of the sheet edges by the reticulons and DP1 and the crosslinking of the two membranes by Climp-63 may explain why ER sheets have a relatively constant luminal width.

How ER sheets are stacked on top of one another is unclear. While it is well established that tubules are linked by three-way junctions (Terasaki et al., 1986), it is unknown how sheets are connected with one another. In order to understand the mechanism of ER sheet stacking, a better picture of the actual three-dimensional (3D) geometry is required. In particular, one needs high-resolution 3D views of a relatively large volume of the cell, which allows visualization of not only the ER sheets themselves, but also the connections between them. This requires EM analysis of serial sections, rather than the visualization of a single section, as was done in most previous studies. The sections need to be thinner than the thickness of ER sheets, which in mammals are typically in the range of ~50 nm, and also thinner than the distance between sheets. Thin-sections for transmission electron microscopy (EM) are usually >60 nm thick, precluding detailed analysis of the sheet connections. EM tomography has the required resolution, but is currently confined to the analysis of a relatively small volume. We have therefore used a new EM methodology that combines improved protocols of membrane staining with the automated collection of a large number of serial ultra-thin sections (Tapia et al., 2012). This technique allowed us to visualize the three-dimensional organization of stacked ER sheets in unprecedented detail, both in neuronal cells, containing only a few stacked sheets, and in salivary gland cells that are specialized in secretion and thus contain densely stacked ER sheets.

Based on our 3D structures of stacked ER sheets, we identified a common structural motif by which sheets are connected. The connections are formed from twisted continuous membrane surfaces with edges of left- or right-handedness. The 3D structure resembles a parking garage, in which the different levels are joined by helicoidal ramps. A theoretical model explains the experimental observations based on the hypothesis that this structure corresponds to a minimum of elastic energy of sheet edges and surfaces. The theory indicates that the structure is the optimal arrangement for the packing of membranes in the restricted space of a cell.

Results

A novel method to visualize the 3D structure of the ER

To accurately visualize ER stacks, EM images of serial sections over several microns are required. We applied a novel ultra-thin sectioning technique, in which the sections are 30–40 nm thick (Tapia et al., 2012). A large number of consecutive sections were collected automatically on a moving tape. Because the sections were placed on an electron-impermeable surface, the samples were imaged by scanning EM, rather than by conventional transmission EM. For visualization, a staining protocol that accentuates membranes was used, which greatly facilitates the tracing of membranes. The contrast of other structures, such as ribosomes and microtubules, is not enhanced. Briefly, after fixing the tissue with a mixture of formaldehyde and glutaraldehyde, small pieces were stained with reduced osmium, followed by treatment with thiocarbohydrazide, which acts as a mordant for a second exposure to osmium. Finally, the samples were stained en bloc sequentially with uranyl acetate, copper, and lead. After dehydration, the samples were embedded in epon, sectioned, and collected serially on a custom-made device.

The new technique was applied to the cell bodies of mouse cortical neurons and to secretory acinar cells of the parotid salivary gland. Both tissues were fixed in situ by cardiac perfusion of mice with fixative. The two tissues were chosen because the ER in neuronal cell bodies would be expected to have only relatively few stacked ER sheets, whereas salivary gland cells are specialized in secretion and thus contain densely stacked ER sheets.

ER stacks in neuronal cell bodies

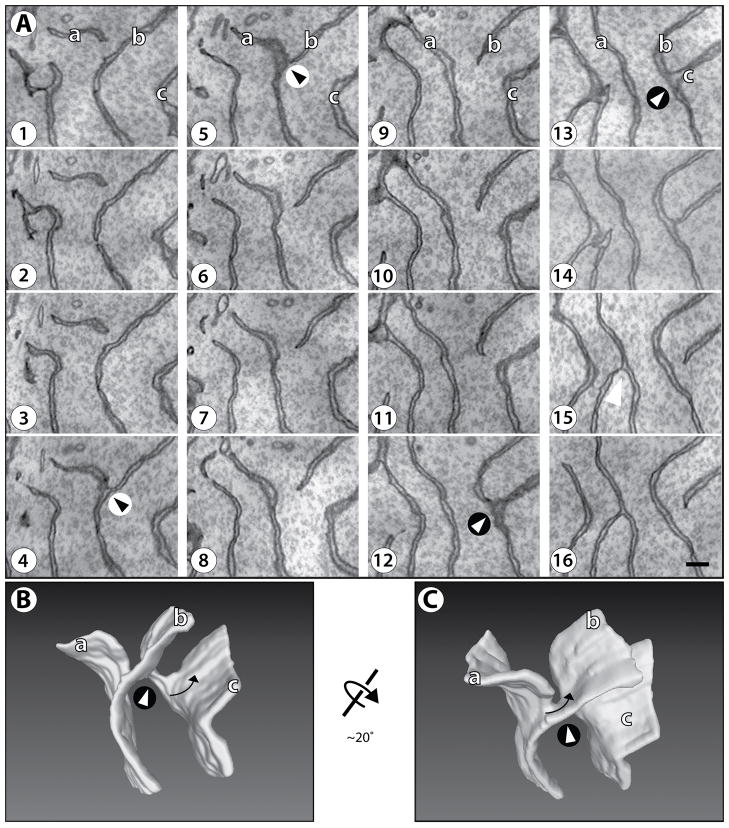
The ER morphology was analyzed in several neuronal cell bodies, each with ~500 serial sections. The ER structure is rather complex, comprising of both tubules and sheets. Here we focus on stacked sheets, which are present in several, irregular regions scattered throughout the cytoplasm. An example of serial sections through a stack of ER sheets is shown in Figure 1A (see also Supplemental Figure S1), and a 3D reconstruction is shown in Figures 1B and 1C (see also Movie S1). The analysis shows that the luminal width of the sheets is ~45 nm. The sheets are clearly stacked with an average distance of ~270 nm (measured between the cytosolic surfaces), but there is significant variability of the spacing (range: 204 to 420 nm). The sheets are all connected, forming a continuous membrane system. The connections between the sheets turned out to be surprisingly complex. From the analysis of many examples, we conclude that there are only rare cases, in which sheets form an extended T-junction, i.e. where a sheet edge fuses with the flat surface of another sheet. The most frequent connection between sheets is by a motif that has not been described before. Serial sections of two of these characteristic sheet connections are shown in Figure 1A. In the first connection, the edge of sheet ‘a’ approaches the surface of sheet ‘b’ to eventually merge (panels 1–4). The three-way junction exists for only two sections (panels 4 and 5). Then, the upper part of sheet ‘b’ disconnects, forming a new edge, while the lower part is now connected with former sheet ‘a’ (panels 6 and higher). A similar pattern is seen with the second connection in Figure 1A, between sheets ‘b’ and ‘c’.

Figure 1. Structure of stacked ER sheets in a neuronal cell body of mouse brain cortex.

Figure 1

Open in a new tab

(A) Membranes were visualized in serial sections, each 30 nm thick, by scanning EM at 3 nm per pixel. The order of the sections is indicated by the numbers. Supplemental Figure S1 shows an Image J stack of the sections. A region of cytoplasm containing only ER sheets (i.e., no tubules) is shown. Two instances of the common connection motif are shown: between sheets ‘a’ and ‘b’ and between sheets ‘b’ and ‘c’; they are highlighted by arrowheads in circles of white and black background, respectively. The arrowhead on black background corresponds to the one shown in the 3D reconstruction in Figures 1B and 1C, and in higher magnification in Figure 2. Scale bar = 200 nm.

(B) A 3D reconstruction of the serial section series in (A). The view is in the same orientation, with the same three sheets labeled. The arrow indicates the twist of the sheet connection (according to convention, this structure is “left handed”, because the edge turns counter-clockwise as it moves into the plane of the paper). Movie S1 shows a Quicktime movie of the reconstruction being rotated.

(C) As in (B), but rotated by 20°, as indicated.

The 3D reconstruction of the overall structure in Figures 1B and 1C illustrates that the connections are formed by twisted membrane surfaces that have a handedness (see arrows, and Movie S1) and possess a continuous edge that runs through the connection (Figure 2; the edge is highlighted; see also Movie S2). Quantification was performed on the sparsely packed sheets from three neurons; in a total volume of 4.8 μm3, there were 42 twisted sheet connections, with 19 being left-handed and 23 right-handed.

Figure 2. Structure of the commonly observed sheet connection.

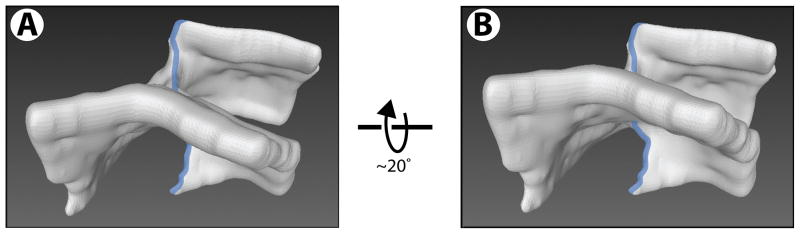
Figure 2

Open in a new tab

(A) Shown is a 3D reconstruction of a single sheet connection. The region corresponds to that indicated by an arrowhead on black background in Figure 1A. The orientation was preserved. Note that a sheet edge (shown as a blue transparent line) runs through the connection and is present on both sides of an apparent three-way sheet junction. Movie S2 shows a Quicktime movie of the reconstruction being rotated.

(B) As in (A), but the reconstruction is rotated around the horizontal axis, as indicated.

ER stacks in secretory cells of the salivary gland

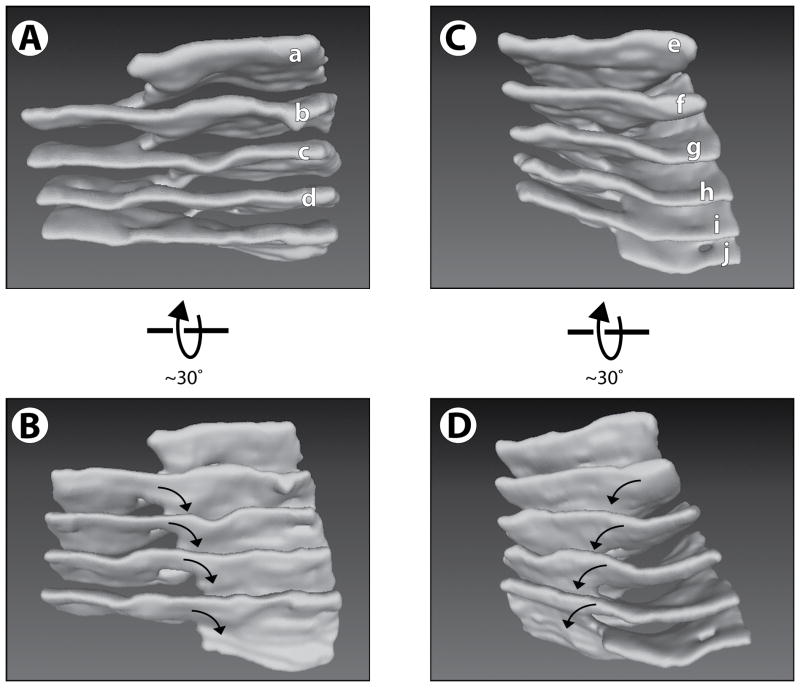
To test whether the same sheet connections exist in cells with abundant ER stacks, we used the new EM technique with acinar secretory cells of the parotid salivary gland. The ER in these cells is more homogeneous than in neuronal cell bodies, containing extensive areas of densely stacked sheets (Hand, 1972). A large number of parallel sheets can be seen, extending over many consecutive sections in a large volume (see serial sections in Figure 3A and Figure S2). The 3D reconstruction shows that the sheets have an almost uniform spacing (Figure 3B; see also Movie S3). Again, connections between the sheets generate a continuous membrane system. Moreover, the connections are formed by a series of the same motif that is seen in neurons (Figures 4 and Figure S2). The edge of the connections forms a helix with one turn between two adjacent sheets (Figure 4). Often, we observed the junctions between adjacent sheets to be lined up along the helical axis, such that a continuous helical edge connects several sheets. Examples of four and five such consecutive junctions are shown in Figures 4A and 4B, respectively (see also Movies S4 and S5).

Figure 3. Structure of stacked ER sheets in an acinar cell of mouse salivary gland.

Figure 3

Open in a new tab

(A) Membranes were visualized in serial sections, each 40 nm thick, by scanning EM at 3 nm per pixel. The top panel shows the region that was analyzed by serial sectioning EM. Supplemental Figure S2 shows an Image J stack of the sections. Serial sections of the regions indicated by the black and white rectangles are shown in the lower panel in the left and right columns. The sheets are labeled with letters ‘a’ to ‘d’ (black rectangle, left column) and ‘e’ to ‘j’ (white rectangle, right column). Note that the sheets break and re-attach to connect adjacent sheets of the stack (for example, in the left column, sheet ‘b’ breaks in frame 3, and rejoins with sheet ‘c’ in frame 4). Scale bar = 200 nm.

(B) 3D reconstruction of the area shown in the top panel of (A). Movie S3 shows a Quicktime movie of this reconstruction being rotated.

Figure 4. Structure of helical ramps connecting stacked ER sheets.

Figure 4

Open in a new tab

(A) A 3D reconstruction of the region within the black rectangle of Figure 3A. The sheets are labeled as in Figure 3A (left column). Movie S4 shows a Quicktime movie of this reconstruction being rotated.

(B) As in (A), but from a different view angle. The arrows indicate the handedness of the helical edge.

(C) A 3D reconstruction of the region within the white rectangle of Figure 3A. The sheets are labeled as in Figure 3A (right two columns). Movie S5 shows a Quicktime movie of this reconstruction being rotated.

(D) As in (C), but from a different view angle. The arrows indicate the handedness of the helical edge, which is opposite to that in (A) and (B). See also Figure S3.

To exclude the possibility that the ER sheet connections are an artifact caused by chemical fixation, we analyzed rapidly frozen samples. Small pieces of parotid gland were excised from anesthesized mice and subjected to rapid freezing under high pressure. After freeze substitution and staining, the samples were processed for serial thin section microscopy in the same manner as the chemically fixed tissue. The rapidly frozen tissue showed the same helical ramps in similar abundance as observed with chemically fixed samples (see Supplemental Figure S3 and Movie S6).

The overall structure resembles a parking garage. In the example shown in Figure 4A, the helix is fortuitously aligned along the plane of section. From this structure, we estimate the luminal width of the sheets to be 48 +/− 8 nm (mean +/− standard deviation), and the distance between the cytosolic surfaces of adjacent sheets, related to the pitch of the inter-sheet connection (see below), to be 84 +/− 14 nm. The inner radius of the helicoidal connections is 36 +/− 10 nm (measured from the central axis of the helicoid to the cytosolic surface of the sheet edge). We found connections with both right- and left- handed helical edges (boxed areas in Figure 3A top panel; the corresponding 3D reconstructions are shown in Figures 4A and 4B). Quantification was performed on the densely packed ER sheets from six cells; in a total volume of 195 um3, there were a total of 22 helical ramp connections of 3–5 complete turns, with 10 being left-handed, and 12 right-handed. Occasionally, we detected planar holes in the sheets, which are reminiscent of the fenestrations that have been described in tissue culture cells (Puhka et al., 2012). Taken together, our results indicate that ER stacks are formed by the same structural motif in different cell types, regardless of whether there are only few sheets connected, as in neurons, or many, as in salivary gland cells.

A theoretical model for ER sheet stacking

To understand the physical basis for the generation of the commonly observed sheet connection, we developed a theoretical model. Our hypothesis is that the observed sheet stack structure corresponds to a minimum of elastic energy of sheet edges and surfaces. The model considers three contributions to the energy: (1) the elastic bending energy of sheet edges, which describes the energy required to bend the edge line of a sheet away from its preferred spontaneous curvature; (2) the elastic bending energy of sheet surfaces, which describes the energy required to bend the initially flat membrane of a sheet; and (3) the energy caused by an effective lateral pressure acting on the external edges of a sheet as a result of spatial confinement. A simplified form of the sheet edge bending energy was used in our previous model, which was suggested for the formation of ER tubules and their interconversion into sheets (Hu et al., 2008; Shibata et al., 2010). The energy of the lateral pressure was introduced here to take into account that the lateral expansion of the sheet area is restricted by the limited space of a cell.

Elastic energies of the sheet edge and surface

A sheet consists of two planar membranes connected by an edge membrane, the shape of which can be approximated by a half-cylinder that bends along the sheet rim (see Figure S4). The half-cylindrical edge sets a constant distance between the two sheet membranes, which thus tend to remain parallel during sheet deformation. Therefore, the membranes of a sheet bend as one unit, described as a plane in the middle between the two membranes. The border of this sheet plane is the axis of the half-cylindrical edge membrane (Figure S4), forming the edge line (see also Supplemental Theory). We model a sheet stack as a pile of sheet planes with connections between them. Each sheet plane has an area, A. The total length Ltot of the edge line per sheet includes both the external edge of the sheet plane and the internal edges lining the connections to adjacent sheet planes.

To account for the elastic properties of the sheet rim, the edge line is considered to resist bending, which is characterized by the line bending elasticity (Shibata et al., 2010) (Supplemental Theory). In our previous model, which considered only tubules and flat sheets (Hu et al., 2008; Shibata et al., 2010), it was sufficient to assume that the preferred shape of the edge is a straight line. In the present model, we take into account that the edge line has an intrinsic tendency to bend and reach a certain curvature ζs, referred to as the line spontaneous curvature. This spontaneous curvature is expected to be negative (ζs < 0), meaning that the edge line tends to form an indentation into a sheet, rather than to bulge outwards. This is explained by a strong tendency of the edge membrane to adopt a saddle-like shape with small mean curvature: the negative curvature along the edge line partially compensates for the positive curvature of the cross-section of the half-cylinder (see Figure S4 and Supplemental Theory). We will treat the absolute value of the edge line spontaneous curvature |ζs| as a free parameter, as it is difficult to estimate; it may depend on numerous factors, such as the protein and lipid composition of the edge membrane. Generation of an edge line curvature ζ that deviates from ζs requires energy. This energy related to unit length of the edge line, fe, was taken to depend on the curvature ζ, according to the simplest Hooke-like law

fe=12ke(ζ+∣ζs∣)2, (1)

where ke is the edge line bending modulus. The total elastic energy of the edge line, Fe, is obtained by integration of Eq.(1) over the length L of the edge line,

Fe=12ke∮(ζ+∣ζs∣)2dL. (2)

The sheet plane is characterized by a bending elasticity, which accounts for its resistance to deformation from a flat shape. The bending energy of the sheet plane, related to its unit area, fs, can be determined by the Helfrich model of membrane bending elasticity (Helfrich, 1973),

fs=12κJ2, (3)

where J is the mean curvature of the sheet surface (Spivak, 1970) and κ is the membrane bending modulus (Helfrich, 1973), multiplied by a factor of two to account for contributions of the two sheet membranes. The total bending energy of the sheet surface, FS, is obtained by integration of Eq.(3) over the area A of the sheet plane,

FS=12κ∫∫J2dA. (4)

The restriction of the sheet expansion is taken into account by a two-dimensional lateral pressure, Π, acting on the external edge of the sheet plane. The corresponding energy, FΠ, is given by integrating this lateral pressure over the total area, Ap, bound by the external edge in the sheet plane,

FΠ=∫∫ΠdAp. (5)

Here, we make the simplifying assumption that the lateral pressure Π is not dependent on deformations of the membrane surface or edge line.

Optimal shape of a single helicoidal connection

We first consider only one connection between the sheets, consisting of an internal edge and a surrounding sheet surface. The energy of the edge line is minimal if the line curvature is constant and equal to the negative spontaneous curvature (see Eqs. (1,3)),

ζ=-∣ζs∣, (6)

whereas the sheet surface energy is minimal if the surface mean curvature equals zero

J=0. (7)

The edge line of constant curvature Eq.(6) corresponds to a helix, whose radius, r, and pitch distance, p, satisfy the relationship

rr2+(p/2π)2=∣ξs∣. (8)

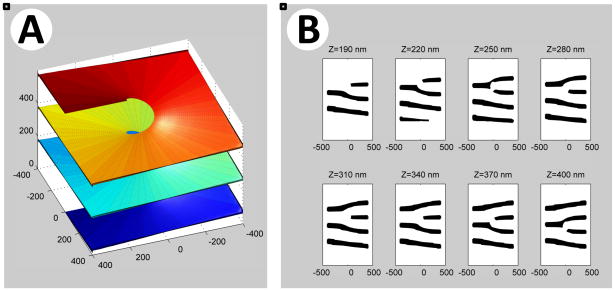
The surface of zero mean curvature Eq.(7) containing a helical internal edge is a hollow element of a helicoidal surface (Catalan, 1842; do Carmo, 1986), which has a saddle-like shape at each point. The resulting structure has minimal elastic energy of both the internal edge and the surface. This optimal shape of a single connection is illustrated in Figure 5A. We refer to it as a “helicoidal connection”. The spacing between two adjacent sheet planes is the pitch of the helical edge. Importantly, the serial sections of a helicoidal connection reproduce the novel motif observed experimentally (Figure 5B). Thus, the occurrence of this motif can be explained on the basis of the fact that a single helicoidal connection between sheets possesses minimal elastic energy and is therefore a favored state.

Figure 5. Model for helicoidal inter-sheet connections.

Figure 5

Open in a new tab

(A) Model for a single helicoidal connection. Shown is a section of a hollow helicoidal element with an internal radius of 75 nm and a pitch of 200 nm. The different levels of the sheet stack are shown in different colors. The helicoid surface is viewed along an axis (Z) that has an elevation angle of 50° from the axis of the helicoid.

(B) Calculated serial cross sections for the helicoidal connection shown in (A). The cross-sections were computed at 30 nm intervals for sheets of 30 nm thickness. The cross sections are calculated along the Z-axis. The Z origin is arbitrary, and units are in nm.

See also Figure S4.

Optimal configuration of an array of helicoidal connections

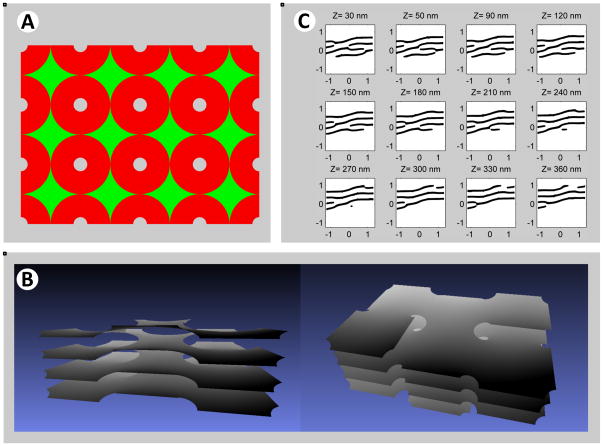
In reality, sheets in a stack have more than one connection, which would distort the ideal configuration seen for a single connection. However, the shape with multiple connections can be obtained by assembling helicoidal connections side-by-side in a mosaic-like manner. Our analysis showed that a regular arrangement, in which neighboring helicoidal connections have opposite handedness, minimizes the geometrical mismatch between them and, hence, the related energy penalty (see Supplemental Theory; see also Figure S5). Thus, one would predict that left- and right- handed helicoidal connections are present in a 1:1 ratio. Specifically, we considered a quadratic lattice, a “checkerboard array”, in which the helicoidal connections with alternating handedness can be smoothly linked by elements of saddle-like surfaces (Figure 6A) (for more details, see Supplemental Theory). These surface elements have a non-vanishing, but fairly small mean curvature J, resulting in low bending energy. The final structure resulting from energy minimization (see Supplemental Theory) resembles a parking garage, in which the different levels are connected by helicoidal ramps (Figures 6B; see also Movie S7). The model reproduces the major features of experimental observations. Most importantly, the serial sections of the model structure are similar to the observed connection motif (Figure 6C). In addition, the predicted one-to-one relationship between left- and right-handed helicoidal connections is in reasonable agreement with the 3D reconstructions of the experimental data.

Figure 6. Optimized structure of stacked sheets connected by helicoidal connections.

Figure 6

Open in a new tab

(A) Top view of the computed optimal shape of sheets joined by helicoidal connections. The helicoidal elements of alternating handedness are arranged in a rectangular array. The surface is composed of slightly deformed helicoidal surfaces, shown in red, and saddle-like surfaces that smoothly connect them, shown in green. The surface is obtained by simultaneous minimization of the energy of the helicoidal and saddle-like elements with the constraint that the surface is continuous across their interface. The helical edges have a pitch of 220 nm and a radius of 65 nm.

(B) Side views of a 3D model of the optimized structure, a sub-region of the surface in (A). Note the similarity with a parking garage. Movie S7 shows a Quicktime movie of this structure being rotated.

(C) Calculated serial cross-sections obtained for the optimal surface shown in (A) and (B), with a 30 nm distance between the section planes. The cross sections were calculated along an axis Z, which corresponds to the viewing direction in the right panel of (B). The origin is arbitrary and the units are in nm.

See also Figure S4 and Figure S5.

Dependence of the membrane stack structure on model parameters

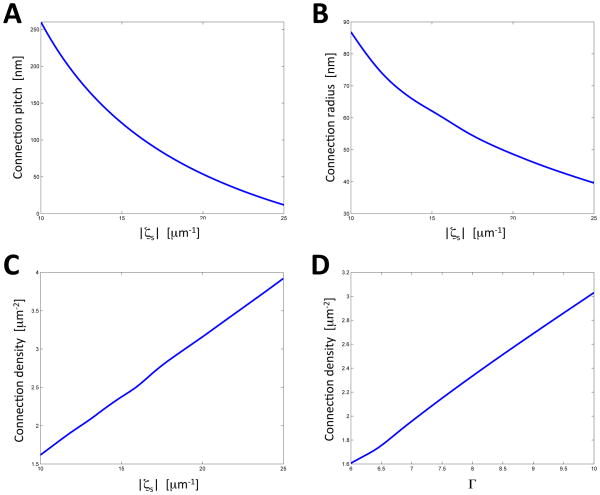
In our model, the geometry of the stacked sheets can be expressed by the pitch distance of the helicoidal connections and the connection density, i.e. the number of connections per unit area of the sheet. We computed these values as functions of two major parameters of the system: the spontaneous curvature of the sheet edge, ζS; and a parameter Γ representing the normalized total edge length (the ratio between the total edge length per sheet plane, Ltot, and the circumference of a circle with the area A equal to that of the sheet plane, Γ=Ltot4πA).

Our results show that the edge spontaneous curvature, ζS, has a strong influence on the helicoidal connections. The connections are only observed if ζS is negative, as expected from the fact that their helical edges have negative curvature. An increase in the absolute value of the spontaneous curvature, |ζS|, results in smaller values of the pitch, p (Figure 7A), and of the internal radius of the cross-section of the connections, r, (Figure 7B). In other words, the helicoidal connections become shorter and thinner, as expected from (Eq.8), and, as a result, the inter-sheet distance decreases.

Figure 7. Variation of ER stack morphology predicted by the model.

Figure 7

Open in a new tab

(A) Optimized structures of stacked sheets with helicoidal connections were calculated. The pitch of the helicoidal connections was determined for different values of the absolute value of the edge spontaneous curvature, |ζs|, (ζs < 0).The calculations were performed for a lateral pressure Π = 4 κ μm−2 (where κ is the sheet plane bending rigidity), and a normalized dimensionless edge length Γ = 6.

(B) As in (A), but the edge radius was plotted versus |ζs|.

(C) As in (A), but the connection density was plotted versus |ζs |.

(D) The connections density was calculated as a function of the normalized edge length, Γ. The calculations were performed for ζs = −10 μm−1 and Π = 4 κ μm−2.

The results of Figures 7A and B give the best fit with the experimental data, obtained for secretory cells of the salivary gland (Figure 4), with parameter values of |ζS| = 15 μm−1 and Π = 4 κ μm−2 (where κ is the sheet plane bending rigidity). In order to compare the computational predictions with experimental results, it has to be kept in mind that the model ignores that the sheets have a thickness of ~48 nm. Thus, this number has to be subtracted from the computed inter-sheet distance to compare with the experimental value, measured as the distance between the cytosolic surfaces of the sheets. Half the sheet thickness (24 nm) has to be subtracted from the computed internal radius of the helicoidal connections. With these corrections, the radius and inter-sheet distance are calculated to be 62 nm – 24 nm = 38 nm and 125 nm – 48 nm = 77 nm, respectively. These estimates are in good agreement with the experimental numbers of 36 nm and 84 nm, respectively.

We also calculated the density of the helicoidal connections as a function of the edge spontaneous curvature, ζS (Figure 7C). The growth of the connection density with increasing |ζS| is explained by the fact that, if the total edge length, Ltot, is kept constant, a decrease of p and r causes a reduction of the edge length, L, of every individual connection, and this is compensated by an increase of the number, and thus density, of the connections. The computations also show that an increase of Γ, i.e. of the total edge length per sheet Ltot, results in a higher connection density (Figure 7D), but has a negligible effect on the connection pitch p and radius r for relevant distances between the connections (not shown).

In summary, our analysis indicates that, in the physiological range, both the pitch p and the cross-sectional radius r of an individual connection are mostly determined by the edge spontaneous curvature |ζS|. The connection density is determined by both |ζS| and the total edge length Γ. It should also be noted that the external sheet edges tend to retain a circular shape.

The calculations indicate that the elastic energy decreases with increasing distance between the helicoidal connections, which means that the connections repel each other. Thus, they are expected to adopt the largest possible distance from each other. For low connection densities, and thus low total edge length, this means that the connections will be so far apart from each other that the membrane configuration around each of them is close to that of a single hollow helicoidal element. Indeed, our experiments show that many connections are relatively distant from each other.

Discussion

Here, we have addressed the long-standing question of how ER sheets are stacked. We show that the sheets are connected by a novel motif, a twisted membrane surface with an internal edge that is right- or left- handed. The three-dimensional structure is a continuous membrane system resembling a parking garage, in which the different levels are connected by helicoidal ramps. Our theoretical model indicates that this structure corresponds to a minimum of elastic energy of sheet edges and surfaces, and that it allows the dense packing of ER sheets in the restricted space of a cell.

The helicoidal connections between sheets were observed both in neuronal cell bodies and in secretory cells of the salivary gland, suggesting that they are a general feature in all cells. However, the “parking garage” structure, which assumes an array of helicoidal connections between multiple sheets, might only exist in cells with abundant stacked ER sheets, such as in “professional” secretory cells of the salivary gland or pancreas. These cells have a particular requirement for membrane-bound polysomes, as secretory proteins account for up to 90% of all synthesized proteins. Thus, there is a need to accommodate in the confined volume of the cell a maximum amount of membrane surface for ribosome binding. The “parking garage” structure provides the solution to this problem, as it allows for an energetically favorable packing of a maximum amount of membrane sheets. Much of the structure consists of flat or almost flat membrane surfaces, which are ideal to accommodate even large membrane-bound polysomes. In addition, ribosomes can also sit on the helicoidal ramps. The existence of lipid connections between sheets guarantees that proteins required for the translocation of secretory proteins across the membrane, as well as modification enzymes and chaperones acting on nascent polypeptide chains, are distributed freely throughout the ER. In addition, cytosolic components can easily diffuse through the stacked sheets. Finally, the variability of the helical pitch and of the corresponding distance between the sheets, allows the cell to adjust to different demands on its secretory capacity; when more secretory proteins are needed, the cell can pack more membrane into the same space, resulting in smaller distances between the sheets.

Our results do not exclude the possibility that stacked ER sheets are also connected by cytoplasmic protein bridges. In fact, deep-etch EM suggested that there may be protein bridges on the cytoplasmic side of ER membranes in silkworm gland cells (Senda and Yoshinaga-Hirabayashi, 1998). Cytoplasmic bridges might be formed by p180 (Becker et al., 1999), but it is not present in all organisms that contain stacked ER sheets. In addition, the distance between stacked ER sheets can vary between cell types and even within a cell, and can be rather large (>300 nm), arguing that cytoplasmic protein bridges are not the major factor for sheet stacking. The situation is drastically different for the Golgi apparatus, where cytoplasmic bridges are likely a major mechanism by which the sheets of the cisternae are stacked on top of each other (Short et al., 2005). Connecting ER sheets by membranes, and Golgi sheets by proteins, is consistent with the fact that the ER functions as a single unit, whereas Golgi cisternae are functionally distinct.

Our results indicate that the minimization of bending energy of membrane edges and surfaces is a major factor determining ER structure. Previous work had shown that such considerations explain how ER sheets and tubules are formed and interconvert between each other (Hu et al., 2008; Shibata et al., 2010). Now, we show that a simple extension of the previous model can also explain how sheets are connected within stacks. The suggested model only involves three parameters: the spontaneous curvature of the membrane edge, the total edge length per sheet area, and the lateral pressure exerted on the sheet edges, caused by the confinement of the membranes in a limited space. In this paper, we have concentrated on how this model can explain the generation of membrane connections between stacked ER sheets and how the elastic parameters of the ER sheets affect the stack structure. However, the same model can be used to explain other experimentally observed ER morphologies, such as tubules and fenestrated sheets, as well as the interconversion between the different structures (unpublished results). Our model does not take into account kinetic barriers in the transition between different states, but it is remarkable that a thermodynamic model, which only considers elastic energy, can explain so extensively the observed ER morphologies.

Structures reminiscent of helicoidal ramps, and referred to as the screw dislocations, have been observed by physicists studying lyotropic liquid crystals (Kamien and Lubensky, 1997) and multi-lamellar phases of diblock copolymers (Gido et al., 1993; Gido and Thomas, 1997). The hollow screw dislocations within stacks of lyotropic membranes are similar to the twisted structures observed by us, but the physical forces causing them are of different origin, related to the chirality of the molecules forming these artificial membranes (Kamien and Lubensky, 1997).

The parking garage configuration appears to be the optimal arrangement to pack in a confined space a stack of membrane sheets connected by membrane surfaces containing internal edges. In our model we introduced a lateral pressure that acts in the sheet plane and pushes on the external edges of the sheets towards the sheet interior. This parameter thus takes into account that the unlimited expansion of a sheet is prevented by the cell boundary or by cytosolic components, for example, the cytoskeleton. Because of the existence of membrane connections between the sheets, the parking garage system can respond to the lateral pressure by moving membrane out of the sheet plane into the connections. Thus, helicoidal connections are not just linkers between sheets, but play a major role in the packing of sheet stacks in a confined space.

Of course, our theoretical model results in an idealized structure. In the extreme case of the model, there would be very scarce connections between stacked sheets, and the membrane configuration in the vicinity of each connection would be close to a purely helicoidal membrane surface. This configuration would be characterized by having a minimal elastic energy. However, we demonstrate that even if the density of the connections is high, the model structure would still have very low elastic energy. In our calculations, we assumed that the helicoidal connections are arranged in a checkerboard-like array. Of course, other arrangements can be considered, but our analysis shows that the energy costs would be small as long as each helicoidal connection has nearest neighbors with opposite handedness. The exact geometry appears to be of lesser importance, and in reality, one would not expect a completely regular arrangement of the connections. Another simplification of the model is that, in nature, the sheets are not exactly parallel to one another and that the helicoidal surfaces connect a variable number of sheets. Although this means that, in principle, the ends of the helicoidal connections could be relevant, qualitative considerations justify that they can be neglected in our model, as they do not make a large contribution to the elastic bending energy, particularly if the helicoidal surfaces connect multiple sheets.

A major discovery of our analysis is that the sheet connections are membrane surfaces with edges. These edges have a nearly half-cylindrical shape with high curvature perpendicular to the membrane surface, similar to the curvature seen in cross-sections of tubules (this curvature is in the tens of nanometer scale and thus significantly higher than the micron scale curvature of the edge lines considered in our present model). Because the high membrane curvature in the ER is generally stabilized by proteins of the reticulon and DP1 families (Shibata et al., 2009), it is likely that the edges of the connections also contain these proteins. They would stabilize the high curvature by forming wedges inside the bilayer, and by forming arc-like scaffolds around the edge. Our previous theoretical considerations indicated that the energetically optimal distance between the arcs is ~40 nm (Hu et al., 2008). Any further increase of the amount of curvature-stabilizing proteins would therefore require an increase of the edge length to accommodate additional arc scaffolds. Thus, we predict that the level of the reticulons and DP1 proteins determines the total length of internal edges in stacked ER sheets. Hence, our calculations show that an increase of the amount of the curvature-stabilizing proteins would result in a higher density of helicoidal connections. The hypothesis that the reticulons and DP1 are required to form the internal edges of stacked ER sheets and regulate the organization of the sheet stack may explain the apparent puzzle that these proteins are quite abundant in cells with proliferated ER sheets (Luckey et al., 2006; Shibata et al., 2010).

Sheet-enriched proteins, such as p180, kinectin, and Climp-63 may also play a role in the stacking of rough ER sheets. These proteins are highly up-regulated in cells containing proliferated stacked ER sheets, such as pancreatic cells or immunoglobulin-secreting plasma cells (Shibata et al., 2010). Based on fluorescence-recovery after bleaching (FRAP) experiments (Nikonov et al., 2007; Nikonov et al., 2002), it seems that one function of these sheet-enriched proteins is to immobilize polysomes on the ER membrane, both by forming oligomers through their coiled-coil domains and by interacting with the cytoskeleton through their microtubule-binding domains (Klopfenstein et al., 1998; Ogawa-Goto et al., 2007; Savitz and Meyer, 1990; Toyoshima et al., 1992). A consequence would be that the concentration of diffusible monosomes and free, non-ribosome associated, sheet-enriched proteins would be minimized, which otherwise could move into the sheet edges and attenuate the negative spontaneous curvature of the edge. As a result, the sheet-enriched proteins would promote sheet stacking.

Increasing the concentration of p180, kinectin, or Climp-63 within a range where they bind to polysomes and cause their progressive immobilization would thus be expected to increase the absolute value of negative curvature of the edge, which, according to our calculations (Figure 7A), would result in a decreased spacing of the sheets. In addition, the sheet-enriched proteins would be expected to concentrate the polysomes in the stacked sheet area. In fact, one may envision a positive feed-back loop, in which the assembly and immobilization of polysomes on a sheet would concentrate more sheet-enriched membrane proteins, which in turn would promote sheet stacking and concentrate more polysomes, and so on. Ultimately, this would lead to a segregated rough ER domain consisting of densely stacked, ribosome-studded membrane sheets.

Much of the new insight in the packing of ER sheets was made possible by new methods for serial section electron microscopy, which produce well stained membranes and thinner sections than previously possible. These methods were originally designed to generate a comprehensive connection diagram of neurons (“connectomics”). However, we demonstrate that this methodology can also be applied to the level of single cells. We expect that the methodology will also be useful for the analysis of the morphology of other organelles, such as mitochondria and lipid droplets, as well as their interactions with the ER.

Experimental procedures

Electron microscopy

Adult mice were deeply anesthetized (Ketamine/Xylazine), and perfused through the left ventricle of the heart with 2.5% glutaraldehyde/2.0% paraformaldehyde in 0.1 M sodium cacodylate buffer, pH 7.4. The tissues were dissected, fixed for an additional 2–4 hrs in the same fixative, then rinsed, and stored at 4°C in 0.1 M cacodylate buffer, pH 7.4. The tissues were trimmed into small pieces, 1–2 mm on a side, and rinsed several times in buffer. The samples were processed according to the ROTO protocol (Tapia et al., 2012). They were post-fixed for 1 hr in a mixture of equal volumes of 4% aqueous osmium tetroxide and 3% potassium ferrocyanide in 0.2 M cacodylate buffer, pH 7.4. The samples were then thoroughly rinsed in distilled water, and treated for 20 min with 1% aqueous thiocarbohydrazide (Sigma Chemical; St Louis, MO). Following thorough rinsing with distilled water, the samples were treated with 2% aqueous osmium tetroxide for 30 min and rinsed again with distilled water. The samples were then treated with 1% aqueous uranyl acetate overnight at 4°C, rinsed in distilled water, and treated for 30 min in 0.066% lead aspartate. The samples were then rinsed thoroughly in distilled water, dehydrated in graded ethanol solutions, and embedded in epoxy resin (Polybed, Polysciences; Warrington, PA) following standard procedures.

To prepare the polymerized specimens for sectioning, the samples were shaped to a ~1 × 4 mm rectangular face using a diamond trimming tool. The block was mounted in a microtome (Leica EM UC7, Buffalo Grove, IL) with the long side of the face oriented vertically, and thin sections, 30–40 nm in thickness, were cut with a diamond knife. The sections were collected on kapton tape (glow-discharged to prevent wrinkling of sections) with the ATUM tape collection device (Hayworth et al., 2006; Tapia et al., 2012). The tape containing the sections was cut into strips, mounted on 4-inch silicon wafers (University Wafers, South Boston, MA), and then carbon coated (Denton 502B, Moorestown, NJ) to provide grounding for the electron imaging.

The sections were imaged using a field emission scanning EM (Zeiss Sigma FE-SEM; Peabody, MA) in backscatter mode (10 keV electrons, ~5 nA beam current). A high-precision map of the sections on the wafer (± 4 μm) was generated, then the Atlas Large Area Imaging software (Fibics Inc.; Ottawa, Ontario, Canada) was used to automatically image a 50 μm × 50 μm field of the serial sections at 3 nm/pixel resolution (16,000 × 16,000 pixels). The images were aligned using the Linear Alignment with SIFT algorithm, and reconstructed using TrakEM2, both in FIJI Image J (Cardona et al., 2012). Reconstructions were processed with nine smoothing steps of the Laplacian smooth function in the program MeshLab (http://www.meshlab.com).

To analyze rapidly frozen samples, small pieces of parotid gland were excised from anesthetized mice, and quickly trimmed to fit into standard gold-plated specimen carriers (1.2 mm diameter × 0.2 mm deep). The samples were frozen in a Leica EM PACT 2 high pressure freezer equipped with a Rapid Transfer System (RTS) (Leica Microsystems, Buffalo Grove, IL). The samples were maintained under liquid nitrogen, then transferred to vials containing frozen 2% osmium tetroxide in anhydrous acetone. Freeze substitution was carried out in a Leica EM AFS machine (Leica Microsystems, Buffalo Grove, IL). After warming to room temperature the samples were processed using a modified ROTO protocol (1% thiocarbohydrazide in 90% acetone/10% water, then 2% osmium in acetone, and finally 0.1% uranyl acetate in acetone; S. Watanabe, personal communication), and finally embedded in Polybed epoxy resin. Further processing was done as described for chemically fixed samples.

Modeling

Determination of the shapes of the stacked sheets and of the helicoidal connections between them was performed numerically by searching for the shapes that minimize the sum of the bending energies of the sheet edge lines (Eq.2), sheet planes (Eq. 4), and the work performed against the lateral pressure (Eq. 5).

The major steps of the energy minimization were performed using Surface Evolver, a software tool developed by Ken Braake of the University of Minnesota (http://www.susqu.edu/brakke/evolver/evolver.html). Surface Evolver represents the surface as an adaptive mesh using the finite elements method, and finds minima of the energy function by the gradient descent technique. Exploration of the phase space of shapes that correspond to possible system parameters was performed by energy minimization using code written in Matlab. The minimal energy shape is computed for each set of the parameters: lateral pressure, sheet area, edge length, and edge spontaneous curvature. The minimization process starts from a shape composed of ideal hollow helicoidal elements of alternating handedness packed in a checkerboard-like lattice and connected by interstice regions of low-detail guess shape. The helicoidal elements are parameterized by their pitch and their internal and external radii. In order to facilitate convergence of the optimization process, the interstice surface is created at each optimization step by fitting previously computed optimal surfaces to the area and edge constraints, using Matlab’s trust-region optimization algorithm. The combined helicoid-interstice surface and associated parameters are parsed into a script to be run by Surface Evolver, which then optimizes and refines the shape, returning the minimal energy and corresponding surface parameters.

Supplementary Material

01
Download video file (969.7KB, mov)
02
Download video file (1.1MB, mov)
03
Download video file (2.1MB, mov)
04
Download video file (1.1MB, mov)
05
Download video file (1.2MB, mov)
06
Download video file (1.5MB, mov)
07
Download video file (2.5MB, mov)
08
09

Highlights.

  • A novel ultra-thin sectioning EM method is used to visualize the ER

  • Discovery of a common structural motif connecting ER sheets

  • Stacked sheets resemble a parking garage with helicoidal ramps between the levels

  • The structure corresponds to a minimum of elastic energy

Acknowledgments

We thank Shigeki Watanabe for providing his unpublished freeze substitution protocol, and Yoko Shibata, Rindy Jaffe, and Adrian Salic for critical reading of the manuscript. We thank Sid Tamm for pointing out the parking garage analogy. M.M.K. is supported by the Israel Science Foundation (ISF) and the Marie Curie network “Virus Entry”, and holds the Joseph Klafter Chair in Biophysics. T.A.R. is a Howard Hughes Medical Institute Investigator. G.H. acknowledges support from the National Science Foundation under grant NSF PHY11-25915, and from the Richard Berlin Center for Cell Analysis and Modeling.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Baumann O, Walz B. Endoplasmic reticulum of animal cells and its organization into structural and functional domains. Int Rev Cytol. 2001;205:149–214. doi: 10.1016/s0074-7696(01)05004-5. [DOI] [PubMed] [Google Scholar]
  2. Becker F, Block-Alper L, Nakamura G, Harada J, Wittrup KD, Meyer DI. Expression of the 180-kD ribosome receptor induces membrane proliferation and increased secretory activity in yeast. J Cell Biol. 1999;146:273–284. doi: 10.1083/jcb.146.2.273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bian X, Klemm RW, Liu TY, Zhang M, Sun S, Sui X, Liu X, Rapoport TA, Hu J. Structures of the atlastin GTPase provide insight into homotypic fusion of endoplasmic reticulum membranes. Proc Natl Acad Sci U S A. 2011;108:3976–3981. doi: 10.1073/pnas.1101643108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Byrnes LJ, Sondermann H. Structural basis for the nucleotide-dependent dimerization of the large G protein atlastin-1/SPG3A. Proc Natl Acad Sci U S A. 2011;108:2216–2221. doi: 10.1073/pnas.1012792108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cardona A, Saalfeld S, Schindelin J, Arganda-Carreras I, Preibisch S, Longair M, Tomancak P, Hartenstein V, Douglas RJ. TrakEM2 software for neural circuit reconstruction. PLoS One. 2012;7:e38011. doi: 10.1371/journal.pone.0038011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Catalan E. Sur les surfaces réglées dont l’aire est un minimum. J Math Pure Appl. 1842;7:203–211. [Google Scholar]
  7. De Craene JO, Coleman J, Estrada de Martin P, Pypaert M, Anderson S, Yates JR, 3rd, Ferro-Novick S, Novick P. Rtn1p is involved in structuring the cortical endoplasmic reticulum. Mol Biol Cell. 2006;17:3009–3020. doi: 10.1091/mbc.E06-01-0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. do Carmo MP, editor. The Helicoid. Braunschweig; Vieweg: 1986. [Google Scholar]
  9. Fawcett DW. The Cell. Philadelphia: W. B. Saunders; 1981. [Google Scholar]
  10. Friedman JR, Voeltz GK. The ER in 3D: a multifunctional dynamic membrane network. Trends Cell Biol. 2011;21:709–717. doi: 10.1016/j.tcb.2011.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gido SP, Gunther J, Thomas EL, Hoffman D. Lamellar diblock copolymer grain-boundary morphology. 1. Twist boundary characterization. Macromolecules. 1993;26:4506–4520. [Google Scholar]
  12. Gido SP, Thomas EL. Lamellar diblock copolymer grain boundary morphology. 3. Helicoid section twist boundary energy source. Macromolecules. 1997;30:3739–3746. [Google Scholar]
  13. Hand AR. The effects of acute starvation on parotid acinar cells. Ultrastructural and cytochemical observations on ad libitum-fed and starved rats. The American journal of anatomy. 1972;135:71–92. doi: 10.1002/aja.1001350107. [DOI] [PubMed] [Google Scholar]
  14. Helfrich W. Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z Naturforsch. 1973;28c:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
  15. Hu J, Prinz WA, Rapoport TA. Weaving the Web of ER Tubules. Cell. 2011;147:1226–1231. doi: 10.1016/j.cell.2011.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hu J, Shibata Y, Voss C, Shemesh T, Li Z, Coughlin M, Kozlov MM, Rapoport TA, Prinz WA. Membrane proteins of the endoplasmic reticulum induce high-curvature tubules. Science. 2008;319:1247–1250. doi: 10.1126/science.1153634. [DOI] [PubMed] [Google Scholar]
  17. Hu J, Shibata Y, Zhu PP, Voss C, Rismanchi N, Prinz WA, Rapoport TA, Blackstone C. A class of dynamin-like GTPases involved in the generation of the tubular ER network. Cell. 2009;138:549–561. doi: 10.1016/j.cell.2009.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kamien RD, Lubensky TC. Chiral lyotropic liquid crystals: TGB phases and helicoidal structures. Journal de Physique II. 1997;7:157–163. [Google Scholar]
  19. Klopfenstein DR, Kappeler F, Hauri HP. A novel direct interaction of endoplasmic reticulum with microtubules. Embo J. 1998;17:6168–6177. doi: 10.1093/emboj/17.21.6168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Luckey CJ, Bhattacharya D, Goldrath AW, Weissman IL, Benoist C, Mathis D. Memory T and memory B cells share a transcriptional program of self-renewal with long-term hematopoietic stem cells. Proc Natl Acad Sci U S A. 2006;103:3304–3309. doi: 10.1073/pnas.0511137103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Nikonov AV, Hauri HP, Lauring B, Kreibich G. Climp-63-mediated binding of microtubules to the ER affects the lateral mobility of translocon complexes. J Cell Sci. 2007;120:2248–2258. doi: 10.1242/jcs.008979. [DOI] [PubMed] [Google Scholar]
  22. Nikonov AV, Snapp E, Lippincott-Schwartz J, Kreibich G. Active translocon complexes labeled with GFP-Dad1 diffuse slowly as large polysome arrays in the endoplasmic reticulum. The Journal of cell biology. 2002;158:497–506. doi: 10.1083/jcb.200201116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ogawa-Goto K, Tanaka K, Ueno T, Kurata T, Sata T, Irie S. p180 is involved in the interaction between the endoplasmic reticulum and microtubules through a novel microtubule-binding and bundling domain. Mol Biol Cell. 2007;18:3741–3751. doi: 10.1091/mbc.E06-12-1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Orso G, Pendin D, Liu S, Tosetto J, Moss TJ, Faust JE, Micaroni M, Egorova A, Martinuzzi A, McNew JA, et al. Homotypic fusion of ER membranes requires the dynamin-like GTPase atlastin. Nature. 2009;460:978–983. doi: 10.1038/nature08280. [DOI] [PubMed] [Google Scholar]
  25. Palade GE, Siekevitz P. Liver microsomes; an integrated morphological and biochemical study. The Journal of biophysical and biochemical cytology. 1956a;2:171–200. doi: 10.1083/jcb.2.2.171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Palade GE, Siekevitz P. Pancreatic microsomes; an integrated morphological and biochemical study. The Journal of biophysical and biochemical cytology. 1956b;2:671–690. doi: 10.1083/jcb.2.6.671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Porter KR, Blum J. A study in microtomy for electron microscopy. Anat Rec. 1953;117:685–710. doi: 10.1002/ar.1091170403. [DOI] [PubMed] [Google Scholar]
  28. Puhka M, Joensuu M, Vihinen H, Belevich I, Jokitalo E. Progressive sheet-to-tubule transformation is a general mechanism for endoplasmic reticulum partitioning in dividing mammalian cells. Mol Biol Cell. 2012;23:2424–2432. doi: 10.1091/mbc.E10-12-0950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Savitz AJ, Meyer DI. Identification of a ribosome receptor in the rough endoplasmic reticulum. Nature. 1990;346:540–544. doi: 10.1038/346540a0. [DOI] [PubMed] [Google Scholar]
  30. Senda T, Yoshinaga-Hirabayashi T. Intermembrane bridges within membrane organelles revealed by quick-freeze deep-etch electron microscopy. Anat Rec. 1998;251:339–345. doi: 10.1002/(SICI)1097-0185(199807)251:3<339::AID-AR9>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
  31. Shibata Y, Hu J, Kozlov MM, Rapoport TA. Mechanisms shaping the membranes of cellular organelles. Annu Rev Cell Dev Biol. 2009;25:329–354. doi: 10.1146/annurev.cellbio.042308.113324. [DOI] [PubMed] [Google Scholar]
  32. Shibata Y, Shemesh T, Prinz WA, Palazzo AF, Kozlov MM, Rapoport TA. Mechanisms determining the morphology of the peripheral ER. Cell. 2010;143:774–788. doi: 10.1016/j.cell.2010.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Shibata Y, Voeltz GK, Rapoport TA. Rough sheets and smooth tubules. Cell. 2006;126:435–439. doi: 10.1016/j.cell.2006.07.019. [DOI] [PubMed] [Google Scholar]
  34. Shibata Y, Voss C, Rist JM, Hu J, Rapoport TA, Prinz WA, Voeltz GK. The reticulon and DP1/Yop1p proteins form immobile oligomers in the tubular endoplasmic reticulum. J Biol Chem. 2008;283:18892–18904. doi: 10.1074/jbc.M800986200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Short B, Haas A, Barr FA. Golgins and GTPases, giving identity and structure to the Golgi apparatus. Biochim Biophys Acta. 2005;1744:383–395. doi: 10.1016/j.bbamcr.2005.02.001. [DOI] [PubMed] [Google Scholar]
  36. Spivak M. A comprehensive introduction to differential geometry. Brandeis University; 1970. [Google Scholar]
  37. Tapia J, Kasthuri N, Hayworth K, Schalek R, Lichtman J, Smith S, Buchanan J. Improved high contrast en bloc staining of neuronal tissue for field emission scanning electron microscopy. Nat Protoc. 2012;7:193–206. doi: 10.1038/nprot.2011.439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Terasaki M, Chen LB, Fujiwara K. Microtubules and the endoplasmic reticulum are highly interdependent structures. J Cell Biol. 1986;103:1557–1568. doi: 10.1083/jcb.103.4.1557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Toyoshima I, Yu H, Steuer ER, Sheetz MP. Kinectin, a major kinesin-binding protein on ER. The Journal of cell biology. 1992;118:1121–1131. doi: 10.1083/jcb.118.5.1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Voeltz GK, Prinz WA, Shibata Y, Rist JM, Rapoport TA. A class of membrane proteins shaping the tubular endoplasmic reticulum. Cell. 2006;124:573–586. doi: 10.1016/j.cell.2005.11.047. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
Download video file (969.7KB, mov)
02
Download video file (1.1MB, mov)
03
Download video file (2.1MB, mov)
04
Download video file (1.1MB, mov)
05
Download video file (1.2MB, mov)
06
Download video file (1.5MB, mov)
07
Download video file (2.5MB, mov)
08
NIHMS508416-supplement-08.pdf (18.9MB, pdf)
09
NIHMS508416-supplement-09.docx (118.5KB, docx)

RESOURCES