Quantifying interactions between real oscillators with information theory and phase models: Application to cardiorespiratory coupling

Abstract

Interactions between oscillators can be investigated with standard tools of time series analysis. However, these methods are insensitive to the directionality of the coupling, i.e., the asymmetry of the interactions. An elegant alternative was proposed by Rosenblum and collaborators [M. G. Rosenblum, L. Cimponeriu, A. Bezerianos, A. Patzak, and R. Mrowka, Phys. Rev. E 65, 041909 (2002); M. G. Rosenblum and A. S. Pikovsky, Phys. Rev. E 64, 045202 (2001)] which consists in fitting the empirical phases to a generic model of two weakly coupled phase oscillators. This allows one to obtain the interaction functions defining the coupling and its directionality. A limitation of this approach is that a solution always exists in the least-squares sense, even in the absence of coupling. To preclude spurious results, we propose a three-step protocol: (1) Determine if a statistical dependency exists in the data by evaluating the mutual information of the phases; (2) if so, compute the interaction functions of the oscillators; and (3) validate the empirical oscillator model by comparing the joint probability of the phases obtained from simulating the model with that of the empirical phases. We apply this protocol to a model of two coupled Stuart-Landau oscillators and show that it reliably detects genuine coupling. We also apply this protocol to investigate cardiorespiratory coupling in anesthetized rats. We observe reciprocal coupling between respiration and heartbeat and that the influence of respiration on the heartbeat is generally much stronger than vice versa. In addition, we find that the vagus nerve mediates coupling in both directions.

I. INTRODUCTION

Coupling of oscillators has broad applicability in physical and biological systems. Interactions between oscillators can be investigated empirically with standard methods of time-series analysis such as cross-correlograms, spectral coherence, or mutual information. However, these approaches are limited by their insensitivity to the directionality of the coupling, i.e., the asymmetry of the interactions.

Rosenblum and collaborators proposed an alternative approach to investigate coupling in real oscillators capable of resolving the directionality [1,2]. Their method is to fit a generic model of coupled phase oscillators to the data and to use the coupling functions of the model to measure coupling. Although the theory is sound, spurious results can be obtained in practice because the fitting is linear and performed in the least-squares fashion. The problem is that a solution to the least-squares minimization problem always exists so an empirical model can be obtained from oscillators that are actually uncoupled.

In this paper, we propose a three step protocol to overcome this limitation. First, we compute the mutual information of the instantaneous phases and determine its statistical significance using a series of randomizations. If the dependency in the data is significant relative to the randomized data, then we fit the coupled oscillator model to the actual data to obtain the interaction functions. Last, we validate the empirical oscillator model by comparing the joint probability of the phases obtained from simulating the model with the joint probability of the empirical phases.

We illustrate the application of our protocol in two different contexts. First, we study a system of two coupled Stuart-Landau oscillators. This type of oscillator is commonly used in theoretical and computational studies in physics as it represents the dynamics of a system close to a supercritical Hopf bifurcation; a frequent mechanism of obtaining a stable limit cycle [3]. Our protocol reliably detects the presence or absence of coupling in this context as well as its directionality. Second, we study cardiorespiratory coupling (CRC) in rats. CRC is defined as the relationship between the rhythms of respiration and the heartbeat [Fig. 1(a)] [4]. Theoretically, CRC minimizes the energy expenditure for gas exchange and plays an integral role in maintaining homeostasis [5–8]. Here, we show that the predominant interaction is the influence of respiration on the heartbeat. Conversely, the influence of the heartbeat on respiration is weak, but significant.

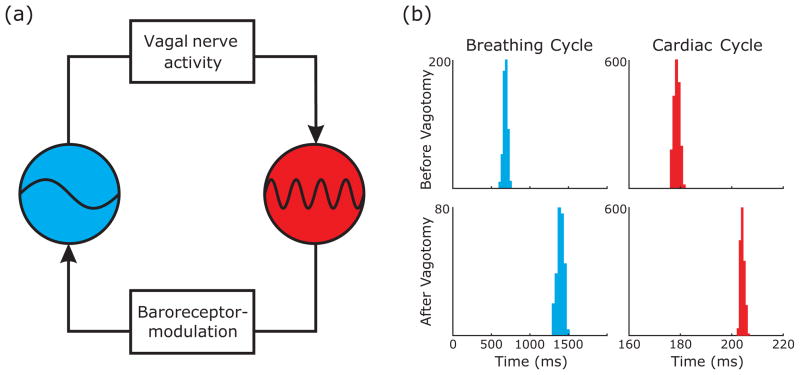
FIG. 1.

(Color online) Cardiorespiratory coupling schematic and interevent intervals for respiratory and heartbeat signals. (a) The blue (light gray) ball is respiration and the red (dark gray) ball is heartbeat. The major pathway which mediates CRC for a given direction is labeled in the boxes. (b) Distribution of interevent intervals for respiration and heartbeat in intact and vagotomized states. Note that vagotomy reduces the mean frequency of both oscillators.

Previous studies have quantified CRC using measures in the time and frequency domains. Recent reports used χ ² statistics to quantify the deviance from uniformity of cross-correlograms of heartbeats relative to each breath [9,10] and spectral coherence at low frequencies [11,12]. Although both approaches are valid, they are unable to resolve the asymmetry of the coupling. The empirical model of coupled phase oscillators proposed in Refs. [1,2] is an ideal candidate for the study of CRC because it is sensitive to the directionality of the interactions [13–15].

In practice, two assumptions are made when using the phase oscillator approach. First, coupling between both oscillators is weak, in the sense that the dispersion around the mean frequency of the oscillator is small compared to the mean frequency, which is verified in Fig. 1(b); and second, the interactions between the oscillators can be truthfully represented by a phase oscillator model; i.e., the angular frequency is the only relevant state variable, and the amplitude of the signal and its temporal modulation are irrelevant, which is verified in Fig. 2.

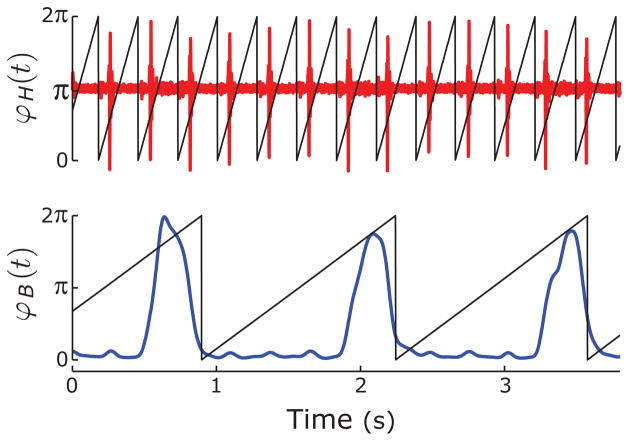
FIG. 2.

(Color online) Phase of ECG and EMG recordings. The phase of each recording is overlaid on the raw traces. (Top) ECG; (bottom) diaphragmatic EMG. B stands for breathing and H stands for heartbeat.

II. METHODS

A. Experimental methods

Adult male Sprague-Dawley rats (Sprague Dawley/Harlan, 375–425 g, n = 15), were anesthetized with isoflurane (0.5%–1.0%). Rats were intubated and breathed spontaneously. Electrocardiogram (ECG) and diaphragmatic electromyogram (EMG) were recorded, filtered (0.01–3 kHz), digitized, and stored on a computer via SPIKE2 software (sampling at 10 kHz). Rats were allowed at least 30 min after surgery to stabilize. Stationary epochs were analyzed from a 5-min epoch before and after bilateral transection of the vagal nerves (vagotomy).

B. Phase estimation

The recordings were first narrow-band pass filtered. The impulse response of the filter was defined by a trapezoid with height 1 and vertices located at 0.5, 0.8, 1.3, and 1.5 Hz for the EMG and 3.5, 4.0, 6.0, and 6.5 Hz for the ECG. Then, the Hilbert transform was computed for each filtered signal to obtain a complex time series, the so-called analytical signal, whose angle represents the instantaneous “protophase,” for each oscillator, θ₁, θ₂. Next, a correction detailed in Ref. [16] was applied to θ₁, θ₂ to obtain the “genuine” phase φ₁, φ₂. Specifically, begin with θ and define

$$S_n=\frac{1}{N}\sum _{j=1}^N{e}^{-in\theta (t_j)},$$

where θ(t_j) indicates the values of the protophase at the ith time sample. Then, the genuine phase is given by

$$\phi (t)=\theta (t)+\sum _{n\ne 0}\frac{S_n}{in}(e^{in\theta (t)}-1).$$

For our analysis, we use n = −10 to 10 because a larger range did not yield different results. An example of the phase in comparison with the raw data is shown in Fig. 2.

C. Mutual information of the oscillatory dynamics

In information theory, mutual information is a nondirectional measure of the dependency of two random variables based on their marginal and joint probability distributions. Intuitively, this measure describes how factorizable a joint distribution is. The mutual information, I, for two oscillators with phases φ₁, φ₂ is given by

$$I({\phi }_1,{\phi }_2)=I({\phi }_2,{\phi }_1)={\int }_0^{2\pi }{\int }_0^{2\pi }P({\phi }_1,{\phi }_2)ln\times \left(\frac{P({\phi }_1,{\phi }_2)}{P_1({\phi }_1)P_2({\phi }_2)}\right)d{\phi }_{1}d{\phi }_2,$$ (1)

where P(φ₁, φ₂) is the joint distribution of the phases and P₁(φ₁) and P₂(φ₂) are the respective marginal distributions. A theoretical definition of P(φ₁, φ₂) is

$$P({\phi }_1,{\phi }_2)=\frac{1}{N}\sum _{j=1}^N\delta ({\phi }_1-{\widehat{\phi }}_1(t_j))\delta ({\phi }_2-{\widehat{\phi }}_2(t_j)),$$ (2)

where φ̂ indicates empirical values of the ith phase at each time sample, j of N total samples (Ndt is the total duration of the recording with dt = 1 ms in our case). To construct a continuous distribution, the δ functions in Eq. (2) are convolved with a sharp symmetric distribution of unitary area and half width σ ≪ 2π. For our analysis, we use the von Mises distribution, which generalizes the Gaussian distribution to the case of wraparound conditions. The von Mises distribution is given by

$$f(x\mid \mu ,\kappa )=\frac{e^{\kappa cos(x-\mu )}}{2\pi J_0(\kappa )},$$ (3)

where J₀ is the modified Bessel function of the first kind and $\kappa =\frac{1}{2\pi {\sigma }^2}$. In the above expression, σ² is the analog of the variance of the typical Gaussian distribution. The bivariate form of the von Mises distribution is the product of Eq. (3), and so the empirical probability distribution for the phases of two oscillators is given by

$$P({\phi }_1,{\phi }_2)=\frac{1}{N{(2\pi J_0(\kappa ))}^2}\sum _{k=1}^{N}exp(\kappa cos({\phi }_1-{\widehat{\phi }}_1(t_k)))\times exp(\kappa cos({\phi }_2-{\widehat{\phi }}_2(t_k))).$$ (4)

This definition of the joint distribution of the phases is more robust than the standard one obtained via a two-dimensional histogram; this is because the calculation of the mutual information is acutely sensitive to the size and edges of the histogram’s bins. In contrast, the mutual information marginally depends on the choice of σ in Eq. (4). As long as σ ≪ 2π, the above method approximates the value for the “true” continuous distribution associated with its empirical estimation, P(φ₁, φ₂). We use σ = 0.12 for our analysis.

Recall that I is a criterion for determining if coupling can be detected using the phase oscillator approach. As mentioned in the Introduction, this constraint is necessary because fitting the model to data always produces a coupling function, even in cases where the oscillators are uncoupled. To determine whether I for a given experiment is significant, we randomize the data to obtain a tolerance for I due to chance interactions. Specifically, we compute I for the empirical phases and compare it to the 95% confidence interval of I ‘s computed from many randomizations of the empirical phases. These randomizations consist of independently permuting the cycles of both oscillators. It is worth noting that this randomization technique preserves the mean and variance of the heartbeat and respiration periods.

For clarity, let I ^* be the tolerance for significance (95th confidence interval). The procedure to calculate I ^* is as follows. First, permute the cycles of the phases of both oscillators arbitrarily and compute I for this particular randomization. Then, repeat this process many times (n = 100 in our case) and determine the 95th percentile of all the I ‘s belonging to the randomizations. Compute the interaction functions only for experiments where the empirical I is greater than I ^*.

D. Empirical phase oscillator model

Following Rosenblum et al. [1,2,17], the generic model of two coupled oscillators is given by

$$\begin{array}{l}{\stackrel{.}{\phi }}_1={\omega }_1+F_{2\to 1}({\phi }_1,{\phi }_2)+{\sigma }_1{\eta }_1(t),\\ {\stackrel{.}{\phi }}_2={\omega }_2+F_{1\to 2}({\phi }_2,{\phi }_1)+{\sigma }_2{\eta }_2(t),\end{array}$$ (5)

where φ̇₁, φ̇₂ are the time derivative of the phases; ω₁,ω₂ are the autonomous frequencies, F_2→1(φ₁, φ₂), F_1→2(φ₂, φ₁) are the coupling functions; η₁(t),η₂(t) are uncorrelated white noise processes with unitary variance and scaled by constants σ₁,σ₂. The coupling functions can be expressed as a complex Fourier series given by

$$\begin{array}{c}{F}_{2\to 1}({\phi }_1,{\phi }_2)=\sum _{n,m}{A}_{n,m}^1{e}^{i(n{\phi }_1+m{\phi }_2)}\\ F_{1\to 2}({\phi }_2,{\phi }_1)=\sum _{n,m}{A}_{n,m}^2{e}^{i(n{\phi }_2+m{\phi }_1)}\end{array}\text{for}\text{which}n\text{or}m\ne 0,$$ (6)

where n,m are indices synonymous to the n : m phase locking indices of two oscillators, and $A_{n,m}^1,A_{n,m}^2$ are the coefficients of the respective Fourier series for given values of n,m. Also, each function possesses a direction: 2 → 1 denotes coupling in the direction from oscillator 2 to 1 and 1 → 2 denotes coupling in the direction from oscillator 1 to 2. Incidentally, a similar approach can be applied to compute the phase-resetting curve of an oscillator from experimental data [18].

In obtaining the empirical model of coupled phase oscillators, the left-hand side of Eq. (5) is directly computed from the data, the right-hand side of Eq. (5) can be expressed as a complex Fourier series where ω_1,2 is given by Eq. (6) for which n and m = 0, and F_1,2 is given by Eq. (6) for which n or m ≠ 0. To avoid overfitting, we first compute A_n,m ∀n,m′s for a desired order, with the inner product of φ̇₁ and e^{−i(nφ̇₁−mφ̇₂)} given by

$$A_{n,m}={\int }_0^{2\pi }{\int }_0^{2\pi }{\stackrel{.}{\phi }}_{1}exp(-in{\phi }_1-im{\phi }_2)d{\phi }_{1}d{\phi }_2,$$

which can be numerically approximated as the temporal average 〈φ̇₁(t) exp(−inφ₁(t) − imφ₂(t))〉. Then, we rank the A_n,m’s and select coefficients with the largest power until 99% of the total power is reached, i.e., Σ_j |A_j|² > 0.99 Σ_n,m |A_n,m|², where A_j denotes the selected coefficients. When fitting the model to the data, we only use the n,m′s predetermined using this criterion. The amount of energy that cannot be accounted for the coefficients is then attributed to the energy of background noise, σ². In the final step, we fit (5) to the data using least squares. Furthermore, we use the parameters c_2→1,c_{1 →2} given by

$$c_{2\to 1}=\frac{\sqrt{{\sum }_{n,m\ne 0}{\left|A_{nm}^1\right|}^2}}{2\pi },c_{1\to 2}=\frac{\sqrt{{\sum }_{n,m\ne 0}{\left|A_{nm}^2\right|}^2}}{2\pi },$$

with units of Hz, to compare the strength of coupling and its directionality. In particular, if c_{2→ 1} > c_{1→ 2}, then heartbeat drives respiration more strongly than vice versa. If c_{2→ 1} < c_{1 →2}, then respiration drives heartbeat more strongly than vice versa.

Finally, we note that the amplitude of the interaction function has units of the reciprocal of time, Hz in our experiments. Thus, its reciprocal value provides a proxy for the time scale of the coupling, which is a few minutes in our experiments. Consequently, we selected 5-min-long stationary epochs for analysis.

E. Validation of the empirical oscillator model

The final step of our protocol is the validation of the empirical phase oscillator model. To this end, we test whether the joint distribution of the empirical phases is statistically different from the joint distribution of the phases obtained from simulating the oscillator model. This step is an additional measure for preventing spurious results. For our protocol, statistical similarity of the two distributions is determined using both Pearson’s linear correlation coefficient, R and Kendall’s τ. The Kendall’s τ coefficient is a nonparametric correlation statistic based on ranks and takes values between −1 and +1, where −1 indicates the ranks are reversely ordered with respect to each other, 0 indicates there is no association with the ranks, and 1 indicates the ranks are identical. Details for computing the p value for a given τ are provided in Ref. [19]. Hypothesis testing is performed using Kendall’s τ, where the null hypothesis is that the two distributions are independent and the alternate hypothesis is that they are dependent. We cannot perform a rigorous hypothesis testing with R since the error is not entirely Gaussian. Finally, we note that to compute Kendall’s τ and R for the empirical and theoretical probability distributions, we discretize them in intervals of 2π/100 for both φ₁ and φ₂.

F. Pseudocode

We implement our protocol with the MATLAB scripting language, made publicly available on our web site [20] as the Empirical Phase Oscillator Model (EPHOM) software package. EPHOM will take pre-processed data as input and produce the coupling functions when applicable. An overview of our protocol is as follows. Begin by computing the empirical joint distribution of the data. Then, compute I and I^* from the empirical joint distribution of the phases. Proceed with the analysis only if I is significant, i.e., I > I^*. Next, fit the coupled phase oscillator model to the data. Following, simulate the phase oscillator model and compute the joint distribution of these surrogate phases. Last, compute the Kendall’s τ for the empirical and the theoretical probability density functions. The results are considered only if τ is significant, i.e., the p-value is less than 0.05.

III. RESULTS

A. Numerical example

We simulate two complex Stuart-Landau oscillators with weak diffusive coupling and weakly driven with uncorrelated white noise:

$$\begin{array}{l}{\stackrel{.}{z}}_1=(1+i{\omega }_1)z_1-{\mid z_1\mid }^2{z}_1+{\epsilon }_1(z_2-z_1)+{\sigma }_1{\eta }_1(t),\\ {\stackrel{.}{z}}_2=(1+i{\omega }_2)z_2-{\mid z_2\mid }^2{z}_2+{\epsilon }_2(z_1-z_2)+{\sigma }_2{\eta }_2(t).\end{array}$$

In Cartesian coordinates, the model is given by

$$\begin{array}{l}{\stackrel{.}{x}}_1=x_1-{\omega }_1{y}_1-x_1\left(x_1^2-y_1^2\right)+{\epsilon }_1(x_2-x_1)+{\sigma }_1{\eta }_1(t),\\ {\stackrel{.}{y}}_1=y_1+{\omega }_1{x}_1-y_1\left(x_1^2-y_1^2\right)+{\epsilon }_1(y_2-y_1),\\ {\stackrel{.}{x}}_2=x_2-{\omega }_2{y}_2-x_2\left(x_2^2-y_2^2\right)+{\epsilon }_2(x_1-x_2)+{\sigma }_2{\eta }_2(t),\\ {\stackrel{.}{y}}_2=y_2+{\omega }_2{x}_2-y_2\left(x_2^2-y_2^2\right)+{\epsilon }_2(y_1-y_2).\end{array}$$

In polar coordinates it reads

$$\begin{array}{l}{\stackrel{.}{r}}_1=r_1(1-{\epsilon }_1-r_1^2)+{\epsilon }_1{r}_{2}cos({\phi }_2-{\phi }_1)+{\sigma }_1{\eta }_1(t)cos({\phi }_1),\\ {\stackrel{.}{\phi }}_1={\omega }_1+{\epsilon }_1\frac{r_2}{r_1}sin({\phi }_2-{\phi }_1)-{\sigma }_1{\eta }_1(t)sin({\phi }_1),\\ {\stackrel{.}{r}}_2=r_2(1-{\epsilon }_2-r_2^2)+{\epsilon }_2{r}_{1}cos({\phi }_1-{\phi }_2)+{\sigma }_2{\eta }_2(t)cos({\phi }_2),\\ {\stackrel{.}{\phi }}_2={\omega }_2+{\epsilon }_2\frac{r_1}{r_2}sin({\phi }_1-{\phi }_2)-{\sigma }_1{\eta }_1(t)sin({\phi }_2).\end{array}$$

Under the weak-coupling assumption, r₁,r₂ are roughly constant and can be approximated as 1. In this case, the model of coupled Stuart-Landau oscillators takes the form of two weakly coupled phase oscillators, as in Eq. (5) with

$$\begin{array}{l}{F}_{2\to 1}({\phi }_1,{\phi }_2)=sin({\phi }_2-{\phi }_1),\\ F_{1\to 2}({\phi }_2,{\phi }_1)=sin({\phi }_1-{\phi }_2).\end{array}$$ (7)

We applied our protocol to four different test cases: asymmetric coupling where oscillator 2 drives oscillator 1 more strongly than vice versa, asymmetric coupling where oscillator 1 drives oscillator 2 more strongly than vice versa, symmetric coupling, and no coupling. For all the test cases, ω₁ = 3, ω₂ = 3π, and σ₁ = σ₂ = 0.05. For the asymmetric cases, ε₁ = 0.5, ε₂ = 0.15 and ε₁ = 0.15, ε₂ = 0.5, for the symmetric case, ε₁ = 0.5, ε₂ = 0.5, and for the uncoupled case, ε₁ = 0, ε₂ = 0. To integrate the model, we use the Euler-Maruyama method with dt = 0.001 s and a total integration time of 5 min. Only one realization was used for the analysis. However, other realizations produce near identical results due to the considerable length and stationarity of the simulated signals.

Our protocol accurately resolves the presence or absence of coupling, its directionality, and its magnitude (Figs. 3 and 4). As expected, the accuracy of coupling estimation decays as ε approaches the value of σ but, notably, the directionality can still be resolved until when ε ≈ σ (not shown).

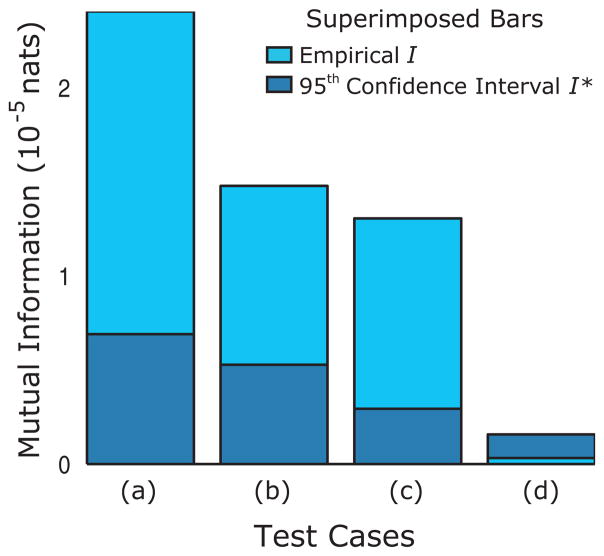
FIG. 3.

(Color online) Mutual information values of simulated coupled Stuart-Landau oscillators. (a) Symmetric coupling. (b) Asymmetric coupling where oscillator 2 drives oscillator 1 more strongly than vice versa. (c) Asymmetric coupling where oscillator 1 drives oscillator 2 more strongly than vice versa. (d) No coupling.

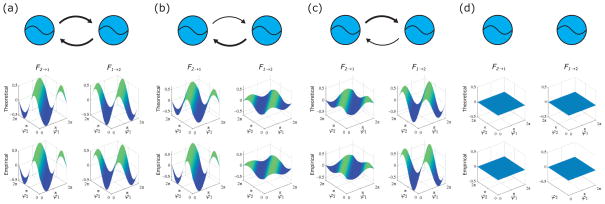
FIG. 4.

(Color online) Theoretical and empirical coupling functions of simulated coupled Stuart-Landau oscillators. In (a), (b), (c), and (d) the top panel is a schematic showing how the oscillators are coupled. The middle panel is the theoretical coupling function, and the bottom panel is the empirical coupling function obtained using our protocol. (a) Symmetric coupling. (b) Asymmetric coupling where oscillator 2 drives oscillator 1 more strongly than vice versa. (c) Asymmetric coupling where oscillator 1 drives oscillator 2 more strongly than vice versa. (d) No coupling.

B. Cardiorespiratory coupling in anesthetized rats

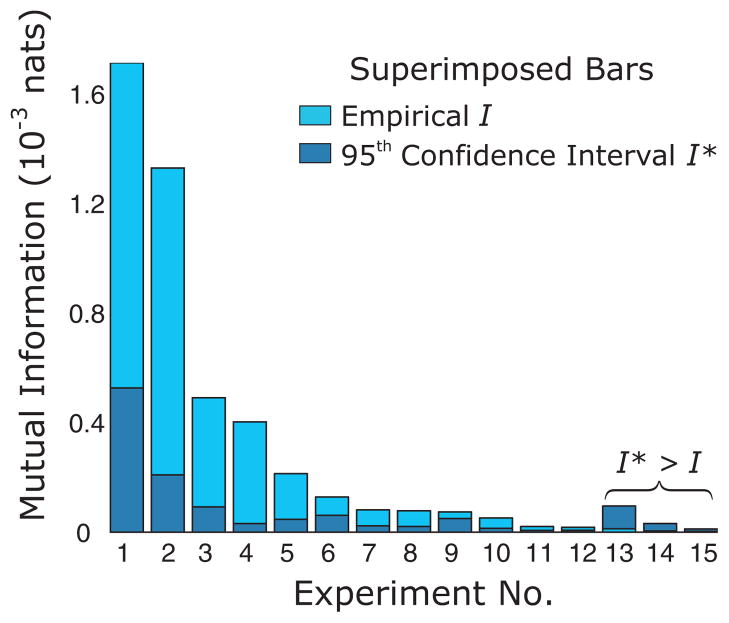
We applied our protocol to a physiologic data set composed of 15 experiments. The values of mutual information ranged from highly significant to insignificant (Fig. 5); data from 12 of 15 passed the mutual information test and 3 (see Fig. 5, 13 through 15) were excluded because the data did not possess a significant value of the mutual information (Fig. 5).

FIG. 5.

(Color online) Mutual information values of data. The empirical and randomized values of the mutual information are presented for the 15 experiments.

The coupled phase oscillator model was obtained for 12 experiments, and importantly, the residuals of these models, η(t), were not correlated. The Pearson’s linear correlation coefficients for η_B (t) and η_H (t) were <6% for all the experiments analyzed. This indicates that the coupling between both oscillators is deterministic and not the result of stochastic synchronization [21–25], i.e., the entrainment of uncoupled oscillators driven by common noise.

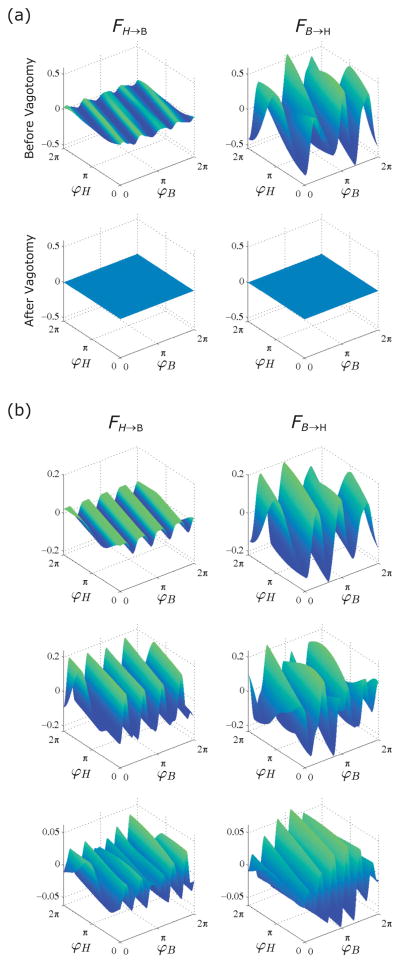
In order to improve the solution of the least squares problem, we removed angular frequencies which differed by more than three standard deviations from the natural frequency. Outlying angular frequencies were removed by eliminating entire segments of the phase corresponding to those values, from both signals. This preserves the paring of the data points in time, and thus any interactions which were present prior to modifying the data. For clarity, no means of interpolation was used to fill in removed segments; they are simply removed in the same way from both signals. An example of the coupling functions for an experiment before and after vagotomy is presented in Fig. 6(a), and examples of the coupling functions for three experiments in the naive state is presented in Fig. 6(b). Overall, the interaction functions are quite consistent across animals in terms of their undulated structure. This is because the dominant coefficient A_n,m corresponds to the closest n:m ratio of heartbeat to respiration.

FIG. 6.

(Color online) Empirical coupling functions of CRC data. In both (a) and (b), on the left is the coupling function corresponding to the influence of heartbeat on the respiration, and on the right is the coupling function corresponding to vice versa. (a) The top panel is before vagotomy and the bottom panel is after vagotomy. The coupling coefficients for this experiment correspond to 1 in Fig. 8. (b) The coupling functions for three experiments are shown. Top, middle, and bottom correspond to 2, 3, and 4 in Fig. 8.

To interpret the shape of the coupling functions one must bear in mind that each coupling function depends on the phases of both oscillators. Thus, the plot of the each coupling function represents an unwrapped toroidal surface. A single heart rate acceleration-deceleration occurs per respiratory cycle in time, but because the heart rate is approximately six (or five, etc.) times faster than respiration in Fig. 6, and because there are wraparound conditions for the phase, when respiration completes a revolution along the toroidal direction, the heartbeat revolves roughly six times along the poloidal direction on the torus. The number of bands in the coupling functions corresponds to the closest n:m synchronization index of these oscillators. The ratios in our data are 1:4, 1:5, 1:6, and 1:7. From a physiological perspective, the ratio 1: n implies that there are n heartbeats per respiration. So, the baroreceptors are activated n times within one respiratory cycle. Thus, the values of the coupling function constrained to a transversal cut at a fixed value of φ_H, for instance, φ_H = π, will have n peaks.

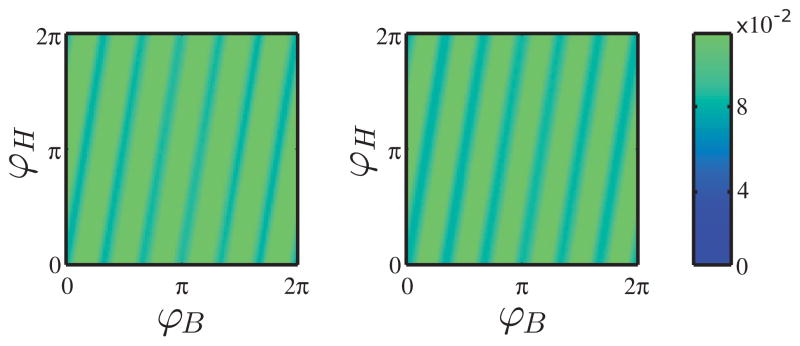
A comparison between the empirical joint distribution and the joint distribution from the model is presented in Fig. 7. The Kendall’s τ, along with the associated p-value, and Pearson’s linear correlation coefficient is presented below (Table I). The coupling coefficients for these experiments are presented in Fig. 8.

FIG. 7.

(Color online) Empirical and theoretical joint probability distributions of the phases. (a) Joint probability of empirical phases corresponding to 2 in Fig. 8. (b) Joint probability of the phases obtained from simulating the model.

TABLE I.

Pearson’s linear correlation coefficient and Kendall’s τ for the empirical and theoretical distributions. Both coefficients are given for the 12 experiments with I > I^*. Statistical significance is determined from the p-value of each τ. Numbering of the experiments is consistent with that of Fig. 5.

Experiment	R	τ	Significant (Y/N)
1	0.99	0.92	Y
2	0.95	0.79	Y
3	0.80	0.52	Y
4	0.99	0.95	Y
5	0.99	0.96	Y
6	0.99	0.95	Y
7	0.95	0.79	Y
8	0.99	0.90	Y
9	0.96	0.86	Y
10	0.96	0.83	Y
11	0.92	0.77	Y
12	0.98	0.89	Y

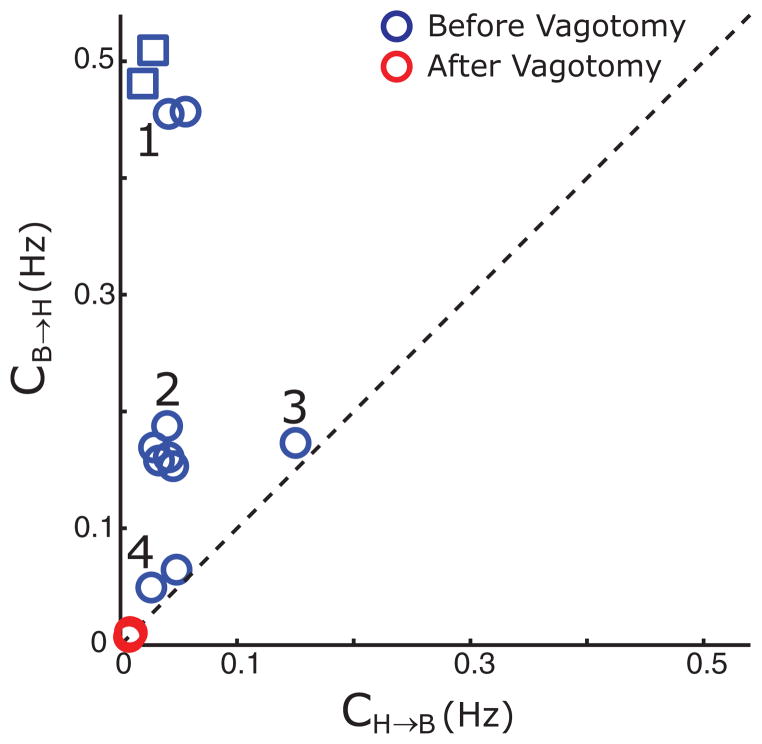
FIG. 8.

(Color online) Coupling coefficients before and after vagotomy. Coupling coefficients (c’s) for both direction are plotted against each other for the 12 experiments with I > I^*. The c’s for experiments where vagotomy was performed are also presented. The squares have c_B→H with values of 2.24 and 1.64. The dotted line emphasizes the directionality.

Our results indicate that coupling in the cardiorespiratory system in the anesthetized state is generally biased in the direction of respiration to heartbeat. Moreover, coupling in both directions is dependent on the vagus nerve, because severing this nerve extinguishes pre-existing coupling.

IV. CONCLUSIONS

We have presented a protocol that combines mutual information with phase oscillator dynamics to quantify coupling in real oscillators. We have successfully tested our protocol with a model of two coupled Stuart-Landau oscillators. In addition, we have applied our protocol to investigate cardiorespiratory coupling in anesthetized rats. From a physiological perspective, we have shown that the interaction between heartbeat and respiration is reciprocal but biased towards the influence of respiration on heartbeat.

Cardiorespiratory coupling is thought to be a good indicator of health, because it reflects a balance between the sympathetic and parasympathetic components of the autonomous nervous systems which control homeostasis and visceral function [26]. Cardiorespiratory interactions are defined and measured in different ways; the most popular is the so called respiratory sinus arrhythmia, by which inspiration tends to delay the upcoming heartbeat. This frequency modulation is apparent in the power spectrum of ECG signals as a second peak in the spectrum below 1 Hz (in humans, but higher in rats), corresponding to the heartbeat’s frequency modulation due to respiration. Consistent with the respiratory sinus arrhythmia, the empirical phase-oscillator model reveals a dominant influence of respiration on the heartbeat. In addition, the model also resolves the reciprocal interaction: our analysis shows that there is a weak but reproducible influence of the heartbeat on respiration. This suggests that the baroreceptor pathway depicted in Fig. 1 is also functionally relevant, at least in anesthetized conditions.

In general, the protocol presented here allows one to efficiently and reliably resolve functional coupling in real oscillators.