Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Jul 24;13(9):4071–4083. doi: 10.1021/cg4009015

Absorbing a Little Water: The Structural, Thermodynamic, and Kinetic Relationship between Pyrogallol and Its Tetarto-Hydrate

Doris E Braun †,‡,*, Rajni M Bhardwaj §, Jean-Baptiste Arlin ∥, Alastair J Florence §, Volker Kahlenberg ⊥, Ulrich J Griesser †, Derek A Tocher ‡, Sarah L Price ‡
PMCID: PMC3767201  PMID: 24027438

Abstract

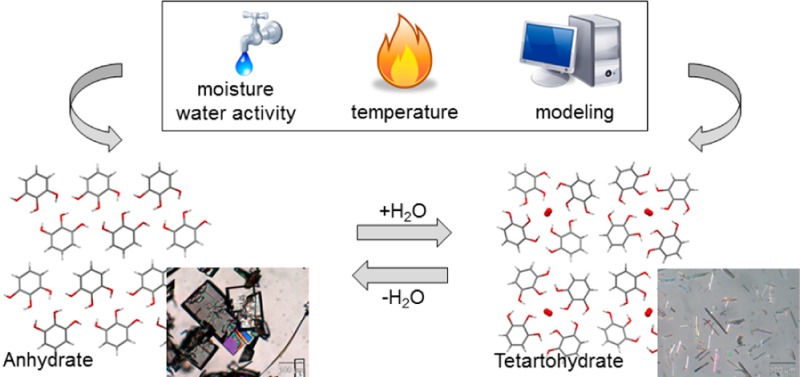
graphic file with name cg-2013-009015_0016.jpg

The anhydrate and the stoichiometric tetarto-hydrate of pyrogallol (0.25 mol water per mol pyrogallol) are both storage stable at ambient conditions, provided that they are phase pure, with the system being at equilibrium at aw (water activity) = 0.15 at 25 °C. Structures have been derived from single crystal and powder X-ray diffraction data for the anhydrate and hydrate, respectively. It is notable that the tetarto-hydrate forms a tetragonal structure with water in channels, a framework that although stabilized by water, is found as a higher energy structure on a computationally generated crystal energy landscape, which has the anhydrate crystal structure as the most stable form. Thus, a combination of slurry experiments, X-ray diffraction, spectroscopy, moisture (de)sorption, and thermo-analytical methods with the computationally generated crystal energy landscape and lattice energy calculations provides a consistent picture of the finely balanced hydration behavior of pyrogallol. In addition, two monotropically related dimethyl sulfoxide monosolvates were found in the accompanying solid form screen.

Short abstract

The structural transformation between anhydrous and hydrated pyrogallol, the only two practically relevant forms emerging from a solid form screen, has been unraveled with complementary experimental techniques (moisture sorption analysis, thermal analysis, X-ray diffraction, and water activity measurements) and crystal energy landscape calculations.

1. Introduction

Understanding the diversity of crystalline forms (polymorphs, hydrates, and solvates) is important in the pharmaceutical and other fine-chemical industries.1−3 The most critical and key parameters that influence the occurrence of solid forms are temperature, pressure, moisture, the nature of the solvent of crystallization (including water activity) and supersaturation. Both kinetic and thermodynamic factors determine which phase results. On the thermodynamic side, contrasting the crystal energy landscape of a molecule4 (i.e., the computer-generated, thermodynamically feasible structures) with the experimentally observed structures can be the first step toward understanding the factors that control crystallization5 and can result in polymorphism.1,6 However, even if relative free energies of the crystal forms could be accurately calculated, the crystal energy landscape does not reflect the kinetic factors.7,8 The control of the kinetics of nucleation and growth requires precise crystallization conditions. Thus, systematic changes in solvent (including mixtures, water activity), temperature, and rate of change of supersaturation need to be considered in solid form screens, with many other variables being possible.9,10

Solvates are formed when the solvent of crystallization becomes part of the crystal lattice,2 with the largest number of solvates containing water (hydrates).11−15 Solvates often crystallize more easily than the solvent-free phases because the presence of solvent molecules may allow stronger interactions between host and guest (solvent) molecules and a more efficient packing.16 This can enable the formation of a more stable hydrogen bonded arrangement than with the molecules of the organic molecule alone.17 Knowing the crystal structures of the solvate and the corresponding solvent free form(s) is important to understand the (de)solvation process, which can often be explained or derived from their structural relationships.18,19 Furthermore, the knowledge of the hydrogen bonding patterns is crucial in understanding the molecular basis of desolvation.1,2,20 Crystal forms hosting solvent or water molecules in open structural voids such as channels often show nonstoichiometric behavior and the solvent may fully or partly escape through these channels without structural collapse of the solvate structure.21 The alternative mechanism involves considerable rearrangement of the host molecules on desolvation. On the basis of these two mechanisms and the corresponding continuity/discontinuity of the sorption/desorption behavior, hydrates are commonly grouped into two main classes, stoichiometric and nonstoichiometric hydrates.22 Stoichiometric hydrates have a well-defined water content, and the crystal structure is clearly different to that of the anhydrate form(s), whereas in nonstoichiometric hydrates the water content is variable within a certain range and removing the solvent is not associated with a significant change in the crystal structure, except some anisotropic distortion of the network. However, though hydrates are usually among the first solid state forms that are discovered in polymorph screens, a clear picture of their thermodynamic and kinetic stability is rarely elaborated. Our strategy to achieve a better understanding of hydrates aims at comprehensive analytical investigations of model hydrates involving computational approaches to connect structural features with relevant properties, particularly stability.

One of the selected model compounds is pyrogallol (1,2,3-trihydroxybenzene, pyrogallic acid, PG, Figure 1), a small organic molecule, used in analytical chemistry as a reagent for antimony and bismuth, as a reducing agent for gold, silver, and mercury salts, and for oxygen absorption in gas analysis. It was used in photography, for dyeing furs, hair, etc. and therapeutically as antipsoriatic and antiseptic.23 Two crystalline forms, one anhydrous and a hydrate with a low water ratio of 4:1 (compound:water, tetarto-hydrate, HY0.25) have been known for decades.24−27 Older investigations on PG focused on thermal analysis of the commercial PG products,24 infrared (IR) spectroscopy of the two crystalline forms, and water uptake of the anhydrous form.26 In 1972 Becker et al.25 reported space groups and lattice parameters of the tetragonal (P4/*) HY0.25 and a monoclinic (P21/c) anhydrate (AH) (Cambridge Structural Database (CSD)28 refcode families: QQQBKD and PYRGAL, respectively). Recently, the crystal structures of the AH and HY0.25 have been published, in addition to solubility/dissolution data and thermal measurements.27 The lattice parameters for the HY0.25 structure27 differ from the earlier report.25 The single crystal structure of a pyrogallol dimethyl sulfoxide monosolvate has also been published recently.29

Figure 1.

Figure 1

Open in a new tab

Pyrogallol (PG) conformers with atom numbering used throughout this study. The conformers (notation according to ref (27)) were derived using isolated ab initio calculations at the MP2/6-31G(d,p) level of theory, with conformer C, a local minimum, being 18.7 kJ mol–1 less stable than the global conformational energy minimum A. Intramolecular hydrogen bonds are indicated with red dashed lines. The intramolecular degrees of freedom (dihedrals) that were optimized in the lattice energy minimizations are indicated with arrows (ϕ1: C2–C1–O1–H, ϕ2: C3–C2–O2–H, and ϕ3: C2–C3–O3–H).

Our study aimed at a comprehensive qualitative and quantitative understanding of the structural, thermodynamic, and kinetic stability of the two practically most important crystalline forms of PG. This was confirmed with an extensive solid form screen, which resulted in two additional solvate forms. We report the single crystal X-ray structure of the AH, the HY0.25 structure solved from powder X-ray diffraction data with corroboration from computer modeling, and the temperature and moisture-dependent relationship between these two solid forms. A variety of analytical techniques were applied: hot-stage microscopy, differential scanning calorimetry, thermogravimetric analysis, X-ray diffractometry (powder and single crystal), vibrational spectroscopy (IR and Raman), and dynamic moisture sorption/desorption analysis. The experimental results were complemented with computational modeling (i.e., generation of the crystal energy landscape for the AH and interaction energy calculations of the water molecule in the HY0.25 structure), using a variety of methods for evaluating lattice energies.30−32

2. Materials and Methods

2.1. Materials

Pyrogallol (purity ≥ 98.0%) was purchased from Sigma-Aldrich and recrystallized from ethanol for purification. For the solvent screen, a set of 29 solvents was chosen, which were all of analytical quality. The solvent screen included evaporation, cooling crystallization, antisolvent precipitation, and liquid-assisted grinding experiments. For liquid-assisted grinding experiments, anhydrous pyrogallol and few drops of each solvent were ground in a Retsch grinding mill MM301 for 7.5 min.

2.2. X-ray Diffractometry

Single crystal X-ray diffraction experiments were performed on an Oxford Diffraction Gemini R Ultra (4-circle kappa-goniometer, 135 mm Ruby CCD detector, Mo Kα radiation, monocapillary collimator) with an Oxford Cryosystems 700 series Cryostream Plus low temperature attachment. Suitable crystals were obtained from slow evaporation experiments from dimethyl sulfoxide. The AH single crystal structure was solved by direct methods using the program package WinGX33 (SIR200434 and SHELXL9735). All non-H atoms were refined anisotropically. The aromatic hydrogen atoms were generated by a riding model on idealized geometries with Uiso(H) = 1.2 Ueq(C); the polar hydrogen atoms were identified from the difference map and refined isotropically. For further details see ref (36).

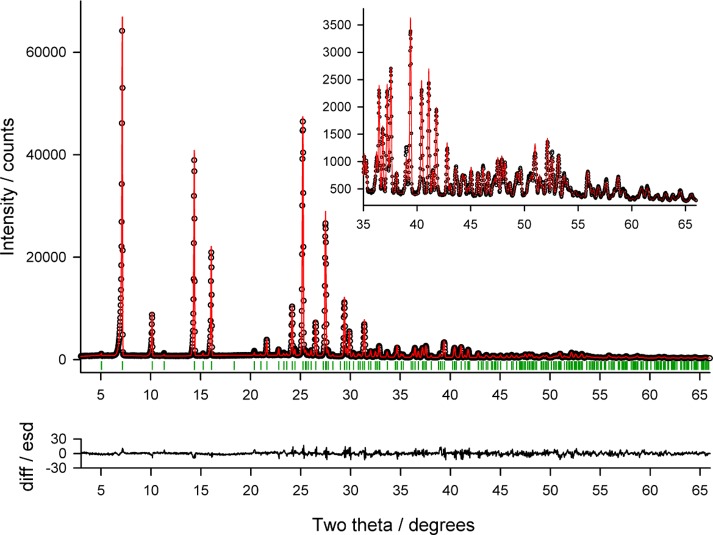
Powder X-ray diffraction (PXRD) data was used to determine the HY0.25 structure. The sample was loaded in a rotating 1.0 mm borosilicate glass capillary and mounted on a Bruker AXS D8 powder X-ray diffractometer equipped with a primary monochromator (Cu Kα1, l = 1.54056 Å) and Lynxeye position sensitive detector. Data was collected at room temperature using a variable count time scheme37,38 (Table S5 of the Supporting Information). The diffraction pattern indexed to a tetragonal unit cell using the first twenty peaks with DICVOL04 and the space group was determined to be P42/n based on a statistical assessment of systematic absences,39 as implemented in the DASH structure solution package.40 From the cell volume, it was derived that there are two PG molecules in the asymmetric unit and from thermogravimetric analysis that there are 0.25 mols of water per mol pyrogallol. The data were background subtracted, and Pawley refinement41 was used to extract the intensities and their correlations. Simulated annealing was used to optimize the hydrate model against the diffraction data set (106 reflections) in direct space. The internal coordinate (Ζ matrix) description was derived from the SCF/6-31G(d,p) gas phase global conformational minimum (Figure 1), with O–H distances normalized to 0.9 Å and C–H distances to 0.95 Å. The structure was solved using 800 simulated annealing runs of 2.5 × 107 moves per run as implemented in DASH. Each of the two PG molecules was allowed 6 external degrees of freedom, and for the water molecule only oxygen was included (i.e., half an oxygen atom with 3 external degrees of freedom). The best solution returned a χ2 ratio of ca. 2.10 (profile χ2/pawley χ2) and was used as the starting point for a rigid body Rietveld refinement42 in TOPAS V4.1.43 The rigid body description was derived from the Ζ matrix used in the simulated annealing runs and the final refinement included a total of 44 parameters (25 profile, 2 cell, 1 scale, 1 isotropic temperature factor, 9 position, and 6 rotation), yielding a final Rwp = 5.57 (Figure 2). For further details see ref (44).

Figure 2.

Figure 2

Open in a new tab

Final observed (points), calculated (red line), and difference [(yobs – ycalc)/σ(yobs)] profiles for the Rietveld refinement of pyrogallol tetarto-hydrate at 25 °C.

The resulting structure from the Rietveld refinement was further scrutinized by allowing all fractional coordinates to refine freely (110 parameters, Rwp = 5.12). As expected, the improvement (Rwp) came at the expense of some chemical sense (e.g., slight distortion in planarity of the benzene ring, movement of H atoms to nonsensical positions), but otherwise, the geometry of the independent molecules was well-preserved, confirming the correctness of the rigid body refined crystal structure.44

Powder X-ray diffraction patterns used for phase identification were obtained using an X’Pert PRO diffractometer (PANalytical, Almelo, The Netherlands) equipped with a θ/θ coupled goniometer in transmission geometry, programmable XYZ stage with a well plate holder, Cu Kα1,2 radiation source with a focusing mirror, a 0.5° divergence slit, and a 0.02° Soller slit collimator on the incident beam side, a 2 mm antiscattering slit, and a 0.02° Soller slit collimator on the diffracted beam side and a solid state PIXcel detector. The patterns were recorded at a tube voltage of 40 kV, tube current of 40 mA, applying a step size of 2θ = 0.013°, with 40 s per step in the 2θ range between 2° and 40°.

2.3. Dynamic Moisture Sorption Analysis

Dynamic moisture sorption and desorption studies were performed with the automatic multisample gravimetric moisture sorption analyzer SPS11-10μ (Project-Messtechnik, Ulm, D). Approximately 750 mg of the AH and 400 mg of the HY0.25 were used for the investigations. The measurement cycles were started at 40% relative humidity (RH) with a desorption cycle to 0% RH (decreasing humidity), followed by a sorption cycle (increasing humidity) up to 90% RH, another desorption cycle to 0% RH, and a final sorption cycle to 43% RH, using variable step sizes (Table S6 of the Supporting Information). The equilibrium condition for each step was set to a mass constancy of ±0.001% over 35 min.

2.4. Water Activity Measurements

Excess of pyrogallol AH and HY0.25 was stirred (500 rpm) in 1 mL of each methanol and water mixture (each containing a different mole fraction of water corresponding to a defined water activity45,46 [Supporting Information, section 1.6)] at 25.0 ± 0.1 °C for ten days. Samples were withdrawn and filtered, and the resulting phase was determined using powder X-ray diffraction and thermogravimetric analysis.

2.5. Thermal Analysis

For hot-stage thermomicroscopic investigations (HTM), a Reichert Thermovar polarization microscope equipped with a Kofler hot-stage (Reichert, A) was used. Photographs were taken with an Olympus ColorView IIIu digital camera (D).

Differential scanning calorimetry (DSC) was performed with a DSC 7 (Perkin-Elmer, Norwalk, CT), using Pyris 2.0. An approximately 3–5 mg sample (UM3 ultramicrobalance, Mettler, CH) was weighed into aluminum pans (25 μL). Dry nitrogen was used as the purge gas (purge: 20 mL min–1). Heating rates of 2.5, 5, 10, and 20 °C min–1 were applied. The instrument was calibrated for temperature with pure benzophenone (mp 48.0 °C) and caffeine (mp 236.2 °C), and the energy calibration was performed with pure indium (mp 156.6 °C, heat of fusion 28.45 J g–1). The stated errors on the given temperatures (extrapolated onset temperatures) and enthalpy values are 95% confidence intervals (minimum five measurements).

Thermogravimetric analysis (TGA) was carried out with a TGA7 system (Perkin-Elmer), using Pyris 2.0. An approximately 3–5 mg sample was weighed into a platinum pan. A two-point calibration of the temperature was performed with ferromagnetic materials (Alumel and Ni, Curie-point standards, Perkin-Elmer). A heating rate of 10 °C min–1 was applied, and dry nitrogen was used as a purge gas (sample purge: 20 mL min–1, balance purge: 40 mL min–1).

2.6. Computational Generation of the Anhydrate Crystal Energy Landscape and Lattice Energy Calculations

The crystal energy landscape of pyrogallol was generated using the two planar conformational minima A and C (Figure 1) held rigid at the optimized isolated conformations obtained at the SCF/6-31G(d,p) level of theory using Gaussian0347 (Supporting Information, section 2.1). The program CrystalPredictor48 was used to randomly generate 50000 Z′ = 1 anhydrate structures in 25 space groups (P1, P1̅, P21, P21/c, P21212, P212121, Pna21, Pca21, Pbca, Pbcn, C2/c, Cc, C2, Pc, Cm, P21/m, C2/m, P2/c, C2221, Pmn21, Pnna, Pccn, Pbcm, Pmmn, and Pnma). An additional 10000 crystal structures containing conformer A(49) were generated in each of the possible hydrate space groups derived from indexing (see X-ray Diffractometry) and the literature25 [i.e., P4/n (Z′ = 1), P42/n (Z′ = 1), and P42/n (Z′ = 2)]. Each crystal structure was relaxed to a local minimum in the intermolecular lattice energy, calculated from the FIT50exp-6 repulsion–dispersion potential and atomic charges, which had been fitted to electrostatic potential around the MP2/6-31G(d,p) charge density using the CHELPG scheme.51 All low-energy structures within 25 kJ mol–1 of the global minimum (ca. 1000 structures, which all contained conformer A) were reminimized using DMACRYS52 with a more realistic, distributed multipole model53 for the electrostatic forces which had been derived using GDMA254 to analyze the MP2/6-31G(d,p) charge density.

Polar proton positions in all Z′ = 1 crystal structures within 10 kJ mol–1 (and within 25 kJ mol–1 for tetragonal structures) of the global minimum were optimized using CrystalOptimizer.55 This was done by minimizing the lattice energy (Elatt), calculated as the sum of the intermolecular contribution (Uinter), and the conformational energy penalty (ΔEintra) paid for distortion of the molecular geometry to improve the hydrogen bonding geometries. Conformational energy penalties (ΔEintra, defined relative to the global conformational minimum, conformer A) and isolated molecule charge densities were computed at the SCF/6-31G(d,p) and MP2/6-31G(d,p) levels, respectively, for each conformation considered in the minimization of Elatt.

To approximate the polarization of the molecular charge distribution in the crystal, as has been found necessary in crystal structure prediction studies of peptides56,57 and similar organic molecules,58,59 the MP2/6-31G(d,p) charge density used in the final evaluation of Elatt was generated in a dielectric constant, ε = 3, using the polarizable continuum model (PCM).60 The intramolecular energy penalty, ΔEintra, was calculated from the MP2 energies in the same PCM ab initio calculation, excluding the interaction energy between the molecule and the polarizable continuum. The result is the PCM crystal energy landscape.

The sensitivity of the relative energies of the structures to the modeling assumptions was investigated by using other methods of evaluating lattice energies. Periodic electronic structure (DFT-D) calculations31 were carried out on the lowest energy computationally generated PCM structures with the CASTEP plane wave code61 using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) exchange-correlation density functional,62 with the addition of the Tkatchenko and Scheffler (TS)63 semiempirical dispersion corrections and ultrasoft pseudopotentials.64 The results reported were obtained using a plane wave cutoff energy of 780 eV and a Monkhorst–Pack Brillouin65 zone sampling grid of spacing 2π × 0.07 Å–1; the required force tolerance for a successful geometry optimization in each run was 0.05 eV Å–1 (section 2.2 of the Supporting Information).

PIXEL calculations32,66,67 were also carried out on these low-energy structures to estimate the repulsive (ER), dispersion (ED), electrostatic (Coulombic, EC), and induction (polarization EP) contributions to the intermolecular lattice energy, and the subdivision of intermolecular lattice energy into contributions from individual pairs of molecules within a crystal. The charge density for the crystal was constructed from the MP2/6-31G(d,p) ab initio charge density of the isolated molecule as extracted from the computed crystal structure. Both the PCM and DFT-D optimized crystal structures were used to test sensitivity of the energies to small differences in the crystal structure68 (section 2.4 of the Supporting Information). The intramolecular energy penalty, ΔEintra, was calculated from the MP2 energies in the same ab initio calculation. The electron density was described using medium cube settings and a step size of 0.08 Å, with the pixels condensed into superpixels with a condensation level n = 4. Intermolecular lattice energy calculations were carried out on a cluster of molecules within a maximum distance of 13 Å from a central molecule.

The differences in crystal structures were examined and quantified with XPac,69,70 using all nonhydrogen atoms and routine medium cutoff parameters (δang = 10°, δtor and δdhd = 14°, VdW search radius of 1.5 Å) and the overlay71 of the largest x molecule cluster (x ≤ 15), rmsdx, as calculated using the Molecular Similarity Module in Mercury.72

3. Results

3.1. Preparation of the Individual Solid Forms (Solid Form Screen)

The experimental solid form screen resulted in four solid forms (AH, HY0.25, and two dimethyl sulfoxide monosolvates), as confirmed with thermal analysis, infrared spectroscopy, and PXRD (sections 1.1, 1.4, and 1.5 of the Supporting Information).

Anhydrate and Tetarto-Hydrate Phases

Needlelike HY0.25 crystals were obtained by crystallization from ethanol and other water-containing solvents (Figure 3a and Tables S1–S4 of the Supporting Information); the AH shows a platelike morphology and crystallized only from water-free solvents or solvents with a very low water activity (aw < 0.15). The AH sample used for this study was prepared by drying the HY0.25 in a drying oven at 75–80 °C for 30 min. We observed a change in color of PG in the presence of water73 (100% relative humidity) after 72 h, suggesting some degradation.

Figure 3.

Figure 3

Open in a new tab

Photomicrographs of (a) tetarto-hydrate crystals crystallized from water, (b) anhydrate crystals obtained from sublimation >110 °C, and (c) spherulithes of the anhydrate grown from the melt at 123 °C.

Dimethyl Sulfoxide Monosolvates I and II

Liquid-assisted grinding experiments of pyrogallol with dimethyl sulfoxide led to the dimethyl sulfoxide monosolvate I (SDMSO-I). The platy SDMSO-I crystals melt at 80–82 °C. Upon quench cooling, molten SDMSO-I, an alternate dimethyl sulfoxide monosolvate (SDMSO-II) crystallized, which undergoes a solid–solid transformation to SDMSO-I at room temperature (Figure 4). The melting points of the two monosolvates determined with DSC are 63.1 ± 0.5 °C and 81.3 ± 0.3 °C for SDMSO-II and SDMSO-I, respectively. From the heat of fusions (higher for SDMSO-I), it could be concluded that the two solvate polymorphs are monotropically related.74 The diffraction pattern of the stable SDMSO-I, using the first twenty peaks, indexed38,39 to an orthorhombic unit cell (Pna21, a = 11.0258 Å, b = 11.0049 Å, c = 8.1265 Å). Space group and lattice parameters are in agreement with the crystal data reported by Polyanskaya and Smolentsev,29 within plausible thermal expansion effects.

Figure 4.

Figure 4

Open in a new tab

Polarized light photomicrographs showing the solid–solid transformation of dimethyl sulfoxide monosolvate II (SDMSO-II) to dimethyl sulfoxide monosolvate I (SDMSO-I) at room temperature. (a–c) show both polymorphs of the solvate, with SDMSO-I growing from the lower left and right-hand side corner, whereas (d) shows only the SDMSO-I polymorph.

3.2. Crystal Structures of Anhydrous and Hydrated Pyrogallol

The crystal structure of the AH form was determined from single crystal and the HY0.25 from PXRD data. The structural details are in agreement with a recent report by Thakuria et al.27 The AH crystallizes in the monoclinic space group P21/n, with Z′ = 1. The PG molecule adopts a molecular conformation similar to conformer A (Figure 1a), with the O2–H proton deviating from the molecular plane by 25° and the O1–H and O3–H protons by approximately 10°. Each of the three hydroxyl groups acts as a hydrogen bond donor and acceptor, leading to three distinct hydrogen-bonding motifs.75 The O1–H···O3 interaction [O1···O3 distance: 2.695(2) Å and O1–H···O3 angle: 163 (2)°] forms linear C11(6) chains (Figure 5). These chains are stacked along [010], forming π···π interactions [centroid distance: 3.807 Å, perpendicular distance: 3.416 Å]. Adjacent C1(6) chains interact through dimeric R22(10) [O2···O1 distance: 2.745(2) Å and O2–H···O1 angle: 150(2)°] and 21 mediated C1(5) hydrogen bonds [O3···O2 distance: 2.850(2) Å and O3–H···O2 angle: 151(2)°], leading to a helical trimer synthon, forming an infinite tape. All hydrogen bonds are located within the π···π stacked infinite tapes.

Figure 5.

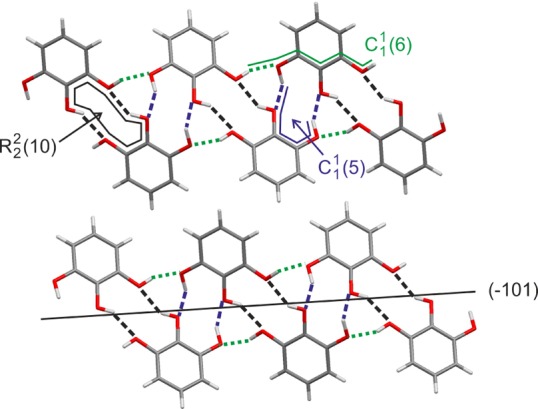
Figure 5

Open in a new tab

Packing diagrams and hydrogen bonding of pyrogallol anhydrate viewed along [010], with the C11(6) chain hydrogen bonding direction horizontal. O–H···O hydrogen bonds indicated with dashed and dotted lines. The (−101) plane is shown as a solid line.

The HY0.25 crystallizes in the tetragonal space group P42/n with two PG molecules in the asymmetric unit. The two molecules adopt conformations similar to conformer A (Figure 1a). The PG molecules are arranged in tetrameric columns, surrounding the water molecules (Figure 6a). The tetrameric columns exhibit four pyrogallol···pyrogallol interactions of the O–H···O type, forming four distinct tetrameric ring motifs (see ref (76)), (Figure 6a). The tetrameric columns are linked through an O6–H···O3 [O6···O3 distance: 2.754(3) Å and O6–H···O3 angle: 147.0(3)°] hydrogen bond to adjacent columns. The tetragonal-coordinated water molecule, located in polar channels along [001], is disordered around the inversion center, leading to a site occupancy factor of 0.5 in positions A and B (Figure 6b). The hydrogen bonding between the pyrogallol O2–H group and water has the traditional “strong” geometry [O2–H···O7: O2···O7 distance: 2.889(7) Å and O2–H···O7 angle: 154.9(3)°]. Furthermore, the position of the water oxygen atoms allows the water protons to act as hydrogen bond donors in a variety of orientations of the water molecule [O5···O7 distances: 2.680(7) Å and 2.838(7) Å].

Figure 6.

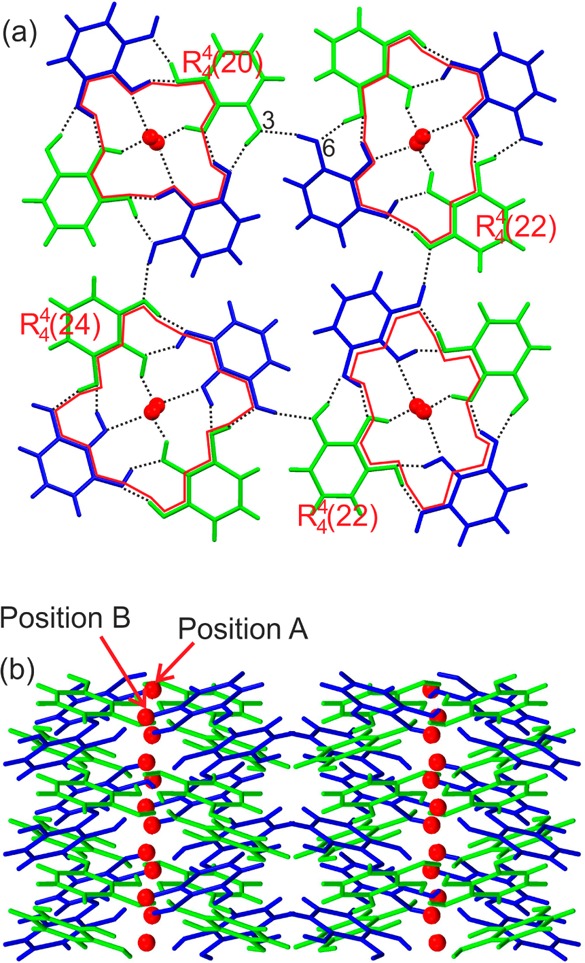
Figure 6

Open in a new tab

Packing diagrams of pyrogallol tetarto-hydrate viewed along (a) [001] and (b) [010], with [001] water channels vertical. Crystallographically unique molecules are colored differently. Positions A and B mark the two water sites (site occupancy factor of 0.5).

3.3. Anhydrate ↔ Hydrate Phase Transformation

Moisture Sorption/Desorption Experiments

The stability of the AH and HY0.25 was investigated under different moisture conditions in the range of 0 to 90% relative humidity at 25 °C. The moisture sorption/desorption isotherms (Figure 7) show that both, pure AH and HY0.25, are stable within a wide range of humidity conditions. The transformation of the pure AH to the hydrate occurs at very high RH values (>82%) in a single step. Complete transformation was achieved within two days at 82% RH. The HY0.25 releases the water only at extremely dry conditions (<5% RH). The dehydration kinetics is very slow and takes about three weeks in a dry atmosphere, as monitored with PXRD (section 1.5 of the Supporting Information). Due to the 48 h time limit for each step in the automatic gravimetric desorption experiments, dehydration was not completed at the lowest humidity condition of the desorption cycles, resulting in a mixture of the AH and HY0.25. This mixture already starts absorbing water at RH ≥ 30%, indicating that the HY0.25 might catalyze its formation in mixed samples. The distinct steps and hysteresis between the sorption and desorption isotherms are characteristic of a stoichiometric hydrate.14,77,78

Figure 7.

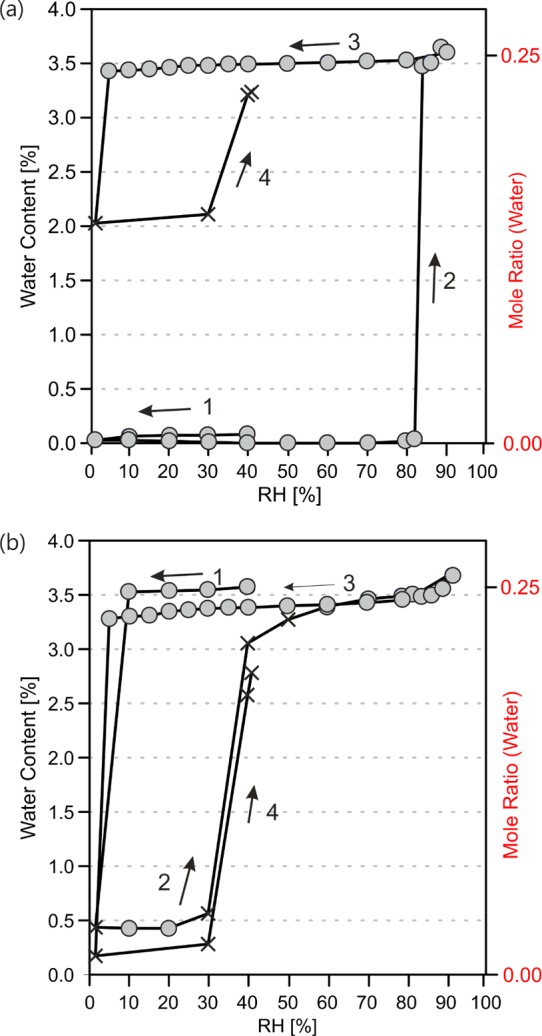
Figure 7

Open in a new tab

Moisture sorption and desorption curves of pyrogallol anhydrate/tetarto-hydrate at 25 °C. The circles present data points that fulfill the preset equilibrium condition (mass change < 0.001% over 35 min), whereas crosses mark measurement values that did not reach the equilibrium within the maximum allowed time limit (set at 48 h). Cycle started using the (a) anhydrate and (b) tetarto-hydrate, both at 40% relative humidity (RH).

Water Activity Experiments

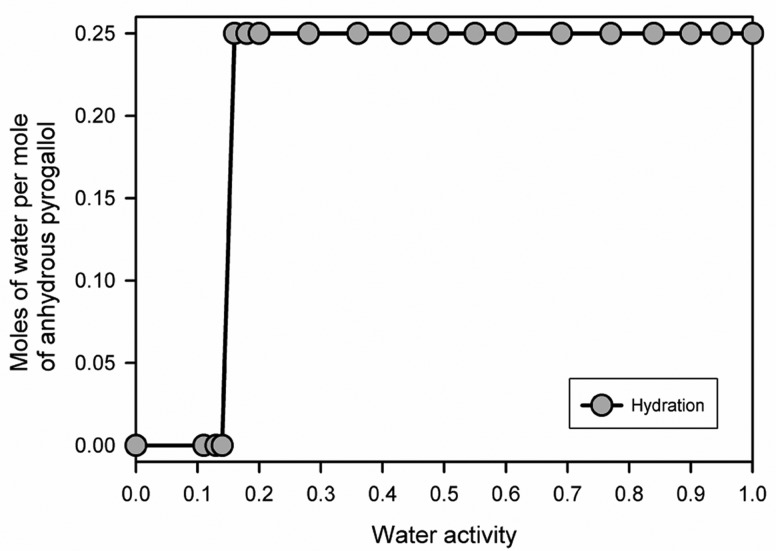
AH and HY0.25 were separately added to methanol/water of various compositions (section 1.6 of the Supporting Information) and equilibrated under stirring for ten days (Figure 8). In contact with methanol/water, at a water activity (aw) < 0.15, the AH was the only solid phase at equilibrium. At aw > 0.15, the HY0.25 was obtained as the most stable form at equilibrium, suggesting that the system, pyrogallol AH ↔ HY0.25, is in equilibrium at aw = 0.15 at 25 °C. Since the water content of the HY0.25, contributes to aw, solutions with aw < 0.15 could not be produced by adding the HY0.25 to the methanol/water mixtures because the HY0.25 is highly soluble in water,23,27 methanol, and mixtures thereof. Therefore, the HY0.25 to AH phase transformation (dehydration) could not be observed using the HY0.25 as starting phase in the water activity experiments. The AH to HY0.25 phase transformation at aw > 0.15 occurs by a solvent-mediated process: the AH dissolves and the HY0.25 nucleates and grows from the supersaturated solution.

Figure 8.

Figure 8

Open in a new tab

Phase diagram after equilibration for ten days showing the dependence of pyrogallol on water activity in methanol/water mixtures during the pyrogallol hydration process at 25 °C. Anhydrous pyrogallol was used as a starting phase; the residual phase, after stirring for ten days, was determined with PXRD.

Thermal Analysis–Thermodynamic Stability

HY0.25 is stable at room temperature (RH ≥ 5%), but with hot stage microscopy it can be observed that the crystals turn opaque on heating. The crystals maintain their original shape but split into numerous small crystallites. This behavior is termed pseudomorphosis24 and is characteristic for stoichiometric solvates, indicating a strong reorganization of the structure on desolvation. The transformation to the AH starts at approximately 75 °C (Figure S4 of the Supporting Information), and the formation of bubbles can be observed in silicon oil. The peritectic melting of the hydrate crystals can be determined at 85 °C, if faster heating rates (heating rate > 10 °C min–1) are applied. At temperatures above 80 °C, anhydrous PG crystals start to sublime. The sublimed crystals appear mainly as plates (Figure 3b), but also bars and grains can be observed. The sublimates correspond to the same anhydrous phase, as confirmed with IR spectroscopy and PXRD. The AH melts at 133 °C and spontaneous crystallization of the same phase occurs about 10° below its melting temperature (Figure 3c).

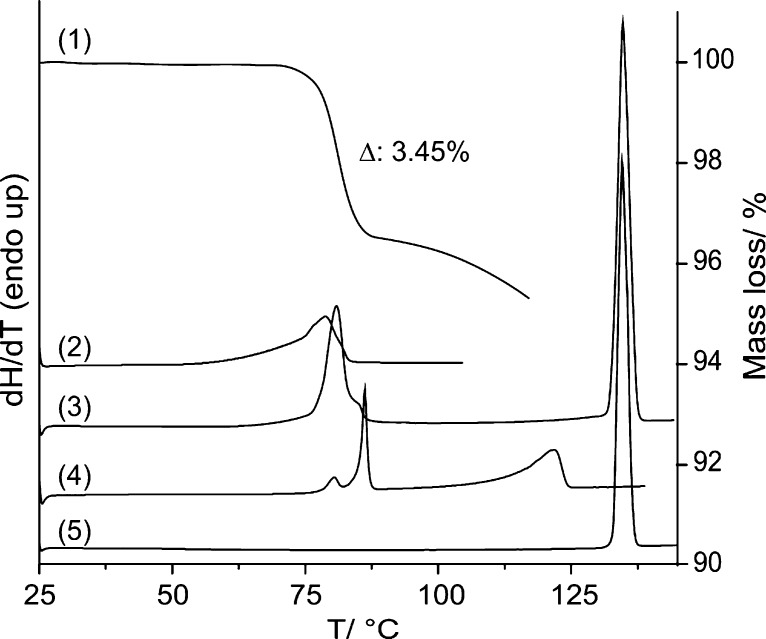
The TGA curve (curve 1 in Figure 9) shows a one-step loss of water. The measured mass loss of 3.45% between 75 and 85 °C corresponds exactly to 0.25 mols equivalent water and is in agreement with values reported elsewhere.24,26,27 The mass loss seen above the dehydration temperature corresponds to the sublimation of the AH.

Figure 9.

Figure 9

Open in a new tab

TGA curve of (1) pyrogallol tetarto-hydrate recorded at a heating rate of 10 °C min–1. DSC thermograms of the tetarto-hydrate in (2) a three pin-holed pan and a heating rate of 2.5 °C min–1, (3) one pin-holed pan at a heating rate of 5 °C min–1, and (4) a sealed pan at a heating rate of 10 °C min–1. DSC thermogram of the anhydrate (5) recoded in a one pin-holed pan at a heating rate of 10 °C min–1.

The DSC curve of the AH (curve 5 in Figure 9) exhibits one sharp melting endotherm at an onset temperature of 133.0 ± 0.2 °C. The measured heat of fusion (ΔfusHAH) is 26.1 ± 0.1 kJ mol–1. DSC measurements of the HY0.25 were either carried out in sealed or in pin-holed pans at different heating rates to investigate the influence of the atmospheric conditions on the dehydration. In a pan with three pin-holes, a broad desolvation endotherm (curve 2 in Figure 9) is observed. The heat of dehydration (ΔdehyHH-A) is 14.3 ± 0.2 kJ mol–1, and the onset temperature for this process varies slightly, depending on the heating rate between 75–80°. In a one pin-holed pan (curve 3 in Figure 9), the dehydration and incongruent melting process (peritectic decomposition) of the hydrate (shoulder) overlap. Two processes are observed (curve 4 in Figure 9) with the use of a sealed pan (isochoric conditions, composition of the binary system is largely maintained). The small endotherm appearing first corresponds to the dehydration process (small amount of water is released from the hydrate to the head space of the pan), and the second peak indicates the peritectic decomposition (Tdiss,H = 85.2 ± 0.5 °C). The third, broad endotherm corresponds to the liquidus curve (anhydrous form dissolves in the melt).

3.4. Computationally Generated Crystal Energy Landscape and Lattice Energy Calculations

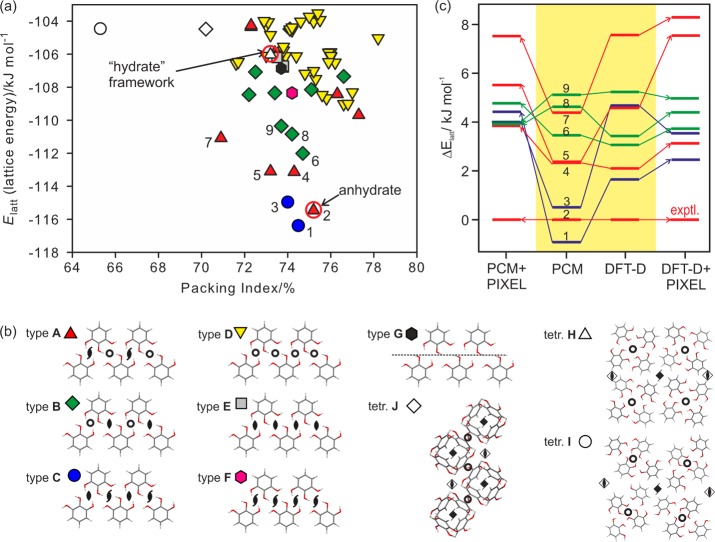
The second lowest energy structure on the PCM crystal energy landscape for anhydrous pyrogallol (Figure 10) corresponds to the observed structure (rmsd15 = 0.09 Å). However, recalculating the lattice energies of the most stable structures in Figure 10a using alternative methods led to a significant reordering of the closely spaced (<6–8 kJ mol–1) relative lattice energies (Figure 10c). The experimental structure becomes the most stable by 1.7 kJ mol–1, using the DFT-D periodic electronic structure optimization (rmsd15 = 0.08 Å, Figure 11) and 2.5 to 4 kJ mol–1, using PIXEL to evaluate the lattice energies of the PCM and DFT-D optimized structures. Both of the latter two methodologies model the polarization in the crystal more specifically than the PCM model, suggesting that this term is crucial to the relative lattice energies of pyrogallol structures.

Figure 10.

Figure 10

Open in a new tab

(a) Lattice energy landscape for pyrogallol anhydrate (Elatt = Uinter + ΔEintra, PCM). Each symbol denotes a crystal structure, which is a lattice energy minimum classified by the most extensive common-packing motif based on the hydrogen bonding shown in (b). (c) Relative lattice energies of the most stable computationally generated pyrogallol structures calculated using different methods: PCM, isolated molecule relaxed structures with average polarization from the PCM model as in (a), DFT-D, periodic density functional theory relaxations with dispersion correction, and PIXEL calculations using either the PCM or DFT-D optimized structure. Tie lines have been added to show the changes in relative ordering. The numbers labeling the symbols in (a) identify the crystal structures by stability order using the PCM model (Table S9a of the Supporting Information). Only selected symmetry operations are drawn in (b).

Figure 11.

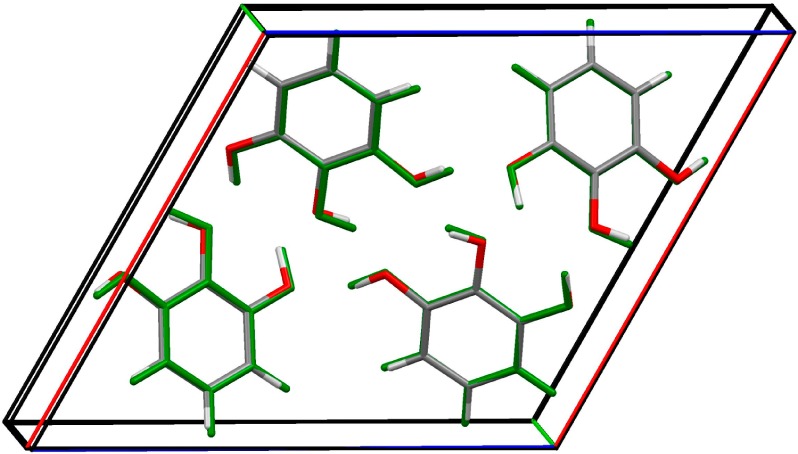
Figure 11

Open in a new tab

Overlay of the experimental crystal structure of pyrogallol anhydrate (colored by element) and the most stable computed structure after full relaxation of the cell and atomic coordinates with DFT-D (green).

Hypothetical Alternative Anhydrate Structures

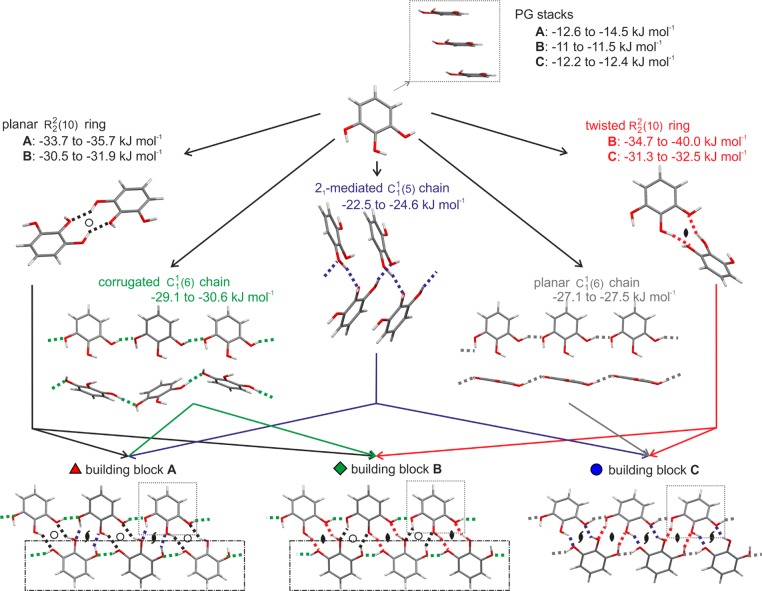
All calculated low-energy structures (Figure 10) have approximately the same conformation as found in the experimental AH, with the θ1–3 torsions defining the proton positions varying by up to 44° from planarity. A consistent feature in all structures are the π···π stacks of pyrogallol molecules (Figure 12 inset). Packing analysis based on the symmetry relationship of the molecules involved in the strong O–H···O intermolecular interactions (e.g., inversion, 2-fold axis, etc.) finds ten possible relationships (A–J, Figure 10b) within about 13 kJ mol–1 of the global minimum. The strong O–H···O intermolecular interactions (A–G) of all structures [except those in tetragonal space groups (H–J)], can be described by only three graph set motifs (Figure 12): linear C11(6) chains, involving the O1 and O3 oxygens, planar (inversion related) or twisted (2-fold axis related) R2(10) dimers, and C11(5) 21-mediated chains. A–G contains the hydrogen bonded O–H···O C1(6) chains, varying in the combination of symmetry operations relating pairs of pyrogallol molecules located in adjacent chains. Two molecular relationships (i.e., two symmetry elements) lead to more stable packings (types A–C) in Figure 10a than structures where only one molecular relationship links adjacent O–H···O C11(6) chains (types D–G). Structures belonging to one type are closely related and differ only in the stacking of 2D building blocks defined by XPac (illustrated in section 2.5 of the Supporting Information). Type A and B have π···π stacks of corrugated O–H···O C1(6) chains in common (Figure 12). Type C structures are distinct from types A and B, only sharing the 1D π···π stacks, despite the hydrogen bonding graph set motifs, C11(6) and C1(5) chains and R22(10) dimers, being the same.

Figure 12.

Figure 12

Open in a new tab

Illustration of the packing similarities and hydrogen bonding motifs of common building blocks in lowest energy structures on the pyrogallol crystal energy landscape (Figure 10). Boxes mark common structural fragments: All structures exhibit 1D stacks of pyrogallol molecules (π···π stacking, square boxes), type A and B structures share a common 2D building block [π···π stacked O–H···O C11(6) chains, rectangular dashed boxes]. PIXEL energies are for a pair of molecules; for chain motifs/PG stacks, each molecule forms two identical interactions of this type (Table S9b of the Supporting Information).

This analysis shows that the two lowest energy structures in Figure 10 (a hypothetical structure rank 1 for PCM, and second in energy for DFT-D and PIXEL, and the experimental structure differ substantially in the packing of the pyrogallol molecules (Figure 13). The corrugated C11(6) chain in the experimental structure is approximately of planar geometry in the hypothetical structure (Figure 12), with all moleules of π···π stacked C1(6) chains being tilted in one direction only (Figure 13b; Figure S9a of the Supporting Information), whereas there are two directions of tilt in the experimental structure (Figure S10a of the Supporting Information). In the experimental structure, a C11(6) chain is linked through inversion related R2(10) dimers to another chain, whereas in the energetically competitive hypothetical structure, adjacent chains cross and each dimeric R22(10) interaction (2-fold) of one chain links to a different C1(6) chain. Thus, a transformation between the two structures would require breaking and reforming the R22(10) and C1(5) hydrogen bonds and reorienting the pyrogallol molecules.

Figure 13.

Figure 13

Open in a new tab

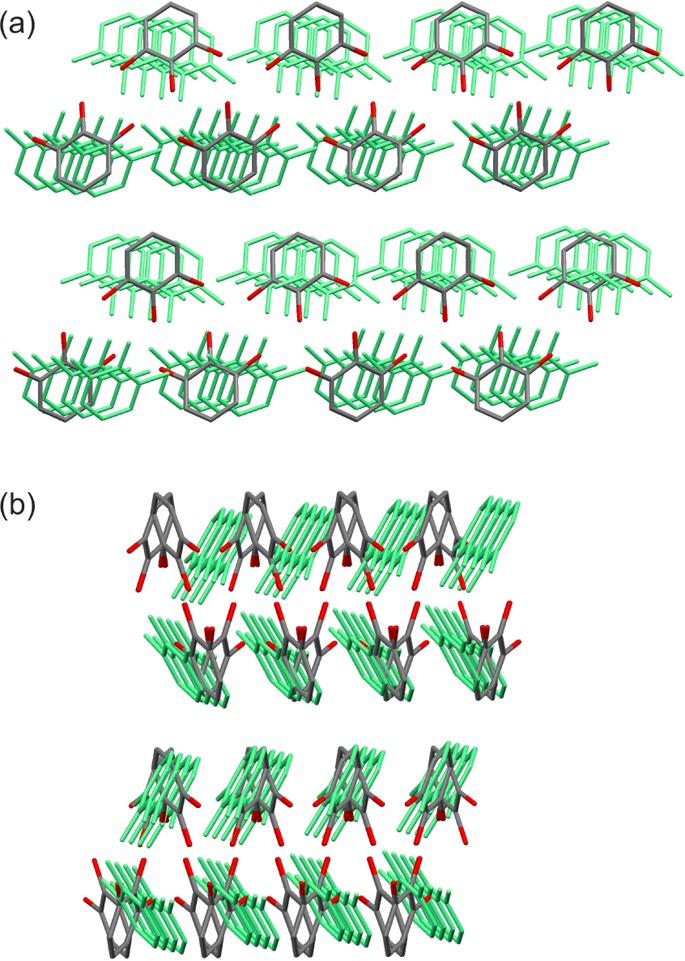
Overlay of the experimental (colored by element) and the hypothetical structure (light green), which is closest in energy [1, Figure 10a; Table S9a of the Supporting Information: label 85_C2(1)], viewed along the (a) experimental [010] and (b) experimental [001], the C11(6) chain axis.

Three tetragonal anhydrate structures are sufficiently stable to appear on the crystal energy landscape within 13 kJ mol–1 of the most stable structure (Figure 10a), each with a different packing arrangement (Figure 10b) and packing efficiency. Only the most stable of the three calculated tetragonal structures (tetr. H, 1_P42/n, Z′ = 2, Table S11 of the Supporting Information) has channels surrounded by polar hydroxyl groups that could accommodate water in a low stoichiometric ratio. The less dense structures, tetr. J (339_P42/n, Z′ = 2) and tetr. I (22_P42/n, Z′ = 2), have voids79 of a size that could accommodate more water, but this void space is mainly surrounded by hydrophobic regions and so seem unlikely to be a hydrate framework.

Computational Modeling of the Tetarto-Hydrate Structure

Five of the calculated P42/n, Z′ = 2 anhydrate structures (1_P42/n, 2_P42/n, 4_P42/n, 15_P42/n, and 32_P42/n, Table S10 and Figure S11 of the Supporting Information), including the lowest tetragonal structure in Figure 10a, closely match our experimentally determined lattice parameters; two of the calculated P4/n, Z′ = 1 anhydrate structures (4_P4/n and 5_P4/n) closely match the hydrate lattice parameters derived by Becker et al.25 Simulating the PXRD patterns from the calculated structures revealed that only the five P42/n structures can be considered as a potential match with our experimental PXRD pattern, as small reflections are present in the experimental pattern (e.g., 5.06°, 11.33°, and 15.25° 2θ) are not allowed in the P4/n space group (Figure S11 of the Supporting Information). The five P42/n, Z′ = 2 anhydrate structures all exhibit narrow channels along [001] surrounded by hydroxyl groups, which could accommodate a low water ratio.

The calculated lowest energy tetragonal anhydrate structure (1_P42/n) matches the atomic coordinates of the pyrogallol framework in the observed HY0.25 (rmsd15 = 0.21 Å, ignoring water), confirming the choice of the PG proton positions in our structure solution from PXRD data. An alternative orientation of hydroxyl protons (conformer C) would be possible, but our calculations show that it is not energetically feasible. We investigated possible water proton positions within the pyrogallol framework 1_P42/n by comparing the PCM lattice energies of the framework and tetarto-hydrate structures having the water in the different orientations shown in Figure 14. The optimization of the cell, molecular positions and orientations, and torsion angles to protons in these structures, using CrystalOptimizer, clearly suggests that the HY0.25 will have water orientation I (Figure 14a). Orientation II (Figure 14b) has a much smaller stabilization energy by over 7.5 kJ mol–1. The hypothetical structure with water···water interactions (Figure 14c) was not a lattice energy minimum, which is why upon optimization the molecule in orientation II rearranged to orientation I.

Figure 14.

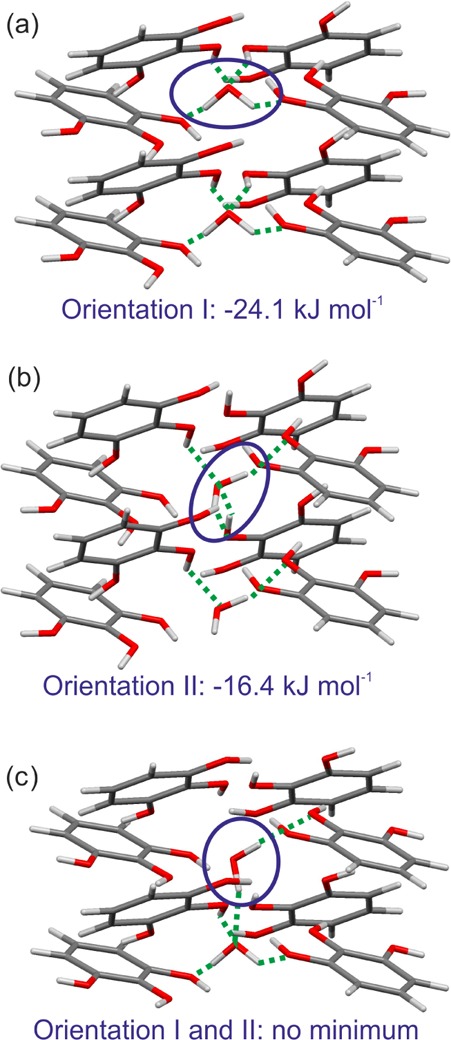
Figure 14

Open in a new tab

Possible orientations and estimated water stabilization energies of the water molecules in the tetarto-hydrate structure with the C and O pyrogallol atom positions initially positioned in the calculated structure 1_P42/n, Z′ = 2. Water molecules were added, after symmetry reducing the anhydrate structure, in different orientations (I and II) in close proximity to the pyrogallol hydroxyl groups (section 2.6 of the Supporting Information). Energy values correspond to the intermolecular energy contribution of the water molecule to the tetarto-hydrate lattice energy.

The computationally derived hydrate structure (1_P42/n, Z′ = 2 anhydrate plus water in orientation I) is in excellent agreement with the experimental HY0.25 structure (rmsd15 = 0.10 Å), as shown in an overlay with the experimental hydrate derived from single crystal X-ray diffraction experiments27 (Figure 15).

Figure 15.

Figure 15

Open in a new tab

Overlay of the experimental crystal structure of pyrogallol tetarto-hydrate27 (colored by element) and computationally derived hydrate structure (green). Energy-minimized tetarto-hydrate (Figure 14a) structure (P4/n) was run through the ADDSYM function of PLATON,80 resulting in P42/n Z′=2, with a water site occupancy of 0.5.

4. Discussion

4.1. Tetarto-Hydrate Structure

In the early structural work on the two pyrogallol solid forms,25 the inability of the instrumentation to record very weak diffraction peaks may have led to the incorrect a (=b) lattice parameter and Z′ for the HY0.25 structure. Forty years later, two groups independently, and using different approaches, corrected the HY0.25 lattice parameters and space group and solved the hydrate structure (including atomic positions). Thakuria et al.27 managed to grow HY0.25 single crystals concomitantly with pyrogallol-pyrazin-amide and pyrogallol-isonicotinamide cocrystals in a cocrystallization screen. This appears to be yet another example where cocrystallizations provided the crystallization conditions needed for growth of otherwise elusive crystals of one of the components, as we were unable to grow single crystals. Therefore, we solved the hydrate structure from PXRD data. As the location of hydrogen atoms based on PXRD data has always been challenging, often resulting in misplaced protons,81 we used lattice energy minimization of hypothetical structures differing only in hydrogen atom positions, to derive the proton positions as those in the energetically most stable structure.82,83 The correctness of this combined experimental and computational approach is confirmed by the excellent match with the experimental single crystal structure.27

4.2. Anhydrate ↔ Hydrate Phase Transformation

Thermal- and moisture-dependent studies indicate a broad stability range for pure HY0.25 and AH (i.e., both forms can be handled and stored under the most relevant conditions without undergoing a phase change). In freshly and partly desolvated mixed phase samples, the transformation to the HY0.25 occurs readily at RH ≥ 30% at 25 °C (i.e., the presence of the HY0.25 in the anhydrous form accelerates the phase transformation and the phase change can occur yet at ambient conditions). The high kinetic stability of both phases with respect to the water vapor pressure is indicated by the considerable hysteresis between sorption and desorption process in the moisture sorption/desorption isotherm (see Figure 7). In slurry experiments, the activation barrier of the transition process can be minimized, enabling the determination of the thermodynamic transition point (water activity where the anhydrate and the hydrate are in equilibrium). The critical water activity at 25 °C was found to be 0.15, which means that HY0.25 is the thermodynamically stable phase above 15% relative humidity (25 °C), whereas the AH is only stable below this value.

The water molecule in the HY0.25 is located at distinct sites in channels. It can form four strong hydrogen bonds and contributes almost 20% of the HY0.25 lattice energy, explaining the stability of the hydrate. The dehydration mechanism could start with the removal of the water through the [001] channels (Figure S12 of the Supporting Information). Indeed, the calculations with the alternative proton positions (Figure 14) are compatible with such a mechanism. On dehydration, a mutual rearrangement of the PG molecules (i.e., structural collapse of the tetrameric columns) has to occur (class I according to the Rouen model,84 destructive process), to result in the stable infinite tape packing of the AH. The energy for this rearrangement can be estimated from Figure 10a, as approximate 10 kJ mol–1 (the difference between tetrameric column packing (1_P42/n, Z′ = 2) and the AH structure). This energy difference is sufficiently large to explain why the HY0.25 does not dehydrate to an isomorphic desolvate, despite the hydrate framework being sufficiently mechanically stable to be found in the search.

Experimentally, the enthalpy of dehydration could be measured by DSC (ΔdehyHH–A = 14.3 ± 0.2 kJ mol–1), a process in which the water within the crystal is also vaporized. The enthalpy of HY0.25 to AH transformation (ΔtrsHH–A) was estimated by subtracting the known enthalpy value for the vaporization of water at the dehydration temperature (Tdehy, max ∼ 80 °C at which ΔvapH°H2O = 41.585 kJ mol–185) from the measured enthalpy of dehydration (ΔdehyHH–A) (eq 1), resulting in a value of 3.9 kJ mol–1.

4.2. 1

The order of magnitude of the HY0.25 ↔ AH transition energy lies within the expected energy range for a polymorphic phase transformation but is lower than the transition energies measured for previously investigated stoichiometric dihydrate ↔ AH systems (barbituric acid86 and phloroglucinol59). This is consistent with the postulated dehydration mechanism through channels for PG. The release of the water molecules from the hydrate structure consumes more energy than gained through the rearrangement of the PG molecules to the more stable AH packing, explaining why the HY0.25 shows such a high stability. Thus, although the tetarto-hydrate has a channel structure, it behaves as a stoichiometric hydrate for both thermodynamic and kinetic reasons.

4.3. Comparison of Experimental and Computational Screening

Modeling at the electronic level (DFT-D and PIXEL calculations) confirms the experimental conclusion that the observed AH is the most stable anhydrous form. The periodic electronic structure calculations (DFT-D) automatically model the polarization of the charge density by intra- and intermolecular hydrogen bonding in the same way but are limited by the quality of the wave function (PBE)87 and size of the cell that could be afforded. The crystal energy landscape (PCM, Figure 10a) energies only include the polarization of the molecule by a continuum model for the crystalline environment, instead of by the structure-specific intermolecular hydrogen bonds. The inclusion of realistic intermolecular polarization might be expected to contribute to the relative lattice energies for pyrogallol, as the deviation of proton positions from coplanar affects the intra- and intermolecular hydrogen bonding balance and is a key distinction between the low-energy structures88 (Figure 10b and Figure 12). This variation in intermolecular polarization energy is confirmed by the PIXEL calculations (Table S9, panels b and c, of the Supporting Information). However, the level of agreement between three very different approaches to modeling the lattice energy of organic crystals for PG (Figure 10b) is promising for the future of crystal structure prediction.

The crystal energy landscape6 shows that there are thermodynamically feasible alternative anhydrate structures which graph-set, symmetry and XPac analysis have similar π···π stacking but different hydrogen bonding arrangements of PG molecules. Since types A and B structures are alternative packing modes of the same stack of O–H···O C11(6) chains, this might result in the occurrence of type B stacking faults in the AH. Having energetically competitive modes of combining 2D sheets has accounted for polymorphism and/or stacking disorder in aspirin,89 phloroglucinol dihydrate,59 or modafinil90 and may account for the occurrence of concomitant polymorphism91 (e.g., aprepitant92 and progesterone93). Since the alternate type A packings (Figure S10 of the Supporting Information) could rearrange easily to the more stable experimental packing, this significantly reduces the possibility that these could be found as long-lived metastable anhydrate polymorphs.

The most energetically competitive computed structure found in the computational search is more distinct from the experimental AH packing (Figure 13). Whether this hypothetical structure could be trapped as an experimental polymorph cannot be assessed from current knowledge of the kinetics of molecular assembly. Since the experimental AH grew easily, including under crystallization conditions that would be expected to yield kinetically favored forms, it can be concluded that the alternate computationally generated structures are not only thermodynamically but also kinetically disfavored. The possibility of changing the relative kinetics of crystallization between the known AH and the more distinct low energy structures seems to be limited. Since our screen aimed to find hydrate form(s) and its dehydration product(s), no precautions were undertaken to avoid moisture or crystallize below the critical water activity of 0.15. Hence, experiments strictly excluding water from playing any role in nucleation, or the presence of impurities, templating surfaces or polymers, etc.,94−97 might produce sufficient change in the mechanism of nucleation and growth in favor of a metastable structure, such as the lowest energy type C structure (Figure 10).

5. Conclusions

Crystallization of pyrogallol, a small druglike model compound, from a variety of organic solvents resulted in four solid forms, an anhydrate, a stoichiometric HY0.25, and two dimethyl sulfoxide monosolvates. It is noteworthy that, to our knowledge, pyrogallol dimethyl sulfoxide solvate II is the first known case of crystallization of a metastable solvate polymorph from the melt. This is facilitated by the large temperature difference of 126 °C between the melting point of the solvate and the boiling point of dimethyl sulfoxide.

The combination of data obtained from calorimetric and moisture-dependent studies indicates that the HY0.25 is the stable phase at ambient conditions. The water loss occurs at higher temperatures (75 °C) or under very dry conditions (relative humidity below 5%). In accordance with the critical water activity of 0.15 (25 °C) determined in the slurry experiments, anhydrous pyrogallol is thermodynamically unstable at moisture conditions greater than 15% relative humidity (RH). The fact that the transformation of the phase pure anhydrate occurs above 82% RH is a nice demonstration of the importance of kinetics in the hydration/dehydration processes. This kinetic stabilization enables the use of metastable anhydrates in practice, which is for example relevant for many drug compounds with low water solubility, since an anhydrous form is always more soluble than a hydrate form.

The computational generation of thermodynamically feasible anhydrate structures clearly identified the role of strong hydrogen bonding, intra-, and intermolecular O–H···O interactions and π···π stacking in pyrogallol. The thermodynamic stability of the anhydrate arises from the balance of these interactions, including the polarization of the molecule in the crystal. The hydrate framework structure was found among the higher energy anhydrate structures (c.f. crystal energy landscapes generating guest-free inclusion compound structures79). This allowed modeling to complement the structure solution of the HY0.25 from powder X-ray diffraction data, confirming the positions of the pyrogallol and water protons and providing insights into the dehydration mechanism. In this case, the fortuitous growth of single crystal X-ray diffraction quality crystals27 confirms the validity of this approach to structure solution of hydrate structures adding to experience of the role of computation in confirming98 or improving83 structures from powder diffraction data. Overall, the study provides atomic-level insight into a system, where both the tetarto-hydrate and anhydrate are practically relevant and demonstrates that a proper set of complementary analytical techniques is required to achieve a high level of understanding of hydrate systems. This knowledge is useful to control the crystallization conditions, handling, storage, and processing of industrially important substances.

Acknowledgments

Prof. Pantelides and Dr. Adjiman (Imperial College London) are thanked for use of CrystalPredictor and CrystalOptimizer. D.E.B. gratefully acknowledges funding by the Hertha Firnberg Program of the Austrian Science Fund (FWF, project T593-N19). This work was supported by the Austrian Ministry of Science BMWF as part of the UniInfrastrukturprogramm of the Research Platform Scientific Computing at the University of Innsbruck and EPSRC funding of Control and Prediction of the Organic Solid State (www.cposs.org.uk).

Supporting Information Available

Conditions and outcomes of the manual solvent crystallization screen; experimental details for hydrate structure solution and dynamic moisture sorption/desorption study; powder X-ray diffraction patterns, infrared and Raman spectra for the AH and hydrate; hydrate to AH phase transformation monitored with hot-stage microscopy, infrared spectroscopy, and powder X-ray diffraction; water activity measurements; crystallographic information (cif files); potential energy surface scans; representation of the experimental structure; computationally generated AH crystal energy landscape; structure comparisons; hydrate modeling. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

cg4009015_si_001.pdf (1.3MB, pdf)
cg4009015_si_002.cif (15.1KB, cif)
cg4009015_si_003.cif (27.7KB, cif)

References

  1. Bernstein J.Polymorphism in Molecular Crystals; Clarendon Press: Oxford, 2002. [Google Scholar]
  2. Byrn S. R.; Pfeiffer R. R.; Stowell J. G.. Solid-State Chemistry of Drugs, 2nd ed.; SSCI Inc.: West Lafayette, IN, 1999. [Google Scholar]
  3. Brittain H. G.Polymorphism in Pharmaceutical Solids; Informa Healthcare USA, Inc.: New York, 2009. [Google Scholar]
  4. Day G. M. Crystallogr. Rev. 2011, 17, 3–52. [Google Scholar]
  5. Davey R. J.; Allen K.; Blagden N.; Cross W. I.; Lieberman H. F.; Quayle M. J.; Righini S.; Seton L.; Tiddy G. J. T. CrystEngComm 2002, 4, 257–264. [Google Scholar]
  6. Price S. L. Phys. Chem. Chem. Phys. 2008, 10, 1996–2009. [DOI] [PubMed] [Google Scholar]
  7. Price S. L. Acc. Chem. Res. 2009, 42, 117–126. [DOI] [PubMed] [Google Scholar]
  8. Dunitz J. D.; Gavezzotti A. Chem. Soc. Rev. 2009, 38, 2622–2633. [DOI] [PubMed] [Google Scholar]
  9. Llinas A.; Goodman J. M. Drug Discovery Today 2008, 13, 198–210. [DOI] [PubMed] [Google Scholar]
  10. Aaltonen J.; Alleso M.; Mirza S.; Koradia V.; Gordon K. C.; Rantanen J. Eur. J. Pharm. Biopharm. 2009, 71, 23–37. [DOI] [PubMed] [Google Scholar]
  11. Sarma J. A. R. P.; Desiraju G. R. In Crystal Engineering, Seddon K. R.; Zaworotko M., Ed.; Kluwer: Norwell, MA, 1999; pp 325–356. [Google Scholar]
  12. Nangia A.; Desiraju G. R. Chem. Commun. (Cambridge, U.K.) 1999, 605–606. [Google Scholar]
  13. Gorbitz C. H.; Hersleth H. P. Acta Crystallogr., Sect. B 2000, 56, 526–534. [DOI] [PubMed] [Google Scholar]
  14. Griesser U. J. In Polymorphism: In the Pharmaceutical Industry; Hilfiker R., Ed.; Wiley-VCH: Germany, 2006; pp 211–233. [Google Scholar]
  15. Braun D. E.Crystal Polymorphism of Drug Compounds: Statistical Aspects, Analytical Strategies and Case Studies. PhD Thesis, University of Innsbruck, 2008. [Google Scholar]
  16. Vippagunta S. R.; Brittain H. G.; Grant D. J. W. Adv. Drug Delivery Rev. 2001, 48, 3–26. [DOI] [PubMed] [Google Scholar]
  17. Desiraju G. R. Chem. Commun. (Cambridge, U.K.) 1991, 6, 426–428. [Google Scholar]
  18. Perrier P. R.; Byrn S. R. J. Org. Chem. 1982, 47, 4671–4676. [Google Scholar]
  19. Braga D.; Grepioni F.; Chelazzi L.; Campana M.; Confortini D.; Viscomi G. C. CrystEngComm 2012, 14, 6404–6411. [Google Scholar]
  20. Desiraju G. R.; Steiner T.. The Weak Hydrogen Bond; Oxford University Press: Oxford, 1999. [Google Scholar]
  21. Brittain H. G.; Morris K. R.; Boerrigter S. X. M. In Polymorphism in Pharmaceutical Solids, 2nd ed.; Brittain H. G., Ed.; Informa Healthcare USA, Inc.: New York, 2009; pp 233–281. [Google Scholar]
  22. Gal S. Chimia 1968, 22, 409–425. [Google Scholar]
  23. The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals, 14th ed.; O’Neil M. J., Ed.; Merck: NJ, 2006. [Google Scholar]
  24. Brandstaetter-Kuhnert M.; Schoeniger W. Microchim. Acta 1962, 1075–1080. [Google Scholar]
  25. Becker P.; Brusset H.; Gillier-Pandraud H. C. R. Acad. Sci., Ser. C 1972, 274111043–1046. [Google Scholar]
  26. Borka L.; Farkas N. Sci. Pharm. 1990, 58, 431–433. [Google Scholar]
  27. Thakuria R.; Cherukuvada S.; Nangia A. Cryst. Growth Des. 2012, 12, 3944–3953. [Google Scholar]
  28. Allen F. H. Acta Crystallogr., Sect. B 2002, 58, 380–388. [DOI] [PubMed] [Google Scholar]
  29. Polyanskaya T. M.; Smolentsev A. I. J. Struct. Chem. 2012, 53, 568–573. [Google Scholar]
  30. Kazantsev A. V.; Karamertzanis P. G.; Adjiman C. S.; Pantelides C. C.; Price S. L.; Galek P. T. A.; Day G. M.; Cruz-Cabeza A. J. Int. J. Pharm. 2011, 418, 168–178. [DOI] [PubMed] [Google Scholar]
  31. Klimes J.; Michaelides A. J. Chem. Phys. 2012, 137, 120901. [DOI] [PubMed] [Google Scholar]
  32. Gavezzotti A. New J. Chem. 2011, 35, 1360–1368. [Google Scholar]
  33. Farrugia L. J. J. Appl. Crystallogr. 1999, 32, 837–838. [Google Scholar]
  34. Burla M. C.; Caliandro R.; Camalli M.; Carrozzini B.; Cascarano G. L.; De Caro L.; Giacovazzo C.; Polidori G.; Spagna R. J. Appl. Crystallogr. 2005, 38, 381–388. [Google Scholar]
  35. Sheldrick G. M. Acta Crystallogr., Sect. A. 2008, 64, 112–122. [DOI] [PubMed] [Google Scholar]
  36. Crystal data of pyrogallol anhydrate: C6H6O3, Mr = 126.11, monoclinic, space group P21/n, T = 173(2) K, size (mm): 0.48 × 0.2 × 0.02, a = 12.1207(6), b = 3.8065(1), c = 13.1647(6), β = 115.478(6), V = 548.32(5), Z = 4, density = 1.528 g cm–3, reflections measured: 3593, independent reflections: 964, observed reflections: 813, θ range for data collection: 2.43–24.99, h, k, l, range: −14 < h < 14, −4 < k < 4, −15 < 1 < 15, data: 964, restraints: 0, parameters: 85, R[F2 > 2σ(F2)] = 0.033, wR(F2) = 0.085, Rint = 0.026, goodness of fit on F2 = 1.03, Δρmax = 0.19, Δρmin (e Å–3) = −0.18, H atoms treated by a mixture of independent and constrained refinement.
  37. Hill R. J.; Madsen I. C. In Structure Determination from Powder Diffraction Data, David W. I. F., Shankland K., McCusker L. B., Baerlocher Ch., Eds.; Oxford Science Publications: Oxford, 2002; pp 98–117. [Google Scholar]
  38. Shankland K.; David W. I. F.; Sivia D. S. J. Mater. Chem. 1997, 7, 569–572. [Google Scholar]
  39. Markvardsen A. J.; David W. I. F.; Johnson J. C.; Shankland K. Acta Crystallogr., Sect. A 2001, 57, 47–54. [DOI] [PubMed] [Google Scholar]
  40. David W. I. F.; Shankland K.; van de Streek J.; Pidcock E.; Motherwell W. D. S.; Cole J. C. J. Appl. Crystallogr. 2006, 39, 910–915. [Google Scholar]
  41. Pawley G. S. J. Appl. Crystallogr. 1981, 14, 357–361. [Google Scholar]
  42. Rietveld H. M. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar]
  43. Coelho A. A. J. Appl. Crystallogr. 2003, 36, 86–95. [Google Scholar]
  44. Crystal data of pyrogallol tetarto-hydrate: 4(C6H6O3)·H2O, Mr = 522.45, tetragonal, space group P42/n, Z′ = 2, T = 298 K, sample formulation: powder, wavelength: 1.54056 Å, a = b = 24.6058(6) Å, c = 3.8524(3) Å, volume = 2332.45(3) Å3, Z = 4, density = 1.494 g cm–3, 2θ range for data collection: 3–70°, background treatment: Chebyshev polynomial, no. of measured reflections: 226; refinement method: rigid body Rietveld; goodness of fit: 3.056 (on Yobs), Rwp = 5.573, Rexp = 1.823, Rp = 5.040.
  45. Goelles F. Monatsh. Chem. 1961, 92, 981–991. [Google Scholar]
  46. Zhu H.; Yuen C.; Grant D. J. W. Int. J. Pharm. 1996, 135, 151–160. [Google Scholar]
  47. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Montgomery J. A. Jr.; Vreven T.; Kudin K. N.; Burant J. C.; Millam J. M.; Iyengar S. S.; Tomasi J.; Barone V.; Mennucci B.; Cossi M.; Scalmani G.; Rega N.; Petersson G. A.; Nakatsuji H.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Klene M.; Li X.; Knox J. E.; Hratchian H. P.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J.; Ayala P. Y.; Morokuma K.; Voth G. A.; Salvador P.; Dannenberg J. J.; Zakrzewski V. G.; Dapprich S.; Daniels A. D.; Strain M. C.; Farkas O.; Malick D. K.; Rabuck A. D.; Raghavachari K.; Foresman J. B.; Ortiz J. V.; Cui Q.; Baboul A. G.; Clifford S.; Cioslowski J.; Stefanov B. B.; Liu G.; Liashenko A.; Piskorz P.; Komaromi I.; Martin R. L.; Fox D. J.; Keith T.; Al Laham M. A.; Peng C. Y.; Nanayakkara A.; Challacombe M.; Gill P. M. W.; Johnson B.; Chen W.; Wong M. W.; Gonzalez C.; Pople J. A.. Gaussian 03; Gaussian Inc.: Wallingford, CT, 2004.
  48. Karamertzanis P. G.; Pantelides C. C. J. Comput. Chem. 2005, 26, 304–324. [DOI] [PubMed] [Google Scholar]
  49. Conformer C structures were found to be too high in lattice energy, and therefore, not included in the additional search.
  50. Coombes D. S.; Price S. L.; Willock D. J.; Leslie M. J. Phys. Chem. 1996, 100, 7352–7360. [Google Scholar]
  51. Breneman C. M.; Wiberg K. B. J. Comput. Chem. 1990, 11, 361–373. [Google Scholar]
  52. Price S. L.; Leslie M.; Welch G. W. A.; Habgood M.; Price L. S.; Karamertzanis P. G.; Day G. M. Phys. Chem. Chem. Phys. 2010, 12, 8478–8490. [DOI] [PubMed] [Google Scholar]
  53. Stone A. J. J. Chem. Theory Comput. 2005, 1, 1128–1132. [DOI] [PubMed] [Google Scholar]
  54. Stone A. J.GDMA: A Program for Performing Distributed Multipole Analysis of Wave Functions Calculated Using the Gaussian Program System, version 2.2; University of Cambridge: Cambridge, U.K., 2010.
  55. Kazantsev A. V.; Karamertzanis P. G.; Adjiman C. S.; Pantelides C. C. J. Chem. Theory Comput. 2011, 761998–2016. [DOI] [PubMed] [Google Scholar]
  56. Cooper T. G.; Hejczyk K. E.; Jones W.; Day G. M. J. Chem. Theory Comput. 2008, 4, 1795–1805. [DOI] [PubMed] [Google Scholar]
  57. Day G. M.; Cooper T. G. CrystEngComm 2010, 12, 2443–2453. [Google Scholar]
  58. Braun D. E.; Karamertzanis P. G.; Price S. L. Chem. Commun. (Cambridge, U.K.) 2011, 47195443–5445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Braun D. E.; Tocher D. A.; Price S. L.; Griesser U. J. J. Phys. Chem. B 2012, 116, 3961–3972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Cossi M.; Scalmani G.; Rega N.; Barone V. J. Chem. Phys. 2002, 117, 43–54. [Google Scholar]
  61. Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. J.; Refson K.; Payne M. C. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar]
  62. Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
  63. Tkatchenko A.; Scheffler M. Phys. Rev. Lett. 2009, 102, 073005-1–073005-4. [DOI] [PubMed] [Google Scholar]
  64. Vanderbilt D. Phys. Rev. B 1990, 41, 7892–7895. [DOI] [PubMed] [Google Scholar]
  65. Monkhorst H. J.; Pack J. D. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar]
  66. Gavezzotti A. J. Phys. Chem. B 2002, 106, 4145–4154. [Google Scholar]
  67. Gavezzotti A. J. Phys. Chem. B 2003, 107, 2344–2353. [Google Scholar]
  68. Bhardwaj R. M.; Price L. S.; Price S. L.; Reutzel-Edens S. M.; Miller G. J.; Oswald I.; Johnson B. F.; Florence A. J. Cryst. Growth Des. 2013, 13, 1602–1617. [Google Scholar]
  69. Gelbrich T.; Hursthouse M. B. CrystEngComm 2005, 7, 324–336. [Google Scholar]
  70. Gelbrich T.; Threlfall T. L.; Hursthouse M. B. CrystEngComm 2012, 14, 5454–5464. [Google Scholar]
  71. Chisholm J. A.; Motherwell S. J. Appl. Crystallogr. 2005, 38, 228–231. [Google Scholar]
  72. Macrae C. F.; Bruno I. J.; Chisholm J. A.; Edgington P. R.; McCabe P.; Pidcock E.; Rodriguez-Monge L.; Taylor R.; van de Streek J.; Wood P. A. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar]
  73. Palmieri A. III. J. Pharm. Sci. 1978, 67, 1338–1339. [DOI] [PubMed] [Google Scholar]
  74. Burger A.; Ramberger R. Mikrochim. Acta 1979, 2, 259–271. [Google Scholar]
  75. Etter M. C. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar]
  76. [O4–H···O2: O4···O2 = 2.750(3) Å, O4–H···O2 = 148.0(3)° and O5–H···O1: O5···O1 = 2.823(3) Å, O5–H···O1 = 137.9(3)°], [O1–H···O6: O1···O6 = 2.868(3) Å, O1–H···O6 = 155.1(3)° and O3–H···O4: O3···O4 = 2.776(3) Å, O3–H···O4 = 128.6(3)°], [O4–H···O2 and O1–H···O6] and [ O5–H···O1 and O3–H···O4].
  77. Braun D. E.; Gelbrich T.; Kahlenberg V.; Tessadri R.; Wieser J.; Griesser U. J. Cryst. Growth Des. 2009, 9, 1054–1065. [Google Scholar]
  78. Braun D. E.; Karamertzanis P. G.; Arlin J. B.; Florence A. J.; Kahlenberg V.; Tocher D. A.; Griesser U. J.; Price S. L. Cryst. Growth Des. 2011, 11, 210–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Cruz-Cabeza A. J.; Day G. M.; Jones W. Chem.—Eur. J. 2009, 15, 13033–13040. [DOI] [PubMed] [Google Scholar]
  80. Spek A. L. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar]
  81. Florence A. J.; Bardin J.; Johnston B.; Shankland N.; Shankland K. Z. Kristallogr. 2009, 30, 215–230. [Google Scholar]
  82. Braun D. E.; Bhardwaj R. M.; Florence A. J.; Tocher D. A.; Price S. L. Cryst. Growth Des. 2013, 13, 19–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  83. Wu H.; Habgood M.; Parker J. E.; Reeves-McLaren N.; Cockcroft J.; Vickers M.; West A. R.; Jones A. G. CrystEngComm 2013, 1853–1859. [Google Scholar]
  84. Petit S.; Coquerel G. Chem. Mater. 1996, 8, 2247–2258. [Google Scholar]
  85. Riddick J. A.; Bunger W. B.; Sakano T. K.. Techniques of Chemistry: Organic Solvents: Physical Properties, 4th ed.; Wiley-Interscience: New York, 1986. [Google Scholar]
  86. Zencirci N.; Gstrein E.; Langes C.; Griesser U. J. Thermochim. Acta 2009, 485, 33–42. [Google Scholar]
  87. Griffiths G. I. G.; Misquitta A. J.; Fortes A. D.; Pickard C. J.; Needs R. J. J. Chem. Phys. 2012, 137, 064506. [DOI] [PubMed] [Google Scholar]
  88. Karamertzanis P. G.; Day G. M.; Welch G. W. A.; Kendrick J.; Leusen F. J. J.; Neumann M. A.; Price S. L. J. Chem. Phys. 2008, 128, No. 244708. [DOI] [PubMed] [Google Scholar]
  89. Bond A. D.; Boese R.; Desiraju G. R. Angew. Chem., Int. Ed. 2007, 46, 615–617. [DOI] [PubMed] [Google Scholar]
  90. Pauchet M.; Morelli T.; Coste S.; Malandain J. J.; Coquerel G. Cryst. Growth Des. 2006, 6, 1881–1889. [Google Scholar]
  91. Bernstein J.; Davey R. J.; Henck J. O. Angew. Chem., Int. Ed. 1999, 38, 3441–3461. [DOI] [PubMed] [Google Scholar]
  92. Braun D. E.; Gelbrich T.; Kahlenberg V.; Laus G.; Wieser J.; Griesser U. J. New J. Chem. 2008, 32, 1677–1685. [Google Scholar]
  93. Lancaster R. W.; Karamertzanis P. G.; Hulme A. T.; Tocher D. A.; Lewis T. C.; Price S. L. J. Pharm. Sci. 2007, 96, 3419–3431. [DOI] [PubMed] [Google Scholar]
  94. Arlin J. B.; Price L. S.; Price S. L.; Florence A. J. Chem. Commun. (Cambridge, U.K.) 2011, 47, 7074–7076. [DOI] [PubMed] [Google Scholar]
  95. Lancaster R. W.; Harris L. D.; Pearson D. CrystEngComm 2011, 13, 1775–1777. [Google Scholar]
  96. Zencirci N.; Gelbrich T.; Kahlenberg V.; Griesser U. J. Cryst. Growth Des. 2009, 9, 3444–3456. [DOI] [PMC free article] [PubMed] [Google Scholar]
  97. Price C. P.; Grzesiak A. L.; Matzger A. J. J. Am. Chem. Soc. 2005, 127, 5512–5517. [DOI] [PubMed] [Google Scholar]
  98. van de Streek J.; Neumann M. A. Acta Crystallogr., Sect. B 2010, B66, 544–558. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cg4009015_si_001.pdf (1.3MB, pdf)
cg4009015_si_002.cif (15.1KB, cif)
cg4009015_si_003.cif (27.7KB, cif)

Articles from Crystal Growth & Design are provided here courtesy of American Chemical Society

RESOURCES