High-Resolution Optical Tweezers for Single-Molecule Manipulation

Abstract

Forces hold everything together and determine its structure and dynamics. In particular, tiny forces of 1-100 piconewtons govern the structures and dynamics of biomacromolecules. These forces enable folding, assembly, conformational fluctuations, or directional movements of biomacromolecules over sub-nanometer to micron distances. Optical tweezers have become a revolutionary tool to probe the forces, structures, and dynamics associated with biomacromolecules at a single-molecule level with unprecedented resolution. In this review, we introduce the basic principles of optical tweezers and their latest applications in studies of protein folding and molecular motors. We describe the folding dynamics of two strong coiled coil proteins, the GCN4-derived protein pIL and the SNARE complex. Both complexes show multiple folding intermediates and pathways. ATP-dependent chromatin remodeling complexes translocate DNA to remodel chromatin structures. The detailed DNA translocation properties of such molecular motors have recently been characterized by optical tweezers, which are reviewed here. Finally, several future developments and applications of optical tweezers are discussed. These past and future applications demonstrate the unique advantages of high-resolution optical tweezers in quantitatively characterizing complex multi-scale dynamics of biomacromolecules.

Introduction

Light carries momentum, which produces the force to blow comet tails away from the sun by solar radiation [1]. Optical tweezers harness the momentum of laser light to trap objects ranging from 0.3 to 30 microns in diameter (Figure 1). Initially developed by Arthur Ashkin and coworkers in Bell Laboratories in the 1970s and 1980s [2,3], optical tweezers have gained increasingly broad applications in biology [4,5]. They are used to apply forces to single biomacromolecules and detect their responses to mechanical forces in the form of distance changes in real time. These force-induced responses include extension increases of the biopolymers, possible decreases in the speed and processivity of molecular motors, and conformational transitions of macromolecules. Modern high-resolution optical tweezers have extremely high resolution and dynamic ranges in measuring force (0.02-250 pN), distance (0.2 nm->50 µm), and time (0.1 ms->3,000 s). These measuring ranges well match the stability and spatiotemporal scales associated with the conformational transitions of most single biomacromolecules (Table 1). For example, the biological functions of macromolecules often critically depend upon their thermal fluctuations, which involve an energy change of 4.1 pN×nm at room temperature (or kBT, where kB is the Boltzmann constant and T the room temperature) [6]. Suppose a macromolecule undergoes a typical conformational transition with a distance change of 1 nm, the average force associated with the structural fluctuation is around 4.1 pN. This rough estimate suggests that the force of biological significance is in the piconewton range. The measured equilibrium forces to mechanically unfold biomacromolecules are generally higher than the above estimated force to prevent global unfolding, typically up to 30 pN (Table 1). Correspondingly, many molecular motors need to generate commensurate forces to remodel or unfold proteins or nucleic acids [7-11]. Thus, optical tweezers are ideal tools to characterize the thermodynamics and kinetics of these biomacromolecules.

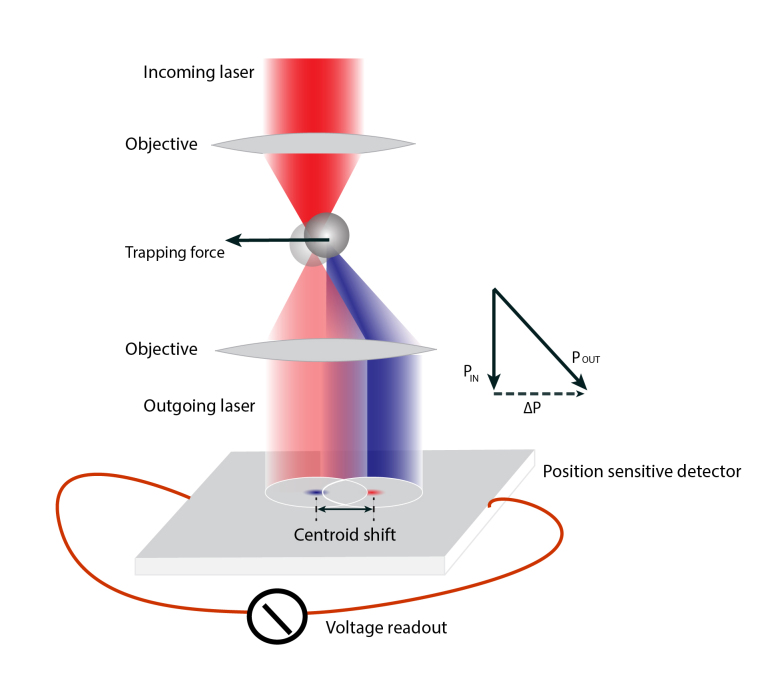
Figure 1.

Principles of optical trapping and displacement detection. As a bead is displaced from the trap center, part of the outgoing laser beam is diffracted. Such diffraction causes a light momentum change to produce the trapping force and a position shift of the beam projected on the position-sensitive detector (PSD). The PSD outputs voltage signals that are proportional to the position of the beam centroid in the PSD surface. The inset shows the light momentum change caused by bead displacement. This diagram is not drawn to scale.

Table 1. Equilibrium unfolding forces of macromolecules and stall forces of molecular motors.

	Molecule	Force (pN)
	ds DNA unzipping	9-20 [128]
	ds RNA unzipping	13-25 [28,92]
	TPP riboswitch	8-9 [63]
Macromolecule	GCN4 leucine zipper	8 [37]
	Strong coiled coil pIL	12 [45]
	Calmodulin	8-12 [129]
	Outer-turn nucleosomal DNA unwrapping	3 [47]
	SNARE C-terminal domain	17 [43]
	Myosin II	3-4 [15]
	Kinesin	7 [13]
Molecular Motor	Bacteria RNA polymerase	15-35 [16]
	RSC complex	30 [21]
	T7 DNA polymerase	34 [18]
	Phage ϕ29 DNA packaging motor	57 [19]

Optical tweezers have been widely used to study molecular motors involved in key biological processes. Molecular motors couple nucleoside triphosphate (NTP†) hydrolysis to actively move along different tracks, such as microtubules, actin filaments, single- or double-stranded DNA or RNA chains, and polypeptides. Numerous motors have been studied by optical tweezers, including kinesin [12-14], myosin [15], RNA polymerases [11,16,17], DNA polymerases [18], DNA or RNA translocases [8,19-22] or helicases [7,23], ribosomes [24,25], and protein unfoldases [9,10]. The characteristic parameters of many molecular motors such as kinesin and bacterial RNA polymerases have been accurately measured, including average speed, processivity, stall force, step size, and detailed mechanochemical coupling of ATP (or NTP) hydrolysis and motor movement [14,22]. Complex motors containing multiple ATPases, such as pentameric phage Φ29 DNA packaging motor [19,22], hexameric protein unfoldase CIpX [9,10] and T7 DNA helicase [26], have been investigated using optical tweezers. These studies show highly coordinated mechanochemical cycles among different ATPase subunits, much like multi-cylinder engines. Optical tweezers are advantageous to measure the motors that move along compliant tracks, such DNA, RNA, and polypeptides [9,20,24]. In these cases, mechanical forces can be used to stretch DNA, RNA or polypeptide chains. The extended chains facilitate measurements of real-time motor movements through extension changes of the chains and investigations of sequence-dependent motor kinetics [26,27]. In conclusion, optical tweezers have contributed much of our current understanding on the molecular mechanisms and biological functions of molecular motors.

Folding dynamics of nucleic acids and proteins constitute another major application category of optical tweezers. The nucleic acids studied by optical tweezers include RNA and DNA hairpins [7,28,29], DNA Holiday junctions [30], telomeric DNA G-quadruplexes, ribozymes [31], and riboswitches [32,33]. The proteins investigated include ribonuclease H [34], T4 lysozyme [35], GCN4 coiled coils [36,37], calmodulin [38], the A2 domain of the von Willebrand factor [39], the Ig domains of filamin A [40], the prion protein PrP [41], the four-helix acyl-CoA binding protein [42], and the SNARE complex [43]. In these studies, the mechanical force exerted by optical tweezers tilts the energy landscapes of biomacromolecules toward their unfolded states [44]. As a result, the external force quantitatively stabilizes the partially or completely unfolded states, increases unfolding rates, and decreases folding rates. Thus, applied force facilitates folding studies of biomacromolecules, especially of extremely stable proteins or nucleic acids [39]. The effects of force also enable optical tweezers to measure the folding energy and kinetics of macromolecules under equilibrium conditions [28]. Compared to other methods for folding studies, a major advantage of optical tweezers is the ability to dissect the complex multiscale reaction networks containing multiple intermediates. Reversible transitions among five or seven different folding states have recently been observed in real time [38,41,43,45], revealing rare misfolded states and cooperative coupling between different protein domains. Finally, optical tweezers can be used to study structures and dynamics of nucleoprotein complexes, such as nucleosome core particles [46-48], chromatin fibers [49], RecA- or Rad51-DNA filaments [50,51], H-NS proteins [52], and single-stranded DNA binding proteins [53]. Thus, optical tweezers have been emerging as indispensable tools to characterize the complex and heterogeneous thermodynamics and kinetics of the folding of macromolecule and their associated functions.

In the following sections, we will first introduce the principles of optical tweezers and compare optical tweezers with other single-molecule manipulation microscopy and ensemble-based experimental approaches. Then we will demonstrate the applications of optical tweezers in protein folding and molecular motor studies. Finally, we will discuss the potential future developments of optical tweezers in instrumentation and applications.

Principle of Optical Tweezers: Optical Trapping and Position Detection

Optical tweezers utilize optical traps to hold micron-sized polystyrene or silica beads as force sensors to manipulate single macromolecules attached to the beads [4,54,55]. An expanded and collimated infrared laser beam (with typical 1064 nm wavelength) is focused by a high-numerical-aperture objective lens to a diffraction-limited spot where an optical trap is formed [2,3]. Spherical beads suspended in water are automatically attracted to and stably trapped in an optical trap. The beads used in such single-molecule experiments are typically 0.5-3 microns in diameter, with a refractive index higher than water. The mechanism of optical trapping can be understood by light momentum changes accompanying bead displacement (Figure 1). As a bead moves away from the trap center to the right, it diffracts part of the outgoing laser light to the right much like a micro-lens. As light carries momentum along its direction of propagation, the light momentum shifts to the right. As a result, the bead experiences a counteracting force to the left, pushing the bead back to the trap center. The trapping force along the axial direction can be explained in a similar manner. Experimental results and theoretical analyses show that the magnitude of this trapping force is proportional to the separation between centers of the bead and trap within 50 to a few hundred nanometers. Thus, within this displacement range, an optical trap can be considered as a spring with a force constant of 0.01-0.5 pN/nm that linearly depends upon the incident laser intensity. The typical force constant used in single-molecule experiments is ~0.2 pN/nm, with an incident light power of ~500 milliwalts per trap.

To detect the displacement of the bead in an optical trap, the outgoing laser beam can be collimated by a second high-numerical-aperture objective lens and projected to a planar position-sensitive detector (Figure 1). The detector registers the centroid of the beam in real time as two voltage signals proportional to the centroid displacement in two orthogonal directions [54,56]. After calibrations, the position of the bead, as well as the average force applied to the bead, can be measured from the voltage readouts. This scheme of position detection, called back focal-plane interferometry [57], can be quantitatively described by interference of the light that is scattered by the bead with the light that is not. Bead position detection can use the same trapping light as shown in Figure 1 for the convenience of instrumentation. Alternatively, a different laser with milliwalt power can be focused on the bead for independent displacement measurement. Unlike any imaging methods, the position detector is not conjugated to the bead in the sample plan. Instead, it “looks at” the back-focal plane of the second objective. Thus, this method of position detection is not limited by light diffraction is capable of magnifying bead movement by more than a thousand fold in the form of beam centroid movement. In addition, modern high-resolution optical tweezers use two optical traps formed by two orthogonally polarized beams split from a single laser beam (Figure 1). When a single molecule is attached to and stretched by two trapped beads, the double-bell detection system is isolated from the environment, including the sample stage [54,58]. Noises common to both traps, such as those from laser pointing instability, are minimized through differential detection for the distance between the two beads. These robust designs of optical tweezers, combined with controlled environments for optical tweezers, such as acoustic isolation, stabilized temperature, and minimal air flow in the optical tweezer room, lead to the extremely high force and spatiotemporal resolution of modern optical tweezers with minimal long-time baseline drift. As a result, current state-of-the-art optical tweezers are capable of detecting position changes at sub-nanometer resolution (~0.2 nm) and sub-millisecond temporal resolution (~0.1 ms) [21,54,58-60].

Advantages of Single-Molecule Manipulation by Optical Tweezers

Optical tweezers have been widely used to investigate the structures and dynamics of macromolecules, especially of large molecular assembly and molecular machines [9,10,28,38,39,41,43,46,61-63]. The single-molecule method has several advantages compared to traditional ensemble-based experimental approaches. First, the single-molecule method can reveal both averages and distributions of the properties of macromolecules, whereas ensemble approaches only yield averages measured from typically billions of macromolecules. Second, the single-molecule approach avoids complications of synchronization required in the ensemble kinetic experiments. In a single-molecule experiment, the conformation transitions of a macromolecule are detected in real time. As a result, different conformational states of a macromolecule show up successively, revealing its transition pathways and kinetics. Under equilibrium conditions, the total dwell time of these states should be Boltzmann-distributed, yielding their relative energies in the presence of force. Thus, both energetics and kinetics of a macromolecule transition can be obtained in one single-molecule experiment [28]. In contrast, only certain average properties of these states can be detected in an ensemble experiment as the synchronized system decays to equilibrium. Once the system reaches equilibrium, no kinetic information can be obtained. Thus, it is intrinsically difficult to dissect the complex reaction network containing more than two states using ensemble approaches, whereas high-resolution optical tweezers have been successfully used to dissect complex kinetic processes containing five or more states [38,41,43,45]. This remarkable capability of optical tweezers crucially depends on their ability to measure long dynamic ranges. Correspondingly, states with energy differences as much as 17 kBT can be directly detected in equilibrium in the presence of a constant force and under optimal conditions, as is estimated from the dynamic range of time measurement. Additionally, the mechanical force offered by optical tweezers can be used to probe rare transitions involving large energy changes in the absence of force [43,46]. For example, the transiently unfolded state of a protein can be stabilized by mechanical force in a native solution, instead of by exposure to urea or other denaturant, to facilitate folding studies. Force lowers the energy of both the unfolded state and the energy barrier of unfolding, enhancing the unfolding rate and equilibrium constant in a quantitatively predictable manner [37,44]. Finally, optical tweezers can reveal the static and dynamic heterogeneity of macromolecules or their assemblies at a single-molecule level [21,64]. A prominent example is the reconstituted chromatin fibers that often differ in numbers and positions of nucleosomes in the same batch of preparation and tend to aggregate and precipitate in bulk [65]. Such heterogeneity imposes remarkable difficulties to study this or similar large molecular assemblies using ensemble approaches.

Single-molecule manipulation can also be carried out by other tools, mainly atomic force microscopy (AFM) and magnetic tweezers [66]. Compared to optical tweezers, these microscopes employ different force and displacement sensors and detection schemes, leading to different force and spatiotemporal resolutions (Table 2). AFM has been widely used in protein folding studies [67-69]. AFM utilizes micro-fabricated silicon or silicon-nitrile cantilevers as a force sensor to manipulate single molecules. These sensors are typically large (~100 µm in length) and stiff (>10 pN/nm), which cause relatively low force resolution (~10 pN) and temporal resolution in water (>1 ms) [66,70]. As a result, only protein unfolding can be directly measured by most of atomic force microscopes, in which proteins are rapidly pulled and unfolded far from equilibrium in a high force loading rate. Protein refolding/unfolding equilibrium has rarely been detected using AFM [71], which makes measurement of protein folding energy difficult. In addition, AFM has not been applied to study real time dynamics of molecular motors. However, AFM has extremely high spatial resolution (~0.2 nm) in single-molecule manipulation and can be used to image single biomolecules deposited on a flat surface [65]. Furthermore, AFM can measure forces greater than 1,000 pN, which is high enough to break covalent bonds [72]. In contrast to optical tweezers and AFM, magnetic tweezers utilize micron-sized magnetic beads placed in a magnetic field to manipulate single macromolecules [66,73-75]. The dynamics of the macromolecule in response to the force is detected through bead movement using a digital camera. Their typical spatiotemporal resolution is around 5 nm and over 1 ms. Magnetic tweezers can easily be used to twist single molecules and detect the structural transitions of molecules in response to an external torque [76,77]. In addition, magnetic tweezers have the advantages of constant force application and relatively easy construction based upon commercial optical microscopy.

Table 2. Comparison of optical tweezers, atomic force microscopy (AFM), and magnetic tweezers for single-molecule manipulation.

	Optical tweezers	AFM	Magnetic tweezers
Spatial resolution (nm)	~ 0.2	~ 0.2	~5
Temporal resolution (ms)	~ 0.1	~ 1	> 1
Stiffness (pN/nm)	0.05-1	>10	~0
Force resolution (pN)	0.02	~10	0.001
Maximum force (pN)	250	>1000	~100
Advantages	High resolution. Easy and specific attachment of biomolecules. Reversible protein folding and unfolding. Applications in molecular motors	High force measurement range. Single-molecule imaging capability.	Capabilities of torque and constant force application. Relatively easy construction.
Disadvantages	Complex construction. Strict environmental requirements. Potential photo-damage [78].	Poor force resolution. Nonspecific interactions. Difficult to study protein refolding and molecular motors.	Relatively poor spatiotemporal resolution.

The above comparisons suggest that optical tweezers generally have high spatiotemporal resolution compared to AFM and magnetic tweezers. In addition, dual-trap optical tweezers have less machine drift due to complete suspension of the detection system and the differential detection described above. In contrast, single molecules have to be directly or indirectly attached to the sample stage in order to be pulled by AFM or magnetic tweezers. This arrangement is susceptible to environmental noises and causes greater machine drift. However, the extremely high light intensity in an optical trap (~10 MW/cm2) tends to cause photo-damage of biomacromolecules in which the biomacromolecules are covalently modified or broken by free radicals [78]. To minimize photo-damage, an oxygen salvaging system is often added in the buffer to reduce light-induced production of free radicals. In addition, polystyrene beads with greater diameters (~2 µm) [37] or silica beads [78] are found to reduce photo-damage. When these precautions were taken, we did not observe significant photo-damage of many DNA and protein samples even for long-time measurement (up to one hour) [37].

Applications of Optical Tweezers in Folding Studies of Strong Coiled Coil Proteins

One of central questions in protein folding studies is how the one-dimensional amino acid sequence of a protein encodes its unique functional three-dimensional structure [79]. Yet, proteins may misfold under certain conditions [80-82]. Such misfolding underlies a wide variety of human diseases, including neurodegenerative diseases, diabetes, mad cow disease, and others [83]. Despite decades of intensive research, it remains challenging to detect the elusive intermediates involved in protein folding and misfolding.

Folding and Misfolding of a Two-Stranded Coiled Coil pIL

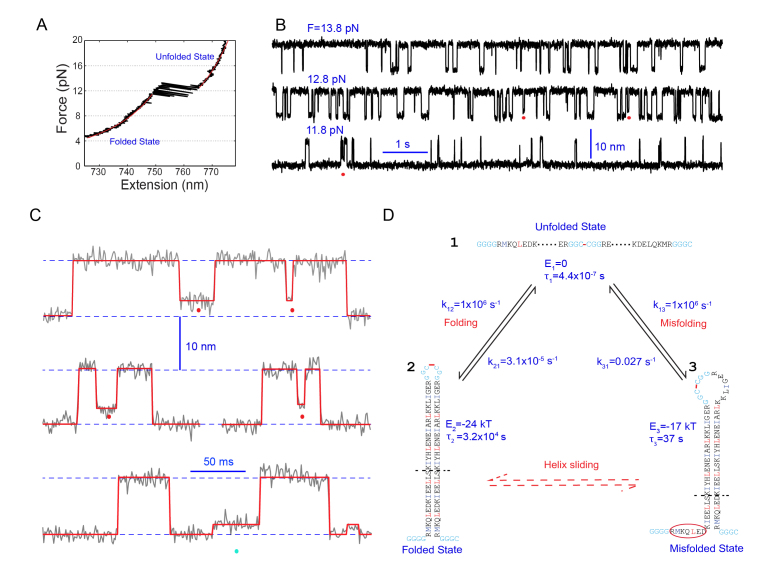
Coiled coils have long been model systems for protein folding studies, partly because they are one of the most common structural motifs in proteins. Xi et al. have recently studied two strong coiled coils using high-resolution dual-trap optical tweezers (Figure 2) [45]. To facilitate attachment of a single protein to two beads as well as force measurement, one or two DNA molecules are utilized as handles [34]. As the protein is pulled to a higher force by separating the two optical traps at a uniform speed, the tension and end-to-end extension of the protein-DNA conjugate monotonically increases if the protein remains folded (Figure 3A). The resultant force-extension curve is mainly derived from the DNA handle, which can be quantified by the worm-like chain model of the DNA [61,84]. In this model, the extension of a semi-flexible polymer chain is related to the force applied to the chain and its contour length (0.34 nm/bp for duplex DNA) and persistence length (~50 nm). However, as the force reaches a critical point around 12 pN, the protein starts to unfold cooperatively, leading to an abrupt extension increase. This transition occurs because the energy of the unfolded state has become either close to or lower than that of the folded state under this tension, corresponding to a low or high energy barrier for the transition. In this former case, reversible folding and unfolding of the protein can be observed if the force is slowly applied to the protein (Figure 3A). This reversible transition represents thermal fluctuations of the protein in two conformations. Further pulling to higher forces will stabilize the protein in the unfolded state, leading again to monotonic force and extension increases. Once this reversible transition is identified, the protein can be held at constant forces in the corresponding force region to detect the equilibrium transitions at higher resolution (Figure 3B). Here, cooperative protein unfolding and refolding is manifested by transitions between discrete extension states. The energetics and kinetics of the protein at zero force can be obtained by extrapolating the force-dependent unfolding probability and transition rates [37,43,44]. The procedure above describes the general process of characterizing protein folding using optical tweezers.

Figure 2.

Typical experimental setup for protein folding studies using high-resolution dual-trap optical tweezers. The protein of interest is tethered between two beads held by two optical traps. The protein is biotinylated at one end and cross-linked to a long DNA handle (> 500 bp) at the other end via a terminal cysteine. For protein complexes such as the coiled coil shown here, the two polypeptides are cross-linked again through a disulfide bridge. The force and extension of the protein-DNA conjugate are measured as the protein is pulled by changing the separation between the two optical traps. This image is not drawn to scale. Typical length scales for the protein, the DNA handle, and the beads are a few nanometers, 300-1000 nm, and ~2000 nm, respectively.

Figure 3.

Formation of staggered coiled coil states through protein misfolding and helix sliding. (A) Force-extension curve (FEC, black) of a single coiled coil complex (pIL) showing reversible two-state transitions at ~12 pN. The FEC regions corresponding to the fully folded and unfolded protein states can be fitted by the worm-like chain model (red lines). (B) Time-dependent extension traces exemplifying two-state transitions of pIL at the indicated pulling forces. Red dots indicate the partially folded and staggered states. (C) Close-up view of the extension traces showing the misfolded states (red dots) and intermediate state (cyan dots). (D) Quantitative model for folding and misfolding of pIL at zero force. One of three misfolded states is shown here, which contains staggered helices with shifted registry. The free energy (E) and lifetime (τ) of different states and their transition rates (k) are indicated.

Surprisingly, Xi and his coworkers discovered three misfolded states for one coiled coil (pIL, a variant of wild type GCN4, Figures 3B-C) and at least one for the other (not shown) [45]. These misfolded states have staggered helical structures with shifted helical registery compared to the correctly folded coiled coils (Figure 3D). Although these misfolded states are much less stable than the folded state, they fold as quickly as the correctly folded states. Thus, protein misfolding efficiently competes with protein folding, leading to a large population of misfolded proteins in the initial phase of the folding process. Further protein folding has to rely on the escape of proteins from the misfolded states, which is generally a slow process. Therefore, the results of the group directly confirm the kinetic partition mechanism for protein folding and misfolding [85]. Such partitioning among different folding intermediates significantly slows down the overall folding rates (Figure 3D). Folding of two-stranded coiled coils is generally considered to be very efficient. Thus, this new observation suggests that misfolding may be a universal property of proteins [80].

Energetics and Kinetics of SNARE Complex Assembly

Gao and her coworkers have recently characterized the folding/assembly energetics and kinetics of neuronal SNAREs (Soluble NSF Attachment protein Receptors) [43]. SNARE proteins are molecular engines that drive membrane fusion [86,87]. They consist of t-SNAREs on the target plasma membrane (syntaxin and SNAP-25 in a binary complex) and v-SNAREs on the vesicle membrane (VAMP2, also called synaptobrevin) [88]. Individual t- and v-SNAREs are largely disordered. They mediate membrane fusion by folding and assembling into an extraordinarily stable zipper-like four-helix bundle, drawing two membranes into close proximity for fusion [89,90].

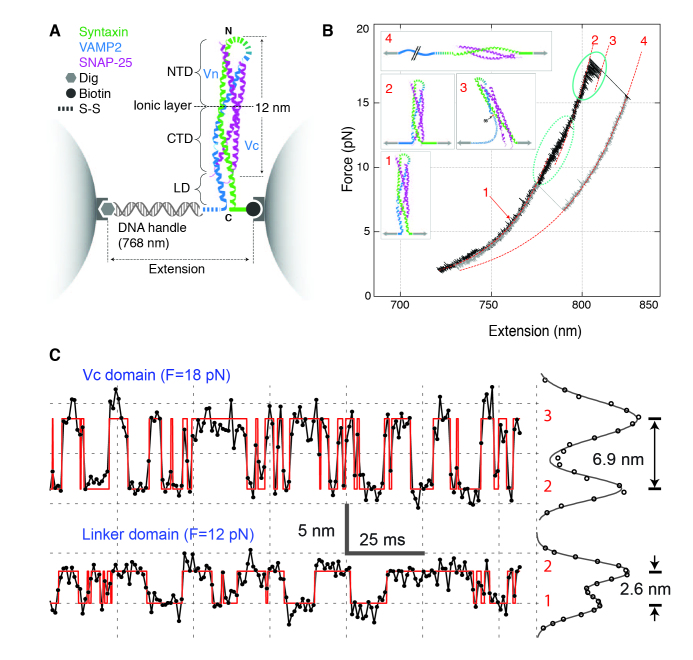
To pull a single SNARE complex, Gao et al. cross-linked the N-termini of syntaxin and VAMP2 by a disulfide bridge and attached syntaxin by its C-terminus to one bead and VAMP2 to another through a DNA handle (Figure 4A). The experiment was started with a single pre-assembled SNARE complex containing its cytoplasmic domain. When pulled to high forces, fast reversible transitions appeared in two force regions. The first region at 8-13 pN has ~3nm average extension change and corresponds to the structural transition of the linker domains (between states 1 and 2). The second region in 14-19 pN has ~7nm extension change and is caused by zippering and unzipping of the Vc domain of the largely structured t-SNARE (between states 2 and 3) (Figure 4B). The binary extension transitions of both domains can be more clearly seen under constant middle forces or trap separations (Figure 4C). From the equilibrium force measured for both transitions, the folding energy of the linker domain and the Vc domain were calculated as 8 (±2) kBT and 28 (±3) kBT, respectively. More extensive measurements also revealed fast zippering rates for both domains, especially for the Vc domain whose zippering rate approaches the diffusion limit. The unusually large zippering energy and rates of the SNARE complex justify SNARE proteins as a powerful engine for membrane fusion. The identified half-zippered state (state 3) may serve as a platform for other proteins to regulate membrane fusion. This single molecule experiment also revealed the unzipped SNARE state (state 4) and the t-SNARE unfolded state (state 5, not shown) at higher force regions.

Figure 4.

Dynamic disassembly and reassembly of a single cytoplasmic SNARE complex. (A) Experimental setup. The SNARE complex contains the N-terminal (NTD) and C-terminal (CTD) SNARE domains, with the corresponding VAMP2 regions designated as Vn and Vc, respectively, the ionic layer, and the linker domain (LD). (B) Force-extension curve (FEC) of the SNARE-DNA conjugate showing sequential disassembly (black trace) and reassembly of the SNARE complex (grey trace). Different segments of the FEC can be fitted by the worm-like chain model (red dashed lines), revealing the structures of SNARE assembly states (inset). The LD and CTD transitions are marked by dashed and solid ovals, respectively. (C) Time-dependent extension corresponding to the unfolding/refolding transitions of the Vc domainn (top panel) or the LD (bottom panel) with their idealized transitions determined by the hidden Markov model analysis (red traces). The histogram distribution of extension (right) from the transition of the Vc (top) or linker (bottom) domain has two distinct peaks, indicating a two-state transition for each domain. Each distribution (circle) can be fitted by a sum of two Gaussian functions (line), revealing the indicated extension change.

Application of Optical Tweezers in A Molecular Motor Study: DNA Translocation by the ATP-Dependent Chromatin Remodeling Complex

Optical tweezers have long been unique tools to study molecular motors [8-10,12,15,19,24,58,62,91,92]. As a result, the mechanical properties of these motors, such as the speed, step size, stall force, and detailed kinetics of movement have been measured for the first time using optical tweezers (Table 1). The Zhang lab at Yale is interested in a large family of poorly characterized DNA translocases contained in ATP-dependent chromatin remodeling complexes (remodelers) [8,21,65]. Remodelers are highly conserved protein complexes that use the energy of ATP hydrolysis to alter chromatin structures [93]. It is not clear how remodelers perform these alterations. Evidence from ensemble experiments suggests that remodelers are capable of moving along DNA in an ATP-dependent manner [94]. However, direct observation of remodeler translocation and accurate measurement of the associated parameters are rare.

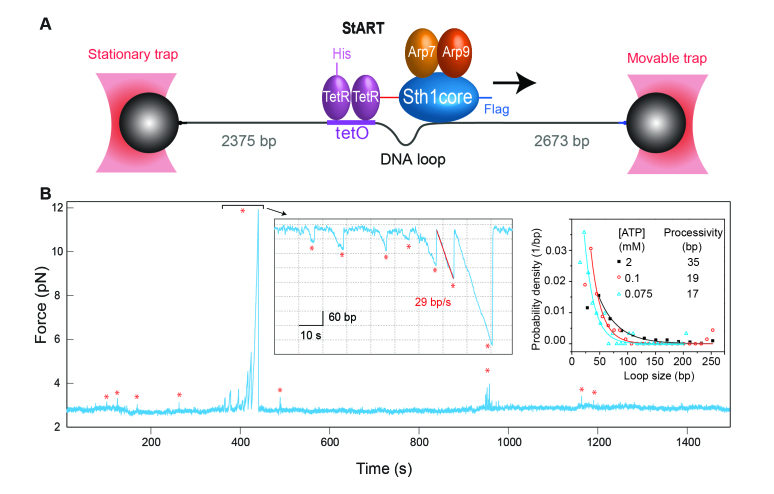
Using high-resolution optical tweezers, Sirinakis and coworkers have characterized the DNA translocation properties of a minimal RSC (Remodel Structure of Chromatin) complex [21]. RSC is a prototypical remodeler containing 15 different subunits with a molecular weight around one million Daltons in total [95]. To dissect its structure and function, they identified a minimal RSC complex containing the ATPase core of RSC and two actin-related proteins. The ATPase was fused with a tetracycline receptor (TetR) that can anchor the minimal complex specifically to the middle of a DNA molecule containing TetR’s cognate binding site (Figure 5A). When the ATPase moves away from the binding site, it shortens the DNA end-to-end extension and increases the force opposing motor translocation, which is recorded by optical tweezers with high resolution (Figure 5B). Thus, the translocation speed (25 bp/s), processivity (35 bp), step size (2 bp), and stall force (>30 pN) at the saturated ATP concentration were measured for this motor. DNA translocation is believed to be the driving force for chromatin remodeling. The extraordinarily high force generation by the RSC motor (>30 pN) suggests that remodelers produce high mechanical force to disrupt strong DNA-histone interactions for nucleosome remodeling.

Figure 5.

ATP-dependent DNA translocation of a tethered minimal RSC complex. (A) Experiment setup. The remodeler complex specifically binds to the DNA through the tetO site. The complex induces a DNA loop as it moves away from the TetO site, which decreases the end-to-end distance and increases the tension of the DNA molecule. These changes can be directly detected by high-resolution optical tweezers in real time. (B) Force-time trace showing a series of distinct spikes (marked by red stars) due to DNA translocation of single remodelers. The time-dependent DNA contour length corresponding to the indicated region is plotted (left inset). The translocation speed and distance of a single translocation event are measured from the slope and size of the translocation phase, respectively. The slope is calculated by a linear regression of the translocation phase (red line). The distributions of the translocation distance at different ATP concentrations are shown in the right inset, revealing the translocation processivity of the remodeler.

Conclusion and Prospective

The above examples and previous studies show that optical tweezers have been successfully used to reveal complex kinetics and energetics of proteins at a single molecule level that prove difficult using ensemble experimental approaches. To further expand the capabilities of optical tweezers, researchers may incorporate more functionality into these tools and explore their new applications.

Current optical tweezers can only detect structural transitions of macromolecules in one dimension at a time, whereas protein folding occurs in three dimensions and may not be completely understood by the measured distance change in one pulling direction. To expand the capabilities of optical tweezers, one major development is the incorporation of single-molecule fluorescence detection, including single-molecule fluorescence resonance energy transfer (smFRET) and imaging [30,53,96]. These new integrated methods allows researchers to not only manipulate the molecule, but also to image it and detect its conformation change orthogonal to the pulling direction in real time based on a fluorescence signal [59,60]. Alternatively, binding of ligands and their associated protein transitions can be simultaneously detected by fluorescence and extension changes, respectively, using fluorophore-labeled ligands added free in solution. In one of such applications, dynamic DNA hairpin unfolding and dye-labeled oligonucleotide binding has been observed [60]. Further applications of combined microscopy into protein folding studies relies on more efficient and orthogonal protein labeling techniques [9,10,97-99], including specific conjugation to fluorophores, DNA handles, or photoactivatable fluorescent proteins [100]. Another notable direction is to add torque measurement to optical tweezers, such that single molecules can be pulled and twisted simultaneously [101].

Protein misfolding and aggregation underlies many prevailing human diseases [81,83]. Proteins misfold and aggregate through a myriad of soluble intermediates called amyloid oligomers and eventually into insoluble β-strand-rich amyloid fibers. Amyloid fibers have been widely detected in the patients with associated amyloid diseases and were once believed to be the culprits of these diseases [102]. However, growing evidence in the past decade has shown that amyloid oligomers are neurotoxic and can cause neuron death [103-105], whereas amyloid fibers are generally inert. Thus, detecting the concentrations of amyloid oligomers in vivo and neutralizing their toxicity has become important for early diagnosis and treatment of amyloid diseases [106], respectively. However, amyloid oligomers are present in low concentrations in vivo (below nanomolar) and generally have limited lifetimes in vitro, and are heterogeneous in size, structure, and toxicity [103]. Thus, it is intrinsically difficult to prepare large amount of homogenous oligomers for structural and pathogenic studies. Therefore, the structures, stabilities, and dynamics of these amyloid oligomers and their interactions with numerous other proteins has not been well characterized so far, despite extensive research using ensemble experimental approaches. Because of their high spatiotemporal resolution and successes in characterizing heterogeneous reaction networks, optical tweezers have great potential to elucidate the dynamic structures of amyloid oligomers. But proper protein constructs, such as the tandem repeats of the amyloid-forming protein sequences [107], must be developed for the folding studies of the oligomers in a single-molecule format.

It remains a great challenge to characterize the energetics and kinetics of membrane protein folding [108]. Folding of helical membrane proteins consists of two either separate or coupled processes: transmembrane helix insertion into and association within membranes [109]. Despite great efforts [110-114], there have been no general methods developed to directly measure the free energy and kinetics associated with both insertion and association of transmembrane helices. It is often impossible to allow transmembrane helices to reversibly partition between the aqueous phase and the membrane using an ensemble approach [115], a necessary condition for free energy measurement. This is because most of membrane proteins aggregate in aqueous solution and produce large energy changes during membrane insertion. Whereas folding studies of cytoplasmic proteins often uses denaturants, detergents, or high temperatures to first synchronize proteins in the unfolded states, such reagents generally cannot be applied to membrane proteins without compromising membrane structures. In addition, the “unfolded states” of membrane proteins in detergents or denaturants are often not completely unfolded and contain certain secondary or tertiary structures [116], which complicate quantitative measurements of folding energy and kinetics. In contrast, mechanical forces can be conveniently used to unfold membrane proteins from a supported bilayer into an aqueous solution, as demonstrated by AFM [117]. Since the experiment is carried out at a single-molecule level, aggregation of the protein in solution is avoided. In principle, high-resolution optical tweezers can be similarly applied to unfold membrane proteins, but under conditions in equilibrium with the folded protein states. This force-induced equilibrium between protein unfolding and refolding makes it possible to measure folding energy and kinetics of membrane proteins. The helix-coil transition of a single transmembrane helix domain only involves estimated extension changes of a few nanometers if the single helix is pulled from both sides of the membrane. To detect such small extension changes, high-resolution dual-trap optical tweezers are required, which necessitate complete suspension of the detection system, including the single membrane protein under tension and its associated membrane. Artificial model membrane systems such as nanodiscs [118,119] may provide a perfect environment for membrane protein folding to be studied by high-resolution optical tweezers.

Finally, as more complex reaction networks are studied using optical tweezers, data analyses of single-molecule trajectories become increasingly challenging [29,43,44,120-122]. Sophisticated data analysis methods, such as those based on hidden-Markov models [123,124], have been developed to reliably extract more kinetic information from single-molecule trajectories [21,37,38,125-127]. However, more efficient and flexible algorithms are required to model the reaction networks associated with protein folding with various constraints, such as the detailed balance of systems under thermodynamic equilibrium.

In summary, optical tweezers have become indispensable tools to study the structures and dynamics of biomacromolecules at a single-molecule level. With new developments in instrumentation and data analysis, optical tweezers have great potential to provide new insights into more complex systems that are difficult to study using traditional ensemble-based experimental approaches.

Abbreviations

AFM

Atomic Force Microscopy

smFRET

Single-Molecule Fluorescence Resonance Energy Transfer

SNARE

Soluble NSF Attachment Protein Receptor

RSC

Remodel Structure of Chromatin

TetR

Tetracycline Receptor

NTP

nucleoside triphosphate