Consequences of domain insertion on sequence-structure divergence in a superfold

Significance

Here, we determine the impact of large-domain insertions on the sequence and structure divergence of a ubiquitous protein scaffold (superfold). By performing quantitative analysis on a distinctive dataset of >150 protein structures, unique protein-design principles have been uncovered. Our work suggests that superfolds are tolerant to relatively large domain insertions when followed by accommodating mutations in the scaffold. This structural robustness may facilitate the development of directed evolution technologies that incorporate domains into existing scaffolds.

Abstract

Although the universe of protein structures is vast, these innumerable structures can be categorized into a finite number of folds. New functions commonly evolve by elaboration of existing scaffolds, for example, via domain insertions. Thus, understanding structural diversity of a protein fold evolving via domain insertions is a fundamental challenge. The haloalkanoic dehalogenase superfamily serves as an excellent model system wherein a variable cap domain accessorizes the ubiquitous Rossmann-fold core domain. Here, we determine the impact of the cap-domain insertion on the sequence and structure divergence of the core domain. Through quantitative analysis on a unique dataset of 154 core-domain-only and cap-domain-only structures, basic principles of their evolution have been uncovered. The relationship between sequence and structure divergence of the core domain is shown to be monotonic and independent of the corresponding type of domain insert, reflecting the robustness of the Rossmann fold to mutation. However, core domains with the same cap type share greater similarity at the sequence and structure levels, suggesting interplay between the cap and core domains. Notably, results reveal that the variance in structure maps to α-helices flanking the central β-sheet and not to the domain–domain interface. Collectively, these results hint at intramolecular coevolution where the fold diverges differentially in the context of an accessory domain, a feature that might also apply to other multidomain superfamilies.

The universe of protein structures is vast and diverse, yet these innumerable structures can be categorized into a finite number of folds (1). Ideally, the protein fold has a robust yet evolvable architecture to deliver chemistry, bind interaction partners, or provide scaffolding. A popular strategy for the acquisition of new function(s) is the topological alteration of the fold to provide a new evolutionary platform. More frequently, existing and stable scaffolds are elaborated to attain diversity that is due to accumulation of stochastic, independent, and near-neutral mutations in the protein sequence. In a large number of cases, the expansion of functional space has been achieved by the tandem fusion of two or three domains to form evolutionary modules known as supradomains (2). An analysis of catalytic domains fused to the nucleotide-binding Rossmann domain has revealed that the sequential order of their connections is conserved because each pairing arose from a single recombination event (3). Another common structural embellishment is that of domain insertion(s) into existing folds (4)—a strategy that is ubiquitous in all structural classes, i.e., all α, all β, α + β, and α/β (5). For example, members of the A, B, and Y DNA polymerase superfamilies, Rab geranylgeranyl transferase superfamily, and alcohol dehydrogenase superfamily have inserted different domains into the native fold to fine tune their cellular functions (6–8). The analysis of such noncontiguous domain organization has been facilitated by the availability of structures bearing insertions of domains that also occur as independent folds. It has been estimated that 9% of domain combinations observed in protein-structure databases are insertions (5). However, the way in which the sequence–structure relationship changes within a protein fold in the context of such domain insertions has yet to be fully understood. In this study, we assess how the insertion of an accessory domain affects the sequence–structure relationship of the Rossmann fold, a superfold used by at least 10 different protein superfamilies (9).

Function-driven changes come with their own costs: most molecular modifications of proteins tend to be thermodynamically destabilizing (10). Although long hypothesized (11), it has been shown only recently that the stability of a fold promotes evolvability by allowing a high degree of structural plasticity (12). As a consequence, protein folds follow a power-law distribution where a few intrinsically stable folds, referred to as superfolds, have numerous members, and a multitude of folds have few members (9). Due to this interplay between stability and evolvability, it has been suggested that superfolds are compatible with a much larger set of sequences than other folds (13). This proposal raises the question of how protein sequence and structural diversity are related to one another. Pioneering work by Chothia and Lesk (14) illustrated that structural similarity is correlated with sequence similarity. Although the 3D structure retains the common fold during neutral drift, it undergoes subtle changes as sequence diverges, mainly due to packing modifications and backbone conformational changes. In a focused study, Halaby et al. (15) have shown that sequence diverges to a greater extent than structure in the Ig fold. More recently, Panchenko and coworkers noted a similar trend in a systematic study spanning 81 homologous protein families (16).

We queried how large inserts into a protein fold shape the relationship between sequence and structure divergence, using as a model system, the Haloalkanoate Dehalogenase Superfamily (HADSF), where the inserts into a Rossmann catalytic domain impart substrate specificity. The HADSF is a highly successful family, and, with close to 80,000 members to date (17), it is one of the largest enzyme superfamilies. The HADSF is well-represented in all domains of life, and the majority of its members catalyze phosphate ester hydrolysis (18, 19). HADSF members have attained functional diversity via accessorization of the conserved core Rossmann-fold domain by the insertion of a cap domain. The Rossmann fold is a primordial nucleotide-binding fold that plays a significant role in maintenance and evolution of life (6). Structurally, it is organized as a three-layered sandwich made up of multiple α/β units. The fold is similar across superfamilies, apart from stochastic thermal fluctuations and structural divergence. Notably, the inserted cap domains in the HADSF have not yet been observed as independent folds in extant organisms (the term domain is defined here as an apparently stable arrangement of secondary structural units). The presence of the cap domains leads to a natural classification of the superfamily into different structural classes—C0 (no or minimal cap insert), C1 (α-helical cap insert after the first strand), C2 (α-helical and β-strand cap insert after the third strand, further subdivided into C2a and C2b depending on topology), and C1 + C2 (inserts in both positions), based on topology and location of the insert (20) (SI Appendix, Fig. S1). These characteristics make the HADSF an excellent model system for the study of the sequence–structure–function relationship in multidomain proteins.

The unique cap–core architecture of the HADSF raises several intriguing biophysical and biochemical questions regarding molecular evolution. In a typical HADSF member, the substrate leaving group and the phosphoryl group are bound by the cap and core domains, respectively. However, binding and catalysis cannot be independent of one another (reflected in the definition of the specificity constant k_cat/K_m). How this functional codependence between the two domains manifests itself in the structure is an important question with implications for evolution and rational design of multidomain proteins. As cap and core domains form a single polypeptide chain, substrate binding and catalysis are inherently linked although the details of this linkage have yet to be defined. Another perplexing issue is the evolutionary mechanism of cap-domain evolution. Did it involve a rapid stage where the cap domain was grafted onto the core domain, followed by a slow stage where neutral mutations were accumulated? Or was there a gradual and continuous change where a small cap domain was inserted followed by subsequent duplication and elaboration? Herein, we attempt to answer such questions by analyzing a unique dataset of core-domain-only and cap-domain-only structures using quantitative informatics analyses. The relationship between sequence and structure divergence in the core fold is shown to be monotonic, as is generally the case, and notably, to be independent of the corresponding cap type. However, core domains with the same cap type bear a greater similarity at the sequence and structure level than do the core domains with different cap types, suggesting interplay between the cap and core domains. Surprisingly, we find that the variation between cap types maps to the flanking helices of the Rossmann fold rather than to the interface, suggesting that the core has changed more globally to accommodate the cap. Overall, our results suggest that the structure space of a superfamily has an underlying organizing principle despite its diversity.

Results

Relationship Between Sequence and Structure Divergence in the Conserved HADSF Core Domain.

To study the relationship between sequence and structure in the HADSF core domain, we constructed a dataset of protein structures representing all known HADSF structures, determined at resolutions better than 3.6 Å, resulting in 154 unique structures (Materials and Methods). To investigate the influence of the cap domain on the core domain, we generated cap-domain-only and core-domain-only datasets by manually dissecting the experimentally determined structures into their respective cap and core domains. For estimating the degree of structural similarity between two proteins, we used the pairwise structure-alignment algorithms TM-align (21) and SAP (22). Results from both alignment algorithms are qualitatively similar (SI Appendix, Fig. S3). Thus, data are presented from one representative algorithm, TM-align, hereon. Root-mean-square deviation (RMSD), the traditional metric of structural similarity, is length-dependent and scales linearly with radius of gyration (23), which makes it problematic for use in making comparisons across different structures and types of alignments. Additionally, the alignment algorithms report different scores as measures of similarity. To circumvent these limitations, structural similarity was assessed using a generic metric—fTM score (24). Significant correlation was observed between the fTM score and RMSD for both datasets (SI Appendix, Fig. S4).

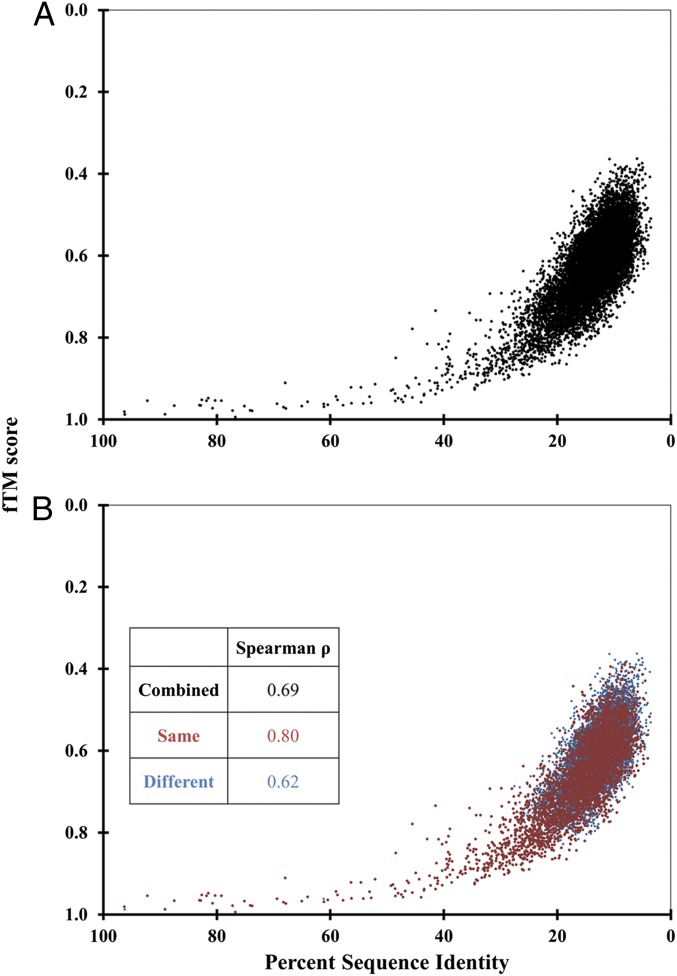
Initially, we analyzed the level of sequence divergence (percent sequence identity) and structure divergence (fTM score) in the core-domain-only dataset using Spearman’s Rank Correlation as it captures nonlinear trends and can tolerate outliers. A strong, statistically significant correlation was observed between percent sequence identity [the metric used by Chothia and Lesk in their studies (14)] and fTM score (Spearman ρ = 0.69, P value < 10⁻¹⁰) (Fig. 1A). Notably, the plot contains many sequences with high structure similarity despite low sequence identity. A qualitatively similar trend is observed using a less stringent measure to estimate sequence divergence—percent sequence similarity (SI Appendix, Fig. S5). The trend indicates that, in the case of the HADSF, the sequence diverges to a greater extent than does the structure. This deduction is consistent with the findings from earlier studies of single domain protein families (14–16).

Fig. 1.

Correlation between sequence identity and structural similarity in the HADSF core domain. Each point denotes one protein pair with percent sequence identity value plotted on the x axis and the fTM score plotted on the y axis. A shows data for the entire dataset (number of points = 11,781) whereas B shows the dataset split into core domains with the same cap type (red, number of points = 3,606) and core domains with different cap type (blue, number of points = 8,175). Inset shows Spearman’s rank correlation coefficient for the three individual sets.

To investigate the influence of the cap domains on the correlation between sequence identity and fTM score, computations were carried out using a dataset of core domains with (1) the same cap type and (2) different cap types. Remarkably, the relationship between the sequence divergence and the structure divergence does not depend on the type of the appended cap domain (Fig. 1B) and is invariant with respect to the choice of cap type (SI Appendix, Fig. S6). However, the correlation is marginally higher for core domains with the same cap type (Spearman ρ = 0.80, P value < 10⁻¹⁰) versus core domains with different cap types (Spearman ρ = 0.62, P value < 10⁻¹⁰). One might argue that the structures corresponding to different cap types represent different protein folds as the only commonality is the topology of the Rossmann fold. It has yet to be shown that the removal of the cap domain does not disrupt the Rossmann-fold architecture (which would argue against treating the two domains as one fold). Unexpectedly, the relationship between sequence and structure divergence in the common-core domain is largely independent of the significant evolutionary event of cap-domain insertion.

Core Domains with the Same Cap Type Have High Similarity.

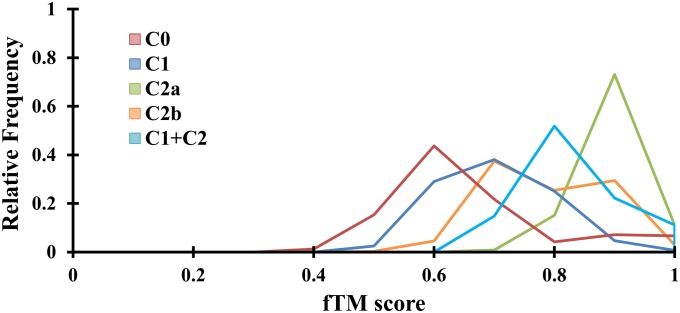
Although the difference in sequence–structure divergence between core domains with the same cap type and core domains with different cap types is only marginal, it is statistically significant. The distributions of sequence and structure similarity scores (sequence alignment is based on pairwise structure alignment) (Materials and Methods) between different core domains show that core domains with the same cap type (mean sequence identity = 16.3%, mean fTM score = 0.66) tend to have higher mean similarity than those with different cap type (mean sequence identity = 12.8%, mean fTM score = 0.60). Next, the distribution of the similarity scores of core domains was subdivided into each cap type to elucidate any underlying trend(s). The distributions (Fig. 2) show that core domains with minimal or no cap (cap type C0) have the lowest mean similarity (mean sequence identity = 15.5%, mean fTM score = 0.62) whereas core domains with the αβ cap type (cap type C2a) have the highest mean similarity (mean sequence identity = 29.9%, mean fTM score = 0.84). The differences in the means are statistically significant (Welch’s two-tailed P value < 10⁻¹⁰). Thus, the type of domain insert influences sequence and structure diversity in the core domain, and core domains freed from cap-domain influence (type C0) display the greatest divergence. The null hypothesis is that all Rossmann folds would be similar apart from stochastic thermal fluctuations and structural divergence. The unexpected finding is that they are not; the structural variation of the core domain is modulated by the appended cap domain.

Fig. 2.

Distribution of similarity scores for the HADSF core domain. The distribution of the fTM structure similarity scores (binned into 0.1-unit intervals) categorized by the cap type insert is shown.

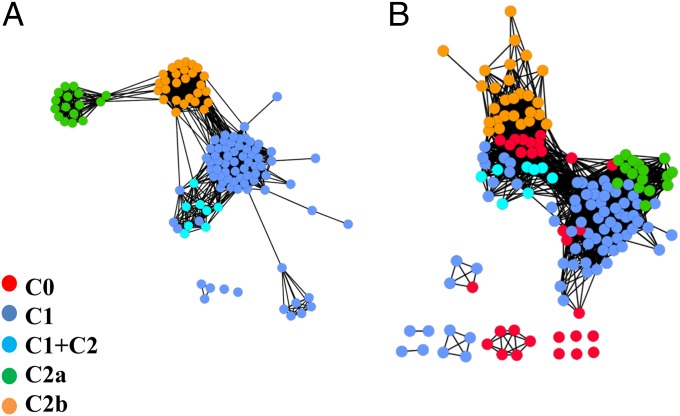
To describe the cap-domain-dependent core domain divergence, we generated structure-similarity networks for the core and cap domains independently (Fig. 3). Structure-similarity networks, graphs where nodes represent protein structures and edges represent structural similarity above a given threshold between the two structures, provide a global view of structure space. Such networks can be used to depict relationships relevant for probing the evolutionary history of protein-structure space (25, 26). In Fig. 3A, similar cap types cluster together (with few edges across cap-type clusters) as cap domains fall into distinct topological classes (as C0 members are the most diverse, they separate into a few clusters on the core domain network; however, examination shows these to be isofunctional proteins so there is no need for further division of the C0 structural class). Surprisingly, we observe distinct clustering in the core domain network based on the corresponding cap type (Fig. 3B). This observation, coupled with the difference in the similarity scores (Fig. 2), suggests that there is a fundamental structural difference between core domains associated with cap domains of a different type.

Fig. 3.

Structure similarity networks for the HADSF cap domain (A) and core domain (B). Each node represents a single protein structure and an edge is drawn if fTM score is higher than the thresholds of ≥0.3 (A) and ≥0.7 (B), respectively. The network shown in A does not contain C0 class members. Annotation information, including cap type (obtained from manual examination of the structures), was associated with each node. The network was visualized using Cytoscape version 2.8 (45) with the yFiles organic layout scheme.

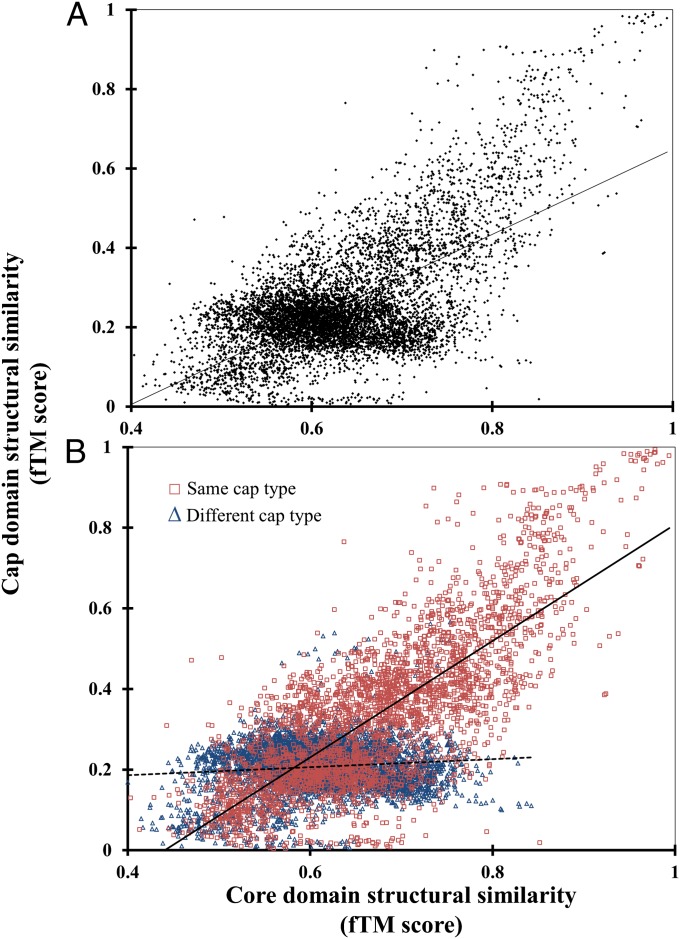
Next, we investigate whether the cap domain affects this cap-type-based core-domain classification. For each pair of proteins, the core domain structural similarity was plotted against the cap domain structural similarity (Fig. 4). Remarkably, a significant correlation between the two (Spearman ρ = 0.47, P value < 10⁻¹⁰) is observed, suggesting a coupling in structural divergence between the two domains (Fig. 4A). This linear relationship between cap and core domain structural similarities is unanticipated as they are spatially separate entities (i.e., the domains are connected by solvent accessible linkers) (SI Appendix, Fig. S1). Next, we recomputed the correlations for comparisons within the same cap type and comparisons across different cap-type classes (Fig. 4B). The correlation can be explained exclusively by the comparisons between core domains with similar cap types (Spearman ρ = 0.75, P value < 10⁻¹⁰). As different cap domains have significantly different topologies, their comparisons have negligible contribution to the overall correlation (Spearman ρ = -0.01, P value = 0.35) and serve as a negative control with all core pairs having a mean fTM score of ∼0.2.

Fig. 4.

Correlation between cap domain and core domain structural similarity. Each point represents a pair of proteins with the core domain fTM score along the x axis and cap domain fTM score along the y axis. (A) All of the pair-wise comparisons with the linear best-squares fit to data represented by the line. (B) The comparisons between core domains with the same type and core domains with different cap type in red and blue, respectively. The continuous line represents the linear best-squares fit to data for all comparisons with the same cap type, and the dotted represents line comparisons with different cap type.

Structural Diversity in the HADSF Has Small Intrinsic Dimensionality.

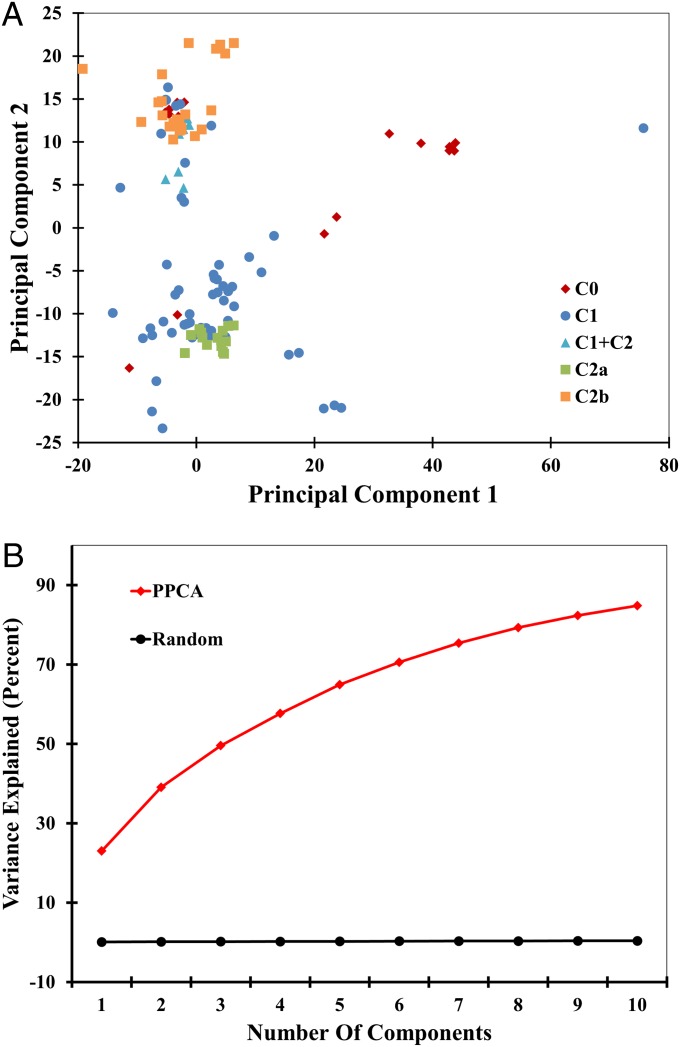
Our results suggested that the cap domain influences the sequence and structural variance of the core domain, but the structural basis of this influence was still unclear. Given the atomic structures determined by X-ray crystallography, the observed structural variance has ∼6,000 degrees of freedom (∼130 residues × 15 atoms per residue × 3 coordinates per atom). However, the number of “effective” degrees of freedom in the evolution of the HAD fold is significantly smaller because it is limited by constraints of secondary structure and packing that preserve the Rossmann fold. To find the most variable degrees of freedom, Probabilistic Principal Component Analysis (PPCA) was performed on all core domain structures (Materials and Methods). PPCA calculates a linear combination of components that describe a characteristic of the data (in this case the atomic positions), thus defining independent descriptors. To bypass any potential bias in this method from the sequence alignment, two different approaches, SALIGN (27, 28), and TM-align and Staccato (29), were used. Both methods yielded similar results (Fig. 5 and SI Appendix, Fig. S7); the results from SALIGN are discussed in detail.

Fig. 5.

Primary Components from Probabilistic Principal Component Analysis using SALIGN. (A) Core domain structural data projected onto Principal Component 1 (PC1) plotted against data projected onto Principal Component 2 (PC2). Core domains are colored according to corresponding cap type. (B) The plot of cumulative variance described by the principal components (red) and random (black).

In contrast to the large number of potential degrees of freedom, the PPCA analysis explains most structural variance with a relatively small number of principal components. Although, no single distinct number can be estimated given the smooth dependence of variance on the number of principal components (SI Appendix, Fig. S8): ∼50% of variance is explained by the first three principal components. Intuitively, as structural differences between core domains become subtler, it takes a greater number of eigenvectors to capture the structural variance. Thus, the plot of contribution of the principal components to structural variance is continuous. Plotting the first two principal components against one another reveals a cap-type-based classification, i.e., core domains with similar cap types cluster together (Fig. 5A). Quantitatively, points derived from core domains with different cap-type insertions are more distant (mean distance = 23.14 ± 0.2) than those from core domains with similar cap types (mean distance = 16.33 ± 0.32) in the coordinate system. The overall classification appears qualitatively similar to the structure similarity network in Fig. 3, showing similar clusters and intercluster connectivity. As a negative control, each of the other principal components was plotted against the first principal component, resulting in the disappearance of the trend (for a typical example, see SI Appendix, Fig. S9). The structural fluctuations we observe are nonstochastic as the variance is significantly greater than the random background (calculated by using unit vectors) where all principal components are needed to explain the entire variance (Fig. 5B).

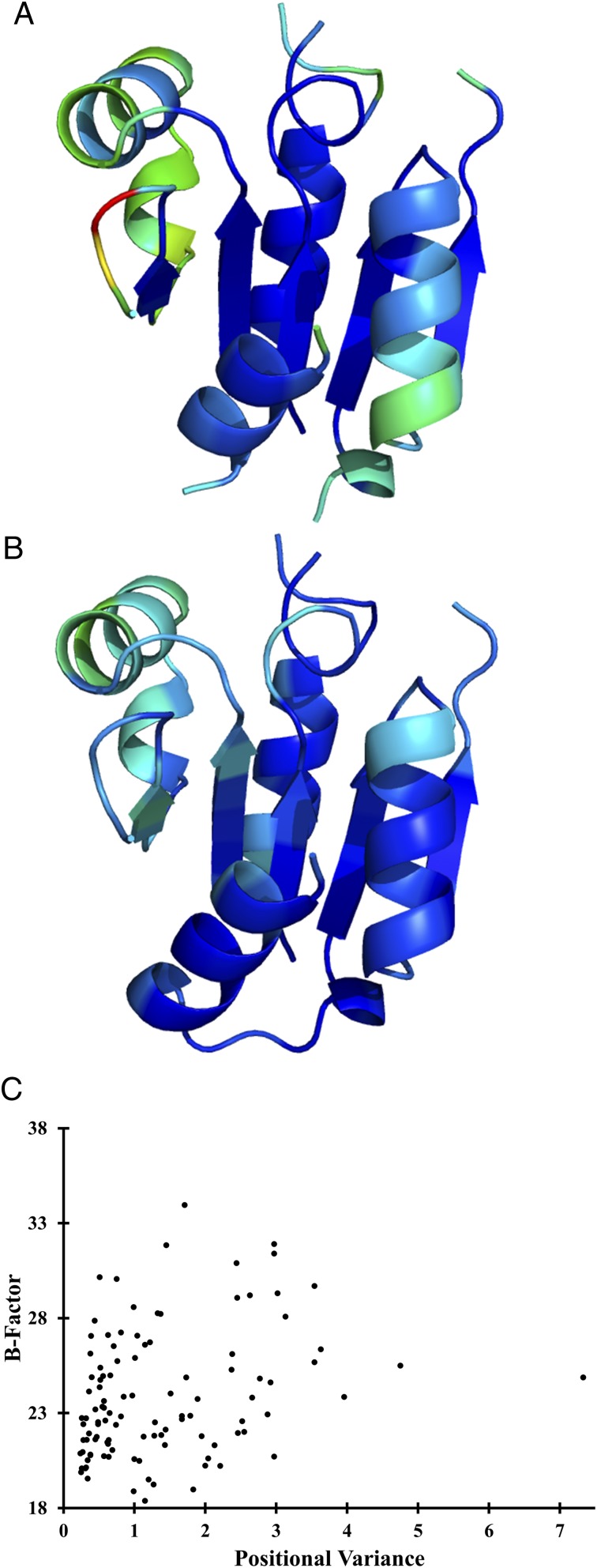
To analyze the structural variation, the positional variance of the C_α-coordinates from the multiple structure alignment was mapped onto a representative structure (PDB ID code 2HSZ) (Fig. 6A); this representative structure was chosen because it lies at the center of the structural similarity network [i.e., on average, it bears the highest structural similarity (fTM score) to all other structures]. The central β-sheet of the Rossmann fold exhibits the lowest structural variance whereas the α-helices flanking the sheet and connecting loops have a high degree of structural variance. Notably, the core face interacting with the cap domain is largely invariant. Moreover, the structural variation does not correlate with the dynamic or static disorder in the structure as there is no correlation between the observed positional variation and the atomic displacement parameters (B-factors) of the representative structure (Fig. 6 B and C). As the cap–core interface is critical for catalysis, we suggest that nonlocal interactions between the two domains control the structural variability. Thus, the interface has significantly less variation than the loops and flanking helices. This analysis suggests a global rearrangement of the Rossmann fold, akin to a “breathing motion,” correlated with the presence of different cap domains. These results are comparable to those obtained by PPCA (whereas SI Appendix, Fig. S10 considers only the first three principal components, the conclusions do not change when the first ten are included). In summary, these findings are indicative of a relatively small number of degrees of freedom in the structural variation of the Rossmann fold that dominate the plasticity of their respective structural classes; moreover, these degrees of freedom are dependent on the presence of different cap domains.

Fig. 6.

Visualizing structural variation in the Rossmann fold. A depicts positional variance of C_α coordinates from multiple structure alignment mapped onto representative core domain 2HSZ, chain A, whereas B depicts B-factors for the same structure. Structures are colored as a color ramp according to corresponding values, with blue denoting the lowest value and red the highest. C shows lack of correlation (Pearson R² = 0.09) between positional variance and B-factor for each residue position for 2HSZ, chain A. The typical HAD Rossmann fold consists of the central β-sheet [strand 1 (6–9), strand 2 (133–118), strand 3 (140–142), strand 4 (171–175), and strand 5 (211–213)] and flanking α-helices [helix 1 (100–110), helix 2 (122–132), helix 3 (154–161), and helix 4 (178–187).

Discussion

The explosion in the amount of sequence and structure information necessitates the development of reliable automated strategies to annotate protein function. However, the availability of these data has enabled large-scale investigation of protein sequence–structure–function relationships. Our approach provides a framework for deconstructing patterns in protein evolution in a systematic and quantitative manner. By using a large protein structure dataset, we have shown that (i) the sequence–structure relationship within the Rossmann superfold is robust toward the significant evolutionary event of domain insertion, (ii) the HADSF Rossmann fold is the product of interplay with the corresponding domain insertions, and (iii) the structural variation of the HADSF Rossmann fold is dominated by relatively few dimensions that are modulated by inserted domains and this variation does not map to the domain–domain interface. Although these relationships have been shown here for the HADSF, they may also occur for other folds.

The Rossmann fold can withstand significant sequence changes; i.e., as many as 90% of residues can change while still maintaining the same fold. For example, a representative pair of HADSF members with 10% sequence identity demonstrate RMSD value of ∼3.2 Å (fTM score ∼ 0.4). This tolerance implies that the fold is highly adaptable as major changes in sequence result in relatively moderate changes in structure, consistent with existing theories that suggest that superfolds can accommodate a significantly higher number of sequences than folds with a relatively small number of members (13). Aravind et al. (6) have proposed the concept of a positive feedback loop where duplication of superfamily members leads to gain of new functions and these new functional frontiers allow further biased selection of additional members from the same superfamily. Presumably, it is primarily due to this process that more than 79,000 HADSF members can currently be identified in the public sequence databases (17). It has been shown that few critical contacts are important to properly maintain a fold (30). Based on that model, we conclude that the interresidue contact network within the Rossmann fold is modular and extremely resilient to mutations. In fact, we have uncovered a much higher degree of permissiveness in the Rossmann fold than resilience to single point mutations as the sequence–structure relationship appears to be capable of withstanding a change as significant as a cap-domain insertion without the loss of secondary and tertiary structural characteristics (Fig. 1).

When the average structural similarity of core domains with no or minimal cap inserts is compared with that of core domains with large cap domains, the core domains without a significant cap domain (C0 cap type, <15 residues) tend to have a lower mean structural similarity and a greater variance. This finding can be rationalized by a biophysical argument. One can imagine the space of all allowable Rossmann fold structures as a “structure cloud.” During evolution, sequences are free to traverse the structure cloud. We propose that the addition of these cap domains imposes limits on this structure cloud. Because cap domains impose unique biophysical constraints on the divergence of the core domain, members with no or minimal cap inserts have the maximum structural diversity. A caveat to this hypothesis is that C0 members may arise by the loss of a cap from a C1 or C2 progenitor; however, such events are rarely observed as only one example has been identified thus far (31). Furthermore, these domain inserts may permit the core domain to traverse an extended, previously inaccessible sector of the structure cloud, thereby allowing unique modifications to the Rossmann fold.

One striking observation is that cap domains of different types tend to have core domains that are different from one another; structural similarities of the cap and core domains are linearly correlated. Two alternative models seem most plausible a priori. First, the linear trend may be a result of structural coevolution between the core and cap domains. When the core domain underwent structural divergence, the cap domain mutations that enhanced functional fitness might have been fixed and/or vice versa. Such fixation of compensatory mutations and structural rearrangements across both domains could allow for interdomain substrate binding and dynamics as well as facilitate catalysis. Second, as the core domains diverged, the cap domains may have diverged independently, also resulting in a correlation between the similarities of the cap and core domains.

Which of these scenarios is more likely? Importantly, Burroughs et al. (20) predicted that the last universal common ancestor (LUCA) had five distinct HAD members—a representative HADSF member from each cap subtype. Additionally, different cap types have evolved to catalyze the various types of chemistries, and, thus, they appear to be under similar selective constraints during evolution. For example, sugar phosphatase, sugar phosphomutase, and nucleotidase activities have been observed in the C1 and C2 cap types (32–37). In such a scenario, structural divergence of the core domain is expected to be similar across all cap types, in contrast to what is observed (SI Appendix, Fig. S11). As discussed earlier, cap type C0, which has a minimal insert, is the most divergent. We suggest that this greater divergence is due to the absence of a domain insert leading to relaxed evolutionary constraints on the core domain. Thus, we speculate that structural coevolution is a more plausible explanation for the observed trend in the HADSF than is the independent divergence. The data are most consistent with a model where a small cap domain was inserted into the core domain (pre-LUCA), followed by subsequent intradomain duplication and elaboration (consistent with the model in ref. 20).

It is of fundamental importance to study molecular evolution via analyzing protein structures to understand how they perform cellular function, how they are regulated, and how improved variants can be rationally designed. Unfortunately, clustering proteins using sequence and structure information is problematic, which makes functional annotation difficult and fraught with errors. In the case of HADSF, these errors in alignment and clustering are mainly due to extensive divergence further complicated by the location of the active site at the domain–domain interface. Our findings hint at protein design principles that might be useful in synthetic biology approaches. We find that protein folds undergo codependent evolution in the case of interacting domains where the sequence–structure diversity is modulated by the inserted domains. Notably, the variation is not located at the domain–domain interface. Thus, a more efficient conformational sampling scheme for improved modeling of multidomain protein structures and multiprotein complexes may be developed. Traditional directed evolution experiments have primarily tested amino acid residue substitution as the modification mechanism, without exploring the role of insertions and deletions. Recently, there has been considerable interest in using domain insertions to regulate protein activity (38). Our work suggests that superfolds are tolerant to relatively large domain insertions when followed by accommodating mutations in the scaffold. This structural robustness may facilitate the development of directed evolution technologies that incorporate domains into existing scaffolds.

Materials and Methods

Data Collection and Curation.

All of the HADSF structures in the Protein Data Bank (PDB) were filtered to yield a representative set of structures related to each other at less than 90% sequence identity according to program uclust (39) or corresponding to a unique UniProt ID (Dataset S1). Preference was given to structures determined at resolutions better than 3.6 Å and having chains with a minimal number of missing residues. For structures containing multiple chains, a single chain was chosen, with a preference for those chains with a minimal number of chain breaks. This set of criteria resulted in a collection of 154 HADSF structures. Subsequently, any additional domains not corresponding to the HADSF core or cap domain regions were removed. Resulting HADSF domains were manually divided into Rossmann-fold core and variable cap domains with the flexible linkers included with the core domains. The termini of the cap domain were judged to be those points where the secondary structural elements began and ended.

The large number of sequences (>79,000) and relatively small number of structures (>150) equates to an apparent coverage of ∼0.25% of the superfamily. However, we estimated the “true” structural coverage, using automated comparative modeling, creating comparative models for all superfamily members that are detectibly related to a known structure [deposited in ModBase (21)], and yielding models for ∼22% of the HADSF member sequences at a cutoff of 40% sequence identity and 90% target-template overlap. As the sequence space is highly redundant and the structure space has reasonable coverage, we posit that the experimental dataset provides a broad sampling of the sequence space with minimal bias due to any one subfamily (as assessed by mapping onto a sequence similarity network (40) (SI Appendix, Fig. S2)). It should be noted that only the experimentally determined coordinates were used in the dataset.

Structure Alignments and Similarity Networks.

The TM-align and SAP programs were used to perform all-by-all structural alignments of both the core and cap region structure sets. To facilitate comparison of scores between the different superposition methods, the fTM score was calculated for each structural superposition. Sequence-identity and sequence-similarity values were computed from sequence alignments (based on structural superpositions) by custom scripts. Structure-similarity networks were created for each domain (core and cap) and each superposition method (TM-align and SAP), using the fTM score as an edge weight.

Sequence-Similarity Networks.

All-versus-all BLAST e-value information was extracted from the Structure–Function Linkage Database (17) using an e-value cutoff of 10⁻²⁰. A representative sequence similarity network was constructed using Pythoscape (41), with mean e-value as edge weight. Each node represents a 40% ID cluster of sequences from CD-HIT (42).

Principal-Component Analysis.

Structure-based Multiple Sequence Alignment (MSA) was generated by the SALIGN (27, 28) module in MODELLER (excluding divergent structures; n = 131). Initially, we divided the structure set into two subsets, followed by aligning the sequences within the subsets using the iterative structure alignment option of SALIGN. We then combined the aligned subsets of sequences iteratively while restraining the alignment of several catalytic residues in the individual structures. Optimal 3D gap penalty parameters were determined by trial-and-error and used to create the final structural alignment. An alternate MSA was generated by combining all pairwise structure-based sequence alignments (made by TM-align) using Staccato (29).

The sequence alignments contained several gaps arising from variable loops and topological variations. A heuristic algorithm was applied to estimate the number of gaps in the alignment as a measure of number of columns included in the analysis. It resulted in a curve (SI Appendix, Fig. S12) that was used to select an appropriate cutoff for the number of columns (L = 132). Similar to Emberly et al. (43), all of the structures were realigned to the “center” structure (2HSZ, chain A). We created an N × 3L coordinate matrix, where each row represents individual structures and each column represents C_α-coordinates of the amino acid residues from the columns in the MSA. As the input matrix contained missing information corresponding to coordinates for gaps in the MSA, traditional principal-component analysis could not be used. Thus, Probabilistic Principal Component Analysis (PPCA) on the resulting coordinate matrix was performed using the PCAMV package (44) and custom scripts in MATLAB. Resulting eigenvectors were mapped onto the center structure using the sum of squares.

Statistical Analysis.

Statistical parameters, including Spearman rank correlation and two-tailed Welch’s t test, were computed using the statlib library in Python. Graphs were generated using Microsoft Excel and MATLAB.