Fractal spatial distribution of pancreatic islets in three dimensions: a self-avoiding growth model

Abstract

The islets of Langerhans, responsible for controlling blood glucose levels, are dispersed within the pancreas. A universal power law governing the fractal spatial distribution of islets in two-dimensional pancreatic sections has been reported. However, the fractal geometry in the actual three-dimensional pancreas volume, and the developmental process that gives rise to such a self-similar structure, have not been investigated. Here, we examined the three-dimensional spatial distribution of islets in intact mouse pancreata using optical projection tomography and found a power law with a fractal dimension, 2.1. Furthermore, based on two-dimensional pancreatic sections of human autopsies, we found that the distribution of human islets also follows a universal power law with fractal dimension 1.5 in adult pancreata, which agrees with the value previously reported in smaller mammalian pancreas sections. Finally, we developed a self-avoiding growth model for the development of the islet distribution and found that the fractal nature of the spatial islet distribution may be associated with the self-avoidance in the branching process of vascularization in the pancreas.

1. Introduction

Improving glucose homeostasis by regenerating insulin-secretion capability in diabetics is a major medical priority. Insulin is secreted by beta cells in the endocrine pancreas. Normal beta-cell function depends on the collective behavior of endocrine cells organized in islets of Langerhans. Thus, apart from the crucial question of increasing beta-cell mass, the process of formation and function of the islet distribution in a normal pancreas is of topical interest in light of rapid advances in bioengineering.

Fractal geometry of self-similar structures is observed in many organs such as lung, kidney, brain, and vasculature [1–5]. Such structures may originate from developmental processes using basic building rules repeatedly, as confirmed in lung formation [6]. A defining property of fractals is the scale independence of self-similar patterns. The space filling property is measured by the fractal dimension, a quantity that can take non-integer values. Methods for measuring fractal dimensions from biological images have been reviewed [7]. The fractal dimensions, D₂, measured usually from two-dimensional (2d) organ images, are 1.8 in the bronchial tree [1], 1.6 in the renal arterial tree [2], 1.5 in cerebral cortex [3], 1.3 in pial vasculature [4], and 1.7 in retinal vasculature [5]. In addition to organ structures, the spatial distributions of islets on pancreas sections have been reported to follow a fractal geometry with D₂ = 1.5 in guinea pigs [8] and also in dogs, pigs, goats, and cows [9].

These fractal dimensions were computed from 2d images of organs. Recent advances in imaging methods, however, have provided three-dimensional (3d) information, e.g., 3d fractal dimension of lung, D₃ = 2.3 – 2.5 [10]. In particular, optical projection tomography has provided 3d spatial distributions of islets in intact mouse pancreata [11]. In addition to such advances in imaging methods, the availability of computational resources has enabled practical advances in automated image analysis [12]. Applying these to human tissues has allowed the examination of the geometry of islet distributions in entire human pancreata, although the data obtained from large human organs is still limited to 2d sections [13]. In this study, we examine the spatial organization of islets in 3d mouse pancreata and 2d human pancreatic sections using data obtained with these advances.

It has been speculated that the fractal geometry of spatial islet distribution is associated with vascularization in the pancreas [8]. Here we explicitly examine this hypothesis with a self-avoiding growth model and show that the spatial fractal distribution of islets may result from self-avoidance in the branching process of vascularization.

2. Self-avoiding growth model

The model starts with a single node (islet) at a 3d position, y₁. At the next growth step, the node can generate (branch into) a new node at y₂ = y₁ + Δy where Δy is a random 3d vector with ∣Δy∣ < l. Here l is a distance scale obtainable from the mean distance between nearest islets in experiments. In the following step, every node including the mother and daughter nodes can generate new nodes. In the growth process, we introduce self-avoidance to inhibit close overlaps between nodes. A standard mechanism for the directionality of growth processes is the diffusion of special molecules such as chemo-attractants and chemo-repellents, e.g., in axon guidance [14]. Using the idea of chemo-repulsion, we assume that every node at y_i produces a chemo-repellent factor, which diffuses out from existing nodes and finally degrades. Given N nodes, the potential (concentration) of the chemo-repellents, φ(x, t), at position x at time t can be described by

$${\partial }_t\Phi =\sum _{i=1}^N\delta (\mathrm{x}-{\mathrm{y}}_i)+D{\partial }_{\mathrm{x}}^2\Phi -d\Phi$$ (1)

where D and d are diffusion and degradation constants. Since the diffusion and degradation are expected to occur much faster than the growth process, we consider a stationary state of the above equation and obtain a spatial gradient of the chemo-repellents. We can solve this differential equation by Fourier transform:

$$\Phi \left(\mathrm{k}\right)=\frac{1}{D{\mathrm{k}}^2+d}\sum _{i=1}^N{e}^{-ı\mathrm{k}\cdot {\mathrm{y}}_i}.$$ (2)

Finally, the inverse Fourier transform of φ(k) gives

$$\Phi \left(\mathrm{x}\right)=\sum _{i=1}^N\frac{\lambda }{\mid \mathrm{x}-{\mathrm{y}}_i\mid }{e}^{-\mid \mathrm{x}-{\mathrm{y}}_i\mid ∕\lambda },$$ (3)

where $\lambda =\sqrt{D∕d}$ is an effective distance of the chemo-repulsion from existing nodes. In this study, we set λ = l to match the effective distance as the mean minimal distance between islets. It is of interest that φ(x) has the form the Yukawa potential in particle physics. Therefore, a new node can be generated in a unit volume around a point, x, near the existing ith node (∣x – y_i∣ < λ) with the probability density,

$$P\left(\mathrm{x}\right)=\mathcal{A}{\Phi }^{-m}\left(\mathrm{x}\right),$$ (4)

that is assumed to be proportional to the inverse of the chemo-repellent gradient from existing nodes. The parameter, m, determines how strongly the chemo-repulsion affects the growth process with a corresponding normalization constant, $\mathcal{A}$. When no additional nodes exist near the ith node, the normalization constant is approximated as ${\mathcal{A}}^{-1}\left(m\right)\approx {\int }_0^1{r}^m{e}^{\mathit{mr}}\mathit{dr}$. However, depending on the exponent, m, a few nodes exist together within the effective distance, λ, from the ith node. For example, there are ten and five nodes on average within the effective distance for m = 0.5 and 3, respectively In practice, it is not necessary to compute the exact normalization constant, $\mathcal{A}$, which requires a heavy computation at every addition of new nodes. Instead, we use a practical normalization constant, ${\mathcal{A}}^{\prime }(<\mathcal{A})$, that equally reduces P(x) at every position, x. We have checked that the growth process is independent of the specific value of ${\mathcal{A}}^{\prime }$, if it is small enough (e.g., ${\mathcal{A}}^{\prime }=0.01\mathcal{A}$), while it must also be large enough not to reject every trial of node addition.

The practical algorithm for adding a new node to existing N nodes is as follows:

1. Calculate the chemo-repellent gradient, φ(x) in Eq. 3, generated by the existing N nodes;

2. Randomly select one node (e.g., the ith node) among the N nodes;

3. Randomly pick a coordinate near the ith node, x = y_i + δy, where y_i is the coordinate of the ith node and δy is a random 3d vector with ∣δy∣ < l;

4. Accept the addition of the new node with a probability, P(x) in Eq. 4;

5. Iterate these steps to add more nodes.

3. Results

3.1. Fractal spatial distribution of pancreatic islets

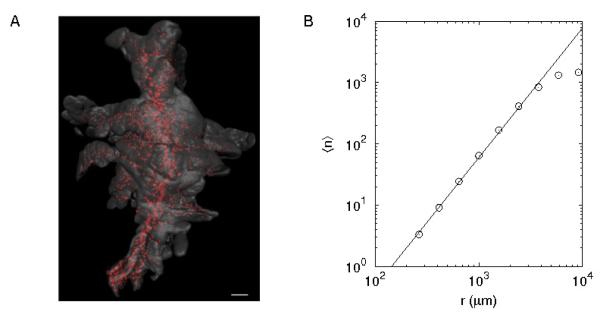
Optical Projection Tomography (OPT) imaging captured the 3d spatial distribution of the islets scattered in the exocrine tissue of the mouse pancreas (Fig. 1A). Based on the centroid coordinate of every islet, we calculated the average number ⟨n⟩ of neighboring islets within a distance r. This allowed to determine the correlation dimension D [15], a type of fractal dimension, from the relation (⟨n⟩ ∝ r^D). For example, when points are homogeneously distributed in a line, surface, and volume, their fractal dimensions become 1, 2, and 3, respectively, as expected in Euclidean space. The logarithmic plot of ⟨n⟩ versus r showed the expected power-law behavior in 3d (Fig. 1B), first observed in 2d pancreatic sections in guinea pigs with a fractal dimension, D_2S = 1.5 [8]. Independent on pancreatic lobes (splenic, duodenal, and gastric lobes), the 3d fractal dimension was D₃ = 2.1 (Table 1). Box-counting method gave a similar 3d fractal dimension, 2.03 ± 0.24 (P = 0.3).

Figure 1.

Spatial distribution of islets in the three-dimensional pancreas. (A) Optical Projection Tomography-based iso-surface reconstruction of a splenic lobe from a C57BL/6 pancreas at 8 weeks. The islets are reconstructed based on the signal from insulin-specific antibody staining (red) whereas the exocrine parenchyma is reconstructed based on the signal from endogenous tissue fluorescence (gray). Scale bar is 1 mm. (B) Average number ⟨n⟩ of islets within a distance r. The linear relation in their log-log plot represents a power law, and its slope (2.1) corresponds to the fractal dimension of the spatial islet distribution. Note that the finite size of pancreata gives a cut-off distance above which power-law behavior disappears. Therefore, we excluded data points at large separations if they changed the first decimal place of the fractal dimension (slope), the confidence interval in this study.

Table 1.

Fractal dimension of spatial islet distributions in mouse and human pancreata. Fractal dimensions of islet distributions in three-dimensional volume (D₃) and two-dimensional projection (D_2P ) and section (D_2S) of the pancreas were calculated based on islet centroid coordinates. N_total represents total number of islets in the pancreas volume, while N_section represents number of islets on the pancreas section. Mean ± s.d. (n samples)

Species	Age	n	Region	Ntotal	Nsection	D 3	D 2P	D 2S
Mousea (C57BL/6)	8 weeks	5	splenic	2036 ± 269	102 ± 18	2:06 ± 0:06	1:60 ± 0:03	1:28 ± 0:04
			duodenal	1672 ± 198	100 ± 13	2:09 ± 0:09	1:60 ± 0:05	1:27 ± 0:02
			gastric	778 ± 73	78 ± 17	2:13 ± 0:09	1:62 ± 0:03	1:37 ± 0:08
	all	15	-	-	-	2:10 ± 0:08	1:61 ± 0:04d	1:31 ± 0:07e
Mouseb (MIP-GFP)	1 day	8	whole	1204 ± 250	-	-	1:57 ± 0:04	-
	3 weeks	3	whole	3335 ± 709	-	-	1:54 ± 0:04	-
	all	11	-	-	-	-	1:56 ± 0:04d	-
Humanc	50 ± 20 years	14	whole	-	370 ± 156	-	-	1:53 ± 0:07e

^aPancreata from female mice were isolated, stained for insulin, and subjected to Optical Projection Tomography as described in our previous study [24]. The 3d islet centroid coordinates were extracted using the Imaris software. For the estimation of 2d projection and section fractal dimensions, the projection plane was selected by rotating the pancreas in 3d to maximize the averaging distance between islets on the projected plane, and the section plane along with the given projection plane was selected to include maximal number of islets within a section depth of 100 μm.

^bPancreata were excised from MIP-GFP mice in which beta cells are genetically tagged with green fluorescent protein under the control of mouse insulin 1 promoter [36]. Fixed and cleared pancreata were then be placed between slide glass and cover slip. To capture entire islets including those that are not in perfect focus, epifluorescent configuration with the uncertainty of Z depth was used with confocal microscope. The islet centroid coordinates were extracted using the ImageJ software. Detailed methods are described in our previous study [37].

^cAutomated image analysis were used to examine centroid coordinates of islets on pancreatic sections from human autopsies [13].

^dThe fractal dimension of projection D_2P showed no significant difference between C57BL/6 and MIP-GFP mice.

^eThe fractal dimension of sections D_2S showed a significant difference between C57BL/6 mice and humans (P < 0.01).

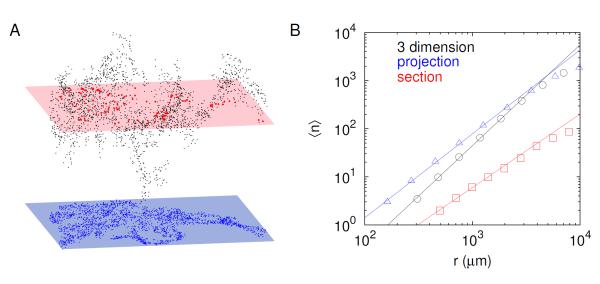
The spatial islet distribution information in the pancreas is usually extracted from 2d pancreatic sections, especially for large animals including humans. To examine the method dependence, we compared islet distributions in 3d, 2d projection, and 2d sections of the full 3d data (Fig. 2A). Note that random sections of the non-symmetric 3d structure in Fig. 1A could result in large variations in the fractal dimension measurement. Therefore, we consistently chose the unique 2d projection plane and section that maximize average distances between islets and number of islets within the section, respectively, by rotating the 3d pancreas. Although all three methods gave power-law behaviors in the spatial distribution, they had different fractal dimensions (Fig. 2B and Table 1). The 3d fractal dimension has been extrapolated as D₃ = D_2S+1 by adding a unit co-dimension based on the fractal dimension D_2S measured on the 2d pancreatic section [8]. Our direct observation demonstrated that D₃ was different from D_2S + 1 (P < 0.01), suggesting that islet distributions are not symmetric in space. This was obvious in the 3d OPT image (Fig. 1A).

Figure 2.

Fractal dimensions depending on organ preparations. (A) Spatial distribution of islets in a splenic lobe of 3d pancreas (3 dimension, black), 2d pancreatic section (section, red), and with uncertain Z values (projection, blue) in an eight-week C57BL/6 mouse. (B) Average number ⟨n⟩ of islets within a distance r for the three preparations: slopes, fractal dimensions, in the log-log plots are 2.1 (3 dimension), 1.6 (projection), and 1.3 (section).

We also examined islet distributions in intact mouse pancreas with uncertainty in Z depth, which corresponds to 2d projection. The fractal dimension did not change with age (Table 1), which is consistent with the age independence found in guinea pigs [9].

Furthermore, the recent availability of human tissues allowed us to examine the spatial islet distribution in human autopsies [13]. We analyzed the fractal dimension with pancreatic sections from adult pancreata. They also followed the power law with a fractal dimension, D_2S = 1.53 ± 0.07 (Table 1), which is very close to 1.5 as reported for other smaller mammals [9]. Note that a relatively smaller animal, mouse, showed a significantly smaller fractal dimension, D_2S = 1.3 (Table 1). In our model, this corresponds to a smaller value of m.

3.2. The emergence of fractal geometry

Pancreatic islets are co-localized with pancreatic ducts [16] and blood vessels [17] in the pancreas. Thus it has been speculated that the fractal geometry of spatial islet distributions is associated with the vascular structure of pancreatic ducts [8, 18]. In pancreatic development, primitive endodermal epithelium differentiates into pancreatic duct, endocrine, and exocrine cells [19]. Note the clusters of endocrine cells finally form islets. Blood vessels play a critical role for the organ development by not only providing oxygen and nutrients but also providing inductive signals for endocrine cell differentiation [20]. On the other hand, endocrine cells produce vascular endothelial growth factor, which attracts endothelial cells of blood vessels. Therefore, the organogenesis of endocrine pancreas results from the mutual interaction between the endocrine cells and blood vessels. Surprisingly, however, Magenheim et al. has recently reported that blood vessels reduce branching and differentiation of epithelial cells [21]. The dual effect of inducing and inhibiting endocrine cell differentiation by blood vessels may lead to a self-avoiding formation of islets in the pancreas.

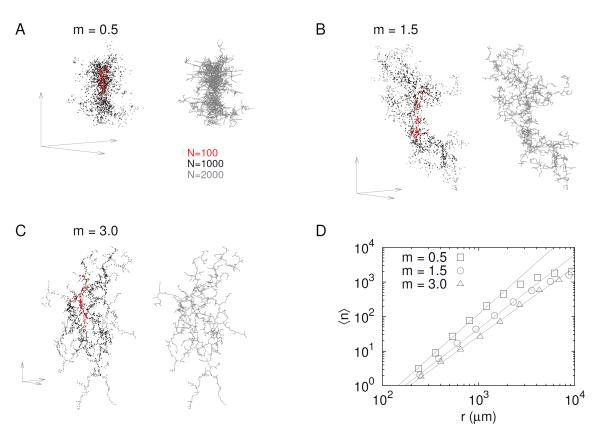
Here we developed an organ growth model considering self-avoidance. The model focused on islet formation without introducing epithelium and blood vessels explicitly. Thus islets, represented as nodes in space, were assumed to produce a chemo-repellent potential, φ, to implicitly incorporate the self-avoiding effect resulting from the mutual interaction between islets and blood vessels. In the model, new islets (nodes) were generated from existing nodes with a probability, P ∝ φ^−m. The parameter, m, controls the degree of self-avoidance. For example, vanishing m amounts to neglecting self-avoidance, while large m limits growth to locations furthest from the existing nodes. Figure 3 showed examples of the self-avoiding growth with various values of m. With a negligible self-avoidance (m = 0.5; Fig. 3A), nodes were densely distributed with a high fractal dimension (D₃ = 2.74 ± 0.04). On the other hand, with a relatively strong self-avoidance (m = 3; Fig. 3C), nodes were sparsely distributed with a small fractal dimension (D₃ = 1.88 ± 0.05). Finally, the self-avoiding growth model with m = 1.5 could produce a node distribution pattern resembling the islet distribution in the pancreas (Fig. 3B). The fractal dimensions of 3d, 2d projection and 2d section of the model were consistent with the fractal dimensions of islet distributions, when the node number is truncated to 2000 as the total islet number in adult mice (Tables 1 and 2). The self-avoiding growth model could generate node distributions with distinct fractal dimensions (Fig. 3D and Table 2). Note that during the growth process with a fixed m, the fractal dimension generally increased until node number became large enough to make finite size effects negligible (Table 2).

Figure 3.

Self-avoiding growth model. In the growth process, new nodes (points) are added with lower probability proximal to existing nodes. Suppose that existing nodes produce a chmo-repellent potential, φ(x) (see text for details). Then, the probability for generating a new node at a position, x, is inversely proportional to the potential, P(x) ∝ φ^−m(x). The exponent, m, determines how strongly the chemo-repulsion affects the growth process: (A) negligible (m = 0.5), (B) medium (m = 1.5), and (C) large (m = 3.0) effects of self-avoidance. The evolution of the growth process is represented by color dots: 100 (red), 1000 (black), and 2000 (gray) nodes added. Axis arrows at every left bottom represent the same scale for the three models. In addition, the right panel for every model displays a skeletal view where neighboring dots are connected by gray lines. (D) Average number ⟨n⟩ of islets within a distance r for the three models: slopes, fractal dimensions, in the log-log plots are 2.5 (m = 0.5), 2.1 (m = 1.5), and 1.9 (m = 3.0).

Table 2.

Fractal dimensions in the self-avoiding growth model. The degree of self-avoidance produced different fractal structures. Larger m produces stronger self-avoidance. The model had finite size effects on the fractal dimension. As the model with m = 1.5 grows from 1000 to 5000 nodes, its fractal dimensions of 3d, 2d projection and section approach to equilibrium. Mean ± s.d. (n = 10)

m	Ntotal	Nsection	D 3	D 2P	D 2S
0.5	2000	134±17	2.47±0.04	1.73±0.02	1.45±0.10
1.0	2000	110±8	2.21±0.05	1.64±0.04	1.29±0.09
1.5	2000	87±12	2.06±0.04	1.60±0.07	1.22±0.08
2.0	2000	84±12	2.00±0.05	1.59±0.07	1.14±0.08
3.0	2000	86±11	1.88±0.05	1.57±0.05	1.11±0.08
1.5	1000	64±7	2.01±0.06	1.55±0.07	1.20±0.09
1.5	2000	87±12	2.06±0.04	1.60±0.07	1.22±0.08
1.5	3000	117±14	2.11±0.04	1.65±0.06	1.25±0.08
1.5	4000	135±21	2.15±0.04	1.67±0.05	1.26±0.06
1.5	5000	159±27	2.18±0.03	1.69±0.05	1.27±0.07

4. Discussion

A universal power law in the spatial distributions of pancreatic islets has been reported in guinea pigs, dogs, pigs, goats, and cows with a fractal dimension, D_2S = 1.5, measured in 2d pancreatic sections. In this study, we demonstrated that humans also followed the universal power law with the same fractal dimension. Furthermore, with the advanced imaging method, OPT, we found the fractal dimension in 3d pancreas as D₃ = 2.1 in mice. Note that the null hypothesis, D₃ = 2 (surface in Euclidean space), was rejected (P < 0.001).

The pancreas has distinct developmental origins of the dorsal (splenic) and ventral (duodenal) pancreas, which later fuse [22]. The gastric lobe is formed by perpendicular growth from the dorsal pancreas a few days after its formation [23]. Our recent study has shown regional differences in the pancreas that the gastric lobe has a higher relative number of islets (i.e., islets/mm³ of pancreatic tissue) than splenic and duodenal lobes [24]. However, we found indistinguishable fractal dimensions of spatial islet distributions in all three lobes of the pancreas, although the higher islet density in the gastric lobe was reflected as a slightly higher fractal dimension that was not statistically significant. This suggests that three regions may be governed by the same developmental rule.

The fractal dimension in 3d pancreas has been extrapolated as D₃ = 2.5 by adding a unit co-dimension to the 2d section fractal dimension, D_2S = 1.5, under the assumption of symmetric islet distributions in space [8]. Because the diffusion-limited aggregation (DLA) in 3d generates a tree-like structure with the fractal dimension, D₃ = 2.4 [25], DLA has been proposed as the underlying mechanism of the spatial distribution of pancreatic islets [18]. However, our direct measurement of the 3d fractal dimension, D₃ = 2.1, was clearly different from D₃ = 2.4 of DLA. Furthermore, endocrine cells are continuously nucleated from the source of endodermal epithelium during the pancreatic development. Therefore, the organ expansion is fundamentally different from DLA in which particles scattered in a large volume aggregate to the center of a cluster [26]. The self-avoiding growth model, however, captured the organ expansion process. The DLA-like branching pattern has also been described by a neurite growth model attracted (not avoided) by chemical gradients [27]. Our model also explained the symmetry breaking, D₃ ≠ D_2S + 1, because the self-avoiding growth prefers to grow in directions as orthogonal as possible to the locations of proximal existing nodes. When the self-avoiding effect becomes negligible (smaller m), spatial symmetry is restored.

The model with m = 1.5 could reproduce similar 3d, 2d projection and 2d section fractal dimensions of spatial islet distributions in mice, considering the uncertainty of measurement. In particular, the uncertainty in 2d section is considerable because the fractal dimension of 2d section depended greatly on the position and orientation of the section plane in the pancreas volume. In general, smaller animals had smaller fractal dimensions (D_2S) in the spatial islet distributions: mice (1.31 ± 0.07), rats (1.42 ± 0.04) [9], and humans (1.53 ± 0.07). To reproduce spatial islet distributions in larger animals including humans, the same model with smaller m (weaker self-avoiding effect) could recreate a larger fractal dimension in the larger pancreas with more islets. This growth algorithm can be generally applicable to generate self-similar structures such as vasculature with flexible fractal dimensions.

The inter-species differences of lung airway structures have been carefully examined by considering a multiplicity of scales [28]. Outer scales, and in more generality, the question of multifractal scaling would indeed be an interesting explanation for the islet data in different species. However, our theoretical attempts were limited by the amount of data we had available. The species difference can be simply understood in terms of self-avoidance, if we accept that different species can have different strengths of self-avoidance in the islet development. Our data is limited to just center coordinates of islets, unlike the lung data with specific branch lengths and diameters. Nevertheless, multi-fractal scaling might lead to a model without self-avoidance that might apply to all species.

Node generation and self-avoidance in the phenomenological model could reflect the dual roles of blood vessels for inducing and inhibiting endocrine cell differentiation. Nevertheless, this model gives little insight into the specific mechanisms of self-avoidance. In addition, the model did not generate conserved fractal dimension during its evolution. Ignoring measurement uncertainty, the fractal dimension does not change with age in guinea pigs [9], and also in mice shown in this study. During the evolution of the model, however, the fractal dimension slightly increased until node number became large enough to overcome finite size effects.

The self-avoidance of islet formation may play a role for producing islets with optimal sizes. Endocrine cells tend to aggregate in embryonic development [29] and even in vitro culture [30]. Continuous generation of proximal cells, therefore, could lead to a gigantic cluster of cells. Constraints on endocrine cell differentiation by blood vessels [21] may inhibit the formation of large aggregates of cells and help to generate optimal sizes of islets evenly distributed throughout the pancreas. The functional importance of islet sizes has been emphasized [31–35]. As progress is made in both tissue scaffold engineering and the induction of desired lineage characteristics in induced pluripotent stem cells, the geometry of how functional replacement organs might be best engineered becomes important. As such, our growth model provides a simple characterization of how to grow finite samples with the desired geometric properties for optimal function of pancreatic islets.