On the Controversy About the Sharpness of Human Cochlear Tuning

Abstract

In signal processing terms, the operation of the mammalian cochlea in the inner ear may be likened to a bank of filters. Based on otoacoustic emission evidence, it has been recently claimed that cochlear tuning is sharper for human than for other mammals. The claim was corroborated with a behavioral method that involves the masking of pure tones with forward notched noises (NN). Using this method, it has been further claimed that human cochlear tuning is sharper than suggested by earlier behavioral studies. These claims are controversial. Here, we contribute to the controversy by theoretically assessing the accuracy of the NN method at inferring the bandwidth (BW) of nonlinear cochlear filters. Behavioral forward masking was mimicked using a computer model of the squared basilar membrane response followed by a temporal integrator. Isoresponse and isolevel versions of the forward masking NN method were applied to infer the already known BW of the cochlear filter used in the model. We show that isolevel methods were overall more accurate than isoresponse methods. We also show that BWs for NNs and sinusoids equate only for isolevel methods and when the levels of the two stimuli are appropriately scaled. Lastly, we show that the inferred BW depends on the method version (isolevel BW was twice as broad as isoresponse BW at 40 dB SPL) and on the stimulus level (isoresponse and isolevel BW decreased and increased, respectively, with increasing level over the level range where cochlear responses went from linear to compressive). We suggest that the latter may contribute to explaining the reported differences in cochlear tuning across behavioral studies and species. We further suggest that given the well-established nonlinear nature of cochlear responses, even greater care must be exercised when using a single BW value to describe and compare cochlear tuning.

Introduction

Our limited ability to separately perceive the frequency components of a complex sound is a fundamental property of human auditory perception. This property, termed auditory frequency selectivity, may be explained by likening the operation of the auditory system to that of a bank of overlapping sound filters (Fletcher 1940). Much effort has been spent on designing accurate methods to characterize the shape and tuning of these filters, and the results have guided the design of a multitude of applications, including artificial speech recognizers (Brown et al. 2010), computer models of loudness perception (Moore and Glasberg 2004) and cochlear signal processing (Zhang et al. 2001; Sumner et al. 2002), sound processors for auditory prostheses (Wilson et al. 2005), or bit-rate sound compression algorithms (Painter and Spanias 2000). The physiological origin of perceptual auditory filters is thought to be in the frequency selectivity of cochlear responses, in the inner ear (Evans 2001; Shera et al. 2002).

The shape and tuning of perceptual auditory filters have been typically characterized using auditory masking techniques (Moore 2012). Methods have been optimized over the years to overcome confounding factors in an attempt to obtain closer estimates to the tuning of physiological cochlear filters. A favored approach consists of measuring the detection of fixed, low-level, sinusoidal probe tones in the presence of a preceding notched noise masker (Shera et al. 2002; Oxenham and Shera 2003). The use of notched noise maskers minimizes off-frequency listening (Patterson 1976; Patterson and Nimmo-Smith 1980); the use of forward maskers minimizes the risk of results being affected by cochlear suppression (Heinz et al. 2002); the use of a fixed-level probe provides isoresponse tuning estimates conceptually similar to neural tuning curves; and the use of low level (“near threshold”) probe tones is thought to facilitate the comparison between behavioral tuning and threshold neural tuning curves (Oxenham and Shera 2003). Results obtained with this method suggest that human cochlear filters are much more sharply tuned than suggested by earlier masking studies (Oxenham and Shera 2003). Furthermore, they also suggest that human cochlear filters are more sharply tuned than those of other mammals (Shera et al. 2002). If confirmed, these results could have important scientific, technological, and clinical implications. The result, however, is controversial (Ruggero and Temchin 2005; Shera et al. 2010; Eustaquio-Martin and Lopez-Poveda 2011; Joris et al. 2011).

A basic assumption of the notched noise method is that auditory filters operate linearly over the range of sound levels involved in the measurements. This assumption has been long disputed on the grounds that auditory masking is a nonlinear phenomenon and that behavioral tuning estimates obtained using fixed-level maskers (isolevel approach) differ from those obtained using fixed-level probes (isoresponse approach) (Vogten 1974, 1978; Verschuure 1980, 1981). Indeed, there has been some controversy about which of the two approaches, isolevel or isoresponse, provides more accurate tuning estimates (Baker et al. 1998; Rosen et al. 1998; Glasberg and Moore 2000; Baker and Rosen 2006). More recently, we have questioned the linearity assumption specifically for the favored forward masking notched noise method (Eustaquio-Martin and Lopez-Poveda 2011). We showed that the original method, which rightly involved fixed-level probes (isoresponse approach) to facilitate comparisons with neural tuning curves, and an alternative version, where the masker level is fixed (isolevel approach), yield different tuning estimates due to peripheral compression on the notched noise maskers. This adds to the abovementioned controversy about the exceptional sharpness of human cochlear tuning and raises two fundamental questions: (1) How accurate is the forward masking notched noise method at characterizing nonlinear (compressive) cochlear filters?, and (2) Which of the two versions of the method, isoresponse or isolevel, provides more accurate estimates of cochlear tuning across levels?

The present study addresses these two questions using a computer model of forward masking (Plack et al. 2002) that includes a well-accepted model of nonlinear cochlear frequency selectivity (Meddis et al. 2001). Isoresponse and isolevel versions of the notched noise method are then applied to the forward masking model, and the power spectrum model of masking (Patterson 1976) is used to infer the already known shape of the cochlear filter used in the model. An accurate behavioral method should provide a close estimate of this cochlear filter. Heinz et al. (2002) used a similar approach to assess the accuracy of the isolevel notched noise method in simultaneous masking.

Methods

Isoresponse vs. isolevel procedures

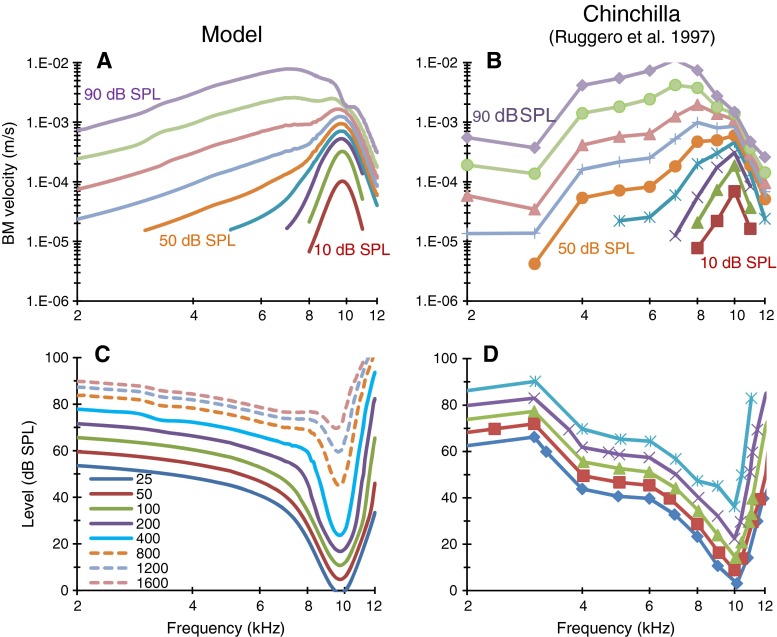
The tuning of a filter may be described based on its response amplitude to fixed-level input sinusoids of varying frequency. The resulting curve is known as the filter shape, frequency response, or isolevel curve of the filter. An alternative description consists of representing the input level required for sinusoids of varying frequency to maintain a fixed output level. The resulting curve is referred to as an isoresponse or tuning curve. Example isolevel and isoresponse curves for actual and modeled basilar membrane (BM) responses are shown in Fig. 1.

FIG. 1.

Left, Actual tuning characteristics of the BM model. A Isolevel curves for pure tones from 10 to 90 dB SPL in 10-dB steps. C Isoresponse (tuning) curves for different BM velocity criteria from 25 to 1,600 μm/s (see legend). Right, Tuning characteristics of the chinchilla BM (case L113 in Ruggero et al. 1997). Note that these data were used to produce the BM model shown on the left panels (Meddis et al. 2001). Matching colors are used to illustrate corresponding model (left panels) and experimental responses (right panels). The tuning curves illustrated by dashed lines in c do not have corresponding experimental curves in D.

The forward masking notched noise method of Shera et al. (2002) consisted of measuring the masker level at the detection threshold of a fixed-level probe for different notch widths. In this case, the threshold masker level is assumed to depend on the relative excitation produced by the masker and probe at the BM place activated by the probe. Because the probe is fixed both in level and frequency, all maskers with different notch widths are assumed to produce an identical excitation on that place. For this reason, the resulting functions are thought of as isoresponse curves. This is the approach typically used to measure auditory nerve tuning curves. Isoresponse bandwidth estimates for different response criteria may be obtained by using different probe levels (Oxenham and Simonson 2006) or different masker–probe time gaps (Eustaquio-Martin and Lopez-Poveda 2011).

In a previous study, we argued that isoresponse masker levels increase with increasing notch width not only as a result of frequency selectivity but also as a result of cochlear compression on the masker (Eustaquio-Martin and Lopez-Poveda 2011). We provided an alternative method to assess cochlear frequency selectivity without the concomitant effects of cochlear compression on the masker. The method consisted of using a fixed-level masker and a fixed-level probe and measuring the masker–probe time gap at the detection threshold of the probe. As in the isoresponse method, in this method, it is also assumed that masking threshold depends on the relative excitation of the masker and probe at the BM place activated by the probe. The excitation of the fixed-level masker increases with decreasing notch width and so longer gaps will be required to just mask the fixed-level probe. Therefore, gap threshold is proportional to the excitation produced by the fixed-level masker at the BM activated by the probe. On the other hand, gap thresholds will be inherently affected by the post-mechanical (or post-compression) rate of recovery from forward masking. We argued that the latter may be accounted for by transforming gap thresholds into BM output levels (in arbitrary decibel units) using a linear reference temporal masking curve; that is, a curve describing the level required for a masker that is processed linearly by the BM to just mask the fixed-level probe as a function of the masker–probe time gap. For more details, see Eustaquio-Martin and Lopez-Poveda (2011).

Here, we assess the accuracy of the bandwidth estimates produced by isolevel and isoresponse forward masking notched noise methods.

Mimicking forward masking with a computer model

An existing phenomenological model of forward masking was used to mimic performance in a notched noise forward masking experiment (Plack et al. 2002). In this model, forward masking is assumed to arise from the persistence of neural activity produced by the masker (Oxenham 2001). The model consisted of a cascade of a linear FIR filter that mimicked the outer–middle transfer function, followed by a dual-resonance nonlinear (DRNL) filter that mimicked the BM response at a particular cochlear site, followed by a square-law rectifier, followed by an exponentially-weighted temporal integrator (or temporal window) that mimicked the persistence of neural activity produced by the masker, followed by a decision device. The parameters of the outer–middle ear and DRNL filters were set to published values optimized to simulate the frequency response of the chinchilla BM for a cochlear site with a characteristic frequency (CF) of ~9.6 kHz (Meddis et al. 2001). The parameters of the temporal window were set to published values optimized to account for human temporal integration in forward masking [Fit 1 set in Table 1 of Oxenham (2001)]. Masked threshold was assumed to occur when the ratio of the model output for the masker plus probe (O_M+P) to the masker alone (O_M) just exceeded a constant value K (Plack et al. 2002). Two different values of K were used here (2.5 and 10 dB) to assess tuning over a wider range of levels. The model was implemented and evaluated digitally in Matlab using a sampling frequency of 100,000 Hz.

The absolute detection threshold for a probe tone at the CF was assumed to occur near neural threshold and there is evidence that neural threshold tuning curves most closely approximate the 5 × 10⁻⁵ m/s isovelocity BM tuning curve (p. 2157 in Ruggero et al. 1997). Therefore, absolute detection for a probe tone at the CF was assumed equal to the level at which the modeled BM response was 5 × 10⁻⁵ m/s. As a result, absolute threshold was equal to 4.7 dB SPL.

Stimuli

The probe was a sinusoid with a frequency (f_P) equal to the CF of the simulated BM response (9,760 Hz). Probe and masker durations were 10 and 200 ms, respectively, including 5-ms onset and offset cosine-squared ramps (i.e., the probe had no steady state). The masker–probe time gap was defined from masker offset to probe onset. Maskers consisted of two bands of Gaussian noise below and above the f_P, each with a bandwidth of 0.25f_P. The notch was defined as the normalized deviation of the closer edge of each noise, ∆f, from the probe frequency, i.e., ∆f/f_P. The accuracy of the isoresponse and isolevel methods was evaluated for typical and ideal application conditions, as defined by the number of placements of the two noise bands around f_P. To assess isoresponse methods in typical conditions, we used eight symmetric notches with normalized deviations of 0, 0.025, 0.05, 0.1, 0.15, 0.2, 0.3, and 0.4, plus four asymmetric notches with normalized deviations of the upper–lower noise bands of 0.1–0.3, 0.2–0.4, 0.3–0.1, and 0.4–0.2, respectively. These conditions are comparable to those used in earlier relevant studies (e.g., Oxenham and Shera 2003; Oxenham and Simonson 2006; Eustaquio-Martin and Lopez-Poveda 2011). To assess isoresponse methods in ideal conditions, we used the same eight symmetrical notch placements as for typical conditions plus 48 asymmetrical notch placements. The latter were placed so that for each of the eight deviations of the lower (or upper) noise band used in the symmetric case, the normalized deviation of the upper (or lower) noise band was equal to the symmetric deviation plus 0.05, plus 0.1, and plus 0.2. For example, for a symmetric normalized deviation of 0.025, six asymmetric notches were used with normalized deviations of the upper–lower noise bands of 0.075–0.025, 0.125–0.025, 0.225–0.025, 0.025–0.075, 0.025–0.125, and 0.025–0.225.

The accuracy of isolevel methods could not be assessed using identical notch widths as were used for isoresponse methods because the range of notch widths that may be used depends on the actual number of masker–probe time gaps that may be measured (e.g., wide notches would sometimes require immeasurably narrow gaps, particularly for low masker levels). Instead, notch widths were set using the data in Fig. 7D of Eustaquio-Martin and Lopez-Poveda (2011) as a guide. In typical conditions, we used ten symmetric notches with normalized deviations uniformly distributed within the ranges 0–0.1 for masker levels of 40, 50, and 60 dB SPL and 0–0.2 for a maker level of 70 dB SPL; we did not use asymmetrical notches. In ideal conditions, we used the same ten symmetrical notch placements as for the typical condition plus 60 asymmetrical notch placements. The latter were placed so that for each of the ten normalized deviations of the lower (or upper) noise band used in the symmetric case, the normalized deviation of the upper (or lower) noise band was equal to the deviation in question plus 0.01, plus 0.03, and plus 0.05 (masker levels from 40 to 60 dB SPL) or plus 0.02, plus 0.6, and plus 0.12 for a masker level of 70 dB SPL. It will be shown, however, that the isolevel method was roughly as accurate in ideal as in typical conditions and so that including asymmetric conditions hardly improved accuracy.

Procedure

The notched noise method was applied in two isoresponse and one isolevel conditions. In the isoresponse conditions, the masker level at the detection threshold of a fixed-level probe was measured for different notch widths. In one of the two conditions, the masker–probe gap was set at 2 ms and different probe levels were used to infer filter shape and tuning over a wide range of responses (Oxenham and Simonson 2006). Probe level ranged from 9 to 24 dB of sensation level (SL; dB above the absolute threshold for the probe) in 5-dB steps. In the second isoresponse condition, the probe level was set at 9 dB SL and different masker–probe gaps were used to infer filter shapes and tuning over a wide range of responses (Eustaquio-Martin and Lopez-Poveda 2011). Masker–probe gaps of 2, 10, 30, 50, and 70 ms were used. Masker levels at the masked detection threshold of the probe were calculated using a one-up, one-down adaptive procedure. The initial masker level was set well below threshold. Masker level was then altered in 6-dB steps until two reversals occurred and in 2-dB steps thereafter. A total of eight reversals were obtained for each run. Threshold was calculated as the mean masker level of the last four reversals in a run. Ten threshold estimates were obtained per condition and their mean was taken as the masker level at threshold. See Eustaquio-Martin and Lopez-Poveda (2011) for further details.

In the isolevel condition, the masker and the probe levels were fixed, and the gap at masked probe threshold was measured for different notch widths. Different maskers levels (from 40 to 70 dB SPL in 10-dB steps) were used to infer filter shape and tuning over a wide range of levels (Eustaquio-Martin and Lopez-Poveda 2011). Probe level was fixed at 9 dB SL. Gaps at the masked detection threshold of the probe were calculated using a one-up, one-down adaptive procedure as described elsewhere (Moore and Glasberg 2003). The gap was changed by a factor of 1.4 until two reversals had occurred and was then changed by a factor of 1.2 until six further reversals had occurred. The threshold was calculated as the geometric mean gap value at the last four reversal points. Ten gap threshold estimates were obtained per condition and their geometric mean was taken as the masker level at threshold (see Moore and Glasberg 2003, for further details). Resulting gap thresholds were then transformed into filter excitation levels using a linear reference temporal masking curve for a sinusoidal masker of 5,000 Hz simulated with the model (Eustaquio-Martin and Lopez-Poveda 2011).

Inference of filter shapes from notched noise data

Filter shape and bandwidth was inferred from data for all three conditions using the power spectrum model of masking (Patterson 1976). The assumed filter shape was an asymmetrical double rounded exponential or roex (Patterson and Nimmo-Smith 1980). Two roex functions were used (after Oxenham and Shera 2003). The first one, denoted roex(p,w,t), allows the filter having different slopes at its tip and tail, with a parameter (w) that determines the relative weights of the tip and tail slopes. In this roex, the tip and tail slopes may be different on the upper and lower frequency sides of the filter. On each filter side, the tip slope is set by parameter p and the tail slope is set as a fraction (1/t) of the tip slope, i.e., the tail slope is set as p/t (Eq. 3 in Oxenham and Shera 2003). The factor determining the tail slope (t) and the weighting factor (w) are assumed identical on both sides. The second roex function, denoted roex(p,w,t,p), is identical to the first one except that t and w are not used on the upper side of the filter. That is, the upper side of the filter is determined by a single slope (Eq. 4 of Oxenham and Shera 2003). Optimal roex parameters were sought considering random initial values. Methods were identical to those described in earlier related studies (Oxenham and Shera 2003; Eustaquio-Martin and Lopez-Poveda 2011).

Bandwidth estimates and analysis

BM and auditory nerve tuning is typically described using pure tones as stimuli (Ruggero et al. 1997) and this has served as the reference for across-species and across-method comparisons (Shera et al. 2002; Oxenham and Shera 2003; Joris et al. 2011). Similarly, the accuracy of isoresponse and isolevel notched noise methods was analyzed here by comparing bandwidth inferred using these behavioral methods with actual values obtained from BM responses to pure tones. The 10-dB-down bandwidth (BW₁₀), 3-dB-down bandwidth (BW₃), and equivalent rectangular bandwidth (ERB) were used. BW₃ and BW₁₀ values were obtained directly from high-frequency resolution isoresponse and isolevel actual or roex curves. The frequency step was 5 and 16 Hz for isolevel and isoresponse curves, respectively. ERBs were calculated by integration of isolevel and normalized isoresponse actual or roex curves over a frequency range from 4,000 to 12,000 Hz. The ratio of inferred to actual bandwidth values was used to quantify the error of the estimates.

Results

BW₃ values were always smaller than BW₁₀ values (on average, BW₁₀ ~ 2.15BW₃), but the overall pattern of results was virtually identical for the two measures and so only the latter are reported. Results for the two isoresponse versions of the notched noise method were virtually identical and so results are reported only for the method where the probe level was fixed and the masker–probe gap was used as a parameter. These will be referred to as isoresponse estimates.

Actual isoresponse vs. isolevel BM tuning

Actual isolevel and isoresponse curves for our BM model are shown in Fig. 1A and B, respectively. For reference, the right panels of Fig. 1 show the experimental BM responses used originally to produce the BM model shown on the left panels (Meddis et al. 2001). Arguably, the model accounts for the main level-dependent characteristics of chinchilla BM isolevel and isoresponse tuning. A complete discussion on the merits of the BM model has been provided elsewhere (Meddis et al. 2001; Lopez-Poveda 2003; Lopez-Najera et al. 2007).

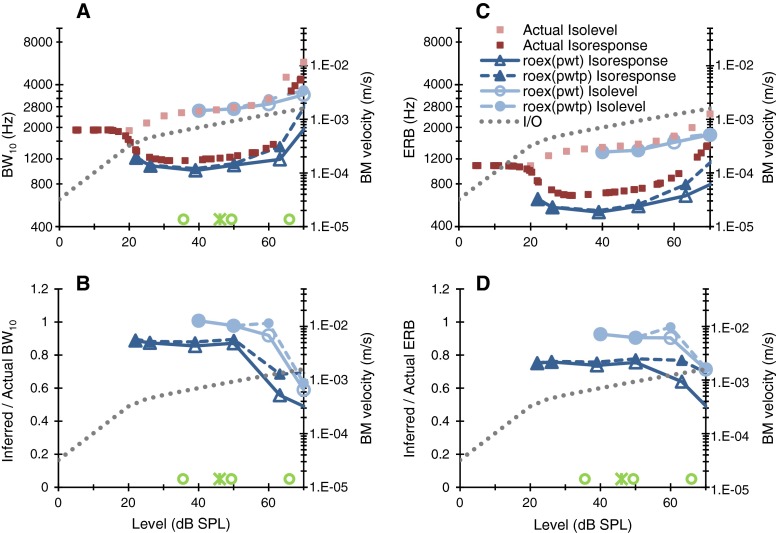
Actual isoresponse and isolevel BW₁₀ values for our BM model are compared in Fig. 2A. Strictly speaking, comparisons for matching levels are not possible because each isoresponse (tuning) curve involves a wide range of stimulus levels. To facilitate an approximate comparison, isoresponse BW₁₀ values are plotted as a function of the level at the tip of their corresponding BM tuning curves (Fig. 1C). Actual isoresponse and isolevel BW₁₀ only matched at very low levels (<20 dB SPL), where the BM model responds linearly. Over the compressive part of the BM input/output (I/O) curve (dotted line in Fig. 2), isoresponse BW₁₀ values were around 0.45 times the isolevel values over the level range from 40 to 60 dB SPL. Furthermore, isolevel BW₁₀ increased monotonically with increasing level, while isoresponse BW₁₀ varied nonmonotonically with level, decreasing at levels where BM responses went from linear to compressive and increasing at higher levels. This pattern of results is consistent with previously reported theoretical and experimental analyses (Eustaquio-Martin and Lopez-Poveda 2011). The decrease in isoresponse BW₁₀ from low to moderate levels is consistent with BM (e.g., Fig. 9 in Temchin et al. 2008) and auditory nerve physiology (e.g., Fig. 3 in Geisler et al. 1974) and indeed has been proposed as an explanation for the comparatively sharper tuning curves of AN fibers with high rate thresholds (Temchin et al. 2008).

FIG. 2.

A A comparison of actual and inferred BW₁₀ values for isolevel and isoresponse versions of the forward masking notched noise method. Inferred values are shown for two roex filter shapes (see “Methods”). Inferred values were obtained using many more symmetric and asymmetric notch placements around the probe frequencies than are typically used in experimental conditions. Note that actual and inferred values are for pure tones and notched noises, respectively. For isolevel series, the abscissa shows the rms level of the two stimuli. For the actual isoresponse series, the abscissa shows the tip level of isoresponse (tuning) curves for pure tones (Fig. 1B); for the inferred isoresponse series, the abscissa shows the rms level of a reference (no notch) masker. Symbols near the abscissa depict rms level values in previous relevant studies: open circles depict reference (no notch) masker levels for a probe frequency of 6 kHz and probe levels of 10, 20, and 40 dB SL (from Fig. 3 of Oxenham and Simonson 2006); the asterisk depicts the reference masker level for a probe frequency of 8 kHz (from Fig. 1 of Oxenham and Shera 2003). B The error of the inferred BW₁₀ values expressed as the ratio between inferred and actual values. C, D As for panels A and B but for ERB instead of BW₁₀. In the four panels, the dotted line (right ordinate) illustrates the I/O curve of the BM model for a tone at CF. Open circles and asterisks are not shown in panel C to avoid clutter.

BW₁₀ and ERBs have been both used in the literature to characterize cochlear tuning. Given the asymmetric, nonlinear nature of BM responses, the two measures need not be linearly related. Figure 2C shows actual isolevel and isoresponse ERBs for our BM model. Clearly, ERBs were smaller than BW₁₀ values over the full range of levels, but the pattern of results was otherwise similar for ERB and BW₁₀ (compare squares in Fig. 2A and C).

Note that BW₁₀ increased quickly with increasing level just above ~60 dB SPL. This is the result of the dual-resonance nature of the DRNL filter used to model BM responses. Around 65 dB SPL, the linear, more broadly tuned resonance of the DRNL filter suddenly influenced the BW₁₀ estimate (Fig. 1A and C). ERBs were affected by this effect to a lesser extent. It is uncertain whether this feature is realistic or is particular to the present DRNL filter. Experimental BM tuning curves are typically measured using sparse frequency spacing and so only provide coarse bandwidth estimates. Nonetheless, some physiological datasets do support rapid bandwidth increases with increasing response criterion; for example, compare the tuning of the 800- and 1,600-μm/s series in Fig. 9A of Temchin et al. (2008). Individual behavioral data also support rapid increases of BW with small level increments. For example, in the bottom-left panel of Fig. 4 in Oxenham and Simonson (2006) (their 4-kHz dataset), the isoresponse normalized ERB of one subject nearly doubled with increasing signal level from 25 to 30 dB SPL.

In summary, Figure 2 shows that care must be exercised when comparing cochlear tuning (expressed as BW₁₀ or ERB) inferred with different (isoresponse vs. isolevel) methods at any given level, or with any given method at different levels.

Isolevel procedures are more accurate than isoresponse procedures in ideal application conditions

Actual and inferred bandwidth values are compared in Fig. 2. Inferred values were obtained using many notch placements around the probe frequency (see “Methods”) to assess the accuracy of the behavioral methods in “ideal” application conditions. Note that actual and inferred values are for pure tones and notched noises, respectively. For inferred isolevel data, the abscissa shows rms masker levels. For inferred isoresponse data, the abscissa shows the rms level of a reference (no notch) masker. Data are restricted to levels below 70 dB SPL because this is the level range over which bandwidth can be typically obtained using the behavioral methods in human. As a guide, the open circles and asterisks near the abscissa illustrate the levels used in earlier relevant studies (see the caption of Fig. 2).

Let us first analyze the BW₁₀ data, shown in the left panels of Fig. 2. Inferred isolevel BW₁₀ values were accurate for levels up to around 60 dB SPL. At 70 dB SPL, however, inferred isolevel values were significantly smaller than actual values (error ratio ~0.6, Fig. 2B). Inferred BW₁₀ values were virtually identical for the roex(p,w,t) and the roex(p,w,t,p) models.

As for isoresponse estimates, inferred BW₁₀ values were around 10 % smaller than actual values for levels up to 50 dB SPL and became smaller at higher levels (Fig. 2B). The roex(p,w,t,p) model provided a more accurate isoresponse bandwidth estimate than the roex(p,w,t) model at high levels. The importance of this observation is further discussed below.

Results for ERBs are shown in Fig. 2C–D. The pattern was nearly identical as for BW₁₀. If anything, inferred isoresponse ERB estimates were less accurate than BW₁₀ estimates below 50 dB SPL (the error ratio was ~0.8 for ERB vs. ~0.9 for BW₁₀).

In summary, in ideal application conditions, the isolevel notched noise method is more accurate overall than the isoresponse method. Furthermore, the isoresponse method provides more accurate BW₁₀ than ERB estimates. No significant differences were observed between roex(p,w,t) and roex(p,w,t,p) models except, perhaps, at 60–70 dB SPL where the latter is more accurate than the former. The accuracy of isoresponse and isolevel methods decreases significantly for levels around 60–70 dB SPL. This is the level range where the actual model bandwidth increases rapidly with increasing level, as explained above.

Tuning is different for sinusoidal and noise stimuli of matching levels

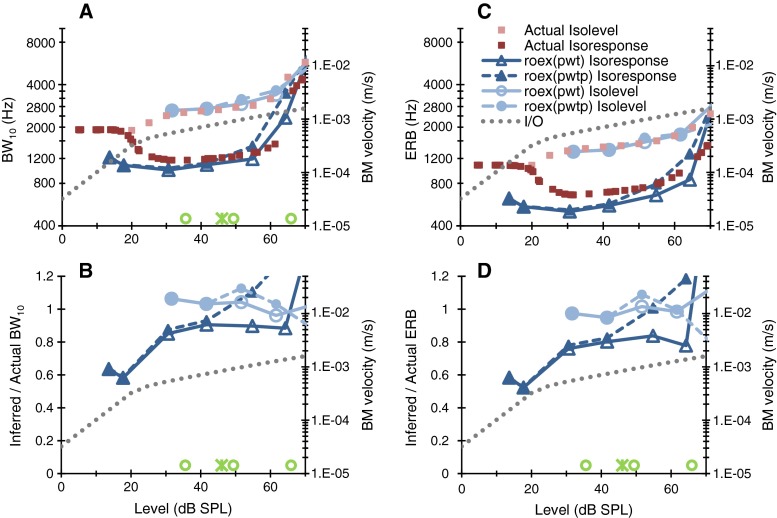
Actual bandwidth values in Fig. 2 are for pure tones while inferred values are for notched noises. It has been shown elsewhere that isolevel BM tuning is comparable for pure tones and noise only when the SPLs of the two stimuli are adequately scaled, specifically, when pure tones are typically 10 dB lower in level than an octave-wide noise or, equivalently, 7 dB lower than a half-octave wide noise like the one used in the present behavioral methods (de Boer and Nuttall 2002). This suggests that more accurate isolevel bandwidth estimates could be obtained by adequately adjusting the level of the notched noises. This was indeed the case. Figure 3 shows that actual and inferred isolevel bandwidth values matched more closely over the range of levels typically measured behaviorally when the inferred curves were horizontally shifted to the left by ~8.3 dB (compare the error ratios for isolevel bandwidth estimates in Fig. 3 with those in Fig. 2). The magnitude of the shift in the present data was comparable to the typical shift found experimentally by de Boer and Nuttall (2002), even though the CFs were different for the two studies [9.6 kHz here vs. 16.7 kHz in the study of de Boer and Nuttall (2002)]. It is uncertain whether this correspondence is just coincidental or has a grounded explanation. Distinguishing between these two possibilities, however, would be important. If it were the latter, we could conclude that the isolevel notched noise method in ideal application conditions (i.e., with a large number of notch placements) provides accurate estimates of nonlinear cochlear tuning for pure tones provided that the level of the two stimuli are adequately scaled. Experimental evidence suggests that for CFs between 15 and 18 kHz, the typical scaling factor is 10 dB for octave-band noises but can vary across cases and levels from 3 to 20 dB [compare the scaling factors across the cases in Fig. 3 to 6 in de Boer and Nuttall (2002)]. The explanation for the actual scalar values or their variability is uncertain.

FIG. 3.

A comparison of actual and inferred bandwidths for level-scaled stimuli. The data and layout are identical to Fig. 2 except that inferred series are shifted to the left by 8.3 dB, and the optimal level shifts to maximize the correspondence between actual and inferred isolevel bandwidths. See the “Results” section.

As for isoresponse tuning, experimental evidence is lacking that appropriate level scaling improves the correspondence between BM tuning curves for tones and noise; de Boer and Nuttall (2002) only addressed the issue for isolevel tuning. The present evidence (Fig. 2) shows, however, that inferred isoresponse bandwidths are always smaller than actual bandwidths throughout the level range, even over the “flat” portion of the curve. Therefore, left shifting the inferred curves (a measure equivalent to level scaling) does not increase the correspondence between actual and inferred isoresponse bandwidths consistently across levels. Indeed, Figure 3 shows that level scaling of inferred isoresponse bandwidths by 8.3 dB can improve accuracy at high levels but decreases accuracy at low levels.

In summary, constant level scaling of the noise stimuli may improve the accuracy of inferred isolevel bandwidths but is unlikely to improve the accuracy of the inferred isoresponse estimates. Further research is necessary to understand the correspondence between BM tuning for noises and tones, as well as to determine the scaling factor and its potential dependence on the method (isoresponse vs. isolevel), level, and/or CF.

The accuracy of the notched noise method in typical experimental conditions

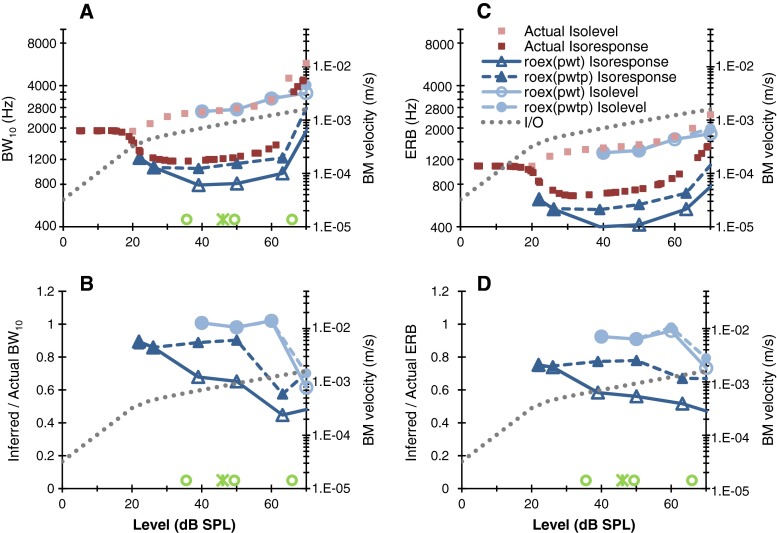
The inferred bandwidth values discussed thus far were obtained using many more symmetric and asymmetric notch placements (see “Methods”) than is typically used in human behavioral experiments (Stone et al. 1992; Shera et al. 2002; Oxenham and Shera 2003; Eustaquio-Martin and Lopez-Poveda 2011). Cochlear filters are asymmetric (Robles and Ruggero 2001) and so the accuracy of the notched noise method may depend strongly on the used number of asymmetrical conditions. Figure 4 shows bandwidth values and error ratios inferred using the conditions typically used in a laboratory experiment (see “Methods”). Visual comparison of Fig. 4 with Fig. 2 reveals that all but one of the notched noise methods were nearly as accurate in this typical case as when many more asymmetrical notch placements were used. The exception was the isoresponse roex(p,w,t) method (shown as open triangles in Fig. 4), which was less accurate in typical application conditions. It is noteworthy that the error of this method was significant even for the lowest masker levels (regarded as “near threshold”) used in earlier relevant studies, depicted as symbols near the abscissa in Fig. 4 (at 40 dB SPL, error ratios were 0.65 and 0.58 for BW₁₀ and ERB, respectively).

FIG. 4.

As in Fig. 1 except that inferred values were obtained using the typical number of asymmetrical notch placements around the probe frequency.

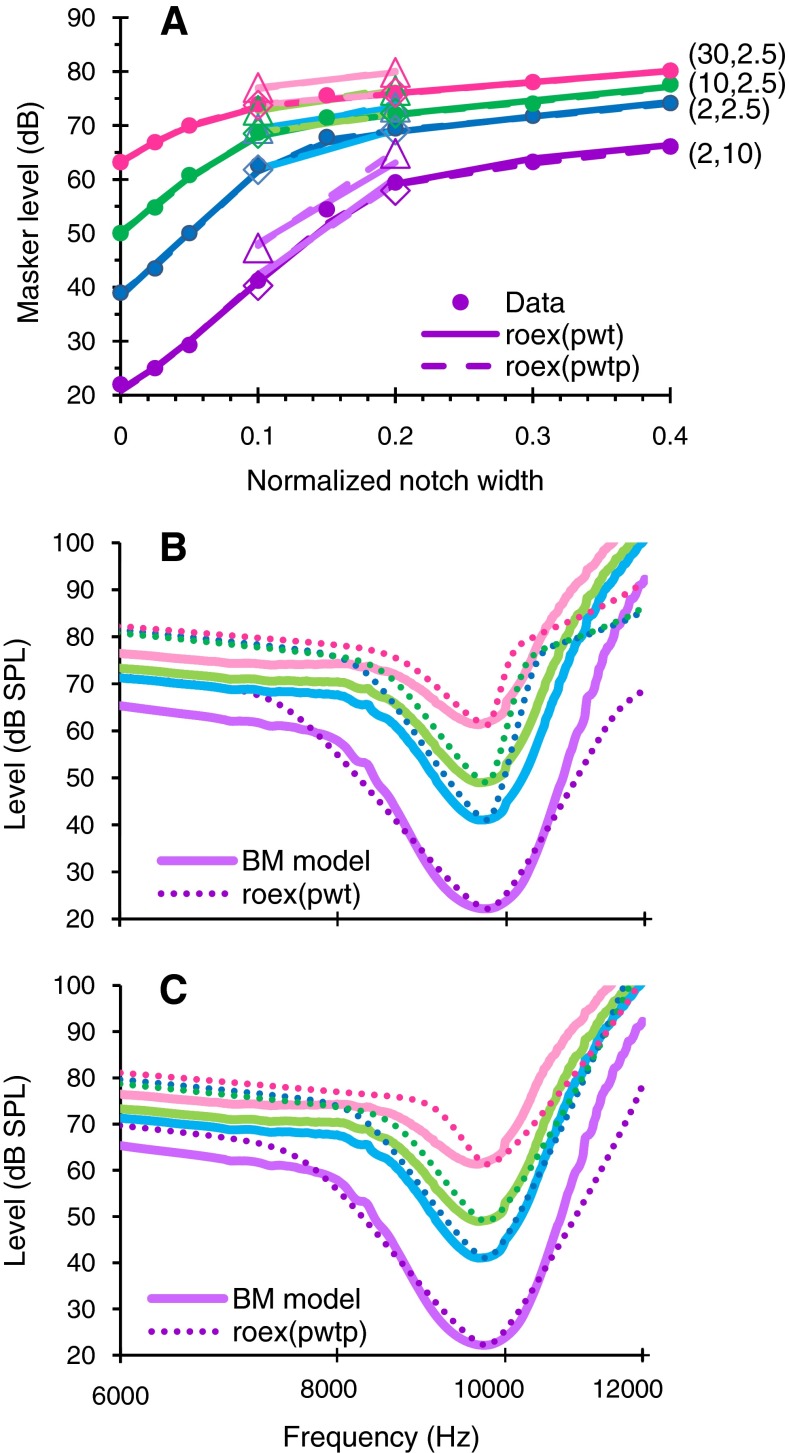
The poorer accuracy of isoresponse roex(p,w,t) bandwidths compared to roex(p,w,t,p) bandwidths in typical application conditions is not due to poorer fits of the power spectrum model of masking to the experimental masker levels. Figure 5A shows that the fits of the power spectrum model of masking to the isoresponse data were actually excellent for the two roex functions (the mean rms fit errors across conditions were 0.9 and 0.7 dB for roex(p,w,t) and roex(p,w,t,p), respectively). Instead, the greater error of the inferred roex(p,w,t) bandwidth values was due to the poorer fits of the resulting roex(p,w,t) to the actual BM tuning curves. Indeed, visual comparison of Fig. 5B and C reveals that the fits to the actual BM tuning curve were clearly poorer for the roex(p,w,t) than for the roex(p,w,t,p) model. In other words, the power spectrum model of masking reproduces the masker thresholds even with a roex(p,w,t) that fits the corresponding tuning curves poorly.

FIG. 5.

A Isoresponse notched noise masker levels as a function of notch width. Symbols illustrate experimental values obtained with the forward masking model. Lines are predictions of the power spectrum model of masking assuming asymmetrical roex(p,w,t) (continuous lines) or roex(p,w,t,p) (dashed lines) filter shapes. The number pair next to each series informs of the masker–probe time gap (millisecond) and K (decibel) values used to obtain the data (see “Methods”). B Inferred roex(p,w,t) curves (dotted lines) for the fits in A compared to actual BM tuning curves (continuous lines). Actual tuning curves were chosen so that their tip levels approximately matched the levels of the reference (no notch) masker in A. C As in B but showing inferred roex(p,w,t,p) curves.

The following questions arise regarding the accuracy of the isoresponse methods: why is the roex(p,w,t,p) model overall more accurate than the roex(p,w,t) model? Why is the roex(p,w,t) model more accurate in ideal than in typical experimental conditions? In either case, why is it more accurate at lower than at higher levels? Why are roex(p,w,t) bandwidth estimates generally biased towards smaller values? The answer to all these questions lies in a common factor: the roex(p,w,t) is a poor model of chinchilla basal BM tuning curves. It assumes that the low- and high-frequency sides of a BM tuning curve are both described with two slopes, one steep near the tip and one shallow on the tail. It further assumes that the shallower slope takes over the steeper slope at identical levels on either side of the tuning curve. Neither assumption is supported by actual BM tuning curves (shown in Fig. 1C and D). Indeed, BM tuning curves are more consistent with the roex(p,w,t,p) model, which assumes two slopes on the low-frequency side and a single (steep) slope on the high-frequency side of the tuning curve. This explains the overall greater accuracy of the isoresponse roex(p,w,t,p) compared to roex(p,w,t) model, as shown in Figs. 2 and 4.

For short masker–probe time gaps (or low probe levels), masker levels are determined mostly by frequency selectivity around the tip of the tuning curve, with little or no contribution from the shallow low-frequency tail. Notice, for example, that masker levels for the lowermost series of Fig. 5A extend a range (from 20 to 60 dB SPL) that broadly matches the level range at the tip of the corresponding actual BM tuning curve (lowermost curve in Fig. 5B or C). This explains the greater and comparable accuracy of the two roex models at low levels (Figs. 2-4). Actual tuning curves become gradually more asymmetric with increasing response criterion because cochlear compression is greater on the high- than on the low-frequency side of the tuning curves, at least for basal cochlear regions (Fig. 1; see also Figs. 8 and 9 of Techmin et al. 2008). As a result, the shallow low-frequency tail of the actual tuning curves contributes gradually more to masking as time gap (or probe level) increases. In these cases, the roex(p,w,t) model still fits the masking functions very well (Fig. 5A) but it does so by forcing shallow tails on both the low- and high-frequency sides even though the latter does not exist in the actual tuning curves. Compare, for example, the different slopes on the high-frequency sides of the resulting roex(p,w,t) and roex(p,w,t,p) functions in Fig. 5B and C. This leads to overestimating the steep slope on the high-frequency side and so to a bias towards narrower bandwidths. This bias is more significant in typical than in ideal experimental conditions because for a fixed notch width range, the masking functions in the ideal case contain many more data points for conditions around the tuning curve tip. Therefore, the fitting error around the tip has more weight than the fitting error on the tails.

Figure 4 also shows that for typical experimental conditions, the accuracy of inferred bandwidths was greater for isolevel than for isoresponse estimates and broadly similar for roex(p,w,t) and roex(p,w,t,p) models. This is because actual isolevel curves are overall more symmetric than isoresponse curves and are not subject to the steepening effects of frequency–asymmetric compression. As a result, the two roex models fitted isolevel BM curves better than they fitted isoresponse curves.

Discussion

We have used a computer model of behavioral forward masking to assess the accuracy of the notched noise method at estimating BM tuning. Our approach was conceptually similar to that of Heinz et al. (2002), but the aims of the two studies were different. They focused on the impact of suppression on “near-threshold” tuning inferred using fixed level (isolevel condition), simultaneous maskers. Here, by contrast, we tested the claim that a particular forward masking version of the notched noise method provides tuning estimates that can be more directly compared with physiological tuning curves (Shera et al. 2002). Furthermore, we have compared the accuracy of isoresponse and isolevel versions of the forward masking notched noise method at estimating BM tuning at different levels.

Accuracy and generalizability of the results

The present study used a specific model of the nonlinear basal BM response in chinchilla. Therefore, some aspects of the results reflect of necessity the characteristics of this model. For instance, modeled BM tuning curves had slightly shallower low-frequency tails than experimental curves (compare Fig. 1C with D). However, insofar as the chosen model incorporated the main nonlinear properties of basal BM frequency selectivity—particularly, asymmetric and level-dependent gain and tuning (Fig. 1) with suppression (Meddis et al. 2001; Plack et al. 2002)—and that the uneven accuracy of the various notched noise methods is indeed the result of these characteristics, it seems reasonable to conclude that the present model results also apply experimentally.

Isoresponse methods were overall less accurate than isolevel methods in typical conditions (Fig. 4B and D) because the roex, particularly the roex(p,w,t), produced a poorer fit to actual isoresponse than isolevel curves (Fig. 5). We have argued that this is because isoresponse (tuning) curves are concomitantly affected by asymmetric frequency selectivity and compression. Compression likely extends a broader frequency range relative to CF in the apex than in the base of the BM (Rhode and Cooper 1996; Lopez-Poveda et al. 2003; Eustaquio-Martin and Lopez-Poveda 2011) and so apical tuning curves may be more symmetric than basal tuning curves. It is uncertain that the present results, which are for a basal cochlear filter, are representative of the accuracy of the notched noise methods at characterizing apical cochlear filters.

It is uncertain to what extent the present chinchilla model is representative of cochlear responses in other species. The accuracy of the notched noise methods at estimating cochlear tuning in other species could differ from the present values (Figs. 2, 3, and 4) depending on the goodness-of-fit of the chosen roex filter at mimicking actual isoresponse and isolevel curves combined with the degree of cochlear compression on the maskers over the measured level range. The generalizability of the present results to human is discussed in more depth below.

What is the most accurate behavioral method for estimating human cochlear filter tuning?

The present results show that inferred isoresponse roex(p,w,t,p) tuning estimates are more accurate than isoresponse roex(p,w,t) estimates (Figs. 2D-4D), a result in agreement with the conclusions of Rosen et al. (1998) and the assertions of earlier studies (Glasberg and Moore 2000; Oxenham and Shera 2003; Oxenham and Simonson 2006). They also show that three of the four methods tested (the isoresponse roex(p,w,t,p) and the two isolevel methods) are as accurate in typical as in ideal application conditions (compare the bottom panels of Figs. 2 and 4). This is not to say, however, that the three methods in question are equally accurate.

We have shown that in typical experimental conditions (Fig. 4), the isolevel notched noise method provides accurate BW₁₀ and ERB estimates for masker levels up to 60 dB SPL and that its accuracy at 70 dB SPL can improve with adequate scaling of the noise level (Fig. 3). This holds true for the two roex models tested. The accuracy of the isoresponse method, by contrast, depends on level, on the roex model and on the chosen bandwidth measure (BW₁₀ vs. ERB) (Fig. 4). This is because the roex models, particularly the roex(p,w,t), is a poor model of actual BM tuning curves for masker levels for which the low-frequency tail of the BM tuning curves contributes to masking (Fig. 5). Furthermore, stimulus level scaling is unlikely to improve the accuracy of isoresponse estimates consistently across levels (Fig. 3). Altogether, the present evidence favors isolevel notched noise methods over isoresponse methods in terms of accuracy. On the other hand, it suggests that isoresponse methods may allow assessing tuning at lower levels than isolevel methods (Figs. 2 and 4).

Alternative interpretations of unusually sharp behavioral estimates of human cochlear tuning

The isoresponse forward masking method of Shera et al. (2002) and Oxenham and Shera (2003) was carefully designed to provide estimates of human cochlear tuning at low levels that were comparable to those of animal threshold neural tuning curves. The present results are for a specific chinchilla model at a CF ~10 kHz. Assuming, nonetheless, that they also apply to human, they suggest that at ~40 dB SPL, the lowest level roughly measured by Oxenham and Shera (2003) for a reference (no notch) masker at 8 kHz, the error ratio of inferred to actual isoresponse ERB is ~0.8 (530 vs. 692 Hz) for the roex(p,w,t,p) filter and ~0.6 (400 vs. 692) Hz for the roex(p,w,t) filter (Fig. 4D). In other words, the present model suggests that inferred isoresponse tuning could be sharper than actual tuning at the lowest level roughly measured in a typical human masking experiment. Although not negligible, this bias would be insufficient to explain the differences between the revised estimates of human cochlear tuning obtained with this method and earlier estimates for human (Oxenham and Shera 2003) or for other mammals (Shera et al. 2002). A more careful analysis of the present results, however, reveals that the differences in question could be more apparent than real, as discussed as follows.

Based on their isoresponse masking estimates of tuning, Oxenham and Shera (2003) claimed that human cochlear filters are more sharply tuned than had been suggested by earlier masking studies [see Fig. 4 of Oxenham and Shera (2003)]. We questioned this claim in a previous study on the grounds that in addition to other methodological differences (e.g., earlier studies had used simultaneous instead of forward masking), most earlier studies used isolevel rather than isoresponse masking methods and that the two procedures can give different tuning estimates over the range of levels where BM compression occurs (Eustaquio-Martin and Lopez-Poveda 2011). The present results show that at ~40 dB SPL, the lowest level roughly measured by Oxenham and Shera (2003) for a reference (no notch) masker at 8 kHz, the actual isoresponse ERB for the BM model was approximately half the actual isolevel ERB (692 vs. 1,446 Hz) (compare the dark and light squares in Fig. 4C). A similar ratio of isoresponse to isolevel tuning occurred for inferred ERB values with the more accurate roex(p,w,t,p) model (530 vs. 1,337 Hz) (compare the filled triangles and circles in Fig. 4C). Therefore, the present results further support our earlier reasoning.

It has also been claimed elsewhere that human cochlear filters are more sharply tuned than those of other mammals (Shera et al. 2002, 2010; Joris et al. 2011). This claim was grounded on the longer latency of stimulus frequency otoacoustic emissions (SFOAEs) for human compared to cat or guinea pig and was corroborated by Shera et al. (2002) with isoresponse roex(p,w,t) notched noise tuning estimates. We have no explanation for the difference in SFOAE latency across species (nor did we aim at providing one). But we have shown here that inferred isoresponse ERBs can be 0.6 and 0.8 times the actual values for roex(p,w,t) and roex(p,w,t,p), respectively, at 40 dB SPL, the lowest masker level obtained in a typical masking experiment, if this low sound level is still within the compressive region of cochlear responses. Most importantly, however, the present results further show that isoresponse tuning decreases with increasing level over the level range where BM responses go from linear to compressive (Fig. 2). As noted in the “Results” section, this trend is consistent with physiology and indeed could explain the decrease in isoresponse BW with increasing level reported by recent behavioral studies (e.g., Fig. 4 of Oxenham and Simonson (2006); Fig. 5 of Eustaquio-Martin and Lopez-Poveda (2011)). Despite the precautions taken when developing the isoresponse notched noise methods, physiological threshold tuning curves are still typically measured over lower levels than those available for human behavioral testing. Therefore, it is likely that inferred isoresponse BW be narrower at the lowest level measurable in human (~40 dB SPL) than at lower levels closer to neural threshold. Indeed, in the present model, the more accurate inferred isoresponse roex(p,w,t,p) ERB at 40 dB SPL was roughly half the actual ERB at (neural) threshold (4.7 dB SPL) (530 vs. 1,077 Hz). If sound levels low enough to be at neural threshold and in the linear region of cochlear responses could be used, behavioral isoresponse estimates would be less biased (Fig. 4D) (see below). Given the practical impossibility of making behavioral measurements using masker levels at neural threshold, and due to the nonlinear nature of the filters, cross-species comparisons should ideally be made using identical stimuli, methods, and levels. These are important considerations that should be taken into account when using behavioral isoresponse tuning estimates to corroborate other indirect estimates of cochlear tuning (e.g., SFOAEs).

Admittedly, the present analysis is based on a specific chinchilla BM model and so it is reasonable to question whether these model predictions also apply to the average human. For example, Oxenham and Shera (2003) reported that there was a tendency for roex(p,w,t) isoresponse ERB estimates to be narrower than roex(p,w,t,p) estimates, but the average difference was less in their data (mean ~6 %, max ~20 %) than in the present model (~32 %). The shallow high-frequency tails assumed in the roex(p,w,t) filter do not occur in the present chinchilla model (Fig. 5) but do sometimes occur in human psychoacoustical tuning curves (Kidd and Feth 1981; Yasin and Plack 2005; Lopez-Poveda et al. 2007). This could explain the greater difference between isoresponse roex(p,w,t) and roex(p,w,t,p) ERB for the present model compared to the human estimates of Oxenham and Shera (2003). Also, some datasets suggest that the compression knee-point occurs at higher levels in human than in the present chinchilla model [e.g., 30–35 dB SPL (Plack and Oxenham 2000; Epstein and Florentine 2005) or 40–50 dB SPL (Johannesen and Lopez-Poveda 2008; Lopez-Poveda and Johannesen 2012)] and, hence, is closer to the lowest level considered by Oxenham and Shera (2003). This suggests that human isoresponse tuning estimates could be less biased than suggested by the present chinchilla model. On the other hand, however, studies reporting compression knee-points at 40–50 dB SPL defined the knee-point as the input level where the cochlear input/output level slope equals 0.5 dB/dB and so compression actually extended to lower levels. Indeed, some studies have reported compressive responses for levels as low as and probably lower than 20 dB SPL across CFs in line with the present chinchilla model (Lopez-Poveda et al. 2003; Nelson and Schroder 2004). Furthermore, in psychoacoustical tuning curves where shallow high-frequency tails occur, they typically do occur at much higher levels than on the low-frequency side [e.g., Fig. 1 in Lopez-Poveda et al. (2007)], in contrast with the equal-level (or equal w) assumption of the isoresponse roex(p,w,t) implementation of Oxenham and Shera (2003). Therefore, it is likely that some of the presently reported bias still applies to the isoresponse tuning estimates of Oxenham and Shera (2003). An important conclusion from the present analysis is that the accuracy of isoresponse methods could improve by using conditions that involve masker levels within the presumed linear region of cochlear response (e.g., lower probe levels) and independent roex parameters (p,w,t) on each filter side to better account for the potential asymmetry of experimental tuning curves. This conclusion is in line with the report of Rosen et al. (1998).

Implications for filterbank auditory models and applications

It is a common, though perhaps unconscious, mistake to think of isoresponse (or tuning) curves as inverted isolevel filter shapes. This would be correct for linear filters but it is certainly incorrect for auditory filters because they are nonlinear (Vogten 1974; Verschuure 1980, 1981; Rosen and Baker 1994; Rosen et al. 1998). Indeed, isoresponse bandwidth values are smaller than corresponding isolevel values over the range of levels where peripheral compression occurs [Figs. 1-4; see also Eustaquio-Martin and Lopez-Poveda (2011)].

Confounding isoresponse with isolevel filter shapes or BWs may have important consequences. For example, it has been suggested (p. 3322–3323 of Shera et al. 2002) that loudness models should be revised to incorporate the exceptionally sharp isoresponse tuning estimates of Shera et al. (2002) or Oxenham and Shera (2003). Also, there is a trend to invoke unusually sharp filters to explain controversial aspects of human sensitivity to temporal fine structure (Moore and Sek 2011). Loudness models and models of temporal fine structure sensitivity, however, are typically based on the “excitation pattern” of the stimulus. The excitation pattern is a graphical representation of the output of the auditory filters to a fixed-level stimulus as a function of the filters’ center frequencies (Moore 2007). Hence, it is, by definition, an isolevel measure. This is not to say, however, that isoresponse tuning estimates are perceptually irrelevant. Sharp isoresponse tuning may be at play, for example, when detecting a fixed-level signal in the presence of fluctuating maskers (e.g., during the tracking of speech in noisy backgrounds). As noted by Shera et al. (2002, p. 3322), “cochlear filtering is a dynamic process that no set of static linear filters can completely represent”. To simultaneously account for isoresponse and isolevel tuning, auditory models should incorporate nonlinear filterbanks with realistic level- and frequency-dependent tuning and compression.

Greater care must be exercised when using a single bandwidth value to characterize cochlear filter tuning

A basic idea we are putting forward here and elsewhere (Eustaquio-Martin and Lopez-Poveda 2011) is that across-species and across-studies differences in cochlear tuning may be more apparent than real. The controversy may be due to the fact that cochlear frequency selectivity is nonlinear and BW is only adequate to describe the tuning of linear filters. Considering that behavioral methods are approximate and that the BW of cochlear responses strongly depends on the procedure (e.g., isolevel vs. isoresponse) as well as on the level and the type of the stimulus used to estimate it, the debate should be conducted even more carefully. Across-species and across-studies comparisons should ideally be made for matching procedures, stimuli, and conditions. Given that the nonlinear nature of cochlear responses is now well established, even greater care must be exercised when using a single bandwidth value to characterize and compare cochlear tuning.