Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Sep 10;3:2608. doi: 10.1038/srep02608

Interplay of cytoskeletal activity and lipid phase stability in dynamic protein recruitment and clustering

Jordi Gómez-Llobregat 1, Javier Buceta 2, Ramon Reigada 3,a
PMCID: PMC3767946  PMID: 24018870

Abstract

Recent experiments have revealed that some membrane proteins aggregate to form clusters. This type of process has been proven to be dynamic and to be actively maintained by external kinetics. Additionally, this dynamic recruiting is cholesterol- and actin-dependent, suggesting that raft organization and cytoskeleton rearrangement play a crucial role. In the present study, we propose a simple model that provides a general framework to describe the dynamical behavior of lipid-protein assemblies. Our results suggest that lipid-mediated interactions and cytoskeleton-anchored proteins contribute to the modulation of such behavior. In particular, we find a resonant condition between the membrane protein and cytoskeleton dynamics that results in the invariance of the ratio of clustered proteins that is found in in vivo experimental observations.

Many membrane proteins are heterogeneously distributed in the bilayer plane even in resting cell conditions1. For example, GPI-anchored proteins and Ras proteins are organized in randomly distributed monomers and in transient clusters of a few proteins in the outer and inner leaflets, respectively2,3. In both cases, the clusters have been revealed to be dynamic, in the sense that they continuously form and break. The clusters are thought to function as transient platforms that are highly efficient at recruiting membrane-associated proteins and that activate the downstream effectors required to produce and deliver biochemical signals4,5,6.

Many proteins have a large affinity for liquid-ordered lipid membrane domains that are rich in saturated lipids and cholesterol (rafts). Because protein association in nanoclusters is abrogated after cholesterol depletion, the involvement of a ‘raft-dependent' mechanism for protein recruitment has been conjectured7. However, analysis of the protein distributions in the plasma membrane has shown that the fraction of clustered proteins remains constant when the protein concentration is increased2,3,8; therefore, clustering of raftophilic proteins violates the law of mass action and is actively maintained away from equilibrium. This finding suggests that protein clustering results from an ordering of lipids by membrane proteins rather than from pre-formed lipid raft complexes in which specific proteins aggregate9,10.

The updated viewpoint of the lipid raft hypothesis11 not only envisages lipid nanodomains as highly dynamic but also stresses the role of proteins (in particular, cytoskeletal proteins) in stabilizing lipid nanodomains and dynamically regulating their behavior12. The interface between the lipid membrane and the actin cortex has been intensely studied in recent years. In vitro experiments are particularly useful for unveiling the basic components that provide the cytoskeleton-membrane interface with its unique functionality and versatility13. Interestingly, recent in vivo experiments have shown that actin filaments that are attached to the membrane induce the formation of liquid-ordered domains14,15. Conversely, cholesterol sequestration alters the ratio between liquid-ordered (raft-like) and liquid-disordered lipid phases, causing dramatic changes in the dynamics of the actin cytoskeleton16. All this evidence suggests a dynamic interplay between the actin cytoskeleton and the lipid membrane that alters the normal diffusion of proteins in the membrane17.

In particular, the interaction between the lipid membrane and the actin cytoskeleton provides a non-equilibrium source that explains active nanocluster formation. Protein raft-like nanoclusters do not form upon actin cytoskeleton disruption, suggesting that the formation of cholesterol-dependent protein clusters is induced by any of these three potential mechanisms: (direct or indirect) binding to actin filaments, actin-associated membrane nanodomains or membrane domains supported by actin filaments10,18,19. The active role of the actin cytoskeleton in membrane organization has been documented previously in giant vesicles: polymerization of dendritic actin networks on the membrane induces phase separation of initially homogeneous vesicles20. Additionally, proteomic studies showed that raft phases are particularly enriched with cytoskeletal proteins, an indication of the affinity between the actin cytoskeleton and membrane rafts10. Furthermore, the assumption that the bilayer pinning sites of the cytoskeleton mesh have a strong preference for either liquid-ordered or liquid-disordered lipid phases has been considered in recent modeling proposals21,22.

The role of the activity of the underlying cortical cytoskeleton in membrane protein clustering can be interpreted in different ways. In this paper, we suggest a mechanism with a direct role for lipids in the protein clustering process. According to our proposal, cytoskeletal activity regulates the spatiotemporal lateral distribution of the lipids in the membrane; the lipid distribution, in turn, determines the protein distribution at the membrane surface. In particular, the mechanism is based on three main assumptions. (i) Actin network activity is responsible for creating nanometric liquid-ordered (raft-like) lipid spots in the membrane surface. (ii) Actin-induced raft-like regions recruit raftophilic proteins to minimize the system's energy. (iii) The actin network is evolving and active; thus, the induced raft-like spots are continuously formed and destroyed at randomly distributed points in the membrane. Assumption (i) is supported by numerous experimental observations; raft-like phases appear in areas of the membrane with a high concentration of actin10,20,21,23. This correlation might be explained by the nucleation effect of the cytoskeleton proteins anchored to the membrane10. Phosphoinositides, such as PI(4,5)P2, which are enriched in lipid rafts, are suggested to play a central role in regulating the activity of actin-binding proteins24. Assumption (ii) arises from simple energetic considerations; raftophilic proteins diffuse in the bilayer plane in a quasi-random manner, showing a preference for the lipid raft phase. Finally, assumption (iii) can be explained by the fact that the cortical actin network is actively evolving25. Actin turnover continuously remodels the cytoskeleton-membrane linking points, either directly by affecting the attachment/detachment kinetics of membrane-associated cytoskeleton proteins or indirectly, e.g., by locally altering the content of PIP2, which regulates the activity of many membrane-associated cytoskeleton proteins24. As an example, active attachment/detachment of the spectrin junctional complex has been quantified in red blood cells; the nonequilibrium dynamics of PIP2 phosphorylation/dephosphorylation powered by ATP metabolism actively regulates the binding of the lipid bilayer to the cytoskeleton26,27. Assumption (iii) is also consistent with recent biochemical studies that show that actin remodeling in the cytoplasm can induce lipid-mediated protein clustering not only in the inner monolayer but also in the outer membrane14.

Other alternatives have recently been suggested for the role of cytoskeleton dynamics in membrane protein clustering behavior. Mayor and Rao28,29 proposed that the actin network continuously forms transient and localized inward-pointing filament structures, known as ‘asters'. Membrane proteins may eventually bind to the actin filaments and become advected toward the core of the ‘asters', forming nanoclusters. The dynamics of these protein aggregates is then suggested to be determined by the active remodeling of actin ‘asters'. In the framework of the proposal of Mayor and Rao, the role of the membrane lipid mixture is reduced to the transversal coupling between the outer and inner leaflets of the membrane. Protein clustering in the outer layer follows the aggregation process in the inner leaflet due to the transbilayer link caused by the local registration of liquid-ordered nanodomains (rich in saturated lipids and cholesterol) at both sides of the bilayer28,29. In this context, our proposal aims to provide a complementary, non-exclusive, lipid-mediated mechanism.

Results

The model

In the present paper, we propose a dynamical model that summarizes the three main assumptions explained above: the actin network locally nucleates liquid-ordered nanodomains, some (raft-like) proteins have a preferential affinity for these domains, and the actin network is being dynamically remodeled. Taken together, these assumptions yield a dynamical picture where proteins are transiently clustered due to lipid-mediated interactions. The model combines a continuous description of membrane lipids using a conserved composition order parameter and a discrete approach for membrane proteins. The lipid mixture can locally be in either a liquid-ordered (raft) phase or a disordered (non-raft) phase. Two types of proteins are considered: raftophilic proteins (P) that follow a biased Brownian motion, showing a preference for raft phases (for example, GPI-anchored proteins), and active proteins (X) that correspond to other proteins that link the cytoskeleton to the membrane and nucleate a lipid raft environment around themselves. The latter accounts for the continuous energy-dependent re-assembly activity of the cytoskeleton by following particular membrane attachment/detachment or activation/deactivation dynamics.

The lipid matrix is characterized by a local composition order parameter ϕ(r,t) that corresponds to the molar fraction difference between generic raft and non-raft lipids. ϕ(r,t) = 1 corresponds to a raft lipid phase, whereas ϕ(r,t) = −1 represents a non-raft lipid phase. The lipid free-energy functional follows a Cahn-Hilliard equation,

graphic file with name srep02608-m1.jpg

which is commonly used to describe the energetics of binary systems. The parameter γ accounts for the line tension between different lipid phases. The local free-energy functional, F(r), is expressed as

graphic file with name srep02608-m2.jpg

where the first two terms correspond to a typical Landau expansion. The interaction parameters are given in kBT energy units. The parameter β is taken with a typical value of 1/3, whereas the value of α accounts for the thermodynamic stability of the lipid mixture. The critical condition corresponds to α = 0; positive values of α lead to lipid miscibility, whereas α < 0 results in spinoidal decomposition of the lipid mixture. In our proposal, phase separation of the lipid mixture is not invoked; thus, α > 0 is considered in the simulations. The third contribution represents the interaction between lipids and cytoskeleton-anchored proteins. For a membrane location r in contact with a cytoskeleton-anchored protein, we set SX(r) = 1, whereas SX(r) = 0 otherwise. The parameter χ is considered positive and equal to 1, corresponding to a preference to nucleate a lipid raft phase around proteins X. The dynamics of the lipid mixture is governed by a conserved kinetic equation,

graphic file with name srep02608-m3.jpg

where D corresponds to the mean lipid diffusivity.

The surface area of membrane proteins is at least 10–20 times larger than the typical area per lipid in a fluid phase membrane; thus, these proteins are described as discrete particles that are inserted in the lipid lattice. Cytoskeleton-anchored proteins X are considered to be active inclusions that are randomly located in the membrane plane. Each X protein remains fixed at its assigned anchoring position for an average time τ, after which, the protein detaches from the membrane and attaches again at another membrane location. Although the attachment/detachment kinetics is probably affected by the (internal) lipid nucleation dynamics, we consider, for simplicity, that the value of τ is exclusively determined by the external cytoskeletal activity. In contrast, proteins P are considered to be permanently inserted and to be laterally diffusing in the membrane surface. The protein motion is, however, biased by energetic preferences for a particular lipid phase. The generic Hamiltonian for the protein P system reads

graphic file with name srep02608-m4.jpg

where ri is the position of the i-th protein, and λ is the interaction parameter that accounts for the lipid-protein affinity (in kBT units). A positive λ implies a preference for lipid raft phases.

A schematic representation of the proposed model is shown in Fig. 1, and its numerical implementation is explained in the Methods.

Figure 1. Schematic representation of the simulation model.

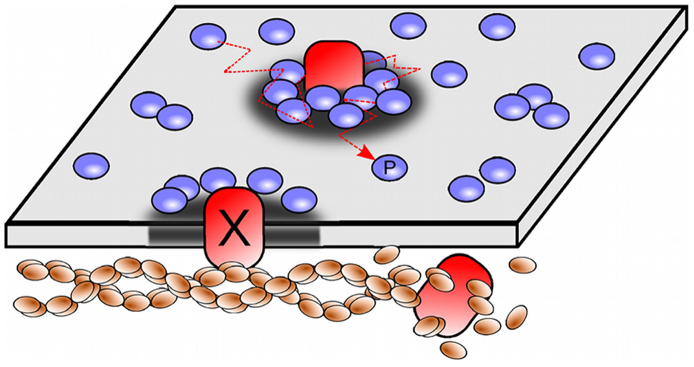
Figure 1

Open in a new tab

The membrane is portrayed as a surface where the relative concentration of lipids ϕ(r,t) is plotted as a grey scale; areas enriched in raft-like lipids are represented as darkened regions. Cytoskeleton-anchored proteins (X) are represented by red inclusions that nucleate lipid rafts. These proteins can eventually detach after an average time τ due to the active re-polymerization of the actin meshwork. Raftophilic proteins (P) diffuse and are attracted to lipid rafts, causing transient aggregation of these proteins in areas enriched with raft-like lipids, forming protein clusters.

Results for permanently anchored proteins

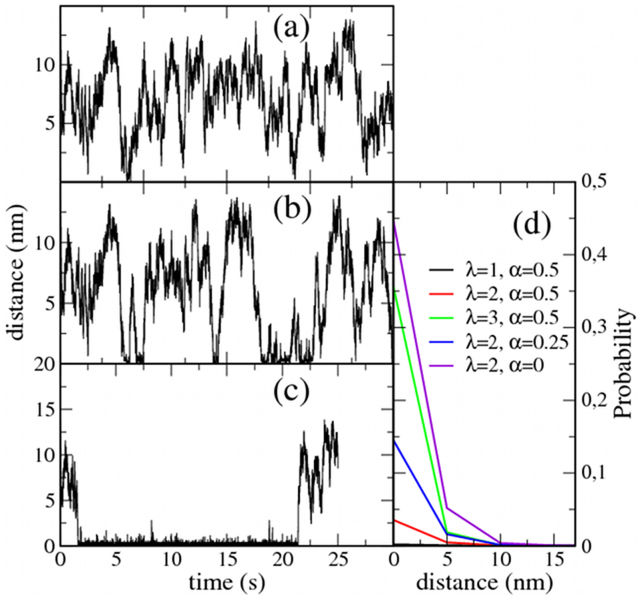
As a simple initial exploration of the proposed lipid-mediated mechanism for protein clustering, simulations with permanently fixed X proteins (τ = ∞) have been conducted. First, we examine the trajectory of a single P protein in a system with one fixed X particle (NX = NP = 1) for different interaction parameters. The distance between the P and X proteins is monitored, and some illustrative results are shown in Fig. 2. In general, increasing the parameter λ promotes trapping periods (compare panels a and b). Similar behavior is observed by increasing χ (data not shown). Interestingly, when approaching phase separation (namely, α → 0+), the trapping periods become extremely long. This latter observation is a consequence of the membrane's ‘gain of lability', which is observed when approaching the critical conditions; this lability increases the sensitivity of the lipid mixture to external perturbations. Strong lipid-protein interactions (large λ and/or χ) and proximity to a phase separation (small α) result in particles that are completely trapped around the static X protein (Fig. 2c). From the simulation trajectories, the probability distribution can be computed for the distance between the two particles. Some illustrative results are shown in Fig. 2d, confirming that mobile proteins are recruited to the area around the X particle when the protein-lipid interactions λ are large or when the lipid mixture approaches the phase boundary.

Figure 2. Trapping effect of static inclusions.

Figure 2

Open in a new tab

Simulations for a system with a single static trapping inclusion (NX = 1) and one mobile protein (NP = 1). The system size is 100 × 100 sites (0.25 μm2). The distance to the trapping inclusion is monitored for different cases. (a) λ = 1, α = 0.5: only a few very short trapping periods. (b) λ = 2, α = 0.5: increasing protein-lipid affinity promotes longer trapping periods. (c) λ = 2, α = 0: when the lipid mixture approaches the phase boundary, the mobile protein remains trapped most of the time. (d) Probability distribution for the P-X distance for different values of λ and α.

Analysis of experimental protein trajectories with state-of-the-art optical methods30 opens new avenues to study the different factors, such as membrane domains or the actin cytoskeleton, that affect protein diffusion. In particular, some of the trajectories in Fig. 2 resemble the transient immobilization of membrane proteins that are observed experimentally using single-particle tracking techniques: the so-called STALL-periods (stimulation-induced temporary arrest of lateral diffusion)18,19. Basically, a STALL period is characterized by a set of points of the protein trajectory where the residency time is unexpectedly long. These zones are approximately or less than 40–50 nm long in diameter9,10; this size was also observed in our simulations (Fig. 2). The jittering motion during recruitment (STALL periods) is due to the diffusion of proteins inside the small raft-like trapping spots. Furthermore, STALLs are actin-dependent and cholesterol sensitive18,19,31, suggesting a mechanism driven by the interplay between the actin meshwork and lipid raft domains rather than actin corrals32 or direct protein-protein interactions. Moreover, the median compartment size of corral-mediated partitioned plasma membranes is much larger than STALL confined trajectories. For example, the compartment size in NRK cells is of the order of 230 nm33. In summary, the transient protein recruitment in the form of STALL periods that is also described in our model is caused by the interaction of the proteins with lipid nanodomains that are induced by cytoskeleton-anchored inclusions.

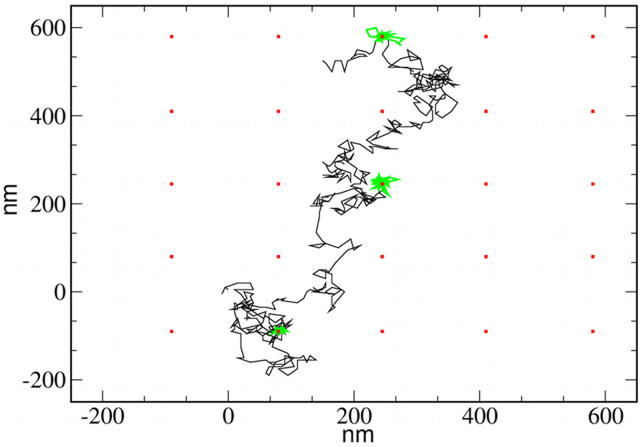
An illustrative simulation has been performed to show that STALL periods appear when combining a biased diffusive motion of proteins P with the nucleation of raft-like lipids caused by the fixed inclusions X. A membrane lipid system is simulated with a number of fixed and equally spaced X inclusions. The trajectory of a single P protein is then tracked, and the STALL periods are analyzed by means of a computational method commonly used to analyze the experimental trajectories of labeled proteins34. Given a particular protein, sets of consecutive M points of the trajectory are taken, and we calculate the probability for the protein to escape from a circle of radius R, with R being the linear distance from the starting point to the furthest point of the set. A STALL period is then identified as the set of consecutive points in the trajectory that have an escape probability larger than a threshold level L. We choose M = 10 and L = 3.16 (see34). In Fig. 3, the trajectory for a mobile protein is shown, and the STALL periods are clearly identified (in green). In all cases, the STALL periods occur at the area surrounding a static inclusion. The STALL periods identified in Fig. 3 (λ = 2 and α = 0.5) are on the order of 0.39 s. As suggested by the P-X distance probability distributions plotted in Fig. 2d, a larger protein-lipid affinity and/or proximity to the lipid phase boundary increases the ability to recruit diffusing proteins and therefore increases the duration of the STALL periods. For example, increasing the lipid-protein interaction λ up to 3 results in an average STALL duration of 2.87 s. In contrast, approaching the phase boundary by setting α = 0.25 and α = 0.1 leads to confinement periods of 1.06 s and 3.90 s, respectively.

Figure 3. A trajectory showing STALL periods.

Figure 3

Open in a new tab

Trajectory of a P protein in a system with an array of fixed inclusions. The interaction parameters are λ = 2 and α = 0.5. STALL periods (green lines) occur around the static proteins (red squares). The lipid mixture is not shown for simplicity. Notice that the STALL periods are only caused by lipid-mediated interactions.

The mechanism underlying the reported lipid-mediated ‘recruitment' and ‘confinement' effects is clear; protein X nucleates a lipid raft phase around itself (controlled by α and χ), and mobile P proteins move in a biased random manner (controlled by λ) toward the nucleated raft domains. Formally, the model can also be described using a continuum approach for the kinetics of the proteins P by defining a scalar field ρ(r) as the local density probability of P particles. The preference for a particular lipid phase is introduced by adding an extra term +λϕ to the chemical potential corresponding to the protein density field. The kinetics of this field can be then described by applying the balance equation

graphic file with name srep02608-m5.jpg

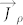where Inline graphic accounts for the compositional internal flux, which can be expressed in terms of the chemical potential, leading to

graphic file with name srep02608-m6.jpg

Combining Eqs. (5) and (6) results in the following biased diffusion equation:

graphic file with name srep02608-m7.jpg

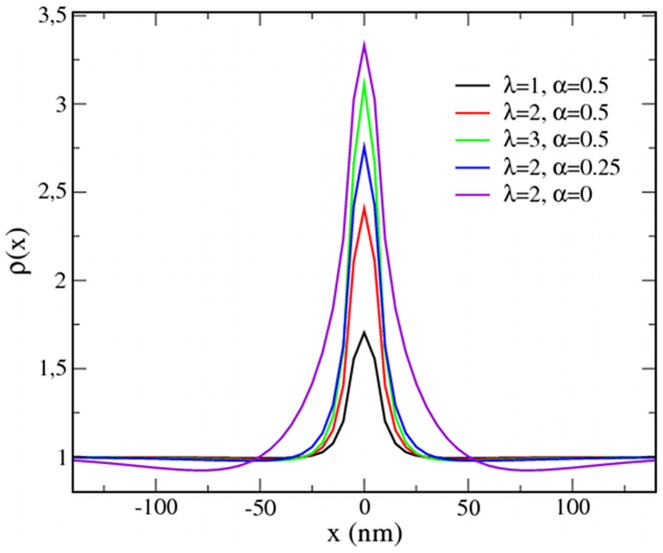
Equation (7) describes the motion of protein particles for typical diffusive behavior (first term) with drifting toward regions of increasing lipid raft fraction (λ > 0, second term). Equations (3) and (7) have been numerically solved for a system with an initial homogeneous protein density ρ = 1 and a static X particle placed in the center of the membrane surface. As shown in Fig. 4, the protein aggregation trends for the variation in the parameters λ and α are the same as those for the discrete description.

Figure 4. Trapping of proteins in a continuous description.

Figure 4

Open in a new tab

Protein density cross-sections, ρ(x), obtained from a continuum (coarse-grained) approach using different interaction parameters λ and α. The mean protein density average is initially fixed to 1. The X particle is placed at x = 0.

Results for actively attaching/detaching anchored proteins

In the simulations performed in the previous section, the nucleating inclusions X were permanently fixed to the membrane, yielding an equilibrium scenario. In this section, cytoskeletal activity is accounted for by considering active attachment/detachment dynamics (finite τ) that lead to a stationary but non-equilibrium situation. The interplay between the recruiting dynamics (determined by the protein dynamics) and the kinetics of the attachment/detachment process (determined by τ) controls the stationary state and the global protein clustering dynamics.

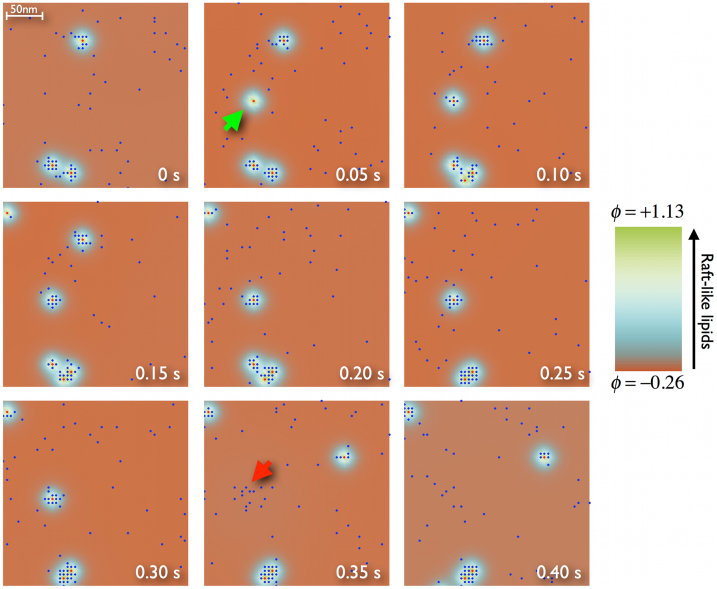
To investigate the non-equilibrium scenario, a reference case is examined in detail. A simulation is performed for a membrane of 1 μm2 (200 × 200 sites) containing 50 nucleating inclusions with a recycling period of 0.5 s and 1000 mobile proteins (NX = 50, τ = 0.5 s, and NP = 1000). The simulation is run for up to 5 s (times much longer than τ); thus, any correlation with the initial state is lost. We choose the energetic parameters to be α = 0.5 and λ = 3. A sequence of snapshots is displayed in Fig. 5 for a piece of the simulated system and illustrates the general behavior. Inclusions attract and trap nearby mobile proteins, thus forming a nanocluster until the inclusion detaches from the membrane. When this happens, the nanocluster breaks up, proteins are dispersed, and another cluster is formed elsewhere at a new attachment point. Temporary nanocluster formation and destruction can also be easily identified in Movie S1 (Supplementary Movie S1 online) where the clustering dynamics from the simulation in Fig. 5 is followed for the entire system for 5 s.

Figure 5. Transient trapping of proteins in clusters.

Figure 5

Open in a new tab

Sequence of snapshots corresponding to a simulated membrane of 1 μm2 containing 50 nucleating active inclusions X (red) and 1000 diffusing P proteins (blue) in a lipid media (color code on the right side). The model parameters are τ = 0.5 s, λ = 3, and α = 0.5. The sequence only shows a 0.4 μm2 subsection to observe the details of the cluster formation (green arrow) and destruction (red arrow) process. From left to right and top to bottom, the sequence covers the last 0.4 s of simulation (almost one time period τ).

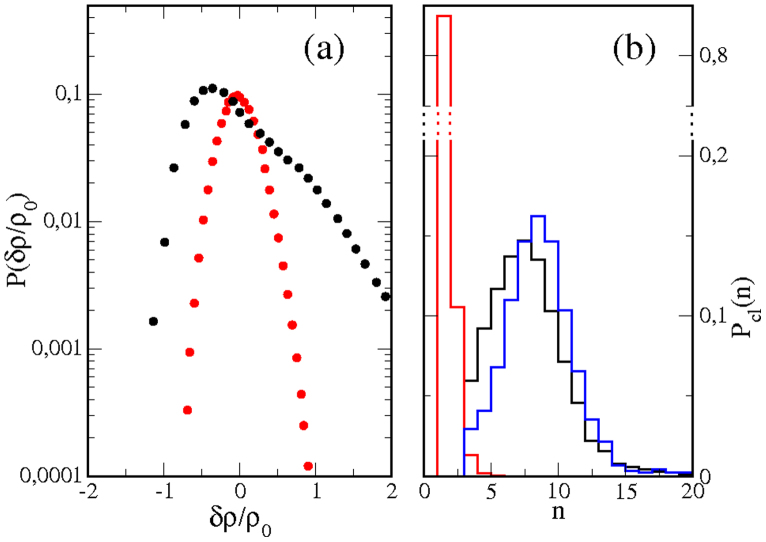
The clustering behavior can be characterized by computing the density fluctuation distribution, P(δρ). In Fig. 6a, the fluctuation distribution for the reference case in Fig. 5 (black symbols) is compared with the distribution corresponding to the random situation (keeping the same number of proteins but removing all the interactions between components, red symbols). The distributions are plotted on a semi-logarithmic scale. In contrast to the random case, which displays the expected Gaussian shape, the interacting system shows a linear tail for positive fluctuations as a consequence of protein aggregation, in agreement with experiments8,29.

Figure 6. Density fluctuations and cluster distribution.

Figure 6

Open in a new tab

(a) Distribution of protein density fluctuations, P(δρ), for NP = 1000. Black: reference case (τ = 0.5 s, λ = 3, α = 0.5). Red: random case (no interactions). (b) Distribution of the probability of finding a protein cluster formed by n proteins, Pcl(n). Black: reference case (τ = 0.5 s, λ = 3, α = 0.5). Red: random case (no interactions). Blue: case with slower cytoskeleton dynamics (τ = 5 s, λ = 3, α = 0.5).

Protein clustering can also be examined by computing the distribution of cluster sizes in the stationary state (t ≫ τ). In our simulations, a cluster is defined as a group of n protein particles that are in direct contact with at least one of the other particles in the cluster. Aggregates of 4 or more particles in a random distribution of 1000 proteins P in a 200 × 200 lattice are extremely rare (see the distribution plotted in red in Fig. 6b corresponding to a random case); thus, we choose n = 4 as the minimum number of particles to form a cluster due to the effect of the lipid-protein interactions proposed in the model. The probability of finding a cluster formed by n proteins, Pcl(n), is plotted in Fig. 6b for the reference case and shows a peak near 7 proteins, which agrees well with experimental estimations of Ras protein aggregates in the inner leaflet of the cell membrane5. From the cluster distribution, the ratio of proteins forming nanoclusters, Φ, can be computed, resulting in Φ = 0.330 for the simulated reference case.

The value of the ratio Φ can be used to determine the role of the different model parameters in the aggregation mechanism. First, the affinity of the mobile proteins for lipid raft phases (λ) determines the attraction to the raft spots nucleated by the X inclusion. A large affinity implies a fast biased motion toward the cytoskeleton-anchored proteins; thus, they recruit a large number of mobile proteins before detaching from the membrane. Reducing the value of λ from 3 to 2 in the reference case decreases the fraction of clustered proteins to Φ = 0.201. A similar effect is found by modifying the affinity of the cytoskeletal inclusions for nucleating a raft-like environment (χ). Protein clustering is also affected by the stability of the lipid mixture (α). Deeply quenched mixtures are barely perturbed. In contrast, when approaching the phase boundary (α → 0+), the lipid system is able to self-organize into regions with different phasic properties (raft and non-raft) in response to a perturbation. Increased proximity to the phase boundary allows weaker perturbations to produce a significant response. Therefore, the effects of the cortical activity and the response of mobile proteins are extraordinarily enhanced close to the phase boundary (small α). For example, reducing the value of α from 0.5 to 0.1 or 0 in the reference case increases the ratio of clustered P proteins to Φ = 0.597 and 0.706, respectively. When approaching the phase boundary, significant protein clustering is obtained, even when the affinity of mobile proteins for raft phases is low. For instance, the reference case results in a very poor clustering effect if λ is set to 1 (Φ = 0.015), but the clustering ability of the lipid mixture is recovered when approaching the phase boundary: Φ = 0.122 for α = 0.1, and Φ = 0.260 for α = 0.

Finally, cytoskeletal activity is the process that drives the membrane system away from equilibrium; thus, its kinetics is fundamental for determining the characteristics of the stationary state. Slow cytoskeletal activity will cause the system to approach equilibrium, namely, the formation of a few long-lasting and very populated protein clusters. Instead, fast cytoskeletal kinetics keeps the system in a very dynamic scenario of many short-lived nanoclusters formed by a reduced number of proteins. For the reference case, reducing τ to 0.1 s leads to Φ = 0.175, whereas increasing τ up to 1 s and 5 s results in larger clustering of Φ = 0.387 and 0.453, respectively. In this latter case, mobile proteins remain recruited for longer times, and the cluster size distribution is slightly shifted to larger clusters (see distribution plotted in blue in Fig. 6b). Experimental observations indicate that several drugs can modify actin polymerization/depolymerization dynamics. In particular, latrunculins slow down actin network turnover by sequestering actin monomers, thus inhibiting actin polymerization. Mild latrunculin treatment slows down the dynamics of GPI-anchored proteins8, in agreement with the effect obtained in our simulations when τ is decreased.

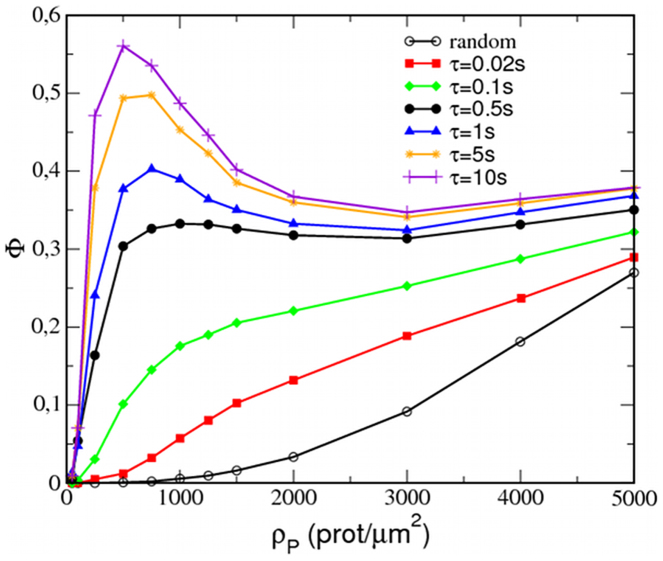
Similarly to experiments2,3, our simulations also capture the violation of the mass action law in the protein aggregation process; the ratio of proteins forming nanoclusters is relatively independent of the total protein density for a large range of protein densities. Simulations of the reference case have been performed while varying the number of mobile P proteins from Np = 50 to 5000, and the ratio of proteins in clusters has been calculated for each protein density and plotted in Fig. 7. For the random situation (black empty circles), the proteins are mostly monomeric for ρP < 1000–2000 prot/μm2, and Φ progressively grows with increasing protein concentration. In contrast, the reference case (black filled circles) displays a sharp increase in Φ slightly above 0.3 at 500 prot/μm2, after which Φ remains relatively constant for, at least, ten times larger protein densities. Variations of only ±3–5% with respect to the average value are found for the clustered protein ratio in the range from ρp = 500 up to ρP = 5000 prot/μm2.

Figure 7. Resonant condition for the invariance of the ratio of proteins forming clusters.

Figure 7

Open in a new tab

Ratio of proteins in clusters, Φ, as a function of the normalized mobile protein density ρP for the reference case (λ = 3, α = 0.5) with different attachment/detachment kinetics: red squares (τ = 0.02 s), green diamonds (τ = 0.1 s), black circles (τ = 0.5 s), blue triangles (τ = 1 s), yellow stars (τ = 5 s), and violet plus symbols (τ = 10 s). Random case (no interactions): black empty circles.

The invariance of the ratio Φ is, however, determined by appropriate tuning of the attachment/detachment kinetics of the nucleating inclusions. Notice that extreme values for the parameter τ result in de facto equilibrium situations. When cytoskeletal inclusions are linked to the membrane for very short periods (low τ), only those proteins that are very close to the inclusion will have sufficient time to approach and form a cluster around the inclusion. As a consequence, little aggregation is observed and will be only noticed for highly populated membranes. In contrast, if cytoskeleton-linking proteins remain attached for long periods of time (large τ), most proteins will have sufficient time to diffuse to a proximal inclusion and form a cluster. In this situation, nucleated raft-like spots become saturated at large protein densities, and as a consequence, the aggregation will be proportionally more pronounced for protein-diluted membranes. The optimal condition can be roughly estimated as follows. On the one hand, the average distance between inclusions in the membrane surface is on the order of (1/ρX)1/2, where ρX is the surface density of inclusions X. On the other hand, the mean squared displacement of a diffusive protein in a time period t follows (2D′t)1/2. Because the inclusions remain attached to the membrane for an average time τ, the resonant condition can be then roughly evaluated to first order by setting (1/ρX)1/2 ≈ (2D′τ)1/2. Such estimation leads to τ ≈ 0.5 s, which shows the clearest invariant behavior for Φ(ρP) in our simulations (see Fig. 7). Importantly, experimental estimations of the lifetime of clusters of Ras proteins5 and GPI-anchored proteins18,19 in cell membranes provide values on the order of a few fractions of second.

Discussion

We have proposed a minimal model that couples the dynamics of lipid phases (raft and non-raft) and proteins (passive and active), allowing a simple spatiotemporal description of the membrane organization. The lipid mixture, although initially homogeneous, can locally be either in a liquid-ordered (raft) phase or in a disordered (non-raft) phase upon external perturbation. The plasma membrane is linked to the cortical cytoskeleton through anchored proteins that act as point-like pinning and raft-nucleation active sites in the membrane. Diffusing proteins show a preference for the lipid raft regions formed around the cytoskeleton-anchored proteins. Cytoskeletal activity is included in the model by considering stochastic changes in the membrane linking point of cytoskeleton-anchored proteins after a given average time.

With these ingredients, our model captures the main experimental observations regarding protein clustering. Once a cytoskeleton protein is attached to the membrane, the protein promotes the nucleation of a small raft-like lipid phase around its location. Neighboring mobile proteins are attracted and become clustered around the cytoskeleton-linking protein. When the cytoskeleton protein detaches from the bilayer, the protein cluster disintegrates. Following this mechanism, clusters are formed at randomly distributed points of the membrane and are dispersed after some time. Our results strengthen the idea that although monomers are free to diffuse, nanoclusters are formed in situ and remain relatively immobile. We also reproduce the main experimental observations. First, the protein fluctuation probability function displays a long-tail that indicates strong protein aggregation8,29. Second, the peaked shape of the cluster size distributions indicates that transient protein aggregates are mostly small and formed by a few (6–8) proteins particles, similarly to Ras nanoclusters5. Third, the fraction of proteins in nanoclusters remains constant, regardless of the global protein concentration2,3. This latter observation has not been accounted for in any existing theory for membrane organization based on equilibrium conditions. In the present model, cytoskeletal activity drives the system to a stationary but dynamic non-equilibrium state that reproduces these types of experimentally observed features. Actually, a resonance phenomenon is found for the time scales of the nonequilibrium process (τ) and the biased protein diffusive motion. At the resonant conditions (found for τ ≈ 0.5 s), the fraction of proteins in nanoclusters becomes invariant. Interestingly, the experimentally measured lifetime of transient clusters of GPI proteins in the outer leaflet18,19 and Ras proteins in the inner leaflet5 of the plasma membrane agree with the attachment/detachment periods that show a resonant behavior in our simulations.

The characteristics of the protein clustering phenomenon described in this study are determined by the three main ingredients of the model. The interplay between the protein-lipid affinity (λ and/or χ), the lipid phase stability (α), and the attachment/detachment kinetics (τ) modulate the duration of the clustering periods and the fraction of clustered proteins, suggesting different and plausible control mechanisms for the aggregation and distribution of proteins in the plasma membrane system. These mechanisms can be implicated in signal-response processes that involve a particular protein distribution in the plasma membrane. At this point it is worth to emphasize the relevance of the cytoskeletal activity as the external process that drives the protein-lipid membrane system out of equilibrium. The competition between the thermodynamics (internal driving force leading to equilibrium by promoting aggregation) and the cytoskeletal activity (external nonequilibrium process that promotes mixing) gives rise to the reported phenomenology. Instead, models based exclusively on equilibrium scenarios are not able to reproduce the protein clustering behavior observed in the cell membrane. For example, one may consider a system of interacting proteins that diffuse in a lipid mixture in the absence of any effect due to the cytoskeletal activity. In this case the system tends to one of the two possible equilibrium states, depending on the values of the protein-protein interaction parameter. For low protein-protein affinity, diffusing proteins are randomly distributed and binary clusters are just occasionally formed. For strong protein interactions, phase segregation takes place and one single cluster is formed containing most of the proteins and raft lipids of the system. Neither the former nor the latter scenario corresponds to the stationary nonequilibrium state observed in the biological context.

Our proposal shares some similarities with other recently published theoretical models. For instance, Lavi et al.35 propose that protein clusters are maintained by a combination of vesicle trafficking, confinement of membrane proteins by the actin cytoskeleton, and dispersion of individual clusters by lateral diffusion35. Alternatively, in the ‘asters model' proposed by Mayor & Rao28,29, passive (not necessarily raftophilic) proteins bound to actin filaments and are advected to the center of ‘aster'-like structures. In our model, this local aggregation process is caused by the preference of diffusing proteins (necessarily raftophilic) for a raft-like lipid phase. In both models, the aggregation centers are continuously forming and reforming elsewhere; thus, the corresponding model outcomes are similar for raftophilic species. It is important to notice that although the dynamics of the mobile proteins follow a diffusive motion that is biased by the presence of the cytoskeleton proteins, our model does not describe an equilibrium situation. This situation would occur if cytoskeleton proteins either diffuse toward equilibrium or remain permanently fixed. Instead, cytoskeleton-anchored proteins display non-equilibrium, externally controlled, attachment/detachment dynamics that keeps the membrane system away from equilibrium; formally, as it is proposed in the ‘asters model'28,29.

Experimental evidence clearly supports these models28,29,35 but, importantly, does not oppose our proposal either. The aim of our proposal is not to be an alternative but to be an additional and complementary contribution to the mechanism of protein aggregation that could be elucidated by further experimental work. In particular, the lipid-mediated mechanism proposed here could be especially useful when addressing the behavior of proteins in the outer membrane leaflet where direct interaction with the cortical cytoskeleton cannot be invoked.

Methods

Simulation procedure

The motion of proteins P follows a lattice-gas scheme and is governed by kinetic Monte Carlo dynamics36. First, all possible protein movements (jumps to neighbor sites) are listed. A Metropolis probability pk is then assigned to each event k: pk = min(1,exp(−ΔkH))/W, where 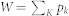Inline graphic, and ΔkH is the energy change due to the jump of the protein. One of these events is chosen according to its probability, and the event is performed. 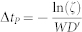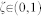The time for the lipid subsystem is then increased by Inline graphic where Inline graphic is a uniform random number, and D′ is the ratio of the protein diffusivity to the lipid diffusion.

The kinetic equation for lipids is discretized and solved using an Euler scheme of mesh size Δx and time step Δtl. tl and tp are the time running for the lipid and protein systems, respectively. To couple both timescales, mobile proteins are only allowed to move if tp < t1; otherwise, the lipid field is updated. Upon doing so, the ‘clocks' of both system components are synchronized and consistent with real time. Lipids diffuse more rapidly than proteins, thus, every time a protein is moved, the local lipid environment is relaxed until it is ‘adapted' to the new protein configuration in a sort of adiabatic approach. In both subsystems, periodic boundary conditions apply.

The mesh size sets the simulation length units, s.l.u = Δx = 5 nm, which we take as the linear size of a small protein. Simulation time units are taken as s.t.u = γ/(D kBT). If we consider γ ≈ (Δx)2kBT, and D = 1 μm2/s, then s.t.u = 2.5 × 10−5 s. The length and time units of all the results shown in this Paper are converted to nanometers and seconds. Proteins are considered to be approximately 50 times slower than lipids (D′ = 0.02). The lipid lattice is initially homogeneous with ϕ (r) = −0.2 (40 mol% of raft-like lipids), and it is decorated with NX cytoskeleton-anchored X proteins and NP diffusing P proteins. The roles of lipid phase stability, lipid-protein affinity, and cytoskeletal activity in protein clustering are investigated by exploring different values for the parameters α, λ and τ.

Author Contributions

J.G.L. and R.R. conducted the simulations. R.R. wrote the main manuscript text. All authors (J.G.L., R.R., J.B.) worked out the model, discussed the results and commented on the manuscript.

Supplementary Material

Supplementary Information

Movie S1 Legends

srep02608-s1.pdf (59.2KB, pdf)
Supplementary Information

Movie S1

Download video file (15.1MB, avi)

Acknowledgments

Computational resources were provided by the Barcelona Supercomputing Center (BSC). Financial support is provided by SEID through projects BFU2010-21847-C02 and by DURSI through project 2009-SGR-1055. The authors would like to thank Drs. Satyajit Mayor and Madan Rao for fruitful discussions.

References

  1. Spira F. et al. Patchwork organization of the yeast plasma membrane into numerous coexisting domains. Nat. Cell Biol. 14, 640–648 (2012). [DOI] [PubMed] [Google Scholar]
  2. Sharma P. et al. Nanoscale organization of multiple GPI-anchored proteins in living cell membranes. Cell 116, 577–589 (2004). [DOI] [PubMed] [Google Scholar]
  3. Mayor S. & Rao M. Rafts: scale-dependent, active lipid organization at the cell surface. Traffic Cph. Den. 5, 231–240 (2004). [DOI] [PubMed] [Google Scholar]
  4. Simons K. & Toomre D. Lipid rafts and signal transduction. Nat. Rev. Mol. Cell Biol. 1, 31–39 (2000). [DOI] [PubMed] [Google Scholar]
  5. Harding A. S. & Hancock J. F. Using plasma membrane nanoclusters to build better signaling circuits. Trends Cell Biol. 18, 364–371 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Anderson R. G. W. & Jacobson K. A role for lipid shells in targeting proteins to caveolae, rafts, and other lipid domains. Science 296, 1821–1825 (2002). [DOI] [PubMed] [Google Scholar]
  7. Park Y.-K., Lee J.-W., Ko Y.-G., Hong S. & Park S.-H. Lipid rafts are required for efficient signal transduction by CD1d. Biochem. Biophys. Res. Commun. 327, 1143–1154 (2005). [DOI] [PubMed] [Google Scholar]
  8. Goswami D. et al. Nanoclusters of GPI-anchored proteins are formed by cortical actin-driven activity. Cell 135, 1085–1097 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Plowman S. J., Muncke C., Parton R. G. & Hancock J. F. H-ras, K-ras, and inner plasma membrane raft proteins operate in nanoclusters with differential dependence on the actin cytoskeleton. Proc. Natl. Acad. Sci. U. S. A. 102, 15500–15505 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chichili G. R. & Rodgers W. Cytoskeleton-membrane interactions in membrane raft structure. Cell. Mol. Life Sci. Cmls 66, 2319–2328 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Owen D. M., Magenau A., Williamson D. & Gaus K. The lipid raft hypothesis revisited--new insights on raft composition and function from super-resolution fluorescence microscopy. Bioessays News Rev. Mol. Cell. Dev. Biol. 34, 739–747 (2012). [DOI] [PubMed] [Google Scholar]
  12. Rodgers W., Farris D. & Mishra S. Merging complexes: properties of membrane raft assembly during lymphocyte signaling. Trends Immunol. 26, 97–103 (2005). [DOI] [PubMed] [Google Scholar]
  13. Vogel S. K. & Schwille P. Minimal systems to study membrane-cytoskeleton interactions. Curr. Opin. Biotechnol. 23, 758–765 (2012). [DOI] [PubMed] [Google Scholar]
  14. Chichili G. R. & Rodgers W. Clustering of membrane raft proteins by the actin cytoskeleton. J. Biol. Chem. 282, 36682–36691 (2007). [DOI] [PubMed] [Google Scholar]
  15. Dinic J., Ashrafzadeh P. & Parmryd I. Actin filaments attachment at the plasma membrane in live cells cause the formation of ordered lipid domains. Biochim. Biophys. Acta 1828, 1102–1111 (2013). [DOI] [PubMed] [Google Scholar]
  16. Chubinskiy-Nadezhdin V. I., Efremova T. N., Khaitlina S. Y. & Morachevskaya E. A. Functional impact of cholesterol sequestration on actin cytoskeleton in normal and transformed fibroblasts. Cell Biol. Int. 37, 617–623 (2013). [DOI] [PubMed] [Google Scholar]
  17. Lenne P.-F. et al. Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. Embo J. 25, 3245–3256 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Suzuki K. G. N. et al. GPI-anchored receptor clusters transiently recruit Lyn and Gα for temporary cluster immobilization and Lyn activation: single-molecule tracking study 1. J. Cell Biol. 177, 717–730 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Suzuki K. G. N., Fujiwara T. K., Edidin M. & Kusumi A. Dynamic recruitment of phospholipase C gamma at transiently immobilized GPI-anchored receptor clusters induces IP3-Ca2+ signaling: single-molecule tracking study 2. J. Cell Biol. 177, 731–742 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Liu A. P. & Fletcher D. A. Actin Polymerization Serves as a Membrane Domain Switch in Model Lipid Bilayers. Biophys. J. 91, 4064–4070 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Machta B. B., Papanikolaou S., Sethna J. P. & Veatch S. L. Minimal model of plasma membrane heterogeneity requires coupling cortical actin to criticality. Biophys. J. 100, 1668–1677 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gómez J., Sagués F. & Reigada R. Effect of integral proteins in the phase stability of a lipid bilayer: Application to raft formation in cell membranes. J. Chem. Phys. 132, 135104–9 (2010). [DOI] [PubMed] [Google Scholar]
  23. Kress A. et al. Mapping the Local Organization of Cell Membranes Using Excitation-Polarization-Resolved Confocal Fluorescence Microscopy. Biophys. J. 105, 127–136 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Saarikangas J., Zhao H. & Lappalainen P. Regulation of the actin cytoskeleton-plasma membrane interplay by phosphoinositides. Physiol. Rev. 90, 259–289 (2010). [DOI] [PubMed] [Google Scholar]
  25. Sheetz M. P., Sable J. E. & Döbereiner H.-G. Continuous membrane-cytoskeleton adhesion requires continuous accommodation to lipid and cytoskeleton dynamics. Annu. Rev. Biophys. Biomol. Struct. 35, 417–434 (2006). [DOI] [PubMed] [Google Scholar]
  26. Park Y. et al. Metabolic remodeling of the human red blood cell membrane. Proc. Natl. Acad. Sci. 107, 1289–1294 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Grzybek M. et al. Spectrin-phospholipid interactions. Existence of multiple kinds of binding sites? Chem. Phys. Lipids 141, 133–141 (2006). [DOI] [PubMed] [Google Scholar]
  28. Chaudhuri A., Bhattacharya B., Gowrishankar K., Mayor S. & Rao M. Spatiotemporal regulation of chemical reactions by active cytoskeletal remodeling. Proc. Natl. Acad. Sci. 108, 14825–14830 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gowrishankar K. et al. Active remodeling of cortical actin regulates spatiotemporal organization of cell surface molecules. Cell 149, 1353–1367 (2012). [DOI] [PubMed] [Google Scholar]
  30. Marguet D., Lenne P.-F., Rigneault H. & He H.-T. Dynamics in the plasma membrane: how to combine fluidity and order. Embo J. 25, 3446–3457 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lajoie P., Goetz J. G., Dennis J. W. & Nabi I. R. Lattices, rafts, and scaffolds: domain regulation of receptor signaling at the plasma membrane. J. Cell Biol. 185, 381–385 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Auth T. & Gov N. S. Diffusion in a fluid membrane with a flexible cortical cytoskeleton. Biophys. J. 96, 818–830 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Suzuki K., Ritchie K., Kajikawa E., Fujiwara T. & Kusumi A. Rapid Hop Diffusion of a G-Protein-Coupled Receptor in the Plasma Membrane as Revealed by Single-Molecule Techniques. Biophys. J. 88, 3659–3680 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Simson R., Sheets E. D. & Jacobson K. Detection of temporary lateral confinement of membrane proteins using single-particle tracking analysis. Biophys. J. 69, 989–993 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lavi Y., Gov N., Edidin M. & Gheber L. A. Lifetime of major histocompatibility complex class-I membrane clusters is controlled by the actin cytoskeleton. Biophys. J. 102, 1543–1550 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Newman M. E. J. & Barkema G. T. Monte Carlo Methods in Statistical Physics. (Clarendon Press, 1999). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Movie S1 Legends

srep02608-s1.pdf (59.2KB, pdf)
Supplementary Information

Movie S1

Download video file (15.1MB, avi)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES