Modeling the measurements of cellular fluxes in microbioreactor devices using thin enzyme electrodes

Abstract

An analytic approach to the modeling of stop-flow amperometric measurements of cellular metabolism with thin glucose oxidase and lactate oxidase electrodes would provide a mechanistic understanding of the various factors that affect the measured signals. We divide the problem into two parts: (1) analytic formulas that provide the boundary conditions for the substrate and the hydrogen peroxide at the outer surface of the enzyme electrode layers and the electrode current expressed through these boundary conditions, and (2) a simple diffusion problem in the liquid compartment with the provided boundary conditions, which can be solved analytically or numerically, depending on the geometry of the compartment. The current in an amperometric stop-flow measurement of cellular glucose or lactate consumption/excretion is obtained analytically for two geometries, corresponding to devices developed at the Vanderbilt Institute for Integrative Biosystems Research and Education: a multianalyte nanophysiometer with effective one-dimensional diffusion and a multianalyte microphysiometer, for which plentiful data for metabolic changes in cells are available. The data are calibrated and fitted with the obtained time dependences to extract several cellular fluxes. We conclude that the analytical approach is applicable to a wide variety of measurement geometries and flow protocols.

1 Introduction

Multianalyte microphysiometers [2–4] are enabling the simultaneous, dynamic electrochemical measurement of extracellular metabolites from ~10⁵ mammalian cells maintained in microfabricated bioreactors with microliter [5,6] or even nanoliter volumes [7–10]. These devices, which make stop-flow measurements of the rates of acidification, consumption of glucose and oxygen, and production or consumption of lactate and other metabolites, are enabling the real-time measurement of metabolic dynamics at sub-minute time scales and may provide a new approach to identification and classification of unknown toxins or toxin cocktails. However, the quantitative interpretation of the data requires a first-principles model that correctly represents the spatiotemporal behavior of various diffusional, biochemical, and electrochemical processes that occur in the transduction of a cellular metabolic flux to an electronic signal. The particular challenge offered by these measurements is their speed—the balance between the rates for these processes is set by the design of the bioreactor and the associated sensors and the goal to optimize the temporal response of the sensor/bioreactor/cell system. Our ultimate design target for our sensor development project is a subsecond to second response; however, as a result we cannot assume that the processes are time-independent, and it is necessary to consider competing processes with similar spatiotemporal scales.

This paper summarizes these processes in a generalized representation of a microbioreactor with electrochemical sensing and then describes a detailed analytical model that can be tailored to our particular measurement geometry. A comprehensive review of analytical and numerical modeling of biosensors and specifically enzyme electrodes recently discusses many of the basics in this area [11,12]. The most significant accomplishment of our work is the formulation of boundary conditions that represent analytically the bioelectrochemistry of the problem, so that the computational effort can be focused on analytical or numerical solutions to a simple diffusion equation. This approach is in contrast to more conventional approaches wherein a numerical model has multiple, connected compartments that have specific properties or functions, such as a particular enzymatic conversion of a metabolite into a substance that can be readily measured electrochemically. The limitation of the conventional approach is the difficulty in obtaining the correct values for the numerous internal parameters that specify or link the various compartments. With our approach, the unspecified parameters appear explicitly in the formulation of the model, and hence their known analytical form can be utilized to simplify the determination of the parameters themselves through calibration experiments.

2 A simple model for electrochemical sensors in a microbioreactor

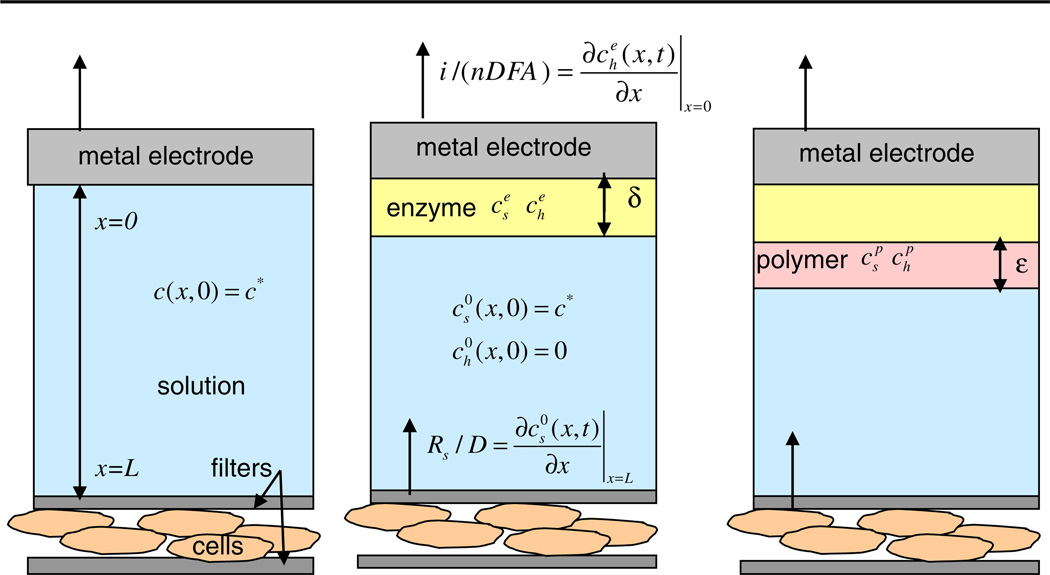
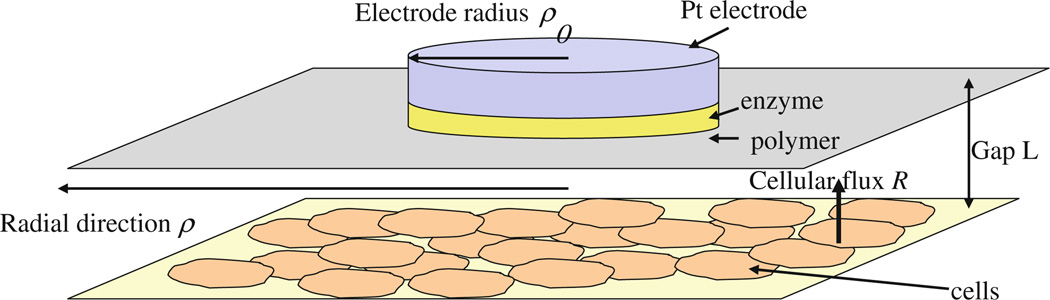
In this paper we consider several simplified models of a microbioreactor consisting of cells that produce metabolic fluxes, located at one surface, and electrodes that allow amperometric measurements at another surface. The cells and the electrodes are coupled through diffusion of the excreted or produced species through the solution inside the volume of the microbioreactor (Fig. 1). The diffusion coupling averages the cellular signals both in space and in time, but at the price of a finite time resolution of the metabolic changes. The solution also nourishes the cells by providing them with oxygen and nutrients and removing waste products. This is achieved through the stop-flow cycle described in Sect. 2.1. Our ultimate aim is to model the stop-flow measurements with the multianalyte microphysiometer (MMP) developed at the Vanderbilt Institute for Integrative Biosystems Research and Education (VIIBRE) [2–4], because it is able to collect large quantities of physiological data that will benefit from automated, model-guided analysis. The upper surface of the microbioreactor is formed by the 10 mm diameter sensor head, which holds two round enzyme electrodes of radii ρ₀ = 0.25 mm for glucose and lactate measurements, an oxygen electrode with a radius of ρ₀ = 0.14 mm, a counter electrode, and intake and output microfluidic tubes through which the solution flows in the MMP chamber. The cells are spread evenly on the lower surface of the reactor and trapped between two porous membranes. Figure 1 presents an idealized one-dimensional picture, where the electrode and the corresponding enzyme layer occupy the entire upper surface, thus the concentrations do not depend on the radial or angular variables. A measurement model with a realistic treatment of the MMP geometry is considered in Sect. 4.2.

Fig. 1.

Three simple models of an instrumented bioreactor or microphysiometer. a Bare sensing electrode, e.g., pH or O₂. b Enzymatic electrode, e.g., lactate. c Enzyme electrode with a polymer layer, e.g., glucose. Concentrations of the substrate c_s (Glu, Lac) and the peroxide c_h have a superscript index e in the enzyme, p in the second polymer layer, and 0 in the liquid. R_s is the cellular flux, D is the diffusion constant, A is the area of the electrode, i is the current, n is the number of donated electrons, and F is the Faraday constant

2.1 Stop-flow measurements

At present, cellular metabolism in a bioreactor can be measured using either stop-flow [2–4] or continuous flow [13] approaches. The stop-flow setup that we have adopted provides the maximum sensitivity to measure slight metabolic changes by integrating the metabolic analytes over the duration of the stop-flow interval. To begin our analysis, and using the simple geometry of Fig. 1, we consider a cylindrical bioreactor that has cells adherent to one end of the cylinder and a plate electrode at the other. We reduce this to a one-dimensional model and consider first the classic case of a metal electrode; for example, one for an amperometric measurement of oxygen (Fig. 1a). We then extend this simple model to include an enzymatically active electrode, such as glucose or lactate (Fig. 1b), and consider the case where the enzyme is sequestered behind a polymer layer (Fig. 1c).

For our present stop-flow measurements, in the flow interval T_f, of typically 80 s, the cells are perfused, and we assume perfect, instantaneous mixing within the bioreactor. In the stop interval T_s, typically 40 s, cellular metabolic activity at the bottom of the bioreactor leads to a local change in nutrient and metabolic concentrations, which diffuse toward the other end of the reactor during T_s. The cellular metabolic activity is integrated over T_s, so a longer T_s will lead to larger concentration changes and electrochemical signals. The duration of T_s is limited by the range of concentrations to which the cells should be exposed, without significantly affecting their metabolism. Too long a T_s may lead to the exhaustion of the measured metabolite and decoupling from the electrode. The length of T_f is set by the time required to flush the bioreactor of metabolites and reestablish the baseline nutrient levels, and for the cells to recover from the previous stop cycle. If a toxin is to be added, the instrument switches fluids at the start of a particular flow interval. The sum of T_f and T_s sets the time resolution of the standard stop-flow technique. Our analysis addresses not only the full cycle, but also the dynamics of the metabolic changes and sensor consumption of analytes during T_s. The main time scale that governs these dynamics is τ = L²/D, where D is the diffusion constant for the measured analyte and L is the distance between the cells and the electrode. Given this understanding of the stop-flow measurement, which is central to our entire approach, we can proceed to specify the boundary conditions.

2.2 Solutions to a simple diffusion boundary problem

In our measurements, the cellular consumption or excretion fluxes serve as a boundary condition for a diffusion boundary problem at the bottom surface of the bioreactor (Fig. 1a). At the electrode at the top, this substance is converted and detected at a rate that is determined by the sensor properties. For example, if the electrode is biased at the correct voltage, the rate of conversion of O₂ to H₂O for electrochemical detection, described by

$${\mathrm{O}}_2+4{\mathrm{e}}^{-}+4{\mathrm{H}}^{+}\stackrel{\mathrm{P}\mathrm{t}}{\to }2{\mathrm{H}}_2\mathrm{O},$$ (2.1)

is sufficiently high that the current is limited solely by the diffusion of O₂ into the sensor region. The diffusion equation and the boundary condition at the cell surface are

$${\frac{\partial }{\partial x}c(t,x)|}_{x=L}=\frac{R(t)}{D}$$ (2.2)

and

$$\frac{\partial c(t,x)}{D\partial t}=\frac{{\partial }^2}{\partial x^2}c(t,x),$$ (2.3)

where c is the substrate concentration, x is the distance from the surface of the electrode, and R(t) is the time-dependent cellular flux (rate) at the surface of the cells, which lies at a distance L from the electrode. The concentration is always zero at the electrode, which consumes the analyte being measured, c(t, 0) = 0. Everywhere else in the chamber, the initial concentration (at t = 0) is c*, c (0, x) = c. The discontinuity at x = 0, t = 0 is a standard idealization of a rapid initialization of the electrical potential at t = 0 and ignores the electrochemical double layer. One way to achieve this initialization is a strong flow of the solution for t < 0, which maintains the constant concentration c* throughout the solution, except in a very thin layer close to the electrode. The flow stop at t = 0 and the metabolic activity of the cells affect concentrations in the media. The electrode current by definition is

$$\frac{I(t)}{nFAD}={\frac{\partial }{\partial x}c(t,x)|}_{x=0},$$ (2.4)

where n = 4 is the number of electrons donated by the electrode, F is the Faraday constant, and A is the surface area of the electrode.

If we look for a solution that is time-independent, the equation and the boundary conditions are satisfied by a linear function in x: c (x) = (R / D) x, where we assume a constant cellular flux R. The stationary solution is the limit of the stop-flow problem for long times. The electrode current is then given by

$$I=-nFAR.$$ (2.5)

The two most popular approaches for solving diffusion boundary problems are the separation of variables (Fourier) and the Laplace transform methods. The first is straightforward but laborious. The second convolves the concentration time dependence with an exponential kernel,

$$\mathrm{c̄}(s,x)=ℒ[c(t,x)]\equiv \underset{0}{\overset{\infty }{\int }}c(t,x)e^{-st}dt.$$ (2.6)

It immediately produces the Laplace transformed result c̄ (s, x) in terms of the Laplace transformed cellular flux; however, the last step—an inverse Laplace transformation—might be more involved. Both methods yield the same well-known answer,

$$c(t,x)=\frac{R_0}{D}(x-\frac{2L}{{\pi }^2}\sum _{n=0}^{\infty }\frac{(-1)\text{sin}\left(\pi \right(n+\frac{1}{2}\left)\frac{x}{L}\right)}{{(n+\frac{1}{2})}^2}\text{exp}(-{\pi }^2{(n+\frac{1}{2})}^2\frac{t}{\tau }\left)\right).$$ (2.7)

The sum consists of exponents whose decay times decrease with increasing index. The largest decay time is $\frac{4}{{\pi }^2}\tau =\frac{4L^2}{{\pi }^{2}D}$, after which the solution approaches the steady-state, linear gradient, given by the first term. Shortly, we will use Eq. 2.7 to determine the time dependence of the stop-flow current, given different scenarios of the cellular metabolic activity.

2.3 Asymptotic time behavior for the inverse Laplace transform

When the Laplace transform method is used to solve a boundary problem with an initial condition, the final step for finding the time dependence of any quantity consists of an inverse Laplace transformation. These transforms are tabulated for many functions, but usually the tables do not provide transforms suitable for boundary value problems, such as Eq. 2.7. The general definition of the inverse transformation involves a contour integral in the complex plane of the Laplace variable s. The integral can be expressed as a sum over the residues of the integrand’s singularities. In most boundary problems, the singularities are poles, located on the imaginary s axis. The singularities away from s = 0 produce decaying exponents, such as in the solution above. They disappear very quickly and can be ignored if we use measurements at times longer than the longest decay time. If there is a remaining time dependence, it comes from a singularity at s = 0, which corresponds to the asymptotic behavior at long times. Such a contribution is missing in the simple problem above, because the asymptotic behavior is time-independent. In the case of enzyme electrodes with two substrates (glucose or lactate, and H₂O₂), the asymptotic temporal behavior is more complicated, as it is in more complicated geometries. Then an easy way to obtain the asymptotic time dependence for any quantity, e.g., the concentration of the substrates or the current, is to expand the Laplace transformed function around s = 0, isolate only the singular part of the expression, and perform an inverse Laplace transform only on it. We present the results of this method later in the paper.

2.4 Time-dependent boundary conditions

When the boundary conditions depend on time, as in the case when the cellular flux changes with time, the solution can be expressed as a convolution of the solution c₀(t, x) for unit boundary conditions (R = 1) and the time derivative of the boundary condition, i.e.,

$$c(t,x)=\underset{0}{\overset{t}{\int }}R(t\prime ){\partial }_t(c_0(t-t\prime ,x)\theta (t-t\prime ))dt\prime =R(0)c_0(t,x)+\underset{0}{\overset{t}{\int }}({\partial }_{t\prime }R(t\prime ))c_0(t-t\prime ,x)dt\prime .$$ (2.8)

This is called the Duhamel formula, and in the Laplace method it reflects the basic properties of the Laplace transformation [14].

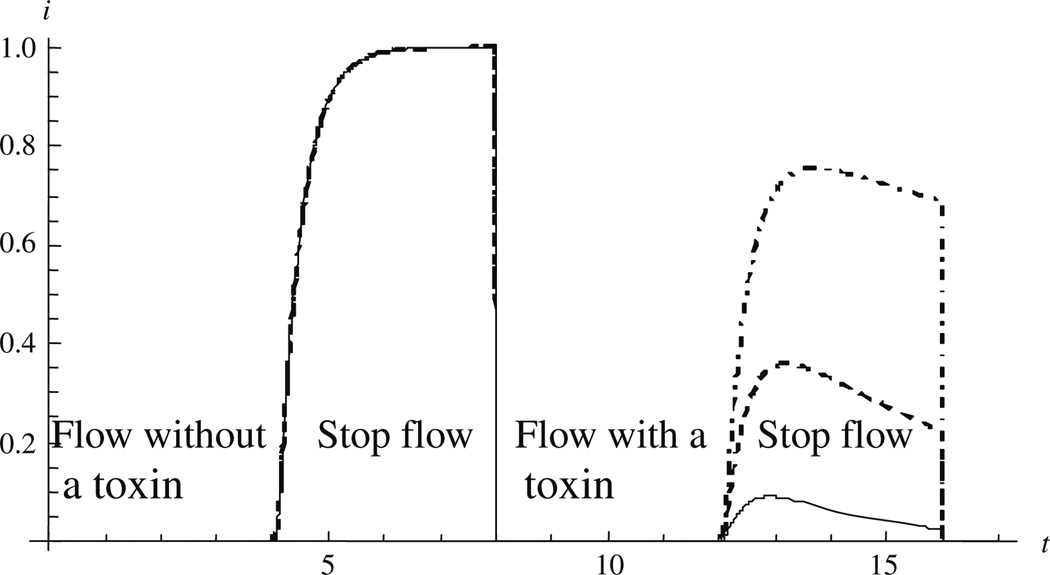
Figure 2 demonstrates the kinetics of a simple measurement. Unlike the example above, where we had a substrate (e.g., O₂) depleted by the cells [2–4], here we consider a substrate produced by the cells (e.g., insulin [15]). At the end of the first stop-phase the cells are exposed to a toxin that suppresses their metabolic activity. The rate of increase of sensor current for 4 < t < 8 is determined by both the constant cellular metabolic flux R and the diffusion properties of the bioreactor. For t > 8 (the beginning of the second flow period), R goes to zero with an exponential time constant σ. The system response is determined by the ratio of σ to the time constant of the bioreactor, τ. Hence the ability to study the dynamics of the cellular response to the toxin is determined in part by the time constant of the bioreactor. As we shall see later, for our system the diffusion of the analyte through the bioreactor is an order of magnitude slower than sensor response. Hence measurement of metabolic dynamics is simplified by using very small bioreactors [5].

Fig. 2.

Electrode current during two sequential stop-flows (4 < t < 8 and 12 < t < 16) with sensor time constant τ = 1. The time constant σ of the toxin-induced cellular response is: solid σ = 2, dashed σ = 5, dotdashed σ = 20

2.5 Extracting the cellular rates

The problem that we aim to solve is an inverse one: extracting the cellular rate from the electrode current data. From the Duhamel formula, we can observe that the flux is convolved with an integral kernel, coming from the solution of the constant flux boundary problem. This smears the flux signal by the characteristic sensor time scale τ. One analogy of the coupling between the cell flux and the electrode current during the stop-flow period is a low-pass electronic signal filter, which prevents the resolution of any signal with a frequency higher than 1/τ. To find the time dependence of the cellular flux for the stop-flow period, we must solve a Volterra type 1 integral equation, which is considered an ill-posed problem. Because of the exponential smearing of the time dependence of the cellular flux signal, the inverse determination of this signal to any desired level of precision requires exponentially higher precision of the measured signal. In other words, any errors of the measured signal are exponentially enhanced in the solution. The same happens with the systematic errors coming from the model itself and the uncertainties of its parameters. This limits the amount of information we can extract from a single stop-flow measurement. The easiest quantity to extract is the time average of the cell flux during the stop-flow period. The next is the average change of the flux during that interval. When the time scales that govern the metabolic changes are long compared to the stop-flow period, these two numbers provide good characterization of a slowly changing cellular flux, which can be approximated by a linear function during the stop-flow interval R (t) = R₁ + R₂t.

At the end of the paper, we discuss the problem of metabolic changes that are faster than the stop-flow interval.

3 Enzyme electrodes

3.1 Description

While unmodified electrodes can measure pH, O₂, and H₂O₂, the use of enzyme coatings enables the measurements of other species that can be enzymatically oxidized. We now extend the simple model discussed above to include the enzyme layer in Fig. 1b. Enzyme electrodes based on glucose oxydase (GOX) and lactate oxydase (LOX) have been studied extensively in recent years [16–19], as have electron transfer and the effects of the inhomogeneity of the enzyme-loaded media on the rate of the reactions [20,21]. Here we consider the simplest possible model of the enzyme reactions, linearized kinetics. One of our typical enzyme electrodes consists of a thin platinum wire with a flat circular end of radius ρ₀. A thin polymer layer that contains the enzymes GOX or LOX is deposited only on that end and exposed to the solution [2]. That layer also includes bovine serum albumin (BSA) and the cross-linking agent glutaraldehyde. The enzyme layer is a porous medium that allows the substrates to diffuse through it. The equation for the effective chemical reaction occurring in the GOX catalyzed enzyme layer is

$$\text{glucose}+{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\to \text{gluconic acid}+{\mathrm{H}}_2{\mathrm{O}}_2.$$ (3.1)

and in the LOX catalyzed layer it is

$$\text{lactate}+{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\to \text{pyruvate}+{\mathrm{H}}_2{\mathrm{O}}_2.$$ (3.2)

The H₂O₂ will then diffuse through the cross-linked BSA to the platinum electrode, where it donates two electrons and is oxidized back to water and oxygen. The potential at which the peroxide is oxidized completely (zero concentration at the electrode) is +0.6 V with respect to an Ag/AgCl reference electrode. While some peroxide escapes from the outer surface of the enzyme layer, most of the available oxygen is recycled within the enzyme layer by reaction (3.1) and the inverse of reaction (2.1) at the electrode surface. A second polymer (Nafion™) layer not containing GOX is deposited on the surface of the GOX layer (Fig. 1c) to limit the diffusion of the glucose, which keeps the reaction in the linearized regime and limits the escape of peroxide, thereby increasing the signal [22]. This layer also minimizes the bio-fouling of the enzyme and the BSA. If a Nafion layer was used with the LOX electrode, the mesoporous, anionically charged Nafion could prevent the diffusion of the negatively charged lactate into the sensor, but because of the much smaller concentrations of lactate in the cell media, such an extra diffusion barrier is not needed for the LOX electrode.

3.2 Scales and assumptions

One of the most important features of the enzyme electrodes is their thinness. The thickness of the enzyme layer δ and the second polymer layer δ is much smaller than the radius of the electrode ρ₀ and the characteristic distance L between the cells and the electrodes, i.e., the microphysiometer height. Hence we consider the diffusion inside the electrode layers as one-dimensional, with concentration depending only upon x. Another approximation that follows from the thinness of the layers is that the characteristic times for diffusion through the layers (δ² / D and ε² / D, where D is the diffusion constant) are much shorter than all other characteristic times, and we do not need to convolve the sensor response with the metabolic and microphysiometer responses; i.e., we treat the sensor response as instantaneous.

Another parameter with a dimension of length is 1/α, where $\alpha =\sqrt{\frac{k_{\text{cat}}{C}_E}{D_1{k}_M}}$ characterizes the enzyme reaction. Here k_cat is the reaction constant, C_E is the enzyme concentration, k_M is the Michaelis constant, and D₁ is the diffusion constant for the substrate. From our calibrations of the electrodes with known concentrations of the substrates we can determine that αδ is small for the glucose (αδ ≈ 0.03), but much bigger for the lactate (0.1 < αδ < 0.9). The condition that the GOX and LOX reactions are in the linearized kinetics regime requires that the concentration of the substrate is very low, i.e., $c_S^0<<k_M$. The linearized kinetics assumption allows the use of linear differential equations and the encapsulation of all the chemical dynamics into a single parameter α. The linearity condition can be controlled by providing sufficient enzyme loading and a diffusion barrier that limits the influx of the substrate and the escape of the peroxide. This condition is violated for certain GOX electrodes used in our MMP cellular metabolic measurements. We can extend the analytic universal boundary conditions, which are developed in Sect. 3.4, for the nonlinear Michaelis–Menten reaction kinetics. We will present these in Sect. 3.5, but the derivation of the relationship between the electrode current and the cellular metabolic activity requires a numerical solution of the usual linear diffusion equations for the bioreactor with nonlinear boundary conditions.

Related to this condition is the assumption that oxygen is sufficiently abundant in the solution (although at lower molar concentrations than the glucose in the solution) that the reaction is controlled by the concentration of the substrate, not by the oxygen. This assumption was experimentally validated for our electrodes during normal measurement conditions [22], although this may not be the case in studies of cellular metabolism under hypoxic conditions. In the hypoxic case, the oxygen can be replaced as an oxidizing agent, through the use of wired enzymes [23].

An important issue is the nature of diffusion inside the enzyme and polymer (Nafion) layers. We adopt the model of a porous substance, where there are large voids through which the substrates can diffuse and an excluded volume unavailable to them. If the diffusion channels are straight enough, the diffusion constant for the corresponding substrate remains unchanged in the porous material. However, the macroscopic concentration is decreased in proportion to the available volume θ_e,p = V_available / V_full, where indices e and p relate to the enzyme and the protective polymer layers. In terms of matching the boundary conditions for diffusion between the different layers, our excluded volume approach produces a concentration jump at the boundary, but a continuous gradient. (The alternative of having two different diffusion constants would result in the concentration being continuous at the boundary and the gradient discontinuous.) Hence we assume that the diffusion constants in the solution and the electrode layers are the same. Numerically, at the temperature of the media (37°C), assuming diluted solutions, D_Lac ≈ D_H2O2 = 1.4 × 10⁻³ mm² / s, D_Glu = 0.9 × 10⁻³ mm² / s, D_O2 = 2.8 × 10⁻³ mm² / s.

3.3 Initial concentrations and quasi-stationary solutions for the electrode layers

The thinness of the electrode layers allows the imposition of simple boundary conditions, involving the concentrations of the glucose or lactate and the peroxide at the outer surface of the electrode layers as well as their gradients and time derivatives. The same boundary conditions also determine the time dependence of the electrode current during the stop-flow period. Because of the thinness, we can ignore the radial direction and consider one-dimensional diffusion equations with a sink term for the substrate and the same term as a source for the peroxide (3.3). As discussed in Sect. 3.2, the design of the enzyme electrodes and the ambient concentration of substrates validate the approximation in which the source/sink term linearly depends only on the concentration of the substrate, but not on the concentration of the oxygen, peroxide, or other products of the enzyme reaction. Our diffusion equations become

$$\frac{\partial c_S^e(t,x)}{D_1\partial t}=\frac{{\partial }^2}{\partial x^2}{c}_S^e(t,x)-{\alpha }^2{c}_S^e(t,x),\frac{\partial c_H^e(t,x)}{D\partial t}=\frac{{\partial }^2}{\partial x^2}{c}_H^e(t,x)-{\alpha }^2{c}_S^e(t,x),$$ (3.3)

where D and D₁ are the diffusion constants for the peroxide and the substrate. The boundary conditions at the platinum electrode surface are simple:

$${\frac{\partial }{\partial x}{c}_S^e(t,x)|}_{x=0}=0,c_H^e(t,0)=0.$$ (3.4)

The electrode current is now defined by

$$\frac{I(t)}{nFAD}=-{\frac{\partial }{\partial x}{c}_H^e(t,x)|}_{x=0}.$$ (3.5)

The equations for the concentrations in the protective layer that lack the source/sink terms are

$$\frac{\partial c_S^p(t,x)}{D_1\partial t}=\frac{{\partial }^2}{\partial x^2}{c}_S^p(t,x),\frac{\partial c_H^p(t,x)}{D\partial t}=\frac{{\partial }^2}{\partial x^2}{c}_H^p(t,x).$$ (3.6)

The matching condition between the concentrations and their derivatives across the enzyme-polymer and polymer-liquid boundaries contains the available volume ratios θ_e and θ_p,

$$\frac{c_S^e(t,\delta )}{{\theta }_e}=\frac{c_S^p(t,\delta )}{{\theta }_p},{\frac{\partial }{\partial x}{c}_S^e(t,x)|}_{x=\delta }={\frac{\partial }{\partial x}{c}_S^p(t,x)|}_{x=\delta },\frac{c_H^e(t,\delta )}{{\theta }_e}=\frac{c_H^p(t,\delta )}{{\theta }_p},{\frac{\partial }{\partial x}{c}_H^e(t,x)|}_{x=\delta }={\frac{\partial }{\partial x}{c}_H^p(t,x)|}_{x=\delta },{c_S^0|}_{\mathrm{\Sigma }}(t)=\frac{c_S^p(t,\epsilon +\delta )}{{\theta }_p},{{\partial }_n{c}_S^0|}_{\mathrm{\Sigma }}(t)={\frac{\partial }{\partial x}{c}_S^p(t,x)|}_{x=\epsilon +\delta },{c_H^0|}_{\mathrm{\Sigma }}(t)=\frac{c_H^p(t,\epsilon +\delta )}{{\theta }_p},{{\partial }_n{c}_H^0|}_{\mathrm{\Sigma }}(t)={\frac{\partial }{\partial x}{c}_H^p(t,x)|}_{x=\epsilon +\delta }$$ (3.7)

where $c_S^0{|}_{\mathrm{\Sigma }}(t),c_H^0{|}_{\mathrm{\Sigma }}(t)$ are the concentrations and ${\partial }_n{c}_S^0{|}_{\mathrm{\Sigma }}(t),{\partial }_n{c}_H^0{|}_{\mathrm{\Sigma }}(t)$ their normal derivatives at the outer surface Σ of the electrodes’ layers. The initial conditions (during the entire flow period) are

$${c_S^0|}_{\mathrm{\Sigma }}(0)=c^{*},{c_H^0|}_{\mathrm{\Sigma }}(0)=0,{{\partial }_n{c}_S^0|}_{\mathrm{\Sigma }}(0)=0,{{\partial }_n{c}_H^0|}_{\mathrm{\Sigma }}(0)=0,$$ (3.8)

where c* is the substrate concentration in the cell media. Solving the stationary equations, we obtain the stationary concentrations inside the layers during the flow periods (which are the initial conditions for the stop-flow concentrations):

$$c_S^e(0,x)=A\text{cosh}(\alpha x),\text{where}A=\frac{{\theta }_e{\theta }_p{c}^{*}}{{\theta }_p\text{cosh}(\alpha \delta )+\alpha \epsilon {\theta }_e\text{sinh}(\alpha \delta )},c_H^e(0,x)=A(1-\text{cosh}(\alpha x))+A\frac{{\theta }_p\text{cosh}(\alpha \delta )+\alpha \epsilon {\theta }_e\text{sinh}(\alpha \delta )-{\theta }_p}{\delta {\theta }_p+\epsilon {\theta }_e}x,c_S^p(0,x)=A\alpha \text{sinh}(\alpha \delta )(x-\delta -\epsilon )+{\theta }_p{c}^{*},c_H^p(0,x)=A{\theta }_p\frac{\text{cosh}(\alpha \delta )+\alpha \delta \text{sinh}(\alpha \delta )-1}{\delta {\theta }_p+\epsilon {\theta }_e}(x-\delta -\epsilon ),$$ (3.9)

and the initial (pump-on) current

$$\frac{I_0}{nFAD}={\alpha }^2\delta {\theta }_e\frac{2\epsilon {\theta }_e+\delta {\theta }_p}{2(\epsilon {\theta }_e+\delta {\theta }_p)}{c}^{*}.$$ (3.10)

The easiest way to find the time-dependent solution of Eq. 3.6 with 3.4 is to perform a Laplace transformation in time (2.6) to obtain the transformed concentration as a function of the Laplace variable s, instead of time t. The s-dependent Laplace transformed solutions are then

$$c_S^{-e}(s,x)={Ā}_S(s)\text{cosh}({\beta }_{1}x)+\frac{1}{s}{c}_S^e(0,x),c_S^{-p}(s,x)={\mathrm{B̄}}_S(s)\text{cosh}({\xi }_{1}x)+{\mathrm{C̄}}_S(s)\text{sinh}({\xi }_{1}x)+\frac{1}{s}{c}_S^p(0,x),c_H^{-e}(s,x)={Ā}_H(s)\text{sinh}({\xi }_{1}x)+\frac{1}{s}{c}_H^e(0,x),c_H^{-p}(s,x)={\mathrm{B̄}}_H(s)\text{cosh}(\xi x)+{\mathrm{C̄}}_S(s)\text{sinh}(\xi x)+\frac{1}{s}{c}_H^p(0,x),\text{where}\xi =\sqrt{s/D},{\xi }_1=\sqrt{s/D_1},{\beta }_1=\sqrt{s/D_1+{\alpha }^2.}$$ (3.11)

We can eliminate the six functions Ā_S(s), Ā_H(s), B̄_S(s), C̄_S(s), B̄_H(s) and C̄_H(s) from the eight matching conditions (3.7) and express ${\partial }_n\overline{c_S^0}{|}_{\mathrm{\Sigma }}(s)$ and ${\partial }_n\overline{c_H^0}{|}_{\mathrm{\Sigma }}(s)$ in terms of $\overline{c_S^0}{|}_{\mathrm{\Sigma }}(s)$ and $\overline{c_H^0·}{|}_{\mathrm{\Sigma }}(s)$.

We are interested in times much longer than the very short time scales δ²/D and ε²/D. These times will correspond to small Laplace variables s, such that ξδ, ξ₁δ, ξε and ξ₁ε are all small. Expanding in all small parameters and keeping the leading terms only, we obtain the boundary conditions and perform an inverse Laplace transform ℒ⁻¹[c̄ (s, x)]. The approximation is quasi-stationary. It neglects fast transient changes in the thin layers. It has some similarity to the Reactor Layer Approximation [24,25]. Next we present the results of this process.

3.4 Universal boundary conditions for the thin enzyme electrodes

We now can write the boundary conditions for all surfaces Σ of the generalized microbioreactor of arbitrary geometry:

$$\text{cells}:{{\partial }_n{c}_S^0|}_{\mathrm{\Sigma }}=\frac{R(t)}{D_1},{{\partial }_n{c}_H^0|}_{\mathrm{\Sigma }}=0,\text{electrode}:{{\partial }_n{c}_S^0|}_{\mathrm{\Sigma }}={{\alpha }^2\delta {\theta }_e{c}_S^0|}_{\mathrm{\Sigma }}+(\delta {\theta }_e+\epsilon {\theta }_p)\frac{{{\partial }_t{c}_S^0|}_{\mathrm{\Sigma }}}{D_1},{c_H^0|}_{\mathrm{\Sigma }}=(\frac{\delta }{{\theta }_e}+\frac{\epsilon }{{\theta }_p}){{\partial }_n{c}_H^0|}_{\mathrm{\Sigma }}+\frac{{\alpha }^2{\delta }^2}{2}{c_S^0|}_{\mathrm{\Sigma }},\text{elsewhere}{{\partial }_n{c}_S^0|}_{\mathrm{\Sigma }}=0,{{\partial }_n{c}_H^0|}_{\mathrm{\Sigma }}=0.$$ (3.12)

The electrode current is expressed through the boundary conditions as

$$\frac{I(t)}{nFAD}=\underset{\mathrm{\Sigma }}{\int }({{\partial }_n{c}_H^0|}_{\mathrm{\Sigma }}+{{\alpha }^2\delta {\theta }_e{c}_S^0|}_{\mathrm{\Sigma }})d^2\mathrm{\Sigma }.$$ (3.13)

These equations have a simple interpretation—they represent the steady-state balances of the substrates. The one for glucose/lactate (S) states that the flux through the electrode boundary is equal to the change of the concentration inside the layer times the volume plus the consumption rate due to the enzyme reaction (also times the enzyme volume). The equation for the peroxide (H) relates the concentration at the boundary to the flux that escapes plus the peroxide created in the enzyme layer. The equation for the current states that the flux of the electrons donated by the peroxide at the metal surface is proportional to the rate of peroxide creation by the enzyme reaction minus the peroxide flux that escapes in the microbioreactor. The fully stationary limit for the enzyme layer is realized when the concentration of the glucose within the layer is constant. In that limit, the time-dependent term $(\delta {\theta }_e+\epsilon {\theta }_p){\partial }_t{c}_S^0{|}_{\mathrm{\Sigma }}/D_1$ in (3.12) disappears. It is also easier to obtain the boundary conditions (3.12), because we must solve time-independent equations. In most of the applications, the time-dependent term above can be neglected, because its dimensionless coefficient Ω = (δθ_e + εθ_p) / L is the smallest among those kept in this approximation.

What remains is to solve the diffusion problem in the microbioreactor,

$$\frac{1}{D_1}\frac{\partial c_S^0(t,x)}{\partial t}=\frac{{\partial }^2}{\partial x^2}{c}_S^0(t,x),\frac{1}{D}\frac{\partial c_H^0(t,x)}{\partial t}=\frac{{\partial }^2}{\partial x^2}{c}_H^0(t,x),$$ (3.14)

consistent with the initial conditions (3.8) and the boundary conditions (3.12). Diffusion problems with boundary conditions that provide a linear combination of the concentrations and their gradients are well defined and can be solved numerically for any geometry of the microbioreactor that couples the cellular fluxes with the electrodes. The addition of a time derivative to the boundary conditions is less common but should be computationally treatable. In the cases when we can neglect Ω, we can simplify the problem by dropping the time derivative.

3.5 Michaelis–Menten regime for the enzyme: nonlinear boundary conditions

It is remarkable that even when the enzyme reaction rate depends nonlinearly on the glucose or lactate concentration, we can solve analytically the nonlinear stationary diffusion-reaction equations for the enzyme layer and again encapsulate all the characteristics of the sensor into nonlinear boundary conditions for the diffusion in the microbioreactor (3.14). The Michaelis–Menten form of the stationary equations for the concentrations in the enzyme layer is

$$\frac{d^2{c}_S^e}{d{x}^2}=\frac{{\alpha }^2{c}_S^e}{1+c_S^e/M},\frac{d^2{c}_h^e}{d{x}^2}=-\frac{{\alpha }^2{c}_S^e}{1+c_S^e/M}.$$ (3.15)

We can reduce these to first order differential equations because they do not depend explicitly on x. The solution for the first one is

$$\sqrt{2}\alpha x=\underset{z_0}{\overset{z}{\int }}\frac{dz}{\sqrt{z-z_0-\text{ln}(1+z)+\text{ln}(1+z_0)}},z=c_S^e(x)/M.$$ (3.16)

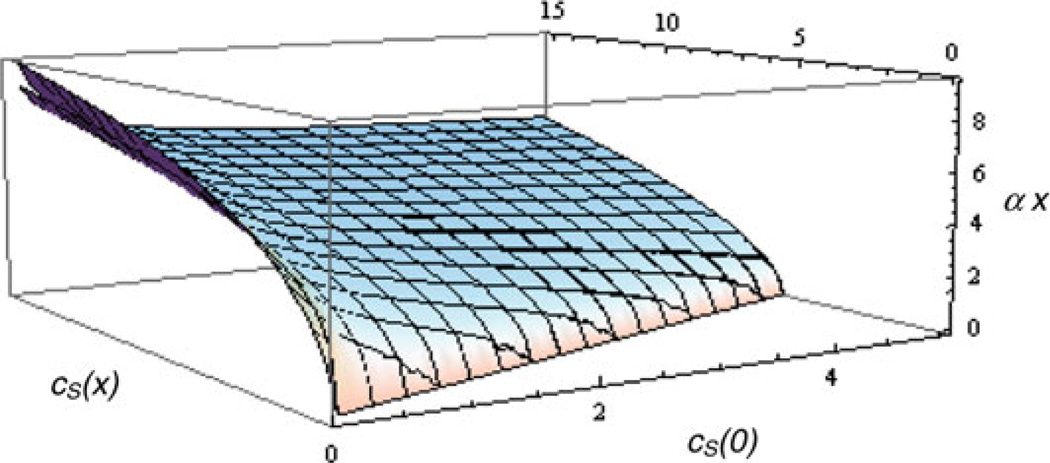
It presents $c_S^e(x)$ as an implicit function (Fig. 3) of x and $c_S^e(0)$,

$$c_S^e(x)=c_S^e(0)F(\alpha x,c_S^e(0)/M).$$ (3.17)

The solution for the peroxide is

$$c_H^e(x)=ax+c_S^e(0)({\partial }_1^{-2}F(0,c_S^e(0)/M)-{\partial }_1^{-2}F(\alpha x,c_S^e(0)/M)),$$ (3.18)

where ${\partial }_1^{-2}F$ means a double indefinite integral with respect to the first argument of F, and a is directly related to the measured current I = nFADa. It is easy to take into account a possible protective Nafion layer to get the following nonlinear boundary conditions:

$${{\partial }_n{c}_S^0|}_{\mathrm{\Sigma }}=\frac{{\theta }_p}{\epsilon }({c_S^0|}_{\mathrm{\Sigma }}-\frac{c_S^e(0)}{{\theta }_e}F(\alpha \delta ,c_S^e(0)/M)),{{\partial }_n{c}_H^0|}_{\mathrm{\Sigma }}=\frac{{\theta }_p}{\epsilon }({c_H^0|}_{\mathrm{\Sigma }}-\frac{a\delta }{{\theta }_e}-\frac{c_S^e(0)}{{\theta }_e}({\partial }_1^{-2}F(0,c_S^e(0)/M)-{\partial }_1^{-2}F(\alpha \delta ,c_S^e(0)/M)\left)\right),$$ (3.19)

where

$${c_S^0|}_{\mathrm{\Sigma }}=c_S^e(0)(\frac{1}{{\theta }_e}F(\alpha \delta ,c_S^e(0)/M)+\frac{a\epsilon }{{\theta }_p}{\partial }_{1}F(\alpha \delta ,c_S^e(0)/M)),a(\frac{\epsilon }{{\theta }_p}+\frac{\delta }{{\theta }_e})-{c_H^0|}_{\mathrm{\Sigma }}=c_S^e(0)(\frac{a\epsilon }{{\theta }_p}{\partial }_1^{-1}F(\alpha \delta ,c_S^e(0)/M)-\frac{1}{{\theta }_e}({\partial }_1^{-2}F(0,c_S^e(0)/M)-{\partial }_1^{-2}F(\alpha \delta ,c_S^e(0)/M)\left)\right).$$ (3.20)

Some of the cellular metabolism data collected with the MMP at VIIBRE are at high concentrations of glucose, which violate the condition $c_S^0<<k_M$. In a future paper we shall present the extraction of the cellular metabolic rates for the nonlinear regime, using the analytical nonlinear boundary conditions presented in this section and a numerical solution for the diffusion equations in the liquid gap.

Fig. 3.

The implicit dependence between c_S(x), c_S(0) and αx in the enzyme layer, using a Michaelis–Menten reaction rate. The second sheet (visible in the upper left-hand corner) is a parameterization of the implicit function using modification of the linearized solution, allowing the explicit expression c_S(x) = c_S(0)F(αx, c_S(0) / M)

4 Analytic solutions for some simple geometries

4.1 One dimension

Equations 3.12–3.14 can be solved analytically for some simple microbioreactor geometries. This is very useful when many of the parameters that appear in the boundary conditions (3.12) are unknown, and it is a fast way to estimate the cellular fluxes by approximating the more complicated geometry of the microbioreactor with a simpler one. For example, one-dimensional analytical solutions to the geometries in Fig. 1b, c can be very useful in deconvolving the experimental data. The concentrations of the substrate and the peroxide will depend only on the distance from the electrode x and not on the other coordinates.

The analytical solution for the Laplace transformed equations (3.14) in the one-dimensional case, using only the cell interface boundary condition, is

$$c_S^{-0}(s,x)={Ḡ}_S(s)(\text{cosh}({\xi }_{1}x)-\text{tanh}({\xi }_{1}L)\text{sinh}({\xi }_{1}x))+(\frac{\mathrm{R̄}(s)\text{sinh}({\xi }_{1}x)}{{\xi }_1{D}_1\text{cosh}({\xi }_{1}L)}+\frac{c^{*}}{s}),c_H^{-0}(s,x)={Ḡ}_H(s)(\text{cosh}(\xi x)-\text{tanh}(\xi L)\text{sinh}(\xi x)).$$ (4.1)

Using the electrode boundary conditions from (3.12), we can find Ḡ_S (s) and Ḡ_H (s), then find the concentrations and their derivatives at the boundary and, from (3.13), finally find the Laplace transformed current

$$\frac{Ī(s)}{nFAD}=\frac{\phi }{L}\left\{\right((1-\phi \frac{\text{coth}({\xi }_{1}L)}{{\xi }_{1}L})(1-\mathrm{\Delta }\xi L\text{tanh}(\xi L))+\mathrm{\Delta }\mathrm{\Xi }{(\xi L\text{tanh}(\xi L))}^2)\frac{c^{*}}{s}+\frac{\mathrm{R̄}(s){\tau }_1}{L}\times \frac{1}{{\xi }_{1}L\text{sinh}{\xi }_{1}L}((1-(\phi +{\tau }_{1}s\mathrm{\Omega })\frac{\text{coth}({\xi }_{1}L)}{{\xi }_{1}L})(1-\mathrm{\Delta }\xi L\text{tanh}(\xi L))+\mathrm{\Delta }\mathrm{\Xi }{(\xi L\text{tanh}(\xi L))}^2\left)\right\},$$ (4.2)

where φ =α²δLθ_e, ${\tau }_{(1)}=\frac{L^2}{D(1)},\mathrm{\Omega }=\frac{\delta {\theta }_e+\epsilon {\theta }_p}{L},\mathrm{\Delta }=\frac{\delta }{2L{\theta }_e},\mathrm{\Xi }=\frac{1}{L}(\frac{\delta }{{\theta }_e}+\frac{\epsilon }{{\theta }_p})$ up to higher order terms in α²δ², δ / L and ε / L. Ignoring Ω, because it contains products of two small quantities (θ_e,p and δ / L, ε / L), using a linearly changing cell rate R(t) = R₁ + R₂t, and taking the large time limit of the inverse Laplace transformation, we get

$$I(t)=nFAD\frac{\phi }{L}\{-c^{*}\phi \frac{t}{{\tau }_1}-R_1\frac{{\tau }_1}{L}(-\frac{t}{{\tau }_1}-\phi \frac{-3t^2+t(6\mathrm{\Delta }\tau -{\tau }_1)}{6{\tau }_1^2})-R_2\frac{{\tau }_1^2}{L}(-\frac{t^2}{2{\tau }_1^2}+\frac{t(\mathrm{\Delta }\frac{\tau }{{\tau }_1}+\frac{1}{6})}{{\tau }_1}+\phi (\frac{t^3}{6{\tau }_1^3}+\frac{t^2}{{\tau }_1^2}(\frac{1}{12}-\mathrm{\Delta }\frac{\tau }{2{\tau }_1})-\frac{t}{{\tau }_1}(\mathrm{\Delta }\frac{\tau }{6{\tau }_1}-\mathrm{\Delta }\frac{{\tau }^2}{3{\tau }_1^2}+\frac{7}{120}\left)\right))+\text{const}\}.$$ (4.3)

When there is no cell flux, and Δ,Ξ are small, we can perform the transform exactly:

$$I(t)=nFAD\phi \frac{c^{*}}{L}(1-\phi (\frac{1}{3}+\frac{t}{{\tau }_1}-\frac{2}{{\pi }^2}\sum _{n=1}^{\infty }\frac{e^{-{\pi }^2{n}^2\frac{t}{{\tau }_1}}}{n^2})-2\mathrm{\Delta }\sum _{n=0}^{\infty }{e}^{-{\pi }^2{(n+1/2)}^2\frac{t}{\tau }}).$$ (4.4)

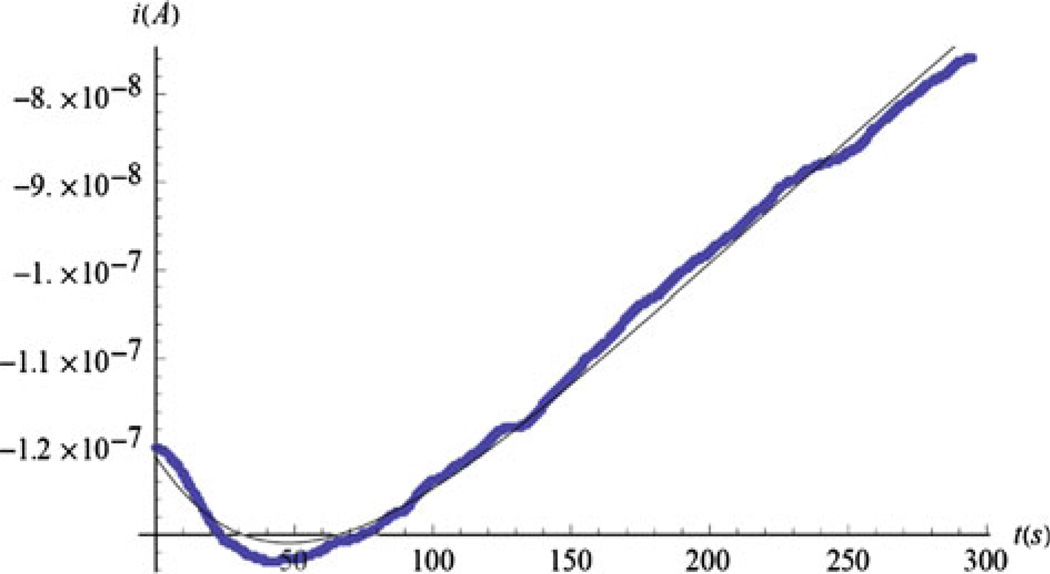
The thick line in Fig. 4 presents no-cell data from a glucose sensor in a nanoliter device, termed a nanophysiometer [26], which is effectively one-dimensional. The thin solid line shows that Eq. 4.4 can provide an excellent three-parameter fit to the data (shown by a thick line). Initially, the current becomes more negative as peroxide begins to accumulate within the enzyme layer after the flow is stopped. During flow, peroxide is lost at the outer electrode layer interface by being washed out so that a zero boundary condition is maintained for the H₂O₂ concentration. When the pump stops, the peroxide loss is decreased and the current grows. Eventually, the glucose concentration in the liquid starts to decrease, the peroxide responds, and the absolute value of the current decreases linearly. The linearity of the time dependence of the no-cell current at long times is a signature for the one-dimensional geometry. The dip is also evident in other geometries.

Fig. 4.

A comparison of the model and experimental data for a thin film glucose sensor. The current without cells in a 1D geometry, with the stop-flow interval beginning at t = 0, fitted using Eq. 4.4: thin curve φ = 0.138, Δ = 0.092. The effective length is L = 0.33 mm. Data courtesy of Franz Baudenbacher

4.2 Solution for the multianalyte microphysiometer (MMP) geometry

The most important geometry, however, is that of our MMP (Fig. 5). If we consider the distance between the electrodes and the outer walls of the head to be much larger than the width of the gap between the upper and lower surfaces (L = 0.1 mm), we can approximate the geometry by two infinite planes, the lower one covered uniformly with cells, and the round enzyme electrode with radius ρ₀ = 0.25 mm in the center of the upper one. Because ρ₀ and L are comparable, we must consider a two-dimensional diffusion within the microphysiometer chamber, where the concentration depends on the time, the vertical distance x, and the radial coordinate ρ. Because of the radial symmetry there is no dependence on the azimuthal angle. In cylindrical coordinates the Laplace transformed diffusion equations are

$$\frac{s\overline{c_S^0}(s,\rho ,x)-c^{*}}{D_1}=\frac{1}{\rho }\frac{\partial }{\partial \rho }\rho \frac{\partial }{\partial \rho }\overline{c_S^0}(s,\rho ,x)+\frac{{\partial }^2}{\partial x^2}\overline{c_S^0}(s,\rho ,x),\frac{s\overline{c_H^0}(s,\rho ,x)-c^{*}}{D_1}=\frac{1}{\rho }\frac{\partial }{\partial \rho }\rho \frac{\partial }{\partial \rho }\overline{c_H^0}(s,\rho ,x)+\frac{{\partial }^2}{\partial x^2}\overline{c_H^0}(s,\rho ,x).$$ (4.5)

We convert the partial differential equations into ordinary ones using another integral transformation, the Hankel transformation ℋ, to obtain the Hankel transformed quantity c̃ (σ):

$$\mathrm{c̃}(\sigma )=\mathscr{H}[c(\rho )]\equiv 2\pi \underset{0}{\overset{\infty }{\int }}c(\rho )J_0(2\pi \rho \sigma )\rho d\rho ,c(\rho )={\mathscr{H}}^{-1}[\mathrm{c̃}(\sigma )]\equiv 2\pi \underset{0}{\overset{\infty }{\int }}\mathrm{c̃}(\sigma )J_0(2\pi \rho \sigma )\sigma d\sigma ,$$ (4.6)

where J_n are the Bessel functions of the first kind. Through this we transform the ρ derivatives in the radial part of the Laplacian into the square of the Hankel variable σ², multiplying the Laplace and Hankel transformed concentration $\tilde{\overline{c}}:\mathscr{H}[\frac{1}{\rho }\frac{\partial }{\partial \rho }\rho \frac{\partial }{\partial \rho }{\mathrm{c̅}}_S^0(s,\rho ,x)]=2\pi {\sigma }^2{\tilde{\overline{c}}}_S^0(s,\sigma ,x)$.

Fig. 5.

The idealized MMP geometry: axial symmetry, and the chamber has infinite radius

A convenient feature of the Hankel transform of the current density is that its value at σ = 0 and x = 0 is the integral of the current density over the upper surface of our bioreactor volume, i.e., the total electrode current we are measuring. The Hankel transformed solution of the diffusion equations within the volume of the bioreactor, without taking into account the boundary conditions, is similar to Eq. 4.1:

$${\tilde{\overline{c}}}_S^0(s,\sigma ,x)={\tilde{\overline{b}}}_S(s,\sigma )(\text{cosh}({\zeta }_{1}x)-\text{tanh}({\zeta }_{1}L)\text{sinh}({\zeta }_{1}x))+(\frac{\mathrm{R̅}(s)\text{sinh}({\xi }_{1}x)}{{\xi }_1{D}_1\text{cosh}({\xi }_{1}L)}+\frac{c^{*}}{s})\frac{\delta (\sigma )}{2\pi \sigma },{\tilde{\overline{c}}}_H^0(s,\sigma ,x)={\tilde{\overline{b}}}_H(s,\sigma )(\text{cosh}(\zeta x)-\text{tanh}(\zeta L)\text{sinh}(\zeta x)),{\zeta }_{(1)}=\sqrt{{\xi }_{(1)}^2+{(2\pi \sigma )}^2},$$ (4.7)

where ${\tilde{\overline{b}}}_{S,H}(s,\sigma )$ are as-yet unspecified functions and δ is the Dirac function. This result is exact for an unbounded plane, but it also contains the singularity of the delta function. For our bounded sensor head we can regularize this solution by considering a large but finite cutoff R₀ for the radial integration that reflects the finite radial size of the MMP: $\frac{\delta (\sigma )}{2\pi \sigma }={\text{lim}}_{R_0\to \infty }\frac{R_0}{\sigma }{J}_1(2\pi R_0\sigma )$. We recognize the right-hand side of this equation as the Hankel transform of θ (R₀ − ρ), which equals 1 for ρ ≤ R₀ and 0 for ρ > R₀.

We now must address the problem of applying the boundary conditions as defined for our untransformed variables (Eq. 3.12) to our Laplace and Hankel transformed variables. At first glance we might assume that this simply requires computing the Hankel transform of the two electrode equations in (3.12). While this is correct for the gradient terms $\left({\partial }_n{c}_{S,H}^0{|}_{\mathrm{\Sigma }}\right)$, the untransformed concentrations must be multiplied by θ (R₀ − ρ) to account for the fact that no conditions are imposed on them outside the small radius of the electrode. Expressing all concentrations in terms of the Hankel transformed ones, we convert the matching conditions (3.12) into an integral equation, where the concentrations ${\tilde{\overline{c}}}_{S,H}^0(s,\sigma ,0)$ are convoluted by an integral kernel

$$K(\sigma ,\sigma \prime )\equiv 2\pi \underset{0}{\overset{\infty }{\int }}{J}_0(2\pi \rho \sigma )\theta ({\rho }_0-\rho )J_0(2\pi \rho \sigma \prime )\rho d\rho =\frac{{\rho }_0}{{\sigma }^2-{\sigma }^{\prime 2}}(\sigma J_0(2\pi {\rho }_0\sigma \prime )J_1(2\pi {\rho }_0\sigma )-\sigma \prime J_0(2\pi {\rho }_0\sigma )J_1(2\pi {\rho }_0\sigma \prime )).$$ (4.8)

The matching conditions (3.12) are now integral equations:

$${{\partial }_n{\tilde{\overline{c}}}_S^0(s,\sigma ,x)|}_{x=0}=2\pi \underset{0}{\overset{\infty }{\int }}K(\sigma ,\sigma \prime )[{\alpha }^2\delta {\theta }_e{\tilde{\overline{c}}}_S^0(s,\sigma \prime ,0)+\frac{\delta {\theta }_e+\epsilon {\theta }_p}{D_1}(s{\tilde{\overline{c}}}_S^0(s,\sigma \prime ,0)-c^{*}\frac{\delta (\sigma \prime )}{2\pi \sigma \prime }\left)\right]\sigma \prime d\sigma \prime ,{{\partial }_n{c}_H^{\simeq 0}(s,\sigma ,x)|}_{x=0}=\frac{{\theta }_e{\theta }_p}{\epsilon {\theta }_e+\delta {\theta }_p}2\pi {\int }_0^{\infty }K(\sigma ,\sigma \prime )\times (c_H^{\simeq 0}(s,\sigma \prime ,0)-\frac{{\alpha }^2{\delta }^2{\theta }_e}{2}{c}_S^{\simeq 0}(s,\sigma \prime ,0))\sigma \prime d\sigma \prime .$$ (4.9)

We can substitute (4.7) into these equations and create the integral equations for ${\tilde{\overline{b}}}_S(s,\sigma )$ and ${\tilde{\overline{b}}}_H(s,\sigma )$, which now provide the linkage between the current based on Eq. 3.13 and the cellular flux R̄ (s) of Eq. 4.7. These are Fredholm equations of the second type. The first contains small parameters under the integral transformation and can be solved iteratively, in our case with two iterations. The second iteration requires an approximation of the integrand with a rational function. This approximation will be the source of the logarithmic corrections with numerical coefficients that will appear in our final result.

The integral in the second equation, however, is multiplied by a large parameter, ρ₀θ_eθ_p / (εθ_e + δθ_p). An iterative solution may not be convergent. The zeroth-order approximation of such an iterative solution corresponds to the case where no peroxide escapes through the outer surface of the enzyme layers. In the one-dimensional case, the zeroth-order approximation produces an electrode current which is twice that of the exact result. Fortunately, the diffusion of the peroxide in the microbioreactor has a zero flux boundary condition everywhere but at the electrode interface, so we can constrain the flux between two limits. The one-dimensional geometry provides a lower limit for the escaping peroxide flux into the microbioreactor. For an upper limit, we can replace the planar electrode with a hemisphere with a radius of $r_0={\rho }_0/\sqrt{2}$ and hence identical area, and consider radial diffusion of the peroxide in the infinite half-space below the x = 0 surface [27].

The solutions for the concentration in the two limiting cases are ${\mathrm{c̅}}_H^0(s,x)={\mathrm{b̅}}_H(s)\text{exp}(-\xi x)$ and ${\mathrm{c̅}}_H^0(s,r)={\mathrm{b̅}}_H(s)\frac{\text{exp}(-\xi r)}{r}$. Writing the boundary conditions for the concentration and its gradient at x = 0, or r = r₀ and excluding ḡ_H(s, σ), we get

$${c_H^{-0}(s)|}_{\mathrm{\Sigma }}=-\frac{{{\partial }_n{c}_H^{-0}(s)|}_{\mathrm{\Sigma }}}{\xi +\frac{\sqrt{2}}{{\rho }_0}m},\text{where}0\le m\le 1\text{for our bounds}.$$ (4.10)

In practice we will keep m ∈ [0, 1] as a free parameter, which (in combination with other parameters) will be determined by our MMP calibration data without cells.

We have now completed our solution in Laplace space and need to compute the inverse Laplace transform. Parts of this process can be performed exactly, while other parts will use the asymptotic behavior, coming from the pole in Laplace space at s = 0, as explained in Sect. 2.3. The exact terms improve the medium-time behavior (t ~ τ) during stop-flow and allow the use of shorter stop-flow times.

The current from our electrode is now given by

$$I(t)={\mathit{I}}_0(1+V(1-e^{B^2\frac{t}{\tau }}\text{erfc}\left(B\sqrt{\frac{t}{\tau }}\right)\left)\right)+\phi \lambda \left(\right(-0.365-\frac{1}{4}\text{log}\left(\frac{1}{\lambda {\tau }_1}\right))(1+V)+\sqrt{\frac{\tau }{t}}\frac{V}{B}(0.401+0.141\text{log}\left(\frac{t}{\lambda {\tau }_1}\right)\left)\right)+\frac{{\mathbf{R}}_1\mathit{\tau }}{{\mathit{c}}^{*}\mathit{L}}\left(\right(\frac{t}{\tau }+\frac{\tau }{6\tau })+)V\left(\right(\frac{t}{\tau }-\frac{2}{B}\sqrt{\frac{t}{\pi \tau }})+(\frac{1}{B^2}-\frac{\tau }{6\tau })\times (1-e^{B^2\frac{t}{\tau }}\text{erfc}\left(B\sqrt{\frac{t}{\tau }}\right)\left)\right)+\phi \lambda (-\frac{t}{\tau }(1+V)(0.115+\frac{1}{4}\text{log}\left(\frac{t}{\lambda {\tau }_1}\right))+\sqrt{\frac{t}{\tau }}\frac{V}{B}(0.238+0.282\text{log}\left(\frac{t}{\lambda {\tau }_1}\right)\left)\right)+\frac{{\mathbf{R}}_{\mathbf{2}}{\tau }^2}{{\mathit{c}}^{*}\mathit{L}}\left(\frac{t}{\tau }\right(\frac{t}{2\tau }+\frac{{\tau }_1}{6\tau })+\frac{V}{B}(\frac{t}{\tau }(\frac{B}{2}\frac{t}{\tau }-\frac{4}{3}\sqrt{\frac{t}{\pi \tau }})+(\frac{1}{B^2}-\frac{{\tau }_1}{6\tau })(B\frac{t}{\tau }-2\sqrt{\frac{t}{\pi \tau }}+\frac{1}{B}(1-e^{B^2\frac{t}{\tau }}\text{erfc}\left(B\sqrt{B\frac{t}{\tau }}\right)\left)\right))+\phi \lambda ({\left(\frac{t}{\tau }\right)}^{\frac{3}{2}}\left)\frac{V}{B}\right(0.034+0.188\text{log}\left(\frac{t}{\lambda {\tau }_1}\right))-{\left(\frac{1}{\tau }\right)}^2(1+V)\times (-0.005+\frac{1}{8}\text{log}\left(\frac{t}{\lambda {\tau }_1}\right))+\sqrt{\frac{t}{\tau }}\frac{V}{B^3}((0.238+0.282\text{log}(\frac{t}{\lambda {\tau }_1}\left)\right)-\frac{{\tau }_1}{\tau }{B}^2((0.025+0.127\lambda )+(0.141+0.070\lambda )\text{log}(\frac{t}{\lambda {\tau }_1}\left)\right))+\frac{t}{\tau }(\frac{V}{B^2}(-0.115-\frac{1}{4}\text{log}(\frac{t}{\lambda {\tau }_1}\left)\right)+\frac{{\tau }_1}{\tau }(1+V(0.025-0.089\lambda -\frac{1}{8}(1+\frac{\lambda }{2})\text{log}(1+\frac{\lambda }{2})\text{log}\left(\frac{t}{\lambda {\tau }_1}\right)\left)\right)\left)\right)),$$ (4.11)

where for convenience we have used the dimensionless (except τ and τ₁) parameters

$$\phi ={\alpha }^2\delta L{\theta }_e,\tau =\frac{L^2}{D},{\tau }_1=\frac{L^2}{D_1},\lambda =\frac{{\rho }_0^2}{L^2},\mathrm{\Delta }=\frac{\delta }{2L{\theta }_e},\mathrm{\Xi }=\frac{1}{L}(\frac{\delta }{{\theta }_e}+\frac{\epsilon }{{\theta }_p}),B=\frac{1}{\mathrm{\Xi }}+m\sqrt{\frac{2}{\lambda }},V=\frac{\mathrm{\Delta }}{\mathrm{\Xi }B(\mathrm{\Xi }-\mathrm{\Delta })}.$$ (4.12)

φ is the key dimensionless parameter that characterizes the enzymatic coupling between the lactate/glucose and the peroxide that donates electrons at the electrode. The slightly different time constants characterizing the diffusion of the metabolic species (Lac or Glu) and the peroxide are τ and τ₁λ is the square of the ratio of the two characteristic scales of the device that make the diffusion essentially two-dimensional. Δ and Ξ are both ratios of two small dimensionless quantities, but the latter also depends on the Nafion layer. When it is absent (for the lactate case) Ξ = 2Δ. B is the reciprocal of Ξ but corrected with our adjustable parameter for the peroxide diffusion m. Our numerical simulations have shown that m ≈ 0. In that case (m = 0) and for the lactate (no Nafion), V = 1. We have neglected terms containing Ω = (δθ_e + εθ_p) / L in the cell flux terms (those with R₁ and R₂), because Ω cannot be determined from the no-cell current, but such terms are small and do not affect the result. I₀ is the stationary current (3.10), which can also be written as $I_0=-nFAD\frac{c^{*}}{L}\phi \left(1-\frac{\mathrm{\Delta }}{\mathrm{\Xi }}\right)$. It can be obtained from the flow-on measurements with different concentrations of the substrate c*.

While (4.11) appears complicated, the origin of each term is easy to track. All the terms are multiplied by I₀, which depends on the glucose or lactate concentration in the media c*, but in reality, only the first terms depend on c*. They represent the no-cell current. The contributions from the cells are presented by the terms proportional to the average cell flux during stop-flow R₁ and its rate of change R₂. The coefficients R₁ and R₂ are made dimensionless by multiplying them by $\frac{\tau }{c^{*}L}$ and $\frac{{\tau }^2}{c^{*}L}$ correspondingly, and the dependence on c* is cancelled. For each of the three contributions (proportional to c*, R₁, and R₂), there are several types of terms as a function of the time. The integer powers of the time, together with some logarithmic corrections, come from the inverse Laplace transform of the solution of the first equation in (4.9). They represent the diffusion of the glucose or lactate inside the microbioreactor. The numerical coefficients are written as decimal numbers because the kernel of the first integral equation in (4.9) is approximated by a rational function. The $e^{B^{2\frac{t}{\tau }}}\text{erfc}\left(B\sqrt{\frac{\tau }{t}}\right)$ terms come from the exact inverse Laplace transform of the solution of the second equation in (4.9). It represents the dynamics of the peroxide escape from the enzyme layer. These terms produce semi-integer powers of the time when their large-time asymptotic is taken. Finally, the semi-integer powers of the time, including the logarithmic corrections, come from the inverse Laplace transform of the product of the two contributions discussed above (i.e., they are mixed terms). To improve the current precision at medium times, we have kept some terms proportional to $\sqrt{\frac{\tau }{t}}$, although they disappear at long times.

The parameters in (4.11) that are poorly known are φ, V, and B, the first two because of the difficulties measuring α, δ, ε, θ_e, and θ_p, and the last one also because of the model parameter m. For the lactate electrode, we must substitute ε = 0, then Ξ = 2Δ, φ = −I₀2L / (nFADc*), and there are only two unknown parameters. For the glucose model, it is also beneficial to express φ through I₀. We have shown that a simpler expression, where the diffusion of the peroxide in the microbioreactor is considered one-dimensional (m = 0) and the complete asymptotic expansion is taken for the time dependence of the current, works well for the lactate model. The simplified formula is

$$I(t)=nFAD\frac{\phi }{L}\left\{c^{*}\right(1-0.56\mathrm{\Delta }\sqrt{\frac{\tau }{t}}-\phi \lambda (0.36+\frac{1}{4}\text{ln}(\frac{t}{\lambda {\tau }_1}\left)\right))+\frac{R_1}{L}t(1-1.13\mathrm{\Delta }\sqrt{\frac{\tau }{t}}-\varphi \lambda (0.11+\frac{1}{4}\text{ln}(\frac{t}{\lambda {\tau }_1}\left)\right)+0.09\mathrm{\Delta }\frac{{\tau }_1}{t}\sqrt{\frac{\tau }{t}}-\frac{{\tau }_1}{t}(\frac{1}{6}+\phi \lambda (0.1+\frac{1}{8}\text{ln}\left(\frac{t}{\lambda {\tau }_1}\right))+\lambda (0.15+\frac{1}{16}\text{ln}\left(\frac{t}{\lambda {\tau }_1}\right)\left)\right))+\frac{R_2}{L}{t}^2(\frac{1}{2}-0.75\mathrm{\Delta }\sqrt{\frac{\tau }{t}}+\varphi \lambda (0.005-\frac{1}{8}\text{ln}(\frac{t}{\lambda {\tau }_1}\left)\right)+0.18\mathrm{\Delta }\frac{{\tau }_1}{t}\sqrt{\frac{\tau }{t}}-\frac{{\tau }_1}{t}\times (\frac{1}{6}+\phi \lambda (-0.026+\frac{1}{8}\text{ln}\left(\frac{t}{\lambda {\tau }_1}\right))+\lambda (0.089-\frac{1}{16}\text{ln}\left(\frac{t}{\lambda {\tau }_1}\right)\left)\right)\left)\right\}.$$ (4.13)

5 Data analysis and discussion

The MMP model depends on several parameters characterizing the electrodes and the geometry of the microbioreactor. Some, such as the electrode radius ρ₀, are known with high precision; others, such as the gap between the cells and the electrode L, are known with 10–20% precision, due to the variability of the chamber size. The diffusion constants D and D₁ and the time constants τ and τ₁ are known with similar precision, although the former can be measured more precisely if necessary. The enzyme and the polymer layer thicknesses are known with much poorer precision. The parameters that are hardest to determine are the porosities θ_e, θ_p, and the enzyme reaction parameter α. The enzyme activity can also change with time. Fortunately all the poorly known parameters enter the formulas in fewer combinations (φ, B, and V in (4.11) and φ and Δ in (4.13)). For the lactate case, we can express φ through the initial current I₀, so we have only one parameter to determine. The poorly known parameters also participate in a few combinations that can be determined through calibration measurements, in the absence of cells, using precisely known concentrations c* of the lactate or glucose in the perfusion medium.

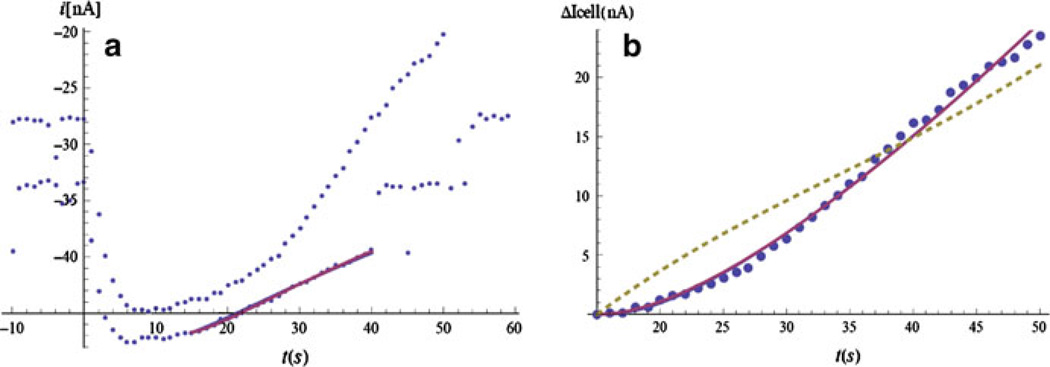
We fit the stop-flow current when the cells are inactivated or not present, in which case we can consider the cell flux R(t) = R₁ + R₂t to be zero. The best case would be to reversibly suppress the cellular activity, without removing or killing the cells. Removing the cells may change the geometry of the device, because of the bulging of the filter and changes in the bioreactor gasket that determines the gap L. Killing the cells may lead to cytolysis and uncontrollable leaking of various substances into the bioreactor. It also prevents the repetition of the calibration procedure at a later time, when the parameters of the enzyme layer, such as α, θ_e, and θ_p, may have changed. In practice, the reversible inactivation is difficult, and the cellular metabolic activity is suppressed using NaF or alamethicin. As discussed in Sect. 4.1, in the beginning of the stop-flow period the electrode current changes rapidly due to transient processes, mostly from the diffusion in the bulk (with time constant τ), but also including even shorter time-constant processes in the enzyme layer and chemical reactions at the surface of the electrode. These processes are difficult to model, and it is sufficient to wait until the system enters a quasi-stationary regime. Thus, the fit is done for electrode current values taken after a certain interval in time (15 s in this case) so that we can use the large-time asymptotic limit for the current (Fig. 6a). The parameters extracted from the fit of the no-cell data are used in the complete formula, when cells are present. The two parameters, R₁ and R₂, are found from the fit of the stop-flow current with cells present (Fig. 6b). The dashed line is a one-parameter fit from a numeric model of the same device presented in Ref. [1]. When we want to extract a single value for the cellular flux from the stop-flow period, we take R(T_s). If we compare this value with a one-parameter fit using (4.11) or (4.13), we find about 20% difference, which might indicate the significance of the cellular fluxes during a single stop-flow period. These changes might be due to exhaustion of certain metabolites and the accumulation of others in the microphysiometer chamber when perfusion is absent.

Fig. 6.

a Lactate data with cells in the MMP (upper points) and no cells (lower ones), with 0.3 Mmol lactate concentration in the solution. The stop-flow starts at t = 0. The stop-flow cell data end at t = 50 s, while the stop-flow no-cell data end at t = 40s, after which some extra lactate is added during the flow for calibration purposes (the step at t = 50 s). The parameters of the model are extracted through data fit (the continuous line). b Current change (ΔI (t) = i (t) − i (15)) for the cell data, starting at t = 15 s. The continuous line is a 2-parameter fit (R₁, R₂) using (4.13). The dashed line is a 1-parameter fit from a numerical model¹ of the same device

When the cellular activity is changing slowly over several stop-flow periods, we expect that the extrapolation of R(t) from one stop-flow measurement to the next will roughly agree with the new flux measurement. Of course, we must assume that the metabolic change due to the stop-flow (discussed above) is smaller than the long-term change over the same period. Discrepancies between the two fluxes may indicate a rapid metabolic process with a time constant comparable to T_s + T_f, such as the one illustrated in Fig. 2.

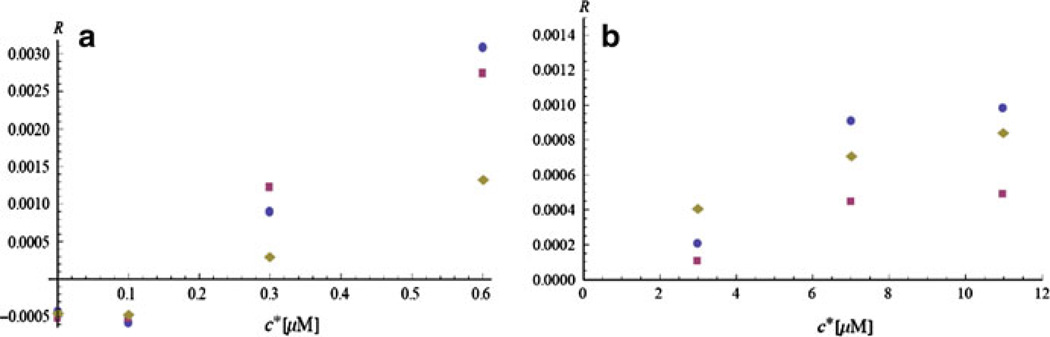
The precision limits of the two-dimensional analytic MMP model are illustrated in Fig. 7a, b. We have extracted the lactate and glucose fluxes for cells that are unperturbed by toxins, but for calibration purposes are exposed to cell media with different concentrations of lactate and glucose. In Fig. 7a the cells’ lactate fluxes are shown at four different values of c*: (0, 0.1, 0.3, and 0.6 mM). The circles use (4.13) and R(T_s); the squares use the same formula, but with R₂ = 0 and a one-parametric fit for R₁; and the diamonds come from a one-parametric fit of the same data using a numeric model of the MMP [1]. Note that both models show that for lactate concentrations in the media below 0.2 mM, the cells excrete lactate (the flux is negative), while for concentrations above this value they consume lactate. Lactate is actively transported by cells in and out. Normally the cell media does not contain lactate, which is added only for calibration purposes.

Fig. 7.

a Lactate cellular fluxes at different initial lactate concentrations. The dots and the squares are different approximations using (4.13). The diamonds come from a numeric model of the MMP. b Glucose cellular fluxes at different initial glucose concentrations. The dots are from the full model (4.12), and the squares use asymptotic expansion. The diamonds are from the numeric model

The glucose fluxes at different concentrations of the glucose in the cell media are shown in Fig. 7b. The concentrations are 3, 7, and 11 mM. The circles indicate the fluxes at the end of the stop-flow extracted from the full formula (4.11), while the squares use the asymptotic expansion of the same formula. The diamonds come again from the numeric model [1]. All models demonstrate that the cells consume glucose at higher rates, when it is more abundant, but there is saturation at high concentrations.

There is about 40% discrepancy between the different models and approximations. Although the two-dimensional analytic MMP model takes into account more parameters of the device (the numeric model ignores the protective layer and the porosity of the enzyme coating), it relies on approximations that are not fully validated. The biggest discrepancy in Fig. 7b is between two different asymptotic expansions of the time dependence of the glucose current. The discrepancy gives an estimate about the model’s precision, which is limited, because at large glucose concentrations, non-linear boundary conditions described in Sect. 3.5 should be used.

If higher precision is desired, we must perform stop-flow calibrations with a known boundary condition at the cellular surface. A device that mimics the cells and provides a known constant flux can be created by substituting the filter that covers the cells (see Fig. 1) with a high diffusion barrier (with diffusion constant D_B) and filling the space underneath with a high concentration of glucose or lactate. We can assume that the difference of the concentrations on the two sides of the diffusion barrier Δc* is constant during the stop-flow. Then the stationary flux through the barrier will be R = Δc*D_B / d, where d is the thickness of the barrier. If D_B is small, the time needed to reach a stationary regime will be large, but we can start the calibration long before the stop-flow period of interest. It is easy to estimate the corrections of Δc* with time, and if d and D_B are known with high precision, we can have an almost perfect calibration, which will strongly reduce the model dependence of the extracted cellular fluxes.

6 Conclusions

We have developed an analytic model for extracting the lactate and glucose fluxes of cells using thin LOX and GOX electrodes and the stop-flow method. The power of our approach is that we decouple the fast diffusion-reaction processes, which happen in the thin enzyme layer, from the diffusion in the body of the microbioreactor, and derive analytic formulas for the boundary conditions that are dependent on the parameters of the enzyme and polymer layers, some of which cannot be easily measured. These parameters, however, can be determined from fits of calibration data where the cellular metabolic activity is suppressed.

Although our main purpose is to create an algorithm for analyzing large amounts of data for cells exposed to different metabolic inhibitors and activators, collected using the multianalyte microphysiometer, the formulas for the boundary conditions at the surface of the electrodes (3.12) and for the electrode current (3.13) can be used for the solution of any diffusion problem containing cell fluxes in a device with different size and geometry. The conditions that make this approach possible are the thinness of the enzyme and protective layers and the requirement that the enzyme reaction is controlled by the substrate (glucose or lactate) and happens in the linearized Michaelis–Menten regime. In particular, this approach is useful for the new generation of nanoliter devices that are being developed at VIIBRE [7–10]. Because of the much smaller characteristic sizes, these devices will have a much better time resolution for the fluxes, which will allow the detailed description of faster metabolic processes. The improved methods for manufacturing these devices will allow the determination of their parameters with better precision and will also limit the parameter deviations between the different electrodes. Having a limited range of device parameters will make the numerical solution for the diffusion in the liquid compartment easier and will make it possible to use any geometry for that compartment.

For the MMP data analysis our aim is to decrease the uncertainties in the parameters and in the model by having better calibration procedures, possibly by developing calibrations with known substrate fluxes. These procedures will greatly decrease the uncertainties of the model due to poorly known parameters and approximations of the diffusion equation solutions due to complicated geometries. Reducing the uncertainties will allow a better time resolution to be obtained even within a single stop-flow cycle, by being able to extract higher derivatives of the cell fluxes R (t) = R₁ + R₂t + R₃t² + R₄t³ + …. This will be another path to studying the fastest metabolic time scales. The extraction of higher derivatives in the MMP setting is possible because, compared to the nanophysiometer, there is less statistical noise in the cell fluxes since the fluxes are averaged over more cells.