Computational modelling of long bone fractures fixed with locking plates – How can the risk of implant failure be reduced?

Abstract

Background and purpose

The Locking Compression Plate (LCP) is part of a new plate generation requiring an adapted surgical technique and new thinking about commonly used concepts of internal fixation using plates. Knowledge of the fixation stability provided by these new plates is very limited and clarification is still necessary to determine how the mechanical stability and the risk of implant failure can best be controlled.

Methods

Upon validation, a finite element model of an LCP attached to a cylinder was developed to simulate and analyse the biomechanics of a transverse long bone fracture fixed with a locking plate. Of special interest were the factors influencing the mechanical conditions at the fracture site, the control of interfragmentary movement and implant failure.

Results

Several factors were shown to influence stability in compression. Increasing translation and/or fracture angle post fixation reduced construct stability. Axial stiffness was also influenced by the working length and plate-bone distance. The fracture gap had no effect on the construct stability when no bone contact occurred during loading.

Stress analysis of the LCP demonstrated that the maximum Von Mises stresses were found in the innermost screws at the screw-head junction.

Interpretation

For the clinical use of the LCP as a locked internal fixator in fractures with an interfragmentary gap of 1 mm, at least two to four plate holes near the fracture gap should be omitted to allow fracture motion and bone contact to occur. This will also achieve a larger area of stress distribution on the plate and reduce the likelihood of fatigue failure due to cyclic loading.

1. Introduction

Since the first plate osteosynthesis reported in 1886 by Hansmann¹ from Hamburg, plating methods and surgical techniques have changed to ensure the best possible fracture healing.

There have been multiple attempts to improve fixation of conventional plates to compromised bone. These have included the use of cement to improve screw torque. Schuhli nuts² and Zespol³ plates were used in early attempts to convert a conventional plate into a fixed-angle device whereby the plate functions like an “internal fixator.” The AO (Arbeitsgemeinschaft fur Osteosynthesefragen) group refined these early attempts and introduced the Point Contact Fixator (PC-Fix)⁴ and the Less Invasive Stabilization system (LISS plate).^5,6 The clinical successes of these plates led to the introduction of the Locked Compression Plate and the recent proliferation of locked-plate designs by several manufacturers.

Traditionally, plate osteosynthesis employed the principles of rigid fixation (leading to primary bone union without the formation of callus) with stability of the construct enhanced by compressing the plate directly onto bone. This method involves the stripping of periosteum and compression of the plate against the bone, both of which can lead to ischaemia and necrosis of bone directly beneath the plate. Locking plates, such as the LCP, provide ‘angular stability’ at the plate-screw interface, which allows extra-periosteal fixation of the plate to the bone. By preserving periosteal blood supply to the bone it addresses the importance of the biological factors involved in fracture healing. The principles of flexible fixation are employed where the goal is for indirect healing with the formation of callus.

Bearing this in mind, one must be aware of a balance between flexible fixation, which encourages callus formation and promotes the healing process, and an unstable fixation, which leads to non-union and implant failure.

Although the LCP system offers a number of advantages in fracture management, its successful use requires careful pre-operative planning, consideration of biomechanical principles, and the use of the appropriate plate and screws combined with good surgical technique. Failure to address these issues can lead to potential pitfalls in terms of implant breakage or non-union.

Little recommendations exist in the current literature for the control of construct stability or how the risk of implant failure can be reduced for internal fixators such as the LCP.

2. Methods

A finite element model of an LCP attached to a cylinder was developed to simulate and analyse the biomechanics of a transverse long bone fracture fixed with a locking plate.

The finite element analysis was performed using ANSYS version 10. The first step in the FE modelling procedure was the idealisation and simplification of the problem. Assumptions were made to simplify the geometry, material behaviour, loads and boundary conditions, and contact mechanics.

A detailed list and explanation of the assumptions used in the FE study are given below:

• •The screw threads in the FE models were neglected and hence the geometry of the screw shaft was simplified into a solid cylinder.^7,8 The inner and outer diameters of a cortical screw's threads are 3.5 mm and 4.5 mm respectively. In the FE models, however, the thread diameters were disregarded and the shaft diameters of the cortical screws were averaged to 3.5 mm. This assumption is made valid by the study by Chao et al.⁹ who showed that the relative importance of the threads in comparison to the root diameter shaft is not a significant factor in screw shaft bending stiffness.
• •The screw heads were simplified to a solid cylinder, with a diameter of 3.5 mm, which provided a perfect fit with screw holes in the plate model.
• •The shaft of the femur was assumed to be perfectly tubular and only a pure transverse diaphyseal fracture was modelled.
• •The underside curvature of the locking plate model and ridges were neglected in the FE model and therefore the plate was assumed to be perfectly flat. The staggered screw holes were perfectly aligned.
• •The material behaviour was assumed to be linear-elastic and isotropic.

2.1. The Locking Compression Plate model

The finite element model (Fig. 1) was created as follows:

• •A hollow cylinder was created to represent the bone. It has an outer diameter of 17.8 mm, an even wall thickness of 4.15 mm, and an inner diameter of 9.5 mm. The total length of the cylinder is 281 mm; however a 1 mm section in the middle of the cylinder is removed to represent the fracture, thus leaving two lengths of 140 mm each.
• •A solid plate (length 138 mm, height 4 mm, width 10 mm) is created symmetrically on the bone with 10 Combi holes (diameter of holes accommodating dynamic compression screws is 4.5 mm and diameter of holes accommodating locking screws is 3.5 mm).
• •Four 19 mm locking screws with a diameter of 3.5 mm were created through the two most proximal and the two most distal locking screw holes. The screws are located 11.5 mm and 24.5 mm from either end of the plate.
• •The volumes are then divided up into smaller more manageable volumes in order to concentrate the mesh at areas of high stress concentrations, and also to allow for bonded contact to be setup between the different volumes. Bonded contacts can be created when two volumes beside each other share similar keypoint positions.
• •Following bonding, the volumes must be assigned their respective material properties. This bone implant complex is represented using two materials, both of which are assumed to be linear-elastic and isotropic. Labelled “Material 1” represents the bone and is assigned a Young's Modulus of 600 MPa and a Poisson Ration of 0.33. The plate and the screws are represented by steel, which has a Young's Modulus of 200 GPa and a Poisson Ration of 0.27.

Fig. 1.

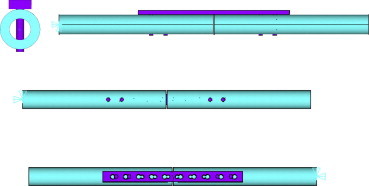
Four views of the finite element model.

2.2. Axial compressive loading

Only axial loading was considered in this study as this is the dominant loading scenario in weight-bearing bones such as the femur and tibia. The application of the axial compressive load is simulated in ANSYS. The axial load is simulated by fixing the distal end of the model and applying a force (400 N) through the bone at the proximal end. This is achieved by selecting only the nodes at the extreme distal end of the bone and constraining them in all degrees of freedom. The nodes at the proximal end of the bone are selected and negative forces in the z-direction are applied to the nodes to simulate the compressive loading situation.

The FE model from above was used to analyse and quantify the magnitude of displacement at the fracture site by applying a load of 400 N and altering the following parameters:

• 1.Fracture gap ranging from 1 mm to 5 mm.
• 2.Fracture translation in the X axis post fixation (i.e. moving the proximal bone segment laterally from 9 mm to −9 mm as shown in the figure below (Fig. 2).
• 3.Fracture angle post fixation, this ranged from 6° to −6° as shown below (Fig. 3).
• 4.Combinations of different fracture translations and angles.
• 5.Number of screws (the displacement in the FE model with all 10 locking screws inserted was compared to removing the 2 innermost screws, 4 innermost screws and 6 innermost screws).
• 6.Plate-bone distance (here the plate was raised from the bone 1 mm at a time, this ranged from 0 to 6 mm.

Fig. 2.

Range of fracture translations used in the FE analysis from −9 to 9 mm in the X-axis post plate fixation.

Fig. 3.

Range of fracture angles used in the FE analysis from 6° to −6° angle at the fracture site post plate fixation.

Displacement results were then logged and analysed using Microsoft Excel spreadsheet.

The same FE model was also used to analyse and quantify the magnitude of stresses experienced by the implant when the innermost sets of screws were removed one at a time. This study also determined the location of stresses experienced by the implant. The results were logged and analysed using Microsoft Excel spreadsheet.

3. Results

3.1. Displacement analysis of load-bearing fixation

3.1.1. Fracture gap

A load of 400 N was applied to the FE model with fracture gaps ranging from 1 mm to 5 mm and the resulting displacement is shown below (Fig. 4).

Fig. 4.

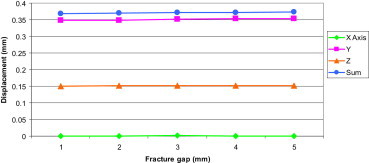
Displacement at the fracture site in FE models with different fracture gaps.

This graph demonstrates that increasing the fracture gap has almost no effect on the resulting displacement at the fracture site.

3.1.2. Fracture translation in the X axis post fixation

Here a load of 400 N was applied to the FE model with a fracture gap of 1 mm at various fracture translations in the X axis. The results are shown in Fig. 5.

Fig. 5.

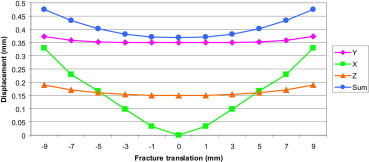
Displacement at the fracture site in FE models with various fracture translations in the X-axis.

This graph shows that increasing the translation results in increase in displacement at the fracture site, especially in the X-axis. The red line in the graph represents the axis of symmetry.

Using the (Sum of displacement) results from above the axial stiffness of the implant construct was calculated (Fig. 6).

Fig. 6.

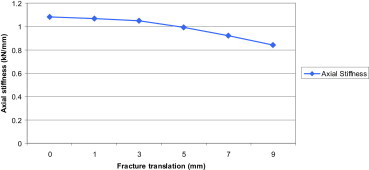
Axial stiffness of the implant construct at increasing fracture translations. The graph demonstrates that increasing the fixation translation results in a decrease in construct stability.

3.1.3. Fracture angle post fixation

In this part of the study a load of 400 N was applied to the FE model with a fracture gap of 1 mm with zero translation at increasing angulation degrees at the fracture site. The results are shown in the graph below (Fig. 7).

Fig. 7.

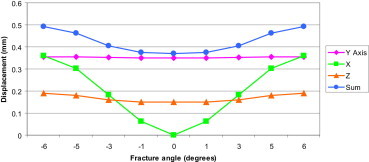
Displacement at the fracture site in FE models with different angulation degrees at the fracture site.

Increasing angulation results in an increase in displacement at the fracture site, more so in the X axis compared to the Y and Z axes. The red line in the graph represents the axis of symmetry.

Using the (Sum of displacement) results from above the axial stiffness of the implant construct was calculated (Fig. 8).

Fig. 8.

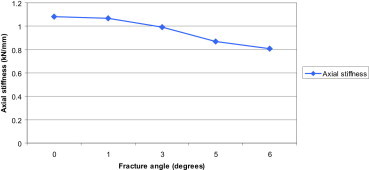
Axial stiffness of the implant construct at increasing fixation angles. The graph demonstrates that increasing fixation angle results in a decrease in construct stability.

3.1.4. Combinations of different fracture translations and angles

In this part of the study a load of 400 N was applied to the FE model with a fracture gap of 1 mm. All possible combinations of fracture translations (−9 to 9 mm) and angles (0–5°) were analysed and the results plotted below (Fig. 9).

Fig. 9.

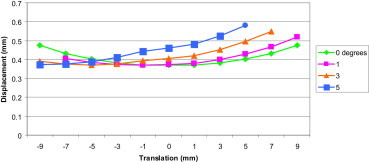
Displacement sum at the fracture site for the various combinations of different fracture translations and angles.

From the graph above it is noted that:

• •For a zero degree fracture angle the displacement is minimal (0.369 mm) when the translation is zero (this represents a perfectly reduced fracture).
• •For a one degree fracture angle the displacement is minimal (0.370 mm) when the translation is −1 mm.
• •For a three degree fracture angle the displacement is minimal (0.370 mm) when the translation is −5 mm.
• •For a five degree fracture angle the displacement is minimal (0.372 mm) when the translation is −9 mm.

From this we can conclude that the minimal displacement in any of the displacement curves above remains almost unchanged, but the fracture translation at which the displacement is minimal varies with different fracture angles.

3.1.5. Number of screws

The displacement in FE models were compared for the cases when all ten locking screws were inserted, followed by removal of the two innermost screws, until 4 screws were remained (two on each side of the plate furthest from the fracture) (Fig. 10).

Fig. 10.

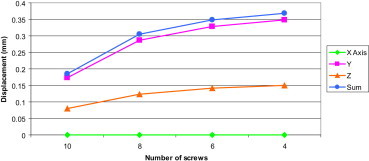
Displacement at the fracture site with different number of screws.

From the results the axial stiffness (Fig. 11) of the implant construct was calculated using the nodal displacements at the fracture sites.

$$\text{Stiffness}=\text{force}/\left(\text{displacement}\right)\text{N}/\text{m}$$

Fig. 11.

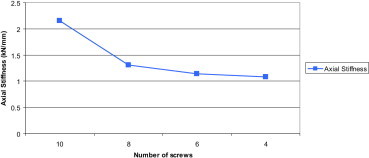
Axial stiffness of the implant construct with different number of screws.

On omission of the two innermost screws near the fracture site, axial stiffness decreased significantly by 39%. Removal of every further pair of innermost screws decreased the stability by about 9%.

3.1.6. Increasing plate-bone distance

Here the plate was raised from the bone 1 mm at a time (range 0–6 mm) and the displacement in the FE models were measured (N.B. for every 1 mm increase in bone-plate distance the lengths of the screws were increased by 1 mm). (Fig. 12).

Fig. 12.

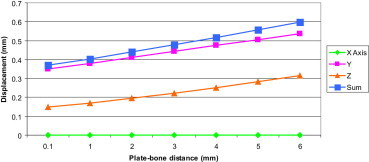
Displacement at the fracture site in the FE models at increasing plate-bone distances.

Using the (Sum of displacement) results the axial stiffness of the implant construct was calculated and plotted in (Fig. 13). Increasing the distance from the plate to bone resulted in a decreased axial stiffness.

Fig. 13.

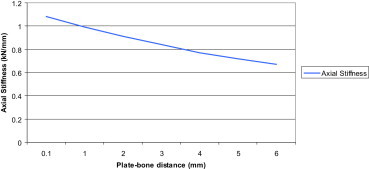
Axial stiffness of the implant construct at increasing plate-bone distances.

3.2. Stress analysis of load-bearing fixation

The same bone and fracture geometries (i.e. same FE model) from the previous chapter was used to analyse and quantify the magnitude and determine the location of stresses experienced by the implant when the innermost sets of screws are removed one at the time.

3.2.1. All screws inserted

When all screws were inserted, the maximum stress in the implant was found at the screw-head junction. This stress concentration (751 MPa) was above yield strength of stainless steel (σ_y = 235 MPa) (Fig. 14), also, when the stresses in the plate were isolated, the maximum Von Mises stress (294 MPa) was still above yield strength of stainless steel (Fig. 15).

Fig. 14.

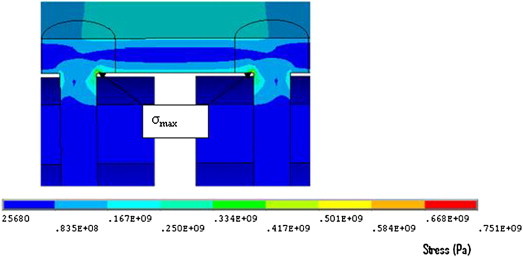
Maximum stress at junction of screw head and shaft.

Fig. 15.

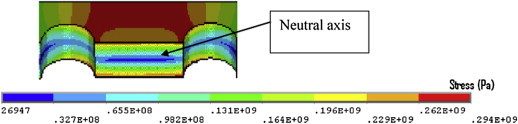
Stresses in experienced by the plate with all screws inserted.

The minimum plate stresses were found in the centre of the plate, where theoretically no stress exists (neutral axis). The maximum stresses were found at the top and bottom of the plate, where it experiences tension and compression, respectively. This agrees with simple beam theory where the minimum stress is in the centre of the plate and the maximum stresses are furthest from the neutral axis (Fig. 16).

Fig. 16.

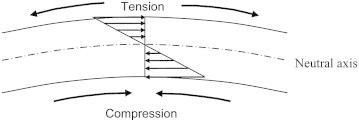
Element of plate under bending, with compression and tension side. The arrows represent the magnitude of stress at a given section of plate.

3.2.2. Two innermost screws removed

When the two innermost screws were removed, the plate stress decreased by 40% (176 MPa) which is considerably lower than the yield strength of stainless steel. The maximum plate stresses were concentrated at the outer edges of the two middle screw holes at the portion of the holes that accommodates the dynamic compression screws (Fig. 17). The maximum stresses were again found in the innermost screws (467 MPa), this represents a reduction of 38% compared to the previous case.

Fig. 17.

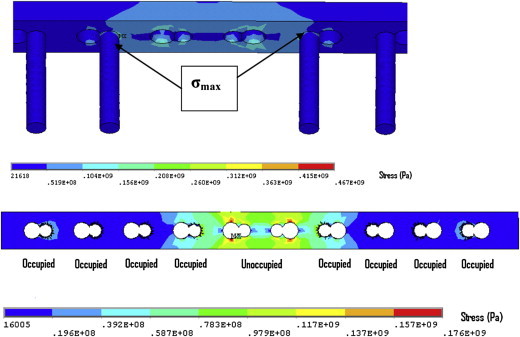
(top) Maximum stress at junction of screw head and shaft with two innermost screws removed, and (bottom) plate stress.

3.2.3. Four-six innermost screws removed

The maximum stresses where again found in the innermost screws (324 MPa with the middle four screws removed) and (298 MPa with the middle six screws removed) (Figs. 18 and 19). The screw stresses changed significantly from when all the screws were fully inserted to when the middle six screws were removed (751–298 MPa). The maximum stresses in the screws were above yield strength of stainless steel.

Fig. 18.

Implant stress contour when four of the innermost screws were removed. Note: the maximum plate stress was 130 MPa.

Fig. 19.

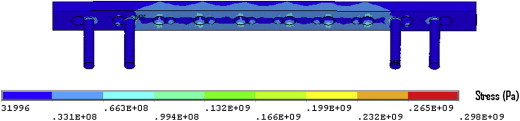
Implant stress contour when six of the innermost screws were removed. Note: the maximum plate stress was 109 MPa.

The maximum plate stresses remained concentrated at the outer edges of the two outermost empty screw holes at the portion of the holes that accommodate the dynamic compression screw, (130 MPa with the middle four screws removed and 109 with the middle 6 screws removed).

3.2.4. Summary

The graph below (Fig. 20) shows the summary of stress analysis results obtained above.

Fig. 20.

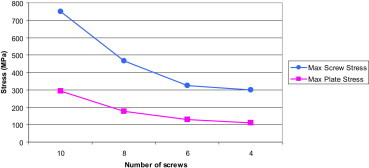
Maximum stresses in the screws and plate as the innermost sets of screws were removed one at a time.

The stress concentrations were localised to a point or a specific region of the implant. The majority of stresses were therefore below the yield stress, and hence the implant would not have deformed permanently. Despite this, these stress concentrations can indicate where fatigue failure might occur.

4. Discussion

In the past, the appearance of callus in plate osteosynthesis was assumed to indicate a lack of stable fixation. Today, indirect healing with callus formation is no longer regarded as a disturbance to healing but a welcome sign of a positive bone reaction. However, in the stabilisation of fractures of long bones there is a fine line between flexible fixation, which enhances callus formation and improves the healing process, and an unstable fixation, which leads to non-union and/or implant failure.

When selecting an internal fixator for plate osteosynthesis, the main problem is to determine how the mechanical environment of the fracture and implant failure can be controlled. The first clinical results with internal fixators were promising,^10,11 although determining the number and position of screws was mainly based on clinical experience with conventional plates as described in numerous studies.^12,13 The present study primarily focused on understanding the control mechanisms of stability and fatigue failure for internal fixators such as the LCP.

The working length had a significant effect on construct stability. By omitting the two innermost screws (one on either side of the fracture), the construct became more flexible by about 39% in compression. These results are in agreement with those of biomechanical investigations for conventional plating techniques.¹⁴ Removal of further pairs of innermost screws further increased flexibility but rather modestly.

It has been shown that axial stiffness is reduced when the same numbers of screws are used in a longer plate than in a shorter plate.⁸ Therefore Stoffel et al⁸ suggests that long plates should be used to optimise axial stability and that the plastic deformation of the plate is reduced when the screws closest to the fracture site are removed. This results because when the working length of the plate is increased, more flexibility is tolerated.

Gautier and Sommer¹⁵ note that the absolute minimal arrangement of screws is two monocortical screws placed in each main fragment of bone. If the two monocortical screws are replaced with bicortical screws the bone-screw interface improves, however, there is no improvement in fatigue life. Therefore, the recommendation is that there are a minimum of three screws in each main fragment.^8,15

Increasing the distance between the plate and the bone significantly affected construct stability. By increasing this distance from 1 mm to 5 mm, axial stiffness decreased by 27% (7–9% for every 1 mm) as the unsupported free part of the screw between the plate and bone increases, it produces a greater lever arm effect during compression testing and hence a weaker construct.

A recent study by Ahmad et al¹⁶ showed that LCPs at 2 mm and flush to the bone responded in a similar manner and failed at significantly higher load than the plates at 5 mm in static loading. The plates at 5 mm also showed a much higher displacement in cyclic axial and torsion testing. Therefore it is recommended to place the plate at a distance less than or equal to 2 mm.

The fracture gap had no effect on the construct stability when no bone contact (load sharing) occurred during loading. Stofell et al⁸ found the LCP plate to behave differently when bridging a small fracture gap, compared to a larger gap when no load sharing can occur during dynamic loading, such that when bridging a large gap the screws should be kept close to the centre of the plate because of the decreased Von Mises stresses and the increased cycles to failure.

Increasing the axial loading resulted in a proportional increase in displacement at the fracture site (linear relationship) when no bone contact occurred. The increase load did not affect the stiffness of the construct.

Increasing fracture angle reduced construct stability. By increasing the angle from 0 (perfect reduction) to 5° in the lateral axis, construct stability decreased by 19%. Similarly increasing the fracture translation from 0 (perfect reduction) to 5 mm in the lateral axis reduced construct stability by 8%.

Analysis of the combinations of different fracture translations and angles showed that the maximum achievable construct stability remained unchanged for the different fracture angles. However, the fracture translation at which the maximum stability is achievable varies with the different fracture angles.

In our finite element calculations under pure axial compression, axial stiffness values were found to be similar to those derived from the in vitro tests carried out by Ahmad et al¹⁶ and Stoffel et al.⁸

The stress analysis demonstrated that the maximum Von Mises stresses were found in the innermost screws at the screw-head junction. When the stresses in the plate were isolated, the maximum Von Mises stresses were concentrated at the outer edges of the two outermost empty screw holes at the portion of the holes that accommodate the dynamic compression screw. Maximum stresses decreased with the removal of the two innermost screws, a pair at a time. The reduction in the stresses were most significant when the first pair of innermost screws were removed.

Hardware failure (plate failure, or screw breakage) is a complication that has been reported to occur in as many as 18% of plate fixations,¹⁷ often as a result of an inappropriate fixation technique, rather than the choice of plate.

The use of locked screws at the level of the fracture passing through the fracture line and short working lengths are examples of such inappropriate techniques,¹⁷ as it reduces the flexibility of the implant⁸ which hinders the micromotion needed for callus formation.

Sommer et al¹⁸ reported on four cases of implant failure as a result of technical error and not of the implant itself. Therefore it is evident that special training and care must be taken in planning such that implant application is optimised.

Conflicts of interest

All authors have none to declare.