The evolution of genetic architectures underlying quantitative traits

Abstract

In the classic view introduced by R. A. Fisher, a quantitative trait is encoded by many loci with small, additive effects. Recent advances in quantitative trait loci mapping have begun to elucidate the genetic architectures underlying vast numbers of phenotypes across diverse taxa, producing observations that sometimes contrast with Fisher's blueprint. Despite these considerable empirical efforts to map the genetic determinants of traits, it remains poorly understood how the genetic architecture of a trait should evolve, or how it depends on the selection pressures on the trait. Here, we develop a simple, population-genetic model for the evolution of genetic architectures. Our model predicts that traits under moderate selection should be encoded by many loci with highly variable effects, whereas traits under either weak or strong selection should be encoded by relatively few loci. We compare these theoretical predictions with qualitative trends in the genetics of human traits, and with systematic data on the genetics of gene expression levels in yeast. Our analysis provides an evolutionary explanation for broad empirical patterns in the genetic basis for traits, and it introduces a single framework that unifies the diversity of observed genetic architectures, ranging from Mendelian to Fisherian.

1. Introduction

A quantitative trait is encoded by a set of genetic loci whose alleles contribute directly the trait value, interact epistatically to modulate each other's contributions, and possibly contribute to other traits. The resulting genetic architecture of a trait [1] influences its variational properties [2–5], and therefore affects a population's capacity to adapt to new environmental conditions [1,6,7]. Over longer time scales, genetic architectures of traits have important consequences for the evolution of recombination [8] and of sex [9], and even reproductive isolation and speciation [10].

Although scientists have studied the genetic basis for phenotypic variation for more than a century, recent technologies, as well as the promise of agricultural and medical applications, have stimulated tremendous efforts to map quantitative trait loci (QTL) in diverse taxa [11–19]. These studies have revealed many traits that seem to rely on Fisherian architectures, with contributions from many loci [20], whose additive effects are often so small that QTL studies lack power to detect them individually [16,21,22]. Other traits, however, are encoded by a relatively small number of loci—including the large number of human phenotypes with known Mendelian inheritance.

The subtle statistical issues of designing and interpreting QTL studies in order to accurately infer the molecular determinants of a trait are already actively studied [16,21,22]. Nevertheless, distinct from these statistical issues of inferences from empirical data, we lack a theoretical framework for forming a priori expectations about the genetic architecture underlying a trait [1,4]. For instance, what types of traits should we expect to be monogenic, and what traits should be highly polygenic? More generally, how does the genetic architecture underlying a trait evolve, and what features of a trait shape the evolution of its architecture? To address these questions, we developed a mathematical model for the evolution of genetic architectures, and we compared its predictions with a large body of empirical data on quantitative traits.

2. Results and discussion

(a). Genetic architectures predicted by a population-genetic model

Our approach to understanding the evolution of genetic architectures combines standard models from quantitative genetics [23] with the Wright–Fisher model from population genetics [24]. In its simplest version, our model considers a continuous trait whose value, x, is influenced by L loci. Each locus i contributes additively an amount α_i, so that the trait value is defined as the mean of the α_i values across contributing loci. This trait definition means that a gene's contribution to a trait is diluted when L is large, which prevents direct selection on gene copy numbers when genes have similar contributions [25,26]. We discuss this definition below, along with alternatives such as the sum. The fitness of an individual with trait value x is assumed to be Gaussian with mean zero and standard deviation σ_f, so that smaller values of σ_f correspond to stronger stabilizing selection on the trait [23]. Individuals in a population of size N replicate according to their relative fitnesses. Upon replication, an offspring may acquire a point mutation that alters the direct effect of one locus, i, perturbing the value of α_i for the offspring by a normal deviate; or the offspring may experience a duplication or a deletion in a contributing locus, which changes the number of loci L that control the trait value in that individual (see Methods). Point mutations, duplications and deletions occur at rates μ, r_dup, r_del, which have comparable magnitudes in nature (see electronic supplementary material, table S1) [27–30]. We assume that deletions are more frequent than duplications, for two reasons. First, in our model, deletions represent both actual deletions and loss-of-function mutations. Second, even ignoring loss-of-function mutations, the frequency of deletions is known to exceed that of duplications [31]. Finally, an offspring may also increase the number of loci that contribute to its trait value by recruitment; that is, by acquiring a recruitment mutation, with probability μ × r_rec, in some gene that did not previously contribute to the trait value (see Methods).

Over successive generations in our model, the genetic architecture underlying the trait (i.e. how many loci contribute to the trait's value and the extent of their contributions) varies among the individuals in the population, and evolves. The genetic architectures that evolve in our model represent the complete genetic determinants of a trait, which may include—but do not correspond precisely to—the genetic loci that would be detected based on polymorphisms segregating in a sample of individuals in a QTL study. We discuss this important distinction below, when we compare the predictions of our model with empirical QTL data.

We studied the evolution of genetic architectures in sets of 500 replicate populations, simulated by Monte Carlo, with different amounts of selection on the trait. We ran each of these simulations for 50 million generations, in order to model the extensive evolutionary divergence over which genetic architectures are assembled in nature. The form of the genetic architecture that evolves in our model depends critically on the strength of selection on the trait. In particular, we found a striking non-monotonic pattern: the equilibrium number of loci that influence a trait is greatest when the strength of selection on the trait is intermediate (figure 1). The distribution of allelic effects also evolves in our model (see electronic supplementary material, figure S1). The variance of allelic effects across loci exhibits a similar pattern as the one observed for the number of contributing loci: it is maximized for traits under intermediate selection. In other words, our model predicts that traits under moderate selection will be encoded by many loci with highly divergent effects, whereas traits under strong or weak selection will be encoded by relatively few loci. Moreover, the distribution of allelic effects determines the typical phenotypic effects of gene deletions and duplications, which are also greatest for traits under intermediate selection (see electronic supplementary material, figure S2).

Figure 1.

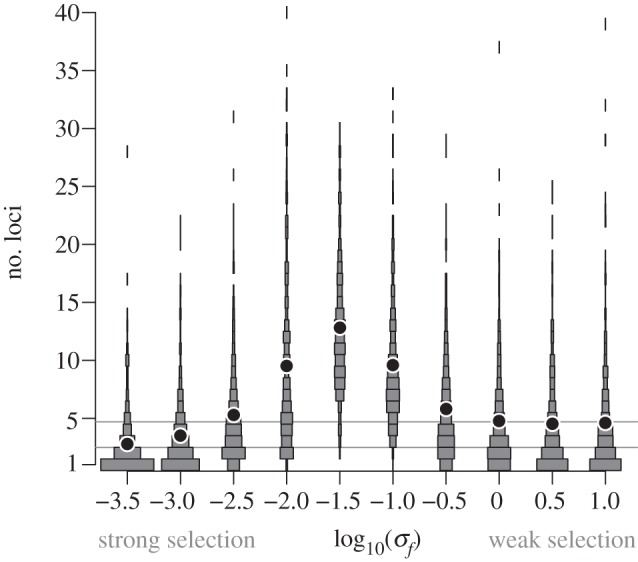
The genetic architecture underlying a trait depends on the strength of selection on the trait, in a population-genetic model. Traits subject to intermediate selection (intermediate values of σ_f) evolve genetic architectures with the greatest number of controlling loci. Dots denote the mean number of loci in the architecture underlying a trait, among 500 replicate Wright–Fisher simulations, for each value of the selection pressure σ_f. The rectangular areas represent the distribution of the number of loci in the architecture. The neutral expectations for the equilibrium number of loci (see Methods) are represented as grey lines, when recruitment events are neutral (top line) or not (bottom line). Parameters are set to their default values (see electronic supplementary material, table S2).

We also studied how epistatic interactions among loci influence the evolution of genetic architecture. To incorporate the influence of locus j on the contribution of locus i, we introduced epistasis parameters β_ji, so that the trait value is now given by

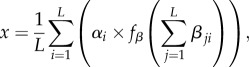2.1

where f_β is a standard sigmoidal filter function (see Methods; see also electronic supplementary material, figure S4a) [8]. As with the direct effects of loci, the epistatic effects were allowed to mutate and vary within the population, and evolve. Although significant epistatic interactions emerge in the evolved populations, and modulate the direct contributions of individual alleles (see electronic supplementary material, figure S3b,c), the presence of epistasis does not strongly affect the average number of loci that control a trait (see electronic supplementary material, figures S3a and S4). Epistasis is not required for the evolution of large L, nor does it change the shape of its dependence on the strength of selection.

(b). Intuition for the results

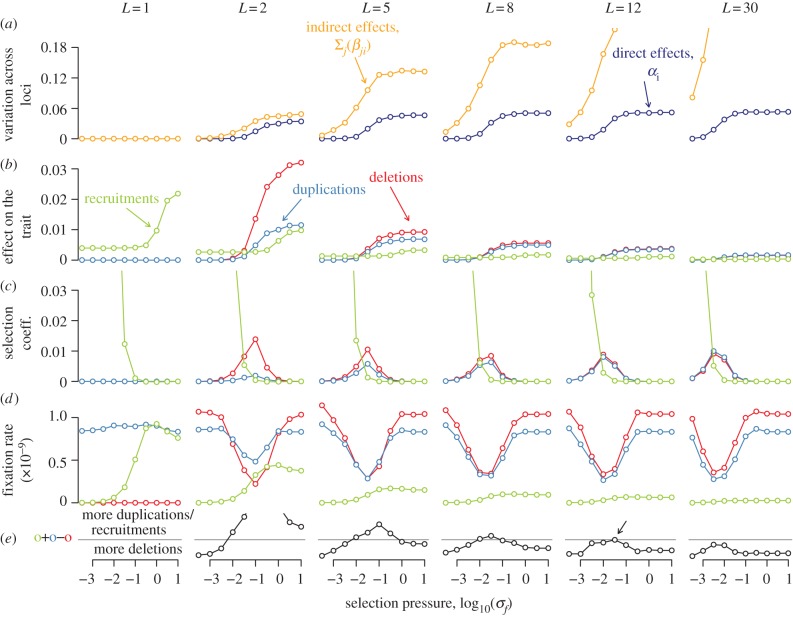
There is an intuitive explanation for the non-monotonic relationship between the selection pressure on a trait and the number of loci that control it. For a trait under weak selection (high σ_f), changes in the trait value have little effect on fitness. Thus, even if deletions, recruitments and duplications change the trait value, these changes are nearly neutral (figure 2). As a result, the number of loci controlling the trait evolves to its neutral equilibrium, which is small because deletions are more frequent than duplications and recruitments (see Methods; figure 1; electronic supplementary material S3). On the other hand, when selection on a trait is very strong (low σ_f), few point mutations, and only those with small effects on the trait, will fix in the population. As a result, all loci have similar contributions to the trait value (figure 2a), and so duplications or deletions again have little effect on the trait or on fitness (figure 2b,c). In this case, the equilibrium number of loci is given by the value expected when deletions and duplications, but not recruitments, are neutral (figure 1; electronic supplementary material S3).

Figure 2.

The consequences of gene duplications, recruitments and deletions in a population-genetic model. Populations were initially evolved with a fixed number of controlling loci L (a), and we then measured the effects of recruitments, deletions and duplications on the trait value (b) and on fitness (c). From the latter, we calculated the rate at which deletions, recruitment and duplications enter and fix in the population (d), and the resulting rate of change in the number of loci contributing to the trait (e). (a) For L > 1, the variation in direct effects (α_i) and indirect effects among controlling loci 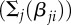increases as selection on the trait is relaxed. (b) As a consequence of this variation among loci, the average change in the trait value following a duplication or a deletion also increases as selection on the trait is relaxed. (c) Changes in the trait value are not directly proportional to fitness costs, because the same change in x has milder fitness consequences when selection is weaker (larger σ_f). As a result, the average fitness detriment of duplications and deletions is highest for traits under intermediate selection. (d) Consequently, the fixation rates of duplications and deletions are smallest under intermediate selection. (e) The equilibrium number of loci controlling a trait under a given strength of selection is determined by that value of L for which duplications and recruitments on one side, and deletions on the other, enter and fix in the population at the same rate. For example, when σ_f = 10^–1.5, these rates are equal when L is close to 12 (black arrow), so that the equilibrium genetic architecture contains ≈12 loci on average (compare electronic supplementary material, figure S3, black arrow). (Online version in colour.)

Only when selection on a trait is moderate can variation in the contributions across loci accrue and impact the fixation of deletions and duplications (figure 2d), by a process called compensation: a slightly deleterious point mutation at one locus, which perturbs the trait value, segregates long enough to be compensated by point mutations at other loci [32–35]. Compensation increases the variance in the contributions across loci (figure 2a), as has been observed for many phenotypes in plants and animals [36]. Owing to this variation, both duplications and deletions move the trait value away from the optimum (figure 2b), and so they are mildly deleterious on average (figure 2c). Nevertheless, there is a bias favouring duplications over deletions among the few such events that fix. This bias arises because duplications increase the number of loci in the architecture, which attenuates the effect of each locus on the trait (figure 2b). Thus, when selection is moderate, duplications and recruitments fix more often than deletions, driving the number of contributing loci above its neutral expectation (figure 2d,e). As the number of loci increases the bias is reduced (figure 2d,e), and so L equilibrates at a predictable value (figure 1; electronic supplementary material S3).

Duplications and recruitments might also be slightly favoured over deletions under intermediate selection, because architectures with more loci also exhibit, in our model, attenuated mutational effects. This effect, which could positively select for an increase in gene copy number [37], is likely weak in our model, because duplications and recruitments are both deleterious on average under intermediate selection, only less so than deletions (figure 2d,e).

(c). Robustness of results to model assumptions

The predictions of our model—notably, that the number of loci in a genetic architecture and the variance of their allelic contributions are greatest for traits under intermediate selection—are robust to choices of population-genetic parameters. The non-monotonic relation between selection pressure on a trait and the size of its genetic architecture, L, holds regardless of population size, but the location of maximum L is shifted towards weaker selection in larger populations (see electronic supplementary material, figure S5). This result is compatible with our explanation involving compensatory evolution: selection is more efficient in large populations, and so compensatory evolution occurs at smaller selection coefficients. Likewise, when the mutation rate is smaller the resulting equilibrium number of controlling loci is reduced (see electronic supplementary material, figure S6). This result is again compatible with the explanation of compensatory evolution, which requires frequent mutations. Increasing the rate of deletions relative to duplications also reduces the equilibrium number of loci in the genetic architecture, but our qualitative results are not affected even when r_del is twice as large as r_dup (see electronic supplementary material, figure S7). Finally, increasing the rate of recruitment r_rec (or the genome size) increases the number of loci contributing to all traits except those under very strong selection, as expected from figure 2. Our prediction that traits under intermediate selection are encoded by the richest genetic architectures is insensitive to changes in this parameter, and it holds even in the absence of recruitment (see electronic supplementary material, figure S8).

Our analysis has relied on several quantitative-genetic assumptions, which can be relaxed. First, we assumed that all effects of locus i (i.e. α_i and all β_ij and β_ji) are simultaneously perturbed by a point mutation. Relaxing this assumption so that a subset of the effects are perturbed does not change our results qualitatively (see electronic supplementary material, figure S9). Second, we assumed that point mutations have unbounded effects so that variation across loci can increase indefinitely. To relax this assumption, we made mutations less perturbative to loci with large effects (see Methods). Even a strong mutation bias of this type led to very small changes in the equilibrium behaviour (see electronic supplementary material, figure S10). Third, we assumed no metabolic cost of additional loci, even though additional genes in Saccharomyces cerevisiae are known to decrease fitness slightly [38,39]. Nonetheless, including a metabolic cost proportional to L does not alter our qualitative predictions (see electronic supplementary material, figure S11).

We defined the trait value as the average of the contributions α_i across loci (equation (2.1)), as opposed to their sum. This definition reflects the intuitive notion that a gene product's contribution to a trait will generally depend on its abundance relative to all other contributing gene products. If a gene is duplicated or deleted, then the concentration of its products will change relative to other genes contributing to the trait. If the number of contributing genes is already large, this change will have generally have a smaller impact on the phenotype. This attenuating effect of additional contributing loci is also supported by direct empirical data: changing a gene's copy number is known to have milder phenotypic effects when the gene has many duplicates [40,41]. Of course, many alternative definitions of the trait value can include such an attenuating effect, to a greater or lesser extent. We have explored alternative definitions of the trait value, spanning from the average to the sum of contributions across loci, and we find that they generically exhibit the same qualitative results as those obtained under the ‘average’ definition in equation (2.1) (see electronic supplementary material S1 and figure S12).

Finally, although robust to model formulation and parameter values, our results do depend in part on initial conditions. When selection is strong, the initial genetic architecture can affect the evolutionary dynamics of the number of loci (see electronic supplementary material, figure S14). This occurs because the initial architecture may set dependencies among loci that prevent a reduction of their number. This result indicates that only those architectures of traits under very strong selection should depend on historical contingencies. We have also studied a multi-trait version of our model, where genes participating in other traits can be recruited or lost through mutation. Even though this model features pleiotropy, and the effects of recruitment mutations evolve neutrally instead of being sampled from an arbitrary distribution, our qualitative results remained unaffected (see electronic supplementary material S3 and figure S15).

(d). The dynamics of copy number

Previous models related to genetic architecture have been used to study the evolutionary fate of gene duplicates. These models typically assume that a gene has several subfunctions, which can be gained (neo-functionalization [42]) or lost (subfunctionalization [43,44]) in one of two copies of a gene. Such ‘fate-determining mutations’ [45] stabilize the two copies, as they make subsequent deletions deleterious. Such models complement our approach, by providing insights into the evolution of discrete, as opposed to continuous or quantitative, phenotypes. Yet there are several qualitative differences between our analysis and previous studies of gene duplication. Most important of these is that our model considers the dynamics of both duplications and deletions, in the presence of point mutations that perturb the contributions of loci to a trait. This coincidence of time scales is important in the light of empirical data [27–30] showing that changes in copy numbers occur at similar rates to point mutations (see electronic supplementary material, table S1). Under these circumstances, a gene may be deleted or acquire a loss-of-function mutation before a new function is gained or lost. Our model includes these realistic rates, and accordingly we find that duplicates are very rarely stabilized by subsequent point mutations. Instead, the number of loci in a genetic architecture may increase in our model, because compensatory point mutations introduce a bias towards the fixation of duplications as opposed to deletions.

(e). Comparison with empirical data

Like most evolutionary models, our analysis greatly simplifies the mechanistic details of how specific traits influence fitness in specific organisms. As a result, our analysis explains only the broadest, qualitative features of how genetic architectures vary among phenotypic traits, leaving a large amount of variation unexplained. This remaining variation may be partly random (as predicted by the distributions of the number of evolving loci; figure 1), and partly due to ecological and developmental details that our model neglects.

A quantitative comparison between our model and empirical data requires information about the genetic architectures for hundreds of traits (see below for our analysis of expression QTLs). Nevertheless, the qualitative, non-monotonic predictions of our model (figure 1) may help to explain some well-known trends in the genetics of human traits. For instance, in accordance with our predictions, human traits under presumably moderate selection, such as stature (Mendelian inheritance in man, MIM no. 606255 [13,46]), or susceptibility to mid-life diseases such as diabetes (e.g. MIM no. 125853), cancer (e.g. MIM nos. 114480, 176807) and heart disease, are typically complex and highly polygenic, whereas traits under very strong selection, such as those (e.g. mucus composition or blood clotting) affected by childhood-lethal diseases such as cystic fibrosis (MIM no. 219700) or haemophilias (e.g. MIM nos. 306900, 306900) often rely on simple architectures with one or a few loci; and so too traits under very weak selection, such as handedness [47], cerumen moisture (MIM no. 117800 [48]) or bitter taste [49], typically rely on simple architectures. Our analysis provides an evolutionary explanation for these differences, and it delineates the selective conditions under which we expect a Mendelian, as opposed to Fisherian, architecture.

It is important to recognize that our analysis describes the emergence of genetic architectures over evolutionary time scales, which pertain to divergences among species. This perspective complements theories over short time scales, which pertain to segregating variation within a single population, such as the common disease/common variants hypothesis, which explains allelic diversity at a human locus in terms of recent population expansion [50,51].

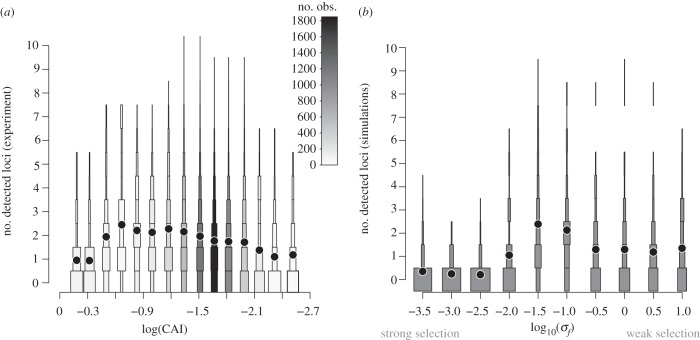
We tested our model for the evolution of genetic architectures by comparison with empirical data on a large number of traits. Such a comparison must, of course, account for the fact that our model describes the true genetic architecture underlying a trait, whereas any QTL study has limited power and describes only the associations detected from polymorphisms segregating in a particular sample of individuals. Accounting for this discrepancy (see below), we compared our model with data from the study of Brem et al. [15], who measured mRNA expression levels and genetic markers in 112 recombinant strains produced from two divergent lines of S. cerevisiae. For each yeast transcript, we computed the number of non-contiguous markers associated with transcript level, at a given false discovery rate (FDR; see Methods). We also calculated the codon adaptation index (CAI) of each transcript, an index that correlates positively with a gene's expression level [52] and that reflects the environmental conditions encountered during the organism's evolutionary history [53]. CAI correlates with gene dispensability [54,55], and thus it is a decent proxy for the strength of selection on a gene's expression level. We found a striking, non-monotonic relationship between the CAI of a gene and the number of loci linked to variation in its expression (figure 3a). Therefore, our analysis of Brem et al.'s [15] data indicates that transcript levels under intermediate selection are regulated by more loci than transcripts levels under weak or strong selection.

Figure 3.

The number of genetic loci controlling a trait inferred (a) from real S. cerevisiae populations and (b) from simulated populations has a non-monotonic relationship with the strength of selection on the trait. (a) In the yeast data of Brem et al. [15], the largest number of eQTLs were detected for those transcripts (i.e. traits) under intermediate levels of selection (intermediate CAI), whereas fewer eQTLs were detected for transcripts under either weak or strong selection. Transcripts were binned according to their log (CAI) values. Squares represent the distribution of the number of one-way eQTLs identified from the study of Brem et al. [15], for traits within each bin of CAI. Grey scale indicates the number of transcripts in each bin. Mean numbers of detected eQTLs are represented by circles. (b) For the simulated experiment, we evolved 100 populations of genetic architectures, using the parameters corresponding to the electronic supplementary material, figure S3. From each such population, we then evolved two lines independently for 25 000 generations in the absence of deletions, duplications and recruitment, to mimic the divergent strains used in the yeast cross in [15]. From these two divergent genotypes, we then created 112 recombinant lines following the genetic map of Brem et al. [15]. We then analysed the resulting simulated data with R/qtl in the same way as we had analysed the yeast data (see electronic supplementary material S2). The distribution of QTLs detected and their means are represented as in figure 1, for each value of selection strength σ_f.

In order to compare the predictions of our evolutionary model with the empirical data on yeast eQTLs (figure 3a), we required to mimic the experimental design of the yeast study. To do so, we first evolved genetic architectures for traits under various amounts of selection (see electronic supplementary material, figure S3), and for each architecture we then simulated a QTL study of the exact same type and power as the yeast eQTL study; that is, we generated 112 crosses from two divergent lines using the empirical yeast genetic map (see electronic supplementary material, figure S2). As expected, the simulated QTL studies based on these 112 segregants detected many fewer loci linked to each trait than in fact contribute to the trait in the true, underlying genetic architecture (figure 3b versus figure 1). This result is consistent with previous interpretations of empirical eQTL studies [16].

We can compare the yeast eQTL data only with the qualitative trends in our model, because we lack absolute estimates of selection pressures on yeast transcript abundances. It is likely that the range of simulated selection strengths in figure 3b is larger than the range of selection pressures in yeast. For instance, point mutations in genes contributing to traits simulated with log₁₀(σ_f) ≤ –2.5 have mean selection coefficients Ns ≤ –140 (see electronic supplementary material, figure S2), which makes them very unlikely to fix (mean fixation probability ≤ 3.5 × 10^–5), whereas for simulated traits with log₁₀(σ_f) ≥ 0, point mutations have a mean selection coefficient Ns ≥ –4.5 × 10^–3 and nearly neutral mean fixation probability ≈0.001. This wide range is guaranteed to include biologically relevant selection pressures, but may be broader than the range of selection pressures on yeast transcript levels.

The simulated QTL studies (figure 3b) also revealed an important bias: the probability to detect a locus contributing to the architecture of a trait depends on the allelic diversity at that locus, such that the architecture of a trait under weak selection is more likely to be correctly identified in a QTL study than the architecture of a trait under strong selection (see electronic supplementary material, figure S16). Furthermore, our simulations demonstrate that the number of associations detected in such a QTL study also depends on the divergence time between the parental strains used to generate recombinant lines (see electronic supplementary material, figure S17).

Genes with low CAI are typically expressed at low levels and may therefore be prone to more measurement noise. To study this effect, we also simulated measurement noise correlated with selection pressure (see electronic supplementary material, figure S18). Despite these detection biases, the relationship between the selection pressure on a trait and the number of detected QTLs in our model (figure 3b; electronic supplementary material, figures S18 and S19) agrees with the relationship observed in the yeast eQTL data (figure 3a). Importantly, both of these relationships exhibit the same qualitative trend: traits under intermediate selection are encoded by the richest genetic architectures.

In principle, a non-monotonic pattern similar to the one shown in figure 3a could also emerge as a result of the two detection biases that we have described. First, the lack of variation at contributing loci could prevent their detection for traits under very strong selection, whereas elevated measurement noise in weakly expressed genes might also impede the detection of any genetic association. We have quantified these biases in genetic architectures with a fixed number of contributing loci across traits (see electronic supplementary material, figure S20). Our analysis indicates that the non-monotonic pattern observed in the empirical data (figure 3a) is unlikely to result from these biases alone. Therefore, detection biases can only accentuate an already non-monotonic pattern in the true architecture.

3. Conclusion

Many interesting developments lie ahead. Here, we have considered only traits under stabilizing selection, whereas some traits might experience fluctuating target phenotypes over the time scales considered, so that periods of stabilizing selection alternate with periods of adaptation. A proper study of the evolution of genetic architectures in fluctuating environments should disentangle these complex dynamics, which is clearly beyond the reach of this paper. Our model is also far too simple to account for tissue- and time-specific gene expression, context-dependent effects, and so on [5,56]. Moreover, we considered the evolution of only haploid genetic architectures. It will be interesting to investigate how architectures evolve when including, for instance, patterns of recombination or dominance and sex-specific effects.

Nonetheless, our work provides intuition that can guide the interpretation and design of empirical studies. Our main finding is that the evolution of genetic architectures is governed by an interaction between the divergence of allelic effects and the number of loci, and this conclusion should hold even in the presence of frequent recombination. More generally, our analysis shows that it is possible to study the evolution of genetic architectures from first principles, to form a priori expectations for the architectures underlying different traits, and to reconcile these theories with the expanding body of QTL studies on molecular, cellular and organismal phenotypes.

4. Methods

(a). Model

We described the evolution of genetic architectures using the Wright–Fisher model of a replicating population of size N, in which haploid individuals are chosen to reproduce each generation according to their relative fitnesses. The fitness of an individual with L loci encoding trait value x is ω_k = G(x, 0, σ_f) × (1 – L × c), where G denotes the density at x of a Gaussian distribution with mean zero and standard deviation σ_f, and the second term denotes the metabolic cost of harbouring L loci, which depends on a parameter c. The trait value of such an individual, given the direct contributions α_i and epistatic terms β_ji, is described by equation (2.1), where 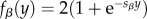is a sigmoidal curve, so that the epistatic interactions either diminish or augment the direct contribution of locus i depending on whether 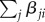is positive or negative (see electronic supplementary material, figure S4). In general, loci do not influence themselves (β_ii ≡ 0) and, in the model without epistasis, all β_ji ≡ 0 and f_β ≡ 1. If an individual chosen to reproduce experiences a duplication at locus i then the new duplicate, labelled k, inherits its direct effect (α_k = α_i) and all interaction terms (β_kj = β_ij and β_jk = β_ji for all j ≠ i,k), with the interaction terms β_ik and β_ki initially set to zero. Recruitment occurs with probability r_rec per mutation of one of the 6000 genes not contributing to the trait. The initial direct contribution α_i of recruited locus i is drawn from a normal distribution with mean zero and standard deviation σ_m; its interaction terms with other loci (k), β_ik and β_ki, are initially set to zero. Note that this assumption is relaxed in the multi-locus version of our model, where the direct and indirect effects of recruitments evolve neutrally (see electronic supplementary material, text S3 and figure S15).

In general, a point mutation at locus i changes its contribution to the trait, α_i, and all its epistatic interactions, β_ij and β_ji, each by an independent amount drawn from a normal distribution with mean zero and standard deviation σ_m. In this model, the impact of a mutation on fitness depends on the ratio σ_f/σ_m, such that an increase in the value of σ_m is strictly equivalent to a proportional decrease of σ_f. The normal distribution satisfies the assumptions that small mutations are more frequent than large ones [57,58], and that there is no mutation pressure on the trait [23]. We relaxed the former assumption by drawing mutational effects from a uniform distribution without qualitative changes to our results (see electronic supplementary material, figure S13). We also used a log-uniform distribution for the mutation effects, such that more mutations have very small effects, again with no qualitative change (see electronic supplementary material, figure S13). In order to relax the latter assumption, we included a bias towards smaller mutations in loci with large effects, so that the mean effect of a mutation at locus i now equals −b_α × α_i and −b_β × β_ij, respectively for α_i and β_ij [59]. We also considered a model in which a mutation at locus i affects only a proportion p_em of the values α_i, β_ij and β_ji.

By default, simulations were initialized with L = 1 and α₁ = 0; alternative initial conditions were also studied, as shown in electronic supplementary material, figure S14. The code for all simulations and figures presented in the paper was deposited in the Dryad repository (http://dx.doi.org/10.5061/dryad.1f217).

(b). Markov chain for neutral changes in copy number

When deletions and duplications are neutral, and recruitments strongly deleterious, the evolution of the number of loci L in the genetic architecture is described by a Markov chain on the positive integers. The probability of a transition from L = i to L = i + 1 equals r_dup × i, and that of a transition from i to i – 1 is r_del × i. We disallow transitions to L = 0, assuming that some regulation of the trait is required. We obtained the stationary distribution of L by setting the density of d₁ of individuals in stage 1 to 1 and calculating the density d_i of individuals in the following stages as

4.1

The equilibrium probability of being in state i was calculated as 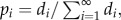and the expected value of L was calculated as 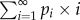. With r_dup = 10^–6 and r_del = 1.25 × 10^–6, we found an equilibrium expected L of 2.485.

When deletions, duplications and recruitments are all neutral, equation (4.1) can be replaced by

4.2

Equation (4.2) illustrates the fact that the rates of deletions (which include loss of function mutations) and duplication depend on the number of loci in the architecture, whereas the rate of recruitments does not. With μ = 3 × 10^–6 and r_rec = 5 × 10^–5, we found an equilibrium expected L of 4.705.

(c). Calculation of 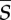and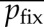

We first evolved populations to equilibrium with a fixed number of controlling loci L, and we then measured the effects of deletions, duplications or recruitments introduced randomly into the population. We simulated the evolution of the genetic architecture with L fixed in 500 replicate populations, over 8 × 10⁶ generations for deletions and 10 × 10⁶ generations for duplications, reflecting the unequal waiting time before the two kinds of events. We used 10 × 10⁶ generations for recruitment as well, although different durations did not affect our results. For each genotype k in each evolved population, we calculated the fitness ω_k(i) of mutants with locus i deleted or duplicated. We calculated the corresponding selection coefficients as s_k(i) = ω_k(i)/〈ω〉 – 1, where 〈ω〉 denotes mean fitness in the population. We calculated 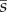as the mean across loci and genotypes of s_k(i), weighted by the number of individuals with each genotype. We calculated the probability of fixation of a duplication, deletion or recruitment as

4.3

and obtained the mean p_fix using the same method as for .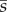

Rates of deletions and duplications fixing were calculated per locus (figure 2) as r_del or r_dup times p_fix. The total probability of a duplication or a deletion entering the population and fixing is, of course, also multiplied by L. However, recruitment rates remain constant as L changes. Therefore, we divided the rate of recruitments by L in figure 2, for comparison with the per locus duplication and deletion rates.

(d). Number of loci influencing yeast transcript abundance

We used the R/qtl [60,61] package to calculate logarithm of odds (LOD) scores for a set of 1226 observed markers and 3223 uniformly distributed pseudo-markers separated by 2 cM, by Haley–Knott regression. We calculated the LOD significance threshold for a FDR of 0.2 as the corresponding quantile in the distribution of the maximum LOD after 500 permutations (an FDR of 0.01 and a fixed LOD threshold of three produced qualitatively similar results). The number of detected loci linked to the expression of a transcript was calculated as the number of non-consecutive genomic regions with an LOD score above the threshold. We downloaded S. cerevisiae coding sequences from the Ensembl database (EF3 release), and calculated CAI values with the seqinr [62] package, using codon weights from a set of 134 ribosomal genes.

Funding statement

We gratefully acknowledge support from the Burroughs Wellcome Fund, the David and Lucile Packard Foundation, the James S. McDonnell Foundation, the Alfred P. Sloan Foundation, the Foundational Questions in Evolutionary Biology Fund (RFP-12-16), the US Army Research Office (grant no. W911NF-12-1-0552) and grant no. D12AP00025 from the US Department of the Interior.

Data accessibility

C++ and R code for simulations and figures is accessible from Dryad at http://dx.doi.org/10.5061/dryad.1f217.