Effect of combined function of temperature and water activity on the growth of Vibrio harveyi

Abstract

Vibrio harveyi is considered as a causative agent of the systemic disease, vibriosis, which occurs in many biological fields. The effects of temperatures (12.9–27.1 °C) and water activity (NaCl% 0.6%-3.4%) on V. harveyi were investigated. The behavior and growth characteristics of V. harveyi was studied and modeled. Growth curves were fitted by using Gompertz and Baranyi models, and the Baranyi model showed a better fittness. Then, the maximum growth rates (μ_max) and lag phase durations (LPD, λ) obtained from both Gompertz and Baranyi model were modeled as a combination function of temperature and water activity using the response surface and Arrhenius-Davey models for secondary model. The value of r², MSE, bias and accuracy factor suggest Baranyi model has better fitness than Gompertz model. Furthermore, validation of the developed models with independent data from ComBase also shown better interrelationship between observed and predicted growth parameter when using Baranyi model.

INTRODUCTION

Vibrio harveyi is a gram-negative, motile rod bacterium ubiquitous in marine and estuarine aquatic ecosystems. Although V. harveyi is non pathogenic to human, it is one of causative agents of the systemic fish disease, vibriosis, and sea food spoilage which occurs in many commercially important fish (20), including sharks, seahorse, lobster, shellfish or shrimps (13). Pseudosciaena crocea (big yellow croaker) is an important commercial marine fish in China, and has been widely cultured in hatcheries recent years. However, infectious vibirosis and spoilage is becoming severe with expanding culture (19).

Traditionally the microbiological safety of food has been established via challenge tests. However, challenge tests have been criticized as an expensive, labor intensive, time consuming and non-cumulative research tool (8). Therefore, mathematical models are being developed for predicting microbial growth. In the research field of predictive microbiology, mathematical modelling is an efficient tool for assessing how individual or combined environmental factors affect microorganisms in foods (17). Various models have been developed in predictive microbiology for fitting growth curves and estimating biological parameters of food-borne pathogens (9, 11). Predictive microbiology is a useful tool in food industry to predict behaviors of microorganisms (24), where primary model describes the growth data under constant environmental conditions and secondary model describes the dependence of primary model parameters on environmental factors such as temperature, water activity, and pH. Primary models such as Logistic, Gompertz and Baranyi model are often used to fitting microbial growth data. At present, the Baranyi model is getting more popular among researchers and several studies have reported that the Baranyi model performs better (25). There are many types of secondary models used by previous researchers to predict microbial growth under dynamic conditions, including Belehradek-type models, response surface model, Arrhenius-type model and artificial neural networks (7). Therefore by gathering a detailed knowledge of the growth rate response to the dominant environmental parameters of temperature and Aw, it is possible to predict the extent of microbial proliferation under conditions within the range of experimental values tested (12).

In the case of V. harveyi, there was few published study reporting the effects of environmental factors like temperature and Aw on its growth using modelling approaches, and it is also difficult to find the growth data related to V. harveyi in the worldwide growth data-base and predictive software, like ComBase or Growth Predictor. The influence of the modelling and prediction on vibriosis infection and spoilage has been a neglected field of study. Besides, to determines whether predictions provide good description of growth in food, models should be validated to evaluate their predictive ability, like r² values, mean square error (MSE), bias factor, and accuracy factor, and can also be used as an indication of the reliability of models when applied to food (6).

The aim of this study was to develop predictive models to describe the combined effects of temperature and Aw on the growth rate of V. harveyi for each tested condition. The temperature and Aw can contribute to understanding the growth dynamics of V. harveyi and the initiation of P. crocea infection by this microorganism. By evaluated and validated with independent data, the developed models could be successfully employed as an empirical approach in modeling and prediction for risk assessment concerning V. harveyi in P. crocea.

MATERIALS AND METHODS

Bacterial strain

The pathogenic strain was isolated from infected cage cultured large yellow croaker (Pseudosciaena crocea) in Luoyuan Bay in the east of Fujian province, China, and the majority of the micro-organisms in the fish was identified as V. harveyi by standard biochemical testing (21) and designated as V. harveyi LIZ-42028.

Experimental design

A central composite design (CCD) was applied using Design-Expert Version 7.1.4 (StatEase, Inc., Minneapolis, Minnesota, USA). The variables were temperature (12.9, 15, 20, 25, and 27.1 °C) and water activity determined by concentration of sodium chloride 0.6% (0.997), 1% (0.995), 2% (0.989), 3% (0.983), and 3.4% (0.981).

Media preparation

Nine different media combinations designed from the software were prepared by adding the corresponding concentration of sodium chloride (0.6%-3.4%) to tryptone soybean yeast extract broth (TSYEB). The cultures were adjusted to an approximately concentration of 10⁸ CFU/ml preliminary determined by plate count after 30 h at 27 °C incubation. The doses of V. harveyi used in this study were then prepared by dilution in TSYEB, 10–15 min prior to use and the CFU were later confirmed by plate counts (3). The TSYEB with 1% agar (TSYEA, pH=7.0) was used for plate counts and 8.5 g/l sodium chloride was used for all serial dilutions of the inoculums. All media were autoclaved at 121 °C for 15 min.

Experimental procedure

Samples of different conditions were incubated in a constant temperature environment stabilized at 12.9, 15, 20, 25, 27.1 °C. At appropriate time intervals during incubation (Fig. 1), decimal dilutions were made from separate battles of TSYEB onto TSYEA. The samples were incubated for 24 h at 30 °C for plate counts. Each experiment was carried out in triplicate, and an average CFU/ml of each sampling point was used to determine estimates of the growth.

Figure 1.

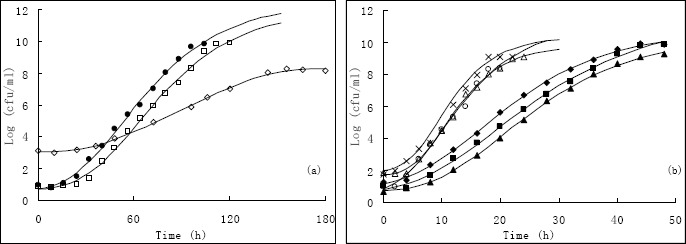
The observed and Gompertz model predicted growth of Vibrio harveyi in different conditions (a), (b); the observed and Baranyi model predicted growth of Vibrio harveyi in different conditions (c), (d). (Scatter dots are observed; curves are predicted). (◇), 12.9 °C, 2%; (﹡), 15°C, 1%; (●), 15 °C, 3%; (◆), 20 °C, 0.6%; (■), 20 °C, 2%; (▲), 20 °C, 3.4%; (×), 25 °C, 1%; (△), 25 °C, 3%; (○), 27.1 °C, 2%.

Primary modelling

One of the recommended models for describing microbial growth is Gompertz model (25)

$$x\left(t\right)=C+A{e}^{-e^{-B\left(t-D\right)}}$$ 1

where x(t) is log₁₀ (CFU/ml) of cell concentration at time, t; C is value of lower asymptote in units of log₁₀ (CFU/ml); A is equal to log₁₀ (x_max/x₀); x₀ is the initial population density; x_max is maximum population density; B is maximum relative growth rate at D in 1/h; D is time at which the absolute growth rate is maximum in hours.

From these parameters, the maximum specific growth rate [μ=B*A/e, log(CFU/ml)h^-1, where e=2.7182], the lag phase duration [LPD=D-(1/B), h] were derived.

The flexible function of Baranyi and Roberts (2) was fitted to the growth data by means of the non-linear function of SPSS Version 10.0 (SPSS Inc., Chicago, USA). This enables the determination of the μ_max and LPD

$$y\left(t\right)=y_0+{\mu }_{\max }F\left(t\right)-\ln (1+\frac{e^{{\mu }_{\max }F\left(t\right)}-1}{e^{\left(y_{\max }-y_0\right)}})whereF\left(t\right)=t+\frac{1}{v}\ln \left(e^{-vt}+e^{-h_0}-e^{\left(-vt-h_0\right)}\right)$$ 2

Where y(t) the ln (CFU/ml) of cell concentration at time, t; y₀ the initial cell concentration in ln (CFU/ml) units; y_max the maximum cell concentration in ln (CFU/ml) units; μ_max the maximum specific growth rate in terms of in (CFU/ml); v the rate of increase of the limiting substrate; h₀ is equal to μ_maxλ; λ is lag-phase duration in h. The growth data were fitted again with the Baranyi model, after fixing the value of h₀ with the mean value (1).

Secondary modelling

Two functions were evaluated for their ability to describe the combined influence of temperature and Aw on the μ_max and LPD. These included a response surface (RS) model (3), and the Arrhenius-Davey (AD) model (4), which with a interaction term (Aw / T), as follows:

$$Ln\left({\mu }_{\max }or1/\lambda \right)=C_0+C_1\times T+C_2\times AW+C_3\times T\times AW+C_4\times T^2+C_5\times A{W}^2$$ 3

$$Ln\left({\mu }_{\max }or1/\lambda \right)=C_0+C_1/T+C_2\times AW+C_3\times AW/T\times AW+C_4/T^2+C_5\times A{W}^2$$ 4

Where T is degree Celsius (°C) and Aw has transformed to NaCl (%).

The coefficients of these two models and the significance of their associated factors were determined by fitting the models onto the estimated cell μ_max or LPD by means of SPSS.

Model validation and statistical evaluation

The quality of fit of a model can be reflected as the regression coefficient (r²), which is often used as an overall measure of the prediction attained. The higher the value (0< r²<1), the better is the prediction by the model.The mean square error (MSE) is a measure of variability remaining. The lower MSE obtained the more satisfying of the model to describe the data.

$$\text{MSE=}\sum {\left({\text{μ}}_{\text{observed}}-{\text{μ}}_{\text{predicted}}\right)}^2/n$$ 5

The bias factor answers the question whether the observed values lie above or below the line of equivalence and by how much. A bias factor<1 indicates a ‘fail safe’ model. The accuracy factor accesses the distance between each point and the line of equivalence as a measure of how close, on average predictions are to observations. The larger the value, the less accuracy is the average estimate (14). n is the number of observations; μ_predicted is the predicted specific growth rate; μ_observed is the observed specific growth rate.

$$biasfactor={10}^{(\frac{\sum \log (\frac{{\mu }_{observed}}{{\mu }_{predicted}})}{n})}$$ 6

$$accuracyfactor={10}^{(\frac{\sum \log \left|\frac{{\mu }_{observed}}{{\mu }_{predicted}}\right|}{n})}$$ 7

The developed secondary models were validated also with independent data from ComBase database for the growth rate of 155 Vibrio spp. at different temperatures and Aw on TSYEB. The selected data for validation were all within the range of experimental conditions (temperature 12.9 °C-27.1 °C, Aw 0.997–0.981, the KEY is start with ‘Tas’ in ComBase), and then the prediction capability of the models were evaluated by MSE, bias and accuracy factors.

RESULTS

Primary model curve fitting

After plate count of each combination, growth curves of V. harveyi were obtained by both the Gompertz and Baranyi model. The growth took approximately 144 and 120 h to reach the maximum concentration, when the temperatures were 12.9 °C and 15 °C respectively. The μ_max and LPD of 12.9 °C, 2% (NaCl%) is 0.0485, 35 h and 0.1112, 35 h fit by Gompertz and Baranyi model respectively. However, it took only 28 h when the temperature is 27.1 °C to reach the maximum concentration. The μ_max and LPD of 27.1 °C, 2% (NaCl%) is 0.193, 2.200 h and 1.060, 1.092 h fit by Gompertz and Baranyi model respectively (Fig. 1). The μ_max is sensitive to both the temperature and Aw, whereas the LPD is more rely on temperature, which could also be seen in Fig. 2, 3. All the experimental data obtained from combined effects have been fitted into both the Gompertz and Baranyi (Fig. 1) models.

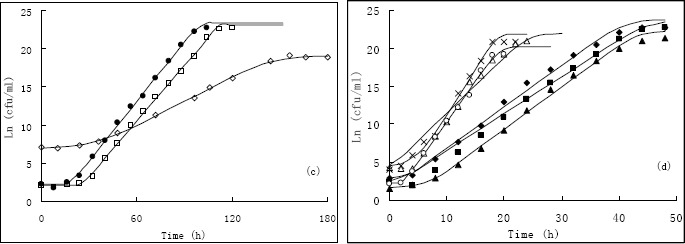
Figure 2.

Surface plots of the growth rates predicted by RS model as a function temperature and NaCl% for (a); and surface plots of the growth rates predicted by AD model as a function temperature and NaCl% for (b). The symbols represent the observed data.. Surface plots of the lag phase duration predicted by RS model as a function temperature and NaCl% for (a); and surface plots of the lag phase duration predicted by AD model as a function temperature and NaCl% for (b). The symbols represent the observed data.

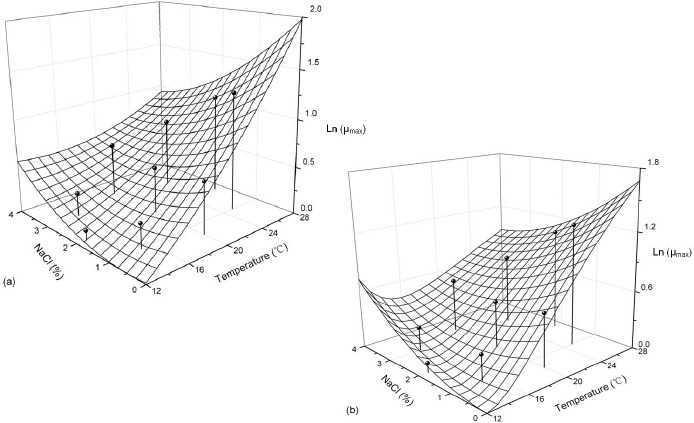
Figure 3.

Surface plots of the lag phase duration predicted by RS model as a function temperature and NaCl% for (a); and surface plots of the lag phase duration predicted by AD model as a function temperature and Nacl% for (b). The symbols represent the observed data.

Table 1 compared the r², MSE, bias and accuracy factor in different combinations of temperature and Aw of Gompertz and Baranyi model. The r² and MSE values were not significant different by one-way ANOVA with the p>0.05 for all the parameters. All the r² > 0.99, and the MSE < 0.1 for Baranyi model, which is better than r² > 0.98 and MSE < 0.2 for Gompertz model. Furthermore, compare with the indices of all the conditions on average, the r², MES, bias and accuracy factor of Baranyi are 0.9965, 0.0463, 0.9885, 1.0621, which is more acceptable than Gompertz model with the values are 0.9944, 0.0467, 0.9918, 1.0492. The F-test value of growth rate is 0.64 and lag phase duration is the same between two models, and the F value of r², MSE, bias and accuracy factor less than the F value from table, so there is no significant difference between two primary models.

Table 1.

Evaluation of specific models predicting Vibrio harveyi in different combinations according to various mathematical/statistical characteristics

Temperature (°C), NaCl (%)	Models
	Gompertz	Baranyi
27.1 °C, 2%
r2	0.9937	0.9964
MSE	0.0446	0.0260
Bias	0.9983	0.9884
Accuracy	1.0663	1.0278
25 °C, 1%
r2	0.9899	0.9924
MSE	0.1780	0.0613
Bias	0.9405	0.9856
Accuracy	1.0711	1.0517
25 °C, 3%
r2	0.9965	0.9952
MSE	0.0247	0.0524
Bias	0.9984	0.9901
Accuracy	1.0358	1.1698
20 °C, 0.6%
r2	0.9985	0.9954
MSE	0.0112	0.0637
Bias	0.9994	0.9818
Accuracy	1.0264	1.0429
20 °C, 2%
r2	0.9982	0.9987
MSE	0.0252	0.0372
Bias	0.9955	0.9961
Accuracy	1.0672	1.1198
20 °C, 3.4%
r2	0.9991	0.9964
MSE	0.0043	0.0424
Bias	0.9988	0.9914
Accuracy	1.0163	1.0391
15 °C, 1%
r2	0.9969	0.9981
MSE	0.0321	0.0416
Bias	0.9971	0.9784
Accuracy	1.0744	1.0411
15 °C, 3%
r2	0.9971	0.9982
MSE	0.0358	0.0295
Bias	0.9987	0.9890
Accuracy	1.0604	1.0391
12.9 °C, 2%
r2	0.9800	0.9980
MSE	0.0644	0.0633
Bias	0.9994	0.9959
Accuracy	1.0252	1.0281

Combined effect of temperature and Aw on growth rate

The coefficient of the models developed describing the combined effect of temperature and Aw on the μ_max and their statistical validation are shown in Table 2, whereas the 3D surface of the models developed for both observation and prediction are given in Fig. 2. The secondary model predicted that the optimum condition was 28 °C, 0%, and the μ_max were1.9826 and 1.6839 for RS model and the AD model, respectively. The lowest μ_maxwas estimated in 12 °C. It can be observed that the μ_max increased with increase of temperature for RS model (Fig. 2). When the NaCl% is lower than 1%, the μ_max also increased with the temperature increase for the AD model, However, when the NaCl% higher than 1% and the temperature lower than 15 °C, the μ_max decreased when the temperature increase for AD model. This may indicate that distinctive reaction to the varied environments of the salt-tolerance and thermophilus bacteria like V. harveyi or other Vibrio spp. Based on Fig. 2, it clearly can be seen from the curvature of the secondary model that synergistic and antagonistic interaction occurs between the temperature and Aw on the μ_max.

Table 2.

Coefficients of growth rate models, describing the combined effects of temperature and NaCl% on V. harveyi.

	Gompertz-RS	Baranyi-RS	Gompertz-AD	Baranyi-AD
C0	0.0453	-0.6522	0.8369	5.0662
C1	-0.0041	0.0269	-22.1187	-120.1110
C2	-0.0489	0.2468	-0.0758	-0.6390
C3	-0.0002	-0.0250	0.0587	7.8723
C4	0.0004	0.0024	161.4295	711.4668
C5	0.0130	0.0472	0.0180	0.0417
r2	0.8703	0.9616	0.8956	0.9413
MSE	0.0046	0.0013	0.0036	0.0014
Bias	1.0405	1.0121	1.0053	1.0000
Accuracy	1.2906	1.1770	1.1539	1.1991

In the secondary model, the r² are 0.9616 and 0.9413 for Baranyi model by using RS and AD model, which is 0.8703 and 0.8956 for Gompertz model. The values of MSE, bias factor, and accuracy factor were all in the acceptable range. The bias factor from Baranyi model was 1.0121 to 1.0000, and the accuracy factor was 1.1770 to 1.1991 (Table 2). The F-test indicated there is difference between the bias and accuracy factor from Baranyi and Gompertz model, and Baranyi model shown better fitness with better r² and MSE value.

The validation between observed μ_max and independent data from ComBase by Baranyi nad Gompertz model with both RS and AD model is presented in Table 3. The growth rate data from ComBase were selected according to the conditions in this study, The MSE is less than 0.02 shown that the models are goodness-of-fit, and the accuracy factor indicated that both the developed models predicted the growth with approximately the same. However, the bias factor of RS model is much higher than AD model, which indicated that the AD model is better. Moreover, the bias and accuracy factor obtained from Gompertz model is higher than1.8, which is unacceptable, whereas which from Baranyi model is lower and acceptable.

Table 3.

Validation indices for the performance of the models on independently derived data from Combase.

		RS	AD
Gompertz	MSE	0.0201	0.0191
	Bias	1.9367	1.8883
	Accuracy	1.9985	1.9590
Baranyi	MSE	0.0152	0.0162
	Bias	0.8919	0.9473
	Accuracy	1.5636	1.5980

Combined effect of temperature and Aw on lag phase

The coefficient of the models developed describing the combined effect of temperature and Aw on the LPD and their statistical evaluation are shown in Table 4, the 3D surface of the models developed for both observation and prediction are given in Fig. 3. Both the secondary models presented satisfactory fitting to the experimental data which obtained from Baranyi model. RS and AD model described the combined effect of temperature and Aw on the LPD correctly. The LPD increased when the temperature decreased, and the LPD last less than 2 hours in 28 °C, whereas more than 30 hours in 12 °C (Fig. 3). The LPD affected less by Aw. For RS model and AD model, the duration hour alters less than 3 hours for different Aw in a same temperature. This temperature and Aw interaction occurred also in some kind of fungi, Apergillus carbonarius, Asperigillus flavus and Asperigillus parasiticus (16, 18).

Table 4.

Coefficient and mathematical/statistical indices used to validate the lag phase duration models, describing the combined effects of temperature and NaCl% on V. harveyi.

	Function	r2	MSE	bias	accuracy
Response surface	LP=83.424-5.518×-T-0.189×NaCl-0.003×T×NaCl+0.093×T2+0.070×NaCl2	0.9971	0.0420	0.9543	1.1249
Arrhenius-Davey	LP=-21.417+623.428/T-0.549×NaCl+0.997/T×NaCl+264.433/T2+0.133×NaCl2	0.9990	0.0146	0.9768	1.1768

The MSE value of secondary model is less than 0.05 for Baranyi model. Furthermore, the bias factors are close to 1, which is in an acceptable range as previously described. Compare the RS model to AD model, the AD model is better than RS mode with a better statistical assessment (Table 4).

DISCUSSION

The aim of study is to predict and control the sea food safety by modeling the V. harveyi. The effect of temperature and Aw was fitted by Gompertz and Baranyi models preliminary. The temperature and Aw effect the μ_max significantly, and in a same temperature, the maximum growth rate occurred when the Aw was approximately 0.99, which was consistent with previous report (12).

The entire bias factor of primary models was between 0.94 and 1 in Table 1 which indicated that the predictive growth rate is, on average, lower than the observed growth rate. Ross (15) proposed the following interpretation of bias factor when used for model performance evaluations involving pathogens: 0.90–1.05 can be consider good; 0.70–0.90 or 1.06–1.15 can be considered acceptable; <0.70 or >1.15 should be considered unacceptable. According to this standard, results of bias factor of Banrayi models in this study were within good range (5). Additionally, there are also other reported standards of bias factor, Dalgaard (4) suggested 0.8–1.3 in seafood spoilage model. The accuracy factor provides indication of the average accuracy of estimate. In the primary model establishment, all the accuracy were slightly higher than 1, and were 1.0277–1.1698 in combined condition, which were in an acceptable ranges. By model evaluation and statistical validation, the parameters derived from Baranyi model performed better than Gompertz model, which was consistent with previously study (22, 23).

The combined temperature and Aw effect on the growth of V. harveyi were conducted by both the RS and AD models. The RS is a classical modelling approach in predictive microbiology area and shown a good performance in growth rate fitting, however with the index of MSE in fitting the LPD, AD model exhibited more reliable. By comparing the r², MSE, bias and accuracy factor of secondary model, it also indicated that AD model is better. By analysis the LPD models, which was almost constant at a same temperature with different Aw, and was highly sensitive to the variation of temperature with a same Aw, especially in the AD model. This result indicated that the LPD is mostly relying on temperature, and these trends were also found in published researches (16, 18).

Validation of the developed models with independent data from ComBase shown good interrelationship between observed and predicted growth rate (Table 3). Although the predictive model and published data of V. harveyi is scanty, we compare the data with very similar species of Vibrio spp. The indices shown a good performance of the developed models, the MSE is around 0.020 for Gompertz model and 0.015 for Baranyi model. However, the bias and accuracy factor are not in the acceptable range for the parameters from Gompertz model. We also compared the validation data with the model data in Figure 4, shown Gompertz model always predicted the rate always higher, whereas Baranyi model distribute more central.

Figure 4.

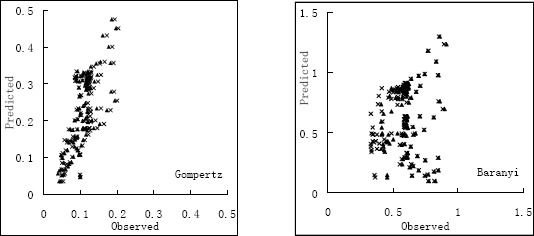
Compare the growth of V. harveyi in broth to 4 models. (▲, RS model; ×, AD model)

In summary, the experiments compared Gompertz with Baranyi models and response surface with Arrhenius-Davey models, established predictive model to reveal the growth characteristics of V. harveyi in combined conditions of temperature and Aw. In this study, Baranyi model and Arrhenius-Davey model showed goodness-of-fit to describe the growth of V. harveyi under different laboratory conditions.

Furthermore, the data of μ_max and LPD could be integrated into a QMRA (quantitative microbial risk assessment) and further for a HACCP (hazard analysis critical control point) software, in monitor the safety of food (10). As there is correlation between broth data and real condtition, the established model could be used to calculate the likely number of organisms before the fishes were captured, and predict the potential hazard of infection, and help to control the disease spread in the batch. Furthermore, if the models predict that growth of a particular micro-organism cannot occur, this information can be used to determine the risk of financial loss and also control the organism from the list of potentially hazardous for the HACCP.