Abstract
The current study was designed to examine potential interlimb asymmetries in controlling movement extent. Subjects made repetitive single-joint elbow extension movements while the arm was supported on a horizontal, frictionless, air-jet system. Four targets of 10, 20, 35, and 45° excursions were randomly presented over the course of 150 trials. For both arms, peak tangential hand velocity scaled linearly with movement distance. There was no significant difference between either peak velocities or movement accuracies for the two arms. However, the mechanisms responsible for achieving these velocities and extents were quite distinct for each arm. For the dominant arm, peak tangential finger acceleration varied systematically with movement distance. In contrast, nondominant-arm peak tangential acceleration varied little across targets and, as such, was a poor predictor of movement distance. Instead the velocities of the nondominant arm were determined primarily by variation in the duration of the initial acceleration impulse, which corresponds to the time of peak velocity. These different strategies reflect previously identified mechanisms in controlling movement distance: pulse-height control and pulse-width control. The former is characterized by a variation in peak acceleration and has been associated with preplanning mechanisms. The latter occurs after peak acceleration and has been shown to depend on peripheral sensory feedback. Our findings indicate that the dominant-arm system controls movement extent largely through planning mechanisms that specify pulse-height control, whereas the nondominant system does so largely through feedback mediated pulse-width control.
INTRODUCTION
Handedness is a prominent feature of human motor control that has been well described phenomenologically through the identification of tasks that are preferentially performed with one or the other arm (Oldfield 1971). However, the neural mechanisms responsible for this behavioral asymmetry are not well understood. The most prevalent theory of motor lateralization suggests that preplanning and feedback mediated mechanisms are differentially controlled by each hemisphere. According to this open/closed loop hypothesis, preferential sensorimotor access of each arm to the contralateral hemisphere and thus to one or the other process, is thought to result in manual asymmetries. The term, “closed-loop,” refers to mechanisms that are mediated by sensory feedback, whereas “open-loop” refers to mechanisms that for any given movement, are not affected by feedback. However, open-loop mechanisms may be influenced through the feedforward use of sensory information obtained during previous movements. This hypothesis has emerged from studies comparing dominant and nondominant arm performance in healthy adults (Annett et al. 1979; Carson 1993; Mieschke et al. 2001) and has been supported by studies examining the ipsilesional arm in unilaterally brain damaged patients (Haaland and Delaney 1981; Haaland and Harrington 1989a,b, 1996; Winstein and Pohl 1995).
We have recently provided evidence for an alternative hypothesis of motor lateralization (Bagesteiro and Sainburg 2002, 2003; Sainburg 2002; Sainburg and Kalakanis 2000; Sainburg and Wang 2002). The dynamic dominance hypothesis suggests that the dominant hemisphere/limb system is specialized for controlling limb trajectory, whereas the nondominant arm system appears specialized for controlling limb position or posture. This hypothesis emerged from studies demonstrating superiority of the dominant arm in controlling intersegmental dynamics as required for specification of hand trajectory during multijoint reaching movements (Bagesteiro and Sainburg 2002, 2003; Sainburg 2002; Sainburg and Kalakanis 2000; Sainburg and Wang 2002). This idea is not contradictory to the open/closed-loop hypothesis, and the two ideas may actually express convergent perspectives of motor lateralization. Control of intersegmental dynamics is, in fact, largely dependent on anticipatory control mechanisms, which for any given trial, are mediated by open-loop mechanisms (Gribble and Ostry 1999; Sainburg et al. 1993, 1995; Schneider et al. 1989; Smith and Zernicke 1987). We have also reported evidence consistent with nondominant-arm superiority for somatosensory-based feedback-mediated control. In a number of studies, the nondominant arm showed greater final-position accuracy for reaching movements made without visual feedback (Bagesteiro and Sainburg 2002, 2003; Sainburg 2002; Sainburg and Kalakanis 2000; Sainburg and Wang 2002). Because accuracy in final position is largely related to events occurring in the later phase of motion, when feedback mechanisms become available, these findings may be associated with an advantage for somatosensory-based, closed-loop control mechanisms. In fact, we recently showed that the nondominant arm is substantially more efficacious in somatosensory-based responses to unexpected inertial perturbations (Bagesteiro and Sainburg 2003). Nevertheless, the roles of feedforward and feedback processes in limb-coordination asymmetries remain poorly understood.
We expect that if these differences in control are fundamental to motor asymmetries, they should not be limited to complex multijoint movements. Instead such differences should be apparent in single-joint-targeted motions. Rapid single-joint movements are typically associated with triphasic electromyographic (EMG) patterns that result in characteristic kinematic patterns that include a biphasic acceleration profile and a typically smooth unimodal velocity profile (Desmedt and Godaux 1977, 1979; Ghez 1979; Ghez and Gordon 1987; Gordon and Ghez 1984). For movements made to different target amplitudes, the initial acceleration profile has been shown to correlate well with both peak velocity and movement amplitude (Ghez and Gordon 1987; Ghez and Vicario 1978; Gordon and Ghez 1984, 1987a; Gottlieb et al. 1990). The duration of the first acceleration pulse is typically fairly consistent, although it varies slightly with target and movement amplitude. This control pattern has been referred to as pulse-step control and has two components: pulse-height and -width, which refer to the peak and duration, respectively, of the initial acceleration pulse, force pulse, or first agonist EMG burst (Ghez 1979; Ghez and Gordon 1987; Gordon and Ghez 1984; Brown and Cooke 1981, 1984, 1986, 1990). Pulse-width control has been shown be substantially affected by peripheral sensory influences, such as force perturbations, whereas pulse-height control is resistant to such influences (Brown and Cooke 1981). Because of this and because peak accelerations occur before peripheral feedback can affect force output, pulse-height control has been attributed largely to the preplanning of movement amplitude. Gordon and Ghez (1987b) have also shown that within a given isometric target, the duration of the force profile varied inversely with force amplitude. They proposed that pulse-width mechanisms, thereby, function to compensate inaccuracies in pulse-height control. These findings have recently been corroborated in a multijoint reaching task (Krakauer et al. 2002). Taken together, these studies support a two-mechanism process for controlling single-joint movement amplitude: pulse-height and pulse-width control. The former results exclusively from preplanning, whereas the latter is substantially influenced by somatosensory feedback and can compensate for inaccuracies in the former.
The purpose of the current study is to examine interlimb differences in control of movement extent. According to both the open/closed-loop and the dynamic-dominance hypotheses, we expect the nondominant system to rely more heavily on pulse-width control, whereas the dominant system might show more reliance on pulse-height control. Alternatively, these mechanisms may not reflect interlimb differences in coordination associated with handedness. In this case, the previously identified interlimb differences in coordination may be specific to the multijoint-coordination requirements of the tasks studied.
METHODS
Subjects
Eleven neurologically intact right-handed adults (3 males and 8 females) aged from 20 to 25 yr old, performed fast point-to-point single-joint elbow-extension movements. Only right-handers were recruited; handedness was determined using a 12-item version of the Edinburgh inventory (Oldfield 1971). The subjects gave informed consent prior to participation. Each subject performed two single 150-trial experimental sessions (1 with each arm). Five subjects performed with their left arm first (LR group) and the other six with their right arm first (RL group).
Experimental setup
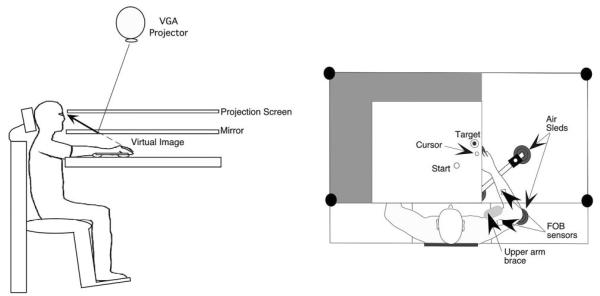
Figure 1 illustrates the experimental setup. Subjects sat facing a projection screen with either the right or left arm supported over a horizontal table top, positioned just below shoulder height (adjusted to subjects' comfort), by an air-jet system, which reduces the effects of gravity and friction. A cursor representing finger position, a start circle, and a target were projected on a horizontal back-projection screen positioned above the arm. A mirror, positioned parallel and below this screen, reflected the visual display so as to give the illusion that the display was in the same horizontal plane as the fingertip. Calibration of the display assured that this projection was veridical. The upper arm and all joints distal to the elbow were immobilized using adjustable braces. This virtual-reality environment assured that subjects had no visual feedback of their arm during an experimental session. Movements of the trunk and scapula were restricted using a butterfly-shaped chest restraint. Position and orientation of the segments proximal and distal of the elbow joint were sampled using a flock-of-birds (FoB; Ascension-Technology) magnetic 6-df movement-recording system. A single sensor was attached to the upper arm segment via an adjustable plastic cuff, and another sensor was fixed to the air sled where the forearm was fitted. The sensors were positioned approximately at the center of each arm segment. The position of the following three bony landmarks was digitized using a stylus that was rigidly attached to a FoB sensor: index finger tip, the lateral epicondyle of the humerus, and the acromion, directly posterior to the acromio-clavicular joint. These positions relative to the sensors attached to each arm segment thus remained constant throughout the experimental session. As sensor data were received from the FoB, the position of these landmarks was computed by our custom software yielding the three-dimensional (3D) position of the index finger tip. Because the table surface defined our x-y plane, perpendicular axis displacement was constant. We, thus used the recorded x-y coordinates of the finger tip to project a cursor onto the screen. Screen redrawing occurred fast enough to maintain the cursor centered on the fingertip throughout the sampled arm movements. During the experiment, the light was turned off such that subjects were unable to view their arm. Digital data were collected at 103 Hz using a Macintosh computer, which controlled the sensors through separated serial ports and stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC (REAL Software), C, and IgorPro (Wavemetric).
FIG. 1.
Experimental setup.
Experimental task
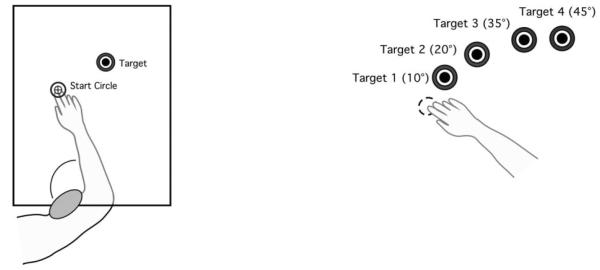
Prior to all trials, the index finger position was displayed in real time as a screen cursor. The shoulder position was restrained by a brace at 20°, while the shoulder-elbow angle (angle formed between upper arm and forearm) established the start and end locations of the movements. The start location was 80°, while the target locations were 90, 100, 115, and 125°; thus target positions required 10, 20, 35, and 45° of elbow extension, respectively (Fig. 2). Although target positions were individually set for each subject according to elbow angles, the average Euclidean distances were 7, 13, 21, and 27 cm, respectively. All targets were displayed as 2.5 cm in diameter. Subjects were to hold the cursor within the starting circle for 200 ms to initiate each trial. They were instructed to move the finger cursor to the target using a single, uncorrected motion in response to an audiovisual GO signal. Feedback of the fingertip position (cursor display) was given to allow subjects to position the hand in the start circle and then was removed at the GO signal. Whereas subjects did not receive specific feedback about final position location, points were awarded based on distance between the final finger position and the center of the target. Final position errors of <2.5 cm were awarded 10 points, whereas errors between 2.5 and 3.5 cm were awarded 3 points and errors between 3.5 and 5 cm were awarded 1 point. Targets were presented in a pseudorandom order such that no single target was presented consecutively. The first 50 trials of each session were discarded to allow for task familiarity. Kinematic analysis was conducted on the following 100 trials.
FIG. 2.
Experimental task.
Kinematic data
The 3D position of the index finger and elbow were calculated from sensor position and orientation data. Then joint angle was calculated from this data. All kinematic data were low-pass filtered at 8 Hz (3rd-order, dual-pass Butterworth) and differentiated to yield angular velocity and acceleration values. Each trial usually started with the hand at zero velocity, but small oscillations of the hand sometimes occurred within the start circle. In this case, the onset of movement was defined by the last minimum (<5% maximum tangential velocity) prior to the maximum in the index finger's tangential velocity profile. Movement termination was defined as the first minimum (<5% maximum tangential hand velocity) after the peak in tangential hand velocity. Elbow displacement and velocity were calculated from joint-angle data. Movement accuracy was measured as the final position error, which was calculated as the distance between the index-finger location at movement end and the center of the target.
Statistical analysis
The individual dependent measures used in this paper were analyzed using two-way repeated-measure ANOVA. The individual dependent measures used in this paper were analyzed using two-way repeated-measure ANOVA. The design was counterbalanced, such that 1/2 of the subjects performed first with the dominant arm, whereas the other 1/2 performed first with the nondominant arm. The two factors assessed were hand and target. Based on our design, we expected main effects for target. Our null hypothesis was that main effects for hand would not be significant, P > 0.05. Post hoc analysis was done using Tukey-Kramer analysis when warranted by significant main effects. We also conducted simple linear regression analysis for select sets of data using the linfit routine in Igor Pro (Wavemetrics). Comparison of correlation coefficients was done by converting r values to z scores (Fisher Transformation) and then averaging these scores. Mean z scores were then converted back into equivalent correlation coefficients and were compared using paired t-test.
RESULTS
Hand paths
Figure 3 shows ensemble averaged hand paths separated by target and hand for a representative subject. Movements were generally well adapted to the amplitude of the targets and showed a tendency to overshoot, which was greater for the longer distance targets (Table 1). The tendency to overshoot targets has previously been demonstrated for planar reaching movements made under low-friction conditions with no visual feedback (Ghez 1979; Sainburg 2002). However, as shown in the inset of Fig. 3, both arms showed comparable final-position errors across all subjects. Our ANOVA revealed no main effect for hand, nor interaction between target and hand (Table 1). There was a tendency for the nondominant arm to overshoot target 3 more than the dominant arm (P < 0.05); however, both arms showed similar performances for the other targets. Overall, the hand-paths of both arms showed similar spatial profiles for this task.
FIG. 3.
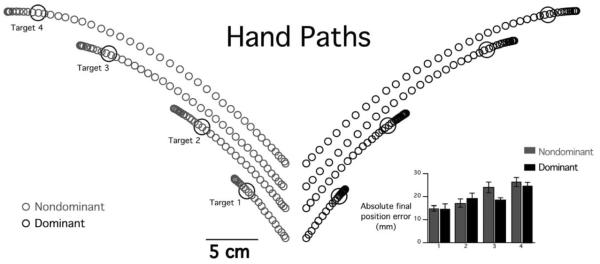
Ensemble averaged hand paths separated by target for nondominant (gray) and dominant (black) arms for a representative subject. Inset: Parametric measures of final position error across subjects for nondominant (gray) and dominant (black) arms by target across subjects.
table 1.
ANOVA: measure of overshoot: final position error
| Factor | F Ratio | Probability > F |
|---|---|---|
| Hand | 0.7049 | 0.4208 |
| Target | 22.839 | <.0001 |
| Hand*target | 2.2288 | 0.1053 |
Velocity and acceleration profiles
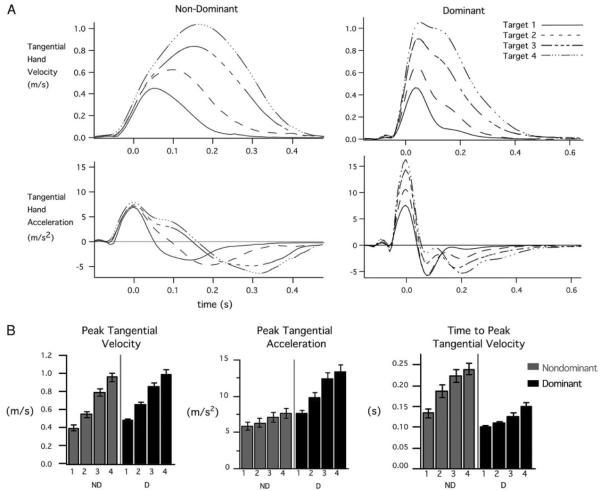
Figure 4A shows the ensemble averaged tangential hand velocity (top) and acceleration profiles (bottom) for individual subjects. Figure 4B shows parametric measures of peak tangential hand velocity, peak tangential hand acceleration, and time-to-peak tangential hand velocity separated by target and averaged across all subjects. Both dominant and nondominant arm trajectories show a strong scaling of peak tangential hand velocity with smaller movements averaging ~0.4–0.45 m/s and the largest movements averaging ~0.9–1.2 m/s. As shown in Fig. 4B (left), this scaling was consistent across both arms of all subjects. No significant main effect for hand occurred, but there was a main effect for target and an interaction effect (Table 2).
fig. 4.
A: ensemble averaged tangential hand velocity (top) and acceleration (bottom) profiles for nondominant (gray) and dominant (black) arms of individual subjects as synchronized to peak acceleration. For display purposes, data have been synchronized to peak tangential acceleration (x = 0). B: parametric measures of peak tangential hand velocity (left), peak tangential hand acceleration (middle), and time-to-peak tangential hand velocity (right) for nondominant (gray) and dominant (black) arms by target across subjects.
table 2.
ANOVA: peak tangential hand velocity
| Factor | F Ratio | Probability > F |
|---|---|---|
| Hand | 1.8374 | 0.2051 |
| Target | 234.303 | <.0001 |
| Hand*target | 3.8173 | 0.0198 |
Whereas both arms showed similar scaling of peak velocities with target distance, the method of achieving these velocities was quite different for each arm. Figure 4A, bottom, shows the acceleration profiles that correspond to the velocity profiles (top). The characteristic unimodal velocity profiles were produced by biphasic acceleration profiles. As reported previously, the scaling of dominant arm velocity profiles with target distance is reflected by scaling of the first peak in the acceleration profile, a phenomenon termed “pulse-height” control (Brown and Cooke 1981; Ghez 1979). Whereas the peak in tangential hand velocity reflects the area of the first acceleration pulse, the duration of this pulse is very consistent across target amplitudes. This is reflected by the near coincident peak velocities, and acceleration zero crosses, for all four movement amplitudes. Thus the width of the acceleration profile is nearly constant for the dominant arm, whereas the height varies with movement amplitude, a reflection of predominantly pulse-height control. In contrast, the nondominant arm shows an opposite pattern for the acceleration profiles. The initial peak in tangential acceleration is nearly constant across all four movement amplitudes, whereas the duration of the first acceleration pulse varies directly with the peak in tangential velocity. As a result, the time-to-peak tangential velocity varies directly with peak velocity. This is most easily observed by the increasingly rightward location of the larger velocity profiles in Fig. 4A (top, left) and of the acceleration cross zero locations (bottom, left). Thus in contrast to the dominant arm, the nondominant arm system specified peak velocity primarily by varying the duration of the first acceleration pulse, a reflection of pulse-width control.
The robust nature of this finding is demonstrated in the bar plots of Fig. 4B. Peak tangential velocity (left) shows a similar scaling across target amplitudes for both arms. No main effect of hand was revealed by ANOVA (Table 2). However, peak tangential acceleration was quite different for the two arms. For the nondominant arm, very little variation of peak acceleration with target occurred. In fact, there was no significant main effect of target (P = 0.23). However, for the dominant arm, substantial scaling of peak acceleration occurred with target as reflected by a main effect of target for this arm (P < 0.0001). Our ANOVA revealed a main effect for hand and interaction between hand and target for this measure (Table 3). As discussed in the preceding text, the nondominant arm scaling of peak velocity with target occurred by scaling the duration, not the amplitude, of the acceleration profile. As a result, the nondominant arm showed, on average, an increase of near 100% [109 ± 0.0096 (SD) ms] in time-to-peak velocity between targets 1 and 4. In contrast, the dominant arm showed less than a 60% change over the same targets. In both cases, a main effect for target occurred for each hand and an interaction between hand and target occurred (Table 4).
table 3.
ANOVA: peak tangential hand acceleration
| Factor | F Ratio | Probability > F |
|---|---|---|
| Hand | 38.175 | <.0001 |
| Target | 42.547 | <.0001 |
| Hand*target | 27.261 | <.0001 |
table 4.
ANOVA: time-to-peak tangential hand velocity
| Factor | F Ratio | Probability > F |
|---|---|---|
| Hand | 45.783 | <.0001 |
| Target | 65.3641 | <.0001 |
| Hand*target | 15.02 | <.0001 |
It should be noted that the duration of acceleration varied for both hands but much more so for the nondominant arm, whereas peak acceleration varied greater for the dominant arm. These findings indicate greater reliance on pulse-width control for the nondominant arm and on pulse-height control for the dominant arm.
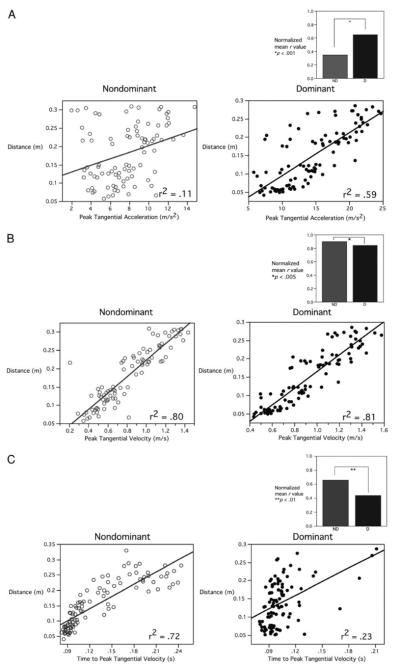
The findings described in the preceding text imply that peak tangential acceleration, which occurred some 50 ms after (58 ± 11 ms) movement onset, served as a reasonable predictor of movement distance for the dominant but not the non-dominant arm. Figure 5A shows movement distance plotted as a function of peak tangential acceleration for both arms of a representative subject. As indicated by the figure, peak tangential acceleration is a relatively strong predictor of distance for the dominant arm (r2 = 0.59) but not for the nondominant arm (r2 = 0.11). This finding was significant across all subjects as indicated by Fig. 5A, inset, showing a comparison of correlation coefficients across subjects. These values were normalized for statistical comparison, which indicated highly significant differences between the limbs (P < 0.001).
fig. 5.
A: movement distance as predicted by peak tangential hand acceleration of nondominant (gray circle) and dominant (black solid) arms for a representative subject. Inset: normalized mean r values for nondominant (gray) and dominant (black) across subjects. B: movement distance as predicted by peak tangential hand velocity of both arms for a representative subject. Inset: normalized mean r values for nondominant (gray) and nondominant (black) across subjects. C: movement distance as predicted by time-to-peak tangential hand velocity of both arms for a representative subject. Inset: normalized mean r values for nondominant (gray) and nondominant (black) across subjects.
Regardless of the poor correlation between movement distance and peak acceleration for the nondominant arm, peak velocity predicted movement distance well for both arms. In fact, as shown by Fig. 5B, inset, this prediction was better for the nondominant arm than for the dominant arm across all subjects (P < 0.005). This indicates that the pulse-width strategy employed by the nondominant arm was effective in producing peak velocities that were comparable to the dominant arm in relation to movement distance. As shown in Fig. 5C, time-to-peak velocity, or acceleration duration, predicted movement distance to a greater degree for the nondominant (r2 = 0.72) than the dominant arm (r2 = 0.23). This finding was significant across all subjects as indicated by the insert graph of normalized correlation coefficients (P < 0.01). As discussed in the preceding text, this suggests that the nondominant arm system utilized sensory feedback mechanisms to adjust the duration of the initial acceleration impulse so as to specify movement speed in accord with intended movement distance. In contrast, the dominant arm system specified distance primarily by adjusting the amplitude of the initial acceleration impulse.
DISCUSSION
In this study, we examined interlimb differences in control of movement extent. Subjects made repetitive single-joint elbow-extension movements to each of four targets of 10, 20, 35, and 45° excursions. Both arms performed the task equally well as there was no significant difference between either peak velocities or movement accuracies. However, the mechanisms responsible for the different movement extents were quite distinct for each arm. For the nondominant arm, peak tangential acceleration varied little across target distances and, as such, was a poor predictor of movement distance. The peak velocities of the nondominant arm were determined primarily by variation in the duration of extensor accelerations. In contrast, for the dominant arm, peak tangential finger acceleration varied with movement distance, whereas the duration of the initial acceleration impulse remained fairly constant. Previous research on dominant-arm movements has indicated that these two processes represent independent neural mechanisms for control of movement distance (Brown and Cooke 1981, 1984, 1986; Ghez 1979; Ghez and Gordon 1987; Ghez and Vicario 1978; Gordon and Ghez 1984, 1987a,b). Our current findings support this idea by showing that each arm system relies differentially on one or the other process to specify movement distance.
The dominant-arm dependence on pulse-height control is consistent with the hypothesis that the dominant control system is specialized for open-loop movement-planning mechanisms. The premise that pulse-height control represents open-loop processes is supported by two lines of experimental evidence. First, studies of load perturbations indicate that appreciable changes in force cannot occur at latencies less than 50 ms, roughly the time of peak acceleration in single-joint studies (Bagesteiro and Sainburg 2003; Bennett et al. 1994; Bizzi et al. 1978; Bock 1993; Brown and Cooke 1981; Shapiro et al. 2002). Second, a number of studies have revealed that pulse-height control mechanisms are resistant to manipulations of sensory information prior to or during rapid single-joint movements (Brown and Cooke 1981, 1984, 1986). When a force perturbation is applied to the stationary limb of an animal or human, the first measurable EMG response that produces substantial force is initiated at a latency of 30–60 ms and has been referred to as the functional stretch reflex (FSR) (Evarts and Tanji 1974, 1976; Ghez and Shinoda 1978; Godaux and Desmedt 1979). Similarly, when unexpected loads are applied just prior to an ongoing voluntary movement, load compensation responses begin some 50–60 ms after the onset of movement (Bagesteiro and Sainburg 2003; Bennett et al. 1994; Bizzi et al. 1978; Bock 1993; Brown and Cooke 1981; Shapiro et al. 2002). It should be emphasized that additional time is required for such changes in EMG to affect force and thus acceleration values (Zajac 1989). These findings provide strong support to the idea that peak acceleration values, measured some 50 ms after movement onset, are unaffected by sensory feedback.
Previous studies that have directly examined pulse-height and -width control provide further support to the hypotheses that the former is a reflection of preprogrammed processes, while the latter largely reflects feedback-mediated events. Rapid, aimed, single-joint movements are typically produced with a characteristic triphasic EMG pattern (Day et al. 1983; Desmedt and Godaux 1979; Ghez 1979; Gordon and Ghez 1984). During targeted isometric force pulses (Gordon and Ghez 1984, 1987a) and rapid elbow-joint movements (Brown and Cooke 1981, 1984, 1986), the amplitude of the first agonist burst (AG1) corresponds to the amplitude of the initial acceleration peak or force, whereas the duration of the initial acceleration impulse, or time-to-peak force, varies with the duration of AG1 and onset of the antagonist muscle burst (ANT). In an elegant series of experiments, Brown and Cooke (1981, 1984, 1986) previously showed that the duration of AG1 and the onset of ANT can be affected by sensory feedback in the form of perturbations prior to or during movement onset. However, the amplitude of AG1 tends to be resistant to such peripheral influences (Brown and Cooke 1981). These authors also showed that the duration of AG1 and onset of ANT continue to vary with movement amplitude in a proprioceptively deafferented patient, suggesting that pulse-width control is at least partially mediated by open-loop mechanisms (Cooke et al. 1985). Nevertheless, these studies support the hypothesis that pulse-height control is dependent on preprogramming, whereas pulse-width control can also be substantially influenced by feedback-mediated processes. Further supporting this idea, Gordon and Ghez (1987) showed that pulse-width control can serve as a mechanism for correcting inaccuracies in pulse-height control. In a targeted force-pulse task, for each single-target amplitude, force rise time varied inversely with computed initial “errors” in the rate of rise of force. When the slope of the force/time curve was too steep for the target amplitude, the timing of peak force was shortened, and when the slope was too shallow, the timing of peak force was prolonged. These findings have recently been supported in a planar reaching task (Krakauer et al. 2002) in which time-to-peak velocity was shown to vary inversely with peak acceleration. As a result, peak velocity remained fairly constant for a given target amplitude. Thus pulse-height and -width control appear to largely reflect the influence of open- and closed-loop mechanisms for controlling movement distance. Our current findings provide support for this model by demonstrating that the two arms rely differentially on one or the other process. In addition, our findings suggest specialization of the dominant hemisphere/limb system for pulse-height control and specialization of the nondominant system for pulse-width control.
Interlimb differences in open/closed-loop processing
The idea that the nondominant arm is specialized for feedback-mediated error-correction mechanisms has previously been proposed, although the effects of sensory feedback on dominant and nondominant arm performance have yielded conflicting results (Carson et al. 1990, 1992, 1995; Elliott et al. 1994; Flowers 1975a,b; Roy and Elliott 1986; Roy et al. 1994; Todor and Cisneros 1985). For example, Flowers (1975a,b) and others (Carson et al. 1993a; Todor and Cisneros 1985; Todor and Doane 1977) suggested that manual asymmetries emerge from differences in the use of visual feedback that arise when the precision requirements of aiming tasks become high as reflected by the index of difficulty (ID) (see Plamondon and Alimi 1997). However, conflicting interpretations developed from studies that failed to alter interlimb differences in accuracy by manipulating the visual feedback conditions of aimed movements (Carson 1992, 1993; Carson et al. 1990, 1993a,b; Roy and Elliott 1986). In contrast to feedback mechanisms, some authors have proposed a dominant arm/hemisphere advantage for movement planning, initiation, or sequencing (Annett et al. 1979; Carson et al. 1995; Todor and Kyprie 1980; Todor and Smiley-Oyen 1987). Other studies have suggested a nondominant arm/hemisphere advantage for movement preparation based on left-hand advantages in reaction time (Carson et al. 1990; Elliott et al. 1993). Thus the idea of differentiating dominant and nondominant arm control by open- or closed-loop control mechanisms alone remains controversial. However, most of these studies used reaction time, peak speed, movement duration, and/or final position accuracy as dependent measures. It should be stressed that our current results show substantial interlimb differences in movement strategy, as revealed by the early phase of the acceleration profiles, with no significant differences in movement accuracy or speed. Therefore the seemingly equivocal results from many previous studies may be due to the dependent variables chosen, regardless of interlimb differences in control strategies.
Studies in unilateral brain-damaged patients have provided consistent and strong evidence to support an open/closed-loop hypothesis of hemispheric control. Haaland and colleagues (Haaland et al. 1977; Haaland and Delaney 1981; Haaland and Harrington 1989a,b, 1996, 1994; Prestopnik et al. 2003) have used perceptual motor tasks, which require rapid reciprocal aimed movements between two targets that vary in size and/or target distance to examine movement deficits in the ipsilesional arm of stroke patients. These experiments have used horizontal movement in the ipsilesional hemispace with the ipsilesional arm in the stroke patients (e.g., right hemispace and arm for patients with right hemisphere damage) to rule out the confounding effects of motor weakness, visual field cuts, and visual neglect. Dominant hemisphere lesions produced deficits in the initial, ballistic component of movement but not in the later component (Haaland and Delaney 1981; Haaland and Harrington 1989a,b, 1994, 1996; Haaland et al. 1977; Prestopnik et al. 2003). Patients with nondominant hemisphere lesions showed no deficits in this task. However, when the precision requirements of the task were increased, patients with nondominant lesions showed deficits in final position accuracy (Haaland and Delaney 1981; Haaland and Harrington 1989a,b, 1994, 1996; Haaland et al. 1977; Prestopnik et al. 2003; Winstein and Pohl 1995). These results suggested that the dominant hemisphere is important for controlling rapid, ballistic components of movement that are more dependent on planning (open-loop), and the nondominant hemisphere is more important for the later movement component that is more responsible for response modification (closed-loop). Consistent with these findings, Winstein and Pohl (1995) showed that nondominant lesions produced slowing of the deceleration phase of motion, whereas dominant lesions produced slowing of the initial, acceleration phase of motion. Our current results support these findings, indicating a reliance of the dominant limb/hemisphere system on open-loop pulse-height control and a reliance of the nondominant system on closed-loop pulse-width control. It should be emphasized that neurologically intact individuals utilize both mechanisms with each limb but seem to rely more heavily on one or the other, depending on the arm being used. Previous studies with stroke patients did not specifically examine pulse-height and -width control mechanisms, and it thus remains to be determined whether these patients will show lesion specific deficits in these mechanisms.
Consistent with the idea that the nondominant hemisphere/limb system is specialized for feedback mediated control, we recently provided strong evidence for nondominant arm advantages in somatosensory-based load-compensation responses (Bagesteiro and Sainburg 2003). Subjects made repetitive 20° elbow flexion movements while the arm was supported on a horizontal, frictionless, air-jet system. On random trials, a 2-kg mass was attached to the arm splint prior to the go signal. Whereas muscle activity recorded prior to peak tangential hand acceleration was the same for loaded and baseline trials, substantial changes in muscle activity occurred after this point. In both limbs, the load-compensation response was associated with a reduction in extensor muscle activity, resulting in a prolonged flexor velocity phase of motion. For the nondominant arm, this resulted in effective load compensation, such that no differences in final position accuracy occurred between loaded and baseline trials. However, the dominant arm response also included a considerable increase in flexor muscle activity, which substantially prolonged the flexor acceleration phase of motion. As a result, the dominant arm overcompensated the effects of the load, producing a large and systematic overshoot of final position. These results indicated more effective load-compensation responses for the nondominant arm, supporting a specialized role of the nondominant arm/hemisphere system in closed-loop somatosensory-based mechanisms. Our current findings, indicating reliance on pulse-width mechanisms for controlling movement amplitude, are consistent with a nondominant arm specialization for feedback mediated control. These findings also may explain previous findings showing nondominant arm advantages in final position accuracy (Bagesteiro and Sainburg 2002; Sainburg and Kalakanis 2000; Sainburg and Wang 2002). This is because final position achievement is largely dependent on deceleration mechanisms that emerge late in the movement, after feedback loops become available. These findings suggest that the open/closed-loop and the dynamic-dominance hypotheses of motor lateralization are convergent ideas that might reflect differential specialization for open-loop trajectory-planning mechanisms and closed-loop control of final position.
ACKNOWLEDGMENTS
We thank Dr. Kathy Haaland for many insightful and scholarly interactions that contributed to the considerations of hemispheric dominance discussed in this paper.
GRANTS This research was supported by National Institute of Child Health and Human Development Grant R01HD-39311.
REFERENCES
- Annett J, Annett M, Hudson PTW. The control of movement in the preferred and non-preferred hands. Qrtly J Exp Psych. 1979;31:641–652. doi: 10.1080/14640747908400755. [DOI] [PubMed] [Google Scholar]
- Bagesteiro LB, Sainburg RL. Handedness: dominant arm advantages in control of limb dynamics. J Neurophysiol. 2002;88:2408–2421. doi: 10.1152/jn.00901.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagesteiro LB, Sainburg RL. Nondominant arm advantages in load compensation during rapid elbow joint movements. J Neurophysiol. 2003;90:1503–1513. doi: 10.1152/jn.00189.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett DJ, Gorassini M, Prochazka A. Catching a ball: contributions of intrinsic muscle stiffness, reflexes, and higher order responses. Can J Physiol Pharmacol. 1994;72:525–534. doi: 10.1139/y94-076. [DOI] [PubMed] [Google Scholar]
- Bizzi E, Dev P, Morasso P, Polit A. Effect of load disturbances during centrally initiated movements. J Neurophysiol. 1978;41:542–556. doi: 10.1152/jn.1978.41.3.542. [DOI] [PubMed] [Google Scholar]
- Bock O. Early stages of load compensation in human aimed arm movements. Behav Brain Res. 1993;55:61–68. doi: 10.1016/0166-4328(93)90007-d. [DOI] [PubMed] [Google Scholar]
- Brown SH, Cooke JD. Responses to force perturbations preceding voluntary human arm movements. Brain Res. 1981;220:350–355. doi: 10.1016/0006-8993(81)91224-5. [DOI] [PubMed] [Google Scholar]
- Brown SH, Cooke JD. Initial agonist burst duration depends on movement amplitude. Exp Brain Res. 1984;55:523–527. doi: 10.1007/BF00235283. [DOI] [PubMed] [Google Scholar]
- Brown SH, Cooke JD. Initial agonist burst is modified by perturbations preceding movement. Brain Res. 1986;377:311–322. doi: 10.1016/0006-8993(86)90874-7. [DOI] [PubMed] [Google Scholar]
- Brown SH, Cooke JD. Movement-related phasic muscle activation. I. Relations with temporal profile of movement. J Neurophysiol. 1990;63:455–464. doi: 10.1152/jn.1990.63.3.455. [DOI] [PubMed] [Google Scholar]
- Carson RG. Manual asymmetries: old problems and new directions. Hum Move Sci. 1993;12:479–506. [Google Scholar]
- Carson RG. Visual feedback processing and manual asymmetries: an evolving perspective. In: Proteau L, Elliott D, editors. Vision and Motor Control. Advances in Psychology. North-Holland; Amsterdam: 1992. pp. 49–65. [Google Scholar]
- Carson RG, Chua R, Elliott D, Goodman D. The contribution of vision to asymmetries in manual aiming. Neuropsychologia. 1990;28:1215–1220. doi: 10.1016/0028-3932(90)90056-t. [DOI] [PubMed] [Google Scholar]
- Carson RG, Chua R, Goodman D, Byblow WD, Elliott D. The preparation of aiming movements. Brain Cogn. 1995;28:133–154. doi: 10.1006/brcg.1995.1161. [DOI] [PubMed] [Google Scholar]
- Carson RG, Elliott D, Goodman D, Thyer L, Chua R, Roy EA. The role of impulse variability in manual-aiming asymmetries. Psychol Res. 1993a;55:291–298. [Google Scholar]
- Carson RG, Goodman D, Chua R, Elliott D. Asymmetries in the regulation of visually guided aiming. J Mot Behav. 1993b;25:21–32. doi: 10.1080/00222895.1993.9941636. [DOI] [PubMed] [Google Scholar]
- Carson RG, Goodman D, Elliott D. Asymmetries in the discrete and pseudocontinuous regulation of visually guided reaching. Brain Cogn. 1992;18:169–191. doi: 10.1016/0278-2626(92)90077-y. [DOI] [PubMed] [Google Scholar]
- Cooke JD, Brown S, Forget R, Lamarre Y. Initial agonist burst duration changes with movement amplitude in a deafferented patient. Exp Brain Res. 1985;60:184–187. doi: 10.1007/BF00237030. [DOI] [PubMed] [Google Scholar]
- Day BL, Rothwell JC, Marsden CD. Interaction between the long-latency stretch reflex and voluntary electromyographic activity prior to a rapid voluntary motor reaction. Brain Res. 1983;270:55–62. doi: 10.1016/0006-8993(83)90791-6. [DOI] [PubMed] [Google Scholar]
- Desmedt JE, Godaux E. Ballistic contractions in man: characteristic recruitment pattern of single motor units of the tibialis anterior muscle. J Physiol. 1977;264:673–693. doi: 10.1113/jphysiol.1977.sp011689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmedt JE, Godaux E. Voluntary motor commands in human ballistic movements. Ann Neurol. 1979;5:415–421. doi: 10.1002/ana.410050503. [DOI] [PubMed] [Google Scholar]
- Elliott D, Chua R, Pollock BJ. The influence of intermittent vision on manual aiming. Acta Psychol. 1994;85:1–13. doi: 10.1016/0001-6918(94)90016-7. [DOI] [PubMed] [Google Scholar]
- Elliott D, Roy EA, Goodman D, Carson RG, Chua R, Maraj BKV. Asymmetries in the preparation and control of manual aiming movements. Can J Exp Psychol. 1993;47:570–589. [Google Scholar]
- Evarts EV, Tanji J. Gating of motor cortex reflexes by prior instruction. Brain Res. 1974;71:479–494. doi: 10.1016/0006-8993(74)90992-5. [DOI] [PubMed] [Google Scholar]
- Evarts EV, Tanji J. Reflex and intended responses in motor cortex pyramidal tract neurons of monkey. J Neurophysiol. 1976;39:1069–1080. doi: 10.1152/jn.1976.39.5.1069. [DOI] [PubMed] [Google Scholar]
- Flowers K. Ballistic and corrective movements on an aiming task. Intention tremor and parkinsonian movement disorders compared. Neurology. 1975a;25:413–421. doi: 10.1212/wnl.25.5.413. [DOI] [PubMed] [Google Scholar]
- Flowers K. Handedness and controlled movement. Br J Psychol. 1975b;66:39–52. doi: 10.1111/j.2044-8295.1975.tb01438.x. [DOI] [PubMed] [Google Scholar]
- Ghez C. Contributions of central programs to rapid limb movement in the cat. In: Asanuma H, Wilson VJ, editors. Integration in the Nervous System. Igaku-Shoin; Tokyo: 1979. pp. 305–319. [Google Scholar]
- Ghez C, Gordon J. Trajectory control in targeted force impulses. I. Role of opposing muscles. Exp Brain Res. 1987;67:225–240. doi: 10.1007/BF00248545. [DOI] [PubMed] [Google Scholar]
- Ghez C, Shinoda Y. Spinal mechanisms of the functional stretch reflex. Exp Brain Res. 1978;32:55–68. doi: 10.1007/BF00237390. [DOI] [PubMed] [Google Scholar]
- Ghez C, Vicario D. The control of rapid limb movement in the cat. II. Scaling of isometric force adjustments. Exp Brain Res. 1978;33:191–202. doi: 10.1007/BF00238059. [DOI] [PubMed] [Google Scholar]
- Godaux E, Desmedt JE. Long loop reflexes during ballistic movements (Proceedings) Arch Int Physiol Biochim. 1979;87:346–347. [PubMed] [Google Scholar]
- Gordon J, Ghez C. EMG patterns in antagonist muscles during isometric contraction in man: relations to response dynamics. Exp Brain Res. 1984;55:167–171. doi: 10.1007/BF00240511. [DOI] [PubMed] [Google Scholar]
- Gordon J, Ghez C. Trajectory control in targeted force impulses. II. Pulse height control. Exp Brain Res. 1987a;67:241–252. doi: 10.1007/BF00248546. [DOI] [PubMed] [Google Scholar]
- Gordon J, Ghez C. Trajectory control in targeted force impulses. III. Compensatory adjustments for initial errors. Exp Brain Res. 1987b;67:253–269. doi: 10.1007/BF00248547. [DOI] [PubMed] [Google Scholar]
- Gottlieb GL, Corcos DM, Agarwal GC, Latash ML. Organizing principles for single joint movements. III. Speed-insensitive strategy as a default. J Neurophysiol. 1990;63:625–636. doi: 10.1152/jn.1990.63.3.625. [DOI] [PubMed] [Google Scholar]
- Gribble PL, Ostry DJ. Compensation for interaction torques during single-and multijoint limb movement. J Neurophysiol. 1999;82:2310–2326. doi: 10.1152/jn.1999.82.5.2310. [DOI] [PubMed] [Google Scholar]
- Haaland KY, Cleeland CS, Carr D. Motor performance after unilateral hemisphere damage in patients with tumor. Arch Neurol. 1977;34:556–559. doi: 10.1001/archneur.1977.00500210058010. [DOI] [PubMed] [Google Scholar]
- Haaland KY, Delaney HD. Motor deficits after left or right hemisphere damage due to stroke or tumor. Neuropsychologia. 1981;19:17–27. doi: 10.1016/0028-3932(81)90040-3. [DOI] [PubMed] [Google Scholar]
- Haaland KY, Harrington D. The role of the hemispheres in closed loop movements. Brain Cogn. 1989a;9:158–180. doi: 10.1016/0278-2626(89)90027-4. [DOI] [PubMed] [Google Scholar]
- Haaland KY, Harrington DL. Hemispheric control of the initial and corrective components of aiming movements. Neuropsychologia. 1989b;27:961–969. doi: 10.1016/0028-3932(89)90071-7. [DOI] [PubMed] [Google Scholar]
- Haaland KY, Harrington DL. Limb-sequencing deficits after left but not right hemisphere damage [published erratum appears in Brain Cogn 27: 134, 1995] Brain Cogn. 1994;24:104–122. doi: 10.1006/brcg.1994.1006. [DOI] [PubMed] [Google Scholar]
- Haaland KY, Harrington DL. Hemispheric asymmetry of movement. Curr Opin Neurobiol. 1996;6:796–800. doi: 10.1016/s0959-4388(96)80030-4. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Gordon J, Veytsman M, Ghez C. Contributions of planning and updating to accuracy of reaching movements in normals and stroke. Soc Neurosci Abstr. 2002:169. [Google Scholar]
- Mieschke PE, Elliott D, Helsen WF, Carson RG, Coull JA. Manual asymmetries in the preparation and control of goal-directed movements. Brain Cogn. 2001;45:129–140. doi: 10.1006/brcg.2000.1262. [DOI] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh Inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Plamondon R, Alimi AM. Speed/accuracy trade-offs in target-directed movements. Behav Brain Sci. 1997;20:279–303. doi: 10.1017/s0140525x97001441. (discussion 303-249. [DOI] [PubMed] [Google Scholar]
- Prestopnik J, Haaland K, Knight R, Lee R. Hemispheric dominance in the parietal lobe for open and closed loop movements. J Int Neuropsychol Soc. 2003;9:1–2. [Google Scholar]
- Roy EA, Elliott D. Manual asymmetries in visually directed aiming. Can J Psychol. 1986;40:109–121. doi: 10.1037/h0080087. [DOI] [PubMed] [Google Scholar]
- Roy EA, Kalbfleisch L, Elliott D. Kinematic analyses of manual asymmetries in visual aiming movements. Brain Cogn. 1994;24:289–295. doi: 10.1006/brcg.1994.1017. [DOI] [PubMed] [Google Scholar]
- Sainburg RL. Evidence for a dynamic-dominance hypothesis of handedness. Exp Brain Res. 2002;142:241–258. doi: 10.1007/s00221-001-0913-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Ghilardi MF, Poizner H, Ghez C. Control of limb dynamics in normal subjects and patients without proprioception. J Neurophysiol. 1995;73:820–835. doi: 10.1152/jn.1995.73.2.820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Kalakanis D. Differences in control of limb dynamics during dominant and nondominant arm reaching. J Neurophysiol. 2000;83:2661–2675. doi: 10.1152/jn.2000.83.5.2661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Poizner H, Ghez C. Loss of proprioception produces deficits in interjoint coordination. J Neurophysiol. 1993;70:2136–2147. doi: 10.1152/jn.1993.70.5.2136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Wang J. Interlimb transfer of visuomotor rotations: independence of direction and final position information. Exp Brain Res. 2002;145:437–447. doi: 10.1007/s00221-002-1140-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider K, Zernicke RF, Schmidt RA, Hart TJ. Changes in limb dynamics during the practice of rapid arm movements. J Biomech. 1989;22:805–817. doi: 10.1016/0021-9290(89)90064-x. [DOI] [PubMed] [Google Scholar]
- Shapiro MB, Gottlieb GL, Moore CG, Corcos DM. Electromyographic responses to an unexpected load in fast voluntary movements: descending regulation of segmental reflexes. J Neurophysiol. 2002;88:1059–1063. doi: 10.1152/jn.2002.88.2.1059. [DOI] [PubMed] [Google Scholar]
- Smith JL, Zernicke RF. Predictions for neural control based on limb dynamics. Trends Neurosci. 1987;10:123–128. [Google Scholar]
- Todor JI, Cisneros J. Accommodation to increased accuracy demands by the right and left hands. J Mot Behav. 1985;17:355–372. doi: 10.1080/00222895.1985.10735354. [DOI] [PubMed] [Google Scholar]
- Todor JI, Doane T. Handedness classification: preference versus proficiency. Percept Mot Skills. 1977;45:1041–1042. doi: 10.2466/pms.1977.45.3f.1041. [DOI] [PubMed] [Google Scholar]
- Todor JI, Kyprie PM. Hand differences in the rate and variability of rapid tapping. J Mot Behav. 1980;12:57–62. doi: 10.1080/00222895.1980.10735205. [DOI] [PubMed] [Google Scholar]
- Todor JI, Smiley-Oyen AL. Force modulation as a source of hand differences in rapid finger tapping. Acta Psychol. 1987;65:65–73. [Google Scholar]
- Winstein CJ, Pohl PS. Effects of unilateral brain damage on the control of goal-directed hand movements. Exp Brain Res. 1995;105:163–174. doi: 10.1007/BF00242191. [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling and application to biomechanics and motor control. In: Bourne JR, editor. CRC Critical Reviews in Biomedical Engineering. 4 ed. CRC; Boca Raton, FL: 1989. pp. 359–411. [PubMed] [Google Scholar]