Computational modeling of epilepsy for an experimental neurologist

Abstract

Computational modeling can be a powerful tool for an experimentalist, providing a rigorous mathematical model of the system you are studying. This can be valuable in testing your hypotheses and developing experimental protocols prior to experimenting. This paper reviews models of seizures and epilepsy at different scales, including cellular, network, cortical region, and brain scales by looking at how they have been used in conjunction with experimental data. At each scale, models with different levels of abstraction, the extraction of physiological detail, are presented. Varying levels of detail are necessary in different situations. Physiologically realistic models are valuable surrogates for experimental systems because, unlike in an experiment, every parameter can be changed and every variable can be observed. Abstract models are useful in determining essential parameters of a system, allowing the experimentalist to extract principles that explain the relationship between mechanisms and the behavior of the system. Modeling is becoming easier with the emergence of platforms dedicated to neuronal modeling and databases of models that can be downloaded. Modeling will never be a replacement for animal and clinical experiments, but it should be a starting point in designing experiments and understanding their results.

Introduction

Multiscale disease

Epilepsy is a multiscale disease involving changes at multiple different spatial and temporal scales. Changes at the scale of ion channels, caused by genetic mutations or the binding of an antiepileptic drug, are known to change the kinetics and excitability of the neuron. Molecular biologists and geneticists have made incredible advances in the recent decades identifying and characterizing ion channel mutations related to this disease (Meldrum and Rogawski, 2007). Changes at the cellular level can bring about seizures. However, seizures are observed at a macroscopic scale, identified in a patient’s behavior and recorded with electroencephalography (EEG) (Johnson et al., 2011). Computational modeling is a powerful tool that can be used to help bridge scales and identify how changes at one level can affect the next. This can help identify how changes at any level may bring about seizures and what sorts of treatments may be affective.

There is a hierarchy of experiments and their perceived relevance to public health. Clinical studies are at the top, being the most translational, followed by in vivo studies down to in vitro studies. The most distant is computational modeling. While clinical studies may be the final stage in establishing a relationship between research and medicine, advances are clearly dependent on the prior steps. In vivo studies are essential to prove the efficacy and safety of a therapy, and in vitro studies are used to establish the basic mechanisms of the disease and treatments. A computational model is arguably the first, fastest, and cheapest step that should be taken towards understanding and treating the disease.

This paper will briefly examine models bridging cellular, network and cortical behaviors. The scale and amount of physiological detail each model uses to describe seizures and epilepsy will be discussed. Models that describe actual physiological processes can be very useful, but we will argue that much can be gained by reducing models to the bare essentials, making them more abstract. We will emphasize how modeling can be useful for an experimentalist. We will provide a list of available modeling platforms and Internet sources for models. This is not intended as a review of epilepsy modeling, but is a review of how and why an experimentalist should use modeling to inform their experiments. From this paper, an experimentalist should be able to identify models available in their field.

What is a model?

A computational model is a set of equations that describe how a neuron, a network, a cortical area, or clinical behavior changes as a function of some variable, such as time. They consist of variables, representing things that change over time, and parameters, which represent values that are static or change on longer time scales than the simulation time. The functions and parameters should be estimated from experiments when modeling epilepsy.

Motivation for modeling can be broken into two types, retrospective modeling, where a model is developed to explain the data that already exists, and prospective modeling, where a model is developed to predict the behavior of a system under new conditions. Retrospective modeling is important for initially developing a model by comparing it to experimental data. However, the true test of a model is in prospective modeling, where the model is verified by examining whether it correctly predicts the experimental outcome. A good model should also match multiple types of experimental data. It is often beneficial to have multiple models per experiment.

Why model?

Models have made important advancements in many fields. One famous example is the debate whether the earth orbits the sun or vice versa. Copernicus was able to present a mathematical model in support of the heliocentric system. The movement of celestial bodies in the night sky is a complicated dynamic system. He was able to explain phenomenon such as proper orbits and eclipses using a model with the sun at the center. This simple model could explain many of the complex patterns observed. His hypothesis was further validated when Kepler, Galileo, Newton, and others collected novel data that the model was able to predict or that fit with the model. In this example a mathematical model was necessary, as technology did not allow for us to see the entire system (Folkerts and Kühne, 2006; Westman, 1975). The interplay between a mathematical model and experimental data helped to create an understanding of the spatial organization of the solar system. A good model should reveal principles that explain a number of interrelated complex behaviors.

As an experimentalist, why should you bother making a computational model when you can simply do the experiment? Even when an experiment can be done, modeling is a powerful approach for developing and designing experiments. We may have working mental models of how the brain works and why it seizes. Making a computational model is a way to formalize this mental model, allowing us to systematically identify the necessary parameters and states of the nervous system to describe its behaviors. Computational models also offer advantages over a mental model. Computational models are portable, allowing others to easily reproduce your findings or test their hypotheses against yours without experimental confounds. Models allow you to perturb parameters, which might not be possible experimentally. They also allow you to look at hidden states not observable experimentally. Models allow you to study interactions between different scales, just as collecting neuronal spikes and LFP data simultaneously allow us to connect different spatial scales. However, it is difficult to combine the data from different scales and experimental techniques except through a correlation analysis. The benefit of a model is that the two scales and their interactions can be explicitly modeled. A model can also determine how and when changes in a system’s behavior will occur, such as when a neuron transitions from resting to spiking.

Models can be useful in many different ways. They may be most useful when experimental outcomes and model predictions are different. This can help us identify important unconsidered factors involved in the system we are studying. Models can also be used in the process of designing and testing protocols. Testing protocols on the model prior to doing the experiment can reveal problems with the experimental design and can reduce wasted experiments. Simulated data can also be used to devise and test statistical analyses prior to starting experiments.

Ideally, models inspire new hypotheses about the biological system. Models may be used to discover which parameters and states increase the likelihood of seizures. Many factors may play a role, such as genetic mutations in ion channels, imbalances of neurotransmitters or ion concentrations, and changes in network topology. Models can be used to determine which therapies may be most effective and identify novel approaches to treating seizures.

Using a model

In generating a model, it is useful to try to define parameters and equations in physiological terms. If possible, variables should be determined from experimental findings, or their values justified. For variables that are unknown, simulations should be run over a range to determine how the model depends on the variable. It is a common misconception that any behavior can be reproduced given a model with enough parameters. Surprisingly, more often than not, a model will not behave as expected. The failure to reproduce a behavior despite attempting to model it realistically can lead to novel hypotheses about important parameters (Kopell, 2005). The failure of a model provides important insights into the shortcomings of our mental model, and forces us to refine both models.

However, the goal of modeling should not be to reproduce the data, but to understand principles about when and why seizures emerge. These principles are the basis from which new hypotheses can be generated. Principles of how and why transitions occur are best illustrated, and arguably best understood, when the model is reduced to its bare essentials. A model using realistic biological detail may be able to reproduce experimental data, but it may be as impenetrable to understand as the biological system. However, a model with less detail, or more abstraction, may allow for a clearer understanding of a complicated system. Different levels of abstraction are appropriate in different situations, and it is important to balance the level of detail you want with what you can learn.

Experimentally, it is often difficult to determine if a change observed is correlated with a perturbation you applied or caused by it. With computational models, it is much easier to determine causation. The change in output given a change in input is what we will define as the behavior in a model. Experimentally, we may be interested in how parameters affect the behavior of a system, such as how extracellular potassium concentration changes a neuron from rest to spiking. In mathematical models, the study of these transitions between behaviors is called “bifurcation theory” (Gurel et al., 1979; Luo, 1997; Wilson, 1999). Mathematical models can be used to understand how and when these behavioral changes come about. Bifurcation theory is a formalism to describe how these changes occur, and has been used in neuroscience to describe transitions in spiking behaviors of neurons, stability of networks, and emergence or termination of seizures (Hoppensteadt and Izhikevich, 1996; Izhikevich, 1998; Rodrigues et al., 2009; Wilson, 1999; Xie et al., 2008).

Changes in the behavior of a model are often caused by changes in the stability of equilibrium points. In a model described using differential equations, we can determine the system’s equilibrium points by setting the differential equations to zero and determining at what parameter values these equations intersect. These points can be stable or unstable. For example, as current applied to the neuron is increased, it will transition from rest to spiking. If the current is low enough, the neuron will return to rest if perturbed, because the resting point is stable. As current is increased, the neuron begins to spike spontaneously when the resting point becomes unstable. The change from stable to unstable is a bifurcation. Effects of drugs and ion channel mutations can be understood by analyzing how they affect these bifurcations.

Bifurcations are classified by the types of behaviors seen before and after the stability changes. Bifurcation types can be used to describe changes in physiological behaviors in a rigorous way. The existence of these equilibrium points and how they change can help establish causation between parameters and the system’s behavior. From the computational model, it is possible to determine if other bifurcations may exist as parameters are changed beyond what has been measured experimentally. The model may predict potential new behaviors not yet identified experimentally.

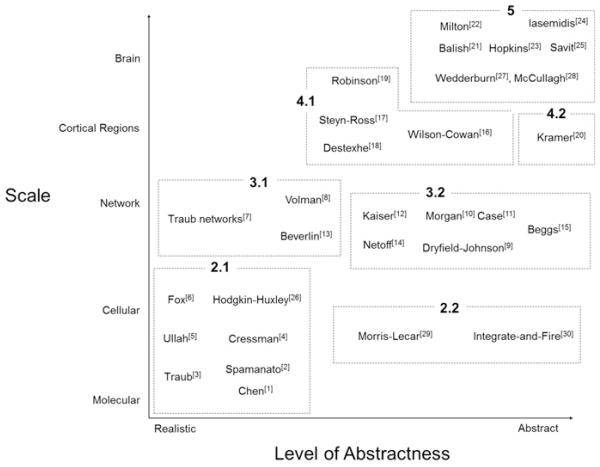
In this paper, we will review examples of models used to understand seizures at different spatial scales with different levels of abstraction. The goal of the paper is to show how and why different models are used. Detail of many of the models included in this paper can be found in a review by Lytton (2008). Fig. 1 is a summary of our paper. One axis represents the different scales of modeling and the other represents different levels of abstraction. Examples of different models reviewed in this paper are grouped by the section number in which they are discussed.

Fig. 1.

Diagram illustrating the range of scales and abstraction of different computational models used in describing epilepsy. Labeled boxes indicate section number in this paper. Names and numbers indicate papers, citations listed below.

1. K. Chen, I. Aradi, N. Thon, M. Eghbal-Ahmadi, T. Z. Baram, and I. Soltesz, Nat. Med. 7, 331 (2001).
2. J. Spampanato, I. Aradi, I. Soltesz, and A. L. Goldin, J. Neurophysiol. 91, 2040 (2004).
3. R. D. Traub and R. Dingledine, J. Neurophysiol. 64, 1009 (1990).
4. J. R. Cressman Jr, G. Ullah, J. Ziburkus, S. J. Schiff, and E. Barreto, J. Comput. Neurosci. 26, 159 (2009).
5. G. Ullah, J. R. Cressman Jr, E. Barreto, and S. J. Schiff, J. Comput. Neurosci. 26, 171 (2009).
6. R. F. Fox and Y. Lu, Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 49, 3421 (1994).
7. R. D. Traub and R. K. Wong, Science 216, 745 (1982).
8. V. Volman, M. Perc, and M. Bazhenov, PLoS One 6, e20572 (2011).
9. J. Dyhrfjeld-Johnsen, V. Santhakumar, R. J. Morgan, R. Huerta, L. Tsimring, and I. Soltesz, J. Neurophysiol. 97, 1566 (2007).
10. R. J. Morgan and I. Soltesz, Proc. Natl. Acad. Sci. U. S. A. 105, 6179 (2008).
11. M. Case and I. Soltesz, Epilepsia 52 Suppl 8, 12 (2011).
12. M. Kaiser and C. C. Hilgetag, PLoS Comput. Biol. 2, e95 (2006).
13. B. Beverlin 2nd, J. Kakalios, D. Nykamp, and T. I. Netoff, J. Comput. Neurosci. (2011).
14. T. I. Netoff, R. Clewley, S. Arno, T. Keck, and J. A. White, J. Neurosci. 24, 8075 (2004).
15. J. M. Beggs and D. Plenz, J. Neurosci. 23, 11167 (2003).
16. H. R. Wilson and J. D. Cowan, Biophys. J. 12, 1 (1972).
17. M. L. Steyn-Ross, D. A. Steyn-Ross, M. T. Wilson, and J. W. Sleigh, Neuroimage 45, 298 (2009).
18. A. Destexhe, J. Neurosci. 18, 9099 (1998).
19. P. A. Robinson, C. J. Rennie, and D. L. Rowe, Phys. Rev. E. Stat. Nonlin Soft Matter Phys. 65, 041924 (2002).
20. M. A. Kramer, H. E. Kirsch, and A. J. Szeri, J. R. Soc. Interface 2, 113 (2005).
21. M. Balish, P. S. Albert, and W. H. Theodore, Epilepsia 32, 642 (1991).
22. J. G. Milton, J. Gotman, G. M. Remillard, and F. Andermann, Epilepsia 28, 471 (1987).
23. A. Hopkins, P. Davies, and C. Dobson, Arch. Neurol. 42, 463 (1985).
24. L. D. Iasemidis, L. D. Olson, R. S. Savit, and J. C. Sackellares, Epilepsy Res. 17, 81 (1994).
25. R. Savit and M. Green, Physica D 50, 95 <last_page> 116 (1991).
26. A. L. Hodgkin and A. F. Huxley, J. Physiol. 116, 473 (1952).
27. R. W. M. Wedderburn, Biometrikia 61, 439 (1974).
28. P. McCullagh and J. A. Nelder, Generalized linear models (Chapman & Hall/CRC, Boca Raton, 1998; 1989), 37, p. 511.
29. C. Morris and H. Lecar, Biophys. J. 35, 193 (1981).
30. L. F. Abbott, Brain Res. Bull. 50, 303 (1999).

Cellular models

Epilepsy and its treatment are known to involve changes at the cellular level, including changes in extracellular potassium concentrations (Rutecki et al., 1985), mutations in ion channels, and binding of antiepileptic drugs affecting ion channel kinetics (Meldrum and Rogawski, 2007). Cellular models enable us to study how molecular level changes affect neuronal behavior. In this section, we will review physiologically realistic models, such as the Hodgkin–Huxley model, followed by more abstract models. An advantage with the more detailed Hodgkin–Huxley models is that every parameter can be measured and directly related to physiological variables. The more abstract models reduce the complex Hodgkin–Huxley model to its bare essentials, more easily enabling large scale network simulations used in the next section.

Physiologically realistic neuronal models — Hodgkin–Huxley

Action potentials are generated by the opening of voltage gated sodium and potassium channels. In the 1950’s Hodgkin and Huxley published a series of papers in which they developed a set of differential equations describing how voltage and membrane conductance change with time to explain the generation of action potentials in the squid giant axon (Hodgkin and Huxley, 1952a, 1952b, 1952c). The parameters for the Hodgkin–Huxley equations (HH) were derived from experimental data. Their experiments and equations helped determine which ionic currents were involved in action potential generation.

The mammalian neuron contains many ion channels that do not exist in the squid giant axon. However, the HH formalism has been extended to describe many different types of ion channels and has been used to model physiologically realistic conductance based neurons. Hodgkin and Huxley were also able to describe how the action potential propagates down the axon. Their equations have been used to understand how synaptic inputs on dendrites travel down to the soma (Rall, 1962). Neuron models can be made even more realistic by including physiological geometries and an array of sodium, potassium and calcium currents (Migliore et al., 1995, 1999; Traub and Dingledine, 1990; Traub and Wong, 1982). These physiologically realistic models have been used to examine molecular changes affecting ionic currents and neuronal firing. Following are examples of how different cellular properties play a role in epilepsy, investigated with HH style models.

Ion channel mutations

Mutations in ion channels, which have been implicated in epilepsy, may lead to alterations in channel dynamics, thereby affecting the dynamics of the neuron (Meldrum and Rogawski, 2007). These properties can be investigated using HH style equations by changing ion channel kinetics. Models have been used to study the effects of epileptogenic mutations in the sodium channel Nav1.1 subunit responsible for Generalized Epilepsy with Febrile Seizures Plus (Spampanato et al., 2004). The effects of the mutations were modeled by positively shifting the voltage dependence of the sodium channel inactivation, which was determined through patch clamp experiments. The model predicted that all mutations studied led to a greater likelihood of firing repetitive action potentials to slow depolarizing stimuli, thereby enhancing the possibility of a seizure.

Ion channel up/downregulation

Experimentally it has been shown that ion channel densities and kinetics change following seizures (Chen et al., 2001; Shah et al., 2004). HH like model neurons can be used to simulate the upregulation or downregulation of channels by changing the maximal gating conductance, which represents the membrane channel density. For example, computational models were used to understand the effects of increased h-currents (noninactivating cation currents activated by a hyperpolarization) following seizures (Halliwell and Adams, 1982; Maccaferri and McBain, 1996; Mayer and Westbrook, 1983; Pape, 1996; Santoro and Tibbs, 1999). H-currents are thought to regularize neuronal activity. Surprisingly, a computational model attempting to explain collected electrophysiology data suggested that increasing the h-current can exist with and possibly contribute to hyperexcitability of the neurons (Chen et al., 2001).

Ion concentrations

The concentration gradient of ions from inside to outside the neuron dramatically affects current flow through ion channels. Experimentally, it has been shown that extracellular potassium concentrations increase 5 to 10 times during a seizure (Cressman et al., 2009; Moody et al., 1974). Typically, HH equations use fixed values for the concentration gradients, but it is possible to calculate the accumulation of ions in microdomains close to the surface of the membrane and recalculate the equilibrium potential. Modeling studies have shown that the change in ion gradients during seizures plays a critical role in neuronal behavior and leads to changes in cellular excitability (Rutecki et al., 1985) and synchronization of the networks (Traub and Dingledine, 1990).

Glial cells have an effect on external neuronal ion concentrations by exchanging ions between the extracellular and glial intracellular space. The single cell model and extracellular microdomains can be further expanded to take into account the effects of glial cells. Glial effects on extracellular potassium can be modeled by including an equation for glial buffering of extracellular potassium. Epileptiform activity occurs in this model when the buffer approaches saturation. Small changes in potassium diffusion dramatically affect the slow, large amplitude oscillations in ion concentrations seen in intracellular recordings during seizure like activity (Cressman et al., 2009; Ullah et al., 2009).

Antiepileptic drug effects on ion channels

Many antiepileptic drugs bind to voltage gated ion channels (Beck, 2007). Patch clamp experiments have determined how the binding affects the kinetics of the channels and the excitability of the neuron (Bentzen et al., 2006; Fisher, 2011; Shin et al., 2011). Computational models can be used to understand how these molecular level changes affect cell behavior. For example, Ethosuximide, an antiepileptic drug used to treat absence epilepsy, affects the low threshold calcium current. The drug was found to alter the dynamics of slow bursting thalamic cells. Experimentally, it was ambiguous whether the drug blocked the channel or caused a shift in the activation curve of the channel. A computational model was able to disambiguate these two hypotheses. In the model, a change in the activation curve could explain the depolarization shift seen at rest experimentally while blocking the channel could not (Lytton and Sejnowski, 1992).

Conclusions from realistic cellular modeling

While the equations and parameters from the HH equations are physiologically inspired, they are still an abstraction of a neuron. The channel gating equation is a statistical mechanic approximation, which assumes that the number of ion channels in the membrane is large, and therefore the current can be approximated by the mean number of open channels. This neglects the probabilistic opening of channels and the resulting noise. More realistic models that account for the individual opening and closing of channels can be made (Fox and Lu, 1994; Goldwyn and Shea-Brown, 2011) but are very computationally intensive. As of yet, we have not seen any computational modeling to ascertain the effects of antiepileptic drugs or mutations on the stochastic properties of the channels. However, we anticipate that there will be interesting effects on the noise properties of neurons that should be taken into account.

While the HH equations have been a triumph in computational modeling, the equations themselves are very complicated. The models are nonlinear; for example a neuronal response to a 2 pA current step may not be exactly twice the response to a 1 pA step, especially when the neuron is near its action potential threshold. Models with reduced physiological detail retain the essential behaviors of the neuron, but their simplicity may provide a better understanding of how changes in parameters relate to changes in behavior. Another purpose for using reduced models is to reduce computational complexity, allowing us to more easily simulate larger networks.

Physiologically abstract cellular models

Realistic neurons are computationally expensive to simulate. To help better understand epilepsy, we need to understand the emergent behaviors that occur when neurons are coupled together. By reducing the model neuron to a simpler model that preserves the dynamics, we are more easily able to generate larger scale networks. Therefore, by abstracting the model of the neuron, we are able to make more physiologically realistic neuronal networks.

Two approaches that have been taken towards reducing the complexity of the HH equations will be discussed in detail. One is to take advantage of symmetries in the model by combining currents that have similar time constants into a single variable. This is done in the Morris–Lecar model (Morris and Lecar, 1981). The other is to ignore the highly nonlinear part of the equations that generate the action potential, and instead focus on the dynamics between action potentials. This is done in integrate and fire (IF) models (Abbott, 1999). These examples are included in this section because they are cellular models, but are more often used to create networks when studying epilepsy, which will be discussed in the following section. These are only two examples used to illustrate the point; however there are many others such as Izhikevich (Izhikevich, 2001, 2010), FitzHugh–Nagumo (FitzHugh, 1961; Nagumo et al., 1962), and the theta-neuron (Ermentrout and Kopell, 1986).

Morris–Lecar model

The Morris–Lecar (ML) model reduces the HH equations from four dimensions to two by combining potassium activation and sodium inactivation, which have similar kinetics, into a single variable and eliminating the fast sodium activation by assuming it is on a time scale faster than any other relevant time values, allowing for the use of the infinite time value (Rinzel, 1985; Santoro and Tibbs, 1999). This retains some physiologically relevant parameters, but greatly reduces the complexity of the equations. The advantage is that it is possible to plot a two dimensional system and see how the equations change with parameter changes. This allows for easier visualization when using a bifurcation theory analysis of the system.

Leaky integrate-and-fire models

A leaky integrate-and-fire (LIF) model is a further abstraction, ignoring the complex dynamics of the action potential and instead focusing on the summation of synaptic inputs between action potentials. In this model the inputs are integrated, and when the voltage reaches a set threshold it resets to a specified value. This reset is used to account for the action potential, but skips modeling the actual shape. Here, we only care that an action potential occurred, so we do not need to know what leads to the actual shape. These models are useful when neurons are strongly coupled and synaptic interactions influence spiking beyond one period (Ermentrout and Chow, 2002), however, because the LIF has a fixed threshold and a single variable it cannot produce many realistic behaviors. Since the model has a fixed threshold, spikes cannot have latencies, and due to the use of a single variable, phasic spiking, bursting, and threshold variability cannot occur. Slightly more complex models, such as the quadratic integrate and fire models, can account for spike latencies, activity dependent thresholds, and the presence of resting and tonic spiking modes (Izhikevich, 2004).

Ion concentrations in seizure termination

To understand why seizure activity terminates, Krishnan and Bazhenov developed a detailed HH-based model including multiple dynamic ion concentrations to simulate seizure termination. Then, they reduced the model to describe just the internal sodium, chloride and external potassium concentrations to understand how these ions cause neurons to transition between rest, spiking/bursting, and depolarization block. Using bifurcation analysis they could determine how accumulation of these ions brings about the termination of the seizure (Krishnan and Bazhenov, 2011).

Conclusions from abstract cellular models

Large scale models, where many neurons are connected together, are limited by the computational cost of each neuron. Therefore, many large scale networks depend on accurate simplifications of the detailed models. These models may only have a few parameters and can then be fitted to reproduce the behaviors observed in experimental data or in physiologically realistic simulations using HH style models. These simple models, because of their computational efficiency, enable the study of large scale network models.

Network models

Epilepsy is a network disorder, and seizures are an emergent behavior of network activity (Bragin et al., 2000; Spencer, 2002). Network activity is determined by the dynamics of the constituent neurons, synapses, network topology and input to the network. It has long been known that there are significant anatomical changes following a seizure, such as mossy fiber sprouting (Sutula et al., 1988), dendritic restructuring (Zeng et al., 2007), and neurogenesis (Parent et al., 1997). Changes that affect synaptic coupling strength, propagation times, and the balance between excitation and inhibition may alter network properties (Zeitler, Daffertshofer and Gielen, 2009). Subtle changes at the scale of the neuron may have large effects when thousands of neurons are involved and may dramatically change the probability of having a seizure, which is a rare and extreme event.

Computational models provide an essential tool that allows us to understand emergent behaviors, such as synchronous bursting or seizure propagation, that occur when large groups of neurons are coupled together. In this section, we focus on network models, where simulations include models of neurons and their connections. We define realistic models as having some aspect that accurately represents the physiology. In this section that happens to be how the topology of the network is modeled. In realistic network models, neurons are connected in ways inspired by experimental evidence. For example, studying how the placement of electrical and synaptic connections on the neuron affects synchrony in the network. Abstract network models connect neurons in a way where the structure of the network is determined by a statistical model or where the network is simply reduced to a model that describes the firing patterns of the neurons with parameters determined by network properties.

Realistic networks

Network simulations with many neurons connected using realistic topologies are now possible due to the availability of low cost computing. In this section, we will present computational models that reproduce epileptiform activity by changing parameters at the cellular scale. Examples of emergent population dynamics are synchronous population oscillations, bursting, or seizures. These behaviors cannot be easily determined by studying neurons in isolation.

Cellular dynamical changes

Intracellular recordings from tissue resected from epileptic foci have revealed that there are many bursting neurons in the focus (Matsumoto and Ajmonemarsan, 1964; Schwartzkroin, 1994). It may only require a small subset of neurons to switch from spiking to bursting to alter the dynamics of the population activity (Destexhe et al., 2001). Large scale network simulations of the CA3 region of the hippocampus indicate that synchronized population bursting emerges when neurons are induced to burst (Traub and Wong, 1982; Wong et al., 1986).

Synaptic changes

Many in vitro seizure models generate epileptiform activity by altering synaptic conductance. For example, seizure like activity can be provoked by blocking inhibitory synapses with penicillin or bicuculline (White, 2002). Conversely, seizures can be generated by enhancing excitatory connections by bathing slices in artificial cerebral spinal fluid low in magnesium, which removes the voltage dependence of the NMDA channels. Models show that the increase in synaptic excitation can promote synchrony in a network resulting in epileptiform activity (Traub et al., 1994). Computational network models have been used to infer network topology because simulations could only reproduce both normal and epileptiform activity when the network contained significant recurrent excitation, and inhibitory connections spread over a greater spatial distance than the excitatory connections (Traub, 1983).

High frequency oscillations (250–500 Hz) have been found in cortex and around the seizure focus (Bragin et al., 1999). These extremely fast oscillations are difficult to explain because the timing of the synchrony occurs faster than should be possible given the delays present in axo-dendritic synapses. In vitro slice experiments have found that the number of gap junctions significantly increases after seizure like stimulation (Mylvaganam et al., 2010; Samoilova et al., 2003). Modeling revealed that excitatory neurons had to be coupled through axo-axonic electrical synapses to explain these highly synchronous events (Traub et al., 2005). Network models using Morris–Lecar neurons connected together in a topologically realistic way with gap junctions lead to epileptiform activity, suggesting that the speed of these connections is critical in epileptogenesis (Volman et al., 2011).

Synaptic changes in network models may help identify effective mechanisms for antiepileptic drugs. The thalamocortical system exhibits synchronous, rhythmic firing in absence epilepsy. It has been shown experimentally that inhibition plays a key role in synchronizing neurons (Kiesmann et al., 1988; Koch, 1991). However, many drugs augmenting GABA_A mediated inhibition are used as antiepileptic drugs. This paradoxical phenomenon found experimentally has been investigated using computer models of the thalamic network. Benzodiazepines are a class of antiepileptic drugs that work through this mechanism. Models have indicated that an isolated increase in GABA_A mediated inhibition in the reticular thalamic (RE) nucleus with the use of benzodiazepines leads to decreased network synchrony (Thomas and Lytton, 1998). The effects of another GABA_A agonist, clonazepam, were also investigated. The model hypothesized that the decrease in IPSP size seen in experiments after the application of the drug was primarily due to its effects on inhibitory connections between RE neurons (Lytton, 1997). In these examples, models were able to provide a possible explanation for this non-intuitive idea by correctly modeling experimental results. By reproducing experimental data under specific biological conditions and failing to reproduce the data using other hypothesized conditions, the model was able to identify a likely mechanism of action for the tested pharmacological agents. The modeling studies also implicated this type of inhibition as a possible effective mechanism in any antiepileptic drug.

Spatiotemporal patterns of seizures

Large scale models have also been useful in understanding spatiotemporal patterns during seizures. Using a modified analysis of EEG data, it has been found that there are distinct initiation and termination dynamics in seizures (Schiff et al., 2005). Until the advent of microelectrode arrays and imaging techniques, propagation of seizures at the cortical column scale could only be measured by placing two recording electrodes in a slice of brain tissue. Computational models of large scale networks have allowed us to understand and predict the spatial extent and propagation of seizures between the two recording sites. In one example, large scale network simulations were used to explain the propagation velocity of seizures in the CA3 region of the hippocampus (Traub et al., 1987). Computational models have also been used to explain spatiotemporal patterns of neuronal activity in response to electric fields produced by stimulating electrodes (Park et al., 2005).

Abstract network models

Large scale realistic networks have played an important role in understanding seizures. However, due to their complexity, it can be difficult to understand how parameter changes bring about changes in the network behavior. The behavior of the network, like of the cell, is the relationship of the output of the network to its input. The output of the network includes behaviors such as bursting, high activity, or low activity. By reducing the network down to a few abstract rules or equations that can describe its behavior, it is possible to establish a causal relationship between its input and output. These reduced models allow us to extract principles about how the system works and to determine the parameter ranges over which behavior of the network will change.

Designing therapies to desynchronize populations

It has long been hypothesized that epilepsy is caused by hypersynchronous neuronal activity (Jackson, 1890). Synchrony’s role in epileptogenesis and ictogenesis is still unclear, but epilepsy may be a pathological deviation from the normal complex, and possibly chaotic, activity (Lehnertz et al., 2009; Netoff and Schiff, 2002). One approach to treating epilepsy is to design therapies that either maximize or minimize synchrony. If a network model is simple enough so that the relationship between features and synchrony can be ascertained, then the model can be used to determine the optimal therapeutic approach for changing network synchrony. Simple networks of oscillators have been used to describe synchronous population oscillations in epilepsy (Feldt et al., 2010; Netoff et al., 2004) and how they may change over time to produce tonic (asynchronous) to clonic (synchronous) shifts seen in a computational model of seizure (Beverlin et al., 2011). Using these models, it is possible to determine stimulation patterns that might be delivered through a deep brain electrode that could desynchronize, or synchronize the population (Bardakjian and Diamant, 1994; Lee et al., 2011; Wilson et al., 2011).

Topology

How does the change in connections following a seizure affect population dynamics, and do certain connections lead to seizures? One limitation with network modeling is that there is limited data measuring network topology. This will soon change with improvements in optical imaging methods (Bhalla, 2008; Bohland et al., 2009). Until much more is known about the precise cellular level topology of the brain different methods can be used in a computational model to account for network topology.

One method if the topology of a network is not known is to assume a random network, where each neuron has an equal probability of being connected with another. Small changes to the probability of connections between individual neurons, a first order statistic, can lead to large changes in behavior. Cultured neuronal networks have been shown to produce epileptiform activity (Kamal et al., 2010). A random network model could explain different epileptiform behaviors, simply by changing the number of connections per neuron in the network. In one model, if there was less than one recurrent connection per neuron, the network was stable, but as the number of connections approached one, seizure like activity emerged, and if more connections were added the network transitioned to bursting (Beggs and Plenz, 2003). When the number of connections equals one, scale-free activity is seen, where the number of events observed is proportional to the size of the events and small events are common but large events are rare.

Another approach to account for unknown network topology is to keep the probability of two neurons being synaptically connected (first order statistic) the same and change higher order statistics, such as the distribution of number of connections per neuron. It is possible to change the behavior from normal to seizing to bursting by changing these higher order statistics without changing the average number of connections. The higher order statistics can be manipulated while preserving the first order statistics are often done by generating small-world network or networks with a scale-free topology. A small-world network involves starting with a ring of connected neurons that are then randomly removed and rewired. This preserves the first order statistics but generates networks where the distance between neurons, measured by number of synaptic connections, is small and neurons are relatively clustered compared to a completely random network (Guare, 1990; Watts and Strogatz, 1998). A scale-free network involves making a power law degree distribution where there is a relationship between the probability of the number of connections and the number of neurons that have those connections. Few neurons have many connections and many neurons have few connections, analogous to citations in scientific papers where famous papers get more citations than less famous, but they are rare. Those with bigger connections, or more citations, tend to grow faster because a newly added neuron is more likely to connect to a neuron with many connections (Barabasi and Albert, 1999).

Functional imaging data has revealed that functional networks display scale free features (Eguiluz et al., 2005), which are more resistant to random changes in the network, but more susceptible to the removal of hub neurons. Scale-free networks have the most synchronizability in weighted networks (Chavez et al., 2005, 2006). However, other groups have suggested that the biological network is more resistant to the removal of hub neurons than a scale free network, suggesting that the brain is not scale-free (Achard and Bullmore, 2007; Achard et al., 2006; Reijneveld et al., 2007; Salvador et al., 2005a, 2005b). Large scale simulations using thousands of realistic model neurons have provided insight into the importance of network topology on the excitability of the dentate gyrus (Dyhrfjeld-Johnsen et al., 2007). A computational study modeling the rat dentate gyrus found that a scale-free topology actually enhanced the hyperexcitability of a network beyond normal after injury (Morgan and Soltesz, 2008), and that the existence of a few neurons with a lot of connections, called hub neurons can dramatically affect the excitability of the dentate gyrus even without a power law distribution of connections (Morgan and Soltesz, 2008). The emergence of this type of connectivity may play a role in the generation of seizures following a brain injury where a portion of the neurons are lost. Other connectivity patterns, such as random connections forming after injury, did not enhance excitability of the network. This suggests that hub neurons may underlie epilepsy, and that targeted removal of these neurons may help restore the excitability of the dentate to normal (Case and Soltesz, 2011). Predictions from these computational models have yet to be confirmed experimentally.

The nervous system of Caenorhabditis elegans was the first to be described as a small-world network, providing biological support for this method (Watts and Strogatz, 1998). In an in vitro preparation of cultured hippocampal networks, network topology was found to lose small-world properties when the networks were injured using glutamate, leading to an increase in the number of bursting events. The fact that the small-world properties, such as mean path length and clustering coefficient, were different between normal and injured networks, suggests that in vitro networks are not scale-free (Srinivas et al., 2007). The free parameters in a small-world network model are the number of neurons, synaptic connections per neuron and the percentage of connections that are random. Using computational models, it has been shown that a bifurcation in the system arises as the number of randomly rewired connections is increased. As changes to the small-world topology were made, the network was shown to transition from normal to seizing to bursting. With a few random connections, the network can be very quiet, but as more random connections are added the network produces sustainable high activity, likened to a seizure, and as more connections are added it begins to burst. The network model was reduced down to two equations that describe the rate at which activity in the network grows and dies off. Analysis of these two equations could determine exactly when these transitions in the behavior would occur (Netoff et al., 2004). In small-world networks, it was also found that long-distance connections play an important role, and that the network does not just optimize for minimal global wiring (Kaiser and Hilgetag, 2006a). These connections lead to faster information processing and facilitated synchronization, and a lack of the long-distance connections has been implicated in epilepsy (Kaiser and Hilgetag, 2006b; Kaiser and Varier, 2011).

Neuronal networks have been shown to have structure that is significantly different from a random network (Song et al., 2005). This was determined by counting the number of different ways three cells could be connected together, called motifs, and comparing them to the expected number under the assumption that connections were random and independent (Sporns, 2011). In homogenous networks, two motifs, divergent and chains, can account for the synchronizability of a network. Divergent motifs are defined as one neuron synapsing onto two others, and chains are when one neuron synapses onto a second which synapses onto a third. An increase or decrease in either of these motifs altered the network’s synchronizability, while other motifs did not (Zhao et al., 2011). These two motifs were analytically related to deeper network properties through graph theory. Using simple measures of network topology like this may help us determine how the anatomical changes following a seizure may affect the network behavior.

Cortical region to whole brain scale models

Even generalized seizures can start focally; however they do not remain focal, but instead spread over the brain. They can spread and may arise by the interaction between different brain regions. This section will focus on models of coupled cortical regions. These models are used to understand the underlying neuronal activity recorded by EEG. We will define realistic models as those that retain some aspect representing the actual physiology of the system, whether it is in how they are connected or the types of neurons that make up the brain region. Abstract models are defined as those that lack any physiological detail of the cortical region.

Realistic models of the corticothalamic loop

Seizures are seen at the scale of cortical regions, and how seizures spread between regions is critical in understanding their underlying mechanisms. Spike and wave discharges occur in absence epilepsy which are generated by 5–9 Hz oscillations occurring in the corticothalamic loop (Pinault et al., 2001). Many cortical models have been developed in order to understand this characteristic seizure pattern.

Model of corticothalamic loop using networks of realistic neurons

Corticothalamic oscillations and spike-and-wave discharges were modeled by simulating networks of excitatory pyramidal cells and inhibitory interneurons in the cortex coupled to excitatory neurons and inhibitory reticular neurons in the thalamus (Destexhe, 1998). Each population was represented by a network of 100 HH style model neurons coupled using a simple topology with the probability of neurons being connected falling off with spatial distance. In this computational model the phasic firing of each population in the model could be understood. The authors could use the model to explore the effects of synaptic and ionic currents on the seizure activity. They found that the oscillations are dependent on GABA_B inhibition in the thalamus.

Mean field models of epileptiform activity

EEG can be simulated using a realistic large scale network and then averaging the neuronal activity, but even large scale simulations of tens of thousands of neurons cannot begin to approximate the brain scale complexity of seizures. Therefore, at some scale it is inevitable that cellular models are replaced with more abstract models describing the population activity of the cortical region. The cortical region can be modeled using equations to describe the average firing rates within a population of neurons; these are mean field models.

Mean field models have been used for over 50 years (Beurle, 1956; Deco et al., 2008; Freeman, 1975; Lopes da Silva et al., 1973; Nunez, 1974), but were adapted to describe the cortex by Wilson and Cowan (1972). They are continuum models, meaning neural activity can be simulated continuously over space and/or time. While the activity of each cortical region is an abstract firing rate model, the parameters can be related to physiologically measurable parameters. This methodology can also incorporate many physiological details such as axonal delays; noise; space, including discrete patches of cortex; and nonlinear features (Rennie et al., 1999; Robinson et al., 1997, 1998; Steyn-Ross et al., 1999; Wright and Liley, 1995) as well as effects of gap junctions (Steyn-Ross et al., 2009). Mean field models have been used to understand the underlying cortical dynamics resulting in the EEG patterns during epileptiform behaviors. The output of these models can be used to simulate EEG data measured during normal and epileptiform activity (Robinson et al., 2002). This single model could explain many different epileptiform behaviors with small changes in parameters. In this parameter space, all the bifurcations between normal epileptiform activities can be diagramed, providing a quantitative framework that relates all the behaviors (Robinson et al., 1997, 2002, 2005).

Mean field models have been used to understand how slight shifts in parameters may lead to different types of epilepsy. Peter Robinson has developed a three-dimensional representation of instability boundaries that allows for an evaluation of which slight parameter shifts lead to the movement from a normal, stable state, to an unstable, epileptic state (Robinson et al., 2002, 2005). This model shows that in emergent types of epilepsy, a slight shift from normal may lead to seizures. However, some types of epilepsy, such as those with a lesion focus, may be completely different from the normal state. The Robinson model has been used to explain why petit mal seizures commonly emerge around the age of four. It is known that myelination increases around this age. By increasing the velocity of cortical conduction to simulate the increased myelination, this model, under certain parameters, could reproduce EEG patters seen in petit mal seizures (Robinson et al., 2002).

A cortical sheet can be modeled by making a spatial continuum of cortical regions. Connections between areas decrease exponentially with distance, and can be modeled using spatial wave equations (Beurle, 1956; Jirsa and Haken, 1996; Lopes da Silva et al., 1973; Marten et al., 2009; Nunez et al., 1994; Robinson et al., 1997; Steyn Ross et al., 2009). These spatially extended mean field models have been used to understand how neuronal activity propagates across the cortex to produce patterns such as traveling waves, standing waves, lurching waves or Turing patterns. These models have been used to describe spatiotemporal patterns during seizures and how they emerge by decreasing inhibition or enhancing excitation (Kramer et al., 2005, 2007).

Classifying epileptiform activity using models of cortical regions

Clinicians use EEG patterns to classify and diagnose seizures (Ebersole et al., 2003; Parisi et al., 2011; Placantonakis and Schwartz, 2009), however, this approach does not link the data to mechanisms. Given that mean field models can produce many different cortical behaviors by changing only a few parameters, one approach to classification is to fit models to data and use the coefficients from the fit model to classify the EEG patterns. This approach has been termed “inverse modeling” (Robinson et al., 2002, 2005). This reduction of the complex behavior to a few coefficients can facilitate the discovery of possible connections between disorders.

Abstract models describing EEG data

Seizures often involve many cortical regions at once. Detecting changes in the interactions between different cortical areas may be useful for identifying state changes in the brain. State changes may occur at the onset of a seizure, during a seizure, at the termination of a seizure, or prior to a seizure. Identifying these state changes may provide insight into the mechanisms behind seizures and may be used to identify a preictal state. Brain states may be a distributed behavior that cannot be fully characterized by analyzing a single EEG electrode. EEG from each signal can be thought to represent the population activity underlying the electrode, and the coupling between electrodes represents statistical association between different cortical areas. Changes in the correlation between cortical areas may indicate a change in behavioral state. This network, where nodes represent different electrodes and links represent the strength of coupling between electrodes (measured in one of many possible ways), can be analyzed using graph theory approaches (Bullmore and Sporns, 2009; Reijneveld et al., 2007; Sporns, 2011). Network analysis measures, such as mean path length, or betweeness centrality, can be used as a summary statistic of the entire EEG activity. For example, in one study, networks were generated using short windows of EEG data. Analysis of these abstract network models of cortical activity found a global decrease in connectivity between the EEG electrodes and a growing importance of a few nodes in the network prior to a seizure (Kramer et al., 2008). Another study analyzing the EEG network found that electrodes within the epileptic zone have higher connectivity than other electrodes (Wilke et al., 2011). The use of these network models constructed from the EEG signals can be helpful in reducing complex multivariate signals into a few features that describe the relationship between cortical regions.

The type of modeling described in this section is more of a statistical model of activity, whereas previous sections have described models of mechanisms. Statistical models predict possible outcomes and the probability distributions of each of those outcomes occurring. Some aspect of the probability distribution likely leads to reproduction of the experimental data.

Abstract models describing seizure frequency

So far we have discussed models of epilepsy on different spatial scales; however, seizures, ictogenesis and epileptogenesis occur on vastly different temporal scales. Models of seizure frequency can be important in determining the efficacy of a treatment. Some seizures do not occur randomly in time, but will often depend on many factors, such as the time to last seizure, the diurnal cycle and seizure type (Balish et al., 1991; Binnie et al., 1984; Hopkins et al., 1985). A statistical model of seizure events may provide a more accurate model to be used as a null hypothesis in a clinical drug study. We will review time independent models and time dependent statistical models.

Time independent models of seizure intervals

Some studies suggest that at least 50% of the patients’ seizures appear to occur randomly (Milton et al., 1987). This means that seizure frequency is independent of time and can be modeled with a Poisson process, where the only variable is seizure frequency. Certain seizure data is well characterized with this model (Milton et al., 1987). However, in many cases seizures cluster in time, or are dependent on external factors such as time of day or menstrual cycle (Balish et al., 1991; Binnie et al., 1984; Hopkins et al., 1985). In one example, a patient’s probability of having a subsequent seizure within an hour after an initial seizure was ten times higher than baseline (Hopkins et al., 1985). In these cases, more complicated statistical models accounting for other factors are needed to accurately predict the probability of a seizure over a given time window.

Time dependent models of seizure intervals

In order to model seizure clustering, the model must take seizure history into account. A Markov model is a statistical model used to describe the probability of a system transitioning from one state to another, such as between a nonepileptic and epileptic state. Markov models can be generated such that the probability of transitioning to a seizure depends on the time since the last seizure. These models can account for the temporal dependency of seizures and can be used to model seizure clustering. It has been shown that Markov chains with just two states can provide a significantly better description of seizure intervals than a Poisson process (Hopkins et al., 1985) and can be used to accurately model daily seizure counts (Albert, 1991). Another type of model, a quasi-likelihood regression model, was found to explain epileptic seizure data more effectively than a Poisson regression model with autoregression terms (Balish et al., 1991; McCullagh and Nelder, 1998; 1989; Wedderburn, 1974). These models differ from the Markov chain in that they can allow for sudden changes in mean seizure rate, which may occur with onset of a treatment.

The nonrandom dependency in seizure frequency data has implications in the use and evaluation of antiepileptic drugs (Hopkins et al., 1985). In clinical trials it is more difficult to analyze effects of treatment on episodic events, such as seizures, than a two state model such as disease free versus death. The goal of antiepileptic drugs is to decrease seizure frequency, and hence increase interseizure interval. How this value is assessed is critical for statistical evaluation. In many studies, seizure frequency is evaluated by: (1) patient evaluation, (2) percentage change in seizure frequency and (3) number of days out of 100 that seizures occur (Beran et al., 1980; Hopkins et al., 1985; Vajda et al., 1978). Statistics of seizure rates in clinical trials often assume that seizures are independent in time, and statistical analyses may be inaccurate if this is not the case. It is important to understand the statistical properties of the data before interpreting the results from a statistical model. A model such as a Markov process or a quasi-likelihood regression model, which allows for time dependency, may improve power in determining the efficacy of a treatment.

Tools for computational modeling

Developing a computational model from scratch may seem like a daunting task, especially if you feel uneasy using differential equations. However, there are many advanced modeling tools and databases of developed models. Brette et al. provide an excellent review of different modeling software (Brette et al., 2007). Often, useful models can be generated by making small changes to an already existing model. For example, the effects of a drug can be simulated by setting a current to zero in an already existing model.

Databases of published models are available for download at ModelDB (http://senselab.med.yale.edu/senselab/modeldb) (Migliore et al., 2003). There is a push in the computational neuroscience field to standardize models to represent any model using a common language. The goal of this is to facilitate sharing of models and implementing models independent of simulation platforms. These common modeling languages in general are called markup languages. One example is NeuroML (Crook and Howell, 2007), http://neuroml.org). Another is International Neuroinformatics Coordinating Facility’s (INCF’s) NineML (http://software.incf.org/software/nineml). Databases are also being generated containing data on all the connections between different cell populations, such as CoCoDat, “The Database of Cortical Microcircuitry” (http://www.cocomac.org/cocodat).

To run simulations there are general tools such as MATLAB (Natick, MA) and Mathematica (Champaign, IL). XPP (http://www. math.pitt.edu/~bard/xpp/xpp.html) and PyDSTool (pydstool.sf.net) are modeling platforms that are especially useful for bifurcation analyses. However, there are software packages specifically dedicated to neuronal modeling, such as NEURON (http://www.neuron.yale.edu/neuron), Brian (http://www.briansimulator.org/), Nest (http://www.nest-initiative.org/?page=Software), Parallel neural Circuit SIMulator (http://www.lsm.tugraz.at/pcsim/), and Genesis (http://www.genesis-sim.org/GENESIS). One system that has focused on large scale simulations enabled by optimization of code is Simatra (http://www.simatratechnologies.com).

Discussion

Epilepsy is a multiscale disease with many etiologies united by the common symptom of seizures. Computational models representing different spatial scales and physiological detail can be used to study the underlying mechanisms of seizures and epileptogenesis. It may seem that models most accurately reflecting the physiology will be most accurate and useful, but a model that abstracts complex activity into the bare essentials can be valuable as well. Abstract models are able to extract principles and predict behaviors that can be difficult to deduce from extremely physiologically detailed models. Ideally, a model will allow you to identify new approaches to developing treatments. Each type of model plays a role in helping us understand the mechanisms and treatment of epilepsy.

Computational models force an experimentalist to formalize their mental models by writing rigorous mathematical equations. The exercise of making a model inevitably leads to a deeper and better understanding of the system being studied. The model can then be used to test hypotheses and design experiments and protocols.

Models help us understand emergent behaviors of systems. Epileptiform activity cannot be seen in isolated neurons, but is an emergent behavior of neuronal populations. Subtle changes at the neuronal scale may lead to dramatic changes at the population scale and the prevalence of extreme events, such as seizures.

Models can be used to understand the relationship between different epileptiform activities and normal neuronal ones. Different types of seizures may be the result of the same neuronal tissue being perturbed in different ways. Understanding what parameters lead to different bifurcations of neuronal activity may provide a way to classify different kinds of seizures. A good model of neuronal activity should be able to reproduce many different epileptiform behaviors by changing a few parameters. This model could then be fit to the data by adjusting the parameters. The fit parameters can then be used to quantify and classify complex behaviors.

Using the appropriate statistical model is important for testing the efficacy of treatment in clinical trials. Accurate models may provide a better estimation of the expected distribution of seizure intervals, which can in turn enable a much more powerful statistical analysis of the data.

Generating a computational model is easier now than ever before with the availability of powerful modeling platforms specifically designed to model neurons and neuronal networks. Many models are now available through online databases. It is possible to model voltage-clamp or current-clamp experiments in simulations.

It is important that, even in abstract models, parameters are kept physiologically meaningful. This makes it possible to assert that the parameters in the model are constrained to physiologically realistic values. It also ensures that changes in parameters, when related to behavior, can be used to generate experimentally testable hypotheses.

The danger in starting a modeling study is that it is easy to begin to study models instead of physiology. A model is only a starting point and should be used to inform experiments, and experiments should then inform the model. The goal of the model should be to identify uniting principles that help reduce a very complex system into one in which a heuristic understanding of the system can be established.