Use of Galvanic Vestibular Feedback for a Balance Prosthesis

Abstract

Activation of vestibular afferents by a bilateral bipolar galvanic vestibular stimulus (GVS) evokes medial-lateral (ML) body sway. By applying a GVS feedback signal that is a function of measured ML head motion, the potential exists for GVS to restore a useful vestibular contribution to ML balance control in vestibular-deficient subjects who remain responsive to GVS. A key to developing an effective balance prosthesis using GVS is to determine the functional relationship between GVS and its influence on the brain’s internal estimate of head motion. We describe how a model-based interpretation of GVS-evoked body sway can be used to identify this functional relationship. Results indicate that the GVS-evoked internal motion estimate is effectively a low-pass filtered version of the GVS current. With preliminary data, we demonstrate that GVS feedback, compensated for the identified low-pass characteristics, can either remove the ability of a subject with normal vestibular function to use vestibular information for balance control, or can restore the ability of a subject with bilateral vestibular loss to maintain balance in a condition requiring vestibular information for balance control.

I. INTRODUCTION

It has long been known that a galvanic vestibular stimulus, provided by a small electrical current introduced near the inner ear’s vestibular receptors, modulates the activity of some of the vestibular afferent nerve fibers [1,2]. When GVS is applied in human subjects using a bilateral bipolar electrode configuration (current passed between electrodes located behind the two ears) an ML body sway is evoked such that subjects lean toward the side of the anodal electrode. Other electrode configurations induce anterior-posterior body sway [3], but in the present study we focus on the more robust ML induced sway evoked using the bilateral bipolar electrode configuration.

GVS has been previously used to alter responses to balance perturbations in both a feed forward mode (i.e., preplanned) [4] and a feedback mode (i.e., as a function of head motion) [5,6]. Both of these studies showed that it was possible to use GVS to alter body movement responses to perturbations. However, both of these studies used subjects with normal vestibular function so there has not been a demonstration that GVS could be used in a prosthesis to improve balance control in subjects with vestibular deficits. Of course, GVS can only contribute to balance control if subjects with vestibular deficits remain responsive to GVS. Fortunately, there is evidence that many vestibular deficient subjects, even those with severe bilateral vestibular loss, remain responsive to GVS [7]. This preserved responsiveness is likely due to activation of remaining vestibular afferents.

To provide the most effective use of GVS in a prosthesis, it is important to understand how the brain interprets GVS-induced changes in vestibular activity. There is evidence that natural vestibular signals from semicircular canals and otolith organs are combined by the brain to provide wide-bandwidth signals encoding head orientation and motion [8]. Due to the unnatural pattern of activation of vestibular afferents by GVS, it is likely that there will be some distortion of the brain’s encoding of head orientation and motion.

One goal of the present study is to show that the system identification and modeling methods we previously applied to identify the dynamic characteristics of the balance control system [9–11] can also be used to characterize the brain’s distorted interpretation of orientation derived from GVS-induced changes in vestibular activation. A second goal is to demonstrate, in two ways, the potential for using GVS feedback for a balance prosthesis. One demonstration identifies the GVS distortion in a subject with normal vestibular function and then compensates for this distortion in order to deliver GVS feedback that subtracts from the natural vestibular signals, thus reducing a subject’s ability to use vestibular cues for balance control. Another demonstration shows that a vestibular contribution to balance can be partially restored using GVS feedback in a subject with bilateral vestibular loss (BVL).

II. Methods

Preliminary data from GVS experiments were from two subjects (one with normal vestibular function and one with BVL) who gave informed consent for a protocol approved by the IRB of Oregon Health & Science University.

A. Experimental Manipulations

The dynamic properties of the balance control system were determined from body sway responses to continuously applied pseudorandom stimuli typically consisting of 6 cycles of either surface-tilt stimuli or GVS. GVS was applied by a battery-powered, optically-isolated voltage-to-current source limited to 12 V across the electrodes (Uni-Patch, 626SS) and 3 mA maximum current. GVS is defined as having a positive sign for anodal current applied to the right side electrode. To simplify body mechanics and to provide better correspondence with balance control models, subjects were constrained to sway as a single-link inverted pendulum using a backboard assembly that only allowed rotation about a single axis located at ankle-joint level. In some tests, the support surface (SS) upon which subjects stood was “sway-referenced” by rotating the SS in proportion to the measured body sway angle. Sway referencing greatly reduces the contribution of proprioceptive information to balance control [12]. Details on test methods, stimulus characteristics, and analysis procedures are given in previous publications [9–11].

B. Simple Model of Balance Control System

Our interpretation of sway responses to GVS are based on a relatively simple model of the balance control system shown in Fig. 1A where the body is modeled as a single-link inverted pendulum. The Fig. 1A model applies to an eyes closed stance condition where visual orientation cues do not contribute to balance. In this condition, orientation cues from the vestibular system (signaling body orientation in space) and proprioceptive system (signaling body orientation relative to the surface) provide the feedback needed to maintain stable stance. Inputs to the model are ML SS tilt angle and GVS, and the output is ML body-in-space (BS) sway angle. The model assumes that GVS generates an orientation signal that is added to the natural vestibular orientation signal. However, the GVS-induced orientation component is not necessarily proportional to the GVS current, but may be distorted in some potentially nonlinear way due to the brain’s processing of the unnatural pattern of vestibular signals produced by GVS. The small-signal linear approximation of this distortion is represented by a “GVS filter”. Identification of the properties of this GVS filter is needed to facilitate development of an effective balance prosthesis. Knowledge of the GVS filter allows for preprocessing of the measured body sway angle through an “Inverse GVS Filter” before generating the GVS feedback signal applied to the subject. Ideally, this inverse GVS filter compensates for the distorted orientation cue that would otherwise be produced by feedback of a GVS current directly proportional to body sway angle.

Figure 1.

A. Feedback model for balance control of a single-segment, inverted-pendulum body with representation of external stimulation from support-surface rotation, GVS, and real-time feedback of GVS. B. FRF gain and phase data from an individual subject with model fit. Error bars show 95% confidence limits. C. Family of FRF gain curves (mean data from 12 subjects with normal vestibular function derived from pseudorandom surface-tilt stimuli that evoke ML sway) showing decreasing gains with increasing stimulus amplitude. D. Sensory weights for subjects with normal vestibular function (mean ± sd, N=8) and 4 subjects with bilateral vestibular loss estimated from fits to FRF data from pseudorandom surface-tilt stimuli that evoke anterior-posterior sway. Modified from [9,11].

III. Results

We first describe characteristics of sway responses to SS stimuli and discuss how the Fig. 1A model can be used to interpret the influence of GVS feedback on balance control. A method to identify the GVS filter characteristics is demonstrated. Finally, results are presented that show the ability of GVS feedback to reduce or restore the availability of vestibular information for balance control in subjects with normal vestibular function and with BVL, respectively.

Fig 1B shows an individual subject’s frequency response function (FRF), expressed as gain and phase data, determined via spectral analysis of stimulus and body sway response data [13]. Sway was evoked by a pseudorandom SS stimulus with 2° peak-to-peak amplitude (eyes closed condition). The solid lines through the experimental data were derived from a curve fit of the Fig. 1A model to the experimental FRF data. The closeness of the fit to the experimental data demonstrate that the Fig. 1A model is able to account for the dynamic characteristics of body sway evoked by SS rotations over stimulus frequencies ranging from 0.016 Hz to about 2 Hz [10,11].

The general shapes of FRFs are similar for FRFs obtained with SS stimuli of different amplitudes. However, the FRF gain is lower for larger amplitude SS stimuli (Fig. 1C). Therefore, there is an amplitude-dependent nonlinearity in the balance control system. Our previous analyses have concluded that this nonlinearity is attributable to a sensory re-weighting phenomenon whereby subjects shift toward increased reliance on vestibular information and decreased reliance on proprioceptive information with increasing stimulus amplitude (Fig. 1D and [9–11]). Intuitively, high reliance on proprioceptive cues results in the balance control system driving orientation toward the tilting surface, thus resulting in large sways and high FRF gains. High reliance on vestibular cues results in the balance control system driving orientation toward earth vertical resulting in small sways and low FRF gains. Subjects with BVL rely entirely on proprioceptive cues in an eyes closed condition (Fig. 1D). This 100% reliance on proprioceptive cues causes their FRF gains to be larger than those in subjects with normal vestibular function even at the lowest stimulus amplitude. Furthermore, BVL subjects show minimal changes in FRFs with stimulus amplitude since they are unable to reduce their reliance on proprioceptive cues because they have no other sensory system to use for balance in an eyes closed condition.

In the case of subjects with normal vestibular function, if the sign of GVS feedback is selected such that the GVS subtracts out the naturally occurring vestibular signal, then their reliance on proprioceptive cues should increase and the FRF gains determined from responses to SS stimuli should be higher. Furthermore, the frequency distribution of gain increases provides information about the bandwidth over which GVS feedback is influencing the vestibular contribution to balance control. In the case of subjects with BVL, if the sign of GVS feedback is selected such that a vestibular contribution to balance is restored, then these subjects should be able to reduce their reliance on proprioceptive cues, and the FRF gains determined from responses to SS stimuli should be lower with GVS feedback.

A. Responses to GVS in Normal Subjects

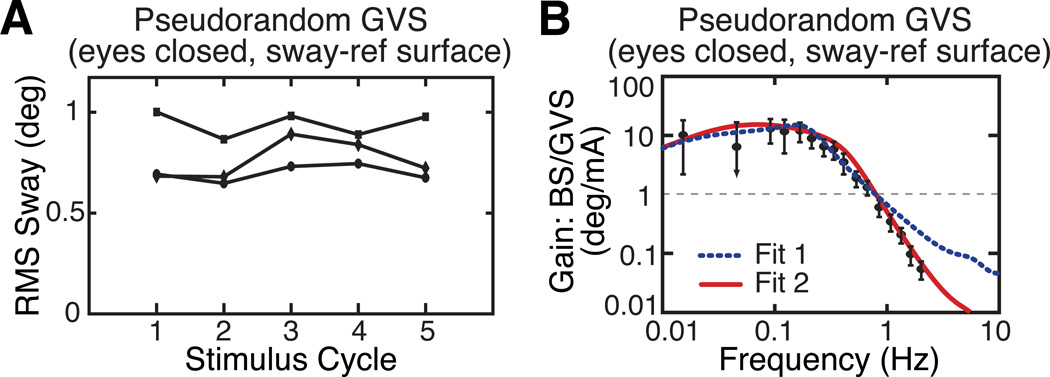
The dynamic characteristics of sway responses to GVS were determined by applying a pseudorandom GVS while subjects stood with eyes closed on a ML sway-referenced SS. In this condition, we assume that subjects are relying 100% on vestibular information for balance control. Consistent with this assumption, subjects show no habituation to the GVS (Fig. 2A). Habituation to GVS, which is commonly reported in galvanic studies that repeatedly apply GVS [14], can be interpreted as a sensory weighting shift away from reliance on vestibular information as the brain learns that the vestibular sensory information is disruptive to balance. However, in an eyes closed, SS sway-referenced condition, there is no possibility of reducing reliance on vestibular information since this is the only information available for balance control. Therefore, no habituation occurs even though GVS perturbs balance.

Figure 2.

A. Sway responses to continuous pseudorandom GVS show no habituation to the stimulus when subjects are tested with eyes closed during stance on a sway-referenced surface. B. FRF gain data derived from sway responses to GVS and 2 fits to FRF data with different assumptions about the functional form of the GVS filter.

Fig. 2B shows FRF data obtained from sway responses to pseudorandom GVS. In comparison to SS FRFs (Fig. 1B,C) the bandwidth of GVS FRFs is reduced. That is, the frequency above which the FRF gain begins to decline is about 0.6 Hz in SS FRFs but is only 0.2 Hz in GVS FRFs. Curve fits of the Fig. 1A model to the GVS FRF data allow for the consideration of different types of GVS filters and for the identification of the parameter values of these GVS filters. Curves fits based on two different GVS filters are shown in Fig. 2B. The GVS filter in Fit 1, which is just a constant value G₁ and therefore does not include any dynamics, does not account well for the experimental FRF data. In contrast, Fit 2, based on a first order lowpass GVS filter (Laplace equation of the lowpass filter: G₂/(T_gs + 1)), provides a much better fit to the experimental data. This particular fit identified filter parameters G₂ = 3.02°/mA and T_g = 1.03 seconds. That is, for stimulus frequencies below the filter cut-off frequency of f_c = 1/(2πT_g) = 0.15 Hz, the balance system interpreted the GVS-induced change in vestibular afferent discharge rates as signaling an ML head tilt of 3° for every mA of applied current. At frequencies above the cut-off frequency, the amplitude of this GVS-induced head-tilt signal was inversely proportional to the stimulus frequency.

For subjects with normal vestibular function or vestibular-deficient subjects able to stand eyes closed on a sway-referenced surface, the procedure described above can be used to identify GVS filter parameters. These parameters could subsequently be used to define an inverse GVS filter to provide more effective GVS feedback. Unfortunately, it is not possible to use this procedure to identify the GVS filter in BVL subjects who cannot stand eyes closed on a sway-referenced surface. However, we anticipate that knowledge of GVS filter characteristics in normal subjects will likely be similar to characteristics on BVL subjects since the GVS filter is indicative of the central nervous system processing of vestibular information and perhaps will not be influenced by the nature of the peripheral vestibular abnormality.

B. GVS Feedback to Eliminate the Vestibular Contribution

Results shown in Fig. 3 demonstrate the use of GVS feedback to reduce the vestibular contribution to balance control in a subject with normal vestibular function. Fig. 3A shows two sets of FRF gain data from responses to a pseudorandom SS stimulus with 4° peak-to-peak amplitude (eyes closed condition). In comparison to FRF results without GVS feedback (blue dashed line connecting gain points), the FRF gains with GVS feedback (red solid line) were greater over a frequency range of 0.05 Hz to about 2 Hz. The inverse GVS filter parameters used to preprocess the GVS feedback were determined following the methods described in Section A assuming that the GVS filter dynamics were those of a 1^st order lowpass filter. Specifically, the inverse GVS filter had the form:

$$GVS(t)=(1/G_2)·h(t)+(T_g/G_2)·ḣ(t)$$

where h and ḣ are head angular tilt and angular velocity, respectively, and G₂ and T_g are the fit parameters defining the GVS filter. For the results shown in Fig. 3A, the inverse GVS filter coefficients were 1/G₂ = 0.3 mA/deg and T_g/G₂ = 0.3 mA s/deg.

Figure 3.

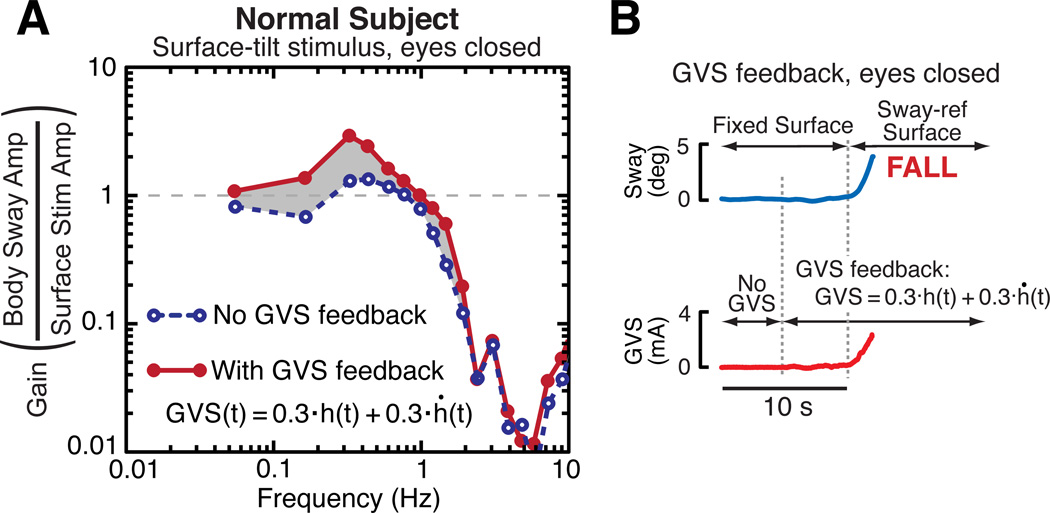
A. Two FRF gain curves derived from responses to ML SS stimuli showing that gain increases when a subject with normal vestibular function has the vestibular contribution to balance reduced by GVS feedback. B. A subject with normal vestibular function is unable to stand eyes closed on a sway-referenced SS when GVS feedback is applied.

The increase in FRF gain seen in Fig. 3A when GVS feedback was active indicates that the test subject had a greatly reduced ability to use vestibular information for balance control and compensated for this by re-weighting toward greater utilization of proprioceptive cues in order to maintain stability. Increased use of proprioceptive cues increases the sway response to SS rotations resulting in larger FRF gains.

Further evidence that GVS feedback greatly reduces a subject’s ability to use vestibular information for balance control is shown in Fig. 3B. Without GVS feedback this subject was able to stand eye closed on a sway-referenced surface (not shown), but with GVS feedback the subject fell soon after SS sway referencing was initiated. In contrast, GVS feedback did not disrupt balance in any noticeable way during stance on a fixed surface prior to the start of sway referencing (i.e., the 5 s period prior to sway referencing).

C. GVS Feedback to Restore the Vestibular Contribution

Preliminary data from one subject with severe BVL demonstrated the necessity of providing training trials where GVS feedback was applied while the subject had access to accurate visual orientation cues. The training consisted of three, 4-minute perturbations (by pseudorandom SS stimulus with 2° peak-peak amplitude), during which time the BVL subject’s eyes were open and GVS feedback was applied. In initial tests performed with eyes closed and prior to training, the subject quickly became unresponsive to GVS feedback and the GVS feedback did not improve her balance. With training, she remained responsive to GVS feedback on eyes-closed tests and her balance did improve.

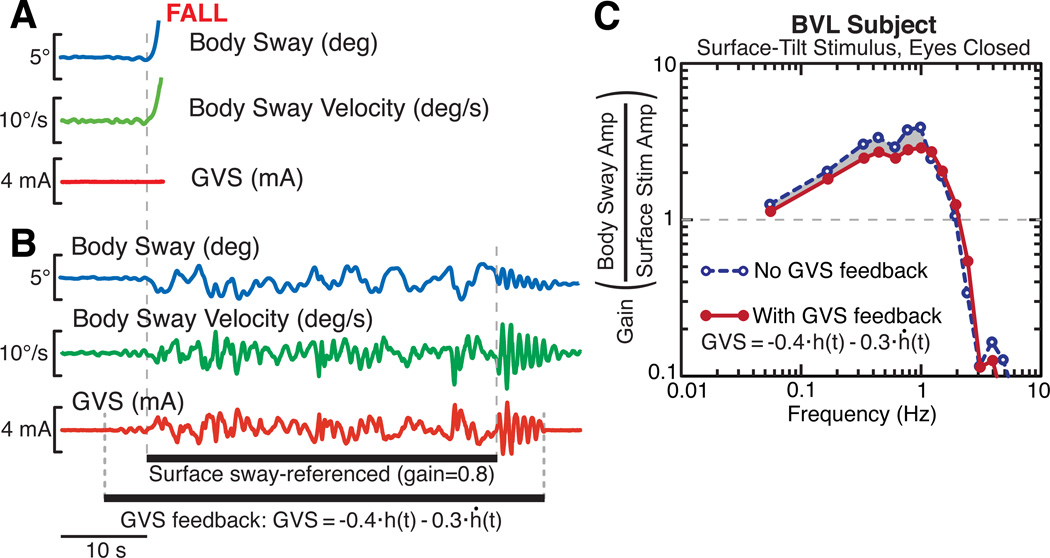
Results from this subject after training demonstrate the extent to which her balance improved. Without GVS feedback, the subject was unable to maintain balance, with eyes closed, on an 80% sway-referenced surface (Fig. 4A). However, when GVS feedback was provided: 1) the subject was able to maintain balance, with eyes closed, on an 80% sway-referenced surface (Fig. 4B), and 2) the subject’s FRF gains, calculated from sway responses evoked by 2° peak-to-peak pseudorandom SS stimulus, with eyes closed, decreased in comparison to the FRF gains when no GVS feedback was applied (Fig. 4C).

Figure 4.

Effects of GVS feedback to restore vestibular contribution to balance in a vestibular loss subject. A. The subject (eyes-closed) fell quickly following onset of surface sway-referencing (sway-reference gain = 0.8). B. GVS feedback restored BVL subject’s ability to maintain stance on a partially sway-referenced surface. C. The subject’s FRFs gain curves from sway evoked by pseudorandom SS stimuli (2° peak-to-peak) with no GVS (blue dashed) or with GVS feedback (red) using an inverse-GVS filter. GVS feedback partially restored the vestibular contribution to balance, causing decreased reliance on proprioceptive cues, which resulted in the subject being less sensitive to the SS stimulus (i.e., lower gains).

In the limited available testing and training time, we were unable to find GVS feedback parameters that restored this subject’s balance to that of a subject with normal vestibular function. Specifically, GVS feedback did not enable this subject to stand with eyes closed on a fully (100%) sway-referenced SS. The results for the FRF analysis (Fig. 4C) are consistent with there being only a partial restoration of a vestibular contribution to balance. If GVS feedback had fully restored a vestibular contribution to balance, the FRF gain reduction would have been about twice what we observed.

IV. Discussion

Our preliminary results demonstrate some potential to use GVS feedback in a balance prosthesis in conditions where the amplitudes of head motion are well matched to the limited capabilities of an externally applied GVS to influence vestibular-derived signals of head orientation. These conditions include quiet stance, moderately perturbed stance, and mild dynamic conditions such as walking. The potential also exists to assist balance in the sagittal plane as well as the frontal plane using different stimulus configurations [3]. A more challenging task will be to integrate this type of prosthesis into more active settings that allow subjects to make large voluntary head motions without evoking excessively large GVS currents.