The Dynamics of Collagen Uncrimping and Lateral Contraction in Tendon and the Effect of Ionic Concentration

Abstract

Under tensile loading, tendon undergoes a number of unique structural changes that govern its mechanical response. For example, stretching a tendon is known to induce both the progressive “uncrimping” of wavy collagen fibrils and extensive lateral contraction mediated by fluid flow out of the tissue. However, it is not known whether these processes are interdependent. Moreover, the rate-dependence of collagen uncrimping and its contribution to tendon’s viscoelastic mechanical properties are unknown. Therefore, the objective of this study was to a) develop a methodology allowing for simultaneous measurement of crimp, stress, axial strain and lateral contraction in tendon under dynamic loading; b) determine the interdependence of collagen uncrimping and lateral contraction by testing tendons in different swelling conditions; and c) assess how the process of collagen uncrimping depends on loading rate. Murine flexor carpi ulnaris (FCU) tendons in varying ionic environments were dynamically stretched to a set strain level and imaged through a plane polariscope with the polarizer and analyzer at a fixed angle. Analysis of the resulting images allowed for direct measurement of the crimp frequency and indirect measurement of the tendon thickness. Our findings demonstrate that collagen uncrimping and lateral contraction can occur independently and interstitial fluid impacts tendon mechanics directly. Furthermore, tensile stress, transverse contraction and degree of collagen uncrimping were all rate-dependent, suggesting that collagen uncrimping plays a role in tendon’s dynamic mechanical response. This study is the first to characterize the time-dependence of collagen uncrimping in tendon establishes structure-function relationships for healthy tendons that can be used to better understand and assess changes in tendon mechanics after disease or injury.

INTRODUCTION

Tendon is a dense, durable connective tissue that transmits forces from muscle to bone. It is comprised of a fluid-saturated, hierarchically structured collagen network aligned along the direction of loading. The well-characterized non-linear and viscoelastic mechanical properties of this tissue are consequences of its elaborate structure and composition. For example, the strain-stiffening behavior of tendon is thought to result from the gradual straightening of wavy or “crimped” collagen fibrils visible at the micron scale (Diamant et al., 1972; Kastelic et al., 1980). Periodic crimp in tendon is typically visualized using high-magnification optical microscopy (Miller et al., 2012a; Miller et al., 2012b) or polarized light microscopy (Rigby et al., 1959), but other imaging modalities including electron microscopy (Dlugosz et al., 1978), optical coherence tomography (Hansen et al., 2002a) and second harmonic-generation microscopy (Houssen et al., 2011) have also been used. While originally thought to result from a helical twisting of the collagen network (Verzar, 1957; Verzar and Huber, 1958), later evidence suggested that the crimp waveform in tendon is planar (Elliott, 1965; Rigby et al., 1959). Crimp is ubiquitous in tendons of all types (Dale et al., 1972), and measured crimp wavelengths in unloaded tendon range from around 30 μm in the mouse supraspinatus tendon (Miller et al., 2012a; Miller et al., 2012b) to roughly 120 μm in the rat tail (Hansen et al., 2002a). Although its origin is not fully understood, one proposed mechanism for collagen crimp in tendon is collagen fibril buckling due to differential shrinkage of the extrafibrillar matrix during development (Dale and Baer, 1974). Under loading, crimp begins to disappear at strains corresponding to the low modulus (i.e., “toe”) region of the stress-strain curve and is difficult to detect once the high modulus (“linear”) region is reached (Diamant et al., 1972; Rigby et al., 1959). Since many tendons operate mostly in the toe region in vivo (Maganaris and Paul, 1999), the process of tendon uncrimping, which has recently been quantified at prescribed loading conditions for the first time (Hansen et al., 2002b; Houssen et al., 2011; Miller et al., 2012a; Miller et al., 2012b), is of high physiological relevance. Similarly, the wide range of strain rates that tendons experience in vivo suggests the importance of understanding whether collagen uncrimping depends on how fast deformation is applied. However, the rate-dependence of collagen uncrimping and its contribution to the well-characterized rate-dependent mechanical properties of tendon have not been investigated.

Another distinct structural response of axially-stretched tendon is extensive contraction in the lateral direction. The Poisson’s ratio of tendon (given by the lateral compressive strain divided by the axial tensile strain) characterizes this effect and has been measured to be between 2 and 5 in tendon and ligament (Hewitt et al., 2001; Lynch et al., 2003; Reese et al., 2010; Reese and Weiss, 2013). For comparison, the highest possible Poisson’s ratio of an isotropic solid is 0.5. The process of tensile stress-induced lateral contraction in tendon may be governed by fluid flow out of the stretched tissue. In articular cartilage, where water comprises roughly 70% of wet weight (Bollet and Nance, 1966), the mechanical effects of fluid exudation resulting from mechanical deformation are well-described by biphasic theory and the theory of poroelasticity (Biot, 1941; Lai and Mow, 1980; Mow et al., 1980). A similar phenomenon may occur in tendon, where water comprises approximately 60% of tissue wet weight (Eichelberger and Brown, 1945). Supporting this idea, experiments have demonstrated that tendon volume and water content are lowered by cyclic tensile strain (Hannafin and Arnoczky, 1994) and that tendons subject to stress relaxation contract laterally in a time-dependent manner consistent with the predictions of biphasic theory (Reese and Weiss, 2013). Moreover, analysis of stress relaxation in mouse tail tendons under uniaxial tension using a mixture theory-based biphasic model suggested that poroelastic effects (i.e., stress-induced transverse fluid-flow) are largely responsible for tendon’s time-dependent mechanical properties (Yin and Elliott, 2004). Importantly, another study measured decreased strain with increased hydration in ligament under a prescribed stress, establishing a clear link between tendon water content and mechanics (Thornton et al., 2001). However, it is unknown whether the fluid component of tendon impacts its dynamic tensile mechanical properties directly or indirectly by altering collagen recruitment, as has been suggested previously (Thornton et al., 2001).

Despite their potential importance during physiological loading, the rate-dependent dynamics of collagen uncrimping and volumetric contraction (i.e., fluid exudation) under tensile deformation have not been simultaneously evaluated. Therefore, the objectives of this study were to a) develop a methodology allowing for concurrent measurement of tendon stress, strain, crimp and lateral thickness under dynamic loading; b) assess the interdependence of collagen uncrimping and lateral contraction by testing tendons in different ionic conditions that alter lateral thickness; and c) evaluate the effects of loading rate on collagen uncrimping. We hypothesized that alterations in tendon thickness and fluid content (mediated by the ionic concentration of the bath) would impact tendon tensile mechanical properties without altering the process of collagen uncrimping. In addition, we hypothesized that for a given applied strain, measured changes in axial stress, crimp and transverse thickness would be rate-dependent.

METHODS

Sample Preparation

A total of 12 female C57BL/6 wild-type mice were sacrificed at 150 days post-natal with IACUC approval. In each mouse, a flexor carpi ulnaris (FCU) tendon from a randomly chosen forelimb (right or left) was detached from the muscle, and the fully-intact pisiform bone was carefully removed from the wrist. Tendon cross-sectional areas were measured using a laser-based device (Favata, 2006), and the proximal (myotendinous) side of the tendon was glued between two small squares of sandpaper 5 mm from the pisiform insertion using cyanoacrylate. Tendon-pisiform complexes were then gripped with custom fixtures and loaded into a bath attached to an Instron 5848 universal testing system (Instron Corp., Norwood, MA). One of three bathing solutions was used: 0.1x phosphate-buffered saline (PBS), 1x PBS or 10x PBS. The 10x PBS solution consisted of 80.1 g/L NaCl, 2.01 g/L KCl, 11.5 g/L Na₂HPO₄ and 2.04 g/L KH₂P0₄ in distilled water and was diluted by 10x and 100x in distilled water to obtain 1x PBS and 0.1x PBS. In-vivo conditions are approximated by 1x PBS and varying the salt concentration of the bath alters the water content of the tendon. For example, in hypotonic conditions, an induced osmotic pressure imbibes the tissue with additional fluid. Following each mechanical test, the bathing solution was replaced and the test was repeated until tests were conducted in all three bathing conditions. The order of bathing solutions was randomized and prior to each test and the tissue was equilibrated in the new bath for 1 hour to ensure proper equilibration (Elden, 1964).

Mechanical Testing

Specimens were tensile tested according to the following protocol: 1) preload to 0.001 N, 2) 10 triangle wave cycles to 4% strain at 0.01 Hz (preconditioning), 3) 5 minute hold, 4) 10 triangle wave cycles to 4% strain at 0.01 or 0.5 Hz, 4) 5 minute hold and 5) 10 triangle wave cycles to 4% strain at 0.01 or 0.5 Hz. According to tests of 31 female C57BL/6 wild-type mice tested to failure at a rate of 0.1% strain/second in 1x PBS, the transition strain between the toe (i.e., non-linear) and linear regions of the FCU tendon stress-strain curve is 3% (Supplementary Material). Thus, the range 0–4% strain spans the entire toe region and the beginning of the linear region. Zero strain was set as the strain at preload in 1x PBS. The order of 0.01 and 0.5 Hz tests (steps 3 and 5) was randomized, and both steps were imaged. Imaging was performed during steps 3 and 5 through a plane polariscope consisting of a light source (L) emitting light along the –z direction, a polarizer (P), the loaded tendon (T), an analyzer (A) oriented perpendicular to P and a camera (C) to detect light passing through the entire system (Figure 1a). In this experimental setup, alternating light and dark bands appear in a crimped tendon (Diamant et al., 1972; Rigby et al., 1959). The crossed polarizers were oriented at the angle θ at which maximal extinction in the dark crimp bands occurred at preload. Images were taken at a rate corresponding to 10 frames per cycle.

Figure 1.

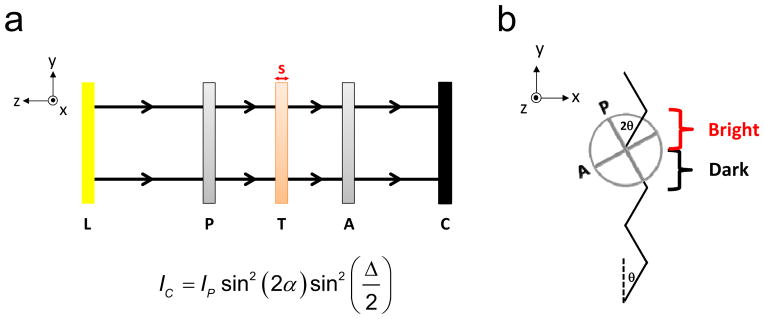
(a) Schematic of the plane polariscope used to visualize tendon crimp and deduce tendon volume. Light from the light source (L) travels along the –z direction through the polarizer (P), tendon (T), analyzer (A) and camera (C). (b) Orientation of the polarizer and analyzer relative to the tendon crimp waveform (jagged black line) at zero strain. The polarizer angle θ is set such that alternating portions of the crimp pattern are parallel to the polarizer (α=0) and completely extinguished, while light passing through the adjacent portions is bright. However, as the tendon is loaded, the angle α between the dark regions of the crimp waveform and the polarizer will increase from zero and the dark bands will brighten. Similarly, the angle between the bright regions of the crimp waveform and the polarizer will decrease from 2θ.

Image Analysis

Since the tendon is a birefringent material, the intensity of light detected by the camera at a particular location (x,y) is given by the equation

$$I_C=I_P{sin}^2(2\alpha ){sin}^2\left(\frac{\mathrm{\Delta }}{2}\right)$$ (1)

where I_p is the intensity of light passing through P, α is the angle between P and tendon’s slow axis (i.e., the aligned axis of the tendon) and Δ is the phase difference of light passing through T along the fast and slow axes (Glazer et al., 1996; Timoshenko and Goodier, 1969). As a result of crimp, the angle α varies with y (Figure 1b). Since the initial angle θ of P is such that maximal extinction occurs in the dark bands, α = 0 for the dark bands and α = 2θ for the bright bands. That is, θ, the angle of rotation of P, is equal to the crimp angle. However, under loading, the tendon begins to straighten out and α for the dark bands increases to γ while α for the light bands decreases to 2θ - γ. Therefore,

$$I_{\mathit{dark}}=\frac{1}{2}{I}_P{sin}^2(2\gamma ){sin}^2\left(\frac{\mathrm{\Delta }}{2}\right)$$ (2)

and

$$I_{\mathit{bright}}=\frac{1}{2}{I}_P{sin}^2\left(2(2\theta -\gamma )\right){sin}^2\left(\frac{\mathrm{\Delta }}{2}\right).$$ (3)

For changes in crimp angle γ > 0, I_dark > 0, so the dark bands brighten with increased strain. In addition, straightening the tendon leads to a decrease in crimp frequency and an increase in the spacing between bright and dark bands. In fact, at high strains, the bright and dark bands become difficult to distinguish (Figure 2a–b). To enhance their visibility, a bandpass filter was applied to each image to eliminate features with spatial frequencies larger than 25 pixels (150 μm) using ImageJ (National Institutes of Health, Bethesda, MD) (Figure 2c–d).

Figure 2.

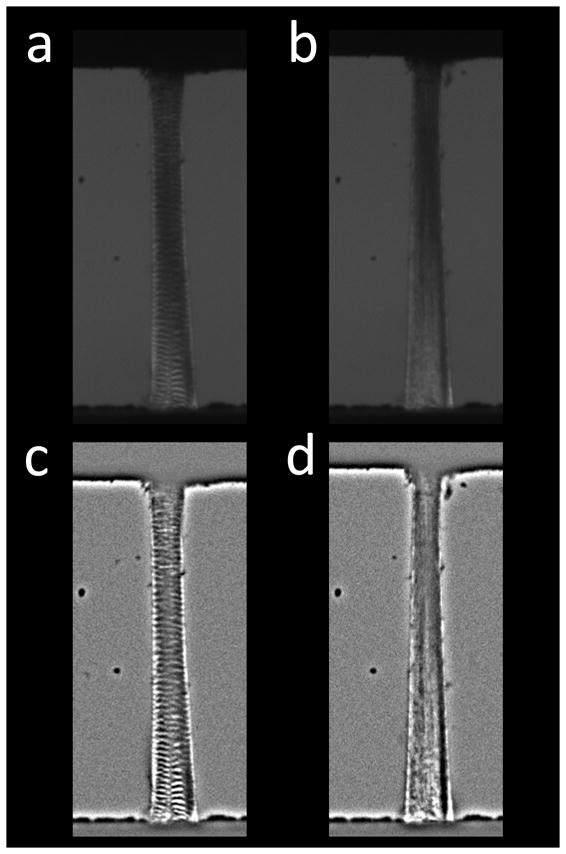
(a) Tendon imaged with the polariscope prior to loading. Crimp bands visible throughout the tissue. (b) At 4% strain, crimp bands disappear. (c–d) Bandpass-filtered tendon images before and after stretching to 4%. Crimp bands are easier to distinguish in the processed images.

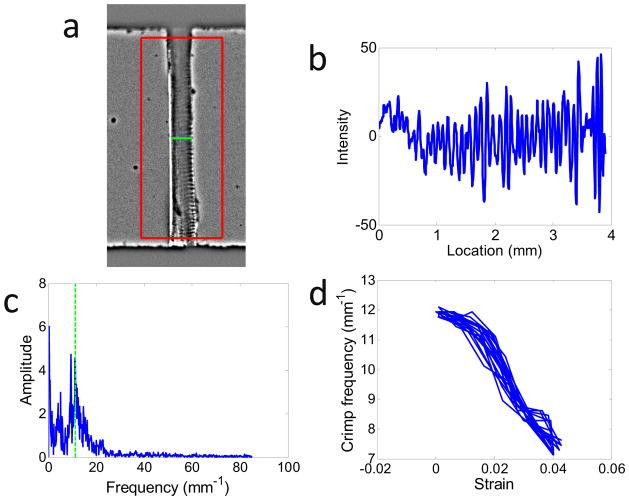
To calculate the crimp frequency, a custom Matlab (Mathworks, Natick, MA) code was written to detect regions of processed images that lie inside the tendon (Figure 3a). Within these regions, the mean intensity across the tendon width was determined as a function of vertical location (Figure 3b). The Fourier transform of this intensity profile was then computed (Figure 3c), and the crimp frequency f_crimp was defined as its mean power frequency (i.e., the frequency at which the Fourier transform was 50% of the total integral of the Fourier spectrum). f_crimp was calculated across all acquired images as a function of the applied strain (Figure 3d).

Figure 3.

Protocol for measurement of crimp frequency in imaged tendons. (a) A region of interest (ROI) was drawn around the tendon (excluding portions near the grips), and the tendon width was detected (horizontal bar). The large box represents the ROI, whose center is denoted by the asterisk. (b) Vertical profile of the mean intensity across the tendon width. (c) Fourier transform of (b). The crimp frequency (green dotted line) was calculated from mean power frequency of (c). (d) Crimp frequency versus strain during dynamic loading at 0.5 Hz. As the tendon is stretched, the crimp frequency decreases.

Now, according to Equations (2) and (3), the mean intensity across the entire tendon (assuming an equal number of bright and dark bands) is

$${\text{I}}_{\mathit{mean}}+\frac{1}{2}\left(I_{\mathit{bright}}+I_{\mathit{dark}}\right)=\frac{1}{2}{I}_P{sin}^2\left(\frac{\mathrm{\Delta }}{2}\right)\left[{sin}^2\left(2(2\theta -\gamma )\right)+{sin}^2(2\gamma )\right].$$ (4)

Since the phase difference Δ is given by (Bloss, 1961)

$$\mathrm{\Delta }\frac{2\pi Bs}{\lambda },$$ (5)

Equation (4) can be written as

$${\text{I}}_{\mathit{mean}}=\frac{1}{2}{I}_P{sin}^2\left(\frac{\pi Bs}{\lambda }\right)\left[{sin}^2\left(2(2\theta -\gamma )\right)+{sin}^2(2\gamma )\right].$$ (6)

where B is the birefringence of the tendon (i.e., the difference in index of refraction between its fast and slow axes), s is the thickness of the tendon (Figure 1a) and λ is the wavelength of emitted light. Assuming the birefringence of the tendon does not vary with load at low strains, for a given change in crimp angle γ and intensity I_p passing through P, I_mean is a function of only the tendon thickness s. The mean unloaded tendon thickness (as measured by a laser-based device was 0.095 mm. Therefore, characterizing λ by a central wavelength of 550 nm and assuming B = 3.0 × 10⁻³ (Maitland and Walsh, 1997), $\frac{\pi Bs}{\lambda }=1.63$ in the unloaded state. Hence, according to Equation (6), an decrease in s will lead to an increase in I_mean until $\frac{\pi Bs}{\lambda }=\frac{\pi }{2}$. To obtain an indirect measurement of tendon thickness, I_mean was calculated within the tendon boundaries in raw (i.e., unfiltered) images.

Data Analysis

To characterize collagen uncrimping and lateral contraction as a function of grip-to-grip strain in different osmotic environments, values of f_crimp, I_mean and tensile stress were averaged across all ten cycles at strains of 0%, 1%, 2%, 3% and 4% for each loading frequency. To characterize the rate-dependent dynamics of uncrimping and lateral contraction, peak changes in tensile stress, f_crimp and I_mean (relative to their values prior to deformation) were computed during the 1st and final (10^th) cycles for 0.01 Hz and 0.5 Hz deformation. These quantities are denoted as Δσ, Δf_crimp and ΔI_mean. The ratios Δσ_{0.5 Hz}/Δσ_{0.01 Hz}, Δf_{crimp, 0.5 Hz}/Δf_{crimp, 0.01 Hz} and ΔI_{mean, 0.5 Hz}/ΔI_{mean, 0.01 Hz} are viscoelastic parameters with values of 1 in solids that deform in a rate-independent manner. These parameters were evaluated in the 1^st and final cycles to elucidate the transient and steady-state response (respectively) of tendon under tension.

Statistics

For each loading frequency, stress, crimp frequency and mean intensity were compared across strain (0, 1, 2, 3 and 4%) and PBS concentration (0.1x, 1x and 10x) using a two-way repeated measures ANOVA with Bonferroni post-hoc analysis to correct for multiple comparisons. The ratios Δσ_{0.5 Hz}/Δσ_{0.01 Hz}, Δf_{crimp, 0.5 Hz}/Δf_{crimp, 0.01 Hz} and ΔI_{mean, 0.5 Hz}/ΔI_{mean, 0.01 Hz} were compared to unity using a Student’s t-test. Significance was set at p ≤ 0.05 for all statistical tests.

RESULTS

At 0.01 Hz, stress increased with strain in all bathing conditions. In the toe region (strain ≤ 3%), stress was higher in 0.01x PBS than in 10x PBS (Figure 4). Crimp frequency decreased with strain but was not affected by PBS concentration (Figure 5). Results were similar at 0.5 Hz.

Figure 4.

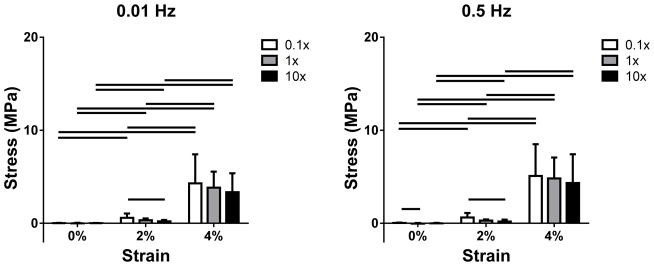
Stress as a function of PBS concentration and strain at (a) 0.01 and (b) 0.5 Hz for 0, 2 and 4% strain (1 and 3% strain are omitted for clarity). Stress increased with strain in all bathing conditions. In addition, a significant decrease in stress was found with increasing salt concentration in the toe region (ε ≤ 3%).

Figure 5.

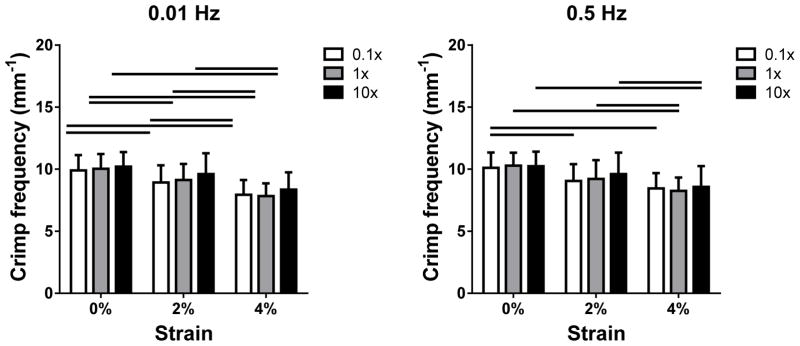
Crimp frequency as a function of PBS concentration at (a) 0.01 and (b) 0.5 Hz for 0, 2 and 4% strain (1 and 3% strain are omitted for clarity). Crimp frequency was generally decreased with increasing strain. No changes in f_crimp with salt concentration were found.

Hysteresis in I_mean versus strain was evident, especially at 0.01 Hz (Figure 6a). At 0.5 Hz, steady-state was not reached over the few cycles (Figure 6b). At 0.01 Hz, with increased strain and decreased PBS concentration, mean tendon intensity increased as the tendon thickness contracted (Figure 7). Similar effects were observed at 0.5 Hz, but changes in I_mean with strain were suppressed. Geometric constraints of the crimp waveform require that each crimp frequency corresponds to a specific crimp angle or change in crimp angle γ. Therefore, since f_crimp was independent of environmental condition, it can be inferred from Equation (6) that for a given strain, changes in I_mean with PBS concentration reflect changes in the tendon thickness s (and possibly the birefringence B) as a result of altered osmotic pressure. Conversely, since f_crimp is decreased with strain, alterations in I_mean with strain may reflect a combination of factors.

Figure 6.

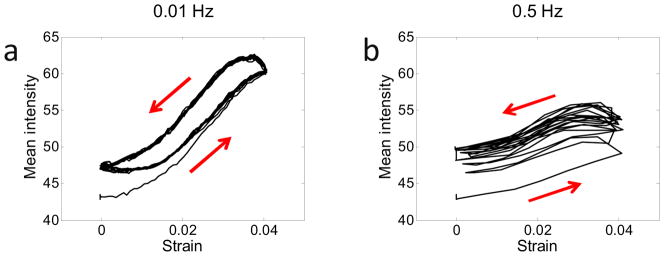
Mean intensity versus strain for a representative FCU tendon in 1x PBS deformed at (a) 0.01 Hz and (b) 0.5 Hz over 10 oscillation cycles. The red arrows denote the directions the curves progress with time. At both frequencies, the mean intensity increased with strain as a result of tendon contraction (Equation 6). However, more contraction occurs at 0.01 Hz, possibly due to the increased time allowed for fluid to flow out of the tendon as it is stretched. Since fluid expulsion continues during the unloading phase, hysteresis is evident, particularly at the lower frequency. At 0.5 Hz, the persistence of fluid expulsion during the short unloading phase could explain the steady increase in mean intensity over the first few cycles.

Figure 7.

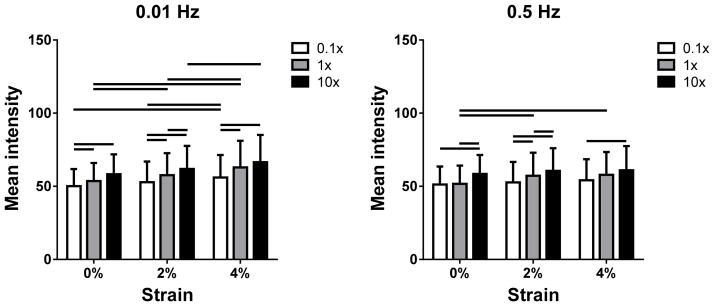
Mean tendon intensity as a function of PBS concentration at (a) 0.01 and (b) 0.5 Hz for 0, 2 and 4% strain (1 and 3% strain are omitted for clarity). I_mean increased with strain, especially at 0.01 Hz. In addition, I_mean generally increased with salt concentration.

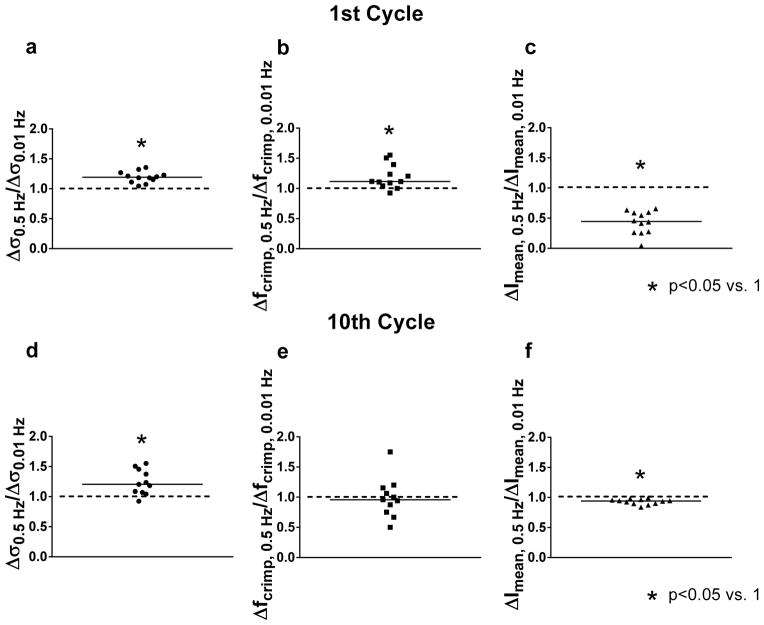
In 1x PBS, over the first cycle, Δσ_{0.5 Hz}/Δσ_{0.01 Hz} and Δf_{crimp, 0.5 Hz}/Δf_{crimp, 0.01 Hz} were significantly higher than 1 while ΔI_{mean, 0.5 Hz}/ΔI_{mean, 0.01 Hz} was significantly lower than 1 (Figure 8). Thus, the initial (transient) stress and degree of uncrimping were enhanced at the higher frequency while lateral contraction and other effects leading to an increase in I_mean were suppressed. Over the final cycle, Δσ_{0.5 Hz}/Δσ_{0.01 Hz} and ΔI_{mean, 0.5 Hz}/ΔI_{mean, 0.01 Hz} were still significantly different than 1, but Δf_{crimp, 0.5 Hz}/Δf_{crimp, 0.01 Hz} was not. That is, uncrimping was no longer rate-dependent in the steady-state. Results were similar in 0.1x and 10x PBS (not shown).

Figure 8.

Ratio of peak changes in stress (Δσ_{0.5 Hz}/Δσ_{0.01 Hz} ), crimp frequency (Δf_{crimp, 0.5 Hz}/Δf_{crimp, 0.01 Hz} ) and mean intensity (ΔI_{mean, 0.5 Hz}/ΔI_{mean, 0.01 Hz} ) for the (a–c) 1^st and (d–f) 10^th cycles. Values significantly different than 1 indicate that the parameter was rate-dependent. While Δσ_{0.5 Hz}/Δσ_{0.01 Hz} and ΔI_{mean, 0.5 Hz}/ΔI_{mean, 0.01 Hz} were different than 1 (i.e., changes in stress and mean intensity were rate-dependent) in both the 1^st and 10^th cycles, Δf_{crimp, 0.5 Hz}/Δf_{crimp, 0.01 Hz} was higher than 1 in the 1^st cycle but not in the steady-state.

DISCUSSION

In this study, real-time reductions in crimp frequency and thickness with increasing dynamic strain were concurrently measured non-destructively during the course of a mechanical test for the first time by imaging the tested tendon through a plane polariscope. As hypothesized, although stress and mean intensity (a parameter sensitive to transverse contraction) were increased in low tonicity bathing solutions that swell the tissue, crimp frequency was unaffected by PBS concentration. Thus, the processes of collagen uncrimping and lateral contraction are not fully coupled and may occur independently. In addition, like axial stress and mean intensity, fibril uncrimping was shown to be rate-dependent in the transient state.

Mean intensity was higher in conditions expected to induce increased lateral contraction: higher strains, lower loading rates and higher ionic concentrations. Moreover, according to Equation (6), I_mean is sensitive to alterations in tendon thickness s, which may be brought on by fluid exudation and volume change as described by biphasic theory. Therefore, the increase in I_mean with strain and ionic concentration likely signifies a decrease in width and volume due to water expulsion. By this logic, the larger intensity increase in I_mean with strain at 0.01 Hz as compared to 0.5 Hz likely results from allowing more time for fluid to flow out of the tendon against fluid-solid drag forces as it is stretched. Moreover, since fluid expulsion initiated by loading continues during the initial stages of unloading until it is overcome by diffusive fluid flow into the tendon, hysteresis is evident in the dependence of I_mean on strain, especially at the lower frequency (Figure 6). Interestingly, at 0.5 Hz, fluid flow into the tendon during the short unloading phase is unable to keep up with strain-induced fluid exudation that persists over both the loading and unloading phases. As a result, the baseline mean intensity increases over the first few cycles (reflecting a continuous decrease in tendon volume) and a steady-state is not immediately reached.

The transient rate-dependence of collagen uncrimping is likely due to flow-independent mechanisms including fibril-fibril interactions and molecular relaxation of collagen. In fact, it is well-established that independent collagen fibrils and collagenous tissues exhibit flow-independent viscoelastic phenomena. However, the results of the current investigation demonstrate that uncrimping is no longer rate-dependent in the steady-state. Conversely, lateral contraction is rate-dependent both in the transient and steady-states. Taken together, these findings suggest that the steady-state viscoelastic response of tendon may be predominantly governed by fluid exudation.

The decreased stress at a given strain level in bathing solutions with increased salt concentration measured in this study is consistent with a prior investigation of rabbit medial collateral ligament (MCL) (Thornton et al., 2001). In that study, ligament water content and strain at a baseline load (0.1 N) increased in a hypotonic sucrose solution as compared to 1x PBS. Although it has been proposed that these effects are due to changes in fibril uncrimping mediated by interactions between collagen and water (Thornton et al., 2001), the current investigation demonstrates that water content impacts tendon mechanics without altering fibril recruitment/uncrimping. That is, the interstitial fluid component of tendon directly affects tendon’s mechanical response. One possible explanation for this effect is that the increased internal swelling pressure under hypotonic conditions could oppose the lateral contraction of the collagen network required for the tendon to stretch along the axis of alignment. Since tendon and ligament are known to have very high Poisson’s ratios (ν>2) (Hewitt et al., 2001; Lynch et al., 2003; Reese et al., 2010; Reese and Weiss, 2013), axial tension must be concomitant with a larger degree of transverse consolidation that may be resisted by the high osmotic pressure in low salt concentrations. Interestingly, the opposite phenomenon has been observed in other tissues. For example, the modulus of the annulus fibrosus was higher in hypertonic conditions than in isotonic conditions (Han et al., 2012). These contrasting findings suggest that structure-function relationships vary between connective tissues that experience different loading conditions in-vivo.

In this study, a novel optical technique was established allowing for real-time measurements of multiple structural parameters in tendon during a mechanical test. In particular, it was demonstrated that both the crimp architecture and a parameter sensitive to changes in lateral thickness (I_mean) can be deduced by analyzing images taken of the tissue through a simple plane polariscope rotated at a constant angle. In addition to changes in ionic concentration, tendon mechanics are altered by genetic alteration, chemical treatment, exercise, fatigue, injury, aging and pathology. The methodology developed in this study could be used to evaluate and better understand the rate- and load-dependent structural changes associated with these processes.

The primary limitation of this study was that the association of the parameter I_mean with tendon thickness and water content was assumed and not validated since direct measurement of these parameters is highly challenging in small mouse tendons like the FCU. The mean intensity is also a function of the birefringence B (Equation (6)) which was assumed to be constant but may be altered by changes in ionic environment or stress in individual collagen fibrils. However, the latter effect is not likely to be important at the low strains investigated in this study. Moreover, the interpretation that increases in I_mean were predominantly consequences of decreases in thickness and water content was established by Equation (6). Furthermore, this interpretation is consistent with the measured increase in I_mean with strain and salt concentration and the observed hysteresis in I_mean as a function of strain (Figure 6). Ongoing experiments in our laboratory are further investigating the relationship between I_mean and tendon thickness using ultrasound. Another limitation of this study is that glycosaminoglycan (GAG) levels can be altered by changes in ionic concentration but were not measured (Han et al., 2012). However, a number of studies have established that GAG content does not affect mechanics in healthy human patellar tendon, human MCL and rat tail tendon (Fessel and Snedeker, 2009; Lujan et al., 2007; Lujan et al., 2009; Svensson et al., 2011), and internal studies in our laboratory comparing tendons incubated overnight in 1x PBS with tendons incubated overnight in chondroitinase ABC have confirmed that this is also the case for the murine FCU tendon (data not shown).

By investigating rate-dependent uncrimping and fluid exudation in tendon in different environmental conditions, this study established structure-function relationships between crimp frequency, lateral thickness and mechanical properties. In particular, changes in crimp frequency of the FCU tendon associated with strain-stiffening were measured for the first time, while rate-dependent mechanical changes were linked to altered uncrimping and volumetric contraction. These findings can be applied to better understand functional changes induced in tendons by alterations in water content and/or crimp morphology known to occur after stress deprivation (Akeson et al., 1987), high-intensity physical activity (Birch et al., 2008), development (Miller et al., 2012b), aging (PattersonKane et al., 1997), injury (Frank et al., 1983; Jarvinen et al., 2004; Williams et al., 1985), disease (Wilmink et al., 1992) and surgical intervention (Sabiston et al., 1990).