Abstract
Nowadays Nuclear Magnetic Resonance diffusion (dNMR) measurements of water molecules in heterogeneous systems have broad applications in material science, biophysics and medicine. Up to now, microstructural rearrangement in media has been experimentally investigated by studying the diffusion coefficient (D(t)) behavior in the tortuosity limit. However, this method is not able to describe structural disorder and transitions in complex systems. Here we show that, according to the continuous time random walk framework, the dNMR measurable parameter α, quantifying the anomalous regime of D(t), provides a quantitative characterization of structural disorder and structural transition in heterogeneous systems. To demonstrate this, we compare α measurements obtained in random packed monodisperse micro-spheres with Molecular Dynamics simulations of disordered porous media and 3D Monte Carlo simulation of particles diffusion in these kind of systems. Experimental results agree well with simulations that correlate the most used parameters and functions characterizing the disorder in porous media.
In the last years, much attention has been devoted to develop techniques for investigating biological tissues in vivo by using non invasive procedures. Among them, Nuclear Magnetic Resonance diffusion (dNMR) has proved to be a successful tool with its ability to provide detailed information about material1,2,3,4,5,6,7 and tissue8,9 properties. The measurement of molecular diffusion is an effective experimental way of probing biological and porous material structures, since the geometrical complexity of heterogeneous systems can be characterized by the way in which small molecules (typically water) diffuse within them.
A complex porous structure implies a multi-scale hindering of diffusing molecules so that its study and characterization can reveal the fingerprint of the medium geometry.
In conventional dNMR studies, structural complexity in heterogeneous media has been investigated by means of tortuosity indices, e.g. the obstruction factor OD10. However, we show here that the parameter OD is not suitable for detecting the most relevant information on global structural complexity (disorder) and structural transitions. In this work we focus on an innovative aspect of dNMR that allows, in the hindered diffusion regime, to describe the disorder properties of a sphere packed medium, to monitor its structural modifications and, if present, to reveal structural transitions.
In particular, we show that the exponent α, a measurable dNMR parameter quantifying the anomalous regime of the time-dependent diffusion coefficient D(t), is related to well known statistical quantities characterizing the disorder in porous media (the bond-orientational order parameters11, and the pair correlation function). Notably, α is able to detect structural transitions and to classify different kinds of disorder.
To achieve this goal, we compare the result of a dNMR experiment made on a sample of random packing monodisperse micro-spheres with the outcome of numerical 3D simulations resulting from an original "collage" of validated algorithms to yield essential results in the characterization of complex systems12,13,14.
Specifically, to highlight the physical meaning and relevance of α we show here a detailed description of structural disorder in random packing of mono-dispersed spheres performing both generative Molecular Dynamics simulations of disordered porous media and extensive 3D Monte Carlo studies of particles diffusion in these kind of systems, eventually connecting the numerical results to experimental dNMR measurements.
We explain the results of particle diffusion in the framework of the continuous time random walk (CTRW), which has been demonstrated to be a general and effective theoretical tool able to quantify anomalous diffusion in both laboratory- and field-scale systems15,16.
The diffusion process of solute particles in dilute homogeneous and isotropic solutions is described by the celebrated Einstein-Smoluchowski equation:
where the expression on the left of Eq.(1) is the mean square displacement (MSD) of solute molecules describing the spatial fluctuations around their coherent motion, d is the effective topological dimension of the medium in which the transport process occurs, and D is the solute diffusion coefficient.
In highly heterogeneous media the migration of solute particles is affected by various combined mechanisms effectively determining trapping into geometrically restricted zones. This leads to a broad spectrum of effective "local" solute particle stopping times, for which the relation (1) is no more valid. In general, natural systems show a range of heterogeneity length scales15,17,18, 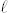 , between a minimum
, between a minimum 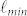 and a maximum
and a maximum 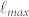 . Both theoretical and experimental studies18,19,20,21,22,23 have shown that three distinct diffusion regimes of solute particles can be identified in heterogeneous media. For
. Both theoretical and experimental studies18,19,20,21,22,23 have shown that three distinct diffusion regimes of solute particles can be identified in heterogeneous media. For 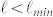 , diffusion is not sensible to heterogeneities and the relation (1) holds with a constant D equal to the bulk diffusivity D0 of the medium.
, diffusion is not sensible to heterogeneities and the relation (1) holds with a constant D equal to the bulk diffusivity D0 of the medium.
On the other hand, when 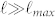 , caging and trapping effects due to heterogeneities are massively averaged out and relation (1) holds again but with an effective constant diffusion coefficient
, caging and trapping effects due to heterogeneities are massively averaged out and relation (1) holds again but with an effective constant diffusion coefficient 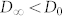 , which takes into account the average effect of traps and barriers24.
, which takes into account the average effect of traps and barriers24.
Finally, on intermediate scales 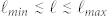 the diffusion is sensible to heterogeneity variations and may show a more complex behavior, known as non-Fickian or anomalous diffusion, which in the case of statistical isotropy takes the form of MSD = 2d
D(t)t, with a D(t) that can be often well fitted by a power law15,17,18
the diffusion is sensible to heterogeneity variations and may show a more complex behavior, known as non-Fickian or anomalous diffusion, which in the case of statistical isotropy takes the form of MSD = 2d
D(t)t, with a D(t) that can be often well fitted by a power law15,17,18
The parameter α is defined as the anomalous diffusion exponent and Γ is a generalized diffusion coefficient. Usually the term anomalous diffusion refers to an asymptotically (in time and scale) anomalous regime, i.e. the tα behavior should persist for t → ∞. This behavior can result from an infinite hierarchy of heterogeneity length scales. However, many complex real porous materials, such as those investigated in this study, exhibit a finite hierarchy of heterogeneity length scales which is a sufficient condition for anomalous diffusion at short times crossing over to normal diffusion at long times. Therefore, in this work, instead of defining away the transient anomalous diffusion, we analyze and quantify the initial period of anomalous diffusion.
This scenario introduces a generalized effective D(t) that in the case of Eq. (2) takes the simple form:
When 0 < α < 1 the diffusion process is sub-diffusive, for α > 1 is super-diffusive and when α = 1 the diffusion is normal and the relation (1) is recovered.
Real heterogeneous porous media are expected to host ordinary or sub-diffusive processes (i.e. α ≤ 1). The transition from the intermediate anomalous diffusion regime to the asymptotic ordinary regime is characterized by the crossover time t*, related to the largest heterogeneity length scale 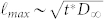 .
.
Conventional dNMR structural characterization of heterogeneous media is based on the measure of the so called obstruction factor OD = D∞/D0, i.e. the inverse of the tortuosity index of the medium10,12. In general, OD depends primarily on the shape and orientation of the geometrical restrictions as well as on the packing ratio φ25. The exact analytical derivation of the OD dependence on φ is a tricky mathematical problem. However, empirical relations with adjustable parameters have been introduced25,26,27 in analogy to well known theoretical results about simple cases.
We classify the degree of disorder in heterogeneous monodisperse sphere packing systems at different angular scales through the widely used11,28,29,30 bond-orientational order parameters Ql. Their values are invariant under rotations of the reference coordinate system and take characteristic values at the crystalline ordered phase. Therefore they can be used to quantify the type and degree of rotational symmetry in the system.
The local bond-orientational order parameter 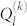 is defined by11
is defined by11
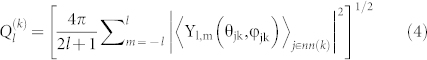 |
with Yl,m spherical harmonics, θjk and ϕjk polar angles of the vector between particles j and k, and 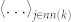 denoting the average over the nearest neighbors j of k.
denoting the average over the nearest neighbors j of k.
The global bond-orientational order parameters, Ql, are often used to quantify global structural disorder30. In order to compute Ql the average 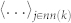 in equation (4) is substituted by the average over all pairs of nearest neighbors.
in equation (4) is substituted by the average over all pairs of nearest neighbors.
We restrict our analysis to l = 4 and l = 6, which bear particular importance in the case of cubic and icosahedral symmetries, respectively11. Since the first non vanishing Ql for the icosahedral, hexagonal and cubic symmetries is Q6, we chose it as an indicator of the degree of local order in the system28,29,30. We normalize Q6 to its value in the perfect fcc crystal and defined the quantity 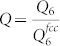 as the normalized bond-orientational order parameter. In the infinite volume limit, Q ranges from 0 (complete disorder) to 1 (perfect fcc order) and therefore can be used to quantify the disorder degree. Hence, a suitable definition of nearest neighbor in a disordered medium is needed. The medium we considered is composed by monodisperse hard spheres. We define a nearest neighbor of a given sphere k any other sphere with its center closer than a certain distance rmin to the center of k. We chose rmin as the length scale of the first relative minimum of the pair correlation function g2(r) defined as usual as
as the normalized bond-orientational order parameter. In the infinite volume limit, Q ranges from 0 (complete disorder) to 1 (perfect fcc order) and therefore can be used to quantify the disorder degree. Hence, a suitable definition of nearest neighbor in a disordered medium is needed. The medium we considered is composed by monodisperse hard spheres. We define a nearest neighbor of a given sphere k any other sphere with its center closer than a certain distance rmin to the center of k. We chose rmin as the length scale of the first relative minimum of the pair correlation function g2(r) defined as usual as
with N being number of spheres, ρ0 = N/V, V the total volume of the system and 〈…〉 the ensemble average.
The expression ρ0g2(r)dV delivers the probability to find the center of a particle in the volume element dV at a distance r around the center of a given sphere.
Details on the numerical estimation of g2(r) are given in the Supplementary materials (SM).
Results
dNMR and numerical experiments
We investigated a system made up of hard and impenetrable monodisperse spherical micro-beads in water at different sphere packing, as a proxy for a simple porous medium.
dNMR experiments were performed on five samples made of beads of nominal mean diameters: 30.0, 20.0, 15.0, 10.00 and 6.00 μm mono-dispersed in water solution. The measured values of the packing ranges from φ = 0.35 to φ = 0.56 (see Methods for details).
The systems used in the NMR experiments were numerically reproduced by 3D Molecular Dynamics simulations of N = 500 mono-sized quasi-hard spheres with periodic boundary conditions on the horizontal plane and reflective conditions on the bottom of the vertical direction. The numerical simulations yielded systems with a broad range of packing values 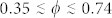 . The face centered cubic (fcc) crystal, corresponding to a perfectly ordered close packed situation with φ = 0.740, was built with the corresponding primitive vectors. A schematic representation of some of the systems simulated in this study is shown in Fig. 1.
. The face centered cubic (fcc) crystal, corresponding to a perfectly ordered close packed situation with φ = 0.740, was built with the corresponding primitive vectors. A schematic representation of some of the systems simulated in this study is shown in Fig. 1.
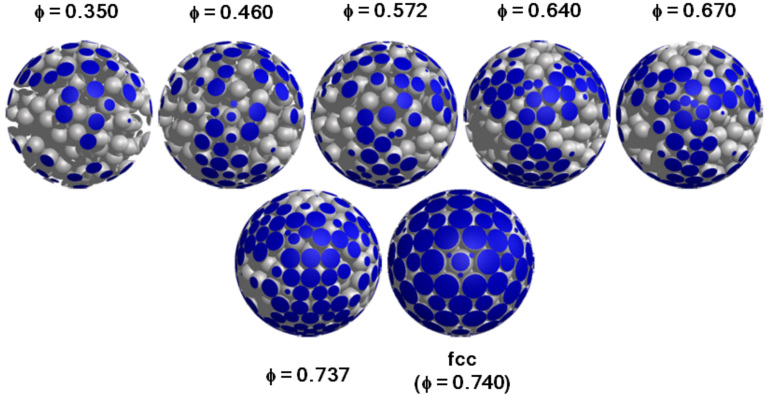
Figure 1. Hard sphere systems.
The spherical regions used for the calculation of some of the statistical quantities described in the text is shown for different hard sphere packing ratios and degrees of disorder. The intersection between the spherical surface and the spheres is depicted in blue color.
Finally, the diffusion of water molecules in the interstitials of such systems, was modeled by a Monte Carlo 3D random-walk process with reflecting boundary conditions at the surface of the spheres that constitute the inaccessible medium.
Geometry-based analysis of numerical results
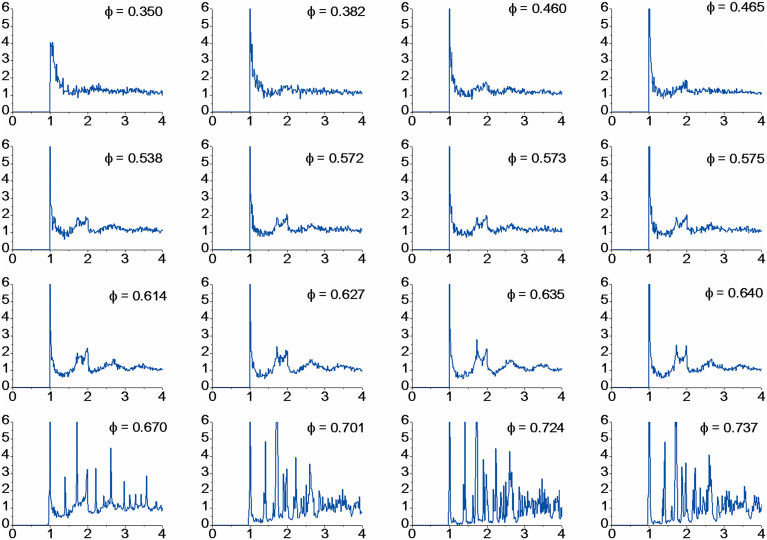
The average structure seen by a generic particle of the system described by g2(r) displayed in Fig. 2, shows a full agreement with the predicted theoretical regimes found in literature28,31. In all cases, we observe a pronounced peak at a distance r = a, with a the sphere diameter that corresponds to the distance of the nearest neighbors in contact. For r > a, the probability to find neighbors decreases reaching a minimum around r ≈ 1.4a. In fluid-like systems, theoretically for 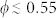 28,31,32, the g2(r) is known to oscillate with decreasing amplitude. By increasing the sphere packing and staying far from a crystallization regime, one gets a random jamming scenario, theoretically for
28,31,32, the g2(r) is known to oscillate with decreasing amplitude. By increasing the sphere packing and staying far from a crystallization regime, one gets a random jamming scenario, theoretically for 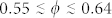 28,31,32, and the g2(r) displays two peaks at
28,31,32, and the g2(r) displays two peaks at 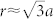 and r ≈ 2a, i.e. at the distances of the second and third neighbors of a closed-packed crystalline structure, still oscillating for larger values of r. The value φ ≈ 0.64 defines the maximum random jamming (MRJ) configuration31,32. Finally, in systems with larger sphere packing
and r ≈ 2a, i.e. at the distances of the second and third neighbors of a closed-packed crystalline structure, still oscillating for larger values of r. The value φ ≈ 0.64 defines the maximum random jamming (MRJ) configuration31,32. Finally, in systems with larger sphere packing 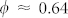 , signs of crystallization become more evident and the g2(r) displays multiple narrow peaks that are the signature of a crystal structure on distances larger than the first neighbor distance33. The graphs in Fig. 2 clearly indicate that in our numerical samples a jamming transition from an unjammed liquid-phase to a disordered jammed phase takes place around the MRJ packing.
, signs of crystallization become more evident and the g2(r) displays multiple narrow peaks that are the signature of a crystal structure on distances larger than the first neighbor distance33. The graphs in Fig. 2 clearly indicate that in our numerical samples a jamming transition from an unjammed liquid-phase to a disordered jammed phase takes place around the MRJ packing.
Figure 2. Pair correlation function.
The g2(r) is shown for selected values of hard sphere packing. The horizontal axis is measured as multiples of the sphere diameter. Three different scenarios can be distinguished: i) a fluid-like behavior for 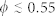 ; ii) random jamming for
; ii) random jamming for 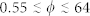 ; iii) a glass or amorphous solid for
; iii) a glass or amorphous solid for 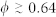 .
.
A deeper analysis of the local packing configurations can be obtained by exploring spherical local neighborhoods and can be useful to identify cooperative effects and possible structural transitions. From the study of the geometric nearest neighbors number distribution (GNNd) and the local spheres density φi distribution (LSDd) we found (see SM) a decreasing number of realizable configurations when the system approaches the random close packing. This behavior can be related to the onset of cooperative effects and of a possible phase transition from unjammed liquid to disordered jammed phase. These results are in good agreement with recent measurements of granular systems34,35,36,37, supporting the existence of a transition from random fluid system to glass or amorphous solid, geometrically frustrated on local crystal structure, but disordered on large scales (polycrystal)38.
The average number nc of spheres in contact with any given sphere, is able to estimate more precisely the two different sphere-density thresholds associated with the two phase transitions known in literature39,40,41, occurring in our simulated disordered systems. The first transition, from fluid to an intermediate phase that is rigid but unstressed39, is identified by the rigidity percolation threshold (RPT) we observe at φ ≈ 0.52 (the theoretical value39,40,41 is found at φ ≈ 0.54). The second transition, from this marginal state to a geometrically frustrated solid state, is identified by the stress percolation threshold (SPT) that we observe at φ ≈ 0.62 (the theoretical value39,40,41 is the MRJ packing found at φ ≈ 0.64) (see SM).
Geometrical frustration, polycrystals and effective anomalous diffusion
It has been often argued that the driving mechanism generating amorphous structures could be the geometrical frustration42. In order to test whether such a frustration mechanism occurs in our simulated systems in the amorphous solid phase for 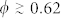 , we searched for configurations that were locally close packed at densities larger than the crystalline ones (details in SM). The geometrical frustration would have an important role in amorphous systems if a non-negligible fraction of such configurations would be found. We found that the geometrical frustration plays a negligible role when φ < 0.70, where the fraction of geometrically frustrated particles fGF was found to be less than 10%, in agreement with previous experimental works40,41. Conversely, at high values of sphere packing
, we searched for configurations that were locally close packed at densities larger than the crystalline ones (details in SM). The geometrical frustration would have an important role in amorphous systems if a non-negligible fraction of such configurations would be found. We found that the geometrical frustration plays a negligible role when φ < 0.70, where the fraction of geometrically frustrated particles fGF was found to be less than 10%, in agreement with previous experimental works40,41. Conversely, at high values of sphere packing 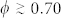 , in the amorphous disordered phase, local sphere arrangements with high local densities, such as the icosahedral packing, play an important role. In that case we found
, in the amorphous disordered phase, local sphere arrangements with high local densities, such as the icosahedral packing, play an important role. In that case we found 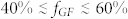 (see SM
Fig. S5). This means that in our highly packed and disordered hard sphere systems an abrupt transition from an unjammed liquid-phase to a disordered jammed phase occurs and frustration arises while the continuous translational symmetry breaks locally. In this case, due to the creation of frustrated areas between locally ordered configurations, systems at high φ values exhibit a broad spectrum of typical heterogeneity length scales (see Fig. 3). This is in fact confirmed by the size distribution of the interstitial voids that has a variance
(see SM
Fig. S5). This means that in our highly packed and disordered hard sphere systems an abrupt transition from an unjammed liquid-phase to a disordered jammed phase occurs and frustration arises while the continuous translational symmetry breaks locally. In this case, due to the creation of frustrated areas between locally ordered configurations, systems at high φ values exhibit a broad spectrum of typical heterogeneity length scales (see Fig. 3). This is in fact confirmed by the size distribution of the interstitial voids that has a variance  showing a minimum at φ ≈ 0.62 and increasing monotonically (see SM).
showing a minimum at φ ≈ 0.62 and increasing monotonically (see SM).
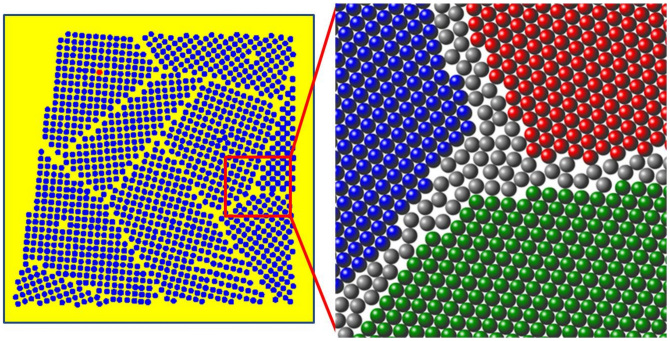
Figure 3. Artistic representation of Polycrystal structure.
Globally disordered structures comprised of frustrated grains locally ordered in crystalline configurations. They are characterized by a wide distribution of voids characteristic length scales that reflect disorder properties. This suggests, according to the CTRW framework, that an effective anomalous diffusion process should be detected in such systems. This means that a straight relation between the properties of structural disorder and diffusion in the hindered regime exists. Unlike OD, the dNMR parameter α embodies information about the properties of structural disorder in an effective way and allows to identify the structural transition from rigid but unstressed random jamming to stressed polycrystal structure (see Fig. 5-b and Fig. 6).
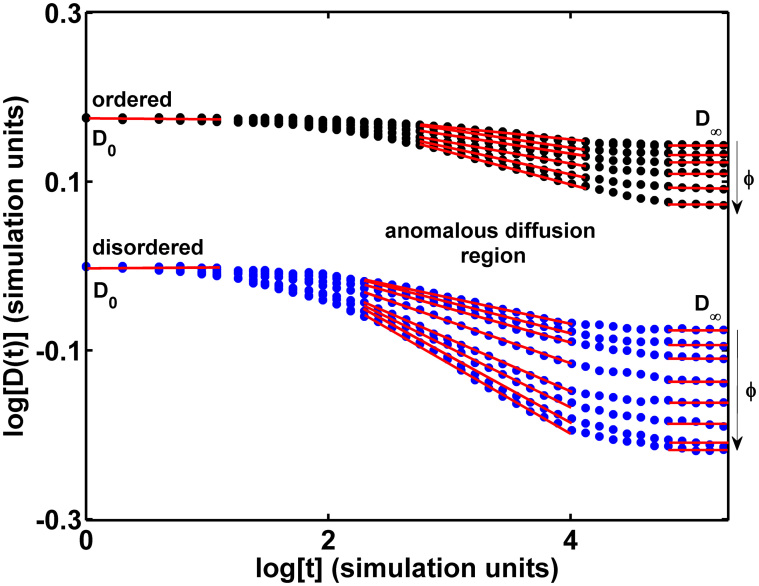
The appearance of multiple heterogeneity length scales by frustration suggests, according to the CTRW framework, that in very dense amorphous packing an effective anomalous diffusion process should be observed. In particular, on the basis of the arguments given above, we expect to measure an α < 1 at these φ values. The behavior of D(t), D vs diffusion time t, for all the simulated systems, i.e. fcc ordered (black points) and disordered (blue points), is reported in Fig. 4, where we notice that the diffusion in disordered systems exhibits a dynamics with a more anomalous character than in ordered ones. Since the decrease of D(t) in ordered systems is due to hindering effects by construction, the corresponding more accentuated decreasing behavior in the disordered regime may be ascribed to the complexity of the system itself. In particular, the decreasing rate at high φ values is more pronounced in disordered samples, while the width of the transient anomalous diffusion region, marked by the red straight lines in Fig. 4, is broader. Moreover, D∞ gets lower values at higher sphere densities, with a trend more noticeable in disordered systems than in ordered ones. All these findings confirm the theoretical and numerical results of previous works12 dealing with the obstruction factor OD.
Figure 4. Time-dependent diffusion coefficient.
Results of Monte Carlo simulations for the set of fcc ordered (black points) and disordered (blue points) hard sphere packing at increasing packing ratio φ ranging from 0.33 to 0.74 (top to bottom). Data corresponding to the ordered systems are suitably shifted on the vertical axis for readability (D0 is the same for all these systems). Red lines are power-law fits and quantify the scaling behavior of D(t) in the anomalous diffusion transient. Fcc ordered hard sphere arrangements at packing ratio less than its maximum value reached at a closed packed geometry, i.e. for φ < 0.74, were obtained by decreasing the diameter α of the spheres and letting their centers lie on the fcc lattice points. The three diffusion regimes are clearly distinguishable for both ordered and disordered systems: free diffusion for t < 10 in simulation units (a time simulation unit correspond to ≈2μs); transient anomalous diffusion when 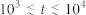 in the case of ordered systems, and
in the case of ordered systems, and 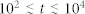 in case of disordered systems; hindered diffusion in tortuosity limit for t > 105.
in case of disordered systems; hindered diffusion in tortuosity limit for t > 105.
Local bond orientational order parameters analysis
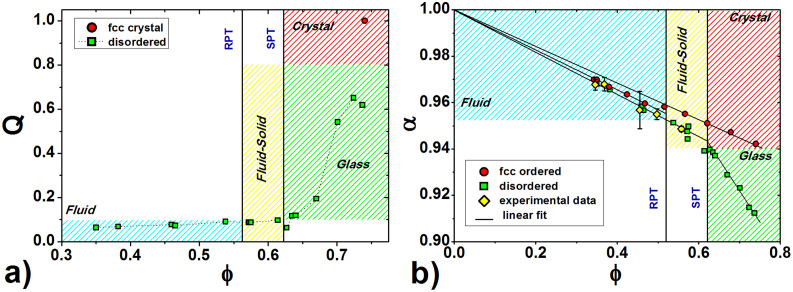
In order to establish the nature of the local internal organization emerging at high packing values, and to measure how close the packing is to an ideal crystal structure, we determined the bond orientational order parameters Q4 and Q6 for all considered systems. Below 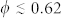 we found (see SM) less than 5% of local configurations with symmetry compatible with either bcc (body centered cubic) or fcc and less than 10% with local symmetry compatible with hcp (hexagonal close-packed). As φ increases, the local close-packed configurations hcp and fcc become more and more significant, reaching more than 30% of the total configurations as φ approaches 0.70. This, together with the previous discussion on the transition of fGF, suggests that a local crystallization process is setting up around φ ≈ 0.70. To highlight the onset of this liquid-polycrystal transition we plot in Fig. 5-(a) the behavior of Q
vs
φ, which shows that Q is very sensitive to any kind of crystallization transition and increases significantly when order appears around φ ≈ 0.70. In particular, Q increases monotonically with φ as the system approaches the rigidity percolation threshold (RPT) at φ ≈ 0.52, indicating that the increase in density yields an increase of short-range order in the fluid. A discontinuous jump in Q is observed at φ ≈ 0.62. At this value of φ a significant amount of structural order appears, in perfect agreement with the stress percolation threshold (SPT). Hence, we deduce that the simulated systems undergo an abrupt transition at φ ≈ 0.62, from an unjammed liquid-phase to a disordered jammed phase.
we found (see SM) less than 5% of local configurations with symmetry compatible with either bcc (body centered cubic) or fcc and less than 10% with local symmetry compatible with hcp (hexagonal close-packed). As φ increases, the local close-packed configurations hcp and fcc become more and more significant, reaching more than 30% of the total configurations as φ approaches 0.70. This, together with the previous discussion on the transition of fGF, suggests that a local crystallization process is setting up around φ ≈ 0.70. To highlight the onset of this liquid-polycrystal transition we plot in Fig. 5-(a) the behavior of Q
vs
φ, which shows that Q is very sensitive to any kind of crystallization transition and increases significantly when order appears around φ ≈ 0.70. In particular, Q increases monotonically with φ as the system approaches the rigidity percolation threshold (RPT) at φ ≈ 0.52, indicating that the increase in density yields an increase of short-range order in the fluid. A discontinuous jump in Q is observed at φ ≈ 0.62. At this value of φ a significant amount of structural order appears, in perfect agreement with the stress percolation threshold (SPT). Hence, we deduce that the simulated systems undergo an abrupt transition at φ ≈ 0.62, from an unjammed liquid-phase to a disordered jammed phase.
Figure 5. (a–b) Structural order phase diagrams.
(a) Normalized bond-orientational order Q vs packing ratio φ, for all the simulated disordered packing (green squares) as well as for the fcc crystal (red cyrcle). (b) anomalous diffusion exponent α vs packing ratio φ. Values of α inferred by Monte Carlo simulations of solute diffusion in the fcc ordered systems (red circles) and in the disordered systems (green squares) reported in Fig. 4, are showed together with dNMR experimental values (yellow diamonds). dNMR experiments were carried on five samples with 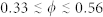 . Experimental error bars for the dNMR data were estimated by a fitting procedure employing a Levenberg-Marquardt algorithm. Values of α were determined from the red line fits showed in Fig. 4 by using the definition of Eq. (3). In both (a) and (b), the planes are subdivided into colored regions, associated to the structural phases of the hard sphere systems. The rigidity percolation threshold (RPT) and the stress percolation threshold (SPT) are highlighted.
. Experimental error bars for the dNMR data were estimated by a fitting procedure employing a Levenberg-Marquardt algorithm. Values of α were determined from the red line fits showed in Fig. 4 by using the definition of Eq. (3). In both (a) and (b), the planes are subdivided into colored regions, associated to the structural phases of the hard sphere systems. The rigidity percolation threshold (RPT) and the stress percolation threshold (SPT) are highlighted.
Discussion
The main result of our study is depicted in Fig. 5-(b) (α
vs
φ graph). The α parameter is able to identify the structural transition occurring at φ ≈ 0.62 (fluid – amorphous solid transition identified by the abrupt change of slope) in similar way to the order parameter Q. Therefore, the diffusion of solute particles is sensitive to the disorder structural transition and can in principle be used as an effective experimental probe to monitor it. By looking the α experimental results displayed as yellow diamonds compared with simulations, it is possible to distinguish the random fluid phase (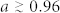 ), the mixed fluid-solid phase (
), the mixed fluid-solid phase (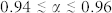 ) and eventually the amorphous solid state (
) and eventually the amorphous solid state (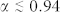 ).
).
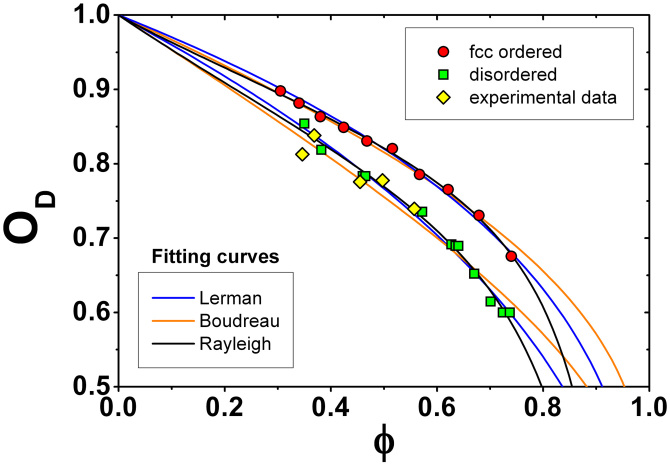
Conversely, OD vs φ showed in Fig. 6, because of its high sensitivity to local properties of the medium, is not able to characterize any transition, and its use is limited to the discrimination between fully ordered and disordered systems25,26,27.
Figure 6. Experimental dNMR OD values as a function of φ compared with simulations results.
Values of the obstruction factor OD inferred by Monte Carlo simulations of solute diffusion in the fcc ordered systems (red circles) and in the disordered systems (green squares). Values were determined from the asymptotic behavior of D(t) at long diffusion times. Yellow diamonds represent values experimentally determined by dNMR, as described in the Methods. The three colored curves represent the fit of the semi-empirical relations derived by Lerman26, Boudreau27 and Rayleigh25 with the values got from simulations. In particular, the Lerman's relation is OD = [A(1 − φ)1−m]−n, with A = 1.00 ± 0.13, m = 1.28 ± 0.11 and n = 1.00 ± 0.10 for the ordered systems and A = 1.00 ± 0.15, m = 1.32 ± 0.14 and n = 1.19 ± 0.13 for the disordered ones; the Boudreau's relation is 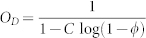 , with C = 0.3266 ± 0.0053 for the ordered systems and C = 0.467 ± 0.011 for the disordered ones; and the Rayleigh's relation is
, with C = 0.3266 ± 0.0053 for the ordered systems and C = 0.467 ± 0.011 for the disordered ones; and the Rayleigh's relation is 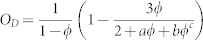 , with a = 0.53 ± 0.10, b = 0.32 ± 0.11 and c = 0.20 ± 0.10 for the ordered systems and a = 0.64 ± 0.12, b = 0.17 ± 0.11 and c = 0.54 ± 0.11 for the disordered ones.
, with a = 0.53 ± 0.10, b = 0.32 ± 0.11 and c = 0.20 ± 0.10 for the ordered systems and a = 0.64 ± 0.12, b = 0.17 ± 0.11 and c = 0.54 ± 0.11 for the disordered ones.
As a first application of the method exposed here, we clarify the nature of the micro-beads systems experimentally studied by dNMR techniques. The measured values of φ, indicate that these samples were in a fluid-like and fluid-solid like phase since 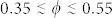 . The measured values of OD ensure that the samples were in a disordered state, well reproduced by our simulations. Moreover, the measured values of α show that the samples lay far from the jamming transition point. Finally, we can assert that three of the five samples were characterized by a random fluid-like microscopic state and the remaining two were in a mixed phase of mixed fluid and solid.
. The measured values of OD ensure that the samples were in a disordered state, well reproduced by our simulations. Moreover, the measured values of α show that the samples lay far from the jamming transition point. Finally, we can assert that three of the five samples were characterized by a random fluid-like microscopic state and the remaining two were in a mixed phase of mixed fluid and solid.
In conclusion, we highlighted here important properties of the α parameter that can be easily measured by using dNMR experiments with faster procedure than in conventional D(t) behavior studies10. Thanks to the ability of NMR to be non-invasive and non-destructive, α measurements could lead to the identification and monitoring of changes in tissue pathology or material structural-properties. In order to demonstrate that anomalous diffusion of particles in heterogeneous porous media can provide information about their structural complexity, a procedure composed of generative Molecular Dynamics simulations and 3D Monte Carlo studies was described. These simulations highlight the relation between the most suitable parameters and functions used to describe disorder in heterogeneous porous systems. Numerical and experimental results show an excellent agreement, confirming the reliability of α to characterize experimentally the structural disorder, opening the way to future developments and applications involving structural transition in heterogeneous media.
Methods
Samples preparation and experimental set-up
Five 10 mm NMR tubes were filled up to a volume of approximately 2 cm3 with polystyrene beads (Microbeads AS, Norway) of nominal average diameters of 30.0, 20.0, 15.0, 10.00 and 6.00 μm, mono-dispersed in a solution of polyoxyethyle-sorbitan-mono-laurat (Tween 20) at 10−6 M and deionized water (conductivity ~ 10−6 Ω−1/cm), and investigated during 4 months after their preparation at fixed temperature of 293 K. The measured values of the packing ranged from φ = 0.35 after two weeks, to φ = 0.56 at the end of the observation after four months.
The effective fractional exponent α was measured by collecting the NMR pulse field gradient (PFG) signal attenuation, S(q, Δ), as a function of the diffusion time Δ and by using the asymptotic expression of the Fourier transform of the motion propagator for the sub-diffusive regime derived in ref. 43:
which holds when 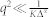 is kept constant at varying Δ, with K a generalized diffusion constant and q the wavevector defined by
is kept constant at varying Δ, with K a generalized diffusion constant and q the wavevector defined by 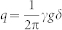 , where γ is the gyromagnetic ratio of the water proton, g is the pulse magnetic field gradient strength and δ is the pulse magnetic field gradient duration. A spectroscopic PFG Stimulated Echo (PFG-STE) sequence with δ = 2.2 ms, g = 0.10 T/m (i.e. q~11240 m−1) along x, y and z directions, repetition time TR = 2.5 s, number of average NS = 32 and 48 values of Δ in the range (10–500)ms was used to extract the αi = x,y,z values. Then the mean value, α, was computed by averaging over the three directions. A second spectroscopic PFG-Stimulated echo experiment was used to obtain experimental OD values. Δ/δ = 400/2.2 ms, TR = 2.5 s, NS = 16 and 48 gradient amplitude steps from 0.026 to 1.02 T/m along x, y and z directions were used to measure the effective diffusion coefficient at long time, D∞, from the slope of
, where γ is the gyromagnetic ratio of the water proton, g is the pulse magnetic field gradient strength and δ is the pulse magnetic field gradient duration. A spectroscopic PFG Stimulated Echo (PFG-STE) sequence with δ = 2.2 ms, g = 0.10 T/m (i.e. q~11240 m−1) along x, y and z directions, repetition time TR = 2.5 s, number of average NS = 32 and 48 values of Δ in the range (10–500)ms was used to extract the αi = x,y,z values. Then the mean value, α, was computed by averaging over the three directions. A second spectroscopic PFG-Stimulated echo experiment was used to obtain experimental OD values. Δ/δ = 400/2.2 ms, TR = 2.5 s, NS = 16 and 48 gradient amplitude steps from 0.026 to 1.02 T/m along x, y and z directions were used to measure the effective diffusion coefficient at long time, D∞, from the slope of 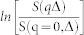 at low q values along each direction and then averaging over the three directions. A Spin Echo imaging sequence with TR = 2.5 s, 48 values of echo time, TE, in the range (3–130)ms, NS = 16, slice thickness STH = 1 mm, field of view FOV = 8 × 8 mm and an in plane resolution of 62.5 μm was used to estimate φ in each sample, as described in ref. 44.
at low q values along each direction and then averaging over the three directions. A Spin Echo imaging sequence with TR = 2.5 s, 48 values of echo time, TE, in the range (3–130)ms, NS = 16, slice thickness STH = 1 mm, field of view FOV = 8 × 8 mm and an in plane resolution of 62.5 μm was used to estimate φ in each sample, as described in ref. 44.
Molecular Dynamic simulation of 3D hard-sphere packing
We simulated numerically and investigated two different sorts of obstructed media: i) systems made of 500 mono-sized hard spheres ordered on a fcc lattice, at different values of sphere packing, 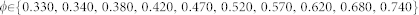 ; ii) systems made of 500 mono-sized hard spheres randomly displaced, at different values of sphere packing,
; ii) systems made of 500 mono-sized hard spheres randomly displaced, at different values of sphere packing, 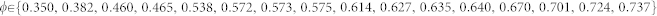 . In the case of the fcc lattices, the different packing were obtained by changing the sphere diameters while leaving the sphere centers on the fcc lattice points. The disordered hard sphere systems were obtained by a Molecular Dynamics (MD) approach. The hamiltonian of the system was taken as
. In the case of the fcc lattices, the different packing were obtained by changing the sphere diameters while leaving the sphere centers on the fcc lattice points. The disordered hard sphere systems were obtained by a Molecular Dynamics (MD) approach. The hamiltonian of the system was taken as
where m is the mass of particle i, U1 the external potential energy and U2 the pair potential. The external field was modeled by a constant gravitational field whose corresponding force acted along the vertical axis z. In order to simulate interactions between hard spheres, the pair potential was chosen harmonic with a suitably high harmonic constant. The corresponding force acts along the radial direction when the distance between two spheres centers is lower than the sum of their radii:
with d = qi − qj the distance between the centers of spheres i and j, r the sum of their radii (their diameter in this case of identical spheres), K ≈ 104 simulation units the harmonic constant and Θ is the Heaviside step function. In order to avoid unrealistic spheres bumpings, a dissipative force, Fγ, was introduced to have a system of harmonic oscillators in overdamped regime:
where ν is the difference between spheres velocities and γ is the damping constant, chosen equal to 0.9 in simulation units.
Moreover, in order for the system to reach a static final state of equilibrium, a viscous friction force, proportional to the velocities of spheres, was also introduced and applied after a proper thermalization time (to obtain a disordered system the viscous friction force has to be applied quite early).
The MD simulations were performed with periodic boundary conditions on the horizontal x, y plane and reflective conditions on the bottom of the simulation box. The initial configuration was chosen from a random poissonian configuration of the spheres with null velocities. We obtained our final systems of spheres with different disorder degree by: 1) changing the density of the initial random configuration, 2) pinning a subset of spheres near the bottom, 3) changing the “switch on” time of viscous friction force. Simulation procedure terminated when the total kinetic energy of the system went below a cutoff value of 10−8 in simulation units.
3D random flight simulation
Diffusion in 3D obstructed media, coinciding with the network of pores of the hard sphere systems, was modeled by random walkers moving among obstructions as a random flight, where each step vector δr is uniformly distributed on the surface of a sphere of fixed radius |δr|.
Once the displacement has been extracted, if the final position of the considered particle is empty the displacement is accepted, otherwise the particle remains in its initial position, and another particle is randomly chosen to move. In other words, attempted steps that would lead the particle into obstructed regions, i.e. inside one of the packed hard spheres, are rejected. This procedure simulates the reflecting boundary condition at the obstructions surface12. Every simulation runs from 104 to 106 time steps and every run was repeated 100 times with a different initial disposition of 500 independent and non-interacting walkers for run. Thus, the ensemble average 〈…〉 was computed by averaging over 5 × 104 random-flight trajectories with random initial positions.
In order to avoid any artifacts in simulation results, the length of the step vector δr is chosen |δr| ≤ a/100, where a is the smallest dimension of the obstructing objects, i.e. the diameter of the hard spheres. This is due to the fact that, although at low values of φ diffusion characteristic parameters as OD are virtually independent of |δr|, at high value of φ (e.g. φ > 0.70) OD was found to increase linearly25 with decreasing |δr|. The length of |δr| chosen is sufficient to avoid this kind of simulation artifacts.
Author Contributions
M.P. carried out analytical calculations, NMR experiments and wrote the manuscript. V.D.P.S. carried out numerical calculations. A.G. collaborated to theoretical interpretation of numerical and experimental results. G.R. and S.C. discussed the results and implications and commented. All authors discussed the results and implications and commented on the manuscript at all stages.
Supplementary Material
Supplementary Materials
Acknowledgments
V.D.P.S. acknowledges the EveryAware project funded by the Future and Emerging Technologies program (IST-FET) of the European Commission under the EU RD contract IST-265432.
References
- Preston C. M. Applications of NMR to soil organic matter analysis: history and prospects. Soil Sci. 161, 144–166 (1996). [Google Scholar]
- Kleinberg R. L. et al. Deep sea NMR: Methane hydrate growth habit in porous media and its relationship to hydraulic permeability, deposit accumulation, and submarine slope stability. J. Geophys. Res. 108, 12–20 (2003). [Google Scholar]
- Callaghan P. T., Coy A., MacGowan D., Packer K. J. & Zelaya F. O. Diffraction-like effects in NMR diffusion studies of fluids in porous solids. Nature 351, 467–469 (1991). [Google Scholar]
- Godefroy S., Korb J. P., Fleury M. & Bryant R. G. Surface nuclear magnetic relaxation and dynamics of water and oil in macroporous media. Phys. Rev. E 64, 021605–021618 (2001). [DOI] [PubMed] [Google Scholar]
- Callaghan P. T. et al. Diffusion in porous systems and the influence of pore morphology in pulsed gradient spin-echo nuclear magnetic resonance studies. J. Chem. Phys. 97, 651–662 (1992). [Google Scholar]
- Blinc R., Pirš J. & Zupančič I. Measurement of Self-Diffusion in Liquid Crystals by a Multiple-Pulse NMR Method. Phys. Rev. Lett. 30, 546–549 (1973). [Google Scholar]
- Matsukawa S. et al. Diffusion processes in polymer gels as studied by pulsed field-gradient spin-echo NMR spectroscopy. Prog. Polym. Sci. 24, 995–1044 (1999). [Google Scholar]
- Basser P. J. & Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. B 111, 209–219 (1996). [DOI] [PubMed] [Google Scholar]
- Pajevic S. & Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: Application to white matter fiber tract mapping in the human brain. Magn. Reson. Med. 42, 526–540 (1999). [PubMed] [Google Scholar]
- Latour L. L., Kleinberg R. L., Mitra P. P. & Sotak C. H. Pore-size distribution and tortuosity in heterogeneous porous media. J. Magn. Reson. A 112, 83–91 (1995). [Google Scholar]
- Steinhardt P. J., Nelson D. R. & Ronchetti M. Bond-orientational order in liquids and glasses. Phys. Rev. B. 28, 784–805 (1983). [Google Scholar]
- Johannesson H. & Halle B. Solvent diffusion in ordered macrofluids: a stochastic simulation study of the obstruction effect. J. Chem. Phys. 104, 6807–6817 (1996). [Google Scholar]
- Rintoul M. D. & Torquato S. Computer simulations of dense hard-sphere systems. J. Chem. Phys. 105, 9258–9266 (1996). [Google Scholar]
- Torquato S. & Jiao Y. Robust algorithm to generate a diverse class of dense disordered and ordered sphere packings via linear programming. Phys. Rev. E 82, 061302–061316 (2010). [DOI] [PubMed] [Google Scholar]
- Metzler R. & Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339, 1–77 (2000). [Google Scholar]
- Cortis A., Chen Y., Scher H. & Berkowitz B. Quantitative characterization of pore-scale disorder effects on transport in “homogeneous” granular media. Phys. Rev. E. 70, 041108–041116 (2004). [DOI] [PubMed] [Google Scholar]
- Havlin S. Ben-Avraham D. Diffusion in disordered media. Adv. Phys. 36, 695–798 (1987). [Google Scholar]
- Bouchaud J. P. & Georges A. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 185, 127–293 (1990). [Google Scholar]
- Saxton M. J. Anomalous diffusion due to obstacles: a Monte Carlo study. Biophys. J. 66, 394–401 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton M. J. A biological interpretation of transient anomalous subdiffusion. I. Qualitative model. Biophys. J. 92, 1178–1191 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y., Prud'homme R. K. & Thomas J. L. Diffusion of mesoscopic probes in aqueous polymer solutions measured by fluorescence recovery after photobleaching. Macromolecules. 35, 8111–8121 (2002). [Google Scholar]
- Wachsmuth M. et al. Diffusion in macromolecular crowded media: Monte Carlo simulation of obstructed diffusion vs. FRAP experiments. Biophys. J. 84, 3353–3363 (2003).12719264 [Google Scholar]
- Weiss M., Elsner M., Kartberg F. & Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 87, 3518–3524 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novikov D. S., Fieremans E., Jensen J. H. & Helpern J. A. Random walk with barriers. Nature Phys. 7, 508–514 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rayleigh L. On the influence of obstacles arranged in rectangular order upon the properties of a medium. Philos. Mag. 34, 481–489 (1892). [Google Scholar]
- Lerman A. Geochemical processes: water and sediment environments. Page 73 (John Wiley & Sons, New York, 1979).
- Boudreau P. B. The diffusive tortuosity of fine-grained unlithified sediments. Geochim. Cosmochim. Acta. 60, 3139–3142 (1996). [Google Scholar]
- Richard P., Orger L., Troadec J. P. & Gervois A. Geometrical characterization of hard-sphere systems. Phys. Rev. E. 60, 4551–4558 (1999). [DOI] [PubMed] [Google Scholar]
- Torquato S., Truskett T. & Debenedetti P. Is random close packing of spheres well defined? Phys. Rev. Lett. 84, 2064–2067 (2000). [DOI] [PubMed] [Google Scholar]
- Truskett T., Torquato S. & Debenedetti P. Towards a quantification of disorder in materials: Distinguishing equilibrium and glassy sphere packings. Phys. Rev. E. 62, 993–1001 (2000). [DOI] [PubMed] [Google Scholar]
- Donev A., Torquato S. & Stillinger F. H. Pair correlation function characteristics of nearly jammed disordered and ordered hard-sphere packings. Phys. Rev. E. 71, 011105–011119 (2005). [DOI] [PubMed] [Google Scholar]
- Aste T. & Di Matteo T. Structural transitions in granular packs: statistical mechanics and statistical geometry investigations. Eur. Phys. J. B. 64, 511–517 (2008). [Google Scholar]
- Gabrielli A. Point processes and stochastic displacement fields. Phys. Rev. E. 70, 066131–066147 (2004). [DOI] [PubMed] [Google Scholar]
- Clusel M., Corwin E. I., Siemens A. O. N. & Brujic J. A ‘granocentric' model for random packing of jammed emulsions. Nature 460, 611–615 (2009). [Google Scholar]
- Corwin E. I., Clusel M., Siemens A. O. N. & Brujic J. Model for random packing of polydisperse frictionless spheres. Soft Matter 6, 2949–2959 (2010). [Google Scholar]
- Schroter M., Goldman D. & Swinney H. Stationary state volume fluctuations in a granular medium. Phys. Rev. E. 71, 030301–030306 (2005). [DOI] [PubMed] [Google Scholar]
- Pugnaloni L. A. et al. Towards a relevant set of state variables to describe static granular packings. Phys. Rev. E. 82, 050301–050306 (2010). [DOI] [PubMed] [Google Scholar]
- Granasy L., Pusztai T., Borzsony T., Warren J. A. & Douglas J. F. A general mechanism of polycrystalline growth. Nature Materials 3, 645–650 (2004). [DOI] [PubMed] [Google Scholar]
- Chubynsky M. V. & Thorpe M. F. Self-organization and rigidity in network glasses. Curr. Opin. Solid State Mater. Sci. 5, 525–532 (2001). [Google Scholar]
- Aste T., Saadatfar M., Sakellaiou A. & Senden T. J. Investigating the geometrical structure of disordered sphere packings. Physica A. 339, 16–23 (2004). [DOI] [PubMed] [Google Scholar]
- Aste T., Saadatfar M. & Senden T. J. Geometrical structure of disordered sphere packings. Phys. Rev. E. 71, 061302–061317 (2005). [DOI] [PubMed] [Google Scholar]
- Aste T. & Weaire D. The pursuit of perfect packing. (Institute of Physics, Bristol, 2000).
- Palombo M. et al. Spatio-temporal anomalous diffusion in heterogeneous media by nuclear magnetic resonance. J. Chem. Phys. 135, 034504–034511 (2011). [DOI] [PubMed] [Google Scholar]
- Turney M. A., Cheung M. K., McCarthy M. J. & Powell R. L. Magnetic resonance imaging study of sedimenting suspensions of noncolloidal spheres. Phys. Fluids 7, 904–911 (1995). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Materials