Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Sep 11;3:2634. doi: 10.1038/srep02634

Next-Generation Anchor Based Phylogeny (NexABP): Constructing phylogeny from Next-generation sequencing data

Tanmoy Roychowdhury 1, Anchal Vishnoi 2, Alok Bhattacharya 1,2,a
PMCID: PMC3769656  PMID: 24022334

Abstract

Whole genome sequences are ideally suited for deriving evolutionary relationship among organisms. With the availability of Next Generation sequencing (NGS) datasets in an unprecedented scale, it will be highly desirable if phylogenetic analysis can be carried out using short read NGS data. We described here an anchor based approach NexABP for phylogenetic construction of closely related strains/isolates from NGS data. This approach can be used even in the absence of a fully assembled reference genome and works by reducing the complexity of the datasets without compromising results. NexABP was used for constructing phylogeny of different strains of some of the common pathogens, such as Mycobacterium tuberculosis, Vibrio cholera and Escherichia coli. In addition to classification into distinct lineages, NexABP could resolve inner branches and also allow statistical testing using bootstrap analysis. We believe that there are some clear advantages of using NexABP based phylogenetic analysis as compared to other methods.

Next-generation sequencing (NGS) techniques have revolutionized genome analysis and consequently enhanced our understanding of genotype-phenotype relationships1. Genome sequences of thousands of micro-organisms including different strains and isolates are now available publicly in repositories, such as Short Read Archive (SRA) of NCBI or European Nucleotide Archive. Variations among these genomes can be used to infer not only their phenotype, but also their evolution including phylogenetic relationship among organisms. Fully assembled genomes have been utilized to generate phylogenetic trees and it is generally recognized that whole genome based methods2,3 provide highly resolved trees as compared to those derived from one or a group of genes4. Some of the approaches developed for whole genome based phylogeny, can also be used for analysis of NGS data. NGS platforms typically generate millions of short genomic reads which can further be assembled into whole genomes. Methods for assembling whole genomes from short read sequence libraries are not efficient and still incapable of merging all the genomic contigs. There are only a few studies where whole genomes have been fully assembled from NGS data5. Therefore, it is difficult to use whole genome based approaches in their present form for construction of phylogeny utilizing unassembled NGS data. Phylogenetic analysis has been done utilizing variable SNPs identified using NGS data6,7. Accurate SNP identification requires high coverage. Moreover, these methods rely heavily on the presence of a closely related complete reference genome.

Since there are not many assembled NGS sequence data available it is useful to have methods that use short read unassembled data to generate trees. The problem is also compounded by the use of different sequencing platforms that provide data with different lengths and error models. Lack of methods that specifically target unassembled NGS data, is mainly due to the problems associated with working on NGS data. In a recent attempt, a novel approach of inferring phylogeny using C-gram and O-gram from short read data has been described (Co-phylog8). The trees generated by Co-phylog are comparable with trees constructed using assembled genomes. However, inner branches of trees generated using Co-phylog was not resolved properly and statistical significance of the derived trees from real NGS data are also not depicted.

In this paper, we have introduced NexABP, an anchor based approach of calculating distances among NGS raw data sets. NexABP is a modified version of our earlier method implemented successfully for comparing whole genome sequences9. The sampling approach used, reduces the data size to be analyzed. The inner branches are well resolved and the statistical significance of the tree can be tested by bootstrap10. Moreover, NexABP can be applied to low coverage data and can generate trees independent of availability of a fully assembled reference genome.

Results

Anchor selection in presence of reference genome

An anchor-based approach to estimate phylogenetic distance among assembled whole genome sequences was described earlier9. Following the same approach, sequences of predefined length termed as “anchors” were chosen from random positions in an assembled reference genome in NexABP. Selected anchors are non-overlapping and are 500 bp long. NGS reads of strains were aligned with individual anchors. Further, a consensus of reads aligned to an individual anchor was created. This was done for all aligned reads along with respective anchor. This procedure generated a set of consensus sequences from a strain for each anchor. Similarly a set of consensus sequences were also generated for other strains. A flowchart of the pipeline is shown in Supplementary Figure S1.

Anchor selection in absence of reference genome

A different approach was used for anchor selection where there is no need of a reference genome. First, a large set of reads were selected randomly from individuals discarding the duplicates as mentioned in Methods. These reads were then locally assembled to generate anchors. Sequence libraries where the number of anchors exceeded above certain threshold were used as references genomes. The threshold was determined by the ability of CNS to reach a steady state as defined later. In this case instead of a single reference genome many reference sequences were available for computation.

Calculation of Cumulative Normalized Score

After extraction of anchors either from assembled or unassembled reference sequence, the score was calculated indicating the distances among the organisms being analyzed. For pair-wise comparison between two strains, consensus sequences from each of the strains corresponding to the same anchor were aligned. The mismatch score between the consensus sequences of the two strains was calculated. The sum of mismatch scores of all the pairs of consensus was called Cumulative Score. This score is further normalized with total number of pairs of consensus to calculate CNS (cumulative normalized score). CNS represents the distance between two sequence libraries. Similarly, CNS was calculated for all pairs of strains and has some intrinsic properties, it reaches a steady state for large number of anchors; the value of CNS lies between 0 and 1; it does not depend on anchor order in reference genome. Also, it fulfills all the three criteria for distance calculation9. CNS is used as a distance measure to construct the phylogeny utilizing Neighbor-joining Method11.

Estimation of typical length of an anchor

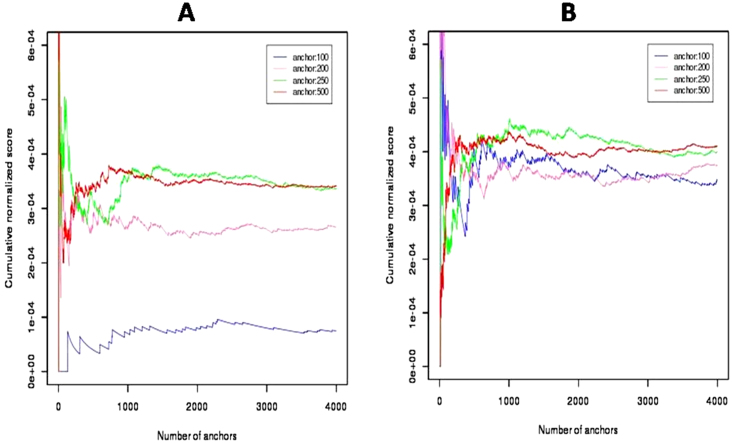
Estimation of anchor length is critical for CNS calculation. The power of an alignment decreases with increasing length. On the other hand the information content of short alignment is less. Therefore, length of an anchor should be a trade-off between these two properties. We did an empirical analysis with anchor lengths of 100, 200, 250 and 500 bp. Both paired-end (PE) and single-end (SE) alignments of the same dataset of M. tuberculosis were performed. CNS reached a steady state with anchor size above 200 bp for PE alignment. For SE, anchor length of 100 bp allowed CNS to reach steady state (Figure 1). We observed that this behavior of CNS is dependent on the size of inserts which is typically around 200 bp for M. tuberculosis dataset used by us. This suggests that the length of an anchor should be greater than the insert size for proper PE alignment. Thus, in this study, we have used anchor size of 500 bp which is frequently a threshold of insert size used for bacterial genome sequencing. In the case of 454 sequencing, anchor length can be further increased to facilitate alignment of larger reads while decreasing appropriately the number of anchors. When an assembled reference genome was not available best results were obtained with an anchor length of 75 nucleotides (read length is 51 nucleotides). On increasing read length, assembled anchor region would also increase due to local assembly, reducing number of anchors required for reaching steady state.

Figure 1. Cumulative Normalized Scores computed using anchors of different size as indicated.

Figure 1

Open in a new tab

M. tuberculosis H37Rv was used as a reference genome along with NGS data from isolates AC74 and LN831 for pairwise comparison. Panels A and B are derived from paired end and single end alignments respectively.

Analysis of M. tuberculosis genome

Using reference genome

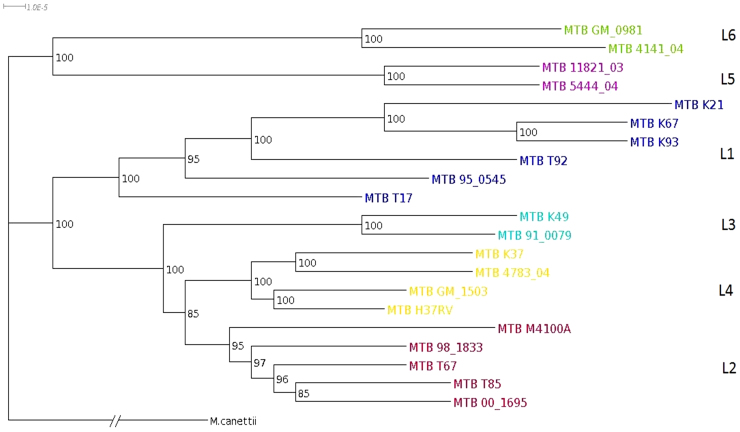
M. tuberculosis is one of the most successful human pathogen in terms of transmission, virulence and drug-resistance. M. tuberculosis complex (MTBC) is believed to undergo a clonal evolution governed mainly by genetic drift. Using molecular markers, such as Single Nucleotide Polymorphism, MTBC could be classified into six major lineages12. We have constructed phylogeny of 21 M. tuberculosis strains from their next generation short sequence reads6 (Figure 2). The tree was rooted with M. canettii. Six different clusters were identified in the tree similar to what has been observed before6,12. These 6 clusters represent 6 major lineages. The East Asia (L2), India-East Africa (L3) and Europe-America-Africa (L4) originated from a common ancestor. The Philippines-Rim of Indian Ocean (L1) and West Africa (L5, L6) are ancient in their origin. High bootstrap values validate the relationships among different M. tuberculosis strains.

Figure 2. NexABP generated phylogenetic tree of M. tuberculosis strains using assembled reference genome M. tuberculosis H37Rv.

Figure 2

Open in a new tab

Six major lineages are represented by different colors. Bootstrap values are shown at nodes. The tree is rooted with M. canettii.

We have used both M. tuberculosis H37RV and M. tuberculosis CDC1551 as reference genomes for generating random anchors (details in method) in this study, both reference genomes gave nearly identical results. It suggests that the distance estimate is independent of the reference genome. To find the effect of slightly distant reference organism on the nature of tree, we carried out an analysis using M. bovis as reference (Supplementary Figure S2). Though, M. bovis is considered to be part of M. tuberculosis complex, it is a different species infecting only bovines. The positions of strains forming L2 and L4 lineages were patchy in this tree. These were not clustered into separate groups, instead encroached the neighboring clusters. For example, MTB M4100A was grouped with strains of L3 lineage, and MTB GM1503, a member of L4 group was found in L2 lineage. In the tree shown in Figure 2, L2 and L4 appear to be monophyletic whereas L4 and L3 lineages are seen to be originated from common ancestor. The variations in the relative position of species and strains in the two trees derived by using different reference strains indicate that M. bovis is not a suitable reference genome for the resolution of evolutionary relationship among the contemporary strains of M. tuberculosis L2 and L4 lineages.

L2 and L4 originated from common ancestor

SNPs can also be used to define evolutionary relationship among organisms. Recently Comas et. al.6 has used 9037 common variable nucleotide positions identified by NGS from 21 strains for phylogeny construction. Since we have also used the same strains for our analysis, we compared the two trees for benchmarking NexABP. The tree generated by NexABP was different in the placement of L3, L2, and L4 lineages from the tree constructed by Comas et al.6, L4 was found to be ancestor to L2 and L3 lineages, in contrast to our observation that L2 and L4 originated from a common ancestor. The AU test significantly supported (p value = 0.920) the interpretation that L2 and L4 have a common ancestor (Supplementary Table S1). Presence of L3 lineage in India and East Africa indicates that the strains may have simultaneously evolved due to migration and trading between these two regions for a long time. M. tuberculosis of L4 and L2 lineages are generally found in Europe-America-Africa and East Asia regions. These lineages may have evolved later in accordance to human migration13.

In absence of reference genome

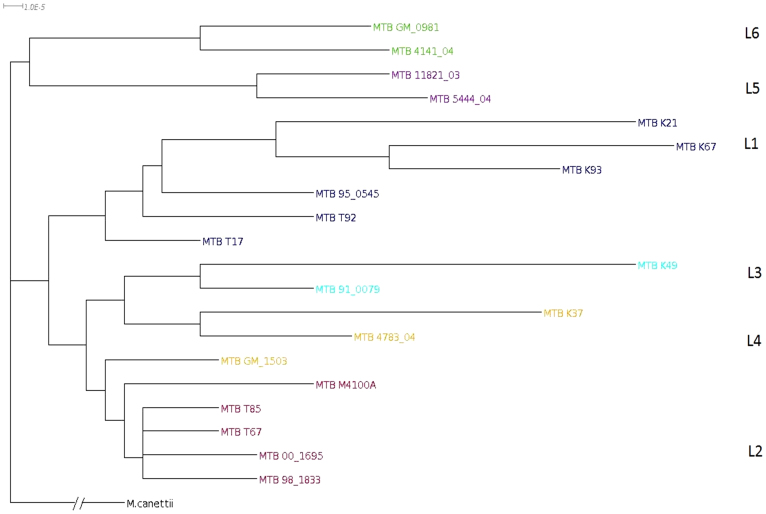
We also constructed phylogeny of M. tuberculosis strains without using assembled reference genome. For this, we first identified a set of strains which can be used as reference genome following an approach described in “Methods”. Randomly picked reads were locally assembled and a consensus sequence was used as an anchor. Typical length of a read and an anchor was ‘51' and ‘75' nucleotides respectively. In this case anchor length is smaller than that extracted from assembled reference genome (100 nucleotides). Therefore, we chose only those strains as references for which the number of anchors were sufficiently large to ensure that CNS reached a steady state (typically 6000). Out of 21 strains under study only 8 namely K21, K49, K37, K67, K93, 00 1695, 5444 04, GM 1503 fulfilled the criteria of being a reference. These strains were used as references to avoid errors caused during the construction of anchors by local assembly. For individual reference CNS was calculated as described before (see Methods). Eight distance matrices were observed for eight references. The tree was constructed from average distance matrix (Figure 3) and the result appeared to be similar to the tree constructed with assembled reference genome. The ancient and contemporary strains were separated out and these further clustered into L1, L2, L3, L4, L5 and L6 lineages.

Figure 3. NexABP generated phylogenetic tree of M. tuberculosis strains without using any reference genome.

Figure 3

Open in a new tab

Analysis of V. cholerae genome

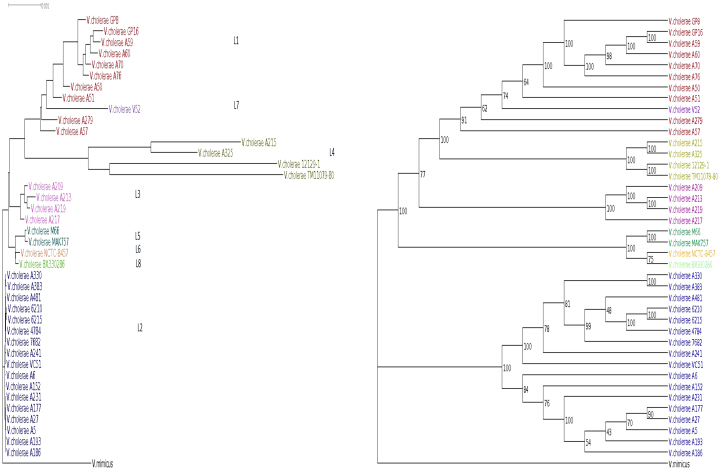
V. cholerae is the etiologic agent of cholera and is endemic in many countries. There are seven known pandemics of V. cholera14. Only strains of O1 sero group (classical and El Tor) and derivative O139 have been known to cause epidemic15. Mutreja et. al.7 sequenced strains representing different lineages and constructed a phylogenetic tree based on SNP. The tree displayed 8 distinct lineages (L1, …, L8). NGS data of 123 El Tor and 19 classical along with other non-O1 strains were used for their study. We used 40 V. cholerae sequence libraries from the same dataset and constructed a phylogenetic tree (Figure 4) utilizing 17 El Tor and 10 classical strains, representing different geographical locations. NGS data was not available for two L4 strains 12129-1, TM11079-80 and L5, L6, L7, L8 strains. Reads were simulated from their available contigs in NCBI and used along with other 33 NGS datasets. V. chlolerae El Tor N16961 and V. mimicus were used as reference and out group genomes respectively. Strains of classical and El Tor belong to clusters L1 and L2 respectively. We observed that the cluster L1 and L2 were distinct in their origin suggesting different origin of these group of strains. Also, distances among the L1 strains are much higher than that observed among L2 strains. L3, L5, L6 and L8 genomes were found to be closer to L2 genomes, suggesting that these genomes are more like El Tor and share a common ancestor as suggested before7. The only exception in NexABP tree is the inclusion of L7 genome among Classical group. This may be due to similar genomic backbone shared with classical strains.

Figure 4. Phylogram and cladogram (with bootstrap values) of V. cholerae strains.

Figure 4

Open in a new tab

Eight different lineages are represented by different colors. The tree is rooted with V. mimicus.

Comparison with Co-phylog and phylogeny of E. coli

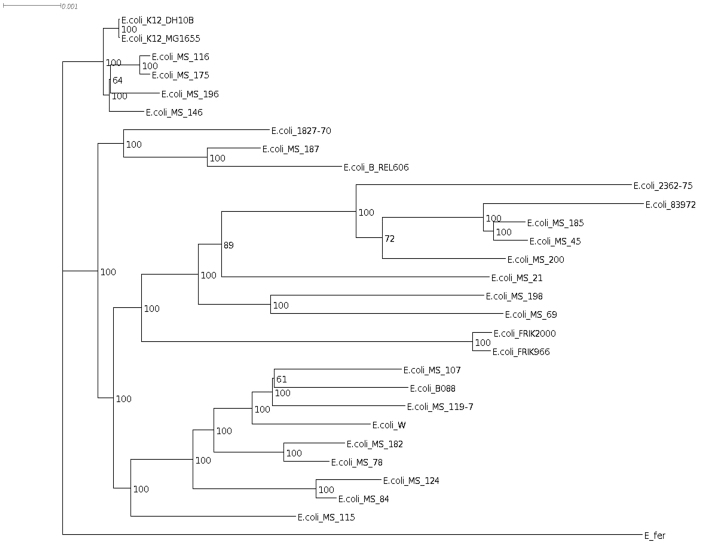
We constructed phylogenetic tree of 29 E. coli strains (Figure 5) originally used in Co-phylog8. Overall grouping of E. coli strains were similar in the two trees (NexABP and Co-phylog). However, the internal nodes were well resolved in the tree constructed by NexABP unlike Co-phylog. For example, internal nodes of leaves representing MS 78, MS 182, MS 119, B088, MS 107 and W (Supplementary Figure S3) were not clearly visible in the Co-phylog tree8 whereas, these were resolved in the NexABP tree. The comparison of internal branch length generated by both methods (Wilcoxon one sided test p value = 0.0134) supported the fact the tree constructed by NexABP was better resolved. In addition to high resolution of internal branches NexABP tree displayed statistical validity as shown by high bootstrap values. Both Co-phylog and NexABP are independent of the NGS platform used for data generation as the data of different E. coli strains used in the study were generated using all the three major platforms (Illumina, Solid and Roche). We also generated Mycobacterial phylogenetic tree (Supplementary Figure S4) using Co-phylog. In contrast to NexABP or Comas et al.6, it didn't place ancient West African strains as an outlier. Position of 98_1333 and K37 are not in concordance with their geographical origin6.

Figure 5. NexABP generated phylogenetic tree of E. coli strains.

Figure 5

Open in a new tab

Bootstrap values are shown at nodes. The tree is rooted with E. fergusonii.

Discussion

It is now recognized that while whole genome information is needed to construct phylogenetic trees and understand evolutionary relationships, one or a few genes may not be suitable for a similar analysis4. A number of methods based on whole genome sequences for phylogenetic tree construction have been developed2,3. However, majority these methods use assembled genome sequences for analysis. Since NGS has become a method of choice for genome sequencing due to low cost and short turn-around time compared to the traditional method, large number of organisms including multiple isolates/strains of different species have been subjected to NGS and the data is available for analysis. Therefore it may be more useful to use NGS data for phylogenetic analysis. However, the ample amount of data generated by NGS and problems during assembly poses major challenges in construction of phylogeny. Recently a method that uses NGS data in phylogeny has been developed (co-phylog8). In this report we describe a new method NexABP which has some features absent in Co-Phylog, such as ability to resolve internal branches of the tree and able to compute statistical validity by bootstrap analysis. The method uses an already described algorithm based on anchors9. We have modified our earlier algorithm for NGS data.

We used an approach in which, neither the assembly of the NGS data is required nor huge size of data act as a hindrance. It has been shown previously that approximately 10% of the whole genome is sufficient to construct the phylogeny from assembled genomes9. Our analysis show that for NGS analysis 20–25% of the data is sufficient, therefore the complexity of the data is reduced to a manageable level. Moreover, the effect of bias in evolutionary rate due to Horizontal Gene Transfer, base composition and differential mutation rate is lowered due to sampling at random positions16.

Phylogeny constructed by any method should give insight about the evolution of organisms under study. We tested NexABP on different strains of M. tuberculosis, V. cholerae and E. coli. The trees constructed by NexABP are well resolved at internal branches with the exception of L2 group of V. cholerae. This is because of lesser number of SNPs present in L2 group genomes as compared to others. The bootstrap values are also very less in that part of the tree for the same reason. The EL Tor strains belong to L2 cluster and are more recent in origin. These strains differ from EL Tor reference genome by 50–250 SNPs7. The clustering of genomes in the tree is similar to that observed by Mutreja et al.7 where they have excluded regions predicted to have undergone recombination whereas the results from NexABP appear to be independent of effects of any recombination event. V. cholerae datasets are of low coverage, thereby displaying the ability of NexABP to work also with low coverage data. Contrary to V. cholerae where geographical differentiation has not been seen, M. tuberculosis strains can be grouped into 6 major lineages pointing their stringent geographical structure12. We not only observed all the known lineages (six) but also inner branches are consistent with ancient (L1, L5, L6) and modern origin (L2, L3, L4). The results are in accordance with classification of strains based on genomic deletion TdD117. Moreover, L5 and L6 lineages representing West African strains are closest to the out group confirming African origin of M. tuberculosis18. Application of NexABP to NGS data of different organisms suggest that this approach is well equipped to handle the complexity of NGS and reveal the underlying biological phenomenon. NexABP overcomes the necessity of assembled reference genome used in alignment based NGS phylogeny6,7. It also resolved internal branches better compared to alignment-free methods8. We believe that availability of methods for deciphering relationship among strains of a species using NGS data may help in understanding some of the important questions, such as evolution of virulence and genetic basis of pathogenecity.

Methods

Our algorithm is based on selection of regions of a genome which we termed as anchors. Here we will briefly describe the selection of anchors from a genome.

Anchor selection in presence of reference genome

Let, T is a reference genome of length ‘K'. We choose a set ‘A' of random anchors which constitute anchors A1, A2, …, Am. An anchor is defined as continuous stretch of nucleotides starting from position ‘i' in the genome T such that,

graphic file with name srep02634-m1.jpg

Where,

graphic file with name srep02634-m2.jpg

Anchor length of 500 bp was selected on the basis of an empirical analysis of various anchor lengths. ‘i' belongs to larger set of random number ‘I' generated by random anchor generator16.

graphic file with name srep02634-m3.jpg

Among i1, i2, i3 …. iN, a set of the random position i1, i2, i3 …. im those fulfill the criteria defined in Vishnoi et al.16 is used for further analysis. This is to ensure that the anchors are non-overlapping. This procedure results in a set of anchors from a reference whole genome.

We want to calculate evolutionary distances for a set of sequence libraries generated by next-generation sequencing. For this, short reads were then aligned with each anchor extracted by the above procedure. Consensus Cj is constructed from the reads aligned to anchor Aj. Consensus was calculated with consensus base ratio 0.9 with minimum read depth of 5 for each position and consensus base should be represented by sequence from both strands of the genome. Otherwise, the same base as the reference was used in the anchor. For all anchors in the reference genome, corresponding consensus were constructed. This was done for each strain under study. For clarity, let us fix notation S1, S2, …, St for the genomes for which the NGS data is to be analyzed. CjSt corresponds to the jth consensus of the tth strain.

Anchor selection in absence of reference genome

The procedure described in the preceding paragraph requires assembled reference genome for anchor selection. The algorithm was modified in a way that non-assembled NGS data can be used. Let say, S1, S2, …, St are unassembled genomes in the form of raw NGS reads. For each of the genome initially a set of random reads are chosen with elimination of duplicated reads (reads representing the same region of the genome). Further, these reads are locally assembled to increase their length. Reads which are >‘s' length are selected for further analysis and constitute a set ‘p' of ‘v' anchors such that pk = {pk1, pk2, …, pkv} where k = {1, 2, …, t}. This whole procedure generated p1, p2, …, pt sets of anchors from S1, S2, …, St genomes. The value of ‘v' varies for each of ‘S', which in turn depends on several factors, such read depth, efficiency of local assembly, which in turn depends largely on error profile and repetitive nature of randomly drawn reads5. Only those pk are used as reference anchors for which the ‘v' is sufficiently large so that the Cumulative Normalized Score described later reaches saturation (data not shown). Pi = {P1, p2, …, pt} was then used a reference anchor set to construct representative consensus anchors for each strain as described in the last section.

Distance calculation

To calculate distance between two strains (genomes), let's say, S1 and S2, the consensus C1S1 of S1 and C1S2 of S2 are aligned. The number of matches and mismatches are calculated based on a binary scheme. A nucleotide match between C1S1 and C1S2 is scored as 0 whereas for mismatch the score is 1. Total sum of these scores normalized over its length is the mismatch score of this consensus pair.

graphic file with name srep02634-m4.jpg

where,

graphic file with name srep02634-m5.jpg

if

graphic file with name srep02634-m6.jpg

C1l is a nucleotide in the consensus C1

For the entire consensus obtained from the anchors in the two genomes under study, the Cumulative Normalized Score (CNS) is given by,

graphic file with name srep02634-m7.jpg

Where, m = Total number of anchors for a reference genome.

When the assembled reference genome is not present there are many sets of unassembled genomes which are used as references genomes. For a pair of genomes, average of CNS calculated for each of these reference genomes is used as a distance measure.

Phylogentic tree construction and bootstrap analysis

Pair wise CNSs were used to construct phylogeny with the help of Neighbour Joining method11. Bootstrap analysis10 was performed to calculate confidence score of the generated phylogenetic tree. CNS between two sequence libraries was calculated using “m” anchors. “m” anchors were re-sampled with substitution from all anchors to calculate CNS and construction of phylogenetic tree. This analysis was performed 1000 times for each tree. Consensus tree was then constructed by majority rule. Bootstrap values were transformed into percentage values. High value in a node, represent high confidence of occurrence of that node in the tree (indicated).

Comparison of tree topology

AU (Approximately unbiased) nonparametric test was performed to compare alternative tree topology hypotheses19. Tree topologies generated by earlier studies and NexABP were compared. First, the branches were swapped around a common backbone by TreeView20 to generate an alternative topology. The site-wise log-liklihood values were estimated by Tree Puzzle21 for each of the tree topologies. These values were fed into CONSEL22 which performs AU nonparametric test.

Softwares

Bowtie23 and Bowtie224 were used to align short reads with the anchors. Samtools25 was used to parse alignment data. Removal of overlapping reads from the random set of reads and local assembly of reads were performed by BLAST26 and CAP327. These modules were used as a part of the PERL script responsible for the entire computation from anchor selection to CNS calculation. Phylogenetic trees were constructed using Phylip28 and visualized using Dendroscope29. Short reads were simulated using MAQ30.

Availability

The set of programs which constitute NexABP and detailed instruction of their use can obtained from the corresponding author on request (alok.bhattacharya@gmail.com).

Datasets

Short read NGS data of 20 M. tuberculosis, 27 E. coli and 33 V. cholerae genomes were used for this study. We have downloaded these freely available datasets from European Nucleotide Archive (www.ebi.ac.uk/ena/). Accession numbers of these sequence libraries are given in Supplementary dataset 1.

Author Contributions

A.B., T.R. and A.V. conceptualized the study. T.R. performed the computational work. A.B., T.R. and A.V. wrote the manuscript. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep02634-s1.pdf (446.1KB, pdf)
Supplementary Information

Dataset 1

srep02634-s2.xls (25KB, xls)

Acknowledgments

The authors thank Department of Biotechnology, Government of India for financial support (AB, AV), Department of Science and Technology, Government of India for J.C. Bose fellowship (AB).

References

  1. Mardis E. R. Next-generation DNA sequencing methods. Annu Rev Genomics Hum Genet 9, 387–402 (2008). [DOI] [PubMed] [Google Scholar]
  2. Snel B., Bork P. & Huynen M. A. Genome phylogeny based on gene content. Nat Genet 21, 108–10 (1999). [DOI] [PubMed] [Google Scholar]
  3. Fitz-Gibbon S. T. & House C. H. Whole genome-based phylogenetic analysis of free-living microorganisms. Nucleic Acids Res 27, 4218–22 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Stine O. C. et al. Phylogeny of Vibrio cholerae based on recA sequence. Infect Immun 68, 7180–5 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Baker M. De novo genome assembly: what every biologist should know. Nat Meth 9, 333–337 (2012). [Google Scholar]
  6. Comas I. et al. Human T cell epitopes of Mycobacterium tuberculosis are evolutionarily hyperconserved. Nat Genet 42, 498–503 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Mutreja A. et al. Evidence for several waves of global transmission in the seventh cholera pandemic. Nature 477, 462–5 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Yi H. & Jin L. Co-phylog: an assembly-free phylogenomic approach for closely related organisms. Nucleic Acids Res (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Vishnoi A., Roy R., Prasad H. K. & Bhattacharya A. Anchor-based whole genome phylogeny (ABWGP): a tool for inferring evolutionary relationship among closely related microorganisms [corrected]. PLoS One 5, e14159 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Efron B. Bootstrap Methods: Another Look at the Jackknife. The Annals of Statistics 7, 1–26 (1979). [Google Scholar]
  11. Saitou N. & Nei M. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol Biol Evol 4, 406–25 (1987). [DOI] [PubMed] [Google Scholar]
  12. Comas I. & Gagneux S. The past and future of tuberculosis research. PLoS Pathog 5, e1000600 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gagneux S. et al. Variable host-pathogen compatibility in Mycobacterium tuberculosis. Proc Natl Acad Sci U S A 103, 2869–73 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Chin C. S. et al. The origin of the Haitian cholera outbreak strain. N Engl J Med 364, 33–42 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Chun J. et al. Comparative genomics reveals mechanism for short-term and long-term clonal transitions in pandemic Vibrio cholerae. Proc Natl Acad Sci U S A 106, 15442–7 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Vishnoi A., Roy R. & Bhattacharya A. Comparative analysis of bacterial genomes: identification of divergent regions in mycobacterial strains using an anchor-based approach. Nucleic Acids Res 35, 3654–67 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Brosch R. et al. A new evolutionary scenario for the Mycobacterium tuberculosis complex. Proc Natl Acad Sci U S A 99, 3684–9 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hershberg R. et al. High functional diversity in Mycobacterium tuberculosis driven by genetic drift and human demography. PLoS Biol 6, e311 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zhang Y. J., Tian H. F. & Wen J. F. The evolution of YidC/Oxa/Alb3 family in the three domains of life: a phylogenomic analysis. BMC Evol Biol 9, 137 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Page R. D. Visualizing phylogenetic trees using TreeView. Curr Protoc Bioinformatics Chapter 6, Unit 6 2 (2002). [DOI] [PubMed] [Google Scholar]
  21. Schmidt H. A., Strimmer K., Vingron M. & von Haeseler A. TREE-PUZZLE: maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics 18, 502–4 (2002). [DOI] [PubMed] [Google Scholar]
  22. Shimodaira H. & Hasegawa M. CONSEL: for assessing the confidence of phylogenetic tree selection. Bioinformatics 17, 1246–7 (2001). [DOI] [PubMed] [Google Scholar]
  23. Langmead B., Trapnell C., Pop M. & Salzberg S. L. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol 10, R25 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Langmead B. & Salzberg S. L. Fast gapped-read alignment with Bowtie 2. Nat Methods 9, 357–9 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Li H. et al. The Sequence Alignment/Map format and SAMtools. Bioinformatics 25, 2078–9 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Altschul S. F. et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res 25, 3389–402 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Huang X. & Madan A. CAP3: A DNA sequence assembly program. Genome Res 9, 868–77 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Felsenstein J. PHYLIP - phylogeny inference package (version 3.2). Cladistics 5, 164–166 (1989). [Google Scholar]
  29. Huson D. H. et al. Dendroscope: An interactive viewer for large phylogenetic trees. BMC Bioinformatics 8, 460 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Li H., Ruan J. & Durbin R. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res 18, 1851–8 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Das S. et al. Genetic heterogeneity revealed by sequence analysis of Mycobacterium tuberculosis isolates from extra-pulmonary tuberculosis patients. BMC Genomics 14, 404 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep02634-s1.pdf (446.1KB, pdf)
Supplementary Information

Dataset 1

srep02634-s2.xls (25KB, xls)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES