Abstract
Many aspects of cell physiology are controlled by protein kinases and phosphatases, which together determine the phosphorylation state of targeted substrates. Some of these target proteins are themselves kinases or phosphatases or other components of a regulatory network characterized by feedback and feed-forward loops. In this review we describe some common regulatory motifs involving kinases, phosphatases, and their substrates, focusing particularly on bistable switches involved in cellular decision processes. These general principles are applied to cell cycle transitions, with special emphasis on the roles of regulated phosphatases in orchestrating progression from one phase to the next of the DNA replication-division cycle.
Introduction
The growth, development, survival, and repair of living organisms depend largely on the ability of individual cells to receive signals, to determine the appropriate response to this information, and to carry out the required actions. Possible responses include cell growth and division, differentiation, movement, protein and hormone secretion, and cell death. This intracellular system for processing information, making decisions, and taking action is carried by complex networks of interacting genes and proteins [1]. Molecular biologists, empowered by the genomics revolution, have been spectacularly successful in identifying the components and pair-wise interactions of these molecular regulatory networks (see Cell, Vol. 100, Issue 1). But the physiological consequences of these interactions are systems-level, dynamic properties of complex networks [2]; properties that are rarely evident from the local or global connectivity of interaction graphs. A major challenge of molecular systems biology is to identify the fundamental dynamic principles that bind the cell’s information processing abilities to its underlying biochemical components and interactions.
Proteins are the primary agents of these regulatory networks. They receive the incoming signals, and the information is represented and processed in terms of fluctuating abundances of specific proteins and changing activities of enzymes and multimeric protein complexes. These signal processing proteins determine the nature of the response: transcription factors control gene expression, motor proteins control cell movement, biosynthetic enzymes determine cell growth and secretions, proteases enable recycling and programmed cell death, and protein kinases and phosphatases control many complex physiological responses, such as the cell division cycle and circadian rhythms.
The effects of a protein are influenced by its abundance, its binding partners, and its covalent modifications. The abundance of a protein is determined by the balance between its synthesis and degradation. Because the rates of synthesis and degradation of any given protein may depend on the abundances and activities of many other proteins, the steady-state level of every protein must be determined simultaneously with the levels of all other proteins in the network. Regulatory proteins rarely act in isolation but are usually part of multimeric protein complexes, with partners that may either activate or inactivate the effector protein. The abundances of such complexes depend on the local concentrations of their constituent proteins and on the binding propensities of the partners. The ability of an enzyme to catalyze a reaction or of a binding partner to enter into a complex can be altered by a panoply of post-translational, covalent modifications: phosphorylation, acetylation, ubiquitinylation, and so on.
In this review, we focus on the effects of protein phosphorylation and dephosphorylation, because phosphoproteins are common regulatory components in a variety of cell decision processes. Because the phosphate group (-O- PO32−) carries a large negative charge at neutral pH, phosphorylation of neutral amino acids (serine, threonine, and tyrosine) may cause significant conformational changes of a folded protein. Furthermore, protein phosphorylation can be done rapidly and is readily reversible, and each cycle is energetically inexpensive (one ATP hydrolyzed per cycle of phosphorylation and dephosphorylation). By contrast, modulating the abundance of a protein by alternating phases of synthesis and degradation is slow and expensive. Changing the makeup of protein complexes can be done rapidly, reversibly, and cheaply, but the breakup and reassembly of complexes is often driven by phosphorylation or dephosphorylation of its components. Similarly, protein synthesis and degradation is often controlled by phosphorylation or dephosphorylation of transcription factors and of proteolytic enzyme complexes. For all these reasons, we focus our review on regulation of protein kinases and phosphatases.
The regulation of protein kinases is a classical theme in molecular biology, especially in the field of cell cycle control by cyclin-dependent kinase (CDK). In recent years, however, the roles of regulated protein phosphatases have become more evident [3–5], and it is time, we believe, to summarize the dynamic consequences of the interplay between protein kinases and phosphatases in cell decision-making. In keeping with the theme of this issue, we illustrate general regulatory principles with specific examples in the control of DNA synthesis and mitosis during the eukaryotic cell cycle.
Reversible phosphorylation of protein substrates
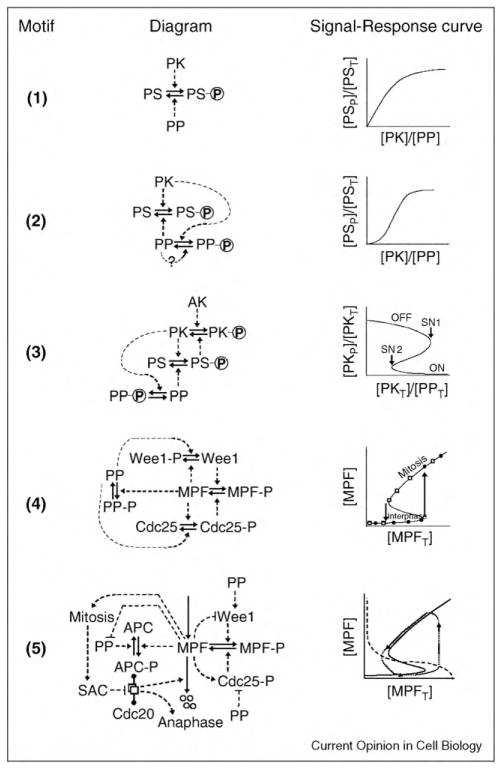
We begin with a simple motif (#1 in Figure 1) whereby a protein kinase (PK) phosphorylates a protein substrate (PS), and the phosphate group can be removed by a protein phosphatase (PP). Plotting the fraction f of phosphorylated substrate (the ‘response’) versus the PK:PP ratio (the ‘signal’) in Figure 1, we see that the signal–response curve for motif #1 changes smoothly from f = 0 to f = 1 as the PK:PP ratio increases, which is the typical characteristic of a rheostat. (See Supplementary Material S1 for how motifs are modeled mathematically.) In some circumstances, a rheostat may be what is needed, but this motif is disadvantaged by considerable futile cycling (pointless ATP hydrolysis) as PS is shuttled back and forth between its phosphorylated and dephosphorylated forms. Futile cycling could be reduced by decreasing the rates of phosphorylation and dephosphorylation, but then the rheostat would become sluggish in its response to changing signal strength.
Figure 1.
Regulatory motifs. In each motif, a solid arrow indicates a chemical reaction, and a dashed arrow indicates an enzyme that catalyzes the reaction. (1) The basic motif. A protein substrate (PS) is phosphorylated by a protein kinase (PK) and dephosphorylated by a protein phosphatase (PP). The incoming ‘signal’ is the ratio of PK activity to PP activity; and the response is the fraction of PS in the phosphorylated form. The response saturates at f = 1 for large values of the PK:PP ratio. [PST] = [PS] + [PSP] = total concentration of the substrate. (2) Coherent feed-forward loop. PK phosphorylates and inactivates PP. The active form of PP may promote its own accumulation by auto-dephosphorylation (the dotted feedback signal marked with a ‘?’). The signal–response curve is now sigmoidal. (3) Positive feedback loop. The protein substrate of motif #2 is now a phosphatase that activates PK by reversing an inhibitory phosphorylation carried out by the ‘antagonistic kinase’ (AK). In this case, the response variable, the fraction of PK in the phosphorylated form, corresponds to the low-activity state of PK. The signal–response curve shows a region of bistability between the points marked SN1 and SN2. (4) Bistability in the activation of MPF. MPF (mitosis promoting factor) is a heterodimer of cyclin B and Cdk1. Wee1 phosphorylates MPF on an inhibitory residue of the Cdk1 subunit. Cdc25 removes the inhibitory phosphate group. PP2A is the phosphatase that opposes the phosphorylation of Wee1 and Cdc25 by MPF. In the signal–response curve, [MPFT] = [MPF] + [MPFP] = total MPF = total concentration of cyclin B, because the Cdk1 subunit is present in excess and free Cdk1 molecules have no kinase activity. The signal–response curve shows a robust region of bistability for intermediate levels of total cyclin B. (5) Negative feedback and oscillations. The positive feedback loops of motif #4 are supplemented by a negative feedback loop, whereby MPF activates the APC/Cdc20 complex, which initiates the proteolysis of cyclin B. The dashed lines from MPF to Wee1, Cdc25, and so on, indicate that MPF has an effect (activation or inhibition) on the target protein, without specifying the precise molecular mechanism of this effect. This is a shorthand convention to simplify the diagram, and the mechanism of the effect can be deduced from previously described motifs. The ‘dumbbell’ notation indicates the reversible formation of a complex between proteins A and B at the ends of the dumbbell, and an icon for the complex (overlapping white rectangles) is placed on the middle of the dumbbell. Four small circles indicate degradation products of a protein. On the signal–response plane, there is no stable steady state, and the system executes periodic oscillations around the trajectory indicated by the dotted line.
A better way to reduce futile cycling is for PK to inhibit PP (motif #2 in Figure 1). This motif (called a coherent feed-forward loop) ensures that PK and PP are not fully active at the same time. It might be objected that this motif simply displaces the futile-cycle problem from PS to PP, but, since a single PK–PP pair is likely to regulate dozens of substrates, the downregulation of PP by PK will significantly reduce the sum total of futile cycling. Coherent feed-forward loops have additional advantages: they suppress noisy fluctuations in the input signal [6], and they generate a sigmoidal signal–response curve, which helps the motif to make more definitive decisions.
There is abundant evidence that coherent feed-forward loops regulate phosphoproteins of the cell cycle. The retinoblastoma protein was possibly the first CDK substrate discovered to be dephosphorylated by a phosphatase (PP1) that is inhibited by CDK phosphorylation [7,8]. Recently PP1 has been identified as one of the major enzymes that dephosphorylate proteins targeted by CDK in Xenopus extracts [9••]. In addition, PP2A, which opposes CDK phosphorylation of Wee1 and Cdc25, appears to be downregulated by CDK activity in Xenopus extracts [10]. Recent data support this notion [11,12••] and suggest that the inactivation of PP2A by CDK is mediated by a different kinase, called Gwl (‘greatwall’) [13••,14••,15,16••]. In fission yeast, a Cdk-counteracting phosphatase Clp1 (also known as Flp1), which is orthologous to Cdc14 of budding yeast, is inhibited by CDK-dependent phosphorylation [17].
Positive feedback and bistable switches
Proper progression through the cell cycle (G1—S/G2—M—G1—…) requires that the transitions from G1 to S/G2, from S/G2 to M, and from M to G1 be ‘irreversible’ in the sense that they not slip back to the earlier state in the face of inevitable fluctuations in the driving signal. A sigmoidal signal–response curve, as for motif #2, can make a clean distinction between two states (f ≈ 0 or f ≈ 1), but it is subject to ‘chatter’ (flipping back and forth between these two states) if the signal fluctuates in the vicinity of the switching point. The best way to implement a clean, irreversible decision between two states is with a bistable signal–response curve, which can be achieved by incorporating positive feedback into the control circuit. For example, in motif #3, we imagine that the substrate of PK is a phosphatase that reverses the inhibitory phosphorylation of PK by an ‘antagonistic kinase,’ AK. (We have in mind here the situation in frog embryos, where PK = CDK, AK = Wee1, PS = Cdc25 and PP = PP2A.) If the phosphorylated form of PS is the more active phosphatase, then PS and PK are involved in a dynamic positive feedback loop. For this case, the signal–response curve shows a region of signal strengths (the ratio of total concentrations of PK and PP) for which the positive feedback loop can exist in either of two stable steady states: the OFF state (PK phosphorylated and inactive) and the ON state (PK unphosphorylated and active). The two stable steady states (‘nodes’) are separated by an unstable steady state (‘saddle point’) with intermediate activity of PK. At low signal strength, PK is phosphorylated and the switch is OFF. As the signal increases, the ON state suddenly appears (at SN2), but the control system remains in the OFF state until the signal increases beyond SN1. Beyond SN1 the system switches ON, and this transition is irreversible, in the sense that, once the ON state is established, the switch will remain ON even if the signal strength drops considerably. To turn the switch OFF, the signal must drop below SN2. The points (SN1 and SN2) where the behavior of the dynamical system undergoes a dramatic change are called ‘bifurcation’ points (in this case, ‘saddle-node’ bifurcation points). At an SN bifurcation, two steady states (a saddle and a node) coalesce and annihilate one another, and the dynamical system must leave the vicinity of the now-missing stable node and proceed to some other attractor (in this case, the other stable node).
In principle, there are more direct ways to build positive feedback into motif #2: PP might activate itself by auto-dephosphorylation (see the dotted line, marked with a ?, in Figure 1), or PK might activate itself by autophosphorylation. Although these feedback effects can increase the sensitivity of the sigmoidal signal–response curve, they do not of themselves create a bistable response (see Supplementary Material S1).
Most substrates of CDK are phosphorylated on multiple sites, and progressive phosphorylation of these substrates can create ultrasensitive sigmoidal response curves [18]. If the sites are phosphorylated in a preferential order, then it could be that the phosphorylation of some sites are activatory and of others are inhibitory (mixed-mode regulation) [19]. In Supplementary Material S2, we present a model of mixed-mode regulation of Wee1, which nicely fits the data in a recent paper from Kirschner’s group [20].
Bistability and irreversible cell cycle transitions
Bistability, as an organizing principle of irreversible cell cycle transitions, was first proposed by Novak and Tyson [21] and has since been discussed by many authors [22–26]. In the context of cell cycle control, the first and clearest example of bistable switching is the Cdc25–MPF–Wee1 system diagrammed in Figure 1, motif #4. (Notice that AK and PK in motif #3 are now involved in a double-negative feedback loop.) This motif, with two reinforcing positive feedback loops, creates a robust bistable switch, which flips itself ON (interphase → mitosis) when the total MPF concentration, [MPFT] = [MPF] + [MPFP], exceeds the SN bifurcation point in the signal–response curve (Figure 1, row 4). The abrupt activation of MPF beyond this point was first observed by Solomon et al. [27], whose experiment is represented schematically by the black circles on the signal–response curve. Novak and Tyson (1993) predicted that, if [MPFT] were gradually decreased, MPF would be inactivated along an entirely different trajectory (the open squares on the signal–response curve). This prediction was confirmed independently by Sha et al. [28] and Pomerening et al. [29].
Negative feedbacks and exit from mitosis
A cell enters into mitosis (the S/G2—M transition) by activating MPF along the path of black circles on the signal–response curve of motif #4. MPF-mediated phosphorylation of many mitotic phosphoproteins [30,31] causes chromosome condensation, mitotic spindle formation, and bipolar attachment of replicated chromosomes to the spindle. Exit from mitosis (the M—G1 transition) involves activation of the Anaphase Promoting Complex (APC; also known as the cyclosome). MPF activates the APC by phosphorylation [32,33], but the spindle assembly checkpoint (SAC) inhibits a crucial component (Cdc20) of the APC [34], see motif #5. When all replicated chromosomes are properly aligned on the mitotic spindle and the SAC is lifted, APC/Cdc20 initiates a series of events that lead to nuclear and cell division. During mitotic exit, MPF-counteracting phosphatases reverse the phosphorylation events that were carried out by MPF during entry into mitosis. APC/Cdc20 promotes this wave of dephosphorylation by degrading the cyclin B subunit of MPF [35,36]. If MPF is an inhibitor of PP (as in motif #5), then APC-mediated downregulation of MPF also promotes activation of its counteracting phosphatase.
Motif #5 provides a good account of cell cycle regulation in early frog embryos and in frog egg extracts [21]. In particular, this model predicts the existence of oscillations (see the signal–response curve for motif #5 and the simulations in Supplementary Material S3), which has been confirmed by elegant experiments of Pomerening et al. [37]. If Motif #5 is supplemented with a mechanism for size control, mediated by the interplay of Wee1 and Cdc25 [38,39], then it can account successfully for cell cycle progression in fission yeast, not only the characteristics of wild-type cells but also the unusual phenotypes of cells mutated at the wee1 and cdc25 loci [40]. Motif #5 is also consistent with experiments on proteasome-inhibited mammalian cells that have been arrested in meta-phase then induced to exit from mitosis by inhibition of CDK activity by a drug (flavopiridol) [41•,42]. Under these conditions, MPF inhibition, in the absence of cyclin degradation, triggered all events of mitotic exit, possibly as a consequence of PP activation [43] followed by inhibitory phosphorylation of MPF by Wee1 [41•].
G1 stabilizers and exit phosphatases
Some of the proteins that are dephosphorylated and activated as a cell exits mitosis have profound negative effects on CDK activity and thereby stabilize G1 phase of the cell cycle (when CDK activity is very low). These proteins, which remain dephosphorylated and active throughout G1 phase, include
Repressors of cyclin transcription.
Stoichiometric inhibitors (CKIs) of Cdk/cyclin complexes.
Cdh1, an activator of APC, which promotes cyclin degradation in G1.
All three G1 stabilizers are involved in positive feedback loops (Figure 2) that have the potential to create bistability between a G1 state (G1-stabilizers active, CDK inactive) and an S/G2/M state (G1-stabilizers inactive, CDK active). These positive feedbacks rather than cyclin destruction make exit from mitosis irreversible [44,45•].
Figure 2.
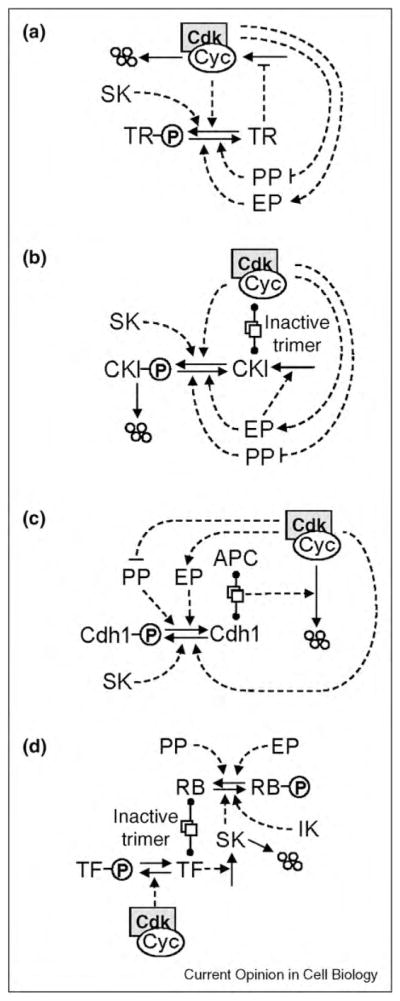
G1-stabilizing motifs. In each case, CDK is involved in a double-negative feedback loop with a protein that stabilizes the G1 state of the cell cycle. (a) A transcriptional repressor (TR) mediates against expression of the cyclin gene. (b) The CDK inhibitor (CKI) binds to and inactivates cyclin/ CDK dimers. (c) Cdh1, an APC partner, assists in the proteolysis of cyclin proteins. In each case, the exit phosphatase (EP) activates the G1 stabilizers, and the starter kinase (SK) promotes inactivation of the G1 stabilizers. (d) Expression of the starter kinase gene is regulated by a transcriptional inhibitor, RB (retinoblastoma-like protein). Initial production of SK requires phosphorylation of RB by an initiator kinase (IK), but thereafter SK can keep RB phosphorylated and inactive. Later in the cell cycle, the transcription factor for SK is inactivated by phosphorylation by cyclin B-dependent kinase.
In the previous section, we attributed mitotic exit to APC-mediated degradation of cyclin and consequential activation of PP. Another possibility is that APC promotes the degradation of a phosphatase-inhibitor other than cyclin/CDK. In this case, phosphatase activation and cyclin degradation could occur in the opposite order, because cyclin destruction might happen only after Cdh1 is dephosphorylated and activated. The paradigm of this scenario is budding yeast, where APC/Cdc20 induces activation of an ‘exit phosphatase’ (EP; called Cdc14 in budding yeast), which then activates Cdh1, CKI, and/or TR (Figure 2), thereby extinguishing CDK activity and establishing the cell in G1. In budding yeast most of the destruction of mitotic cyclins is caused by Cdh1 rather than Cdc20, and, in a particular mutant strain (cdc20Δ pds1Δ clb5Δ), the activation of Cdc14 precedes the destruction of any mitotic cyclin, which is solely dependent on APC/Cdh1 [36,46]. Some experiments with mammalian cells resemble the situation in budding yeast. In metaphase-arrested, proteasome-inhibited mammalian cells, downregulation of MPF activity by roscovitin did not induce mitotic exit [47•], suggesting that exit phosphatase(s) are not active in mitosis and cannot be activated by MPF inhibition. Presumably mitotic exit in these experiments requires APC-mediated activation of EP, similar to the case of budding yeast.
The G1–S transition
To complete the cycle, a cell must leave G1 and enter S/ G2/M phase (DNA replication and nuclear division). This transition is initiated, not surprisingly, by transiently upregulating a ‘starter’ kinase (SK) that inactivates one or more of the G1 stabilizers as indicated in Figure 2. Production of SK requires an ‘initiator’ kinase (IK in Figure 2d) that helps to inactivate an inhibitor of the transcription factor for SK. (In mammalian cells, SK is cyclin E-dependent and cyclin A-dependent kinase, IK is cyclin D-dependent kinase, the inhibitor is the retinoblastoma protein, and the transcription factor is E2F.) In addition to initiating DNA replication, rising levels of SK dispose of CKI (Figure 2b) and inactivate Cdh1 (Figure 2c) so that MPF can make a comeback.
Summing up
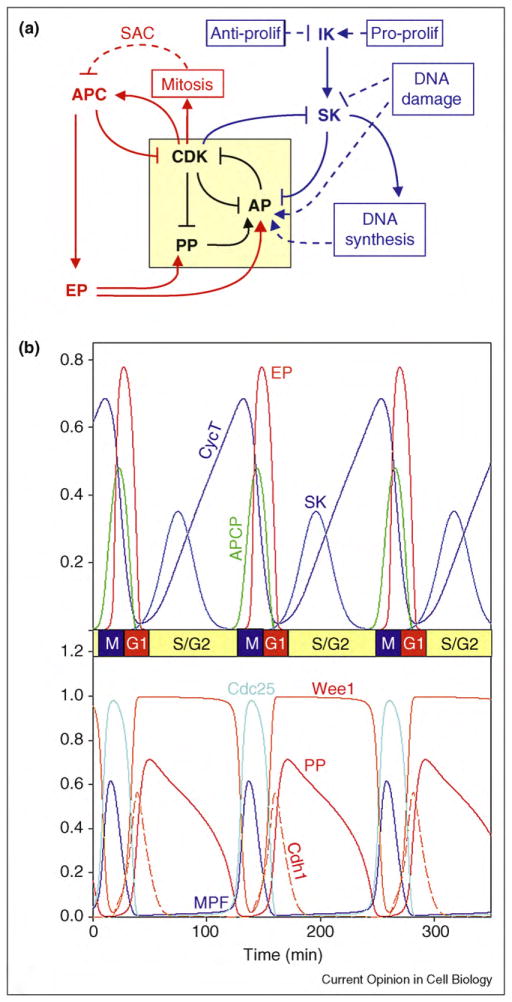
Based on these considerations, we propose in Figure 3a a general framework for viewing regulation of the eukaryotic cell cycle, based on a fundamental antagonism between cyclin B-dependent kinase and its counteracting phosphatase: cyclinB/CDK phosphorylates and inactivates PP, whereas PP dephosphorylates and activates antagonistic proteins (AP = Cdh1, CKI, and Wee1) that extinguish cyclin B/CDK activity. The double-negative feedback loops evident in the yellow box in Figure 3a create alternative stable steady states: a G1 state (PP and all APs active, cyclin B low, no CDK activity), an S/G2 state (Cdh1 and CKI inactive, PP active and Wee 1 active, cyclin B rising, MPF activity low), and an M state (PP and all APs inactive, MPF activity high). In G1, the phosphoprotein substrates of CDK are unphosphorylated, and in S/G2/M, they are phosphorylated (which activates proteins involved in DNA synthesis and mitosis). Flipping the switch from G1 to S/G2 is the job of starter kinases (SK) that are transiently activated at the G1—S transition. Flipping the switch back to G1 is the job of exit phosphatases (EP) that are transiently activated at the M—G1 transition. The G2—M transition is driven by the steadily increasing level of cyclin B in G2 phase, as explained in motif #4. In Figure 3b we show a simulation of this generic picture, based on a mathematical model described in Supplementary Material S4. The simulation confirms the sequence of events during a ‘generic’ eukaryotic cell cycle, as envisioned in this review.
Figure 3.
General framework for cell cycle regulation by protein kinases and phosphatases. (a) Wiring diagram. The yellow box highlights the central toggle switch created by the ‘battle’ between CDK (cyclin B-dependent kinase) on one side and PP (protein phosphatase) and AP (antagonistic proteins) on the other side. In G1 phase, PP and AP are winning the battle, and CDK activity is low. The G1—S transition is promoted by an initiator kinase (IK) that upregulates a starter kinase SK. SK initiates DNA synthesis and downregulates AP. Rising activity of CDK drives the cell into mitosis and promotes mitotic-exit functions of the APC: degradation of cohesins, of cyclin B, and of an inhibitor of the exit phosphatase (EP). EP promotes return to G1 phase by activating PP and AP. Checkpoint signals are indicated by dashed lines. DNA synthesis delays progression into mitosis by activating an AP (Wee1). The spindle assembly checkpoint (SAC) delays exit from mitosis by inhibiting a component of APC (namely, Cdc20). Pro-proliferative and anti-proliferative signals determine whether a cell will start a new round of DNA replication and cell division by regulating the level of IK. DNA damage prevents DNA replication by inhibiting SK, and it prevents entry into mitosis by activating AP (Wee1 and CKI). (b) Numerical simulation. We convert scheme A into a set of nonlinear ordinary differential equations and compute an oscillatory solution for a reasonable choice of kinetic parameter values (for details, see Supplementary Material S4).
The actual sequence of events in any specific type of eukaryotic cell will depend, of course, on how the generic control elements are actually wired together. As we have emphasized, there are alternative ways to establish the basic phases of the cell cycle (G1, S, G2, and M) and trigger the transitions between them. But we propose that, in all cases, the same fundamental dynamic principles are at work. Alternative stable states of the control network are established by positive (or double-negative) feedback loops, regions of bistability are bounded by saddle-node bifurcation points; transitions between stable states are driven by negative feedback loops that transiently activate a kinase or a phosphatase that pushes the control system past a saddle-node bifurcation and then subsides to its basal level.
The eukaryotic cell cycle is only one example of cellular decision-making based on reversible phosphorylation and dephosphorylation of proteins. The MAP kinase signaling pathway provides another famous example [48], and also the generation of circadian rhythms in fruit flies, bread molds, flowering plants, and cyanobacteria [49]. Of course, not all cellular decision-making is based on protein phosphorylation. For example, gene expression is controlled by the formation of large complexes of activators and inhibitors on the promoter regions of genes, and protein phosphorylation may play little or no role in the assembly and disassembly of these complexes. Similarly, the commitment to programmed cell death is made by the formation and dissolution of protein complexes among BH3-families, BCL2-families, and BAX-families of proteins [50], with no significant role played by protein phosphorylation. Nonetheless, the same sorts of dynamical motifs are involved in all cases, whether or not the protein–protein interactions are implemented by phosphorylation and dephosphorylation or by some other molecular mechanism.
Evolutionary Scenario.
The ‘general framework’ in Figure 3a suggests a scenario for the evolutionary origins of the eukaryotic cell cycle control system. Initially, CDK may have been part of a protein kinase signaling pathway in a protoeukaryote. It is well known that the catalytic subunit of CDK requires an activatory phosphorylation of the T-loop of its ATP binding site [51]. This phosphate group is put on by Cdk-activating kinase (CAK) and removed by a phosphatase [52,53] that we propose to be a forerunner of PP. We imagine that CDK evolved the capacity to phosphorylate and inactivate PP (motif #6), thereby creating a double-negative feedback loop, that is, a toggle switch, that could have been advantageous in controlling the phosphorylation of CDK’s substrates (PS).
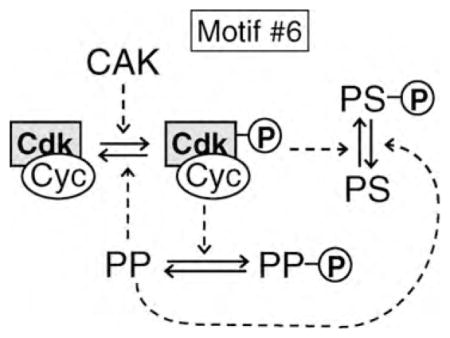
By transferring PP’s role to dephosphorylating PS rather than CDK, the protoeukaryote would have evolved motif #2 in Figure 1. The final step would then have been to transfer the double-negative feedback loop from CDK—PP to CDK—PS, to obtain motif #3 in Figure 1, which is identical to the highlighted box in Figure 3.
Supplementary Material
Appendix A. Supplementary data
Supplementary data associated with this article can be found, in the online version, at doi:10.1016/j.ceb.2010. 07.001.
References and recommended reading
- 1.Bray D. Protein molecules as computational elements in living cells. Nature. 1995;376:307–312. doi: 10.1038/376307a0. [DOI] [PubMed] [Google Scholar]
- 2.Tyson JJ, Chen K, Novak B. Network dynamics and cell physiology. Nat Rev Mol Cell Biol. 2001;2:908–916. doi: 10.1038/35103078. [DOI] [PubMed] [Google Scholar]
- 3.Bollen M, Gerlich DW, Lesage B. Mitotic phosphatases: from entry guards to exit guides. Trends Cell Biol. 2009;19:531–541. doi: 10.1016/j.tcb.2009.06.005. [DOI] [PubMed] [Google Scholar]
- 4.De Wulf P, Montani F, Visintin R. Protein phosphatases take the mitotic stage. Curr Opin Cell Biol. 2009;21:806–815. doi: 10.1016/j.ceb.2009.08.003. [DOI] [PubMed] [Google Scholar]
- 5.Queralt E, Uhlmann F. Cdk-counteracting phosphatases unlock mitotic exit. Curr Opin Cell Biol. 2008;20:661–668. doi: 10.1016/j.ceb.2008.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mangan S, Alon U. Structure and function of the feed-forward loop network motif. Proc Natl Acad Sci USA. 2003;100:11980–11985. doi: 10.1073/pnas.2133841100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dohadwala M, da Cruz e Silva EF, Hall FL, Williams RT, Carbonaro-Hall DA, Nairn AC, Greengard P, Berndt N. Phosphorylation and inactivation of protein phosphatase 1 by cyclin-dependent kinases. Proc Natl Acad Sci USA. 1994;91:6408–6412. doi: 10.1073/pnas.91.14.6408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu CW, Wang RH, Dohadwala M, Schonthal AH, Villa-Moruzzi E, Berndt N. Inhibitory phosphorylation of PP1alpha catalytic subunit during the G(1)/S transition. J Biol Chem. 1999;274:29470–29475. doi: 10.1074/jbc.274.41.29470. [DOI] [PubMed] [Google Scholar]
- 9••.Wu JQ, Guo JY, Tang W, Yang CS, Freel CD, Chen C, Nairn AC, Kornbluth S. PP1-mediated dephosphorylation of phosphoproteins at mitotic exit is controlled by inhibitor-1 and PP1 phosphorylation. Nat Cell Biol. 2009;11:644–651. doi: 10.1038/ncb1871. The authors identify PP1 as a major mitotic exit phosphatase in Xenopus extracts. During mitosis PP1 is inhibited by inhibitor-1 and Cdk-mediated phosphorylation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Clarke PR, Hoffmann I, Draetta G, Karsenti E. Dephosphorylation of cdc25-C by a type-2A protein phosphatase: specific regulation during the cell cycle in Xenopus egg extracts. Mol Biol Cell. 1993;4:397–411. doi: 10.1091/mbc.4.4.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mochida S, Hunt T. Calcineurin is required to release Xenopus egg extracts from meiotic M phase. Nature. 2007;449:336–340. doi: 10.1038/nature06121. [DOI] [PubMed] [Google Scholar]
- 12••.Mochida S, Ikeo S, Gannon J, Hunt T. Regulated activity of PP2A-B55 delta is crucial for controlling entry into and exit from mitosis in Xenopus egg extracts. EMBO J. 2009;28:2777–2785. doi: 10.1038/emboj.2009.238. The cell cycle regulated phosphatase identified in Ref. [11] turned out to be PP2A, which is active in interphase and inactive during mitosis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13••.Castilho PV, Williams BC, Mochida S, Zhao Y, Goldberg ML. The M phase kinase Greatwall (Gwl) promotes inactivation of PP2A/B55delta, a phosphatase directed against CDK phosphosites. Mol Biol Cell. 2009;20:4777–4789. doi: 10.1091/mbc.E09-07-0643. Greatwall kinase promotes mitotic entry and blocks mitotic exit by inhibiting a Cdk-counteracting PP2A phosphatase. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14••.Zhao Y, Haccard O, Wang R, Yu J, Kuang J, Jessus C, Goldberg ML. Roles of Greatwall kinase in the regulation of cdc25 phosphatase. Mol Biol Cell. 2008;19:1317–1327. doi: 10.1091/mbc.E07-11-1099. The newly discovered Greatwall kinase mimics the action of phosphatase inhibitor, okadaic acid, and it regulates the inhibitory tyrosine-modifying enzymes of Cdk1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yu J, Zhao Y, Li Z, Galas S, Goldberg ML. Greatwall kinase participates in the Cdc2 autoregulatory loop in Xenopus egg extracts. Mol Cell. 2006;22:83–91. doi: 10.1016/j.molcel.2006.02.022. [DOI] [PubMed] [Google Scholar]
- 16••.Vigneron S, Brioudes E, Burgess A, Labbe JC, Lorca T, Castro A. Greatwall maintains mitosis through regulation of PP2A. EMBO J. 2009;28:2786–2793. doi: 10.1038/emboj.2009.228. These authors argue that Greatwall stabilizes the mitotic state by inhibiting PP2A but not via Cdk1 autoactivation loop as suggested by Ref. [14••] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wolfe BA, McDonald WH, Yates JR, 3rd, Gould KL. Phosphoregulation of the Cdc14/Clp1 phosphatase delays late mitotic events in S. pombe. Dev Cell. 2006;11:423–430. doi: 10.1016/j.devcel.2006.07.016. [DOI] [PubMed] [Google Scholar]
- 18.Kapuy O, Barik D, Domingo Sananes MR, Tyson JJ, Novak B. Bistability by multiple phosphorylation of regulatory proteins. Prog Biophys Mol Biol. 2009;100:47–56. doi: 10.1016/j.pbiomolbio.2009.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Harvey SL, Charlet A, Haas W, Gygi SP, Kellogg DR. Cdk1-dependent regulation of the mitotic inhibitor Wee1. Cell. 2005;122:407–420. doi: 10.1016/j.cell.2005.05.029. [DOI] [PubMed] [Google Scholar]
- 20.Deibler RW, Kirschner MW. Quantitative reconstitution of mitotic CDK1 activation in somatic cell extracts. Mol Cell. 2010;37:753–767. doi: 10.1016/j.molcel.2010.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Novak B, Tyson JJ. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J Cell Sci. 1993;106(Pt 4):1153–1168. doi: 10.1242/jcs.106.4.1153. [DOI] [PubMed] [Google Scholar]
- 22.Ferrell JE., Jr Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr Opin Cell Biol. 2002;14:140–148. doi: 10.1016/s0955-0674(02)00314-9. [DOI] [PubMed] [Google Scholar]
- 23.Ferrell JE., Jr Feedback regulation of opposing enzymes generates robust, all-or-none bistable responses. Curr Biol. 2008;18:R244–245. doi: 10.1016/j.cub.2008.02.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Thron CD. A model for a bistable biochemical trigger of mitosis. Biophys Chem. 1996;57:239–251. doi: 10.1016/0301-4622(95)00075-5. [DOI] [PubMed] [Google Scholar]
- 25.Yang L, MacLellan WR, Han Z, Weiss JN, Qu Z. Multisite phosphorylation and network dynamics of cyclin-dependent kinase signaling in the eukaryotic cell cycle. Biophys J. 2004;86:3432–3443. doi: 10.1529/biophysj.103.036558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yao G, Lee TJ, Mori S, Nevins JR, You L. A bistable Rb-E2F switch underlies the restriction point. Nat Cell Biol. 2008;10:476–482. doi: 10.1038/ncb1711. [DOI] [PubMed] [Google Scholar]
- 27.Solomon MJ, Glotzer M, Lee TH, Philippe M, Kirschner MW. Cyclin activation of p34cdc2. Cell. 1990;63:1013–1024. doi: 10.1016/0092-8674(90)90504-8. [DOI] [PubMed] [Google Scholar]
- 28.Sha W, Moore J, Chen K, Lassaletta AD, Yi CS, Tyson JJ, Sible JC. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc Natl Acad Sci USA. 2003;100:975–980. doi: 10.1073/pnas.0235349100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pomerening JR, Sontag ED, Ferrell JE., Jr Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat Cell Biol. 2003;5:346–351. doi: 10.1038/ncb954. [DOI] [PubMed] [Google Scholar]
- 30.Ubersax JA, Woodbury EL, Quang PN, Paraz M, Blethrow JD, Shah K, Shokat KM, Morgan DO. Targets of the cyclin-dependent kinase Cdk1. Nature. 2003;425:859–864. doi: 10.1038/nature02062. [DOI] [PubMed] [Google Scholar]
- 31.Errico A, Deshmukh K, Tanaka Y, Pozniakovsky A, Hunt T. Identification of substrates for cyclin dependent kinases. Adv Enzyme Regul. 2010;50:375–399. doi: 10.1016/j.advenzreg.2009.12.001. [DOI] [PubMed] [Google Scholar]
- 32.Shteinberg M, Protopopov Y, Listovsky T, Brandeis M, Hershko A. Phosphorylation of the cyclosome is required for its stimulation by Fizzy/cdc20. Biochem Biophys Res Commun. 1999;260:193–198. doi: 10.1006/bbrc.1999.0884. [DOI] [PubMed] [Google Scholar]
- 33.Kraft C, Herzog F, Gieffers C, Mechtler K, Hagting A, Pines J, Peters JM. Mitotic regulation of the human anaphase-promoting complex by phosphorylation. EMBO J. 2003;22:6598–6609. doi: 10.1093/emboj/cdg627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Musacchio A, Salmon ED. The spindle-assembly checkpoint in space and time. Nat Rev Mol Cell Biol. 2007;8:379–393. doi: 10.1038/nrm2163. [DOI] [PubMed] [Google Scholar]
- 35.Oliveira RA, Hamilton RS, Pauli A, Davis I, Nasmyth K. Cohesin cleavage and Cdk inhibition trigger formation of daughter nuclei. Nat Cell Biol. 2010;12:185–192. doi: 10.1038/ncb2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Thornton BR, Toczyski DP. Securin and B-cyclin/CDK are the only essential targets of the APC. Nat Cell Biol. 2003;5:1090–1094. doi: 10.1038/ncb1066. [DOI] [PubMed] [Google Scholar]
- 37.Pomerening JR, Kim SY, Ferrell JE., Jr Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell. 2005;122:565–578. doi: 10.1016/j.cell.2005.06.016. [DOI] [PubMed] [Google Scholar]
- 38.Novak B, Csikasz-Nagy A, Gyorffy B, Chen K, Tyson JJ. Mathematical model of the fission yeast cell cycle with checkpoint controls at the G1/S, G2/M and metaphase/ anaphase transitions. Biophys Chem. 1998;72:185–200. doi: 10.1016/s0301-4622(98)00133-1. [DOI] [PubMed] [Google Scholar]
- 39.Novak B, Pataki Z, Ciliberto A, Tyson JJ. Mathematical model of the cell division cycle of fission yeast. Chaos. 2001;11:277–286. doi: 10.1063/1.1345725. [DOI] [PubMed] [Google Scholar]
- 40.Fantes P, Nurse P. Control of cell size at division in fission yeast by a growth-modulated size control over nuclear division. Exp Cell Res. 1977;107:377–386. doi: 10.1016/0014-4827(77)90359-7. [DOI] [PubMed] [Google Scholar]
- 41•.Potapova TA, Daum JR, Byrd KS, Gorbsky GJ. Fine tuning the cell cycle: activation of the Cdk1 inhibitory phosphorylation pathway during mitotic exit. Mol Biol Cell. 2009;20:1737–1748. doi: 10.1091/mbc.E08-07-0771. Transient inhibition of Cdk activity induces metaphase-arrested mammalian cells to exit mitosis, by flipping the Cdk1 phosphorylation switch to the OFF state. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Potapova TA, Daum JR, Pittman BD, Hudson JR, Jones TN, Satinover DL, Stukenberg PT, Gorbsky GJ. The reversibility of mitotic exit in vertebrate cells. Nature. 2006;440:954–958. doi: 10.1038/nature04652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kapuy O, He E, Uhlmann F, Novak B. Mitotic exit in mammalian cells. Mol Syst Biol. 2009;5:324. doi: 10.1038/msb.2009.86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Novak B, Tyson JJ, Gyorffy B, Csikasz-Nagy A. Irreversible cell-cycle transitions are due to systems-level feedback. Nat Cell Biol. 2007;9:724–728. doi: 10.1038/ncb0707-724. [DOI] [PubMed] [Google Scholar]
- 45•.Lopez-Aviles S, Kapuy O, Novak B, Uhlmann F. Irreversibility of mitotic exit is the consequence of systems-level feedback. Nature. 2009;459:592–595. doi: 10.1038/nature07984. Mitotic exit in budding yeast is irreversible because of positive (and double-negative) feedback loops rather than cyclin degradation per se. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shirayama M, Toth A, Galova M, Nasmyth K. APC(Cdc20) promotes exit from mitosis by destroying the anaphase inhibitor Pds1 and cyclin Clb5. Nature. 1999;402:203–207. doi: 10.1038/46080. [DOI] [PubMed] [Google Scholar]
- 47•.Skoufias DA, Indorato RL, Lacroix F, Panopoulos A, Margolis RL. Mitosis persists in the absence of Cdk1 activity when proteolysis or protein phosphatase activity is suppressed. J Cell Biol. 2007;179:671–685. doi: 10.1083/jcb.200704117. In contrast to Refs. [40,41•], these authors argue that mitotic exit requires APC-dependent phosphatase activation in addition to Cdk1 inactivation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kholodenko BN. Cell-signalling dynamics in time and space. Nat Rev Mol Cell Biol. 2006;7:165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bell-Pedersen D, Cassone VM, Earnest DJ, Golden SS, Hardin PE, Thomas TL, Zoran MJ. Circadian rhythms from multiple oscillators: lessons from diverse organisms. Nat Rev Genet. 2005;6:544–556. doi: 10.1038/nrg1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang T, Brazhnik P, Tyson JJ. Computational analysis of dynamical responses to the intrinsic pathway of programmed cell death. Biophys J. 2009;97:415–434. doi: 10.1016/j.bpj.2009.04.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Solomon MJ, Lee T, Kirschner MW. Role of phosphorylation in p34cdc2 activation: identification of an activating kinase. Mol Biol Cell. 1992;3:13–27. doi: 10.1091/mbc.3.1.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lee TH, Solomon MJ, Mumby MC, Kirschner MW. INH, a negative regulator of MPF, is a form of protein phosphatase 2A. Cell. 1991;64:415–423. doi: 10.1016/0092-8674(91)90649-j. [DOI] [PubMed] [Google Scholar]
- 53.Lee TH, Turck C, Kirschner MW. Inhibition of cdc2 activation by INH/PP2A. Mol Biol Cell. 1994;5:323–338. doi: 10.1091/mbc.5.3.323. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.