Multi-band accelerated spin-echo echo planar imaging with reduced peak RF power using time-shifted RF pulses

Abstract

Purpose

To evaluate an alternative method for generating multi-banded RF pulses for use in multiband slice-accelerated imaging with slice-GRAPPA unaliasing, substantially reducing the required peak power without bandwidth compromises. This allows much higher accelerations for spin-echo methods such as SE-fMRI and diffusion-weighted MRI where multi-banded slice acceleration has been limited by available peak power.

Theory and Methods

Multi-banded “time-shifted” RF pulses were generated by inserting temporal shifts between the applications of RF energy for individual bands, avoiding worst-case constructive interferences. Slice profiles and images in phantoms and human subjects were acquired at 3T.

Results

For typical sinc pulses, time-shifted multi-banded RF pulses were generated with little increase in required peak power compared to single-banded pulses. Slice profile quality was improved by allowing for higher pulse bandwidths, and image quality was improved by allowing for optimum flip angles to be achieved.

Conclusion

A simple approach has been demonstrated that significantly alleviates the restrictions imposed on achievable slice acceleration factors in multiband spin-echo imaging due to the power requirements of multi-banded RF pulses. This solution will allow for increased accelerations in diffusion-weighted MRI applications where data acquisition times are normally very long and the ability to accelerate is extremely valuable.

INTRODUCTION

The use of multi-banded RF pulses to accelerate volume coverage along the slice direction is becoming increasingly common in multi-slice 2D acquisitions, especially for whole-brain coverage. The approach relies on simultaneously exciting and acquiring multiple slices and subsequently unaliasing them using parallel imaging principles and the spatial information available in multi-channel radiofrequency (RF) array coils (1–7). The strategy allows for a direct reduction in the volume T_R by the number of simultaneously excited slices (i.e., the multiband (MB) factor or the slice acceleration factor). Recently, the approach has been employed with significant success in studies of the brain, first for task or stimulus based functional brain imaging (T/S-fMRI) (4,5), and subsequently for resting-state fMRI (R-fMRI) (1,2,7) and diffusion weighted imaging (dMRI) (1,6) as employed in tractography to extract information on anatomical connectivity. In all of these applications, slice acceleration was utilized together with 2D echo planar imaging (EPI) (8) for fast k-space coverage. The resulting rapid sampling in an R-fMRI time series was shown to yield improved detection of resting state networks (RSNs) (1) and permit new analysis strategies that account for the temporal dynamics of such networks (7). For dMRI, the very long (e.g., 30 to 60 min.) image acquisition time needed to cover the numerous directions and magnitudes of diffusion weighting in techniques like high angular diffusion weighted imaging (HARDI) (9,10) and DSI (11,12) was significantly reduced with slice acceleration (1,13), making the use of this approach practical and indispensable for efforts like the Human Connectome Project (HCP) (14).

In slice-accelerated multiband imaging, the number of simultaneously excited slices dictates the number of bands required in the RF pulse. Conventionally, increasing the number of bands in a RF pulse also increases linearly the required peak B₁ of the pulse and the voltage applied to the RF coil to generate that B₁. Given the quadratic relationship between voltage and power, this implies a significant increase in peak power requirements for multi-banded pulses. This does not present a significant problem in applications such as gradient recalled echo (GRE) based fMRI, since only an excitation pulse is needed, and the short T_R values attained with slice acceleration are accompanied by a reduction in the excitation flip angle employed for optimum signal-to-noise ratio (SNR). When spin echo (SE) acquisitions are required, as in SE-fMRI (15–18) and dMRI, however, the acceleration factor becomes easily limited by the peak power needed to achieve the 180° flip angle for the refocusing pulses to yield optimum SNR. Using controlled aliasing techniques for MB-EPI applications (13,19), we have reported MB factors of up to ~12 for GRE EPI acquisitions at 3 tesla with a 32-channel RF coil (19,20), while the maximum practically achievable MB factor demonstrated for dMRI has been limited to ~3 at 3T (6).

The conventional method employed to generate an RF pulse with N bands is to simply compute the complex sum of N frequency-shifted single-banded waveforms (21). With this method, the peak B₁ (and therefore the peak voltage) required for the multi-banded pulse increases by a factor of N over the original single-banded pulse, and the peak power increases by a factor of N². In practice, the peak power can be reduced to achievable levels by increasing the pulse duration, or by using a technique such as VERSE (22). Increasing the pulse duration also increases minimum achievable T_E and T_R, and decreases the RF bandwidth, leading to degraded slice profiles, especially in the presence of B₀ inhomogeneities. VERSE, on the other hand, is particularly sensitive to B₀ inhomogeneity. While VERSE has been successfully demonstrated for SE MB with acceleration factors of three (6), using VERSE with higher accelerations would likely incur unacceptable degradations in slice profile quality.

In this work, we demonstrate a simple approach for generating multi-banded RF pulses with reduced peak power without incurring a reduction in bandwidth, as is the case with VERSE, or resorting to the use of periodic modulation techniques such as PINS (2,23) which have an essentially unlimited field of view in the slice direction, requiring careful selection of a restricted set of slice orientations in order to avoid undesired aliasing.

The approach considered here relies on the addition of a small temporal shift between the bands. This temporal shift is optimized to avoid direct overlapping of the central regions of the pulses where the required B₁ magnitude is the greatest. This approach had been proposed previously in the context of Hadamard imaging and spectroscopy (24,25). However, applications of this approach have not been widespread. Furthermore, its use in SE imaging requires additional considerations in pulse sequence design that were not previously demonstrated experimentally. Here, we demonstrate that this technique can be applied to slice-accelerated multiband SE EPI in combination with slice-GRAPPA for unaliasing, and that reductions in peak B₁ approaching the MB factor are achievable without compromising bandwidth compared to a conventional single-banded pulse. The approach does not reduce SAR, however. When the peak power limitation is overcome, SAR will ultimately emerge as the primary impediment; this remains a challenge to be addressed for high acceleration factors and at higher field strengths.

A comparison of time-shifted RF pulse designs to matched unshifted pulses is presented, along with example pulse sequences for single spin-echo (monopolar) (26) and double spin-echo (bipolar) (27,28) EPI dMRI acquisitions and experimental results.

THEORY

RF Pulse Design

Beginning with a single-banded sinc pulse of duration t_s, bandwidth BW, and peak RF field requirement B₁, conventional N-banded pulses are formed by summing N frequency-shifted copies of the single-banded pulse in the complex domain. Frequency shifts are applied to each band according to the desired slice position of each band, which is determined by the total number of slices in the imaging protocol, the desired overall spatial coverage of the slices, and the slice acceleration (i.e., the MB factor). The spatial inter-slice distance is typically maximized to optimize coil encoding and allow for the most effective unaliasing performance.

The total duration, t, of the conventional N-banded pulse is the same as the base single-banded pulse: t = t_s. The peak RF field requirement of the conventional N-banded pulse is N·B₁, assuming there is no phase offset between the bands. It has been demonstrated that the phase offset between bands can be optimized for the express purpose of peak power reduction, ideally reducing the peak power by a factor of √N (24,25,29,30). This “phase scramble” optimization can be easily used in conjunction with the technique proposed here, and the combination has been evaluated and is presented.

N-banded time-shifted pulses are created using the same basic calculation as the conventional technique, with the addition of temporal shifts between the bands. As the temporal shift Δ_S is increased from 0 to t_s, the peak RF field requirement of the N-banded time-shifted pulse decreases from N·B₁ and approaches B₁ very rapidly such that for a typical sinc pulse, Δ_S < 0.25·t_s produces an N-banded pulse with a peak RF field of close to B₁. The total duration, t, of the N-banded time-shifted pulse increases with the temporal shift factor so that t = N·Δ_S + t_s.

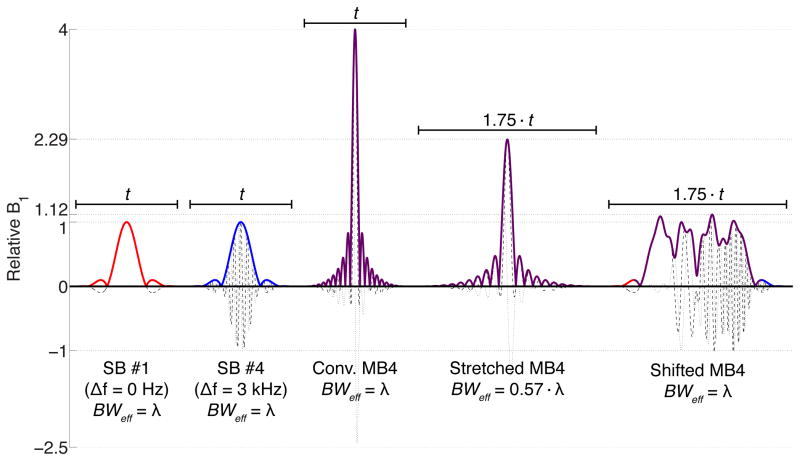
A comparison of four-banded (MB4) RF pulses generated with the conventional method vs. a four-banded pulse generated with the proposed method including a 25% temporal shift between the bands is shown in Figure 1. Two of the base single-banded (SB) pulse envelopes are also shown for reference (with and without frequency shift). When the total duration t is held constant between the SB and conventional MB4 pulses, the effective bandwidth (BW_eff) is also constant, but the peak B₁ required for the conventional MB4 pulse is four times that of the base SB pulse. When the conventional MB4 pulse is stretched in duration to 1.75·t, the peak B₁ decreases linearly, but so does the BW_eff, with deleterious consequences in the pulse profile. The time-shifted MB4 pulse, with the same duration of 1.75·t as the stretched pulse, requires little more peak B₁ than the original SB pulse, but preserves the original effective bandwidth.

Figure 1.

From left to right: single-banded (SB) sinc RF pulse (R = 5.2) for band #1 (no frequency offset), SB pulse for band #4 (~3 kHz frequency offset), conventional four-banded (MB4) pulse with matched duration t, conventional MB4 pulse with stretched duration 1.75·t, time-shifted MB4 pulse generated with the proposed technique with duration 1.75·t (25% temporal shift between bands). For all plots, solid lines represent the magnitude, dashed lines the real component, and dotted lines the imaginary component.

Pulse Sequence Implementation

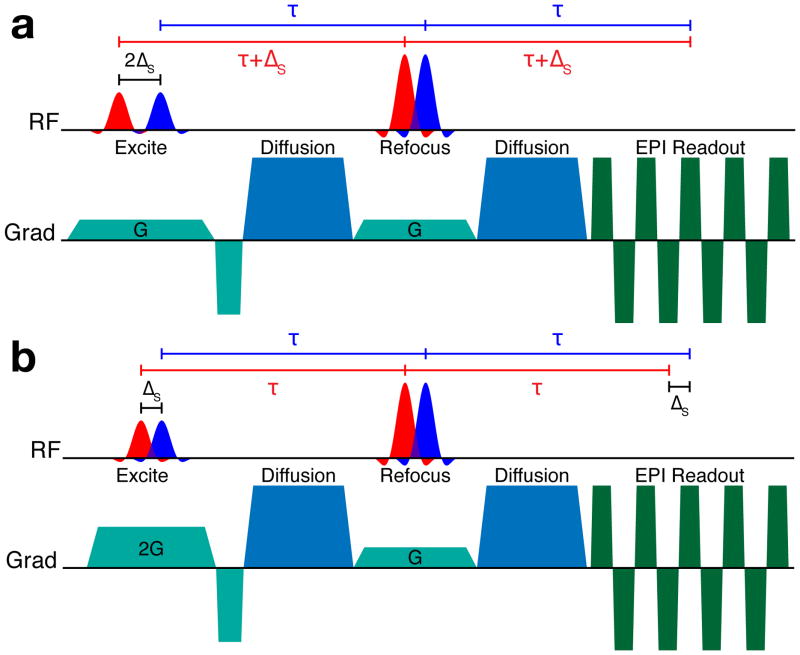
The pulse sequence proposed for bipolar dMRI acquisition with time-shifted multi-banded RF pulses is presented in Figure 2. A two-banded pulse is shown for simplicity. This sequence is based on the standard bipolar dMRI sequence supplied by the scanner vendor, which is often preferred due to its reduced sensitivity to eddy currents (27,28). Since two refocusing RF pulses are used in this approach, time-shifted multi-banded refocusing RF pulses can simply be used in place of single-banded pulses without further modifications to the sequence. The dephasing induced by the asymmetry of the slice selection gradient moment around the RF of a given band in the first refocusing pulse is balanced exactly by an opposing moment around the second refocusing pulse. In this sequence, no shift is applied to the (nominally 90°) multi-banded excitation pulse.

Figure 2.

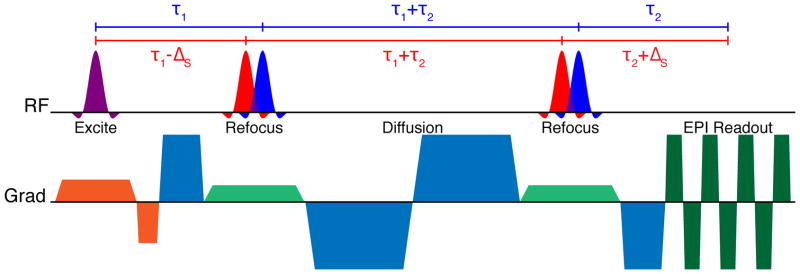
Bipolar diffusion-weighted EPI sequence diagram using time-shifted multi-banded refocusing RF pulses. No time shift is used for the multi-banded excitation RF pulse.

Two pulse sequences proposed for monopolar dMRI acquisition with shifted multi-banded RF pulses are presented in Figure 3. The monopolar approach is advantageous primarily because it allows for significantly reduced minimum T_E resulting in an SNR gain that is critical in dMRI. The historical drawback of the monopolar sequence is increased sensitivity to eddy currents compared to the bipolar sequence, but recent improvements in gradient coil design (31) and post-processing corrections (32) now allow for it to be used routinely and effectively.

Figure 3.

Monopolar diffusion-weighted EPI sequences using time-shifted multi-banded refocusing and excitation RF pulses. The top diagram (a) shows the “aligned-echo” variant, where all spin echoes form at the same time, but the effective T_E of each band differs by 2Δ_S. The bottom diagram (b) shows the “aligned-T_E” variant, where the T_E of each band is the same, but the formation of the spin echoes for each band is separated in time by Δ_S.

In the monopolar scheme, it is necessary to apply time shifts to both the refocusing and the excitation pulses in order to balance the slice select gradient moments experienced by each band. The slice select gradients G_exc, G_ref and the time shift between bands Δ_S,exc, Δ_S,ref for the excitation and refocusing, respectively, must satisfy the condition G_exc·Δ_S,exc = 2·G_ref·Δ_S,ref (24). It follows that there are two “extreme” approaches in sequence design to consider, i.e. the case where G_exc = G_ref and the case where Δ_S,exc = Δ_S,ref.

In the first monopolar approach, shown in Figure 3(a), single-banded pulses were selected such that the excitation and refocusing pulse bandwidths, and therefore the slice select gradient amplitudes G_exc and G_ref, were equal. In this case, it is necessary to use a time shift between the bands of the excitation pulse that is double that of the refocusing pulse time shift in order for the slice select gradient moments to balance (i.e. Δ_S,exc = 2·Δ_S,ref). A consequence of this approach is that the effective T_E of each band differs by 2·Δ_S,ref. The spin echo for each band is formed at the same time, however. We refer to this approach as “aligned-echo” monopolar.

In the second monopolar approach, (Figure 3(b)), the RF bandwidth and therefore the slice select gradient amplitude required for excitation was double of that used for refocusing (G_exc = 2·G_ref). In this case, the slice select gradient moments balance when the time shifts between bands for excitation and refocusing are equal (Δ_S,exc = Δ_S,ref). It then follows that the same T_E is realized for all bands. Unlike in the first approach, however, the spin echoes are formed at different times for each band, separated by Δ_S. We refer to this approach as “aligned-T_E” monopolar. For both monopolar approaches, the slice rephase gradient is calculated from the overall center of the excitation RF pulse.

METHODS

All experiments were conducted on the Siemens MAGNETOM Skyra ConnectomS 3T MR scanner (Siemens, Erlangen, Germany), which was developed specifically for the Human Connectome Project carried out by the WU-Minn (Washington University-University of Minnesota) consortium. This system is equipped with gradients capable of 100 mT/m maximum amplitude and 200 T/m/s maximum slew rate, a custom 56 cm inner diameter transmit RF coil, and a 32-channel receive RF coil optimized for brain studies (31).

Time-shifted RF pulses were implemented within the framework of the multiband EPI sequence described previously (5,19), with minor modifications specific to bipolar and monopolar diffusion schemes as described in the Theory section. The RF pulses were calculated in real time by the sequence. Inter-band frequency shifts were calculated automatically according to the imaging protocol prescribed by the operator using the standard graphical user interface of the scanner. The operator defined the single-banded base pulse durations and temporal shift parameters freely.

For experimental validation of the proposed time-shifted RF pulses, slice profiles were measured in a cylindrical oil phantom. The same measurements were performed for conventional multi-banded pulses, time-shifted multi-banded pulses, and single-banded pulses for comparison. These measurements were acquired using the “aligned-T_E” variant of the monopolar dMRI sequence, moving the readout gradient to the slice select axis. The maximum available RF voltage for this study was 292.4 V (RMS) = 1710 W, as measured by the integrated power detector supplied by the vendor (located only a short distance from the coil input).

Slice profile measurements of six slices were acquired with single-banded RF pulses. The excitation pulse flip angle, duration, and pulse voltage were 90º, 2560 μs, and 127.2 V, respectively. Refocusing flip angle, duration, and pulse voltage were 180°, 5120 μs, and 136.7 V, respectively. Slice thickness = 5 mm, gap = 10 mm, T_E = 28 ms. Time-shifted six-banded pulses were generated using the single-banded pulse described above as a base, with a 640 μs temporal shift between bands. The total excitation pulse duration for the time-shifted six-banded pulse was 5760 μs, excitation pulse voltage 168.9 V, refocusing pulse duration 8320 μs, refocusing pulse voltage 258.9 V. The minimum T_E for this acquisition was 38.1 ms. A conventional six-banded pulse was also generated; in order to bring the RF peak voltage for this pulse below the system maximum, the conventional six-banded excitation pulse was stretched to 7040 μs to reach a peak voltage of 277.5 V; the refocusing pulse was stretched to 14720 μs to reach a peak voltage of 285.4 V. The minimum T_E for this acquisition was 51.7 ms.

Additionally, multiband accelerated images were acquired in human subjects using conventional and time-shifted multi-banded pulses (“aligned-T_E” variant) in the monopolar diffusion sequence for comparison. Acquisition parameters were: FOV (readout × phase) = 210 × 175 mm, matrix size = 168 × 140, slice thickness = 1.25 mm, resolution 1.25 mm isotropic, T_E/T_R = 92/5500 ms, phase partial Fourier = 6/8, echo spacing = 0.78 ms (readout G_max ~= 42 mT/m), bandwidth = 1488 Hz/pixel, 100 slices. An inter-band temporal shift of 640 μs was used for time-shifted MB3 and MB4 pulses, while a shift of 720 μs was used for time-shifted MB5 and MB6 pulses. The base pulse durations were held constant at 2560 μs for excitation and 5120 μs for refocusing in order to maintain the same the pulse bandwidths between acquisitions. For all acquisitions, 90° excitation and 180° refocusing flip angles were specified. Human subjects provided written informed consent to the imaging protocol, which was approved by the institutional review board (IRB) at the University of Minnesota. SAR was monitored using the standard hardware and software supplied by the scanner manufacturer and was held within FDA/IEC limits.

RESULTS

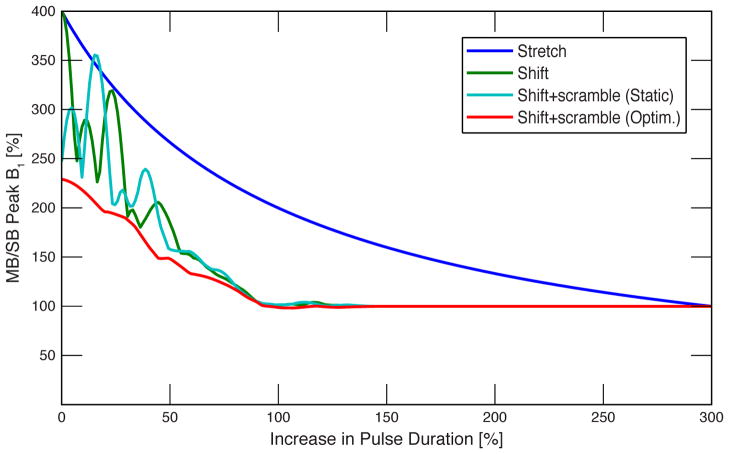
A plot of required peak B₁ vs. total pulse duration is shown in Figure 4 for four-banded pulses with 1.25 kHz frequency offsets between bands created with the proposed technique and the conventional technique. The axes are scaled to use the base single-banded pulse as a reference. For the conventional four-banded pulse, stretching to 300% above the original pulse duration is required for peak B₁ to match the equivalent B₁ of the time-shifted pulse. The significantly longer duration of the stretched pulse increases the T_E for the spin echo (undesirable because of consequent SNR losses in dMRI) and significantly decreases the bandwidth leading to further deleterious consequences. The peak B₁ can be further reduced by applying phase offsets between the bands (“phase scrambling”). If only a static set of pre-calculated offsets is applied (30), it can be seen that the peak B₁ is reduced significantly as expected when no time shift is used (Δ_S = 0), but this advantage vanishes as the time shift increases (light blue plot). It is therefore necessary to re-optimize the phase scramble taking the particular time shift into account. If the optimization is calculated for each selected value of Δ_S (using the optimization described in (30)), the peak B₁ can be reduced for any Δ_S (red plot).

Figure 4.

Plot of required peak B₁ vs. total pulse duration for four-banded pulses with 1.25 kHz inter-band frequency offsets: stretched conventional pulse (dark blue), time-shifted pulse (green), time-shifted with static inter-band phase offsets (light blue), and time-shifted with optimized phase offsets for each shift (red). B₁ and duration are shown relative to the base single-banded sinc pulse.

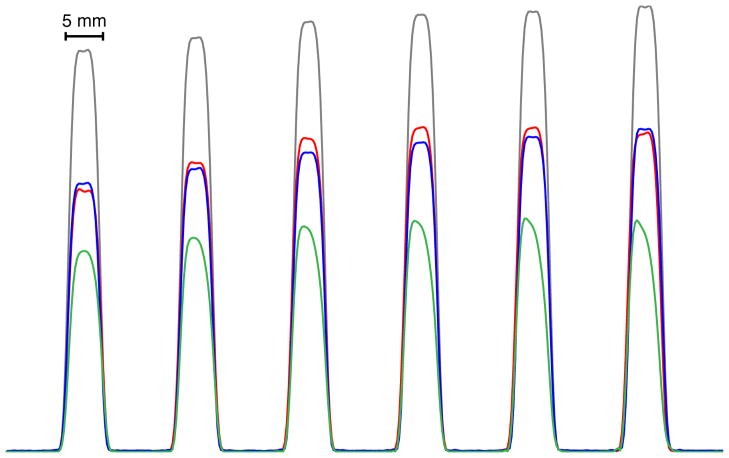
Since the bandwidth is unaltered in time-shifted pulses, the slice profile of the time-shifted six-banded pulse (red) matches very well the profile of the single-banded pulses (blue and gray traces, Figure 5) applied separately at the positions corresponding to that of the six-banded pulse. The difference between the blue and gray traces for the single banded applications is the T_E in the SE sequence, which, for the blue trace, matches that of the six-banded pulse. The peak intensity of the time-shifted six-banded trace is reduced compared to the single-banded traces with shorter T_E (gray trace), as expected given the short T₂ of the oil phantom, but for matching T_E they are very similar. The stretched conventional six-banded pulse trace (green) has the lowest signal intensity due to the significant increase in T_E required to accommodate the large degree of stretching needed to reach the desired flip angles under the constraint of the maximum peak B₁ available from the scanner. The slice profile sharpness of the conventional six-banded pulse is also significantly degraded due to the decrease in bandwidth.

Figure 5.

Slice profiles measured in a cylindrical oil phantom. For reference, slice profiles acquired separately with single-band pulses at the minimum T_E of 28 ms are shown in gray. The six slices simultaneously acquired with a time-shifted six-banded RF pulse are shown in red (T_E = 38 ms); this is compared to single-band acquisition at the same T_E is shown in blue. The same six slices acquired with a stretched conventional six-banded RF pulse are shown in green (T_E = 52 ms).

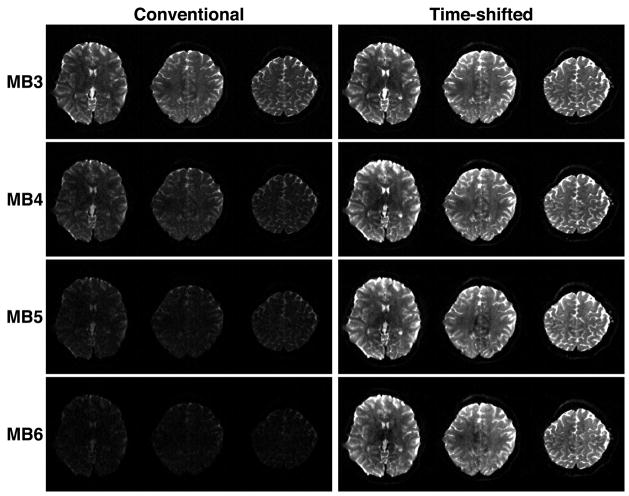
A comparison of human brain images acquired using the monopolar diffusion sequence is shown in Figure 6 for accelerated acquisitions with conventional and time-shifted RF pulses (“aligned-T_E” variant) for MB3-MB6. For display purposes, three slices are shown out of a whole-brain dataset.

Figure 6.

Comparison of human brain images acquired with multi-band slice accelerations of 3–6 (MB3-MB6) using conventional multi-banded RF pulses (left column) and time-shifted RF pulses (right column) with equivalent effective bandwidth. The display window and level are the same for all images.

For MB3 with conventional multi-banded pulses, it is only possible to achieve flip angles of 69°/128° at the maximum power available. For MB3 with time-shifted pulses, applying a 640 μs inter-band shift results in excitation/refocusing pulses with total duration 3840/6400 μs and flip angles of 90°/180°, but with the same effective bandwidth as the conventional pulses.

For MB6 with conventional multi-banded pulses, it is only possible to achieve flip angles of 35°/64° at the maximum power available. SNR in these images is significantly degraded. It would be necessary to increase the pulse durations beyond 6690/14370 μs in order to achieve optimum 90°/180° flip angles, which is not practical due to the consequent increase in T_E and the extremely low bandwidth of the pulses. Using MB6 with time-shifted pulses, flip angles of 90°/180° are easily achieved with a 720 μs inter-band shift, resulting in pulses of total duration 6160/8720 μs which maintain the same effective bandwidth as the conventional pulses. Accelerations greater than MB6 were not achievable at this T_R due to SAR limitations. When the minimum T_R achievable for the increased MB factor was employed, MB4 was possible with these parameters within the SAR limit.

DISCUSSION

For time-shifted pulses, the total pulse duration increases as the shift factor is increased but bandwidth remains unchanged. For conventional pulses, the pulse is simply stretched in time and the bandwidth decreases in consequence. The required peak B₁ decreases much more rapidly with increased pulse duration attained with time shifting. It is even possible for the peak B₁ to be less than that required for the base single-band pulse for certain shift factors where the waveforms for the bands interfere destructively (e.g. at +100% duration, Figure 4). The total power deposited, however, remains unaltered, a consequence of Parseval’s theorem as in the case where individual band phases are changed to reduce peak power (25,30). Therefore, the maximum achievable accelerations will still be constrained by SAR if minimum T_R is desired. The SAR constraint can potentially be ameliorated by parallel transmission techniques (33) without negatively affecting bandwidth. In MB diffusion acquisitions, ultimately T₁ limits the minimum practical T_R due to SNR reduction. However, even operating at T_R values above minimum, using higher MB accelerations can be useful to avoid other instrumental constraints such as gradient duty cycle.

When the product of MB factor and inter-band time shift is smaller than T₂, significant differences in image quality between the “aligned-T_E” and “aligned-echo” extremes of the monopolar sequence are not expected and were not observed. When this condition is not fulfilled, the differences will become more significant and the optimum sequence to use will depend on the application.

In the case of SE-BOLD, the “aligned-echo” sequence will produce images with differing T_E between bands, and therefore different T₂ weighting. For T_E ≈ T₂, SE-BOLD contrast is relatively insensitive to T_E as shown previously (18). The “aligned-T_E” sequence will instead produce images with differences in T₂^* weighting across k-space, similar to what is observed in asymmetric spin echo imaging (34).

As long as the condition G_exc·Δ_S,exc = 2·G_ref·Δ_S,ref (24) is satisfied, it is even possible to compromise between the two aligned extremes as desired. SIR-EPI, a sequence where neither the spin echoes nor the T_E are aligned across slices, has been shown to produce high-quality dMRI data (1,35). In SIR, the minimum time shift between slices is the total duration of the RF pulse, which far exceeds the nominal 25% inter-band shift that would typically be used with the technique proposed in this work.

CONCLUSIONS

In this work, we demonstrate an approach that significantly alleviates peak power imposed slice acceleration limits in multiband spin-echo imaging. The proposed solution provides increased accelerations in dMRI applications such as HARDI and DSI where data acquisition times are normally very long, especially when high resolution is desired and the ability to accelerate is extremely advantageous.