Comparative effectiveness of dynamic treatment regimes: an application of the parametric g-formula

Abstract

Ideally, randomized trials would be used to compare the long-term effectiveness of dynamic treatment regimes on clinically relevant outcomes. However, because randomized trials are not always feasible or timely, we often must rely on observational data to compare dynamic treatment regimes. An example of a dynamic treatment regime is “start combined antiretroviral therapy (cART) within 6 months of CD4 cell count first dropping below x cells/mm³ or diagnosis of an AIDS-defining illness, whichever happens first” where x can take values between 200 and 500. Recently, Cain et al (2011) used inverse probability (IP) weighting of dynamic marginal structural models to find the x that minimizes 5-year mortality risk under similar dynamic regimes using observational data. Unlike standard methods, IP weighting can appropriately adjust for measured time-varying confounders (e.g., CD4 cell count, viral load) that are affected by prior treatment. Here we describe an alternative method to IP weighting for comparing the effectiveness of dynamic cART regimes: the parametric g-formula. The parametric g-formula naturally handles dynamic regimes and, like IP weighting, can appropriately adjust for measured time-varying confounders. However, estimators based on the parametric g-formula are more efficient than IP weighted estimators. This is often at the expense of more parametric assumptions. Here we describe how to use the parametric g-formula to estimate risk by the end of a user-specified follow-up period under dynamic treatment regimes. We describe an application of this method to answer the “when to start” question using data from the HIV-CAUSAL Collaboration.

1 Introduction

In an ideal world, all policy and clinical decisions would be based on the findings of randomized experiments (with perfect adherence to the assigned treatment arm and no loss to follow-up). Unfortunately, randomized experiments are often unethical, impractical, or simply too lengthy for timely decisions. The difficulties of conducting randomized experiments increase when they are used to compare the long-term effectiveness of clinical strategies in terms of clinically relevant outcomes. For example, randomized clinical trials have demonstrated that combined antiretroviral therapy (cART) reduces the risk of AIDS and death in HIV-infected patients (Hammer et al, 1997; Cameron et al, 1998). However, the optimal time to start cART remains under debate (European AIDS Clinical Society, 2009; World Health Organization, 2009; Panel on Antiretroviral Guidelines for Adults and Adolescents, 2009; Thompson et al, 2010) and no randomized clinical trials have yet been completed to answer this question (http://insight.ccbr.umn.edu/start/, accessed 2011; NIH,2009).

Consider a clinical trial in which HIV-infected individuals are randomly assigned to one of several initiation strategies indexed by CD4 cell count. For example, individuals could be randomized to cART initiation when CD4 cell count first drops below either 500 or 350 cells/mm³ (or there is a diagnosis of an AIDS-defining illness, whichever happens first). Each arm of this trial, differing by the two thresholds for CD4 cell count, implements a dynamic treatment regime because whether an individual does or does not start treatment depends on her own evolving history of prognostic factors. Under full adherence to the assigned regime and no loss to follow-up, the data from this trial can be used to compare the effectiveness of these two regimes. One could, for example, estimate the 5-year mortality risk under each regime and choose the one that resulted in the lowest risk (or, equivalently, the highest survival).

However, one would ideally want to compare multiple initiation strategies, each of them under a different CD4 threshold. For example, one might want to estimate the 5-year risk under each of the 7 dynamic regimes: “start cART within 6 months of CD4 cell count first dropping below x or diagnosis of an AIDS-defining illness, whichever happens first”, with x taking on values between 200 and 500 in increments of 50 cells/mm³. Such a trial with 7 arms would require extremely large sample sizes and is unlikely to be conducted. Rather, we can use observational data to obtain preliminary answers to the “when to start” question. At the very least, the findings from properly analyzed observational studies may guide the design of future randomized experiments.

There are relatively few examples of analyses of observational data to compare dynamic regimes similar to those described above (Cain et al, 2011, 2010; Murphy et al, 2001; Hernán et al, 2006; van der Laan and Petersen, 2007; Petersen et al, 2007). Cain et al (2011) applied inverse probability (IP) weighting of dynamic marginal structural models (Hernán et al, 2006; Orellana et al, 2010a,b; Cain et al, 2010) to observational data from the HIV-CAUSAL Collaboration, and emulated a randomized clinical trial with multiple initiation strategies similar to the ones described above. Unlike standard regression/stratification approaches, IP weighting may be used to appropriately adjust for measured time-varying confounding and selection bias in observational studies as well as in randomized clinical trials with imperfect adherence and loss to follow-up.

The parametric g-formula is an alternative to IP weighting that also appropriately adjusts for the measured time-dependent confounders and selection factors when comparing the effectiveness of dynamic regimes. This method was first described by Robins (1986) to estimate the causal effect of arsenic on heart disease in an occupationally exposed cohort and has since been applied by Robins et al (2004) and Taubman et al (2009) to estimate risk under dynamic interventions. Estimators based on this approach are more efficient (i.e. have smaller variance) than those obtained via IP weighting but will generally require more parametric modelling assumptions. In this paper we describe how to apply the parametric g-formula to data from the HIV-CAUSAL Collaboration to estimate the 5-year risk of all-cause mortality under several dynamic strategies for cART initiation. We start by introducing notation and a description of the study data.

2 Data and notation

The HIV-CAUSAL Collaboration has been described elsewhere (Ray et al, 2010). Briefly, the collaboration includes several cohort studies from five European countries and the United States: UK CHIC (United Kingdom), ATHENA (Netherlands), FHDH-ANRS CO4 (France), SHCS (Switzerland), PISCIS (Spain), CoRIS/CoRIS-MD (Spain), VACS-VC (United States veterans), UK Register of HIV Seroconverters (United Kingdom), ANRS PRIMO (France), ANRS SEROCO (France), and GEMES (Spain). All cohorts included in the HIV-CAUSAL Collaboration were assembled prospectively and are based on data collected for clinical purposes within national health care systems with universal access to care.

Our analysis was restricted to HIV-infected individuals who met the following eligibility criteria between 1996 and 2009: age 18 years or older, antiretroviral therapy-naïve, no history of an AIDS-defining illness (CDC, 1992), no pregnancy (when information was available), no history of CD4 cell count less than 500 cells/mm³, and CD4 cell count and viral load (HIV RNA) measurements within six months of each other at baseline.

Let k = 0, 1, 2, … , K, … , 151 represent month of follow-up where K +1 = 60 months is the follow-up of interest and 151 months is the maximum observed follow-up length. An individual’s baseline (k = 0) was defined as the first time her CD4 cell count dropped into the range 200–499 cells/mm³ and all of the above criteria were met. There were n = 8, 392 individuals at baseline. Individuals’ observations were assumed i.i.d.

Let A_k be an indicator of treatment (cART) initiation before the end of month k. cART was defined as either three or more antiretroviral drugs, or two ritonavir-boosted protease inhibitors, or one non-nucleoside reverse transcriptase inhibitor plus one boosted protease inhibitor. We denote the history of a random variable using overbars; for example Ā_k = (A₀, … , A_k) is the observed treatment history through the end of month k.

Let V be a vector of variables measured at or before k = 0 containing sex, geographic origin (Western countries, other or unknown), mode of transmission (heterosexual, homosexual/bisexual, injection drug use, other or unknown), race (white, black, other or unknown), cohort, calendar year (1996 – 1998, 1999 – 2000, 2001 – 2003, ≥ 2004), years since HIV diagnosis (< 1, 1 – 4, ≥ 5 years, unknown) and age (< 35, 35 – 49, ≥ 50 years).

Let L_1,k be an indicator of whether viral load was measured during month k, L_2,k the most recently measured viral load by the end of month k (on the natural log scale), L_3,k an indicator of whether CD4 cell count was measured during month k, L_4,k the most recently measured CD4 cell count by the end of month k (on the natural log scale) and L_5,k an indicator of AIDS-defining illness by the end of month k. For k > 0, we define L_k = (L_1,k, L_2,k, L_3,k, L_4,k, L_5,k) and define L₀ = (V, L_1,0, L_2,0, L_3,0, L_4,0, L_5,0). We constructed the data set such that, when treatment was initiated during month k, L_k represents the last measurements of covariates preceding treatment initiation.

Let Y_k+1 represent the indicator of death from any cause by the end of month k+1, and C_k+1 the indicator of censoring by the end of month k+1 with Y̅₀ = C̅₀ = 0 by definition. An individual was censored at pregnancy or after 12 months without a viral load or CD4 cell count measurement. An individual was also censored at the cohort-specific administrative end of follow-up for this analysis (between December 2003 and September 2009). For notational convenience we set L̅₋₁ and Ā₋₁ to be identically 0. We assume the order (C_k, Y_k, L_k, A_k) within each measurement interval k.

3 Deterministic dynamic regimes

As in Robins and Hernán (2009), we define a deterministic treatment regime or intervention as a collection of functions {g_k(ā_k−1, l̄_k); k = 0, … , K} which determine treatment assignment during month k for a possible realization (ā_k−1, l̄_k) of (Ā_k−1, L̅_k) under that regime. We say a treatment regime g is static if the rule for assigning treatment at each k does not depend on past treatment or covariates; otherwise we say g is dynamic. For example, the intervention “initiate cART at baseline” or g_k(ā_k−1, l̄_k) = 1 for all k = 0, … , K and any (ā_k−1, l̄_k) is a static regime.

In contrast, the interventions “start cART when CD4 cell count first drops below x or there is a diagnosis of an AIDS-defining illness, whichever happens first” are deterministic dynamic treatment regimes. They are dynamic because the treatment value at k depends on the history of the time-varying covariates CD4 cell count and AIDS diagnosis. They are deterministic because treatment history through k − 1 and covariate history through k determines (with probability 1) whether an individual will initiate treatment at k. In §6 we will consider random dynamic regimes where, for a given treatment history through k − 1 and covariate history through k, treatment may be initiated at k with probability between 0 and 1.

We formalize regimes of the form “start cART when CD4 cell count first drops below x or there is a diagnosis of an AIDS-defining illness, whichever happens first,” which we index by x, as follows:

Let g_k(ā_k−1, l̄_k) = 1 if either

1. g_k−1(ā_k−2, l̄_k−1) = 0 and l_4,k < ln(x) or l_5,k = 1 or

2. g_k−1(ā_k−2, l̄_k−1) = 1

and let g_k(ā_k−1, l̄_k) = 0 otherwise for k ≥ 0 and ln(x) the natural log of x.

Because k = 0 is the time when each subject’s CD4 cell count first drops below 500 cells/mm³, Pr[L_4,0 < ln(500)] = 1. Thus, this dynamic regime for x = 500 is equivalent to the static regime “initiate treatment at baseline” as all subjects will meet the criteria for starting treatment at baseline.

Finally, all regimes x discussed in this paper implicitly include an intervention to abolish censoring throughout the follow-up. That is, all regimes set C_k+1 = 0 for all k even if, for simplicity of presentation, this intervention on censoring is not explicitly stated in the definition of the regimes x.

4 The g-formula and identifying assumptions

In general, let ${\overline{Y}}_{K+1}^g$ and ${\overline{L}}_K^g$ represent the outcome and covariate histories, respectively, a subject would have experienced had she, possibly contrary to fact, followed any deterministic treatment regime g, whether static or dynamic. We can write the risk of death through month k + 1 had all subjects followed regime g as $\text{Pr}[Y_{k+1}^g=1]$, for each k = 0, … , K. These represent our population parameters of interest for g defined at the end of §3 (our regimes x).

Recursively, for s = 0, … , k, define $a_s^g$ and ${ā}_s^g=(a_0^g,\dots ,a_s^g)$ by $a_s^g=g_s({ā}_{s-1}^g,{\mathrm{l̄}}_s)$. We make the following identifying assumptions for each k (Robins and Hernán, 2009):

1. Consistency: If ${Ā}_k={ā}_k^g$ then ${\overline{Y}}_{k+1}={\overline{Y}}_{k+1}^g$ and ${\overline{L}}_k={\overline{L}}_k^g$

2. Exchangeability:

   $$(Y_{k+1}^g,\dots ,Y_{k+1}^g)\coprod (A_k,C_{k+1})|{\overline{L}}_k={\mathrm{l̄}}_k,{Ā}_{k-1}={ā}_{k-1}^g,C_k=Y_k=0$$

3. Positivity: $f_{{Ā}_{k-1},{\overline{L}}_k,C_k,Y_k}({ā}_{k-1}^g,{\mathrm{l̄}}_k,0,0)\ne 0\Rightarrow \text{Pr}[A_k=a_k^g,C_{k+1}=0|{\overline{L}}_k={\mathrm{l̄}}_k,{Ā}_{k-1}={ā}_{k-1}^g,C_k=Y_k=0]>0$ w.p.1.

Exchangeability and consistency will hold in a sequentially randomized trial defined as follows:

Definition 1: A sequentially randomized trial is equivalent to a dynamic regime associated with an intervention density f^int(a_k|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) – for ā_k ∈ 𝒜̅_k with 𝒜̅_k the support of 𝒜̅_k – which is chosen by the investigator and in which each subjects’ treatment A_k in month k is an independent draw from this choice of intervention density.

Exchangeability also holds under weaker assumptions (see Robins, 1997). Note that a sequentially randomized trial where the intervention density is chosen such that it may only equal zero or one for any history and any follow-up interval is equivalent to a deterministic dynamic regime. By contrast, if chosen such that it may take on values between zero and one for some history and follow-up interval, this sequentially randomized trial is equivalent to a random dynamic regime (see §6).

Under the consistency, exchangeability and positivity assumptions as defined above and the data structure described in §2, $\text{Pr}[Y_{k+1}^g=1]$ for any k = 0, … , K and deterministic dynamic regime g can be written as the g-formula (Robins, 1986, 1997):

$$\sum _{{\mathrm{l̄}}_k}\sum _{j=0}^k\text{Pr}[Y_{j+1}=1|{\overline{L}}_j={\mathrm{l̄}}_j,{Ā}_j={ā}_j^g,{\overline{Y}}_j={\overline{C}}_{j+1}=0]\times \prod _{s=0}^j\{\text{Pr}[Y_s=0|{\overline{L}}_{s-1}={\mathrm{l̄}}_{s-1},{Ā}_{s-1}={ā}_{s-1}^g,{\overline{Y}}_{s-1}={\overline{C}}_s=0]\times f(l_s|{\mathrm{l̄}}_{s-1},{ā}_{s-1}^g,{\overline{Y}}_s={\overline{C}}_s=0)\}$$ (1)

where $\text{Pr}[Y_j=0|{\overline{L}}_{j-1}={\mathrm{l̄}}_{j-1},{Ā}_{j-1}={ā}_{j-1}^g,{\overline{Y}}_{j-1}={\overline{C}}_j=0]$ represents the probability of surviving through month j conditional on remaining uncensored through j, surviving through j − 1 and adhering to the regime g through j − 1 for specific history $({ā}_{j-1}^g,{\mathrm{l̄}}_{j-1}),j=0,\dots k+1;f(l_j|{\mathrm{l̄}}_{j-1},{ā}_{j-1}^g,{\overline{Y}}_j={\overline{C}}_j=0)$ represents the density for L_j conditional on surviving and remaining uncensored to j and adhering to regime g through j − 1, for specific history $({ā}_{j-1}^g,{\mathrm{l̄}}_{j-1})$, j = 0, … k; and l̄_j represents the first j + 1 components of l̄_k, j = 0, … k. Thus, under our identifying assumptions, the g-formula expresses the counterfactual risk in terms of only the observed data distribution.

One minus expression (1) is equivalent to

$$\sum _{{\mathrm{l̄}}_k}\text{Pr}[Y_{k+1}=0|{\overline{L}}_k={\mathrm{l̄}}_k,{Ā}_k={ā}_k^g,{\overline{Y}}_k={\overline{C}}_{k+1}=0]\times \prod _{s=0}^k\{f(l_s|{\mathrm{l̄}}_{s-1},{ā}_{s-1}^g,{\overline{Y}}_s={\overline{C}}_s=0)\times \text{Pr}[Y_s=0|{\overline{L}}_{s-1}={\mathrm{l̄}}_{s-1},{Ā}_{s-1}={ā}_{s-1}^g,{\overline{Y}}_{s-1}={\overline{C}}_s=0]\},$$ (2)

which, under our identifiability assumptions, is $\text{Pr}[Y_{k+1}^g=0]$, or survival through k + 1 had all subjects followed regime g. For pedagogic purposes, we provide a proof in the appendix of the equivalence between $\text{Pr}[Y_{k+1}^g=0]$ and expression (2) under the identifying assumptions as defined in this section and the interval-censored observed data structure described in §2. Original proofs can be found in Robins (1986, 1997).

5 Estimation of the risk under a dynamic regime

In low-dimensional data, we can compute the g-formula for the counterfactual risk of death by k + 1 in expression (1) by non-parametrically estimating the value of each density function for all possible covariate histories and then taking the sum over these histories. This computation, however, is not possible in the presence of even one continuous covariate. In general, for high-dimensional data, we can only estimate the g-formula (1) by estimating these density functions under parametric modelling assumptions and then approximating the sum over all histories via Monte Carlo simulation.

In the estimation algorithm that follows for expression (1), we use the equivalence between f(l_k|l̄_k−1, ā_k−1, Y̅_k = C̅_k = 0) and

$$\text{Pr}[L_{5,k}=l_{5,k}|l_{4,k},l_{3,k},l_{2,k},l_{1,k},{\mathrm{l̄}}_{k-1},{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0]\times f(l_{4,k}|l_{3,k},l_{2,k},l_{1,k},{\mathrm{l̄}}_{k-1},{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0)\times \text{Pr}[L_{3,k}=l_{3,k}|l_{2,k},l_{1,k},{\mathrm{l̄}}_{k-1},{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0]\times f(l_{2,k}|l_{1,k},{\mathrm{l̄}}_{k-1},{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0)\times \text{Pr}[L_{1,k}=l_{1,k}|{\mathrm{l̄}}_{k-1},{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0]$$ (3)

for each k = 0, … , K.

Note that under our observed data structure described in §2, we have a priori knowledge of some of the conditional densities/probability functions in the product (3) for certain histories. Specifically:

1. f(l_2,k|L_1,k = 0, l̄_k−1, ā_k−1, Y̅_k = C̅_k = 0) = 1 whenever l_2,k = l_2,k−1 and f(l_4,k|L_3,k = 0, l_2,k, l_1,k, l̄_k−1, ā_k−1, Y̅_k = C̅_k = 0) = 1 whenever l_4,k = l_4,k−1; that is, the last measured viral load or CD4 cell count during month k will be the same as the last measured viral load or CD4 cell count during month k−1 if viral load or CD4 cell count was not measured during month k, respectively.

2. Pr[L_1,k = 1 |l̄_k−1, ā_k−1, Y̅_k = C̅_k = 0] = 1 whenever ${\sum }_{s=1}^{12}{l}_{1,k-s}=0$ if k ≥ 12 and Pr[L_3,k = 1|l_2,k, l_1,k, l̄_k−1, ā_k−1, Y̅_k = C̅_k = 0] = 1 whenever ${\sum }_{s=1}^{12}{l}_{3,k-s}=0$ if k ≥ 12; that is, by the definition of censoring, an individual whose viral load or CD4 cell count remains unmeasured for 12 consecutive months must have a measurement in the next month.

3. Pr[L_5,k = 1|L_5,k−1 = 1, l̄_4,k, l̄_3,k, l̄_2,k, l̄_1,k, ā_k−1, Y̅_k = C̅_k = 0] = 1; that is, if an AIDS-defining illness is diagnosed by month k−1 then it is diagnosed by month k.

Thus, in estimating expression (1), we do not have to impose parametric models on all of the component densities of that expression over all histories. Some of these densities are known and need not be estimated. Further, we do not require parametric estimation of the density f(l₀|l̄₋₁, ā₋₁, Y̅₀ = C̅₀ = 0) because we can use the empirical distribution of L₀ as an estimate of this density.

We now present a consistent estimation algorithm for the risk of death by k + 1 under each regime x for any k = 0, … , K as defined in (1) which incorporates the above described a priori knowledge of the data.

For each x, do the following:

STEP I: Parametric modelling of conditional densities

1. Fit models for the conditional densities of the covariates (for k = 1 to the maximum length of follow-up). Specifically, model:

   1. Pr[L_1,k = 1|L̅_k−1 = l̄_k−1, Ā_k−1 = ā_k−1, Y̅_k = C̅_k = 0], for l̄_k−1 such that ${\sum }_{s=1}^{12}{l}_{1,k-s}>0$ if k ≥ 12; that is, the probability that viral load is measured during month k conditional on viral load not remaining unmeasured for the 12 consecutive prior months, past history, surviving and remaining uncensored through k
   2. f(l_2,k|L_1,k = 1, L̅_k−1 = l̄_k−1, Ā_k−1 = ā_k−1, Y̅_k = C̅_k = 0); that is, the density of natural log of viral load during month k conditional on viral load being measured during month k, past history, surviving and remaining uncensored through k
   3. Pr[L_3,k = 1|l_2,k, l_1,k, L̅_k−1 = l̄_k−1, Ā_k−1 = ā_k−1, Y̅_k = C̅_k = 0], for l̄_k−1 such that ${\sum }_{s=1}^{12}{l}_{3,k-s}>0$ if k ≥ 12; that is, the probability that CD4 cell count is measured during month k conditional on CD4 cell count not remaining unmeasured for the 12 consecutive prior months, past history, surviving and remaining uncensored through k
   4. f(l_4,k|L_3,k = 1, l_2,k, l_1,k, L̅_k−1 = l̄_k−1, Ā_k−1 = ā_k−1, Y̅_k = C̅_k = 0); that is, the density of natural log of CD4 cell count during month k conditional on CD4 cell count being measured during month k, past history, surviving and remaining uncensored through k
   5. Pr[L_5,k = 1|l̄_4,k, l̄_3,k, l̄_2,k, l̄_1,k, L_5,k−1 = 0, ā_k−1, Y̅_k = C̅_k = 0]; that is, the probability of diagnosis of AIDS-defining illness by month k conditional on no prior diagnosis, past history, surviving and remaining uncensored through k

2. Fit a model for the outcome (for k = 0 to the maximum length of follow-up). Specifically, model: Pr[Y_k+1 = 1|L̅_k = l̄_k, Ā_k = ā_k, Y̅_k = C̅_k+1 = 0]; that is, the probability of death by month k+1 conditional on past history, surviving and remaining uncensored through k

Detailed modelling assumptions for step I are described in the appendix.

STEP II: Monte Carlo simulation under regime x

For k = 0, … , K and υ = 1, … , n:

1. If k = 0 set l_0,υ to the observed values for subject υ. Otherwise if k > 0

   1. Set l_1,k,υ = 1 if ${\sum }_{s=1}^{12}{l}_{1,k-s,\upsilon }=0$ and k ≥ 12. Otherwise, draw l_1,k,υ from the probability function estimated in step I.1.a based on previously drawn covariates l̄_k−1,υ and assigned treatment ā_k−1,υ under x (see step II.2).
   2. Set l_2,k,υ = l_2,k−1,υ if l_1,k,υ = 0. Otherwise, draw l_2,k,υ from the density function estimated in step I.1.b based on previously drawn covariates l̄_k−1,υ and assigned treatment ā_k−1,υ under x.
   3. Set l_3,k,υ = 1 if ${\sum }_{s=1}^{12}{l}_{3,k-s,\upsilon }=0$ and k ≥ 12. Otherwise, draw l_3,k,υ from the probability function estimated in step I.1.c based on previously drawn covariates l_2,k,υ, l_1,k,υ, l̄_k−1,υ and assigned treatment ā_k−1,υ under x.
   4. Set l_4,k,υ = l_4,k−1,υ if l_3,k,υ = 0. Otherwise, draw l_4,k,υ from the density function estimated in step I.1.d based on previously drawn covariates l_2,k,υ, l_1,k,υ, l̄_k−1,υ and assigned treatment ā_k−1,υ under x.
   5. Set l_5,k,υ = 1 if l_5,k−1,υ = 1. Otherwise, draw l_5,k,υ from the probability function estimated in step I.1.e based on previously drawn covariates l̄_4,k,υ, l̄_3,k,υ, l̄_2,k,υ, l̄_1,k,υ, and assigned treatment ā_k−1,υ under x
2. Assign the treatment a_k,υ under x. Specifically,

   • Set a_−1,υ = 0.
   • (a)
     If a_k−1,υ = 0

     1. if l_4,k,υ < ln(x) (based on step II.1.d) or l_5,k,υ = 1 (based on step II.1.e) then set a_k,υ = 1;
     2. otherwise set a_k,υ = 0
   • (b)
     If a_k−1,υ = 1 then set a_k,υ = 1

3. Estimate probability of death by month k+1 given survival to k, remaining uncensored to k + 1 for the υ^th simulated treatment and covariate history under x based on the estimated coefficients from step I.2.

STEP III: Computation of risk under regime x

For k = 0, … , K, estimate the g-formula (1) as

$$\frac{1}{n}\sum _{\upsilon =1}^n\sum _{j=0}^k\widehat{Pr}[Y_{j+1}=1|{\overline{L}}_j={\mathrm{l̄}}_{j,\upsilon },{Ā}_j={ā}_{j,\upsilon },{\overline{Y}}_j={\overline{C}}_{j+1}=0]\times \prod _{s=0}^j\{1-\widehat{Pr}[Y_s=1|{\overline{L}}_{s-1}={\mathrm{l̄}}_{s-1,\upsilon },{Ā}_{s-1}={ā}_{s-1,\upsilon },{\overline{Y}}_{s-1}={\overline{C}}_s=0]\}$$ (4)

where

$$\widehat{Pr}[Y_{k+1}=1|{\overline{L}}_k={\mathrm{l̄}}_{k,\upsilon },{Ā}_k={ā}_{k,\upsilon },{\overline{Y}}_k={\overline{C}}_{k+1}=0]$$

k = 0, … , K is obtained in step II.3.

Expression (4) is our estimate of the risk of death by each month k+1 had all subjects followed regime x and one minus expression (4) is our estimate of survival through k + 1 had all subjects followed this regime.

Note that the Monte Carlo simulation in step II is based on n samples. However, if there is concern about the Monte Carlo variance, the algorithm may be generalized to a larger number of samples. Further, the algorithm described above models (or constrains using a priori knowledge) the components of the product in (3) which is based on the permutation (L_1,k, L_2,k, L_3,k, L_4,k, L_5,k) of the variables in L_k. Expression (3) is clearly only one of several ways we could write f(l_k|l̄_k−1, ā_k−1, Y̅_k = C̅_k = 0) in terms of the product of the conditional densities of the components of L_k. In principle, we could modify the above algorithm for any of the 119 alternative permutations of the five variables in L_k. Only permutations where L_1,k precedes L_2,k and L_3,k precedes L_4,k would allow us to incorporate constraints based on our a priori knowledge and, therefore, these are the only reasonable permutations to consider. Our main results described in §8 are based on the algorithm described above using the permutation (L_1,k, L_2,k, L_3,k, L_4,k, L_5,k). We performed sensitivity analyses under the five alternative permutations of the variables in L_k such that L_1,k immediately precedes L_2,k and L_3,k immediately precedes L_4,k.

6 Random dynamic regimes

The regimes “start cART when CD4 cell count first drops below x or there is a diagnosis of an AIDS-defining illness, whichever happens first” require that patients initiate treatment immediately after their CD4 cell count drops below x or an AIDS diagnosis is made. This requirement makes regimes of this form difficult to implement in practice as the expectation of immediate treatment is often unrealistic due to administrative delays and other factors.

To address this issue, Cain et al (2011) considered random dynamic regimes which allow for a grace period during which starting treatment is required. A random dynamic regime is equivalent to a sequentially randomized trial, as defined in Definition 1 of §4, where the user-specified intervention density may take on values between zero and one for a given follow-up interval and history. Here we will also extend consideration to random regimes that allow for a grace period, specifically “start cART within m months of CD4 cell count first dropping below x or diagnosis of an AIDS-defining illness, whichever happens first” for m > 0.

If CD4 cell count first drops below x during month k, then we define the end of the grace period as the end of month k + m. If CD4 cell count was measured the first day of month k, then the length of the grace period is m+1 months. If measured the last day of month k, then the length is m months plus 1 day. Thus, whenever we refer to regimes with grace period m, we are actually referring to regimes with grace period somewhere between m and m + 1 months.

As discussed in Cain et al (2010), the regimes as stated above are ill-defined because they do not specify a particular initiation schedule during the grace period. For example, do all patients eligible for initiation start right at the end of the grace period? Alternatively, are the initiation times uniformly distributed during the grace period?

We define f^obs(a_k|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) as the observed data treatment density for a given history with the restriction that, by the definition of A_k, f^obs(1|l̄_k, A_k−1 = 1, Y̅_k = C̅_k = 0) = 1, k = 0, … , K. As in Cain et al (2011), we chose to compare random regimes x that assign treatment up until the last month of the grace period according to the observed data treatment density (i.e., according to how treatment is initiated in the observed data). That is, we will consider random dynamic regimes x with grace period m of the form:

“start cART m months after CD4 cell count first drops below x or diagnosis of an AIDS-defining illness, whichever happens first, if the subject is still alive and has not initiated treatment during the grace period on her own”.

To formalize these random regimes x with a grace period m, let f^x(a_k|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) be the intervention density associated with this random regime. Specifically, f^x(1|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) is the probability of initiating treatment by k under this random regime x and f^x(0|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) is the probability of not initiating treatment by k under this regime, conditional on survival and remaining uncensored to k and for a given history (l̄_k, ā_k−1).

Define r_k(x) as the indicator that CD4 cell count first dropped below x or an AIDS diagnosis was first made by month k; in other words, this is an indicator that the threshold for entering the grace period has been crossed either during month k or in some prior month. Though not shown in the notation for simplicity, r_k(x) is clearly a function of the history l̄_k. By definition if r_k−1(x) = 1 then r_k(x) = 1 (if you have crossed the threshold at k − 1 then you have crossed it by k) and r̄₋₁(x) = 0 (before baseline all observations will have CD4 cell count above 500 and no prior diagnosis of AIDS-defining illness and thus will not have crossed the threshold).

Then, for any m ≥ 0, the random dynamic regime x is defined as follows:

1. if r_k(x) = 0, f^x(0|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) = 1;

2. otherwise if r_k(x) = 1

   1. for m > 0, if r_k−m(x) = 0 then

      $$f^x(a_k|{\mathrm{l̄}}_k,{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0)=f^{\mathit{\text{obs}}}(a_k|{\mathrm{l̄}}_k,{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0)$$
   2. otherwise if r_k−m(x) = 1 then f^x(1|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) = 1

Note that for m = 0 this definition of regime x reduces to:

1. if r_k(x) = 0 then f^x(0|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) = 1

2. otherwise if r_k(x) = 1 then f^x(1|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) = 1

for any follow-up month k, which is equivalent to the definition given for the deterministic dynamic cART regimes indexed by x in §3. Thus, it is only the allowance for a grace period (m > 0) that introduces a “random component” to the rule for treatment assignment under x.

Generalizing to any m ≥ 0, we show in the appendix that under our identifying assumptions of §4, the generalized g-formula for risk of death by month k + 1 had all subjects followed the random dynamic regime characterized by the intervention density f^x(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0), s = 0, … , k is:

$$\sum _{{ā}_k}\sum _{{\mathrm{l̄}}_k}\sum _{j=0}^k\text{Pr}[Y_{j+1}=1|{\overline{L}}_j={\mathrm{l̄}}_j,{Ā}_j={ā}_j,{\overline{Y}}_j={\overline{C}}_{j+1}=0]\times \prod _{s=0}^j\{\text{Pr}[Y_s=0|{\overline{L}}_{s-1}={\mathrm{l̄}}_{s-1},{Ā}_{s-1}={ā}_{s-1},{\overline{Y}}_{s-1}={\overline{C}}_s=0]\times f(l_s|{\mathrm{l̄}}_{s-1},{ā}_{s-1},{\overline{Y}}_s={\overline{C}}_s=0)\times f^x(a_s|{\mathrm{l̄}}_s,{ā}_{s-1},{\overline{Y}}_s={\overline{C}}_s=0)\}$$ (5)

When m = 0, note that this expression is equivalent to the g-formula (1) of §4 for the deterministic regimes indexed by x defined at the end of §3.

One minus expression (5) is equivalent to

$$\sum _{{ā}_k}\sum _{{\mathrm{l̄}}_k}\text{Pr}[Y_{k+1}=0|{\overline{L}}_k={\mathrm{l̄}}_k,{Ā}_k={ā}_k,{\overline{Y}}_k={\overline{C}}_{k+1}=0]\times \prod _{s=0}^k\{\text{Pr}[Y_s=0|{\overline{L}}_{s-1}={\mathrm{l̄}}_{s-1},{Ā}_{s-1}={ā}_{s-1},{\overline{Y}}_{s-1}={\overline{C}}_s=0]\times f(l_s|{\mathrm{l̄}}_{s-1},{ā}_{s-1},{\overline{Y}}_s={\overline{C}}_s=0)\times f^x(a_s|{\mathrm{l̄}}_s,{ā}_{s-1},{\overline{Y}}_s={\overline{C}}_s=0)\}.$$ (6)

In the appendix, not only do we show that under our identifying assumptions the generalized g-formula (6) gives survival through k + 1 had all subjects followed this random regime indexed by x, but also that expression (6) is equal to a weighted average of survival distributions of deterministic regimes.

To consistently estimate (5), we must slightly modify the algorithm described in §5 such that we

1. Add a step I.3: Fit a parametric model for treatment (for k = 0 to the maximum length of follow-up). Specifically model:

   $$f^{\mathit{\text{obs}}}(1|{\mathrm{l̄}}_k,A_{k-1}=0,{\overline{Y}}_k={\overline{C}}_k=0)=\text{Pr}[A_k=1|{\mathrm{l̄}}_k,A_{k-1}=0,{\overline{Y}}_k={\overline{C}}_k=0];$$

   that is, the probability of initiating treatment by k conditional on not having initiated prior to k, covariate history and surviving and remaining uncensored to k.
2. Change step II.2 to: Assign the treatment a_k,υ under x. Specifically:

   1. If r_k,υ(x) = 0 based on the previously drawn l̄_k,υ then set a_k,υ = 0;
   2. otherwise if r_k,υ(x) = 1 based on the the previously drawn l̄_k,υ then

      1. for m > 0, if r_k−m,υ(x) = 0 and a_k−1,υ = 1 then set a_k,υ = 1; otherwise if r_k−m,υ(x) = 0 and a_k−1,υ = 0 then draw a_k,υ from the estimated density in step I.3 based on previously drawn covariates l̄_k,υ and assigned treatment ā_k−1,υ under x;
      2. otherwise set a_k,υ = 1.

Under the data generating assumptions of §2, the estimation algorithm described here extends that described in Taubman et al (2009) and Robins et al (2004) to allow for incorporation of a priori knowledge of the observed data densities conditional on certain histories. This algorithm is implemented in a publicly available SAS macro which we used to obtain the results presented in §8 (http://www.hsph.harvard.edu/causal/software/).

7 Estimation of the risk under the “natural course”

The estimation procedure described in the previous sections relies heavily on the correct specification of parametric models for the conditional densities of the outcome and covariates. If the parametric modelling assumptions described in the appendix are incorrect, then our risk estimates will be biased. One way to explore the validity of our parametric assumptions is to use the above estimation procedure to estimate the mortality risk that would have been observed under no treatment intervention; equivalently, under a random dynamic regime where the intervention density is chosen to be f^obs(a_k|l̄_k, ā_k−1, Y̅_k = C̅_k = 0) at each k = 0, … , k. We refer to this risk as the “natural course” risk.

If censoring is independent – i.e. if $(Y_{k+1}^{\mathrm{c̄}=0},\dots ,Y_{K+1}^{\mathrm{c̄}=0})\coprod C_{k+1}|C_k=Y_k=0$, where ${\overline{Y}}_{K+1}^{\mathrm{c̄}=0}$ represents the outcome history had all subjects followed the “natural course” – the “natural course” risk by k + 1 should be equivalent to the observed risk by k + 1 in the study population. The former can be estimated by the algorithm described in the previous section by assigning a_k,υ for any k in step II according to the observed data treatment density. The latter is estimated as

$$1-\prod _{j=0}^k(1-\frac{e_k}{n_k})$$

where n_k is the number of individuals still at risk (alive and uncensored) at the beginning of month k and e_k is the number of individuals who died in month k + 1 amongst those still at risk at the beginning of month k.

Analogously, the observed means of the time-varying covariates and treatment in each month will be equivalent to those under the “natural course” under independent censoring for treatment, covariates and survival. Estimates of covariate means under the “natural course” may be obtained from the simulated data generated in the estimation algorithm described in §5 and §6.

Thus under independent censoring for both the outcome and covariates, any discrepancy between the observed and “natural course” estimates of risk and covariate means suggests misspecification of the parametric models described in the appendix. It follows, however, that if censoring is informative for the outcome or covariates, then discrepancy between these estimates may be all or partly due to the fact that the “natural course” estimands differ from the estimands to which our observed estimators converge.

To assess the possible role of random sampling variation in the differences between estimated observed and “natural course” survival and covariate means in each month we calculated point-wise 95% confidence intervals for these differences based on 500 bootstrap samples.

8 Data analysis

Table 1 presents characteristics of the 8, 392 study participants at baseline. Of these 8,392, 197 died, 4,006 were censored for having more than 12 consecutive months of unmeasured viral load or CD4 cell count, 3,985 by administrative end of follow-up and 204 by pregnancy. The proportion of subjects with a CD4 cell count above 350 cells/mm³ was 89%.

Table 1.

Characteristics of 8,392 therapy-naive HIV-infected individuals when CD4 first falls between 500 and 200^*, HIV-CAUSAL Collaboration

Characteristic		No. of individuals (%)
Sex	Male	6, 500 (77.5)
	Female	1, 892 (22.6)
Age, years	< 35	3, 391 (40.4)
	35 – 50	4,242 (50.6)
	> 50	759 (9.0)
Transmission group	Heterosexual	2, 457 (29.3)
	Homosexual	4, 122 (49.1)
	Injection drug use	779 (9.3)
	Other/Unknown**	1, 034 (12.3)
CD4 cell count, per mm3	200 – 349	914 (10.9)
	350 – 499	7, 478 (89.1)
HIV RNA, copies/mL	< 10,000	2, 767 (33.0)
	10,000 – 100,000	4, 255 (50.7)
	> 100,000	1, 370 (16.3)
Calendar year	1996 – 1998	1, 299 (15.5)
	1999 – 2000	1, 191 (14.2)
	2001 – 2003	2, 298 (27.4)
	≥ 2004	3, 604 (43.0)
Cohort	UK CHIC	1, 785 (21.3)
	ATHENA	650 (7.8)
	FHDH-ANRS CO4	3, 390 (40.4)
	SHCS	523 (6.2)
	PISCIS	343 (4.1)
	CoRIS	451 (5.4)
	Seroconverters	641 (7.6)
	VACS-VC	609 (7.3)

^*Table is identical to last two columns of Table 1 in Cain et al (2011)

^**Other/Unknown included all VACS-VC participants.

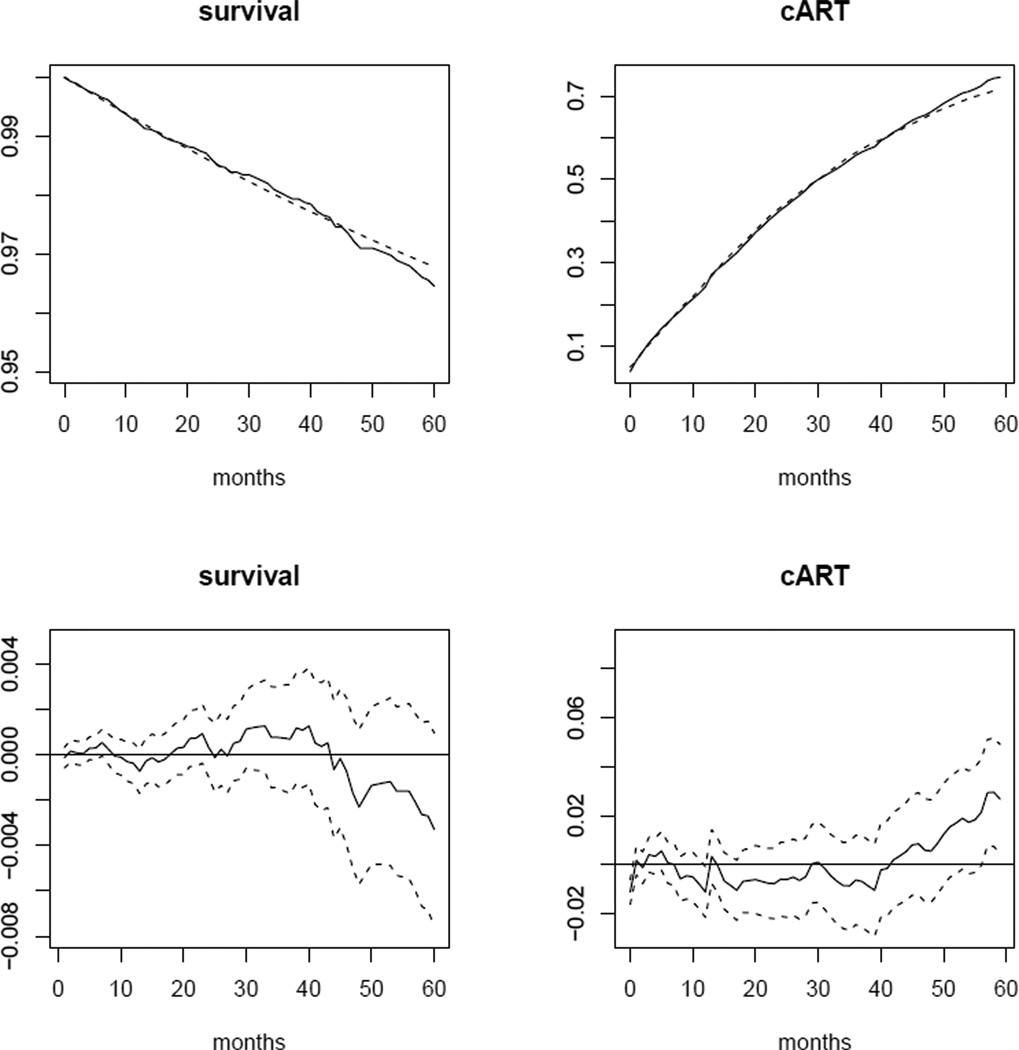
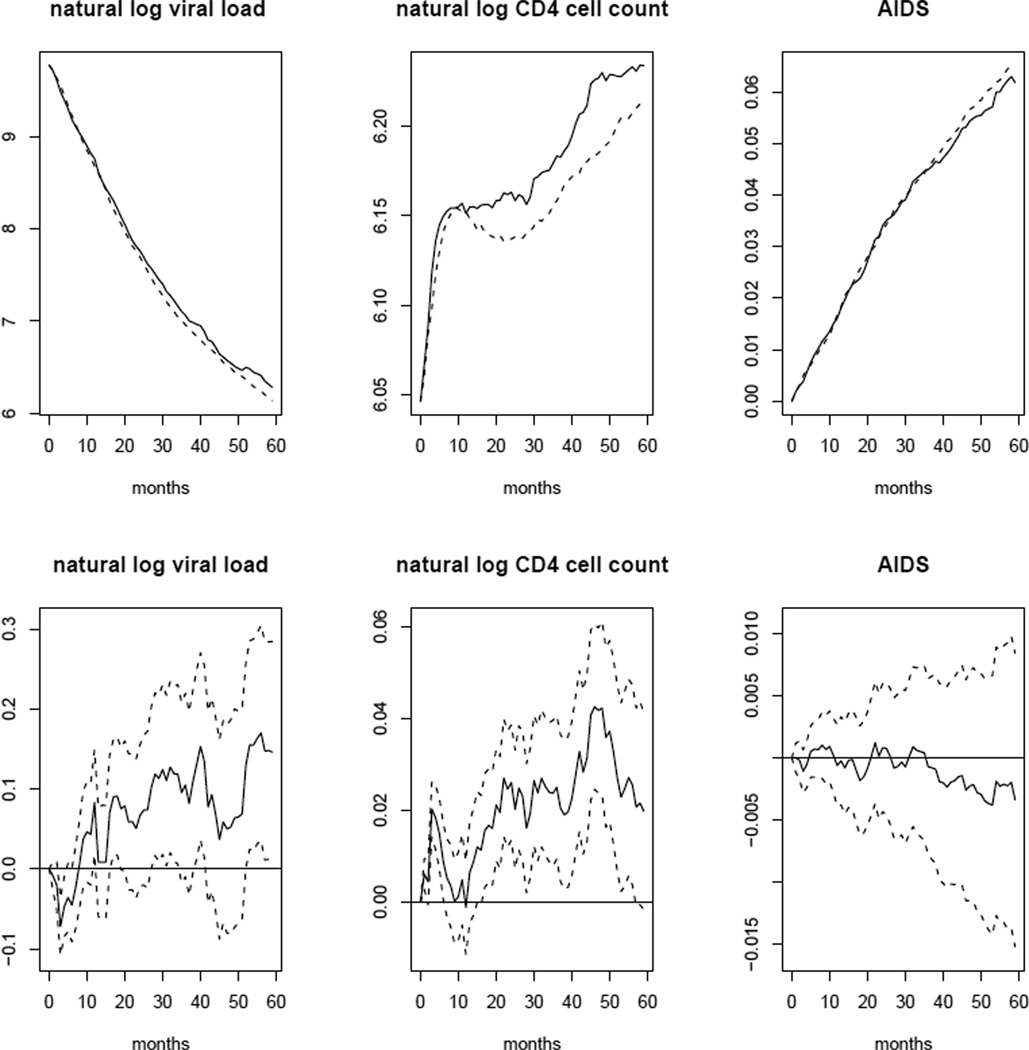
The top panel of Figure 1 shows estimates of observed and “natural course” survival, as well as means of the indicator of cART initiation by each month of follow-up in the population based on the estimators defined in §7. The bottom panel depicts differences between these estimates by month, along with point-wise 95% confidence intervals. Similarly, the top panel of Figure 2 presents the estimated observed and “natural course” means of natural log viral load, natural log CD4 cell count, and the indicator of AIDS-defining illness by follow-up month. Again, the bottom panel depicts differences and point-wise 95% confidence intervals. Only the point-wise confidence intervals for differences in survival and mean of the AIDS indicator contained zero for all months. The differences in means of natural log CD4 cell count and other variables, while small, may suggest misspecification of some of the parametric models described in the appendix. However, as discussed in §7, these discrepancies may also be due to informative censoring.

Fig. 1.

Top panel: estimated observed (solid line) and “natural course” (dotted line) survival and mean cART indicator by month. Bottom panel: estimated differences between observed and “natural course” survival and mean cART indicator by month (solid line) and point-wise 95% confidence intervals based on 500 bootstrap samples (dotted lines).

Fig. 2.

Top panel: estimated observed (solid line) and “natural course” (dotted line) mean natural log viral load, natural log CD4 cell count and AIDS indicator by month. Bottom panel: estimated differences between observed and “natural course” mean natural log viral load, natural log CD4 cell count and AIDS indicator by month (solid line) and point-wise 95% confidence intervals based on 500 bootstrap samples (dotted lines).

The estimated 5-year mortality risk and 95% confidence interval under the regime x = 500 with a grace period m = 6, specifically: “start cART 6 months after CD4 cell count first drops below 500 or diagnosis of an AIDS-defining illness, whichever happens first, if the subject is still at risk and has not initiated treatment during the 6-month grace period on her own”, was 2.65 (2.15, 3.43). The estimated 5-year risks for x = 350 and x = 200 were 3.06 (2.59, 3.67) and 3.65 (3.01, 4.44), respectively.

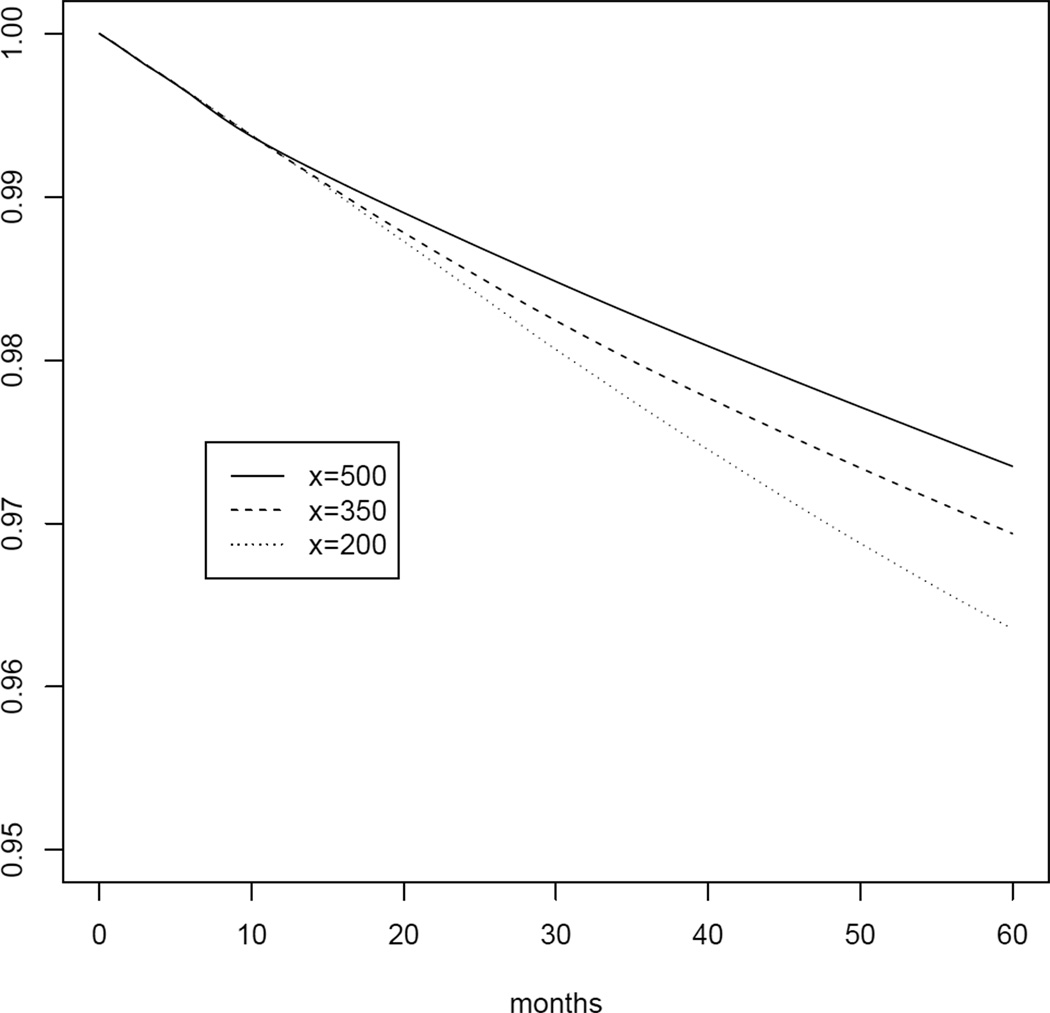
Table 2 presents the 5-year mortality risks as well as risk ratios and risk differences for the 7 random regimes with x between 200 and 500 in increments of 50 cells/mm³ and with a grace period m = 6 months. The risk was estimated to be 38% higher under regime x = 200 and 16% higher under regime x = 350 compared with x = 500. All 95% confidence intervals were based on 500 bootstrap samples. Figure 3 shows the survival estimates by month of follow-up under regimes x = 500, 350 and 200.

Table 2.

Five-year mortality risks, risk ratios, and risk differences under 7 regimes of the form “start cART 6 months after CD4 cell count first drops below x or diagnosis of an AIDS-defining illness, whichever happens first, if the subject is still at risk and has not initiated treatment during the 6-month grace period on her own”.

x	Risk (%)	Risk Ratio	Risk Difference
500	2.65 (2.15, 3.43)	1.00 (ref)	0.00 (ref)
450	2.77 (2.28, 3.47)	1.05 (0.99, 1.09)	0.12 (−0.02, 0.21)
400	2.92 (2.43, 3.55)	1.10 (0.99, 1.18)	0.27 (−0.02, 0.44)
350	3.06 (2.59, 3.67)	1.16 (1.00, 1.29)	0.41 (−0.01, 0.71)
300	3.22 (2.73, 3.81)	1.22 (1.02, 1.41)	0.57 (0.05, 0.99)
250	3.44 (2.87, 4.07)	1.30 (1.03, 1.55)	0.79 (0.08, 1.32)
200	3.65 (3.01, 4.44)	1.38 (1.05, 1.71)	1.00 (0.15, 1.76)

Fig. 3.

Survival by each month of follow-up k = 0, … , 60 under regimes “start cART 6 months after CD4 cell count first drops below x or diagnosis of an AIDS-defining illness, whichever happens first, if the subject is still at risk and has not initiated treatment during the 6-month grace period on her own” for x = 500, 350, 200

The estimated risk ratios and risk differences (with x = 500 reference group), were little changed by alternative modelling choices to those defined in the appendix including: addition of a knot at 50 to h(k), the function of month; addition of a knot at ln(700) to s₄(L_4,k), the function of CD4 cell count; replacement of I^*(t(L_1,k, L_3,k)), the indicator functions for categories of number of months since last measured CD4 cell count or viral load by month k, with linear and squared terms of number of months since either measurement by k; replacement of $A_k\times {\sum }_{j=0}^{k-1}{A}_j$, the interaction term between the treatment initiation indicator by k and number of months since treatment initiation by k − 1, with a vector of interaction terms, each component the product of the treatment initiation indicator by k and an indicator that number of months since initiating is in each of the categories (≤ 1, 2 – 10, 11 – 20, 21 – 40).

We also found estimates were not sensitive to restriction to follow-up starting in 1999 or later, restriction to men, restriction of step I of the algorithm in §5 to only the 60-month follow-up of interest (as opposed to using all 151 months of available follow-up), exclusion of injection drug users, alternative definitions of cART (Cole et al, 2003; Mocroft et al, 2007), and changing the criteria that an individual is censored in the observed data if she has had either no viral load or CD4 cell count measurement within the last 12 months to 18 months or 24 months. Alternative permutations of covariates within L_k (as described in §5) also did not have a substantial impact on mortality risk estimates, risk ratios or differences.

9 Discussion

We used the parametric g-formula to compare the effectiveness of several dynamic treatment regimes for cART initiation in HIV-infected patients. Specifically, we considered the 7 dynamic regimes “start cART 6 months after CD4 cell count first drops below x cells/mm³ or diagnosis of an AIDS-defining illness, whichever happens first, if the subject is still alive and has not initiated treatment during the 6-month grace period on her own” with x taking on values between 200 and 500 in increments of 50 cells/mm³. Our findings, which are based on observational data from the HIV-CAUSAL Collaboration, suggest that the 5-year mortality risk is lowest for x = 500 and increases as x decreases, i.e., when cART initiation is delayed.

The parametric g-formula is an alternative to IP weighting of dynamic marginal structural models to appropriately adjust for measured time-varying confounders when comparing the effectiveness and safety of dynamic interventions. Specifically, for a given target population and underlying observed data generating distribution, these two estimation methods can both give consistent estimates of the same counterfactual population parameter of interest (here, risk under a specified dynamic treatment regime). The consistency of each estimator will rely on the same identifying assumptions but will require parametric assumptions on different component densities of the observed data. Under correct parametric assumptions on these components, the parametric g-formula estimator will be more efficient than its IP weighted counterpart because the former is based on parametric maximum likelihood estimation (under the assumption of exchangeability) and the latter is a semi-parametric estimator. Further, unlike IP weighted estimators, parametric g-formula estimators do not generally become unstable in the presence of near violations of the positivity assumption (see Petersen et al, 2010 for a discussion).

These advantages of the parametric g-formula estimator are at the expense of a greater reliance on parametric assumptions and thus more opportunity for bias. That is, the validity of our parametric g-formula estimates requires correct specification of the conditional distribution of the outcome Y_k+1, the treatment A_k (because our regimes use the observed treatment density to assign treatment during the grace period, otherwise we would not have needed to specify this density) and each of the five time-varying covariates in L_k in all follow-up months k. In contrast, the validity of an analogous IP weighted estimate would require correct specification of the conditional distribution of the treatment A_k, the censoring indicator C_k+1, and the marginal structural model for the relation between x and the risk of death had all subjects followed x for all k.

Parametric g-formula estimators are further subject to the “g-null paradox” theorem, which implies it can be essentially impossible to specify correct parametric models under the causal null hypothesis (i.e. the true risk difference under any two choices of x is exactly zero). As a consequence, the method will reject the causal null even when true in sufficiently large samples. In this particular application, it is reasonable to assume that the causal null does not hold overall.

Doubly robust methods are alternative approaches to the parametric g-formula for estimating risk under interventions that do not involve the observed data treatment density. These estimators are then consistent if either the model for treatment given the past (as needed to implement IP weighting) is correctly specified or the models for the outcome and covariates given the past (as needed to implement the parametric g-formula) are correctly specified, without knowing which of the two sets of models is correct. See Bang and Robins (2005); van der Laan (2010a,b) for further discussion. We did not compute doubly robust estimators here as our regimes of interest involved the observed data treatment density, although, as discussed in §6, we might have chosen an alternative treatment assignment rule during the grace period. Further, the software required to compute such estimators in this context was unavailable.

The parametric g-formula algorithm described in §6 has been previously applied to compare the effectiveness of dynamic regimes involving lifestyle interventions (Robins et al, 2004; Taubman et al, 2009). In these previous applications, the follow-up was divided into 5 to 10 intervals during which time-varying variables were assessed. Our application of the parametric g-formula to the HIV-CAUSAL Collaboration demonstrates the computational feasibility of this software in settings with many more follow-up intervals - specifically, 60 intervals.

Cain et al (2010) described how to use IP weighting to compare the effectiveness of the 7 dynamic cART regimes considered here in the FHDH observational cohort (a subset of the HIV-CAUSAL Collaboration). Cain et al (2011) also used IP weighting to compare the effectiveness of similar dynamic regimes in the HIV-CAUSAL Collaboration. Table 3 shows estimated 5-year risks, risk ratios, and risk differences for x = 500, 350 and 200 reported in Cain et al (2011). The 95% confidence intervals for the IP weighted estimates of the risk ratio have substantial overlap with those for our parametric g-formula estimates. Further, the 95% confidence intervals for the IP weighted estimates of the risk ratios include the parametric g-formula estimates. As expected, the 95% confidence intervals around our parametric g-formula estimates are narrower than those around the IP weighted estimates.

Table 3.

Five-year mortality risks, risk ratios, and risk differences comparing cART initiation regimes with CD4 thresholds of x = 500, 350 and 200 cells/mm³ from Cain et al (2011).

x	Risk (%)	Risk Ratio	Risk Difference
500	2.45 (1.34,3.56)	1.00 (ref)	0.00 (ref)
350	2.43 (1.83,3.04)	0.99 (0.53, 1.46)	−0.02 (−1.20, 1.20)
200	2.91 (2.06,3.77)	1.19 (0.62,1.76)	0.50 (−0.80,1.80)

However, the estimates in Table 3 are not fully comparable with ours in Table 2 because Cain et al (2011) considered slightly different dynamic regimes. Specifically, these authors compared random regimes of the form “do not start cART while the CD4 cell count is at or above x cells/mm³, unless an AIDS-defining illness is diagnosed, and start cART 6 months after CD4 cell count first drops below x cells/mm³ or diagnosis of an AIDS-defining illness, whichever happens first, if the subject is still alive and has not initiated treatment during the 6-month grace period on her own” with x ranging from 500 to 200. That is, Cain et al (2011) considered interventions that started when patients had a CD4 cell count above 500 cells/mm³ rather than (as we did) when their CD4 cell count first dropped below 500 cells/mm³.

When possible, we recommend using both the parametric g-formula and IP weighting for comparative effectiveness research. Similar estimates from the two methods will increase our confidence in the results as each requires parametric assumptions on different components of the observed data generating distribution. Discrepant estimates will force us to question our parametric assumptions for one or both estimators.

Appendix

10.1 Parametric modelling assumptions

Results provided in §8 are based on the following set of parametric modelling assumptions for step I of the estimation algorithm described in the main text:

1. Models for densities of covariates (for k = 1 to maximum length of follow-up):

   1. $\text{logit}\{\text{Pr}[L_{1,k}=1|{\overline{L}}_{k-1}={\mathrm{l̄}}_{k-1},{Ā}_{k-1}={ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0]\}={\beta }_{l_1}^T{X}_{l_{1,k}}$ where β_l1 is a coefficient vector, X_l1,k is the vector

      $$\{1,V,h(k),s_2(L_{2,k-1}),s_2(L_{2,k-2}),s_4(L_{4,k-1}),s_4(L_{4,k-2}),L_{5,k-1},I^{*}(t(L_{1,k-1},L_{3,k-1})),A_{k-1},A_{k-1}\times \sum _{j=0}^{k-1}{A}_j\}$$

      and

      • –
        h(k) contains terms based on transformation of k needed to fit a restricted cubic spline with knots (1, 6, 24, 132);
      • –
        s₂(L_2,j) contains terms based on transformation of L_2,j needed to fit a restricted cubic spline with knots (6.215, 7.601, 9.211, 10.597, 11.513) for j = 0, … , K and s₂(L_2,−1) = 0;
      • –
        s₂(L_4,j) contains terms based on transformation of L_4,j needed to fit a restricted cubic spline with knots (3.912, 4.605, 5.298, 5.858, 6.215) for j = 0, … , K and s₄(L_4,−1) = 0;
      • –
        t(L_1,j, L_3,j) is number of months since last measured CD4 cell count or viral load by month j for j = 0, … K and t(L_1,−1, L_3,−1) = 0;
      • –
        I^*{t(L_1,j, L_3,j)} is a vector of the following indicator variables: {I(t(L_1,j, L_3,j) < 1), I(1 < t(L_1,j, L_3,j) ≤ 3), I(3 < t(L_1,j, L_3,j) ≤ 5), I(5 < t(L_1,j, L_3,j) ≤ 7)}, j = 0, … K.

      Note that, by the definition of A_j, ${\sum }_{j=0}^{k-1}{A}_j$ represents the number of months since treatment initiation by k − 1.
   2. $L_{2,k}={\beta }_{l_2}^T{X}_{l_{2,k}}+{\epsilon }_2$ where β_l2 is a coefficient vector, X_l2,k = X_l1,k and ε₂ is distributed $𝒩(0,{\sigma }_2^2)$.
   3. $\text{logit}\{\text{Pr}[L_{3,k}=1|l_{2,k},l_{1,k},{\mathrm{l̄}}_{k-1},{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0]\}={\beta }_{l_{3,k}}^T{X}_{l_{3,k}}$ where β_l3,k is a coefficient vector and X_l3,k = {X_l2,k, s₂(L_2,k), L_1,k}.
   4. $L_{4,k}={\beta }_{l_4}^T{X}_{l_{4,k}}+{\epsilon }_4$ where β_l4 is a coefficient vector, X_l4,k = X_l3,k and ε₄ is distributed $𝒩(0,{\sigma }_4^2)$.
   5. $\text{logit}\{\text{Pr}[L_{5,k}=1|{\mathrm{l̄}}_{4,k},{\mathrm{l̄}}_{3,k},{\mathrm{l̄}}_{2,k},{\mathrm{l̄}}_{1,k},L_{5,k-1}=0,{ā}_{k-1},{\overline{Y}}_k={\overline{C}}_k=0]\}={\beta }_{l_5}^T{X}_{l_{5,k}}$ where β_l5 is a coefficient vector and X_l5,k = {X_l4,k, s₄(L_4,k), L_3,k}
2. Model for the outcome (for k = 0 to maximum length of follow-up): $\text{logit}\{\text{Pr}[Y_{k+1}=1|{\overline{L}}_k={\mathrm{l̄}}_k,{Ā}_k={ā}_k,{\overline{Y}}_k={\overline{C}}_{k+1}=0]\}={\beta }_y^T{X}_{y_k}$ where β_y is a coefficient vector and X_yk is the vector

   $$\{1,V,h(k),s_2(L_{2,k}),s_2(L_{2,k-1}),s_4(L_{4,k}),s_4(L_{4,k-1}),L_{5,k},I^{*}(t(L_{1,k},L_{3,k})),A_k,A_k\times \sum _{j=0}^k{A}_j\}$$
3. Model for treatment (for k = 0 to maximum length of follow-up): $\text{logit}\{\text{Pr}[A_k=1|{\overline{L}}_k={\mathrm{l̄}}_k,A_{k-1}=0,{\overline{Y}}_k={\overline{C}}_k=0]\}={\beta }_a^T{X}_{a_k}$ where β_a is a coefficient vector and X_ak is the vector

   $$\{1,V,h(k),s_2(L_{2,k}),s_2(L_{2,k-1}),s_2(L_{2,k-2}),s_4(L_{4,k}),s_4(L_{4,k-1}),s_4(L_{4,k-2}),L_{5,k},L_{5,k-1},I^{*}(t(L_{1,k},L_{3,k}))\}$$

Note that ${\sigma }_2^2$ and ${\sigma }_4^2$ were estimated by the sample variances of viral load and CD4 cell count over all person-months, respectively. Further, in step II of the estimation algorithm, simulated values of these covariates were truncated to the observed minimum (if below) and maximum (if above).

10.2 Proof of equivalence between the g-formula and survival by k +1 had all subjects followed a dynamic regime

10.2.1 Deterministic dynamic regimes

Here we present a proof of the equivalence between $\text{Pr}[Y_{k+1}^g=0]$ and the g-formula (2) for any deterministic dynamic regime g under the interval-censored data structure described in §2.

Assume the identifying conditions of §4 hold.

In the following set ${Ā}_{t-1}={ā}_{t-1}^g$, t ≤ k. If f(L̅_t, Ā_t−1, C_t = 0, Y_t = 0) ≠ 0 then define $b^g(k,{\overline{L}}_t,{Ā}_{t-1})=\text{Pr}[Y_{k+1}^g=0|{\overline{L}}_t,{Ā}_{t-1},C_t=Y_t=0]$. Note that by $b^g(k,{\overline{L}}_{-1},{Ā}_{-2})=\text{Pr}[Y_{k+1}^g=0]$ definition.

By the definition of $Y_{k+1}^g$ we have

$$b^g(k,{\overline{L}}_t,{Ā}_{t-1})=\text{Pr}[Y_{t+1}^g=\dots =Y_{k+1}^g=0|{\overline{L}}_t,{Ā}_{t-1},C_t=Y_t=0]$$

By exchangeability and positivity

$$b^g(k,{\overline{L}}_t,{Ā}_{t-1})=\text{Pr}[Y_{t+1}^g=\dots =Y_{k+1}^g=0|A_t=a_t^g,{\overline{L}}_t,{Ā}_{t-1},C_{t+1}=Y_t=0]$$

By consistency and probability rules

$$b^g(k,{\overline{L}}_t,{Ā}_{t-1})=\text{Pr}[Y_{t+2}^g=\dots =Y_{k+1}^g=0|A_t=a_t^g,{\overline{L}}_t,{Ā}_{t-1},C_{t+1}=Y_{t+1}=0]\times \text{Pr}[Y_{t+1}=0|A_t=a_t^g,{\overline{L}}_t,{Ā}_{t-1},C_{t+1}=Y_t=0]$$

By probability rules

$$b^g(k,{\overline{L}}_t,{Ā}_{t-1})=\sum _{l_{t+1}}\text{Pr}[Y_{t+2}^g=\dots =Y_{k+1}^g=0|L_{t+1}=l_{t+1},A_t=a_t^g,{\overline{L}}_t,{Ā}_{t-1},C_{t+1}=Y_{t+1}=0]\times f(l_{t+1}|{ā}_t^g,{\mathrm{l̄}}_{t-1},C_{t+1}=Y_{t+1}=0)\times \text{Pr}[Y_{t+1}=0|A_t=a_t^g,{\overline{L}}_t,{Ā}_{t-1},C_{t+1}=Y_t=0]$$

By exchangeability and positivity

$$b^g(k,{\overline{L}}_t,{Ā}_{t-1})=\sum _{l_{t+1}}\text{Pr}[Y_{t+2}^g=\dots =Y_{k+1}^g=0|A_{t+1}=a_{t+1}^g,L_{t+1}=l_{t+1},A_t=a_t^g,{\overline{L}}_t,{Ā}_{t-1},C_{t+2}=Y_{t+1}=0]\times f(l_{t+1}|{ā}_t^g,{\mathrm{l̄}}_{t-1},C_{t+1}=Y_{t+1}=0)\times \text{Pr}[Y_{t+1}=0|A_t=a_t^g,{\overline{L}}_t,{Ā}_{t-1},C_{t+1}=Y_t=0]$$

Arguing recursively we have for j = 0, … , k

$$b^g(k,{\overline{L}}_{j-1},{Ā}_{j-2})=\sum _{l_j}\cdots \sum _{l_k}\text{Pr}[Y_{k+1}^g=0|A_j=a_j^g,\dots ,A_k=a_k^g,L_j=l_j,\dots ,L_k=l_k,{\overline{L}}_{j-1},{Ā}_{j-2},C_{k+1}=Y_k=0]\times \prod _{s=j}^k\{f(l_s|{ā}_{s-1}^g,{\mathrm{l̄}}_{s-1},C_s=Y_s=0)\times \text{Pr}[Y_s=0|{\overline{L}}_{s-1},{Ā}_{s-1},C_s=Y_{s-1}=0]\}$$

The result follows by setting j = 0 and invoking consistency once more such that we have

$$b^g(k,{\overline{L}}_{-1},{Ā}_{-2})=\text{Pr}[Y_{k+1}^g=0]=\sum _{{\mathrm{l̄}}_k}\text{Pr}[Y_{k+1}=0|{\overline{L}}_k={\mathrm{l̄}}_k,{Ā}_k={ā}_k^g,C_{k+1}=Y_k=0]\times \prod _{s=0}^k\{f(l_s|{ā}_{s-1}^g,{\mathrm{l̄}}_{s-1},C_s=Y_s=0)\times \text{Pr}[Y_s=0|{\overline{L}}_{s-1},{Ā}_{s-1},C_s=Y_{s-1}=0]\}$$ (7)

10.2.2 Random dynamic regimes

We will show that the generalized g-formula (6) is a particular weighted average of the g-formula (2) for the survival probabilities associated with the set of all deterministic dynamic regimes that a) satisfy positivity under the joint distribution of the data when f^obs(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0) is replaced by f^x(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0) and b) only depend on past covariate history. Now (i), under our exchangeability and consistency assumptions, the g-formula (2) for the survival probabilities associated with any deterministic dynamic regimes satisfying positivity is equal to the counterfactual survival probability had all subjects followed that regime and (ii) a random dynamic regime satisfies our exchangeability and consistency assumptions. It follows that the the survival probabilities of the random dynamic regime with intervention density f^x(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0) is also given by (6) and equals the aforementioned weighted average of the survival probabilities associated with the set of deterministic dynamic regimes satisfying positivity under f^x(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0) that only depend on past covariate history.

Let g_t : l̄_t ↦ g_t (l̄_t) denote a function with domain ℒ̅_t and range A_t. Then the deterministic dynamic regime g ≡ ḡ : l̄ ↦ ḡ (l̄), ḡ (l̄) ∈ 𝒜 (that only depends on past covariate history) is the vector (g_t; t = 0, …, K). Let $“\text{Pr}”[Y_t^g=0]$ denote the survival probability through t given by the g-formula (2) for the deterministic dynamic regime g where the quotes around “Pr” denote the formal survival probability given by this expression. Note $“\text{Pr}”[Y_t^g=0]$ equals the true counterfactual survival probability $\text{Pr}[Y_t^g=0]$ under our identifying conditions.

Let f^x(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0) be the intervention density defined in the main text.

Let 𝒢̅ denote the set of all such dynamic regimes (that only depends on past covariate history) for which positivity holds under intervention density f^x(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0). Let |𝒢| denote its cardinality.

We now use f^x(a_s|l̄_s, ā_s−1, Y̅_s = C̅_s = 0) to a construct a specific density q : g ↦ q {g} for regimes in 𝒢̅. Note as a density ${\sum }_{j=1}^{|\overline{𝒢}|}q\{g^j\}=1$ and q {g^j} ≥ 0, g^j ∈ 𝒢̅. Our density is constructed as follows.

Given g ∈ 𝒢̅, let $f_t(a_t^g|{ā}_{t-1}^g,{\mathrm{l̄}}_t)$ equal the intervention density f^x(a_t|l̄_t, ā_t−1, Y̅_t = C̅_t = 0) evaluated at ${ā}_t^g$, where ${ā}_t^g$ in $f_t(a_t^g|{ā}_{t-1}^g,{\mathrm{l̄}}_t)$ is the treatment history determined by g and l̄_t.

In the following we assume L_t is discrete and we choose an ordering such that {l_t,1, …, l_t,|ℒt|} = ℒ_t, with ℒ_t the support of L_t and |ℒ_t| its cardinality.

Let $q_K^g({\mathrm{l̄}}_{K-1})=\prod _{h=1}^{|{ℒ}_K|}{f}_K(a_K^g|{ā}_{K-1}^g,{\mathrm{l̄}}_{K-1},{\mathrm{l̄}}_{K,h})$. For t = K − 1, …, 0, let $q_t^g({\mathrm{l̄}}_{t-1})=\prod _{h=1}^{|{ℒ}_t|}{f}_t(a_t^g|{ā}_{t-1}^g,{\mathrm{l̄}}_{t-1},l_{t,h})q_{t+1}^g({\mathrm{l̄}}_{t-1},l_{t,h})$. Let $q(g)=q_0^g$.

The following is Lemma 4.2 in Robins (1986) with his γ (·i_tj_t) equal to f^x(a_t|l̄_t, ā_t−1, Y̅_t = C̅_t = 0) and his m^A equal to q. The proof of Robins’ Lemma (4.2) is immediate from his tree graph representation of the distribution of the data.

Theorem: Given f^x(a_t|l̄_t, ā_t−1, Y̅_t = C̅_t = 0) and derived density q(g), g ∈ 𝒢̅, then expression (6) through t equals

$$\sum _{j=1}^{|𝒢|}q(g^j)“\text{Pr}”[Y_t^{g_j}=0]$$