Genetic Evidence for Recent Population Mixture in India

Abstract

Most Indian groups descend from a mixture of two genetically divergent populations: Ancestral North Indians (ANI) related to Central Asians, Middle Easterners, Caucasians, and Europeans; and Ancestral South Indians (ASI) not closely related to groups outside the subcontinent. The date of mixture is unknown but has implications for understanding Indian history. We report genome-wide data from 73 groups from the Indian subcontinent and analyze linkage disequilibrium to estimate ANI-ASI mixture dates ranging from about 1,900 to 4,200 years ago. In a subset of groups, 100% of the mixture is consistent with having occurred during this period. These results show that India experienced a demographic transformation several thousand years ago, from a region in which major population mixture was common to one in which mixture even between closely related groups became rare because of a shift to endogamy.

Introduction

Genetic evidence indicates that most of the ethno-linguistic groups in India descend from a mixture of two divergent ancestral populations: Ancestral North Indians (ANI) related to West Eurasians (people of Central Asia, the Middle East, the Caucasus, and Europe) and Ancestral South Indians (ASI) related (distantly) to indigenous Andaman Islanders.¹ The evidence for mixture was initially documented based on analysis of Y chromosomes² and mitochondrial DNA^3–5 and then confirmed and extended through whole-genome studies.^6–8

Archaeological and linguistic studies provide support for the genetic findings of a mixture of at least two very distinct populations in the history of the Indian subcontinent. The earliest archaeological evidence for agriculture in the region dates to 8,000–9,000 years before present (BP) (Mehrgarh in present-day Pakistan) and involved wheat and barley derived from crops originally domesticated in West Asia.^9,10 The earliest evidence for agriculture in the south dates to much later, around 4,600 years BP, and has no clear affinities to West Eurasian agriculture (it was dominated by native pulses such as mungbean and horsegram, as well as indigenous millets¹¹). Linguistic analyses also support a history of contacts between divergent populations in India, including at least one with West Eurasian affinities. Indo-European languages including Sanskrit and Hindi (primarily spoken in northern India) are part of a larger language family that includes the great majority of European languages. In contrast, Dravidian languages including Tamil and Telugu (primarily spoken in southern India) are not closely related to languages outside of South Asia. Evidence for long-term contact between speakers of these two language groups in India is evident from the fact that there are Dravidian loan words (borrowed vocabulary) in the earliest Hindu text (the Rig Veda, written in archaic Sanskrit) that are not found in Indo-European languages outside the Indian subcontinent.^12,13

Although genetic studies and other lines of evidence are consistent in pointing to mixture of distinct groups in Indian history, the dates are unknown. Three different hypotheses (which are not mutually exclusive) seem most plausible for migrations that could have brought together people of ANI and ASI ancestry in India. The first hypothesis is that the current geographic distribution of people with West Eurasian genetic affinities is due to migrations that occurred prior to the development of agriculture. Evidence for this comes from mitochondrial DNA studies, which have shown that the mitochondrial haplogroups (hg U2, U7, and W) that are most closely shared between Indians and West Eurasians diverged about 30,000–40,000 years BP.^3,14 The second is that Western Asian peoples migrated to India along with the spread of agriculture; such mass movements are plausible because they are known to have occurred in Europe as has been directly documented by ancient DNA.^15,16 Any such agriculture-related migrations would probably have begun at least 8,000–9,000 years BP (based on the dates for Mehrgarh) and may have continued into the period of the Indus civilization that began around 4,600 years BP and depended upon West Asian crops.¹⁷ The third possibility is that West Eurasian genetic affinities in India owe their origins to migrations from Western or Central Asia from 3,000 to 4,000 years BP, a time during which it is likely that Indo-European languages began to be spoken in the subcontinent. A difficulty with this theory, however, is that by this time India was a densely populated region with widespread agriculture, so the number of migrants of West Eurasian ancestry must have been extraordinarily large to explain the fact that today about half the ancestry in India derives from the ANI.^18,19 It is also important to recognize that a date of mixture is very different from the date of a migration; in particular, mixture always postdates migration. Nevertheless, a genetic date for the mixture would place a minimum on the date of migration and identify periods of important demographic change in India.

Material and Methods

Data Sets

To learn about population history in India at higher resolution than was previously possible, we assembled genome-wide data for 571 individuals from 73 well-defined ethno-linguistic groups from South Asia (71 Indian and 2 Pakistani groups). We refer to all these groups in what follows as “Indian.” For samples genotyped on Affymetrix 6.0 arrays, we required at least 99% completeness for all SNPs and samples; this resulted in 383 individuals from 52 groups (27 groups newly genotyped for this study)¹ genotyped at 494,863 SNPs. For samples genotyped on Illumina 650K arrays, we required at least 95% completeness, yielding 188 individuals from 21 groups^7,20 genotyped at 543,980 SNPs. Sample collection was in accordance with the ethical standards of the responsible committees on human experimentation (institutional and national), and informed consent consistent with genetic studies of population history was obtained from all participants.

We filtered the data set in two stages. First, we filtered out data from 49 individuals with the following characteristics: (1) duplicate individuals (for each pair of individuals that match at least 90% of genotypes, we remove one individual); (2) related individuals (for mother-father-child trios we exclude the child, and for first-degree relative pairs we remove one of the two individuals); (3) all individuals previously excluded by Metspalu et al.;⁷ and (4) six Pakistani groups (Hazara, Kalash, Burusho, Makrani, Balochi, and Brahui) that had previously been shown to have a complex history involving more than a simple mixture of two ancestral populations¹ (Table S1 available online). Second, we excluded an additional 194 individuals based on principal component analysis (PCA): (1) all individuals with evidence of recent ancestry from populations other than ANI and ASI^1,21 or visual identification of outliers in Figure 1, which led us to exclude all Austro-Asiatic and Tibeto-Burman speakers; (2) all individuals from groups that were not homogenous in PCA in the sense of having multiple clusters in the scatterplot; and (3) individuals who were ancestry outliers compared with the majority of individuals from their own group based on visual inspection of the PCA clusters (Table S1). After curation, we had 211 individuals (30 groups) genotyped on Affymetrix arrays and 117 individuals (15 groups) genotyped on Illumina arrays.

Figure 1.

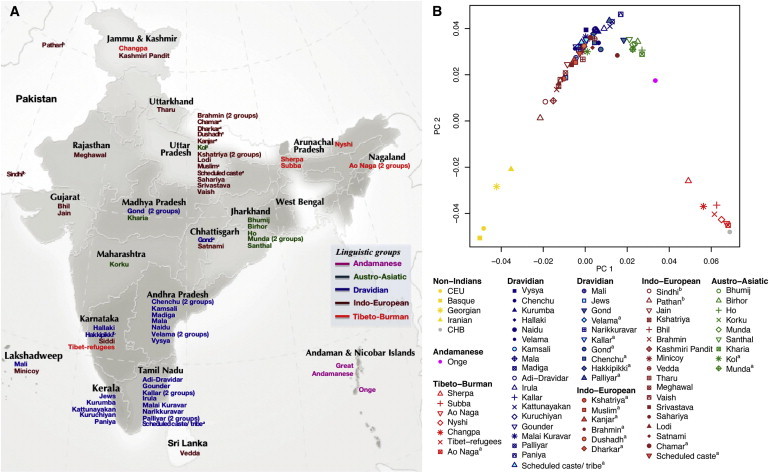
Principal Component Analysis

(A) Map showing the sampling locations for Indian groups in our study (except central_mix1_nihali⁷).

(B) Principal component analysis (PCA) of 70 of 73 groups with non-Indians (European Americans [CEU], Georgian, Iranian, Basque, and Han Chinese [CHB]) highlights the “Indian cline,” a gradient of West Eurasian relatedness. Great Andamanese and Siddi are not included because of their evidence of relatively recent admixture with non-Indian groups, and central_mix1_nihali⁷ is not included because it includes multiple ethno-linguistic groups under one label. To aid visualization, we represent each group by the average PCA coordinates of all the individuals in it. Footnote a indicates groups from Metspalu et al.⁷ and footnote b indicates groups from HGDP.

We coanalyzed the Indian data with HGDP-CEPH data from 51 groups (257 individuals genotyped on Affymetrix 500K SNP arrays²² and 940 on Illumina 650K arrays²⁰); International Haplotype Map Phase 3 (HapMap) data from 11 groups (1,158 individuals genotyped on Affymetrix 6.0 arrays and Illumina 1M arrays²³); Behar et al.²⁴ data from 41 groups (466 individuals genotyped on Illumina 610K arrays); and Yunusbayev et al.²⁵ data from 13 groups (214 individuals genotyped on Illumina 610K arrays). Our “Affymetrix” merged data set consisted of 210,482 SNPs obtained by merging data from 211 Indians (30 groups) with data from non-Indians typed on Affymetrix arrays (HapMap and Affymetrix HGDP). Our “Illumina” merged data set consisted of 500,703 SNPs obtained by merging data from 117 Indians (15 groups) with data from non-Indians typed on Illumina arrays (HapMap, Illumina HGDP; Behar et al.,²⁴ and Yunusbayev et al.²⁵). Our “Illumina-Affymetrix” merged data set consisted of an intersection of these two data sets and included 328 Indian individuals (45 groups) genotyped at 86,213 SNPs.

F₄ Ratio Estimation

We use f₄ ratio estimation as implemented in ADMIXTOOLS²⁶ to estimate the proportion of ANI ancestry in Indian groups. Specifically, we compute the ANI ancestry proportion (α) as:

$$\alpha =\frac{f_4\left(YRI,Basque;India,Onge\right)}{f_4\left(YRI,Basque;Georgians,Onge\right)}.$$ (Equation 1)

This assumes the model of Figure S1 with Pop1 = Georgians and Pop2 = Basque.

For f₄ ratio estimation to provide unbiased results, it requires access to four outgroup populations that branch off at four distinct positions on the ancestral lineage relating ANI and ASI.²⁶ We chose to work with Yoruba (YRI), Andamanese (Onge),²⁷ and two West Eurasian populations (Pop1 and Pop2) that are at successively increasing phylogenetic distances from the ANI (that is, the tree for West Eurasian populations is (Pop2, (Pop1, ANI))) (Figure S1). We first searched for a population to use as Pop1. For each Indian group (X), we compute D(Onge, X; YRI, Y) where Y = any West Eurasian population from a panel of 43 groups including Europeans, Central Asians, Middle Easterners, and Caucasians. For all 45 Indian groups on the Indian cline (described in the Results section), we find that Georgians along with other Caucasus groups are consistent with sharing the most genetic drift with ANI (Tables S2 and S3), as was also previously observed in Metspalu et al.⁷ based on clustering analysis. Therefore, we use Georgians as Pop1 (Figure S1). We next determined a second population to use as Pop2. We examined all possible West Eurasian populations to find groups that provide a good fit to the model (YRI, (Pop2, (Georgians, ANI)), [(ASI, Onge])) by using our admixture graph phylogeny testing software.²⁶ Within the limits of our resolution, we find six groups (Pop2 = Italian, Tuscan, Basque, Kurd, Abhkasian, Spaniard) that are consistent with this model in the sense that none of the f statistics relating the groups are greater than three standard errors from expectation. To evaluate the uncertainty in the ANI ancestry proportions ranging over these six candidates for Pop2, we ran f₄ ratio estimation with two choices of Pop2 representing different geographic extremes (Pop2 = Abhkasian and Pop2 = Basque). We obtain similar ANI ancestry estimates (Table S4). Our ancestry estimates are also statistically consistent (within two standard errors) with those of Reich et al.¹ (Table S4).

Estimating Admixture Dates via Rolloff

For each pair of SNPs (x,y) separated by a distance d Morgans, we compute the covariance between (x,y), which we use to measure the linkage disequilibrium (LD) resulting from population mixture. Specifically, we use the rolloff^26,28,29 statistic

$$R\left(d\right)=\frac{\sum _{|x-y|\approx d}z\left(x,y\right)w\left(x,y\right)}{\sum _{|x-y|\approx d}w{\left(x,y\right)}^2},$$ (Equation 2)

where z(x,y) is the covariance between SNPs x and y, and w(x,y) is a weight function. The weight can be either (1) the allele frequency difference between the two groups we use as surrogates for the ancestors (Europeans, Onge), (2) the allele frequency difference between a tested Indian group and one reference group (Europeans), or (3) the PCA-based loadings for SNPs (x, y) computed by performing PCA with Europeans and various Indian cline groups. We plot the weighted covariance with distance and obtain a date by fitting an exponential function with an affine term $y=A{e}^{-nd}+c$, where d is the distance in Morgans and we interpret n as the number of generations since admixture. We compute standard errors with a weighted block jackknife,³⁰ with one chromosome dropped per run.

Admixture Dates and Their Difference in Indo-European and Dravidian Speakers

For many analyses in this study, we cluster Indians into two categories based on their linguistic affiliation: “Indo-Europeans” to indicate groups that speak Indo-European languages and “Dravidians” to indicate groups that speak Dravidian languages. For the dating analysis shown in Figure 2, we applied rolloff to the merged Illumina-Affymetrix data set of 86,213 SNPs, with weights from PCA-based SNP loadings computed with Basque and speakers of the language group other than the one being analyzed (for example, for estimating the dates of mixture for Indo-Europeans, we use Dravidians and Basque to compute the PCA-based SNP loadings). To compute the significance of the difference in the date estimates, we leave out each of the 22 chromosomes in turn and use a weighted block jackknife procedure to convert the variability into a standard error. As a robustness check, we repeat this analysis with the Affymetrix data set of 210,482 SNPs for the four Indo-European and five Dravidian groups that we found were consistent with a simple ANI-ASI mixture (described in the Results section). For this analysis we use Basque and all other Indian cline groups to compute SNP loadings. We confirm a younger date for Indo-Europeans than for Dravidians, with the difference of 44 ± 18 generations being statistically significant at Z = 2.4 standard errors from zero.

Figure 2.

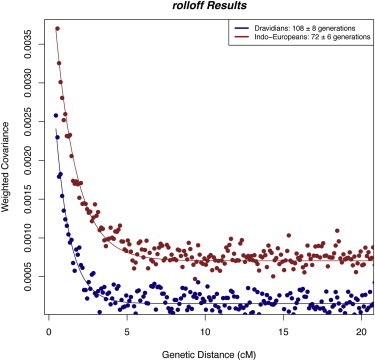
Dates of Mixture

We pool samples based on linguistic affiliation (Indo-Europeans [n = 175] and Dravidians [n = 144]) and run rolloff (with the merged Illumina-Affymetrix data set of 86,213 SNPs) to measure the LD resulting from mixture between ANI and ASI. To obtain weights proportional to the allele frequency differences between ANI and ASI at each SNP (needed to run rolloff), we use SNP loadings obtained from a PCA of Basque and a pool of groups from the linguistic cluster whose admixture is not being dated (e.g., we run PCA with Indo-European and Basque when we are dating Dravidian admixture). The output of rolloff is represented as points and the line shows the exponential fit $\left(y=A{e}^{-nd}+c\right)$ used for estimating the time in generations (n) since mixture. The nonzero constant c allows for variability in the mixture proportion among the groups we pooled and d is the genetic distance in Morgans. Standard errors are computed via a weighted block jackknife (see Material and Methods).

Identifying Groups Consistent with Simple ANI-ASI Admixture

For each of the 37 Indian groups including Onge (this is less than the total number of groups on the Indian cline because we applied a minimum sample size requirement of 5), we tested whether they are consistent with deriving all their ancestry from the same ANI and ASI ancestral populations by studying the matrix of all possible statistics of the form f₄(Indian_base, Indian_other; NonIndian_base, NonIndian_other) with a panel of 38 non-Indian populations. Many f₄ statistics can be written as linear combinations of each other, and therefore we need to pick a basis for the space of f₄ statistics. In practice, we fix one Indian group as “Indian_base” and compute the f₄ statistic for each of the 36 remaining Indian groups as “Indian_other.” We use an African group (YRI) as “NonIndian_base” and the “NonIndian_other” groups include Dai, Papuans, Karitiana, and diverse West Eurasian groups including Europeans, Middle Easterners, and Caucasians (the choice of base has no mathematical impact on the test). To identify sets of Indian groups consistent with having the same relationship to the panel of non-Indians, we use a Hotelling T test as in Reich et al.³¹ to evaluate whether the matrix of all f₄ statistics has exactly one linearly independent component (rank 1). For sets of Indian groups that are consistent with being rank 1, we also run the admixture graph testing software to evaluate whether the relationships in Figure S1 (where Pop1 = Georgians, Pop2 = Basque) are consistent with the data. We began by applying this procedure to all possible sets of three Indian groups. For the sets that passed, we added each possible fourth Indian group in turn and tested the consistency with a simple ANI-ASI mixture. We applied this process iteratively until no additional Indian groups could be added to the rank 1 set.

Admixture Graph Analysis

We applied the admixture graph²⁶ formal phylogeny testing software to evaluate whether the model of simple ANI-ASI admixture in rank 1 Indo-European and Dravidian groups provides a fit to the data. Admixture graph studies the correlations in allele frequency differentiation statistics (f₂, f₃, and f₄)²⁶ among groups, comparing the observed values to those specified by the model (with a standard error from a block jackknife) to test hypotheses about population relationships. To test whether a proposed model provides a fit to the data, the software examines individual f statistics and considers statistics more than three standard errors from expectation to be indicative of a poor fit. We also use this method to estimate the internal genetic drift lengths required by ALDER for estimating admixture proportions (on the lineages separating (ANI, X”) and (ASI, X”) in Figure S2).

Estimating the Date and Proportion of Mixture via ALDER

We run ALDER³² with one reference population (a West Eurasian group; we tried seven diverse West Eurasian groups). The ALDER statistic for measuring admixture LD is similar to the rolloff statistic:

$$a\left(d\right)=\frac{\sum _{S\left(d\right)}z\left(x,y\right)w\left(x,y\right)}{\left|S\left(d\right)\right|}.$$ (Equation 3)

As before, z(x,y) is the covariance between SNPs x and y. Here w(x,y) is the product of the allele frequency differences at x and y between the two reference groups (in this case, a West Eurasian group and the admixed group itself), and $S\left(d\right)=\left\{\left(x,y\right):|x-y|<d-\epsilon /2\right\}$ (where ε is a discretization parameter).

We plot the weighted covariance against genetic distance and perform a least-squares fit by $y=A{e}^{-nd}+c$, where n is the number of generations since admixture and d is the genetic distance in Morgans. Under a single-wave mixture model, the amplitude of admixture LD decay defined as $a_o=A+c/2$ is analytically predicted by the ANI ancestry proportion (α):

$$a_o=2\alpha \left(1-\alpha \right){\left(\alpha f_2\left(ANI,X^{\text{″}}\right)-\left(1-\alpha \right)f_2\left(ASI,X^{\text{″}}\right)\right)}^2.$$ (Equation 4)

Here, X″ is the common ancestor of the reference West Eurasian group (X) and the ANI lineage (Figure S2). We estimate $f_2\left(ANI,X^{\text{″}}\right)$ and $f_2\left(ASI,X^{\text{″}}\right)$ via our admixture graph software with one West Eurasian outgroup (because we do not have access to Georgians in the 210,482 SNP Affymetrix data set). Having only a single West Eurasian outgroup in the admixture graph makes the model poorly constrained, but we address this limitation by fixing the value of the admixture proportion to be equal to the ANI ancestry inferred from f₄ ratio estimation. We compare the expected amplitude a_o (from Equation 4) and the observed amplitude â_o (from the weighted LD curve) to test whether the model of a single wave of mixture between ANI and ASI provides a good fit to the data. The entire procedure is repeated, dropping each chromosome in turn to generate block jackknife standard errors on the quantities of interest.

95% Confidence Interval on the ANI Ancestry Proportion prior to Mixture

Consider the model that an Indian group derives its ancestry from two waves of admixture involving ANI-related populations (assumed to have the same allele frequencies), where the older wave is old enough that its contribution to the measured LD is negligible. If so, the group would have ancestry from three sources: old ANI ancestry (α_old), recent ANI ancestry (α_new), and ASI ancestry (1 − α_total = 1 − (α_old + α_new)). The expected one-reference ALDER amplitude is then

$$a_o=\frac{2{\alpha }_{new}{\left(1-{\alpha }_{total}\right)}^2}{{\alpha }_{old}+\left(1-{\alpha }_{total}\right)}{\left({\alpha }_{total}{f}_2\left(ANI,X^{\text{″}}\right)-\left(1-{\alpha }_{total}\right)f_2\left(ASI,X^{\text{″}}\right)\right)}^2.$$ (Equation 5)

We estimate the internal drift lengths by using admixture graph and estimate α_total by using f₄ ratio estimation. Substituting â₀ (inferred from the weighted LD curve) and solving the above equation for each jackknife run, we estimate the range of α_old. We find that the central 95% confidence intervals always include zero. Therefore, we instead compute a one-sided 95% confidence interval ranging from 0% to the mean plus 1.65 times the standard error.

Results

Principal Component Analysis of 73 Indian Groups

We assembled the most comprehensive sampling of Indian genetic variation to date: genome-wide SNP data collected from 571 individuals belonging to 73 well-defined ethno-linguistic groups. Figure 1 presents the PCA showing the qualitative relationships of these individuals to West Eurasians (Northern Europeans, Basque, Georgians, and Iranians) and East Asians (Han Chinese). Almost all groups speaking Indo-European or Dravidian languages lie along a gradient of varying relatedness to West Eurasians in PCA (referred to as “Indian cline”), which we have previously shown reflects variable proportions of ANI-ASI ancestry.¹ Groups speaking Austro-Asiatic and Tibeto-Burman languages fall away from the Indian cline, consistent with ancestry from distinct populations; the history of these groups is important but is not our focus here. We curated our data by using PCA, removing individuals who did not cluster with others from the same group, and restricting the analysis to 45 groups that fall on the Indian cline, all of which speak Indo-European or Dravidian languages (Table S1; Material and Methods).

Mixture Proportions

By using f₄ ratio estimation²⁶ that analyzes allele frequency correlation patterns to infer mixture proportions, we estimate that ANI ancestry along the Indian cline ranges from as low as 17% (Paniya) to as high as 71% (Pathan) (Table S4). Traditionally lower caste, Dravidian, and tribal groups tend to have lower proportions of ANI ancestry than traditionally upper caste and Indo-European groups (p < 0.001).¹ Our estimates of ANI ancestry are lower than we previously reported (although within two standard errors),¹ because of the fact that we previously used Papuans, Adygei, and Northwest Europeans as outgroups for ancestry estimation, whereas here we use YRI, Basque, and Georgians (Figure S1, Table S4). Since the publication of that study, we have found that some of the groups used in the statistic have a more complex history than is captured by the assumed model.³³ The reason for replacing the Papuans with YRI is that Papuans are now known to harbor gene flow from archaic humans (Denisovans),³³ which could bias ancestry estimates. We use different West Eurasians because the Adygei derive a small proportion of their ancestry from an East Asian-related source, which could again bias estimates, and because a model in which Georgians are the most closely related West Eurasian group to the ANI provides a good fit to the data for many models that we tested, whereas models with Europeans in their place do not provide as good a fit. Although we believe that the Onge are only distantly related to ASI, we do not replace the Onge in our analysis because this is the only group we have data from that is consistent with forming a clade with the ASI (the only requirement for our method to work is for the outgroup to form a clade with the ASI).

Admixture Dates

To date ANI-ASI mixture, we capitalized on the fact that admixture between two populations generates allelic association (linkage disequilibrium [LD]) between pairs of SNPs.³⁴ The LD decays at a constant rate as recombination breaks down the contiguous chromosomal blocks inherited from the ancestral mixing populations. The expected value of the admixture LD is related to the genetic distance between SNPs (the probability of recombination per generation between them) and the time that has elapsed since mixture.³⁴ We previously reported simulations showing that dating population mixture based on the scale of admixture LD is robust to the use of imperfect surrogates for the ancestral populations, fine-scale errors in the genetic map, and a history of founder events in the admixed population, and is able to provide unbiased estimates for the dates of events up to 500 generations ago.^26,28,29 We confirmed this by using new simulations with demographic parameters relevant to India (Appendix A).

We estimated admixture dates for all the groups on the Indian cline with more than five samples (a minimum sample size is important for measuring LD with precision). We observe a decay of LD with genetic distance for all groups (Figures 2 and S3). By fitting an exponential function using least-squares (via rolloff), our point estimates for the dates range from 64 to 144 generations ago, or 1,856 to 4,176 years assuming 29 years per generation.³⁵

We highlight two implications of these dates. First, nearly all groups experienced major mixture in the last few thousand years, including tribal groups like the Bhil, Chamar, and Kallar that might be expected to be more isolated. Second, the date estimates are typically more recent in Indo-Europeans (average of 72 generations) compared to Dravidians (108 generations). A jackknife estimate of the difference is highly significant at 35 ± 8 generations (Z = 4.5 standard errors from zero) (Table 1). A possible explanation is a secondary wave of mixture in the history of many Indo-European groups, which would decrease the estimated admixture date.

Table 1.

Characterization of Population Admixture along the Indian Cline

Pop	Data Set	n	Language Family	Traditional Caste or Social Group	State/Territory	Latitude, Longitude	ANI%	Date of Mixture (gens)	Date of Mixture (years)
Madiga	Reich et al.1 and this study	13 (9)	Dravidian	lower caste	Andhra Pradesh	17°58′N, 79°35′E	32.0 ± 1.7	120 ± 21	3,480
Mala	Reich et al.1 and this study	13 (10)	Dravidian	lower caste	Andhra Pradesh	17°22′N, 78°29′E	34.3 ± 1.7	96 ± 16	2,784
Kallara	Metspalu et al.7	8	Dravidian	tribal	Tamil Nadu	10°99′N, 78°22′E	37.7 ± 1.8	113 ± 15	3,277
Vysya	Reich et al.1 and this study	14 (10)	Dravidian	middle caste	Andhra Pradesh	14°41′N, 77°39′E	37.9 ± 1.8	144 ± 27	4,176
Chamara	Metspalu et al.7	10	Indo-European	tribal	Uttar Pradesh	25°37′N, 83°04′E	38.7 ± 1.7	113 ± 13	3,277
Bhil	Reich et al.1 and this study	17 (10)	Indo-European	tribal	Gujarat	23°02′N, 72°40′E	38.9 ± 1.6	78 ± 7	2,262
Scheduled caste/tribea	Metspalu et al.7	6	Dravidian	lower caste	Tamil Nadu	21°46′N, 86°78′E	40.5 ± 1.9	83 ± 21	2,407
Dushadha	Metspalu et al.7	7	Indo-European	lower caste	Uttar Pradesh	25°44′N, 84°56′E	41.0 ± 1.8	107 ± 13	3,103
Velamaa	Metspalu et al.7	9	Dravidian	upper caste	Andhra Pradesh	17°05′N, 79°27′E	43.4 ± 1.7	85 ± 15	2,465
Dharkara	Metspalu et al.7	11	Indo-European	nomadic group	Uttar Pradesh	25°44′N, 83°1′E	47.8 ± 1.5	64 ± 11	1,856
Kanjara	Metspalu et al.7	8	Indo-European	nomadic group	Uttar Pradesh	26°45′N, 80°32′E	48.2 ± 1.7	75 ± 10	2,175
Kshatriyaa	Metspalu et al.7	7	Indo-European	upper caste	Uttar Pradesh	27°56′N, 78°65′E	54.6 ± 1.6	78 ± 9	2,262
Kshatriya	this study	15	Indo-European	upper caste	Uttar Pradesh	25°45′N, 82°41′E	60.9 ± 1.3	76 ± 10	2,204
Brahmina	Metspalu et al.7	8	Indo-European	upper caste	Uttar Pradesh	26°06′N, 83°18′E	61.2 ± 1.4	86 ± 7	2,494
Brahmin	this study	10	Indo-European	upper caste	Uttar Pradesh	25°45′N, 82°41′E	62.8 ± 1.4	65 ± 9	1,885
Sindhib	Li et al.20	10	Indo-European	urban groups	Pakistan	24°27′N, 68°70′E	64.3 ± 1.3	67 ± 8	1,943
Kashmiri Pandit	Reich et al.1 and this study	15 (10)	Indo-European	upper caste	Kashmir	34°22′N, 75°50′E	65.2 ± 1.3	103 ± 17	2,987
Pathanb	Li et al.20	15	Indo-European	urban groups	Pakistan	32°35′N, 69°72′E	70.4 ± 1.2	73 ± 9	2,117

We estimate the ANI ancestry proportion and date of admixture by using f₄ ratio estimation and rolloff, respectively, for all the groups on the Indian cline that have greater than five samples (the requirement of a minimum sample size is important for measuring LD with precision). Because inferences of dates based on admixture LD are greatly improved by higher SNP density, we performed the date analysis with either the Illumina data set of the 500,714 SNPs or the full Affymetrix 6.0 data set of 494,863 SNPs (this contains approximately double the number of SNPs compared to the merged Affymetrix data set we discuss in the Material and Methods because it removes the HGDP samples typed on the smaller Affymetrix 500K array). For the five instances marked Reich et al.¹ and this study, we indicate the number of newly genotyped samples in parentheses. To convert dates in generations to years, we assume 29 years per generation.

^aSamples from Metspalu et al.⁷

^bSamples from HGDP.

Testing for Multiple Layers of Admixture in the History of Indian Groups

A caveat for these dating analyses is that they assume that the entire admixture occurred instantaneously (or over a small number of generations). However, population mixture can be noninstantaneous, such that the date we obtain from our method may actually be an average of multiple dates spread out over a substantial period. One way to detect a history of noninstantaneous gene flow is to fit a sum of exponential functions to the decay of admixture LD and to show that this provides a better fit to the data than a single exponential function, as we in fact find for the Kashmiri Pandit, Kshatriya, Sindhi, and Pathan (Table 2, Appendix B). However, even if we fail to detect a nonexponential decay, we cannot rule out noninstantaneous gene flow, because the decay can be noisy, making the statistical detection of a mixture of exponential functions difficult.³⁶ A particularly important scenario we could not rule out by this method is that several thousand years ago, Indian groups were already admixed, and thus the LD decay we detect is the result of mixture of already admixed ancestral groups with different proportions of ANI ancestry. If the initial admixture was more than 10,000 years old, the associated admixture LD would have decayed to such a short distance that our methods would have poor power to detect it. The LD we measure might in this case reflect only the final admixture events, complicating interpretation of the results.

Table 2.

Tests for Consistency with a Single-Pulse Admixture Model

Group	Language Family	Social Group	n	p Value
Kashmiri Pandit	Indo-European	upper caste	15	0.0191∗
Brahmin	Indo-European	upper caste	10	<0.0001∗
Kshatriya	Indo-European	middle caste	15	0.0035∗
Bhil	Indo-European	tribal	17	0.0010∗
Vysya	Dravidian	middle caste	14	0.0936
Madiga	Dravidian	lower caste	13	0.0980
Mala	Dravidian	lower caste	13	<0.0001∗
Chamara	Indo-European	tribal	10	0.1883
Dharkara	Indo-European	nomadic group	11	<0.0001∗
Sindhib	Indo-European	urban group	10	0.0001∗
Pathanb	Indo-European	urban group	15	<0.0001∗

Asterisks (^∗) indicate p < 0.05 (rejection of the null model of single pulse of admixture).

^aSamples from Metspalu et al.⁷

^bSamples from HGDP.

To assess whether the admixture LD we are detecting could plausibly account for all the ANI-ASI mixture in an Indian group’s history, we compared the observed amplitude of the LD curves (the amount observed at short genetic distances) to what would be expected if the dated LD accounts for the entire ANI-ASI admixture. We took advantage of our recently developed method ALDER,³² which computes weighted LD statistics and also provides a theoretical expectation for the amplitude under the model of a single wave of mixture, even in cases where the populations used as surrogates for the ancestral populations are highly genetically drifted from the true ancestral populations.^32,37 The ALDER expected-amplitude formula requires estimates of the admixture proportion (which we have from f₄ ratio estimation) as well as the genetic drift separating the true ancestral populations and the surrogates we use for the analysis, which we obtain by fitting a model of population relationships to our data via admixture graph²⁶ (Material and Methods). By comparing the observed and the expected values of the amplitude, we can evaluate whether the admixture LD we are dating can account for the entire ANI-ASI admixture in the group’s history. Our simulations show that for a single-wave admixture history, the weighted LD amplitude measured by ALDER is consistent with the expectation (Table S5).

In Some Groups, the ANI-ASI Admixture Is Multilayered

To make this analysis maximally robust, we restricted it to sets of Indian groups that are consistent with a model of mixture between the same ANI and ASI ancestral populations to within the limits of our resolution. To evaluate formally whether this model fits the data for a proposed set of Indian groups, we compared the allele frequency differences among the Indian groups to the allele frequency differences among a set of 38 non-Indian groups including many West Eurasians, searching for differences that would be expected if the Indian groups did not derive all their ancestry from the same two ancestral populations (Appendix C). Specifically, we computed f₄ statistics measuring the correlation in allele frequencies between each possible pair of Indian groups in the set and diverse pairs of non-Indian groups. If the ANI ancestry in all the Indian groups in the tested set derives from the same ancestral population(s), then the f₄ statistics measuring the correlations are expected to be proportional, and thus the matrix of all f₄ statistics is expected to have one linearly independent component (rank 1). We tested this null hypothesis (rank = 0) with a Hotelling T test as described in Reich et al.³¹ Our simulations show that this test has power to detect a history of multiple ancestral ANI populations even when they are closely related and that genetic drift in the admixed groups cannot increase the rank (Appendix C). For all the sets that pass as rank 1, we performed a further level of testing, running admixture graph to evaluate whether the relationships in Figure S1 (with Georgians forming a clade with ANI and Basque as a second West Eurasian outgroup) are supported by the data in the sense that no f statistic measuring allele frequency correlation is more than three standard errors from model expectation (Appendix C).

Applying this procedure to all possible sets of three Indian groups, and adding in additional Indian groups until we could add no more (without increasing the rank), we identified previously undetected complexity in Indian history, with many sets of Indian groups not consistent with a simple ANI-ASI admixture. This analysis produces two notable findings. First, although aboriginal Andaman Islanders (Onge) are consistent with being a sister group of ASI for many sets of Indian groups,¹ the Onge cannot be added to the model for other sets of Indian groups. Such a pattern would be expected if there was ancient gene flow into the Andaman Islanders from a group more closely related to the ASI ancestry of some present-day Indian groups than others. This would also be consistent with the finding that the closest known matches to Andamanese mitochondrial DNA haplotypes in Eurasia are rare haplotypes found in India.³⁸ Second, we find that the Indian groups consistent with simple ANI-ASI mixture are most often from tribal and traditionally lower-caste groups. Middle- and upper-caste groups tend to have evidence of more complex histories, with signals of multiple layers of ANI ancestry from slightly different ANI ancestral populations (Appendix C). Further evidence for multiple waves of admixture in the history of many traditionally middle- and upper-caste groups (as well as Indo-European and northern groups) comes from the more recent admixture dates we observe in these groups (Table 1) and the fact that a sum of two exponential functions often produces a better fit to the decay of admixture LD than does a single exponential (as noted above for some northern groups; Appendix B). Evidence for multiple components of West Eurasian-related ancestry in northern Indian populations has also been reported by Metspalu et al.⁷ based on clustering analysis.

In Some Groups, the ANI Admixture Is Consistent with Being Simple and All due to Events in the Last Few Thousand Years

Focusing on the largest set of Indo-Europeans (four groups) and the largest set of Dravidians (five groups) consistent with mixture of the same ANI and ASI ancestral populations, we find that the expected and observed admixture LD amplitudes are equivalent to within the limits of our resolution. We restricted this analysis to Indian groups genotyped on Affymetrix arrays because this allowed us to analyze about 2.5 times more SNPs (n = 210,482), which improves the accuracy of inferences based on admixture LD. Limiting our analysis to samples genotyped on Affymetrix arrays raised the challenge that we could not use Georgians as part of our admixture graph fitting (we need a second West Eurasian outgroup to obtain tight constraints on the absolute estimates of ANI-ASI admixture), but in Appendix D we show that we can accurately infer the difference between the two amplitude values (observed − expected) even without access to Georgians by constraining the admixture proportions estimated via f₄ ratio estimation. For both the Indo-European and Dravidian rank 1 sets, the observed amplitudes are statistically consistent with the expected values (Table 3). Thus, our data are consistent with all of the ANI ancestry in some selected sets of Indians (including groups speaking both Indo-European and Dravidian languages) being due to admixture events that we can date to within the past few thousand years. Accounting for statistical uncertainty, we estimate that the ANI ancestry that cannot be explained by a single wave of admixture in the last few thousand years has a 95% confidence interval (truncated to 0) of 0%–19% for Indo-Europeans and 0%–16% for Dravidians. Thus, all the ANI ancestry in some groups is consistent with deriving from admixture events that have occurred in the past few thousand years.

Table 3.

Consistent Estimates of the Amplitude of Admixture LD for the Indo-European and Dravidian Rank 1 Sets

Reference West Eurasian (X)	Expected Amplitude × 10,000	Observed Amplitude × 10,000	Z Score for Difference
Indo-European Rank 1 Set
Basque	0.7 ± 0.2	0.6 ± 0.1	−0.5
CEU	0.6 ± 0.2	0.5 ± 0.1	−0.8
French	0.9 ± 0.2	0.8 ± 0.1	−0.6
Italian	0.5 ± 0.2	0.6 ± 0.1	0.1
Orcadian	0.8 ± 0.2	0.7 ± 0.1	−0.5
Sardinian	0.7 ± 0.2	0.7 ± 0.1	0.4
Tuscan	0.7 ± 0.2	0.7 ± 0.1	−0.2
Dravidian Rank 1 Set
Basque	1.1 ± 0.2	0.8 ± 0.1	−1.7
CEU	0.9 ± 0.1	0.5 ± 0.1	−2.7
French	1.1 ± 0.2	0.6 ± 0.1	−2.4
Italian	0.8 ± 0.1	0.8 ± 0.2	−0.1
Orcadian	0.9 ± 0.1	0.3 ± 0.4	−1.6
Sardinian	0.9 ± 0.2	0.9 ± 0.2	0.0
Tuscan	1.0 ± 0.2	1.0 ± 0.1	0.2

We use Equation 4 to compute the expected amplitude of admixture LD where α, f₂(ANI, X”), and f₂(ASI,X”) are computed by admixture graph (Figure S2). α represents the weighted average of the ANI ancestry in the set (weighted by the sample size of the groups in the set). The observed amplitude is estimated by ALDER with X as the reference population. We ignore inter-SNP distances less than the threshold automatically chosen by ALDER after comparing shared LD between the reference and the admixed group. To infer statistical uncertainty in (observed − expected) amplitude, we use a weighted block jackknife dropping each chromosome in turn. This produces a standard error and allows us to test whether the difference is consistent with zero (|Z| < 3).

Discussion

Our analysis documents major mixture between populations in India that occurred 1,900–4,200 years BP, well after the establishment of agriculture in the subcontinent. We have further shown that groups with unmixed ANI and ASI ancestry were plausibly living in India until this time. This contrasts with the situation today in which all groups in mainland India are admixed. These results are striking in light of the endogamy that has characterized many groups in India since the time of mixture. For example, genetic analysis suggests that the Vysya from Andhra Pradesh have experienced negligible gene flow from neighboring groups in India for an estimated 3,000 years.¹ Thus, India experienced a demographic transformation during this time, shifting from a region where major mixture between groups was common and affected even isolated tribes such as the Palliyar and Bhil to a region in which mixture was rare.

Our estimated dates of mixture correlate to geography and language, with northern groups that speak Indo-European languages having significantly younger admixture dates than southern groups that speak Dravidian languages. This shows that at least some of the history of population mixture in India is related to the spread of languages in the subcontinent. One possible explanation for the generally younger dates in northern Indians is that after an original mixture event of ANI and ASI that contributed to all present-day Indians, some northern groups received additional gene flow from groups with high proportions of West Eurasian ancestry, bringing down their average mixture date. This hypothesis would also explain the nonexponential decays of LD in many northern groups and their higher proportions of ANI ancestry. A prediction of this model is that some northern Indians will have genomes consisting of long stretches of ANI ancestry interspersed with stretches that are mosaics of both ANI and ASI ancestry (inherited from the initial mixture). Although we have not been able to test the predictions of this hypothesis, it may become possible to do so in future by developing a method to infer the ancestry at each locus in the genome of Indians that can provide accurate estimates even in the absence of data from ancestral populations.

The dates we report have significant implications for Indian history in the sense that they document a period of demographic and cultural change in which mixture between highly differentiated populations became pervasive before it eventually became uncommon. The period of around 1,900–4,200 years BP was a time of profound change in India, characterized by the deurbanization of the Indus civilization,³⁹ increasing population density in the central and downstream portions of the Gangetic system,⁴⁰ shifts in burial practices,⁴¹ and the likely first appearance of Indo-European languages and Vedic religion in the subcontinent.^18,19 The shift from widespread mixture to strict endogamy that we document is mirrored in ancient Indian texts. The Rig Veda, the oldest text in India, has sections that are believed to have been composed at different times. The older parts do not mention the caste system at all, and in fact suggest that there was substantial social movement across groups as reflected in the acceptance of people with non-Indo-European names as kings (or chieftains) and poets.⁴² The four-class (varna) system, comprised of Brahmanas, Ksatriyas, Vaisyas, and Sudras, is mentioned only in the part of the Rig Veda that was likely to have been composed later (the appendix: book 10).⁴² The caste (jati) system of endogamous groups having specific social or occupational roles is not mentioned in the Rig Veda at all and is referred to only in texts composed centuries after the Rig Veda, for example, the law code of Manu that forbade intermarriage between castes.⁴³ Thus, the evolution of Indian texts during this period provides confirmatory support as well as context for our genetic findings.

It is also important to emphasize what our study has not shown. Although we have documented evidence for mixture in India between about 1,900 and 4,200 years BP, this does not imply migration from West Eurasia into India during this time. On the contrary, a recent study that searched for West Eurasian groups most closely related to the ANI ancestors of Indians failed to find any evidence for shared ancestry between the ANI and groups in West Eurasia within the past 12,500 years³ (although it is possible that with further sampling and new methods such relatedness might be detected). An alternative possibility that is also consistent with our data is that the ANI and ASI were both living in or near South Asia for a substantial period prior to their mixture. Such a pattern has been documented elsewhere; for example, ancient DNA studies of northern Europeans have shown that Neolithic farmers originating in Western Asia migrated to Europe about 7,500 years BP but did not mix with local hunter gatherers until thousands of years later to form the present-day populations of northern Europe.^15,16,44,45

The most remarkable aspect of the ANI-ASI mixture is how pervasive it was, in the sense that it has left its mark on nearly every group in India. It has affected not just traditionally upper-caste groups, but also traditionally lower-caste and isolated tribal groups, all of whom are united in their history of mixture in the past few thousand years. It may be possible to gain further insight into the history that brought the ANI and ASI together by studying DNA from ancient human remains (such studies need to overcome the challenge of a tropical environment not conducive to DNA preservation). Ancient DNA studies could be particularly revealing about Indian history because they have the potential to directly reveal the geographic distribution of the ANI and ASI prior to their admixture.

Appendix A: Statistics Used for Estimating Dates of Admixture

Here we describe the rolloff and ALDER linkage disequilibrium (LD) statistics that we use for dating admixture events in India.

Both rolloff and ALDER are based on the insight that mixture between populations creates allelic correlation (or LD) between alleles whose frequencies differ between the ancestral populations. This LD decays exponentially as recombination occurs, and explicitly as e^−nd, where n is the number of generations since admixture and d is the genetic distance between SNP pairs.

The rolloff statistic introduced in Moorjani et al.²⁸ estimates admixture LD by computing pairwise correlation between SNPs and weighting them by the differences in allele frequencies between the reference populations:^26,28

$$A\left(d\right)=\frac{\sum _{|x-y|\approx d}z\left(x,y\right)w\left(x,y\right)}{\sqrt{{\sum _{|x-y|\approx d}z\left(x,y\right)}^2}\sqrt{{\sum _{|x-y|\approx d}w\left(x,y\right)}^2}}.$$ (Equation A1)

Here, x, y are SNPs separated by a distance d Morgans; z(x,y) is the correlation between alleles at SNPs x and y; and the weight function w(x,y) is the product of the allele frequency differences between the reference populations at x and y. We plot the weighted correlation with genetic distance and obtain a date by fitting an exponential function with a constant offset (affine) term $y=A{e}^{-nd}+c$, where n is the number of generations since admixture and d is the distance in Morgans. Standard errors are computed via a weighted block jackknife,³⁰ with one chromosome dropped per run.

Although this statistic provides accurate results under most scenarios, Moorjani et al.²⁹ found that for groups that have a history of a very strong bottleneck after admixture, the normalization term z(x,y)² exhibits an exponential decay, thereby biasing the estimated dates of admixture.²⁹ Although this does not affect the estimates in outbred groups such as Europeans and Africans, it could cause a bias in the case of Indian groups such as Vysya and Chenchu that have a history of strong founder events in the past 100 generations.

Following Moorjani et al.,²⁹ we modify the rolloff Equation A1 as follows. (1) We substitute z(x,y) with the covariance between SNPs x and y. This makes the statistic more mathematically tractable, allowing us to use the amplitude of the exponential decay to estimate admixture proportions as in ALDER.³² (2) We remove the normalization term z(x,y)² to remove the bias in the date. The resulting statistic is shown in Equation 2. Simulations show that these changes provide accurate date estimates even in groups with a history of founder events.²⁹

The rolloff statistic requires access to estimates of the allele frequency differences between the reference groups to weight the SNPs and to make the statistic sensitive to admixture-related LD. This means that we need data from reference groups that are related to the true ancestral populations. A challenge is that the ASI are not closely related to any extant group. Although they are anciently related to indigenous Andaman Islanders (Onge), the Onge provide poor estimates of ASI allele frequencies because their population size has been small for the tens of thousands of years since separation from the ASI so that allele frequencies have experienced substantial genetic drift. To overcome these limitations, we further modified the implementation of rolloff as follows.

(1) Use of SNP loadings estimated based on PCA as the weights in rolloff. For India, we do not have access to samples of unadmixed ASI but we have access to multiple admixed groups differing in their mixture proportions. Thus, we can use SNP loadings from PCA of multiple admixed groups and a surrogate for ANI (say, Europeans) in place of frequencies in Equation 2. This idea was first introduced in Moorjani et al.,²⁹ where simulations showed that PCA-based SNP loadings can be used to accurately infer dates.

(2) Using the admixed group as one reference population. Loh et al.³² extended the ideas from rolloff in the new method ALDER. ALDER can infer admixture dates with just one reference population (with the admixed group itself as the other reference) and can also relate the amplitude of the fitted exponential to admixture proportions (see also Appendix D). Specifically, we compute the statistic shown in Equation 3. Simulations show that ALDER provides accurate estimates for the date with one reference population, even when groups that are highly diverged from the true ancestral populations are used as reference populations.³²

We applied both rolloff and ALDER to infer the dates of admixture by using PCA-based loadings and single reference populations and show that we obtain qualitatively similar results from both methods (Table S6).

Simulations with Demographic Parameters Relevant to Indian Groups

Moorjani et al.²⁸ reported that rolloff estimates can be upwardly biased in the cases of low admixture proportion and small sample sizes. To evaluate how this might affect our results in India, we created simulated chromosomes of mixed European and Asian ancestry for demographic parameters relevant to Indian groups (Table S7). The choice of Europeans and East Asians as the ancestral populations for these simulations was motivated by the fact that F_st(ANI, ASI) is approximately equivalent to F_st(CEU, CHB) = 0.09.¹

We simulated data based on the framework described in Moorjani et al.²⁸ For each Indian group (Brahmins, Mala, Pathan, Dravidian rank 1, and Indo-European rank 1), we ran 100 simulations where we set the mixture proportion, time since mixture, and number of samples to match the parameters estimated for the specific group. Table S7 shows that the average date of mixture from the 100 simulations is consistent with the expected date (within one standard error).

Appendix B: Test for Multiple Waves of Admixture

Here we describe a method for identifying groups that have evidence for more than one wave of admixture in their history. The method is based on a likelihood ratio test (LRT) for whether the admixture LD decay curves fit the simple exponential decay expected for a single wave of admixture. For this purpose we use the output obtained from rolloff by using PCA-based SNP loadings as the weights (Appendix A).

The null hypothesis is that there has been a single pulse of admixture. We use least-squares to estimate the parameters of the null model by fitting $y=A{e}^{-nd}+c$, where n = the date of admixture and d = the genetic distance.

The alternative hypothesis is that the population has a history of two pulses of admixture. We fit $y=A{e}^{-n_{1}d}+B{e}^{-n_{2}d}+c$ where n₁ = date of the first pulse of admixture and n₂ = date of the second pulse of admixture. The log likelihood of each model is

$$\frac{-N}{2}\left({\log }_e\left(2\pi \right)+1-{\log }_e\left(N\right)+{\log }_e\left(\sum _{i=1}^n{\epsilon }_i^2\right)\right),$$ (Equation A2)

where N = the number of data points in each simulation and ε_i = the residuals of the fitted model (true(y) − fitted(y)).

The difference between the log likelihood of the null versus the alternative hypothesis (−2∗log_e(likelihood of null model) + 2∗log_e(likelihood of the alternate model)) is expected to be chi-square distributed with two degrees of freedom.

To test whether the ${\chi }^2$ approximation holds true in our case, we performed 100,000 numerical simulations of data under the null model of a single pulse of mixture (date range of 1–300 generations) with normal noise (mean = 0, standard deviation = 0.02). We then used least-squares to estimate the parameters of the null $\left(y=A{e}^{-nd}+c\right)$ and alternative $\left(y=A{e}^{-n_{1}d}+B{e}^{-n_{2}d}+c\right)$ models and record the p value of the likelihood ratio test assuming a distribution with 2 d.f. We reject the null hypothesis in 5.7% of the simulations (Figure S4).

We applied the LRT method to all groups with ≥10 samples (the requirement of a minimum sample size is motivated by the sensitivity of the test to noise in the case of few samples). For most traditionally upper-caste Indo-European groups, there is evidence to reject the null hypothesis (Table 2). In contrast, other groups can be reasonably well fit by the null model to within the limits of our resolution.

We conclude by highlighting three caveats of this LRT.

(1) Without comparing the model of two pulses of admixture with models of multiple pulses (>2) or gradual admixture, we cannot conclude that a group has a history of exactly two waves of admixture. In general, the true histories of the groups consistent with the null model almost certainly involved some amount of noninstantaneous gene flow, so with sufficiently high sample size, our test for a nonexponential decay would be almost guaranteed to reject the null model.

(2) A second caveat is that our method might reject the null because of sources of LD other than admixture, such as LD due to founder events or ancestral LD. In theory, however, this problem is mitigated by using PCA loadings as weights.

(3) A third caveat is that autocorrelation across distant bins in rolloff will make our likelihood scores anticonservative; we do not currently know how to correct for this autocorrelation. Thus, we treat the evidence of multiple waves of admixture as suggestive only and apply other formal methods to identify groups that are consistent with a single wave of ANI-ASI admixture.

Appendix C: Inferring the Number of Admixture Events

Here we describe how we identified sets of Indian groups consistent with mixture of the same two ancestral populations within the limits of our resolution.

Our approach was first introduced in Reich et al.,³¹ where it was applied to estimate the number of migrations from Siberia into the Americas. Here, we coanalyze a panel of Indian groups (m) along with a panel of non-Indian groups (n). The idea is to compute f₄ statistics measuring the correlation in allele frequencies between each possible pair of Indian groups (m(m − 1)/2 comparisons) and each possible pair of non-Indian groups (n(n − 1)/2 comparisons). Specifically, we compute statistics like f₄(Indian₁, Indian₂; NonIndian₁, NonIndian₂). If the analyzed Indian groups harbor ancestry from exactly the same pair of ancestral populations ANI and ASI (but in different proportions), then the f₄ statistics should be proportional up to a scaling factor, and we can test this null hypothesis.

To implement this procedure, we need to address the fact that many of the f₄ statistics can be written as linear combinations of each other, and therefore we need to pick a basis for the space of f₄ statistics. We fix one Indian group as “Indian_base” and compute the f₄ statistic for each of the 36 remaining Indian groups as “Indian_other.” We fix an African group (YRI) as “NonIndian_base” and use 37 diverse Eurasian groups as “NonIndian_other” (the choice of base has no impact on the statistical findings). We then compute all possible f₄ statistics:

$${\text{f}}_4\left({\text{Indian}}_{\text{base}},{\text{Indian}}_{\text{other}};{\text{NonIndian}}_{\text{base}},{\text{NonIndian}}_{\text{other}}\right).$$

This yields a matrix of m − 1 × n − 1 dimensions. By using a variant of singular value decomposition (SVD) as in Reich et al.,³¹ we estimate the number of independent components or rank of the f₄ relationship matrix.³¹ If the ANI and ASI ancestry in all tested Indian groups derives from the same ancestral populations, the f₄ statistics measuring these correlations are expected to all be proportional, and thus the matrix will have one independent component or rank = 1. However, if a tested Indian group has a history of multiple gene flow events, the rank is expected to be greater than 1. We test this null hypothesis (rank = 0) with a Hotelling T test as in Reich et al.³¹ An extension of the same approach allows us to also compute the minimum rank of the f₄ matrix needed to explain the data.³¹ Assuming no back-migration from India into the panel of non-Indian groups, we can interpret a rank of r as implying at least r +1 ancestral populations.

Simulations

To test the method for demographic parameters relevant to Indian groups, we performed coalescent simulations by ms.⁴⁶ For each simulation, we generated data for ∼250K independent SNPs for 15 groups (Pop1–15, 10 samples for each group). We set the effective population size (N_e) for all groups to be 12,500 and the mutation and recombination rates at 2 × 10⁻⁸ and 1 × 10⁻⁸ per base pair per generation, respectively. Pop1 is the outgroup that diverged from Pop2 and Pop3 about 1,800 generations ago. Pop2 and Pop3 diverged 900 generations ago. The relationship of Pop1, Pop2, and Pop3 can be considered analogous to the relationship of YRI, Onge, and CEU, respectively. Pop4–9 are related to Pop3 analogously to the relationship of West Eurasians to ANI, and these populations diverged from Pop3 200–450 generations ago (Figure S5).

Simulation 1: Single Gene-Flow Event with the Same Admixing Populations

Consider the model in Figure S5. Pop10–15 are admixed and derive between 20% and 80% ancestry from Pop2′, which is closely related to Pop2 (the remaining ancestry is from Pop3′, which is related to Pop3). The date of admixture for all groups (Pop10–15) is 100 generations ago. These groups are analogous to the Indian cline with the range of admixture proportions and dates set to be similar to those inferred from real data. We estimate the rank of the f₄ relationship matrix, f₄(Pop10–15; Pop1–9). Here, Pop10 is analogous to Indian_base and Pop1 (an outgroup to Pop2–15) is analogous to NonIndian_base. We infer that the number of independent components is 1 (rank 1 at p > 0.05).

Simulation 2: Two Gene-Flow Events Involving Different Ancestral Populations

Pop10–15 are admixed and Pop10–14 have ancestry from Pop2′ and Pop3′, with Pop3′ ancestry varying between 20% and 80% (the remaining ancestry is from Pop2′). Pop15 has 35% Pop4′ and 65% Pop2′ ancestry. All admixture events occurred 100 generations ago. We estimate the rank of the f₄ relationship matrix as f₄(Pop10–15; Pop1–9) and infer the number of independent components to be 2. If we remove Pop15 from the analysis, that is f₄(Pop10–14; Pop1–9), the inferred rank is 1, as expected.

Simulation 3: Three Independent Gene Flows with Different Mixing Populations

Pop10–15 are admixed and Pop10–13 have ancestry from populations 2′ and 3′, with Pop3′ ancestry between 20% and 80% (the remaining ancestry is from Pop2′). Pop14 has 70% Pop5′ and 30% Pop2′ ancestry, and Pop15 has 35% Pop4′ and 65% Pop2′ ancestry. All admixture events occurred 100 generations ago. We estimate the rank of the f₄ relationship matrix f₄(Pop10–15; Pop1–9) and infer the number of independent components is 3.

Simulation 4: Two Independent Gene-Flow Events at Different Time Periods

Pop10–15 are admixed and have ancestry from Pop2′ and Pop3′, with Pop3′ ancestry between 20% and 80%. Admixture occurred 100 generations ago. Pop15 also has ancestry from an older gene-flow event that occurred 150 generations ago with 50% Pop2′ and 50% Pop3′ ancestry. Thus overall, Pop15 has 70% Pop2′ and 30% Pop3′ ancestry. We estimate the rank of the f₄ relationship matrix f₄(Pop10–15; Pop1–9) and infer the number of independent components is 2.

Simulation 5: Multiple Independent Gene-Flow Events at Different Time Periods

Pop10–15 are admixed with ancestry from Pop2′ and Pop3′. Pop3′ ancestry is between 20% and 80%. Admixture occurred 50–300 (intervals of 50) generations ago (such that Pop10 was admixed 50 generations ago, Pop11 was admixed 100 generations ago, etc.). We estimate the rank of the f₄ relationship matrix, f₄(Pop10–15; Pop1–9), and infer the number of independent components is 3.

In conclusion, our simulations demonstrate that we can accurately estimate the minimum number of gene flow events and that postadmixture drift alone does not change the rank of the f₄ relationship matrix.

Results

We performed a systematic analysis to identify groups that have a similar history of ANI-ASI mixture, meaning that all their ancestry is consistent with deriving from the same ANI and ASI ancestral populations to within the limits of our resolution. We restrict this analysis to Indian groups with at least five samples and non-Indian groups that have at least ten samples, including groups from East Asia, Europe, the Middle East, the Caucasus, and Africa. We remove Central Asian and South Asian populations from the list of non-Indian groups because these have an increased likelihood of back-migration from India in the recent past that can complicate interpretation. We include Vedda (four samples), an aboriginal population from Sri Lanka, they appeared to have a relatively simple history of ANI-ASI mixture in our preliminary analysis. The analyzed data thus consists of m = 37 Indian groups (including Onge) and n = 38 non-Indian groups.

To identify sets of Indian populations that are consistent with deriving all their ancestry from exactly the same ANI-ASI ancestral populations, we systematically explored sets of these Indian groups. We used an iterative procedure, as follows.

(1) Testing all possible sets of three Indian groups. We start by computing

$${\text{f}}_4\left({\text{Indian}}_{\text{set}\text{of}\text{three}\text{groups}};\text{YRI},{\text{NonIndian}}_{\text{other}}\right)$$

and estimate the ranks of the resulting 2 × (n − 1) matrix by a likelihood ratio test. We repeat this for all (37 × 36 × 35)/6 possible triples of Indian groups.

For each set of three Indian groups consistent with a simple mixture of ANI and ASI (rank 1 at p > 0.05), we performed a further level of testing for whether the model is consistent with our data. Specifically, we run the admixture graph phylogeny-testing software^1,26 to test whether the relationships shown in Figure S1 with Pop1 = Georgians, Pop2 = Basque, and India = set of three Indian groups being tested is consistent with the data to within the limits of our resolution (this is the same set of reference populations we use for estimating ancestry proportions in f₄ ratio estimation and thus we are formally testing whether the model underlying the estimation is valid). To evaluate significance, we use the criterion than none of the f₂, f₃, and f₄ statistics relating the seven analyzed groups in the admixture graph is more than three standard errors from expectation.

(2) Testing sets of four Indian groups. For all sets of three Indian groups that pass these two tests, we advanced to the next round, testing sets of four Indian groups for consistency with being a simple mix of exactly the same ANI and ASI ancestral populations. Specifically, we took each of the passing sets of three Indian groups and added in turn each of the remaining groups that were part of at least one set that was rank 1. We applied the same two tests for consistency with a simple ANI-ASI mixture, leading to passing quadruples.

(3) Testing sets of five, six, and seven Indian groups. We applied the same procedure to test larger sets of groups. The results of each round are recorded in Tables S8 and S9. We stopped finding sets of groups that pass the test after m = 6.

We highlight two qualitative results that emerge from this analysis:

• •Onge is often included in the sets of groups consistent with rank 1, consistent with their being an ancient sister group for ASI.¹ However, for some sets of Indian groups qualifying as rank 1, we cannot add in Onge, suggesting that there also might be differences in ASI ancestry within India.
• •A higher proportion of sets including lower-caste and tribal groups have rank 1 than is the case for sets including upper-caste groups.

Appendix D: Test for a Single Wave of Admixture: Comparison of Predicted and Observed ALDER Amplitudes

To evaluate whether the admixture LD we are detecting in India could plausibly reflect a single wave of gene flow accounting for all the ANI-ASI mixture, we compared the observed amplitude of LD decay and the ALDER theoretical expectation for a model of single wave of mixture.³²

We run ALDER with one reference population (X) and plot the weighted covariance against genetic distance and perform a least-squares fit by using $y=A{e}^{-nd}+c$, where n is the number of generations since admixture and d the genetic distance in Morgans. Under a single-wave mixture model, the amplitude of admixture LD $\left(a_o=A+c/2\right)$ is analytically predicted by the ANI ancestry proportion (α) and the genetic drift separating the ANI-ASI lineages by Equation 4 (see population relationships in Figure S2).

The ANI ancestry proportion (α) can be estimated by admixture graph or f₄ ratio estimation, and the genetic drift $f_2\left(ANI,X^{\text{″}}\right)$ and $f_2\left(ASI,X^{\text{″}}\right)$ (Figure S2) can be estimated by fitting a model of population relationships by using admixture graph to the data for an analyzed set of populations. By comparing the observed amplitude inferred from LD (measured with ALDER) and the expected amplitude from frequency correlations (using admixture graph or f₄ ratio estimation that use similar information), we can infer how much of the total ANI ancestry in each Indian group is due to mixture in the last few thousand years.

We applied this analysis to two sets of Indian groups, an Indo-European rank 1 set consisting of four groups and a Dravidian rank 1 set consisting of five groups. We chose these from all the sets identified in Appendix C based on two criteria. (1) All groups are genotyped on the Affymetrix arrays. This allows us to use significantly more SNPs (n = 210,482 SNPs), thus improving the accuracy of ALDER. It also allows us to include Onge, an essential population for our admixture graph analysis. (2) The groups in the sets span as large a range as possible of ANI ancestry, which is valuable for constraining internal branch lengths in admixture graph.

Based on these criteria, we chose the following two sets: Indo-European rank 1 set (n = 4 groups; 32 samples), consisting of Bhil, Jain, Lodi, and Tharu; and Dravidian rank 1 set (n = 5 groups, 33 samples), consisting of Adi-Dravidar, Kuruchiyan, Madiga, Malai Kuravar, and Narikkuravar.

We used the population relationships shown in Figure S1, but now with only one West Eurasian outgroup (because we do not have access to Georgians on the Affymetrix array) as input to admixture graph. We confirmed that the Indo-European (n = 32) and Dravidian (n = 33) rank 1 sets are still good fits to the proposed model by using the larger number of SNPs (n = 210,482 rather than n = 86,213 used in Appendix C). Specifically, none of the f₂, f₃, and f₄ statistics comparing all possible sets of groups are more than three standard errors from the model-based expectation.

The fit generated by admixture graph allows us to estimate the genetic drift that occurred between (1) ANI and the population X″ that was ancestral to ANI and the sister group (X) that we use in our admixture graph analysis (we tried a range of West Eurasian groups X), and (2) ASI and the population that was ancestral to ASI and the sister group we use for them (Onge) (Figure S2). We are able to estimate these branch lengths because we have access to several admixed populations that we hypothesize descend from the same admixture event based on the results of Appendix C.

We compare the predicted amplitude of the admixture LD from admixture graph (based on allele frequency correlation and the expectation of Equation 4) to the observations from ALDER for a variety of proposed West Eurasian outgroups X and for the Indo-European and Dravidian rank 1 sets (Table 3).

A complication of having only a single West Eurasian outgroup in the admixture graph is that it causes the model to be poorly constrained, but we can address this limitation by fixing the value of the admixture proportion (α) to be equal to the ANI ancestry inferred from f₄ ratio estimation by using the merged Illumina-Affymetrix data set. In this merged data set, we have access to two West Eurasian outgroups, allowing us to obtain precise ancestry estimates. We use Georgians and Basque, based on the admixture graph testing of Appendix C, and observe that this model provides a good fit to the data for many Indian groups.

To test whether the expected amplitude based on the model of single admixture is consistent with the observed amplitude, we measure the difference between expected amplitude and observed amplitude. For expected amplitude, we use f₄ ratio estimation on the set of Indian groups to obtain a point estimate of the admixture proportion, and we use admixture graph analysis on the same set of Indian groups (using the constrained model described above) to infer the genetic drift lengths $f_2\left(ANI,X^{\text{″}}\right)$ and $f_2\left(ASI,X^{\text{″}}\right)$. Substituting these numbers into the ALDER amplitude formula (Equation 4) provides a precise mathematical expectation for the amplitude of admixture LD for the scenario that all the ANI-ASI admixture is due to a single admixture event. For observed amplitude, we obtain this by performing ALDER analysis for the same set of Indian groups with Basque as the reference population.

To infer statistical uncertainty of (observed − expected) amplitude, we use a weighted block jackknife, dropping each chromosome in turn and repeating the entire procedure. This produces a standard error and allows us to test whether the difference is consistent with zero (consistent with the null model of a single wave of ANI-ASI admixture).

In practice, we did not find significant evidence for a difference between the observed and expected amplitudes in India. However, it is also valuable to estimate an upper bound on the proportion of ANI ancestry that could possibly derive from an earlier wave of admixture under the assumption that there were multiple waves but we cannot detect significant evidence for them. To do this, we consider the alternative hypothesis that there were two waves of admixture and infer the maximum proportion of ANI ancestry from the earlier wave that could possibly be consistent with the observed LD decay.

Specifically, the model we are considering is two waves of admixture from ANI-related ancestral populations with the same allele frequencies, with the older wave old enough that its contribution to the measured LD is negligible. In this model, present-day Indian groups derive their ancestry from three sources: old ANI (α_old), recent ANI (α_new), and ASI (1 − α_total = 1 − (α_old + α_new)). Hence, the second wave of ANI ancestry (proportion: α_new) enters an admixed population (proportion: 1 − α_new) whose allele frequencies can be written as a linear combination from the first wave:

$$\left(\frac{{\alpha }_{old}}{\left(1-{\alpha }_{new}\right)}\right)\ast A+(1-\left(\frac{{\alpha }_{old}}{\left(1-{\alpha }_{new}\right)}\right))\ast B$$ (Equation A3)

where A is the allele frequency in ANI and B is the allele frequency in ASI.

The expected one-reference-population ALDER amplitude is then

$$a_o=\frac{2{\alpha }_{new}\left(1-{\alpha }_{new}\right){\left(1-{\alpha }_{total}\right)}^2}{{\left(1-{\alpha }_{new}\right)}^2}{\left({\alpha }_{total}{f}_2\left(ANI,X^{\text{″}}\right)-\left(1-{\alpha }_{total}\right)f_2\left(ASI,X^{\text{″}}\right)\right)}^2,$$ (Equation A4)

which reduces to Equation 5 shown earlier.

The last squared factor remains the same as in the single-wave case because we have assumed that the two ANI populations have the same allele frequencies. Note that replacing α_old = 0 (so that α_new = α_total) reduces Equation 5 to Equation 4. The amplitude with the two-wave model is lower than the corresponding value for a single wave of admixture, because the admixture LD resulting from the older wave is no longer detectable beyond the shortest genetic distances. Thus, if the observed amplitude is lower than the expected (single-wave) amplitude, we can find the value of α_old that would explain the difference under a two-wave model. We run a weighted block jackknife (removing one chromosome in each run) to estimate the range of α_old. In practice, our 95% central confidence interval overlaps zero. Thus, we compute a one-sided 95% confidence interval for α_old of 0% to the mean + 1.65^∗(standard error).

Simulations

We tested the accuracy of the methodology in scenarios simulated to resemble hypothetical admixture histories of India. To capture some of the complexities of real human populations, we built our simulated data sets by using phased haplotypes from real groups from HGDP and HapMap via the method described in Moorjani et al.²⁸ Specifically, we simulated two sets of admixed groups. Set 1 consisted of three groups with [30%, 50%, 70%] ancestry from Europeans (HapMap CEU) and the remaining ancestry from East Asians (HGDP Han). Set 2 consisted of three groups with [20%, 30%, 40%] ancestry from Europeans and the remaining ancestry from East Asians.

For each group, we generated 14 diploid individuals under two alternative admixture histories: (1) a single CEU-Han admixture event 100 generations ago and (2) two waves of CEU admixture into Han, 300 and 75 generations ago, that together produce the same total fraction of CEU ancestry as shown above.

To perform the admixture graph analysis, we require additional outgroups. For this we use real data from HGDP French, Basque, Yoruba, and Dai and use the model shown in Figure S6. We use the drift lengths and admixture proportions estimated by admixture graph to compute the expected amplitude (note that the constraint of fixing the admixture proportion from f₄ ratio estimation is not required because we have two West Eurasian outgroups here). We performed ALDER single-reference analysis for each set of admixed groups with the Basque and Dai as single reference populations (independently). We note that we do not reuse the CEU or Han populations (used for generating the simulated data) in our inference procedure, to account for the fact that we do not have access to the true ancestral populations (ANI and ASI) for India. We created simulated populations in groups of three to allow us to infer the necessary f₂ values in the amplitude formula.

We designed our simulations to qualitatively match the scenario relevant to India. In Figure S6, the four outgroups (French, Basque, Yoruba, and Dai) take the place of Georgians, Basque, YRI, and Onge in Figure S1. For the simulated histories, we chose a date of 100 generations ago to be similar to the observed average age of ANI-ASI admixture in India. The two-wave dates of 300 and 75 generations ago provide a plausible alternative scenario yielding an ALDER curve similar to the expectation for a single-wave mixture 100 generations ago. Finally, the two simulated population sets covered distinct ranges of admixture proportion space, one with larger CEU ancestry components and higher ancestry proportion variation than the other. For both sets, our inference methods provide reliable results (Table S5).

Our simulation results demonstrate that for a single-wave admixture history, the weighted LD amplitude measured by ALDER is consistent with the expectation of our formula, whereas in the case of two-wave admixture, the measured ALDER amplitude is smaller than the expectation of Equation 4 (Table S5). Out of the 12 population-reference pairs, the difference in the amplitudes is statistically consistent with zero (|Z| < 3) for all single-wave simulations, whereas the difference is significantly different from zero in 8 of the 12 two-wave simulations, including all 6 with Basque as the reference population. The estimates of the mixture proportion α_old required to explain the amplitude discrepancy under the alternate model are considerably smaller for the single-wave simulated data, with zero always within the confidence interval (Table S5).

Results

(1) Indo-European rank 1 set: For all West Eurasian groups, the model of relationships shown in Figure S2 provides a good fit to the Indo-European rank 1 data as assessed by admixture graph (such that none of the f statistics are greater than three standard errors from expectation). Therefore we substitute the admixture proportions and drift lengths $f_2\left(ANI,X^{\text{″}}\right)$ and $f_2\left(ASI,X^{\text{″}}\right)$ computed by admixture graph in Equation 4 to estimate the expected amplitude. We observe that the expected amplitude is consistent with the observed amplitude (|Z| < 3 for a difference between the two estimates over all seven West Eurasian groups we tested) (Table 3).

For the constrained analysis, we focused on Basque as the reference population and fixed the ANI ancestry proportion from f₄ ratio estimation as described above. We compute the difference in amplitude (observed − expected) and find that the two estimates are statistically consistent (Z = −0.35). This suggests that the model of a single wave of ANI-ASI admixture is consistent with our data.

Applying the alternate two-wave amplitude formula (Equation 5), we estimate α_old to be 4.5% ± 8.5%, giving a 95% confidence interval of 0%–18.6%. Therefore we find no evidence to reject a single-wave model with all ancestry contributing to the measured admixture LD.

(2) Dravidian rank 1 set: Similar to the Indo-European rank 1 set, we applied admixture graph and ALDER to the Dravidian rank 1 data with various West Eurasian groups as references and found that the expected and observed amplitudes are consistent (|Z| < 3) for all reference populations tested (Table 3).

We focused next on Basque as the reference population and used the ANI estimate from f₄ ratio estimation. The expected amplitude is consistent with the observed amplitude in ALDER (Z = −1.06), suggesting that the model of a single wave of ANI-ASI ancestry provides a fit to the data. The proportion of ANI ancestry unexplained by our model (α_old) is 7.1% ± 5.5%, with a 95% confidence interval of 0%–16.2% (truncated at 0).

In conclusion, our data are consistent with the null model of a single wave of ANI-ASI admixture in selected Indo-European and Dravidian groups in India.

Supplemental Data

Supplemental Data include six figures and nine tables and can be found with this article online at http://www.cell.com/AJHG/.