Risk-Standardizing Survival for In-Hospital Cardiac Arrest to Facilitate Hospital Comparisons

Abstract

Objectives

The purpose of this study is to develop a method for risk-standardizing hospital survival after cardiac arrest.

Background

A foundation with which hospitals can improve quality is to be able to benchmark their risk-adjusted performance against other hospitals, something that cannot currently be done for survival after in-hospital cardiac arrest.

Methods

Within the Get With The Guidelines (GWTG)-Resuscitation registry, we identified 48,841 patients admitted between 2007 and 2010 with an in-hospital cardiac arrest. Using hierarchical logistic regression, we derived and validated a model for survival to hospital discharge and calculated risk-standardized survival rates (RSSRs) for 272 hospitals with at least 10 cardiac arrest cases.

Results

The survival rate was 21.0% and 21.2% for the derivation and validation cohorts, respectively. The model had good discrimination (C-statistic 0.74) and excellent calibration. Eighteen variables were associated with survival to discharge, and a parsimonious model contained 9 variables with minimal change in model discrimination. Before risk adjustment, the median hospital survival rate was 20% (interquartile range: 14% to 26%), with a wide range (0% to 85%). After adjustment, the distribution of RSSRs was substantially narrower: median of 21% (interquartile range: 19% to 23%; range 11% to 35%). More than half (143 [52.6%]) of hospitals had at least a 10% positive or negative absolute change in percentile rank after risk standardization, and 50 (23.2%) had a ≥20% absolute change in percentile rank.

Conclusions

We have derived and validated a model to risk-standardize hospital rates of survival for in-hospital cardiac arrest. Use of this model can support efforts to compare hospitals in resuscitation outcomes as a foundation for quality assessment and improvement.

In-hospital cardiac arrest is common, affecting approximately 200,000 patients annually in the United States (1). Rates of survival, however, can vary substantially across hospitals (2). As a foundation for improving quality in their cardiovascular registries, the American Heart Association (AHA) and the American College of Cardiology have developed methods to risk-standardize hospital outcomes for other conditions and procedures. More recently, the Joint Commission and the AHA have expressed interest in developing performance metrics for in-hospital cardiac arrest to facilitate benchmarking and comparison of survival outcomes among hospitals.

Unlike process-of-care measures for resuscitation (e.g., timely defibrillation), which do not require risk adjustment as their performance should be independent of patient characteristics, survival measures require risk standardization to account for variations in patient case-mix across sites so as to facilitate a more unbiased comparison across hospitals (3). Although risk-adjustment models for survival already exist for other medical conditions, such as acute myocardial infarction, heart failure, and community-acquired pneumonia (4,5), a validated model to risk-standardize survival after in-hospital cardiac arrest has not been developed. This current deficiency in the methodology for in-hospital cardiac arrest is a significant barrier to identifying high and low performing hospitals to disseminate best practices and promote quality improvement.

To address this current gap in knowledge, we derived and validated a hierarchical regression model to calculate risk-standardized hospital rates of survival after in-hospital cardiac arrest. We used data from Get With The Guidelines (GWTG)-Resuscitation—the largest repository of data on hospitalized patients with cardiac arrest. We also assessed the stability of the model over time by examining model performance in multiple years and different time periods. Creating this outcome model can assist ongoing efforts to support ongoing quality assessment and improvement efforts.

Methods

Study population

GWTG-Resuscitation, formerly known as the National Registry of Cardiopulmonary Resuscitation, is a large, prospective, national quality-improvement registry of in-hospital cardiac arrest and is sponsored by the AHA. Its design has been described in detail previously (6). In brief, trained quality-improvement hospital personnel enroll all patients with a cardiac arrest (defined as the absence of a palpable central pulse, apnea, and unresponsiveness) treated with resuscitation efforts and without do-not-resuscitate (DNR) orders. Cases are identified by multiple methods, including centralized collection of cardiac arrest flow sheets, reviews of hospital paging system logs, and routine checks of code carts, pharmacy tracer drug records, and hospital billing charges for resuscitation medications (6). The registry uses standardized “Utstein-style” definitions for all patient variables and outcomes to facilitate uniform reporting across hospitals (7,8). In addition, data accuracy is ensured by rigorous certification of hospital staff and use of standardized software with data checks for completeness and accuracy, and a prior report had determined an error rate in data abstraction of 2.4% (6).

From 2000 to 2010, a total of 122,746 patients 18 years of age or older with an index in-hospital cardiac arrest were enrolled in GWTG-Resuscitation. Since in-hospital survival rates have improved over time (9), we restricted our study population to 48,841 patients from 356 hospitals enrolled between 2007 and 2010 to ensure that our risk models were based on a contemporary cohort of patients.

Study outcome and variables

The primary outcome of interest was survival to hospital discharge, which was obtained from the GWTG-Resuscitation registry.

In all, 26 baseline characteristics were screened as candidate predictors for the study outcome. These included age (categorized in 10-year intervals of <50, 50 to 59, 60 to 69, 70 to 79, and ≥80), sex, location of arrest (categorized as intensive care, monitored unit, nonmonitored unit, emergency room, procedural/surgical area, and other), and initial cardiac arrest rhythm (ventricular fibrillation, pulseless ventricular tachycardia, asystole, pulseless electrical activity). In addition, the following comorbidities or medical conditions present before cardiac arrest were evaluated for the model: heart failure, myocardial infarction, or diabetes mellitus; renal, hepatic, or respiratory insufficiency; baseline evidence of motor, cognitive, or functional deficits (CNS depression); acute stroke; acute non-stroke neurologic disorder; pneumonia; hypotension; sepsis; major trauma; metabolic or electrolyte abnormality; and metastatic or hematologic malignancy. Finally, we considered for model inclusion several critical care interventions (mechanical ventilation, intravenous vasopressor support, pulmonary artery catheter, intra-aortic balloon pump, or dialysis) already in place at the time of cardiac arrest. Race was not considered for model inclusion, as prior studies have found that racial differences in survival after in-hospital cardiac arrest are partly mediated by differences in hospital care quality for blacks and whites (3,10).

Model development and validation

We randomly selected two-thirds of the study population for the derivation cohort and one-third for the validation cohort. We confirmed that a similar proportion of patients from each hospital and calendar year were represented in the derivation and validation cohorts. Baseline differences between patients in the derivation and validation cohorts were evaluated using chi-square tests for categorical variables and Student t tests for continuous variables. Because of the large sample size, we also evaluated for significant differences between the 2 cohorts by computing standardized differences for each covariate. Based on prior work, a standardized difference of >10 was used to define a significant difference (11).

Within the derivation sample, multivariable models were constructed to identify significant predictors of in-hospital survival. Because our primary objective was to derive risk-standardized survival rates for each hospital, which would require us to account for clustering of observations within hospitals, we used hierarchical logistic regression models for our analyses (12). By using hierarchical models to estimate the log-odds of in-hospital survival as a function of demographic and clinical variables (both fixed effects) and a random effect for each hospital, this approach allowed us to assess for hospital variation in risk-standardized survival rates after accounting for patient case-mix.

We considered for model inclusion the candidate variables previously described in the Study Outcome and Variables section. Multicollinearity between covariates was assessed for each variable before inclusion (13). To ensure parsimony and inclusion of only those variables that provided incremental prognostic value, we employed the approximation of full model methodology for model reduction (14). The contribution of each significant model predictor was ranked, and variables with the smallest contribution to the model were sequentially eliminated. This was an iterative process until further variable elimination led to a greater than 5% loss in model prediction as compared with the initial full model.

Model discrimination was assessed with the C-statistic, and model validation was performed in the remaining one-third of the study cohort by examining observed versus predicted plots. We also evaluated the robustness of our findings by reconstructing the models with data from: 1) only 2010; 2) 2009 to 2010; and 3) 2008 to 2010, and comparing the predictors and estimates of these models with that from the main study period (from 2007 to 2010). On validation of the model, we pooled patients from the derivation and validation cohorts and reconstructed a final hierarchical regression model to derive estimates from the entire study sample for risk standardization.

Hospital risk-standardized survival rates

Using the hospital-specific estimates (i.e., random intercepts) from the hierarchical models, we then calculated risk-standardized survival rates for the 272 hospitals with at least 10 cardiac arrest cases by multiplying the registry’s unadjusted survival rate by the ratio of a hospital’s predicted to expected survival rate. We used the ratio of predicted to expected outcomes (described in the following text) instead of the ratio of observed to expected outcomes to overcome analytical issues that have been described for the latter approach (15–17). Specifically, our approach ensured that all hospitals, including those with relatively small case volumes, would have appropriate risk standardization of their cardiac arrest survival rates.

For these calculations, the expected hospital number of cardiac arrest survivors is the number of cardiac arrest survivors expected at the hospital if the hospital’s patients were treated at a “reference” hospital (i.e., the average hospital-level intercept from all hospitals in GWTG-Resuscitation). This was determined by regressing patients’ risk factors and characteristics on in-hospital survival with all hospitals in the sample, then applying the subsequent estimated regression coefficients to the patient characteristics observed at a given hospital, and then summing the expected number of deaths. In effect, the expected rate is a form of indirect standardization. In contrast, the predicted hospital outcome is the number of survivors at a specific hospital. It is determined in the same way that the expected number of deaths is calculated, except that the hospital’s individual random effect intercept is used. The risk-standardized survival rate was then calculated by the ratio of predicted to expected survival rate, multiplied by the unadjusted rate for the entire study sample.

The effects of risk standardization on unadjusted hospital rates of survival were then illustrated with descriptive plots and statistics. In addition, we examined the absolute change (either positive or negative) in percentile rank for each hospital after risk standardization. This approach overcomes the inherent limitation of just examining the proportion of hospitals that are reclassified out of the top quintile with risk standardization, as some hospitals may be reclassified with only a 1% decrease in percentile rank (e.g., from 80% percentile to 79% percentile), whereas other hospitals would require up to a 20% decrease in percentile rank to be reclassified (e.g., hospitals with an unadjusted 99% percentile rank).

Because rates of do-not-resuscitate (DNR) orders may vary across hospitals and influence rates of in-hospital cardiac arrest survival, we conducted the following sensitivity analysis to examine the robustness of our findings. For hospitals in the lower 2 quartiles of risk-standardized survival, we assumed that the rate of DNR status for all admissions was 5%. We then assigned DNR rates at hospitals in the top and second highest quartiles to be 100% and 50%, respectively, greater than that of the lower 2 quartiles. We assumed that the rate of in-hospital cardiac arrest for DNR patients to be 5% and calculated the number of cardiac arrests at each hospital that would have occurred if no patients were made DNR. For instance, for a hospital in the highest quartile of survival with 10,000 annual admissions, an additional 50 cardiac arrests (10,000 × 0.10 [DNR rate] × 0.05 [rate of cardiac arrest]) were added to the denominator for each year of data submission.

For each of these “imputed” patients, we assigned an age of ≥80 years and 1 of the following characteristics: renal insufficiency, cancer, or hypotension. We then recalculated risk-standardized survival rates for the entire hospital sample and examined what proportion of hospitals in the original analysis was no longer classified in their quartile of risk-standardized hospital survival rates. If only a minority of hospitals were recategorized into a different quartile, that would suggest that our classification of hospitals in the top 2 quartiles was robust and persisted despite a higher DNR rate for their admitted patients.

All study analyses were performed with SAS version 9.2 (SAS Institute, Cary, North Carolina) and R version 2.10.0 (18). The hierarchical models were fitted with the use of the GLIMMIX macro in SAS.

Dr. Chan had full access to the data and takes responsibility for its integrity. All authors have read and agree to the manuscript as written. The institutional review board of the Mid America Heart Institute waived the requirement of informed consent, and the AHA approved the final manuscript draft.

Results

Of 48,841 patients in the study cohort, 32,560 were randomly selected for the derivation cohort and 16,281 for the validation cohort. Baseline characteristics of the patients in the derivation and validation cohorts were similar, based on comparisons of both p-values and standardized differences (Table 1). The mean patient age in the overall cohort was 65.6 ± 16.1 years, 58% were male, and 21% were black. More than 80% of patients had a nonshockable cardiac arrest rhythm of asystole or pulseless electrical activity, and nearly half were already in an intensive care unit during the arrest. Respiratory insufficiency and renal insufficiency were the most prevalent comorbidities, whereas one-quarter of patients were hypotensive and one-third were receiving mechanical ventilation at the time of cardiac arrest.

Table 1.

Characteristics of the Derivation and Validation Cohorts

	Derivation Cohort (n = 32,560)	Validation Cohort (n = 16,281)	p Value	Standardized Difference*
Demographics
Age, yrs	65.6 ± 16.1	65.6 ± 16.0	0.91	0.10
Age, yrs, by deciles			0.54
18 to <50	5,269 (16.2%)	2,594 (15.9%)
50 to 59	5,476 (16.8%)	2,832 (17.4%)
60 to 69	7,137 (21.9%)	3,556 (21.8%)
70 to 79	7,562 (23.2%)	3,793 (23.3%)
80 to 89	7,116 (21.9%)	3,506 (21.5%)
≥90
Male	18,996 (58.3%)	9,500 (58.4%)	0.99	0.02
Race			0.77
White	22,576 (69.3%)	11,337 (69.6%)
Black	6,678 (20.5%)	3,288 (20.2%)
Other	1,268 (3.9%)	618 (3.8%)
Unknown	2,038 (6.3%)	1,038 (6.4%)
Hispanic	2,254 (6.9%)	1,060 (6.5%)	0.09	1.65
Pre-existing conditions
Respiratory insufficiency	13,301 (40.9%)	6,640 (40.8%)	0.89	0.14
Renal insufficiency	10,850 (33.3%)	5,358 (32.9%)	0.36	0.88
Arrhythmia	9,974 (30.6%)	4,973 (30.5%)	0.84	0.19
Diabetes mellitus	10,001 (30.7%)	4,928 (30.3%)	0.31	0.97
Hypotension	8,413 (25.8%)	4,308 (26.5%)	0.14	1.42
Heart failure this admission	5,370 (16.5%)	2,678 (16.4%)	0.90	0.12
Prior heart failure	6,278 (19.3%)	3,094 (19.0%)	0.46	0.71
Myocardial infarction this admission	5,184 (15.9%)	2,501 (15.4%)	0.11	1.54
Prior myocardial infarction	4,791 (14.7%)	2,319 (14.2%)	0.16	1.34
Metabolic or electrolyte abnormality	4,765 (14.6%)	2,280 (14.0%)	0.06	1.80
Septicemia	5,519 (17.0%)	2,777 (17.1%)	0.77	0.28
Pneumonia	4,342 (13.3%)	2,239 (13.8%)	0.20	1.22
Metastatic or hematologic malignancy	4,046 (12.4%)	1,997 (12.3%)	0.61	0.49
Hepatic insufficiency	2,474 (7.6%)	1,175 (7.2%)	0.13	1.46
Baseline depression in CNS function	3,640 (11.2%)	1,853 (11.4%)	0.51	0.64
Acute CNS non-stroke event	2,250 (6.9%)	1,139 (7.0%)	0.73	0.34
Acute stroke	1,234 (3.8%)	605 (3.7%)	0.69	0.39
Major trauma	1,399 (4.3%)	668 (4.1%)	0.32	0.97
Characteristics of arrest
Cardiac arrest rhythm			0.99
Asystole	10,997 (33.8%)	5,491 (33.7%)
Pulseless electrical activity	15,327 (47.1%)	7,653 (47.0%)
Ventricular fibrillation	3,691 (11.3%)	1,862 (11.4%)
Pulseless ventricular tachycardia	2,545 (7.8%)	1,275 (7.8%)
Location			0.92
Intensive care unit	15,780 (48.5%)	7,809 (48.0%)
Monitored unit	5,034 (15.5%)	2,539 (15.6%)
Nonmonitored unit	5,632 (17.3%)	2,824 (17.3%)
Emergency room	3,307 (10.2%)	1,687 (10.4%)
Procedural or surgical area	2,132 (6.5%)	1,073 (6.6%)
Other	675 (2.1%)	349 (2.1%)
Interventions in place
Mechanical ventilation	10,747 (33.0%)	5,422 (33.3%)	0.51	0.63
Intravenous vasopressor	9,549 (29.3%)	4,800 (29.5%)	0.72	0.34
Pulmonary artery catheter	833 (2.6%)	378 (2.3%)	0.11	1.53
Dialysis	1,163 (3.6%)	598 (3.7%)	0.57	0.54
Intra-aortic balloon pump	482 (1.5%)	228 (1.4%)	0.49	0.67

Values are mean ± SD or n (%).

^*For binary variables, because of the large sample size, standardized differences of >10 indicate a significant difference between groups.

Overall, 10,290 (21.1%) patients with an in-hospital cardiac arrest survived to hospital discharge. The survival rates were similar in the derivation (n = 6,844; 21.0%) and validation cohorts (n = 3,446; 21.2%). A comparison of baseline characteristics between patients who survived and did not survive to hospital discharge is provided in Online Table 1. In general, patients who survived were younger, more frequently white, more likely to have an initial cardiac arrest rhythm of ventricular fibrillation or pulseless ventricular tachycardia, and to have fewer comorbidities or interventions in place (e.g., intravenous vasopressors) at the time of cardiac arrest.

Initially, 18 independent predictors were identified in the derivation cohort with the multivariable model, resulting in a model C-statistic of 0.738 (Table 2; see Online Table 2 for variable definitions). After model reduction to generate a parsimonious model with no more than 5% loss in model prediction, our final model comprised 9 variables, with only a small change in the C-statistic (0.734). The predictors in the final model included age, initial cardiac arrest rhythm, hospital location of arrest, hypotension, septicemia, metastatic or hematologic malignancy, hepatic insufficiency, and requirement for mechanical ventilation or intravenous vasopressor before cardiac arrest. The beta-coefficient estimates and adjusted odds ratios are summarized in Table 3. Importantly, there was no evidence of multicollinearity between any of these variables (all variance inflation factors <1.5).

Table 2.

Full Model for Predictors of Survival to Hospital Discharge

Predictor	Beta-Weight Estimate	Odds Ratio	95% CI
Age, yrs
<50	0	Reference	Reference
50–59	−0.0202	0.98	0.88–1.08
60–69	−0.0408	0.96	0.87–1.05
70–79	−0.2877	0.75	0.68–0.83
≥80	−0.6931	0.50	0.46–0.56
Male	−0.0834	0.92	0.87–0.98
Hospital location
Nonmonitored unit	0	Reference	Reference
Intensive care unit	0.5653	1.76	1.59–1.93
Monitored unit	0.4700	1.60	1.45–1.78
Emergency room	0.5188	1.68	1.49–1.89
Procedural or surgical area	1.1217	3.07	2.71–3.49
Other	0.6259	1.87	1.54–2.26
Initial cardiac arrest rhythm
Asystole	0	Reference	Reference
Pulseless electrical activity	0.0392	1.04	0.97–1.12
Ventricular fibrillation	1.2238	3.40	3.10–3.72
Pulseless ventricular   tachycardia	1.1086	3.03	2.73–3.36
Myocardial infarction this   admission	0.1484	1.16	1.07–1.25
Prior heart failure	−0.0619	0.94	0.87–1.01
Renal insufficiency	−0.2231	0.80	0.75–0.86
Hepatic insufficiency	−0.6539	0.52	0.45–0.59
Hypotension	−0.4463	0.64	0.59–0.69
Septicemia	−0.4308	0.65	0.59–0.71
Acute stroke	−0.3147	0.73	0.63–0.86
Diabetes mellitus	0.1310	1.14	1.06–1.21
Metabolic/electrolyte   abnormality	−0.1625	0.85	0.77–0.94
Metastatic or hematologic   malignancy	−0.7550	0.47	0.42–0.53
Major trauma	−0.3425	0.71	0.60–0.83
Mechanical ventilation	−0.5447	0.58	0.54–0.63
Dialysis	−0.3011	0.74	0.61–0.90
Intravenous vasopressor	−0.7340	0.48	0.44–0.52

CI = confidence interval.

Table 3.

Final Reduced Model for Predictors of Survival to Discharge

Predictor	Beta-Weight Estimate	Odds Ratio	95% CI
Age, yrs
<50	0	Reference	Reference
50–59	0.0031	1.00	0.91–1.11
60–69	−0.0096	0.99	0.90–1.09
70–79	−0.2560	0.77	0.70–0.85
≥80	−0.6562	0.52	0.47–0.57
Initial cardiac arrest rhythm
Asystole	0	Reference	Reference
Pulseless electrical activity	0.0478	1.05	0.98–1.13
Ventricular fibrillation	1.2631	3.54	3.24–3.86
Pulseless ventricular   tachycardia	1.1289	3.09	2.79–3.43
Hospital location
Nonmonitored unit	0	Reference	Reference
Intensive care unit	0.5643	1.76	1.60–1.93
Monitored unit	0.4816	1.62	1.46–1.79
Emergency room	0.5618	1.75	1.56–1.97
Procedural or surgical area	1.1550	3.17	2.80–3.60
Other	0.6210	1.86	1.54–2.25
Hypotension	−0.4749	0.62	0.57–0.67
Sepsis	−0.4879	0.61	0.56–0.68
Metastatic or hematologic   malignancy	−0.7345	0.48	0.43–0.53
Hepatic insufficiency	−0.7240	0.48	0.42–0.56
Mechanical ventilation	−0.5662	0.57	0.53–0.61
Intravenous vasopressor	−0.7329	0.48	0.44–0.52

CI = confidence interval.

When the model was tested in the independent validation cohort, model discrimination was similar (C-statistic of 0.737). Calibration was confirmed with observed versus predicted plots in both the derivation and validation cohorts (R² of 0.99 for both). When we repeated the analyses using data from year 2010 only, 2009 to 2010, and 2008 to 2010, our model predictors were unchanged, and the estimates of effect for each predictor were similar.

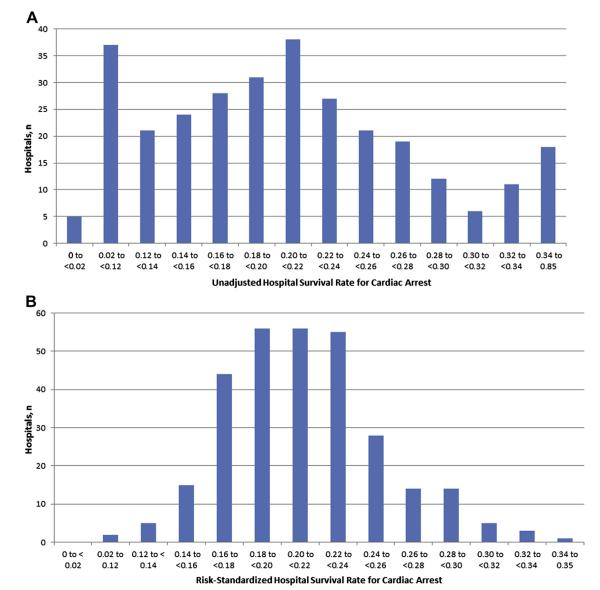
Figure 1 depicts the unadjusted and risk-standardized distribution of hospital rates of cardiac arrest survival (see Online Table 3 for calculations of the risk-standardized rates). The mean unadjusted hospital survival rate was 21 ± 13%, whereas the mean risk-standardized hospital survival rate of 21 ± 4% showed a much narrower distribution. Similarly, the median unadjusted hospital survival rate was 20% (interquartile range 14% to 26%; range 0% to 85%), whereas the interquartile range and range for the risk-standardized hospital survival rates were substantially smaller: median of 21% (interquartile range: 19% to 23%; range 11% to 35%). Nine (3.3%) of the 272 hospitals had risk-standardized survival rates of ≥30%, or ~50% higher than the average hospital.

Figure 1. Distribution of Unadjusted and Risk-Standardized Hospital Survival Rates for In-Hospital Cardiac Arrest.

(A) Observed hospital rates: the number of hospitals for each range of survival rates is displayed. A total of 276 hospitals with ≥10 in-hospital cardiac arrest cases were evaluated. (B) Risk-standardized hospital rates: the number of hospitals for each range of survival rates is displayed. A total of 276 hospitals with ≥10 in-hospital cardiac arrest cases was evaluated.

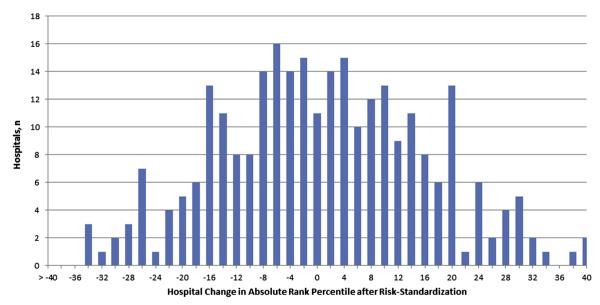
To examine the effect of risk standardization at individual hospitals, the change in percentile rank for each hospital was examined (Fig. 2). Of 272 hospitals, 143 (52.6%) had at least a 10% positive or negative absolute change in percentile rank after risk standardization (e.g., hospital ranked at 39% percentile before and at 53% percentile after risk standardization). Moreover, 50 hospitals (23.2%) had a substantial ≥20% absolute change in percentile rank, with 24 having a 20% or greater increase and 26 having a 20% or greater decrease.

Figure 2. Hospital Change in Absolute Rank Percentile After Risk Standardization.

The change in a hospital’s percentile rank in survival rates for in-hospital cardiac arrest after accounting for patient case-mix is depicted. Of 272 hospitals, 143 (52.6%) had at least a 10% positive or negative absolute change in percentile rank after risk standardization, and 50 hospitals (23.2%) had a substantial ≥20% absolute change in percentile rank.

Finally, we found that our study findings were unlikely to be influenced by higher rates of DNR at hospitals with higher risk-standardized survival. Only 1 of 68 hospitals in the top quartile of risk-standardized survival was reclassified to a different quartile, even after assuming that hospitals in the top quartile had DNR rates that were twice the DNR rate of the lower 2 quartiles. Similarly, only 1 of 68 hospitals in the second highest quartile of risk-standardized survival was reclassified, even after assuming that these hospitals had DNR rates that were 50% higher than those in the lower 2 quartiles (Online Table 4).

Discussion

Within a large national registry, we derived and validated a risk-adjustment model for survival after in-hospital cardiac arrest. The model was based on 9 clinical variables that are easy to identify and collect. Moreover, the model had good discrimination and excellent calibration. Importantly, our model adhered to recommended standards to be employed for public reporting, including the use of hierarchical models, timely and high-quality data, and clearly defined study population and outcomes (3). As a result, we believe this model provides a mechanism to generate risk-standardized survival rates to facilitate more accurate comparisons of resuscitation outcomes across hospitals.

Because substantial variation in hospital survival rates after in-hospital cardiac arrest exists (2), there are currently efforts to measure hospital performance for this condition. The Joint Commission, for instance, is developing a number of metrics to assess hospital performance in resuscitation. The AHA’s GWTG-Resuscitation national registry has also developed a number of target benchmarks to highlight hospitals with exceptional performance. Most of these performance metrics are process-oriented, such as time to defibrillation and time to initiation of cardiopulmonary resuscitation, and are therefore independent of confounding by patient case-mix. However, both organizations also plan to profile survival outcomes after cardiac arrest.

In contrast to process measures, several key challenges exist in comparing survival outcomes across hospitals. First, and most important, hospital variation in survival may be simply due to heterogeneity in patients’ case-mix. Hospitals with cardiac arrest patients who have higher illness acuity may have lower survival rates. To date, a risk-adjustment model that uses appropriate analytical techniques to account for nesting of data within hospitals (i.e., hierarchical models) has not been derived and validated. Although several multivariable models for in-hospital cardiac arrest exist (19,20), these have not been validated, were based on less contemporary cohorts of patients, and used analytical approaches that do not adequately account for clustering of patients within hospitals. Therefore, these other models may have under-estimated standard errors, which can lead to type I errors in inferences regarding statistical significance and inappropriately label certain hospitals as performing better, or worse, than average (21). Moreover, unlike hierarchical models used in this study, these other approaches do not have a mechanism to weight the number of observations contributed by each hospital to account for differences in the sample sizes across hospitals.

Second, prior efforts in risk standardization for other disease conditions have been based on the ratio of observed to expected outcomes. This approach has significant limitations (16,17), especially the inability to risk-standardize rates for sites with low case volumes. In this study, we overcame both of these barriers by deriving and validating a risk-adjustment model using hierarchical random-effects models and basing our risk standardization on the ratio of predicted to expected outcomes (15), thereby allowing us to generate risk-standardized rates for hospitals in the study.

Without risk standardization, differences in hospital survival rates for in-hospital cardiac arrest may be due to differences 1) patient case-mix; and 2) quality of care between hospitals. From a quality perspective, only the last difference is of interest. With our risk-standardization approach, which controlled for differences in patient case-mix across hospitals, the range of hospital survival rates narrowed enormously, with the interquartile range decreasing from 12% to 4%. Even more importantly, we found that more than half of hospitals changed in percentile rank by at least 10%, and nearly a quarter of hospitals changed in percentile rank by 20% or greater, suggesting a significant impact of risk standardization (to account for differences in case-mix) in assessing a hospital’s survival outcomes for in-hospital cardiac arrest. Both of these findings suggest that simple comparisons of unadjusted hospital survival rates would be problematic and likely to lead to incorrect inferences.

Importantly, despite the reduction in variability with our risk-adjustment methodology, there remained notable differences in risk-standardized rates of survival. That suggests that some hospitals were able to achieve higher survival rates than others. For instance, some (9 of 272 [3.3%]) hospitals had risk-standardized survival rates of ≥30%, or ~50% higher than the average hospital. Which hospital factors or quality improvement initiatives are associated with the higher survival outcomes in these hospitals remain unknown. Therefore, identifying best practices at these top-performing hospitals should be a priority (22), as their dissemination to all hospitals has the potential to significantly improve survival for all patients with in-hospital cardiac arrest.

Study limitations

Our study should be interpreted in the context of the following limitations. First, although our risk model was able to account for a number of clinical variables, unmeasured confounding may exist. Specifically, our model did not have information on some prognostic factors, such as creatinine or the severity level for each comorbid condition. In addition, thorough documentation of patients’ case-mix (e.g., comorbidities) and access to telemetry and intensive care unit monitoring may differ across sites, which could account for some of the hospital variation in risk-standardized survival rates. Second, our model did not adjust for intra-arrest variables (such as quality of cardiopulmonary resuscitation and time to defibrillation) which are known to influence survival outcomes. However, because these latter variables are attributes specific to a hospital’s performance, their inclusion in a model developed to profile hospitals for resuscitation performance would be improper (3). Third, we did not have information on DNR status for all admitted patients or the proportion of deaths with attempted resuscitation at each hospital, and this rate is likely to vary across hospitals. Such variation is likely to affect a hospital’s crude rank performance for cardiac arrest survival. However, in our sensitivity analyses, we found that a hospital’s risk-standardized rank performance was relatively unaffected by variation in DNR rates across sites, thus underscoring the importance of risk standardization for meaningful comparisons of in-hospital cardiac arrest survival across hospitals.

Fourth, our study population was limited to hospitals participating within the AHA’s GWTG-Resuscitation program. Therefore, our findings may not apply to non-participating hospitals. Fifth, our model was developed in patients with in-hospital cardiac arrest. Because the reasons for cardiac arrest and comorbidity burden differ for patients with out-of-hospital cardiac arrest, our findings do not apply to cardiac arrests occurring outside hospitals. Finally, we have not developed a model for survival with good neurological outcome. Although this is an important consideration for patients with in-hospital cardiac arrest and should be the focus of a future study, our goal was to develop a risk-standardization model for in-hospital survival, as this is the outcome proposed by national organizations for a performance measure.

Conclusions

Given poor survival outcomes for in-hospital cardiac arrest, there is growing national interest in developing performance metrics to benchmark hospital survival for this condition. In this study, we have developed and validated a model to risk-standardize hospital rates of survival for in-hospital cardiac arrest. We believe that use of this model to adjust for patient case-mix represents an advance in ongoing efforts to profile hospitals in resuscitation outcomes, with the hope that clinicians and administrators will be stimulated to develop novel and effective quality improvement strategies to improve their hospital’s performance.

Abbreviations and Acronyms

AHA

American Heart Association

DNR

do not resuscitate

GWTG

Get With The Guidelines