STABILITY OF HETEROGENEOUS ELASTOGRAPHY PHANTOMS MADE FROM OIL DISPERSIONS IN AQUEOUS GELS

Abstract

A set of five tissue-mimicking phantoms with cylindrical inclusions were produced for assessing long-term stability of geometry and elastic properties and assessing accuracy of determination of elastic properties. The base aqueous materials were either gelatin or a mixture of agar and gelatin. Stiffness was controlled by selection of the volume percent consisting of microscopic safflower oil droplets. Cylinder diameters remained unchanged within 1% or 2% over many months. Strain ratios from elastograms of the phantoms were stable over many months, implying that elastic contrasts were also stable. Test samples, called production samples, for measurement of Young’s moduli were made at the time of manufacture of each phantom and were stored separately from one another. Each production sample was homogeneous and consisted of either inclusion material or background material. For all five phantoms, it was found that the elastic contrast computed using Young’s modulus values determined using the production samples accurately represented the true elastic contrasts in the corresponding phantom. This finding was established by the fact that the (true) elastic contrasts determined using samples excised from the phantoms themselves agreed with the elastic contrasts obtained using the homogeneous production samples.

INTRODUCTION

Use of oil-in-gelatin dispersions to make heterogeneous phantoms for use in elastography has been previously reported. (Madsen et al. 2003) In that work, two different 9 cm × 9 cm × 9 cm phantoms with 1-cm diameter cylindrical inclusions were used to assess temporal stability of geometry (cylinder diameter) and accuracy of elastic contrast determination. Temporal stability of geometry was verified by comparison of strain profiles made over an 8-week period. Samples for measurement of the quasistatic Young’s moduli were made for the inclusion and background materials at the time of production of each phantom; such samples are referred to in the current report as production samples. Evidence was given that the elastic contrast (Young’s modulus of the inclusion material ÷ Young’s modulus of the background), computed using Young’s moduli determined using the production samples, correctly specified the elastic contrast for the phantoms, themselves. This evidence involved comparing the strain ratios determined from elastograms of the phantoms with elastic strain ratios predicted by the model of Kallel et al. (2001), using the elastic contrast corresponding to the production samples. The two strain ratios agreed well for both phantoms, implying that the elastic contrasts obtained using the production samples equaled those inside the corresponding phantoms.

In the present study, more direct methods were used for assessing temporal stability of geometry and elastic contrast¹ and for assessing the reliability of the assumption that elastic contrast for a heterogeneous phantom is correctly given by that computed from Young’s moduli of samples of inclusion and background materials made at the time of production of the phantom. The methods include manufacture of cubic heterogeneous phantoms with cylindrical inclusions along with production samples for measurement of Young’s moduli. Cylinder diameters were monitored periodically using an ultrasound (US) scanner and, 7 weeks or more after production of a phantom, it was sliced perpendicularly to the cylindrical inclusions into 1-cm and 2-cm slabs allowing samples of those thicknesses to be excised for determination of Young’s moduli. Young’s moduli for the excised samples and for the production samples were then compared. Before excising the samples, however, cylinder diameters were accurately measured directly on the slabs with a machinist’s calipers.

The composition of the aqueous gel components of each phantom was the same throughout that phantom; this gel component was either gelatin-based or agar-plus-gelatin-based. The agar-plus-gelatin type phantom contained Cu²⁺-ethylenediaminetetraacetic acid (EDTA) to lower the magnetic resonance imaging (MRI) longitudinal relaxation time (T₁) to tissue-like values and NaCl to produce realistic coil loading (Rice et al. 1998). Three of the gelatin-based phantoms contained propylene glycol to raise the US propagation speed to tissue-like values. Also, some materials contained a small concentration of microscopic glass beads to provide adequate backscatter for US elastography systems.²

MATERIALS AND PRODUCTION METHODS

The materials composing the inclusions and background in each phantom were oil-in-gel dispersions, where the (aqueous) gel was either gelatin or a mixture of agar and gelatin. The method of production of the oil-in-gelatin dispersions has been described in detail previously. (Madsen et al. 2003) When the aqueous gel suspending the dispersion of microscopic oil droplets was an agar + gelatin mixture, the same basic procedure was used to produce the oil-in-agar/gelatin dispersions as in the case of the oil-in-gelatin dispersions.

However, because the detailed procedure for producing the oil-in-agar + gelatin dispersions has not yet been reported, an example is given here, where the method for producing about 1200 mL of the background material corresponding to phantom B is described. First, make an aqueous gelatin solution by mixing together 307 mL of distilled water (at room temperature) with 54 g of (dry) 200 bloom gelatin derived from calfskin. (Vyse Gelatin Co., Schiller Park, IL, USA) After covering the beaker with a thin plastic membrane, such as Saran Wrap^®, heat the mixture in a double boiler to about 90 °C until the mixture becomes optically transparent. The hot clarified mixture is referred to as “molten gelatin.” At the same time that the molten gelatin is being made and, in the same manner, prepare a quantity of molten agar starting with a mixture of 533 mL of distilled water at room temperature and 10.9 g of dry agar (Fisher Scientific, Pittsburgh, PA, USA). Mix together 307 mL of the molten gelatin at 90 °C and 480 mL of the molten agar, also at 90 °C. After raising the beads to 50 °C in an oven, add 4.8 g of 48 to 53 micrometer diameter E-type glass beads (Potters Industries, Parsippany, NJ, USA) to the hot mixture of molten gelatin and molten agar. Add 2.73 g of EDTA tetrasodium salt hydrate (catalog no. E26290, Aldrich Chemical Co., Inc., Milwaukee, WI, USA), 0.93 g CuCl₂-2H₂O, 6.4 g NaCl and 12 g of liquid Germall-plus^® (Sutton Laboratories, Inc., Chatham, NJ, USA). Next, combine, in a 1.5-L beaker, 600 mL of the above mixture at 50 °C with 600 mL of safflower oil (Hollywood brand, The Hain Celestial Group, Inc., Melville, NY, USA), also at 50 °C. Using a stainless-steel tablespoon bent at a right angle where the spoon bowl and handle meet, stir the mixture, keeping the bowl well below the surface and stirring with a motion about a horizontal axis to minimize introduction of air bubbles. This procedure should produce oil droplets of 1-mm diameter or less. Add 12 mL of surfactant (liquid Ultra Ivory^®, Proctor and Gamble, Cincinnati, OH, USA) and continue the vigorous stirring for 1 or 2 min, producing an off-white emulsion. Cool to 40 °C by partially immersing the beaker in cold tap water while stirring continuously. Add 3.2 g of formalin and cool to about 35 °C, stirring well to assure uniformity of all components. (Note that formalin is 37% formaldehyde.) Pour the emulsion into one or more molds and seal under positive gauge pressure. To avoid possible gravitational sedimentation during congealing, attach the mold and contents to an apparatus that rotates about a horizontal axis at a constant rate of about 2 rpm for a sufficient time that congealing and cross-linking of gelatin molecules by the formaldehyde has occurred (24 h is sufficient).

At the time of manufacture of each component material in the phantoms (inclusion or background), test samples, called production samples, were made for measurement of Young’s moduli. These test samples were 2.6 cm in diameter, 1.0- or 2.0-cm thick discs. Except for phantoms C and D, samples for determination of US and nuclear magnetic resonance (NMR) properties were also made. For ultrasonic measurements, 2.5-cm thick, 7.6-cm diameter samples were enclosed in a cylindrical container with 6-mm thick acrylic walls and 25-µm thick Saran Wrap^® (polyvinylidene chloride, Dow Chemical Co., Midland, MI, USA) covering the parallel faces. For NMR relaxation time measurement, a 5-mm diameter glass NMR tube (catalog no. 512, Wilmad LabGlass, Buena, NJ, USA) was filled to within 5 mm of the top and was then sealed from air with petrolatum.

The 2-cm diameter cylindrical inclusion in phantom B consisted of the agar + gelatin mixture described above, without addition of safflower oil or surfactant. Thus, the agar + gelatin material composing the inclusion had the same chemical composition as the agar + gelatin matrix surrounding the oil droplets in the background material. The reason that the inclusion material and matrix material had the same composition was to minimize changes in the phantom properties caused by osmotic effects.

Five phantoms were produced for this study and were designated A to E. Each phantom contained one inclusion material and one background material. Tables 1 and 2 show the weight percents of the component materials in the aqueous parts of the phantoms. Table 3 shows the volume percents of safflower oil in inclusions and backgrounds.

Table 1.

Weight percents of components in the inclusion of phantom B and in the aqueous gel matrix surrounding the oil droplets in the background material

Agar	Gelatin	CuCl2-2H2O	EDTA tetra-Na hydrate	NaCl	formalin	Germall Plus	Glass bead scatterers
1.15	5.62	0.11	0.324	0.763	0.51	1.43	0.57

The weight percent water, which composes the balance, is not shown. 50% of the volume of the background consists of microscopic droplets of safflower oil. The volume of liquid surfactant equals approximately 1% of the volume of the matrix gel (or of safflower oil) in the background material.

Table 2.

Weight percents of components in the inclusions of phantoms A and D and in the gel matrix surrounding the microscopic safflower oil droplets when oil is present (backgrounds of phantoms A and D and both materials in phantoms C and E)

	Gelatin	Germall Plus	Propylene glycol	Formalin	Glass beads
Phantom A	12.77	1.24	0	0.735	0.083
Phantoms C, D and E	13.25	0	5.16	0.735	0

When oil droplets are present, the volume of liquid surfactant equals approximately 1% of the volume of the gel matrix.

Table 3.

Volume percents consisting of safflower oil in the inclusions and background materials of phantoms A–E

Phantom A		Phantom B		Phantom C		Phantom D		Phantom E
Inclusion	Backgrnd	Inclusion	Backgrnd	Inclusion	Backgrnd	Inclusion	Backgrnd	Glandular	Fat
0	50	0	50	30	70	0	50	50	70

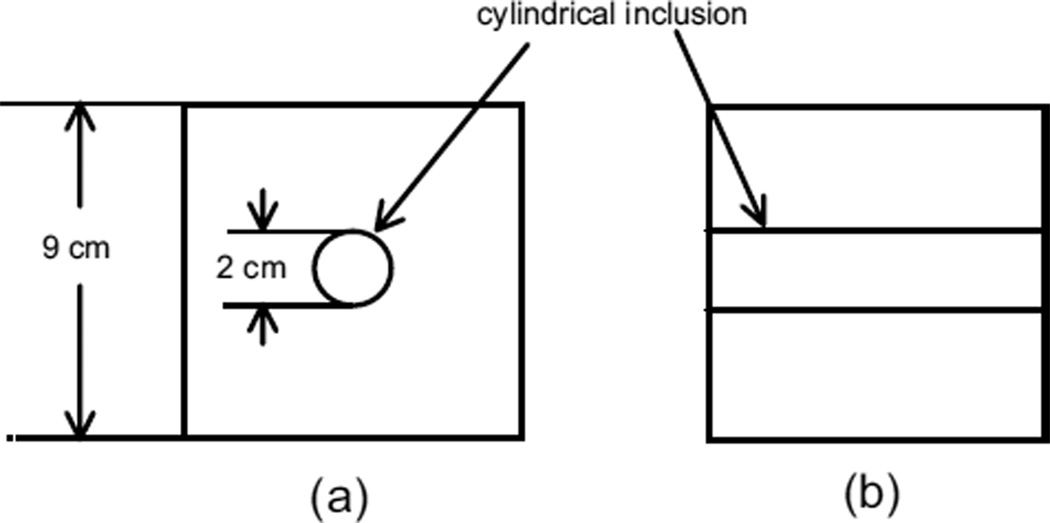
Phantoms A to C were 9 cm × 9 cm × 9 cm cubes of background material with cylindrical inclusions. A diagram of phantoms A to C is shown in Fig. 1. The molds and procedure for making a phantom with the geometry shown in Fig. 1 have been described previously (Madsen et al. 2003). Briefly, the background is made first, surrounding a 2-cm diameter acrylic rod. After the background material has congealed, the rod is removed and the hole filled with the inclusion material.

Fig. 1.

Heterogeneous phantom geometry corresponding to phantoms A to C; (a) view with axis of cylindrical inclusion perpendicular to figure, (b) view with axis parallel to plane of figure.

Making smooth parallel cuts of the cylindrical inclusion in phantom A to obtain samples for measurement of complex Young’s moduli (see Methods of procedure section, following) was not as satisfactory as in the case of the other phantoms because of the rubbery, but easily fractured, nature of the pure cross-linked gelatin. Thus, an alternative phantom, D, in which the cutting difficulties were avoided, was constructed of the same materials as those in phantom A, except that, in phantom D, propylene glycol was introduced to increase the US propagation speeds (see Fig. 2). First, six 2-cm thick, 2.6-cm diameter cylindrical samples were produced with molten gelatin, but no oil dispersion. The next day, two of these discs (cylindrical samples) were placed in the constraining apparatus diagrammed in Fig. 2; this apparatus allowed the curved surfaces of the discs to be in direct contact with surrounding 50% oil-in-gelatin background material, and the discs themselves could be removed intact after long-term contact with the background material. Three 250-µm thick Teflon^® discs separated the sample discs from each other and from the acrylic blocks above and below them. (In an earlier attempt to do this experiment without the Teflon separators, it was found that, when the gelatin discs had been in direct contact for an extended period of time, the discs bonded tightly to one another and could not be separated.)

Fig. 2.

Structure of phantom D; (a) side view of constraining apparatus in the cubic container, (b) top view of constraining apparatus.

A stainless-steel screw and the acrylic constraining block provided for slight pressure to be applied to the gelatin discs so that the discs maintained adequate contact with the Teflon^® discs and no background emulsion could flow between the Teflon^® and gelatin sample discs. The constraining apparatus with two sample discs were placed at the bottom of a cubic acrylic container with inner dimensions 10 cm × 10 cm × 10 cm and open at the top. The 50% safflower oil emulsion used to form the background was made using molten gelatin with the same composition as that used to make the discs, and the emulsion was poured around the apparatus constraining the gelatin discs so that the emulsion contacted the entire curved surfaces of the discs, but did not contact the screw. After the background had congealed, the stainless-steel screw was withdrawn, relieving pressure on the sample discs. A second layer of the 50% emulsion was then poured in to completely submerge the remainder of the constraining apparatus. Finally, the remaining four sample discs were removed from their molds, immersed in safflower oil in small glass jars and sealed in with a cover; these were the inclusion production samples.

Phantom E is an anthropomorphic breast phantom that will be reported in more detail in a future paper. Externally, this phantom has the shape of a right circular cylinder. The central part consists of a 50% safflower-oil-in-gelatin dispersion simulating glandular parenchyma, and the surrounding jacket consists of a 70% safflower-oil-in-gelatin dispersion simulating subcutaneous fat.

At the completion of production of each phantom, it was completely immersed in a safflower oil bath for storage. The surrounding oil prevents desiccation of aqueous components.

METHODS OF PROCEDURE

Measurement of intrinsic physical properties

Young’s moduli, ultrasonic parameters and NMR relaxation times were measured at 22 °C. The method for determining ultrasonic propagation speeds and attenuation coefficients was the commonly used through-transmission water-substitution method described, for example, in Madsen et al. (1999).

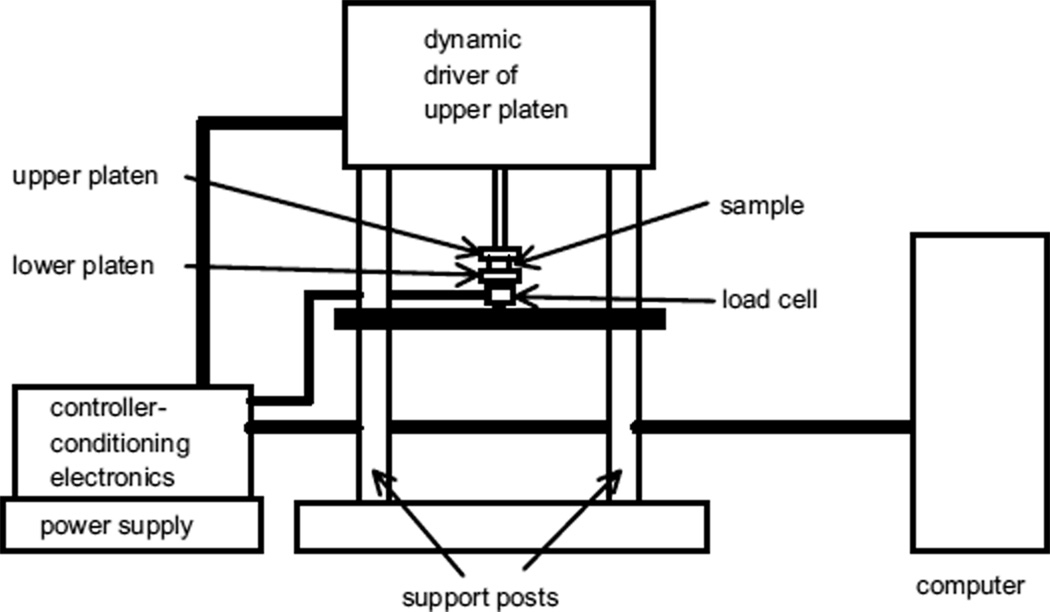
For the 2.6-cm diameter, 1.0- or 2.0-cm thick samples of the tissue-mimicking (TM) materials, dynamic measurements of complex Young’s moduli were made using an EnduraTEC 3200 ELF system (Bose Corporation, EnduraTEC Systems Group, Minnetonka, MN, USA) with a 250-g or 1000-g load cell. The computer controls data acquisition parameters through the controller-conditioning electronics unit. The latter operates the dynamic driver of the upper platen and detects load cell voltages, converting them to force values. Both the monitored force and displacement values are relayed to the computer through the controller-conditioner. The computer uses these values with the DMA software to calculate the complex Young’s modulus.

Test samples were kept immersed in safflower oil when measurements were not being made, to prevent desiccation. To make a measurement, a sample disc was removed from the oil and placed between two horizontal parallel circular platens made of Teflon^®. The platens were 3 cm in diameter. The lower platen has a circular lip around the edge, assuring that the entire flat surfaces of the sample were in contact with the platens at all times. The inner diameter of the lip was 2.8 cm; thus, there was no constraint on the diameter of the sample. Residual safflower oil was left on the surfaces of the sample disc to assure that nearly frictionless slipping could occur at the interfaces between the platens and the sample disc. A simple schematic of the measurement system is given in Fig. 3.

Fig. 3.

Schematic of the EnduraTEC 3200 ELF system used to measure dynamic Young’s moduli of test samples.

The actual measurement procedure was programmed using the EnduraTEC WinTest:version 2.56^® dynamic mechanical analysis (DMA) software (Bose Corporation, EnduraTEC). Initially, the upper platen is not in contact with the sample disc. It is lowered until contact was detected, and then the program completes the procedure as follows. After taring the load cell, the sample is compressed at 0.04 mm/s to a mean compression value M selected by the user and that compression is maintained for a user-selected time (typically 5 s), after which a “precycle” compression variation is done, ending at compression M. Then, a 1-Hz sinusoidal oscillation in compression proceeds at a displacement amplitude chosen by the user. Ten cycles are completed, after which the Fourier analysis of both waveforms allows analysis at the peak frequency. Displacement and force are monitored simultaneously. Amplitudes of displacement and force are determined, as is the lag of the displacement relative to the force. These values, along with entered values for the sample diameter and thickness, allow computation by the software of the real (storage) and imaginary (loss) parts of Young’s modulus. The procedure is repeated at least once more and an averaging of the real and imaginary parts is taken.

At the time of production of each component material in a phantom, typically two disc samples (production samples) were made. The Young’s modulus for a component material was taken to be the mean Young’s modulus for the pair. The uncertainty was taken to equal the standard error (SD of the mean) ≡ the sample standard deviation ÷ √2 (Bevington 1969), unless the resulting standard error is less than the estimated day-today reproducibility uncertainty, namely, 3% of the Young’s modulus value (i.e., the minimum uncertainty for a mean Young’s modulus value is 3% of that mean value).

The NMR relaxation times T₁ and T₂ were measured using the inversion-recovery pulse sequence for T₁ and the Carr–Purcell–Meiboom–Gill pulse sequence for T₂. The relaxometer uses a 60-MHz Bruker mq 60 minispec^® NMR analyzer (Bruker Optics, Inc., Minispec Division, The Woodlands, TX, USA) operating at a probe (sample) temperature of 22 °C. Monoexponential fitting sufficed for both T₁ and T₂.

Assessment of long-term stability of geometry

Geometric stability was monitored by periodic measurement of inclusion cylinder diameters on US images and by direct measurement using machinist’s calipers on phantom slices when the phantoms were cut up (see Fig. 4). For phantoms B, C and D, US diameter measurements were made using electronic calipers on proximal and distal specular reflections, using a Siemens Antares unit (Siemens Ultrasound, Mountain View, CA, USA) equipped with a VFX 9–4 linear-array operating at 9 MHz.

Fig. 4.

Photograph of a slice of a phantom and machinist’s calipers used for direct measurement of cylinder diameter.

In the case of phantom A, US diameter measurements were done retrospectively by recalling data obtained during acquisition of elastograms to reconstruct B-mode images; the images correspond to a 4.5% compression of the phantom. Specular reflections were not well-defined on the images, so the distance between abrupt proximal drop-off and distal recovery of signal on axial B-mode profiles (A-modes) was taken to equal the cylinder diameter.

Assessment of long-term stability of strain ratios and elastic contrasts

The strain ratio corresponding to a given elastogram is defined as the mean strain of the inclusion divided by the mean strain of the background. To assess the stability of the strain ratio, periodic determinations of strain ratios were made from elastograms of phantoms A–C obtained using an Aloka model SD-2000 scanner with a 7.5-MHz linear-array transducer, focused at 5.5 cm. Elastogram data resulted from an initial compression of 4 mm and a final compression of 4.5 mm.

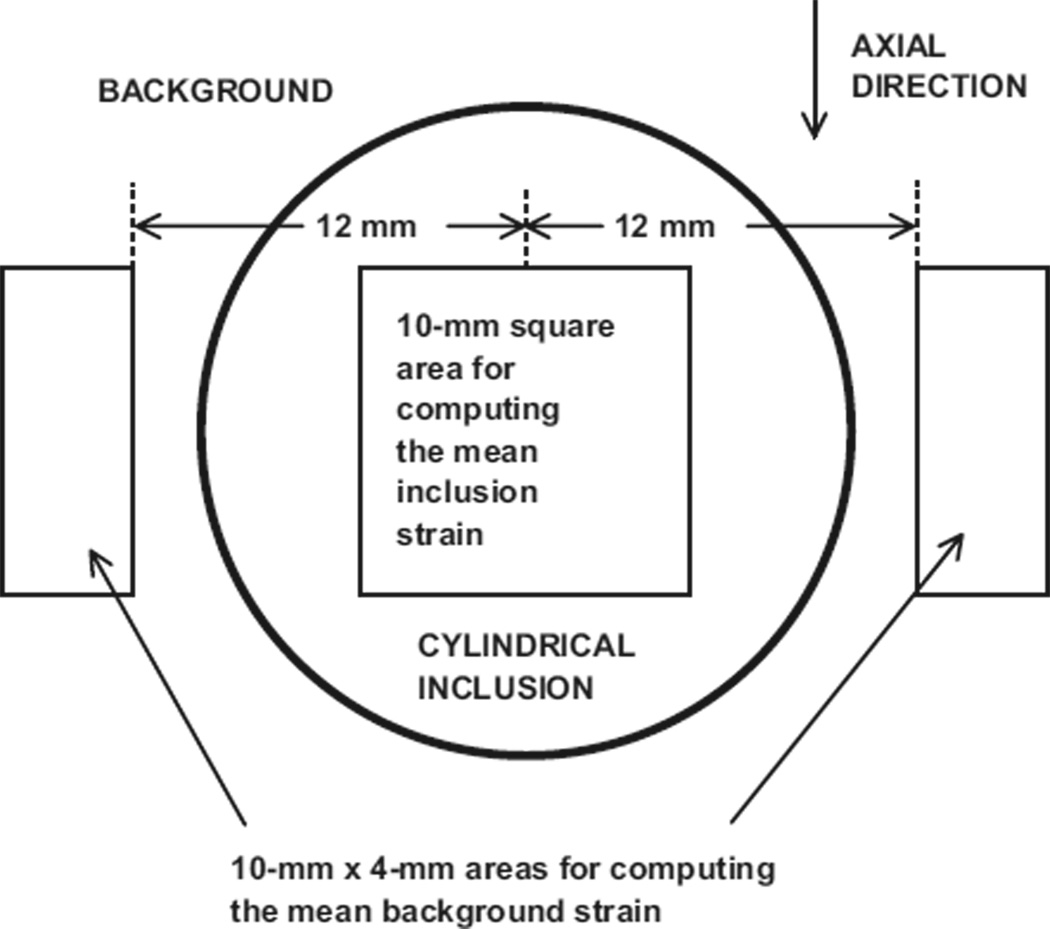
The following method was used for consistent selection of areas on the elastogram to determine mean strains (see Fig. 5). The center of the inclusion was located on the elastogram and its pixel coordinates noted. Then, the mean strain value and SD for the inclusion were determined from all pixel values for pixels lying inside the 10 mm × 10 mm area. The standard error was set equal to the SD divided by the square root of the number of pixel values (strain values) (Bevington 1969).

Fig. 5.

Diagram showing areas on elastograms for computation of strain ratios.

The mean strain value and SD for the background was computed using the two 4-mm × 10-mm areas positioned relative to the 10-mm square area, as shown in Fig. 5. The standard error was again set equal to the SD divided by the square root of the number of pixel values (strain values).

After the mean strain values and their standard errors for the inclusion and the background had been determined, the value of the strain ratio was computed. The error in its value was computed by straightforward propagation of errors using the computed standard errors for the inclusion mean strain and background mean strain.

The final strain ratio was the mean of two independent strain ratios corresponding to scan slices displaced elevationally relative to one another by about 5 mm. Propagation of errors resulted in a final standard error value.

It was assumed that stability of strain ratio implies stability of elastic contrast, where elastic contrast is defined as the ratio of the storage modulus of the material composing the inclusion to the storage modulus of the material composing the background surrounding the inclusion. The storage modulus was defined as the real part of the complex Young’s modulus.

Validity of production sample Young’s moduli to represent Young’s moduli in the phantom

The production samples for a phantom were isolated from one another in sample jars from the time of production of the phantom. The inclusion and background materials in the phantom, however, were in direct contact and the possibility exists that changes in elastic properties occurred because of that direct contact. Thus, samples were excised from each phantom long after production of the phantom and measurements of complex Young’s moduli made on both excised and production samples for comparison.

Samples for measurement of complex Young’s moduli were excised from the phantoms A, B and C as follows. At least 7 weeks after its production, the phantom was sliced into 1-cm and 2-cm thick slabs by pushing it through a “cheese-cutter” type device in which the cutting object was a 100-µm diameter stainless-steel wire stretched tautly either 1 cm or 2 cm above a smooth surface. The cuts were perpendicular to the axes of the cylindrical inclusions. Diameters of inclusions were measured at the cut surfaces. Then, a razor blade or microtome blade was used to excise the cylindrical inclusion samples for measurements of complex Young’s moduli. Square 2 cm × 2 cm samples of the background material were also cut from the slabs for measurements of complex Young’s moduli.

In the case of phantom A, it was found that the “cheese cutter” type of slicing produced a fractured surface on the “pure” gelatin (0% oil) composing the inclusion. An alternative slicer was constructed, in which a thin microtome blade was passed through the inclusion with a slicing motion. Although fracturing at the cut was avoided, the cuts were still not adequately planar or parallel, as evidenced by large SDs in storage moduli measured on the resulting excised samples. The SD was reduced, however, by using a greater average compression during measurement than used ordinarily. The compression² range for the phantom A samples was 5% to 6%, corresponding to an average compression of 5.5%, and the range for the other samples was 2 to 4%, corresponding to an average of 3%.

In the case of phantom E, the cuts were approximately perpendicular to the interface between the simulated glandular parenchyma and subcutaneous fat layer. Square samples were cut from the fat and glandular regions of the slices.

In the case of phantom D, the two discs of gelatin (no oil dispersion) were excised from the surrounding material. Diameter and thickness measurements were made with a machinist’s calipers and the discs immersed in safflower oil in sealed jars until measurements of complex Young’s moduli were undertaken. Slices of the background material were produced with the method used for the other phantoms and square samples were excised from the slices.

RESULTS AND DISCUSSION

Stability of strain ratios and elastic contrasts

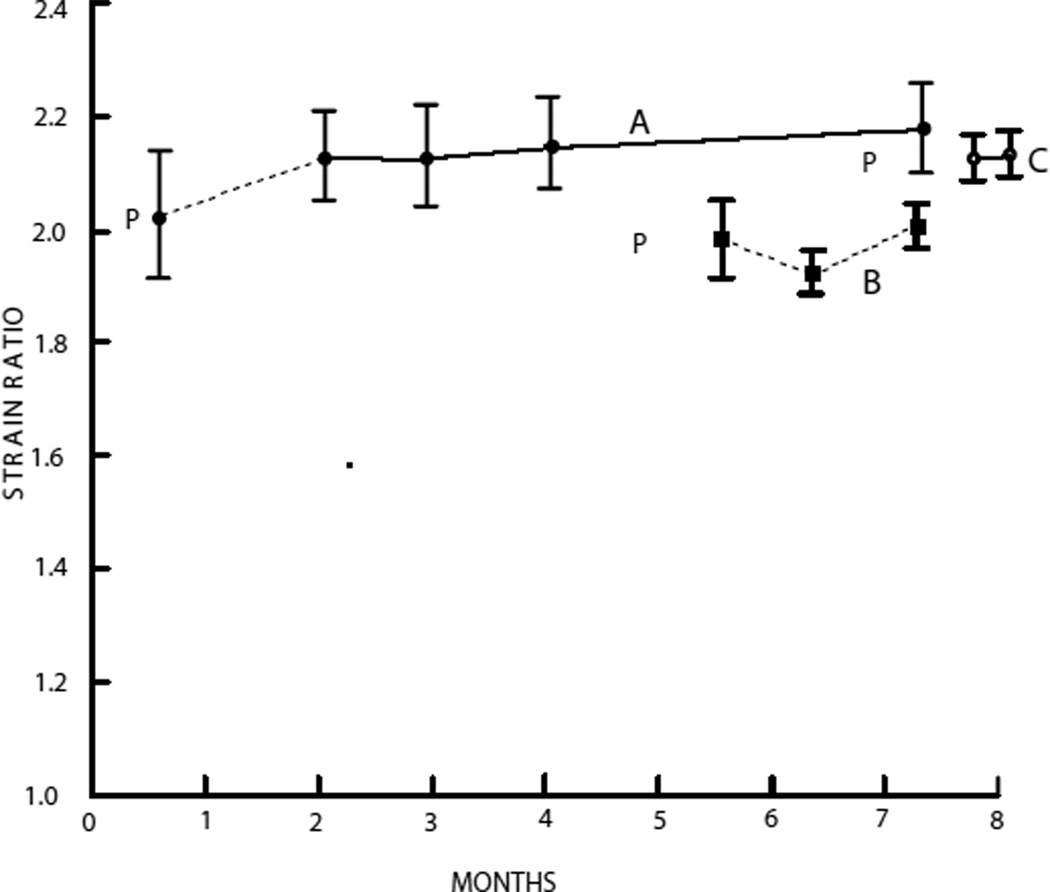
It was assumed that stability of strain ratios for a phantom implies stability of elastic contrast. Figure 6 shows strain ratios for phantoms A, B and C. Strain ratios for phantom D were not monitored because the materials were essentially the same as those in phantom A and, also, the disc-constraining apparatus and Teflon^® layers separating the sample discs were complicating. Strain ratios for phantom E were also not monitored because the geometry of phantom E did not allow for a well-defined method for determining strain ratios.

Fig. 6.

Strain ratios of phantoms A, B and C as a function of time. P = time of production of each phantom. Mean strain ratios with standard error bars are shown.

Excluding the initial strain ratio of those corresponding to phantom A, the strain ratios are remarkably stable, the smallest value being 2.13 ± 0.08 and the largest, 2.18 ± 0.08. The initial strain ratio was not considered because this strain ratio was obtained only 6 days after production of the phantom and it is our experience that strain ratios do not stabilize for 2 to 4 weeks after production.

Strain ratios for phantom B were made over a period of between 22 days after production and 72 days after production of the phantom. Values and error bars are consistent with temporal stability. In order of increasing time after production, the values were 1.98 ± 0.07, 1.91 ± 0.04 and 2.05 ± 0.04.

Strain ratios for phantom C were monitored from 26 days after production through 36 days after production. Unfortunately, because of an oversight, phantom C was sliced up for excising test samples 18 days after the last strain ratio shown, without obtaining a final strain ratio. The two strain ratios obtained were 2.13 ± 0.04 and 2.14 ± 0.04.

Stability of geometry

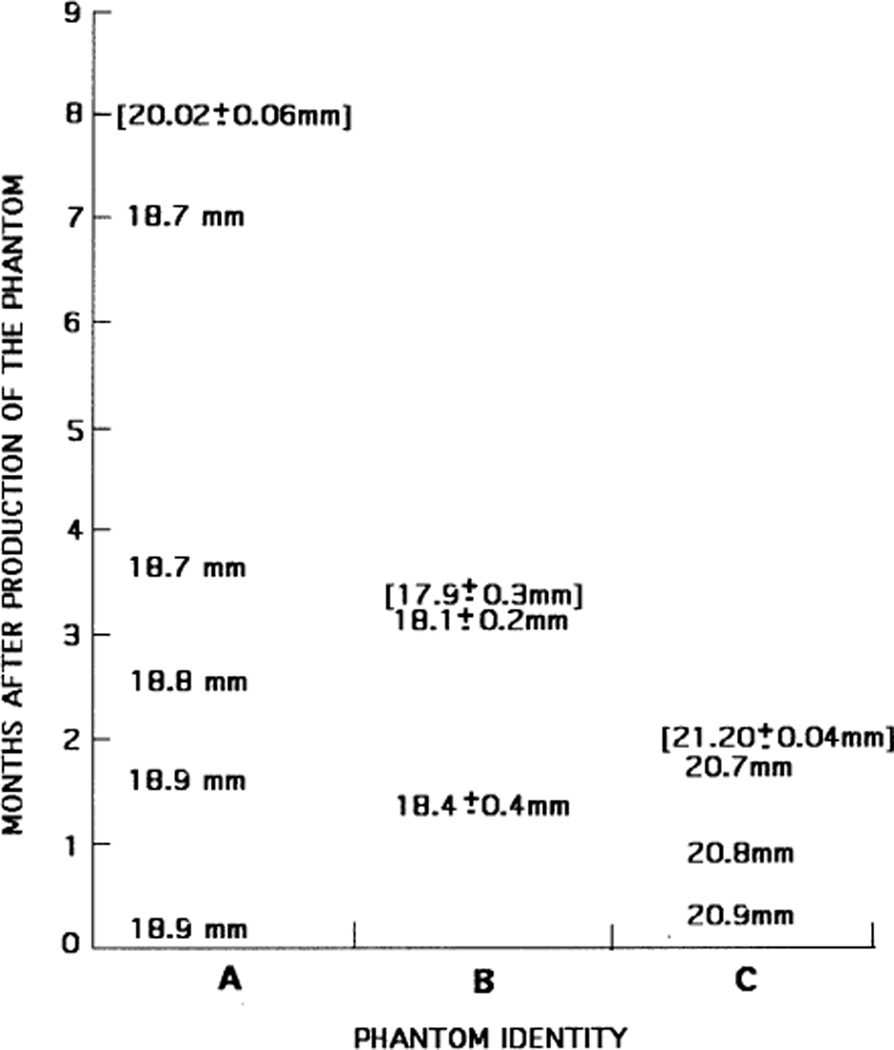
Measured values of inclusion diameters for phantoms A, B and C are shown in Fig. 7. Values in brackets result from direct determinations using machinist’s calipers on slices of the phantom; typically, eight values were averaged and the uncertainties correspond to SDs. All other values in the figure were measured on US images.

Fig. 7.

Values of inclusion cylinder diameters measured with US or with calipers on excised phantom slabs (brackets). Uncertainties correspond to SDs.

The US values indicate a slight decrease in diameter over time. For example, the decrease was about 1% over a 7-month period for phantom A. Recall that the values for phantom A were obtained retrospectively from reconstructed A-mode signals using data at a 4.5% axial compression. Specular reflections were not well defined and the diameter was taken to be the distance between an abrupt proximal drop-off in A-mode signal and an abrupt distal recovery. Both the compression and method of determining the diameter contributed to a reduction in determined diameter, which may explain the fact that the diameter measured with a machinist’s calipers on slices of the phantom was about 7% greater than the value measured with US. The directly-measured value agrees very well, however, with the expected diameter of the inclusion, based on the diameter of the acrylic rod used to form the hole filled by the molten inclusion material during manufacture. Thus, for phantom A, both stability of geometry and fidelity to the expected diameter were demonstrated.

The ultrasonically determined diameters for phantom B were made using images generated by the Siemens Antares. For each value, three images were made with the imaging slice perpendicular to the cylinder axis, one centrally located and the others displaced about +2 cm and −2 cm from the central slice. Considerable diameter variation from one end to the other was found and the mean value is much less than the 2-cm diameter acrylic rod mold. Also, there was considerable variation in diameters measured with machinist’s calipers on the slices of the phantom.

It is likely that most, if not all, of the discrepancy between acrylic rod diameter and measured diameter in phantom B is related to the very soft nature of the background material (about 5 kPa). When the acrylic rod was withdrawn during manufacture before introducing the molten inclusion material, the background material sagged, considerably narrowing the opening. With introduction of the molten inclusion material, the narrowed hole did not fully recover, as evidenced by some of the inclusion material flowing between the top of the background and the cubic acrylic mold. Notice that the mean diameters measured with US agree rather well with the mean determined by direct measurement on slices of the phantom. The average diameter decreased modestly, perhaps 2%, over 2 months.

The values of the diameter of the cylinder in phantom C measured with US electronic calipers decreased over 7 weeks by about 1%. The diameter is larger than the 2.0-cm value expected from the manufacturing method by about 4%. The mean diameter measured on excised samples 7 weeks after production was 21.20 ± 0.04 mm, 6% greater than the 2.0-cm value expected and about 4% greater than that measured with US immediately before the phantom was sliced up.

As in the case of phantom A, the dimensions of the cylindrical samples in phantom D remained unchanged over the 7 weeks after production. Phantoms A and D were made from almost identical materials, the difference being that phantom D contained propylene glycol and phantom A did not. The diameters of the two samples excised from the phantom were 25.68 mm and 25.60 mm. These values are essentially identical to the diameters of the acrylic/Saran Wrap^® molds used to form the samples, namely, 25.7 mm. The thicknesses of the two phantom D samples were 19.98 mm and 19.95 mm, again essentially identical to the 20.0-mm thickness of the acrylic/Saran Wrap^® molds.

It is important to note that the diameters of the cylindrical inclusions in all phantoms monitored with US changed very little (decreased by about 1%) during the periods monitored with US. Thus, the dimensions of inclusions in phantoms made with these oil-in-gel-dispersion materials can be considered invariant. However, there may be a few percent change in diameter from the originally molded inclusion.

Storage moduli for production samples and for excised samples and derived elastic contrasts

Results are shown in Tables 4 and 5. Notice in Table 4 that, for both inclusion and background materials in phantoms A and B, the tendency is for the storage modulus of the excised sample to be elevated significantly relative to that for the corresponding production sample. Why this discrepancy exists is not understood. The percent elevation for each phantom, however, is nearly the same for both inclusion and background material, resulting in rather good agreement between elastic contrast predicted from production sample values and elastic contrast computed from excised sample values; that agreement is shown in Table 5. For phantoms C, D and E, there is very good agreement of corresponding storage moduli resulting from measurements on production samples and on excised samples.

Table 4.

Means and uncertainties of storage moduli (kPa) of production and excised samples for all five phantoms

Phantom identity	Inclusion		Background
	Production samples	Excised samples	Production samples	Excised samples
A	134 ± 4	170 ± 15	41.5 ± 1.2	51.0 ± 1.5
B	16.4 ± 0.5	22.5 ± 0.7	5.0 ± 0.3	6.6 ± 0.2
C	65.4 ± 2.0	65.5 ± 2.6	17.2 ± 0.5	17.4 ± 0.5
D	135.5 ± 4.1	128.4 ± 3.4	46.3 ±1.4	46.7 ±1.4
E	30.5 ± 0.9	31.4 ± 0.9	17.2 ± 0.5	16.7 ± 0.5

Uncertainties equal SDs of the means (standard errors) (Bevington 1969), unless that error is less than 3%, in which case the latter value is assumed because ± 3% is about the day-to-day reproducibility. For each phantom, all measurements were made on the same day. The compression range for all but phantom A was 2–4%. For phantom A, the range was increased to 5–6% for all samples to partially compensate for the fact that the “flat” surfaces of the excised samples were not quite parallel or planar. Note that, for phantom E, the storage moduli for the glandular material are listed in the inclusion columns and those for the subcutaneous fat are listed in the Background columns.

Table 5.

Elastic contrasts computed using the mean storage moduli for the production samples vs. the mean storage moduli for the excised samples using the values in Table 4

Phantom identity	Elastic contrast predicted from storage moduli of production samples	Elastic contrast computed from storage moduli of excised samples
A	3.23 ± 0.13	3.33 ± 0.31
B	3.28 ± 0.22	3.41 ± 0.15
C	3.80 ± 0.16	3.76 ± 0.18
D	2.93 ± 0.12	2.75 ± 0.12
E	1.77 ± 0.07	1.88 ± 0.08

Standard errors in Table 4 were propagated to give standard errors for the elastic contrasts in Table 5.

It was learned in earlier work on oil-in-gelatin phantoms (Madsen et al. 2003) that storage moduli of production samples rise to a maximum about 2 months after production and then drop off during the next 6 or more months by 10 to 15%. It is possible that, for some reason, the drop-off of storage moduli occurs more slowly in the phantoms than in the production samples, which would correspond to the generally higher values for excised samples relative to production samples for phantoms A and B in Table 4. However, phantom E, for which comparisons of storage moduli from production samples with excised were made 9 months after production of the phantom, exhibits nearly identical storage moduli for production vs. excised samples.

As shown in Table 5, elastic contrasts obtained from production sample measurements agree well with those obtained from excised sample measurements for all five phantoms. Thus, measurements on production samples can be considered adequate for determination of elastic contrasts in oil-in-gel-type phantoms.

Loss moduli

Loss moduli were very small compared to the storage modulus for all samples. In terms of tan δ = (loss modulus ÷ storage modulus) = (imaginary part of the complex Young’s modulus ÷ real part of the complex Young’s modulus), the mean for any set of equivalent materials reported was between 0.03 and 0.08.

Ultrasound and NMR properties

Ultrasound and NMR properties are shown in Table 6. Temporal stability of NMR properties was assessed over periods of many months.

Table 6.

US and NMR properties measured at 22 °C on samples of each of the 10 different materials formed at the times of production of each material

Phantom identity and component	US properties			NMR relaxation times
	Propagation speed (m/s)	Atten. coeff. ÷ freq. (dB/cm/MHz)	Density (g/mL)	T1 (ms) (first)	T1 (ms) (second)	T2 (ms) (first)	T2 (ms) (second)	2nd - 1st tim (months)
A (background)	1498	0.34	0.97	340	300	111	111	14
A (inclusion)	1547	0.14	1.02	1350	1150	290	256	14
B (background)	1496	0.4 (at 5 MHz)	0.97	274	277	106	107	3.5
B (inclusion)	1539	0.1 (at 5 MHz)	1.02	506	494	103	104	3.5
C (background)	1492*	0.47*	0.95	239*	239*	95*	103*	11
C (inclusion)	1533*	0.32*	0.99	350*	350*	132*	137*	11
D (background)	1512*	0.33*	0.97	280*	280*	110*	115*	11
D (inclusion)	1575*	0.15*	1.02	1080*	1110*	268*	232*	3.5
E (glandular)	1512	0.33	0.97	280	280	110	115	11
E (subcut. fat)	1492	0.47	0.95	239	239	95	103	11

Density values were computed based on knowledge of densities of component materials.

^*Measured on test samples with the same composition, but made at a different time. US attenuation coefficient ÷ frequency values for the materials in phantom B apply only at 5 MHz. To assess temporal stability, two sets of measurements of NMR relaxation times were made on all samples, the time elapsing between the first and second measurements being given in the far right column.

SUMMARY AND CONCLUSIONS

A variety of heterogeneous phantoms with cylindrical inclusions were produced from oil-in-gelatin and oil-in-agar + gelatin dispersions. Stability of geometry and elastic properties were demonstrated. Also demonstrated was the adequacy of isolated samples (production samples), produced at the time of the phantoms, for use in determining elastic contrasts in the phantoms. Storage moduli ranged from 5 kPa through 130 kPa, and elastic contrasts ranged from 1.8 through 3.8.

The sizes of inclusions, although essentially invariant after production of phantoms, may differ by a few percent from the sizes expected based on dimensions of molds used to produce the inclusions.

The phantoms are tissue-mimicking regarding elastic, US and NMR properties. US propagation speeds can be increased with increase in concentration of propylene glycol in the aqueous parts of a phantom, as seen by comparing phantom A with phantom D in Table 6. The NMR T₁ values in a phantom can be lowered through increase in concentration of the Cu²⁺-EDTA chelate. Good temporal stability of NMR samples was demonstrated; the largest changes included the decrease by about 15% of T₁ of inclusion and background samples for phantom A and the same percentage decrease of T₂ for the inclusions of phantoms A and D.

The oil-in-gelatin and oil-in-agar + gelatin materials should be particularly useful for producing stable complex anthropomorphic phantoms with well-defined properties.