A Bayesian model for cluster detection

Abstract

The detection of areas in which the risk of a particular disease is significantly elevated, leading to an excess of cases, is an important enterprise in spatial epidemiology. Various frequentist approaches have been suggested for the detection of “clusters” within a hypothesis testing framework. Unfortunately, these suffer from a number of drawbacks including the difficulty in specifying a p-value threshold at which to call significance, the inherent multiplicity problem, and the possibility of multiple clusters. In this paper, we suggest a Bayesian approach to detecting “areas of clustering” in which the study region is partitioned into, possibly multiple, “zones” within which the risk is either at a null, or non-null, level. Computation is carried out using Markov chain Monte Carlo, tuned to the model that we develop. The method is applied to leukemia data in upstate New York.

1. Introduction

The detection of disease clusters has a long and controversial history in spatial epidemiology. A major area of debate is on the definition of a cluster, with initial efforts examining all pairs of cases to see if they are “close” or “not close” in space and time (Knox, 1964). Following Wakefield and others (2000), we define cluster detection as, “the identification of areas of high residual risk”. Residual here acknowledges that we have controlled for known risk factors (e.g., age and gender). This definition requires a specification of what we mean by “high”, which will be disease-specific. The method we describe recognizes that even in the absence of any true elevated risk, area-level relative risks will “wobble” around the value 1, and we do not wish to highlight every small fluctuation. The interpretation of cluster detection studies is hazardous since data anomalies (problems with population estimates, under- or over-count of disease cases) may be responsible for apparent increased risk (Besag and Newell, 1991). The situation on which we concentrate considers a study region containing n areas (with associated geographical centroid), typically administrative subdivisions, with each providing an aggregate disease count and an associated population count or expected number of disease cases.

There is a large literature on spatial scan statistics, in which a (usually) circular window is passed over the study region and the significance of the observed number of cases in the window is determined. Different proposals base the circle size on distance (Openshaw, 1984), the number of cases (Besag and Newell, 1991), or the population (Kulldorff, 1997). By far the most popular cluster detection method is based on the latter, in part because of the availability of the easy-to-use software, SatScan (http://www.satscan.org/). The method allows the circular clusters to be centered on each of the n area centroids, with varying radii, up to a maximum that gives a circle with no more than a certain proportion of the total population (common choices include 20% and 50%). We refer to the circles as “zones”. In the unconditional version of the test, a Poisson likelihood is assumed, while the conditional version conditions on the total number of cases, and uses a binomial likelihood. A likelihood ratio statistic is then computed for each zone; for example, in the unconditional version of the test the null and alternative consist of the relative risk being either 1, or >1. Clearly, this strategy leads to a large number of tests, and the multiplicity problem is circumvented by evaluating the significance of only the maximum of the likelihood ratio statistics over all circles, using a Monte Carlo p-value. The method we describe has elements in common with that of Kulldorff (1997), in particular, in the way in which we describe cluster configurations in terms of zones, but attempts to rectify a number of the drawbacks that we discuss in Section 2. In this section, we also apply the SatScan method to leukemia data in upstate New York. Our model is described in Section 3 and Section 4 outlines computation. We return to the upstate New York data in Section 5 and conclude with a discussion in Section 6.

2. Deficiencies of the scan statistic

Clearly, a key component of cluster detection using SatScan is deciding upon a threshold for significance at which to call a collection of areas (a zone) a “cluster”. A review of the literature reveals that current practice is the use of a 0.05 threshold, regardless of the number of areas, or the distribution of expected numbers within those areas, both of which affect the power. Appendix A of the supplementary material available at Biostatistics online gives examples of the use of SatScan. This appendix also contrasts the use of p-values and Bayes factors, in particular showing that the latter is a consistent model selection procedure in a simplified hypothesis-testing setting.

A further difficulty arises when the possibility of multiple clusters is entertained. In both Kulldorff and others (1997) and Jemal and others (2002) secondary clusters were reported with an informal measure of significance. In an investigation one would not expect a large number of clusters (at least not in the way in which we have defined a cluster), but a cluster detection method should not be restricted to finding a single cluster only. In Kulldorff and others (1997) and Jemal and others (2002) (and numerous other studies) p-values for secondary clusters are computed by comparing their likelihood ratios to the simulated null distribution of the likelihood ratios of the most likely cluster. This procedure is conservative since the secondary p-values are being calculated by comparison to the null distribution of the maximum statistic and not the second highest which is the correct reference. More recently, Zhang and others (2010) proposed a modification to the original approach in which, after identifying a statistically significant cluster, they drop the data corresponding to that cluster (possibly along with some neighboring areas), recompute the internally standardized expected numbers for the new reduced dataset, and repeat the Kulldorff procedure until no statistically significant further cluster is found. The resulting sequentially computed p-values are not necessarily monotonically non-increasing but are less conservative than those of the original method. However, a major problem is that the p-values are not directly comparable since they are based on different sample sizes and hence have different power. One should also consider the multiple testing aspect of the multiple comparisons that are being made but it would be very difficult to determine the appropriate error rate of the sequential procedure defined by Zhang and others (2010).

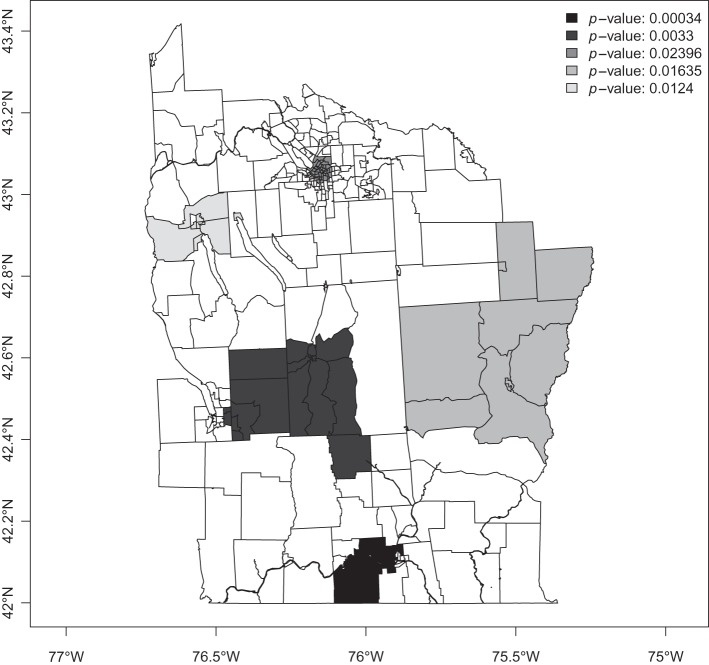
As a motivating example, we consider leukemia data in eight counties of upstate New York, and described by Turnbull and others (1990). These data have provided a test bed for a number of methods. We consider data collected from 1978 to 1982 in n=277 census tracts from the 1980 census. Using an upper limit of 15% of the total population, the spatial scan statistic was evaluated over 12 675 zones (circles). In Figure 1, we present the results of Zhang and others (2010) method on the upstate New York leukemia data with α=0.05 and p-values calculated from 99 999 Monte Carlo simulations under the null. In order of discovery, the significant clusters were: (1) the area surrounding Binghamton in Broome County, (2) the western half of Cortland County, (3) the area surrounding Syracuse in Onondaga County, (4) Central Cayuga County and (5) the area surrounding Ithaca in Tompkins County. Appendix G of the supplementary material available at Biostatistics online contains a figure in which the counties are labeled, to aid in identifying areas of interest. The p-values cannot be interpreted independently as they are computed sequentially, e.g. the interpretation of the third p-value is that: after removing the first two significant clusters we obtained a cluster with observed significance level 0.024.

Fig. 1.

Highlighted clusters for leukemia in upstate New York, under the spatial scan statistic of Zhang and others (2010), and with a significance level of 0.05.

3. A Bayesian partition model for cluster detection

3.1. Notation

Let y_i and E_i denote disease counts and expected counts in i=1,…,n areas that partition a study region. Following Kulldorff (1997), we define single zones as contiguous collections of areas that form “jagged circles”. We create the list of single zones by sequentially aggregating neighboring areas, by taking each area in turn, and continually adding the areas whose centroids are closest to the area center. For each area this procedure is continued until the zone's population reaches a pre-specified maximum allowable proportion of the total study region's population. Suppose there are N₁ single zones; we emphasize that there are multiple zones centered on each area centroid. The model that we define partitions the study region so that each area is either in a cluster/anti-cluster, or is at a null level. Areas within a cluster are associated with increased relative risk, while areas within an anti-cluster are associated with decreased relative risk.

The number of clusters/anti-clusters is j=0,…,J, where J is specified in advance. Each of the clusters/anti-clusters corresponds to a single zone though for a partition with j≥2 single zones, the constituent single zones are not allowed to overlap. We define a configuration as a set of non-overlapping single zones; for j=1,…,J suppose there are N_j configurations of such zones. For j=0, we set N₀=1 for notational consistency. We label the null (i.e., no lows/highs) configuration as c_0N0 and c_jl as the lth configuration of j single zones, for j=1,2,…,J, and l=1,…,N_j. More precisely, c_jl consists of the j single zone labels that constitute configuration l. For example, c_2l is the pair of (non-overlapping) single zones that correspond to configuration l; the label l ranges over the set of all pairs that are “legal”, i.e. non-overlapping, with N₂ such pairs. For the null configuration c₀₁=∅. Examples of c_jl are contained in Appendix B of the supplementary material available at Biostatistics online. There are 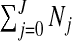possible values of c_jl, which grows very quickly as J increases. For the New York State data N₁=12 675 and N₂=59 455 392.

Define S_z as the set of area indices associated with (single) zone z, z=1,…,N₁. Finally, let 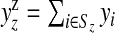and 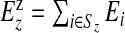be the observed and expected numbers of cases in single zone z, with y^z_z={y_i,i∈S_z} and E^z_z={E_i,i∈S_z} the vectors of observed and expected numbers, respectively, for z=1,…,N₁ (the superscript z therefore distinguishes observed and expected counts in single zones from observed and expected counts in areas).

3.2. A model for clusters and anti-clusters

For a rare disease, we assume that counts are conditionally independent to give: y_i|θ_i∼_iidPoisson(E_iθ_i), where θ_i is the relative risk associated with area i. The prior we assign to θ_i depends on whether area i lies within a cluster/anti-cluster or not. If in a cluster/anti-cluster a “wide” gamma prior is assumed while if null, a “narrow” gamma prior is assumed. The narrow prior reflects variation around 1 that is due to small levels of confounding and small data anomalies (errors in the population and disease counts). These two specifications are what allows us to distinguish between “null” areas and “non-null” areas contained within clusters/anti-clusters. For all i∈S_z, that is, areas in single zone z, we have 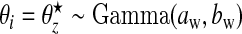, i.e. a common relative risk. Therefore, consistent with our earlier definition, an area is in a cluster/anti-cluster if its relative risk is deemed high/low. The choices of a_n,b_n,a_w, and b_w are study-specific since different diseases have differing inherent “null” spatial variability. The wide model assumes that for single zone z in configuration c_jl, all the constituent areas of the single zone share a common relative risk 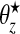, and the counts {y_i,i∈S_z} are conditionally independent given 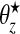. For null areas i, θ_i∼_iidGamma(a_n,b_n).

We may integrate the θ parameters from the model so that the distribution for a generic null area with count y and expected number E, 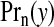, is Neg-Bin(a_n,b_n/(E+b_n)), i.e.

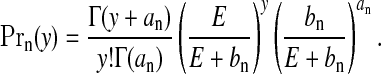Similarly, for a non-null area 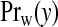is Neg-Bin(a_w,b_w/(E+b_w)). Under this construction, the only unknown parameter in the model is the configuration {c_jl,j=1,…,J;l=1,…,N_j}, a discrete parameter with 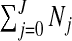possible values.

Given these specifications, we can derive the likelihood. For the null configuration, the study region is entirely comprised of null areas:

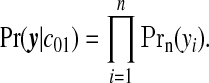Non-null configuration c_jl, j≥1, contains j single zones each with summed counts y^z_z and expected numbers E^z_z, for z∈c_jl. We assume that the vectors of counts 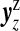associated with each single zone z∈c_jl are independent. Therefore, the likelihood for the set of counts y is

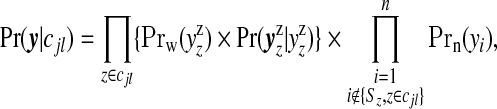for j=1,…,J;l=1,…,N_j. The first term on the right-hand side contains a product of j terms for the cluster/anti-cluster contribution and the second term is for the remaining null areas. The distribution 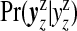is multinomial with dimension equal to the number of areas in zone z, |y^z_z|, with total counts y^z_z and vector of probabilities 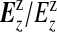. It is useful to define the Bayes factor comparing the probability of the data under configuration c_jl to the probability of the data under the null:

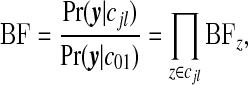(3.1)

a product over zones, where

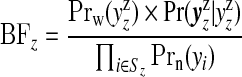(3.2)

is the Bayes factor comparing the distribution of the data within single zone z under the non-null cluster/anti-cluster model to that under the null model.

One consequence of (3.1) is that computation for our model is vastly simplified since we only need to consider calculations for single zones. In the case of a single zone, (3.1) may be compared with the likelihood ratio statistic:

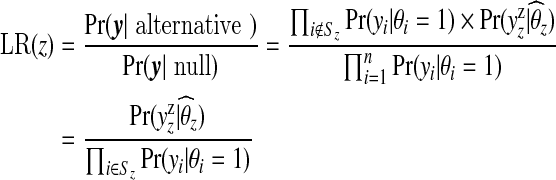of the scan statistic used within SatScan. In the denominator, the scan statistic conditions on θ=1 while the Bayes approach integrates over the narrow prior. In the numerator, up to a constant, the scan statistic maximizes over θ_z (subject to θ_z>1) while the Bayes approach integrates over the wide prior. The multiple zone version of SatScan looks at sequential likelihood ratio statistics (removing parts of the data), whereas the Bayes approach (roughly speaking) averages over products of Bayes factors.

3.3. Prior distribution

In this section, we describe the priors we place on the 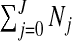possible configurations c_jl. This choice implies a prior on the number of non-overlapping single zones in the partition, τ∈{0,…,J} since 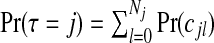. When constructing the probabilities 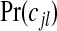there are a number of considerations. We wish to pay particular attention to the j=0 case and set 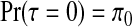, which is the prior probability of the null configuration c_0N0. This value will be typically close to 1 given the rarity of true clusters/anti-clusters. Given the existence of one cluster/anti-cluster (τ=1), the probabilities should reflect our prior belief of each of the N₁ single zones being the cluster/anti-cluster. When extending to combinations of j≥2 single zones, configurations of non-overlapping single zones are assigned prior probability proportional to the prior probability of each of the component single zones being a cluster/anti-cluster. All combinations of single zones with overlap are dropped from consideration.

The simplest form is to take a uniform prior over the total number of single zones, i.e. π_z=1/N₁. This is consistent with SatScan within which all single zones are treated equally. In what follows this form is labeled the uniform prior. A second specification is based on ideas of Gangnon and Clayton (2003) in which an area center is selected with probability proportional to its area with a radius then selected with probability proportional to its size. Suppose that there are m_i single zones centered on area i so that 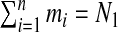. A single zone is defined by its center and its radial area and let l=1,…,m_i index the radial area of single zone z(i,l) centered at area i. Now, let r_i,1<⋯<r_i,mi denote the distances of the centroids of each of the m_i possible radial areas to centering area i, with r_i,1=0, and let r_i,mi+1 denote the distance to the next area beyond area m_i. Then the prior for the single zone centered on area i with radius r_i,l is

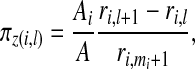(3.3)

where A_i is the surface area of area i, i=1,…,m and A is the total surface area of the study region. We label this form the modified dartboard prior.

The prior on configurations of two or more single zones, i.e. c_jl, is specified in two stages. First, a partition (cluster/anti-cluster) size is selected with probability 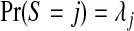for known λ_j, j=0,…,J. Second, given S=j, a set of j zones are sampled, with replacement, from the N₁ single zones with probabilities π_z, z=1,…,N₁, using one of the two forms just described. If the j randomly generated zones are “non-overlapping” this j and configuration are retained, otherwise we repeat this procedure until a legal configuration is sampled.

Let

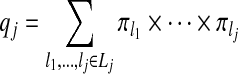(3.4)

be the probability that the j randomly selected zones are non-overlapping, with L_j the set of indices of j non-overlapping zones, for j=2,…,J. Define q₀=q₁=1 since there is no concept of overlapping for j=0,1. Then, given the construction of our prior,

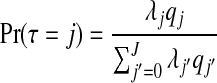and 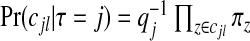. Consequently, the required prior probabilities are

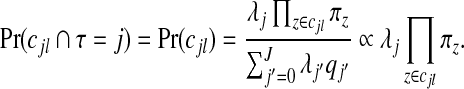If we choose the λ_j's as

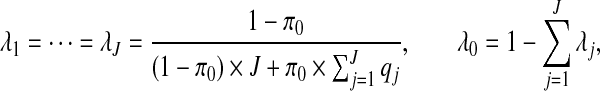then, as detailed in Appendix E of the supplementary material available at Biostatistics online, we obtain 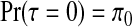and

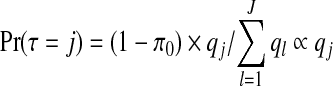for j=1,…,J. Therefore, after dropping all combinations of single zones with overlaps, the prior probability of no clusters/anti-clusters is π₀, as desired, and the prior probabilities for j=1,…,J are defined in a natural fashion (as proportional to the probabilities of obtaining j non-overlapping single zones under random sampling of single zones).

The model that we have described is closest to that of Gangnon and Clayton (2003) and we describe this approach here in some detail. Other approaches (Denison and Holmes, 2001; Gangnon and Clayton, 2000; Knorr-Held and Raßer, 2000; Neill and others, 2006) are described in Appendix F of the supplementary material available at Biostatistics online. We emphasize that the detection of disease clusters is a very different endeavor to disease mapping. In contrast to cluster detection, Bayesian approaches to disease mapping are commonplace, but the usual random effects models that are fitted (for example, Besag and others, 1991) produce both strong global shrinkage of relative risk estimates and strong local smoothing across neighboring areas; the latter is undesirable in a cluster detection context. In particular, the spatial smoothing of abrupt changes/discontinuities in the relative risk surface is not desirable. For evidence of this behavior, see the simulation results of Richardson and others (2004).

Our model differs from that of Gangnon and Clayton (2003) in the following respects. We assume conjugate gamma priors for the “small” and “wide” components while Gangnon and Clayton (2003) assume lognormal random effects. We exclude overlapping zones when constructing configurations of zones; this is not done by Gangnon and Clayton (2003) and it is even possible for the same zone to be included twice in the same configuration, which is clearly not appealing. The priors on the number of clusters/anti-clusters are quite different. We construct a prior to have a user-specified value on the null, and then the mass on j=1,…,J clusters/anti-clusters is spread out in a way that is consistent with our prior construction for multiple non-overlapping zones. Gangnon and Clayton (2003) emphasize a uniform distribution on the number of zones (including the null configuration) in the methods description of their paper, but then also use a geometric prior in their analysis of the New York data. The computation required for the Gangnon and Clayton (2003) model is more complex than for our model since they use a non-conjugate formulation. In particular, reversible jump MCMC (Green, 1995) is used, which is difficult to implement (for the uninitiated) and there are no available implementations (as far as we know). We only have to sample configurations which makes the computation far more straightforward.

3.4. Summaries of the posterior distribution

The posterior distribution can be expressed as

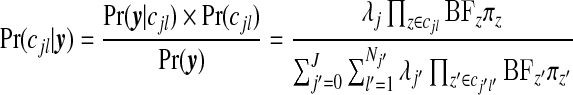(3.5)

where the BF_z terms are given by (3.2); see Appendix D of the supplementary material available at Biostatistics online for this derivation. This form for 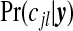emphasizes that for any configuration c_jl the posterior is proportional to a product BF_z×π_z over the component unit zones, multiplied by λ_j.

A first summary of interest is the posterior on the number of clusters/anti-clusters, τ:

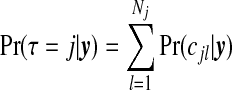(3.6)

and this may be compared with the prior on this quantity. If there are clusters in the data the posterior distribution of any one c_jl will be small, because many configurations are overlapping and, if a non-null region exists, the posterior probability will be spread over similar alternatives. A number of summaries are informative, however. We may evaluate the posterior probability that an area lies in a cluster/anti-cluster. Let C_i={the event that area i is in a cluster/anti-cluster}. Then, summing over all configurations c_jl that contain area i:

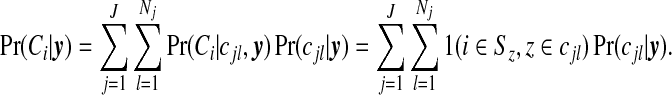(3.7)

Often we will be specifically interested in clusters (i.e., highs), and so we define 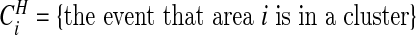. For each configuration c_jl this event occurs when both area i is in c_jl and θ_i is “high”. We define the latter as 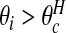where the high crossover point 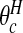is a threshold that we take as the larger of the two intersection points of the narrow and wide priors. The posterior probability of area i being in a cluster is therefore

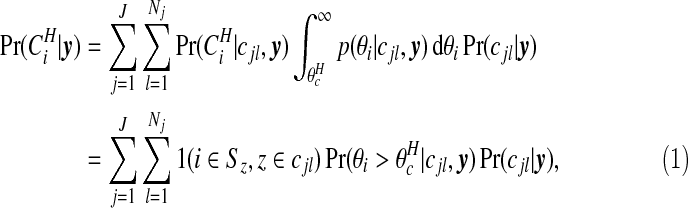(3.8)

where

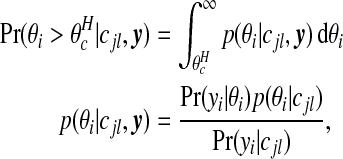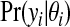is Poisson, and the prior p(θ_i|c_jl) is Gamma(a_w,b_w). We note that the conditional posterior p(θ_i|c_jl,y) is gamma also, by conjugacy.

The probabilities 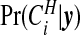are therefore straightforward to evaluate, and may be mapped to indicate areas of clustering. If one wishes to remove the effect of the prior, we may consider the Bayes factor of area i being in a cluster 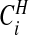versus not being in a cluster :

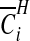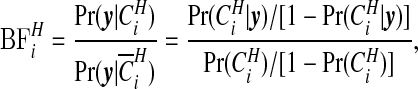(3.9)

where 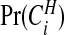is the prior counterpart to (3.8)

We may also provide a map of 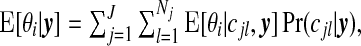which gives the expected relative risk surface based on the cluster model and aids in interpretation of clusters. In addition, this surface may be compared with maps of the raw SMRs and other modeled summaries. Each of these summaries help one to give a context within which public health decisions may be considered. Finally, we may map 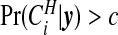, for different thresholds 0<c<1, to provide a more succinct visual summary of areas of clustering.

4. Computation

Recall from Section 3.3 that we specify the prior up to a normalizing constant. For sampling from the posterior, we do not require this constant, but its calculation is required to achieve the prior on the null configuration 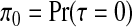. Normalization of the posterior probability of configuration c_jl requires estimation of q_j, as given by (3.4), which we achieve using importance sampling; details are available in Appendix E of the supplementary material available at Biostatistics online.

We now turn to simulation from the posterior for c_jl, a discrete parameter that can take a very large number of values 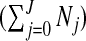. We implement an MCMC algorithm whereby the current configuration is perturbed via one of five moves. A detailed description of the algorithm is presented in Appendix G of the supplementary material available at Biostatistics online and here we provide an outline of the main steps. Recall that c_jl consists of a set of j single zone labels with S_z the set of area labels within zone z. The moves are:

1. Growth: The index set for a particular single zone z {i∈S_z,z∈c_jl} is increased by adding the nearest free neighbouring area (in terms of distance to its center) to the selected single zone. If the zone selected is the largest single zone with this particular center then a growth move is not possible.

2. Trim: The index set for a particular single zone z {i∈S_z,z∈c_jl} is reduced by dropping the area that is furthest from the centering area from the single zone selected for trimming. If the single zone consists of only one centering area, then such a move is not possible. Trim moves are reciprocal to growth moves.

3. Replacement: Replace a single zone z∈c_jl with another single zone with a different centering area.

4. Death: Drop one of the j single zones z∈c_jl to form a configuration with j−1 single zones.

5. Birth: Add a new single zone to c_jl to form a new configuration of j+1 single zones. Birth moves are reciprocal to death moves.

In the first three moves, the newly adjusted single zone that modifies c_jl must not overlap the remaining j−1 single zones in c_jl and in move 5 the newly added single zone must not overlap the existing j single zones. The first three moves are such that the number of single zones remains the same, whereas moves 4 and 5 modify j. In the application to the upstate New York data each of the five moves are proposed with equal probability. The above represents a generic scheme, but we tune to the cluster model. Specifically, single zones are proposed randomly via one of two mechanisms: uniformly from the N₁ single zones, or proportional to the posterior probabilities 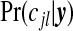with j=1. The latter are known, up to a normalizing constant, and so are available for sampling. Convergence is monitored via examination of the sample paths of various key summaries, including the number of clusters/anti-clusters.

5. Example: Leukemia in upstate New York state

We use the uniform prior on single zones, set π₀=0.95 and take J=7 as the maximum number of clusters/anti-clusters. We first calibrated the prior (i.e. chose the λ's) to give π₀=0.95, which lead to the histogram of prior probabilities in Figure 2. For these data, we choose the priors on θ in the following way. For both the narrow and wide choices, we require the mode to be at 1 so that the prior is decreasing either side of this “null” value. We further require the upper 95% points of the narrow and wide priors to be 1.03 and 4, respectively. This specification leads to the choices (a_n,b_n)=(2976.3,2977.3) and (a_w,b_w)=(2.31,1.31). These choices are shown in Appendix C of the supplementary material available at Biostatistics online. The high crossover point 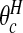is 1.05.

Fig. 2.

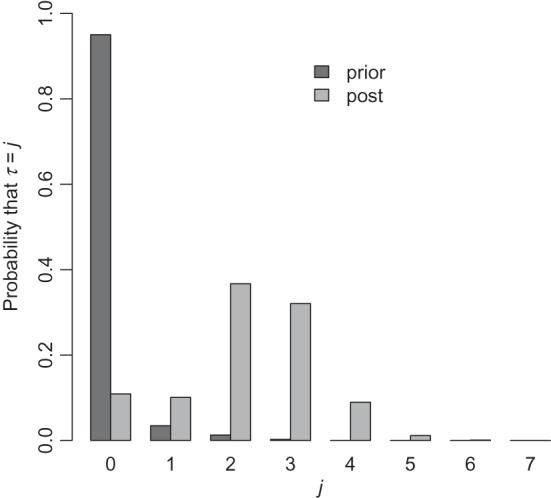
Prior and posterior probabilities on the number of clusters/anti-clusters for the New York data.

We ran the importance sampling algorithm to estimate the (λ₀,λ₁,…,λ_J) using 10⁵ points and the Markov chain algorithm for estimating 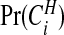and 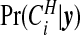for 10⁵ and 10⁶ iterations, respectively. We picked each of the five moves types with probabilities 0.2, and sampled zones alternately using probabilities proportional to the single zone posterior and from a uniform distribution on the number of legal single zones. The analysis took 66 min on a 2 GHz Intel Core i7 processor with 8 GB of 1333 MHz DDR3 RAM. Appendix I of the supplementary material available at Biostatistics online contains details and plots of how convergence of the Markov chain was assessed in this example and also reports the acceptance rates of the different MCMC moves.

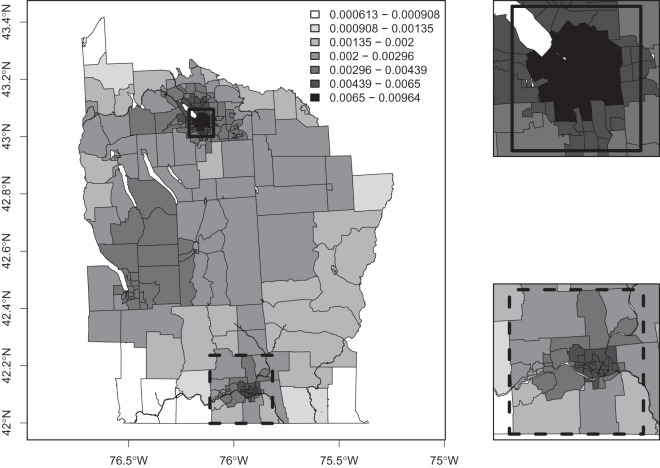
Using the uniform prior 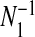, we plot 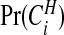for each area in Figure 3, with all areas surrounding Syracuse and Binghamton zoomed in on the right-hand panels. We see that our model puts higher prior probability on urban areas, most notably the areas surrounding Syracuse, Binghamton and Cortland. This is primarily because urban areas tend to be smaller in geographical size, and hence are contained within more single zones, than are rural areas.

Fig. 3.

Prior probability of clusters for New York State.

Figure 2 compares the posterior probabilities 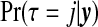(grey columns) against the prior probabilities for j=0,1,…,7. We see that around 80% of the prior probability on the null has moved to 1,2,3,4 clusters/anti-clusters, strongly indicating that there are clusters and anti-clusters in these data. In Figure 4, we display the estimated posterior probability 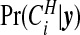of cluster membership for each area i. We observe that even with a prior that is skeptical to the existence of clusters (π₀=0.95), there is strong evidence that areas surrounding Binghamton in Broome County and areas in the western half of Cortland County are in a cluster, while there is milder evidence of cluster areas in Syracuse in Onondaga County.

Fig. 4.

Posterior probability 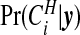of cluster membership for each area i, using π₀=0.95.

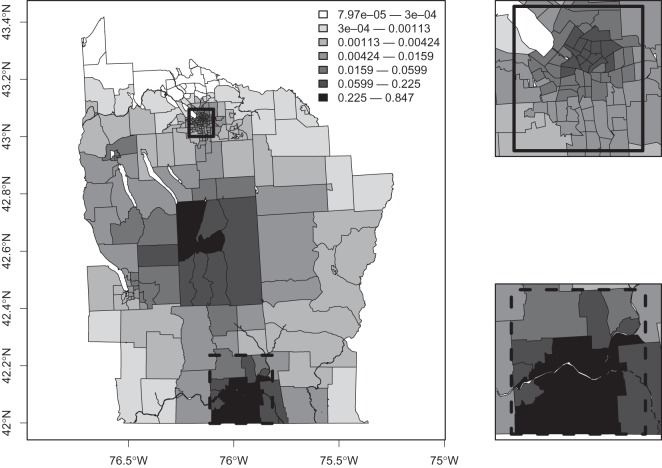
In Figure 5, we plot the 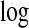Bayes factors 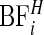of each area being in a cluster, as defined in (3.9). We observe that even after accounting for the prior 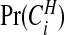, which favors urban areas, there is still relatively strong evidence of clusters. Appendix H of the supplementary material available at Biostatistics online provides further summaries for these data, with sensitivity analyses to the various tuning parameters including the crucial choice of π₀ (Appendix D of the supplementary material available at Biostatistics online contains details of how prior sensitivity to π₀ can be computed efficiently). Also included are mapped relative risk summaries from our model and a comparison with the SMRs, an empirical Bayes model and the ICAR model of Besag and others (1991). Appendix J of the supplementary material available at Biostatistics online compares our conclusions for these data with those of other authors.

Fig. 5.

Log of Bayes factor of area i being in a cluster versus not being in a cluster, 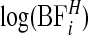, using π₀=0.95, see equation (3.9) for the form of the Bayes factor.

6. Discussion

In this paper, we have described a Bayesian model for cluster detection. The model is designed so that the computation is relatively efficient. In particular, we lean on conjugacy so that the unknown parameter is a single discrete parameter, the configuration c_jl. By defining multiple zones as the product of independent non-overlapping single zones the posterior is an interpretable function of single zone Bayes factors. The prior is built in a natural way, given our multiple non-overlapping single zone construction. The methods described in the paper are implemented within the SpatialEpi R package. The code to reproduce the upstate New York example can be found in Appendix H of the supplementary material available at Biostatistics online.

Our aim was to provide a Bayesian version of the approach considered by SatScan and to this end we have only considered circular windows. A critical feature of our model is that we can account probabilistically for the presence of more than one cluster in the study region. Recently, there has been increased interest in constructing methods for arbitrarily shaped clusters, see for example Duczmal and Assunção (2004) and Kulldorff and others (2006). Our model can be extended to allow for non-circular regions by redefining the set of single zones from which the multiple zones are constructed.

The model we have proposed does not lead to each area having a uniform prior probability of lying within a cluster/anti-cluster. The non-uniformity arises from our definition of single zone and from how single zones are combined to form configurations. The limit on zone size (in terms of population) also has implications. One way in which the effect of these factors can be determined is by plotting the posterior to prior odds ratio of lying in a cluster, i.e. the Bayes factor, and the use of this measure was illustrated in Section 5. The number of clusters is critically dependent on the prior on the null configuration π₀, and addressing the sensitivity to this choice is a key step. If one has area-level covariates then these may be incorporated in the expected numbers. The introduction of a log-linear model is possible, but would break the conjugacy of the model and hence increase computation.

In terms of “cluster detection” one may proceed in a variety of ways but examining multiple posterior summaries is recommended. A starting point will always be comparison of the prior and posterior on the number of clusters/anti-clusters. Following this step, the posterior probabilities of each area falling in a cluster can be mapped. These maps may be thresholded to reveal more clearly areas of high relative risk. “Clusters” in our model are determined with respect to the narrow (null) and wide (non-null) priors and careful thought is required in these specifications, since these choices are defining the answer to the key epidemiological question of: What is a “high” relative risk?

Supplementary material

Supplementary materials, including extensive sensitivity analyses for the New York data and R code to reproduce the example, are available at http://www.biostatistics.oxfordjournals.org.