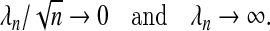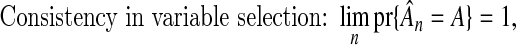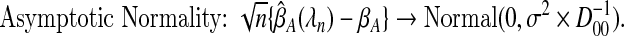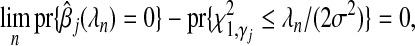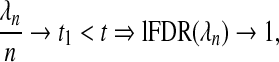Abstract
The Lasso shrinkage procedure achieved its popularity, in part, by its tendency to shrink estimated coefficients to zero, and its ability to serve as a variable selection procedure. Using data-adaptive weights, the adaptive Lasso modified the original procedure to increase the penalty terms for those variables estimated to be less important by ordinary least squares. Although this modified procedure attained the oracle properties, the resulting models tend to include a large number of “false positives” in practice. Here, we adapt the concept of local false discovery rates (lFDRs) so that it applies to the sequence, λn, of smoothing parameters for the adaptive Lasso. We define the lFDR for a given λn to be the probability that the variable added to the model by decreasing λn to λn−δ is not associated with the outcome, where δ is a small value. We derive the relationship between the lFDR and λn, show lFDR=1 for traditional smoothing parameters, and show how to select λn so as to achieve a desired lFDR. We compare the smoothing parameters chosen to achieve a specified lFDR and those chosen to achieve the oracle properties, as well as their resulting estimates for model coefficients, with both simulation and an example from a genetic study of prostate specific antigen.
Keywords: Adaptive Lasso, Local false discovery rate, Smoothing parameter, Variable selection
1. Introduction
The Lasso procedure offers a means to fit a linear regression model when the number of parameters p is comparatively large (Tibshirani, 1996, 2011). The Lasso estimates coefficients by minimizing the residual sum of squares plus a penalty term. Let there be n subjects, let Y =(Y 1,…,Y n)T be their outcomes, let Xj=(Xj1,…,Xjn)T be their measurements for variable j=1,…,p, and let X=(X1,…,Xp). Then the estimated coefficients are
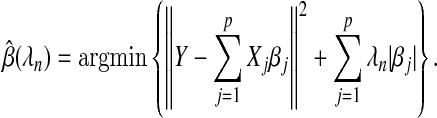 |
A major benefit of the L1 penalty is that the Lasso also serves as a variable selection method, as a large proportion of 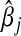 are reduced to 0 when λn is large.
are reduced to 0 when λn is large.
The adaptive Lasso modifies the original version by adding a data-defined weight, 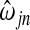 , to the penalty term (Zou, 2006). For our purposes, we consider only
, to the penalty term (Zou, 2006). For our purposes, we consider only 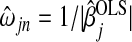 , where
, where 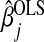 is the ordinary least squares estimate. The adaptive Lasso minimizes
is the ordinary least squares estimate. The adaptive Lasso minimizes
 |
(1.1) |
When 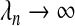 and
and 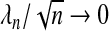 , the adaptive Lasso is an oracle procedure (Cai and Sun, 2007; Fan and Li, 2001). Let the true relationship be described by the linear equation E(Y |X)=β1X1+⋯+βpXp where only a strict subset of the β-coefficients are non-zero, this subset being A={j:βj≠0}. An oracle procedure is defined by having the following two properties:
, the adaptive Lasso is an oracle procedure (Cai and Sun, 2007; Fan and Li, 2001). Let the true relationship be described by the linear equation E(Y |X)=β1X1+⋯+βpXp where only a strict subset of the β-coefficients are non-zero, this subset being A={j:βj≠0}. An oracle procedure is defined by having the following two properties:
Consistent variable selection:
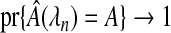 where
where 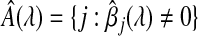 is the estimated set of influential variables.
is the estimated set of influential variables.Asymptotic efficiency for
 , where Σ is the inverse of the information matrix when A is known.
, where Σ is the inverse of the information matrix when A is known.
In practice, with finite sample sizes, a sequence, λn, that satisfies the oracle requirements results in a model that includes a large number of false positives (i.e. the set 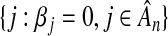 is large) (Martinez and others, 2010). In this manuscript, our three objectives are the following: (1) To demonstrate, mathematically, that choosing λn to meet the oracle properties will result in a high false positive rate for finite samples. (2) To quantify the probability that a variable selected into the model is a false positive. This probability can provide confidence that the included variable is independently associated with the outcome. (3) To show how to identify a sequence of smoothing parameters that controls the number of false positives, instead of achieving the oracle properties.
is large) (Martinez and others, 2010). In this manuscript, our three objectives are the following: (1) To demonstrate, mathematically, that choosing λn to meet the oracle properties will result in a high false positive rate for finite samples. (2) To quantify the probability that a variable selected into the model is a false positive. This probability can provide confidence that the included variable is independently associated with the outcome. (3) To show how to identify a sequence of smoothing parameters that controls the number of false positives, instead of achieving the oracle properties.
In order to measure and control the number of false positives, we introduce the concept of the local false discovery rate (lFDR) into the selection of λn (Efron and others, 2001; Efron and Tibshirani, 2002; Benjamini and Hochberg, 1995). Specifically, we define lFDR(λn) to be the probability that a variable added to the model is a false positive when the penalty term is incrementally lowered below λn. Our first goal is to derive the relationship between lFDR and λn. We then show that lFDR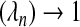 , an unusual choice for most problems, if λn satisfies the oracle requirements, thus explaining the observation that the adaptive Lasso results in a large number of false positives when the effect sizes are not too large. In more traditional problems, a value of 0.05 is often the targeted FDR or lFDR. Finally, we offer a parametric bootstrap method for selecting λn to achieve a desired lFDR which is similar to a step described by Hall and others (2009). Others have also noted this high false positive rate and proposed Bootstrapped and Bayesian versions of the Lasso for handling this problem (Bach, 2008; Hans, 2010; Park and Casella, 2005).
, an unusual choice for most problems, if λn satisfies the oracle requirements, thus explaining the observation that the adaptive Lasso results in a large number of false positives when the effect sizes are not too large. In more traditional problems, a value of 0.05 is often the targeted FDR or lFDR. Finally, we offer a parametric bootstrap method for selecting λn to achieve a desired lFDR which is similar to a step described by Hall and others (2009). Others have also noted this high false positive rate and proposed Bootstrapped and Bayesian versions of the Lasso for handling this problem (Bach, 2008; Hans, 2010; Park and Casella, 2005).
Our motivating example comes from a Genome-Wide Association Study (GWAS). Both the Lasso (Wu and others, 2009) and the adaptive Lasso (Kooperberg and others, 2010; Sun and others, 2010) have become popular tools for GWAS because variable selection is an important step given that 100 000's of single nucleotide polymorphisms (SNPs) are available for testing. In our specific study, we focus on modeling the prostate specific antigen (PSA) level, a biomarker indicative of prostate cancer (Parikh and others, 2010).
The order of this paper is as follows. In Section 2, we introduce notation and review the adaptive Lasso. We then formalize our definition of the lFDR, derive the relationship between the lFDR and λn, and provide asymptotic theory. Finally, we describe our bootstrap approach for choosing λn. In Section 3 and supplementary material available at Biostatistics online, we evaluate the behavior of λn when selected by the lFDR through simulation and our motivating example. We conclude with a short discussion in Section 4.
2. Methods
2.1. Notation
We assume that there is a continuous outcome Y i and its true value is defined by
 |
(2.1) |
where ϵi=Normal(0,σ2). Further, we assume  , where D is a positive-definite matrix. Recall that A is the set of covariates that are associated with a non-zero β, A≡{j:βj≠0}, and βA≡{βj:j∈A}. We say that covariate j is influential if j∈A or that it is superfluous if j∉A. Without loss of generality, assume that A={1,…,p0}, let z=1−p0/p, and let D00 be the corresponding p0×p0 submatrix of D.
, where D is a positive-definite matrix. Recall that A is the set of covariates that are associated with a non-zero β, A≡{j:βj≠0}, and βA≡{βj:j∈A}. We say that covariate j is influential if j∈A or that it is superfluous if j∉A. Without loss of generality, assume that A={1,…,p0}, let z=1−p0/p, and let D00 be the corresponding p0×p0 submatrix of D.
Let  be the parameter estimates produced by the adaptive Lasso,
be the parameter estimates produced by the adaptive Lasso,
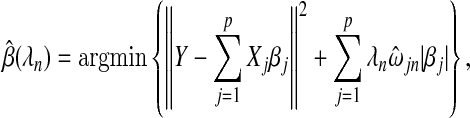 |
where, for our purposes, 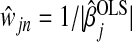 . The sequence λn is the set of smoothing parameters. We let
. The sequence λn is the set of smoothing parameters. We let 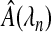 be the set of covariates predicted to have a non-zero β, so
be the set of covariates predicted to have a non-zero β, so 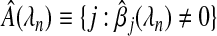 .
.
Finally, we include the notation and definitions for the local FDR and related terms. We denote the probabilities, Pfp(λn) and Pfn(λn), that a variable will be a false positive and a false negative by
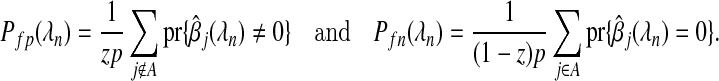 |
We define the lFDR by
 |
(2.2) |
where
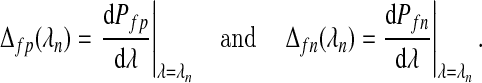 |
By a Taylor series expansion, the expected difference in the number of false positives, (1−z){Pfp(λ)−Pfp(λ−δ)}, at λ and λ−δ, is approximately (1−z)δΔfp(λ). Similarly, the expected difference in the number of false negatives and the total number of variables included in the model are zδΔfp(λ) and zδΔfp(λ)+(1−z)δΔfn(λ). Therefore, we define the lFDR by (2.2) as the probability that a variable added to our model will be superfluous, if added when the smoothing parameter is lowered below λn. Our definition of lFDR differs from that traditionally given for two reasons: (i) we interpret the lFDR from a frequentist point of view and (ii) we focus on the smoothing parameter λn instead of on a test statistic. The traditional definitions of lFDR and FDR have also been used for purposes of variable selection, usually by including only those variables with a q-value below a given threshold (Storey, 2002). However, such an approach would not be as appropriate for Lasso procedures, which try to avoid this post hoc selection. Note, an equivalent definition for FDR is available by replacing Δ(λn) with P(λn) in (2.2).
2.2. Prior results
The adaptive Lasso has many theoretical properties. Here, we build on two previous results. Zou (2006) states the requirements needed for the adaptive Lasso to have the oracle properties.
Theorem 1 —
Suppose that
(2.3) Then the adaptive Lasso estimates must satisfy the following:
(2.4)
(2.5)
If our focus is on variable selection, then a theorem identified by Pötscher and Schneider (2009) proves equally useful.
Theorem 2 —
Let XTX=nI, where I is the identity matrix. then
Because
is asymptotically normal with mean βj, we immediately see
(2.6) where
follows a non-central χ2 distribution with one degree of freedom and non-centrality parameter
.
2.3. Local false discovery rates
When X is orthogonal, the total number of variables included in the model is monotonically non-decreasing as λn decreases. The lFDR is the proportion of added variables that are expected to be false positives. When X is orthogonal and σ2=1, then
 |
(2.7) |
where C(λ), which can be interpreted as the cost of removing a false positive, is
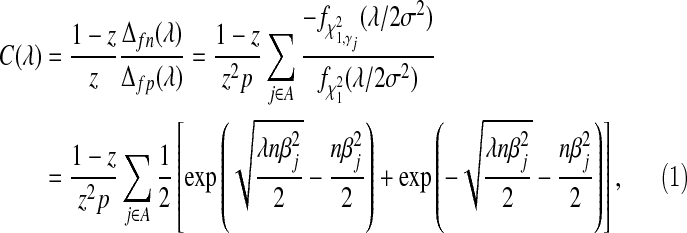 |
(2.8) |
where 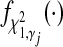 is the density for a χ2 variable with non-centrality parameter
is the density for a χ2 variable with non-centrality parameter 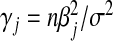 .
.
Equations (2.7) and (2.8) allow us to choose λn to achieve a specific lFDR. For example, if, in addition to σ2=1 and X being orthogonal, all βj=β, then the lFDR will never exceed q if
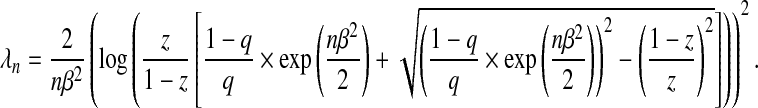 |
(2.9) |
The sequence λn, when defined by (2.9), is independent of the number of variables p. Moreover, all properties discussed hold regardless of the size of β (e.g. β is constant or decreasing at a rate of 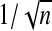 ). Therefore, although there is no λn that can attain the oracle property when β is decreasing at a rate of
). Therefore, although there is no λn that can attain the oracle property when β is decreasing at a rate of 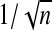 (Pötscher and Schneider, 2009), the sequence defined by (2.9) would still attain the stated lFDR. As expected, we note that the lFDR decreases with increasing λn confirming that those variables added when λn is small are more likely to be false positives. We define λqn to satisfy lFDR(λqn)=q.
(Pötscher and Schneider, 2009), the sequence defined by (2.9) would still attain the stated lFDR. As expected, we note that the lFDR decreases with increasing λn confirming that those variables added when λn is small are more likely to be false positives. We define λqn to satisfy lFDR(λqn)=q.
2.4. Constant β
The term  in (2.8) can be ignored when
in (2.8) can be ignored when  is large. Specifically, when
is large. Specifically, when 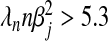 ∀j, the lFDR at a given value of λn can be approximated within 1% of its true value by
∀j, the lFDR at a given value of λn can be approximated within 1% of its true value by
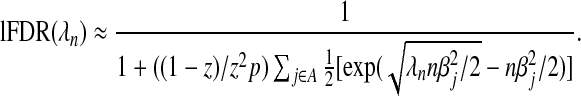 |
(2.10) |
Equation (2.10) shows more clearly that if we choose λn to achieve the oracle property (i.e.  ), then we are choosing a λn that results in an
), then we are choosing a λn that results in an  . As an lFDR=1 implies that all variables being added to the model are false positives, purposely choosing such a λn would seem counterintuitive. Therefore, even when λn can be chosen to achieve the oracle properties, it is unclear whether such a choice is desirable. An alternative approach would be to choose λn to ensure that lFDR<q. In the previous example, where σ2=1, X is orthogonal, and βj=β, we now see lFDR<q if
. As an lFDR=1 implies that all variables being added to the model are false positives, purposely choosing such a λn would seem counterintuitive. Therefore, even when λn can be chosen to achieve the oracle properties, it is unclear whether such a choice is desirable. An alternative approach would be to choose λn to ensure that lFDR<q. In the previous example, where σ2=1, X is orthogonal, and βj=β, we now see lFDR<q if
 |
(2.11) |
Purposely choosing a λn such that the lFDR  0 seems equally counterintuitive, limiting the reasonable choices for λn. If σ2=1, X is orthogonal, and βj=β, where β is a constant, we see that for the lFDR not to diverge to 0 or 1,
0 seems equally counterintuitive, limiting the reasonable choices for λn. If σ2=1, X is orthogonal, and βj=β, where β is a constant, we see that for the lFDR not to diverge to 0 or 1,  .
.
Lemma 1 —
When βj=β ∀j, β is constant, σ2=1, X is orthogonal, and t=0.5β2, then
(2.12)
(2.13)
(2.14) where
.
If λn were chosen to achieve an lFDR strictly between 0 and 1, then only the first of the two oracle properties holds, 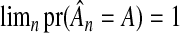 from (2.4). However, we claim that forgoing the second oracle property, in exchange for an lFDR between 0 and 1, is no loss. Although performing variable selection and fitting in a single step is convenient, it is unnecessary. Clearly, there is a two-step method that recovers the second oracle property. After using the adaptive Lasso with
from (2.4). However, we claim that forgoing the second oracle property, in exchange for an lFDR between 0 and 1, is no loss. Although performing variable selection and fitting in a single step is convenient, it is unnecessary. Clearly, there is a two-step method that recovers the second oracle property. After using the adaptive Lasso with 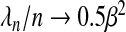 for variable selection, we can refit the model using OLS with only that subset of variables. This two-step procedure not only satisfies both oracle properties, but offers improved efficiency over the single-step procedure, reminding us that the oracle procedure is not an optimal procedure. Although an oracle procedure promises that
for variable selection, we can refit the model using OLS with only that subset of variables. This two-step procedure not only satisfies both oracle properties, but offers improved efficiency over the single-step procedure, reminding us that the oracle procedure is not an optimal procedure. Although an oracle procedure promises that  for all superfluous variables, it makes no claim as to the rate at which this occurs. Asymptotically, we can increase the rate at which
for all superfluous variables, it makes no claim as to the rate at which this occurs. Asymptotically, we can increase the rate at which 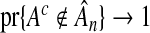 without decreasing the rate at which
without decreasing the rate at which 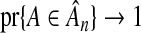 . Returning to (2.6), this potential improvement is clear because, asymptotically,
. Returning to (2.6), this potential improvement is clear because, asymptotically, 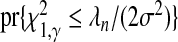 , is unchanged by λn so long as
, is unchanged by λn so long as  .
.
2.5. Empirical choice of λn
In the idealized scenario, where X is orthogonal, βj=β ∀j∈A, and both z and β are known, (2.9) can be used to choose a sequence λn to achieve a specified lFDR. If all values of {βj:j∈A} are not identical, then the solution to (2.8) would need to be obtained numerically. Although β and z are unknown, in practice, we could use an estimate of z and either an estimate of β or a lower bound for a biologically meaningful β. However, when (2.9) is evaluated with these estimates, the chosen λn tends to produce an lFDR above the desired value when X is not orthogonal. Therefore, we prefer a bootstrap approach similar to one of the steps discussed by Hall and others (2009). The algorithm is as follows. Let us first fit a simple model of Y on X to obtain estimates of β. In practice, as done in our simulations, we suggest identifying those β to have non-zero values by the adaptive Lasso with λdn, and then defining  by the OLS estimates. Let us then denote the variance of the residuals from this model by
by the OLS estimates. Let us then denote the variance of the residuals from this model by  . Next, set all components of
. Next, set all components of 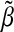 below some threshold equal to zero. In practice, when n>p, we use
below some threshold equal to zero. In practice, when n>p, we use 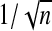 as this threshold. Then generate B sets of data, assuming the true model is
as this threshold. Then generate B sets of data, assuming the true model is  , where
, where  . For each value of λn in a given set, we calculate the number of true,
. For each value of λn in a given set, we calculate the number of true, 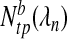 , and false,
, and false, 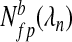 , positives added to the model between λn−δ and λn+δ where δ is an appropriately small number and the superscript b denotes the dataset. We can then estimate the lFDR for each λn by
, positives added to the model between λn−δ and λn+δ where δ is an appropriately small number and the superscript b denotes the dataset. We can then estimate the lFDR for each λn by
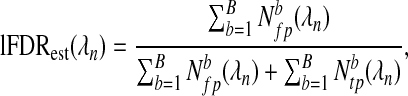 |
(2.15) |
and select the smoothing parameter that achieves a specified lFDR, q:
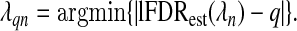 |
For completeness, we define 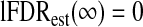 and
and 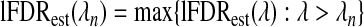 when
when  . In practice, B=10, but we base our estimates of lFDRest on a monotonically smoothed version of lFDRest(λn).
. In practice, B=10, but we base our estimates of lFDRest on a monotonically smoothed version of lFDRest(λn).
For purposes of comparison, we consider the standard method for selecting λn to be cross-validation aimed at minimizing the prediction error of future estimates. Recall that standard 10-fold cross-validation starts by dividing the set Sn of n subjects into 10 mutually exclusive sets, s1∪s2∪⋯∪s10=Sn, of roughly equal size. Let 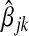 , 1≤k≤10 be the adaptive Lasso estimate for βj based on those subjects not in sk. Then
, 1≤k≤10 be the adaptive Lasso estimate for βj based on those subjects not in sk. Then
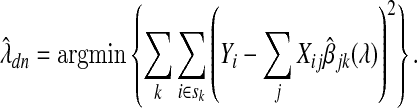 |
Also, 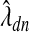 is an estimate of the deviance-optimized smoothing parameters:
is an estimate of the deviance-optimized smoothing parameters:
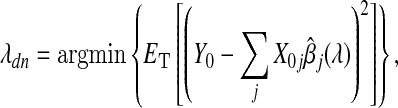 |
where 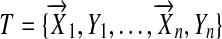 are the data input into the adaptive Lasso to obtain the estimates
are the data input into the adaptive Lasso to obtain the estimates  ,
,  are the data from a new individual, and T={T,T0}. When β is fixed and X is orthogonal, the smoothing parameters minimizing the deviance must satisfy the oracle properties.
are the data from a new individual, and T={T,T0}. When β is fixed and X is orthogonal, the smoothing parameters minimizing the deviance must satisfy the oracle properties.
2.6. High-dimensional adaptive Lasso: p > n
As defined in (1.1), the weights in the adaptive Lasso are 1/ . However, when p>n, the weights must substitute a different estimate of β in place of
. However, when p>n, the weights must substitute a different estimate of β in place of  . Two possible substitutes that have been studied include
. Two possible substitutes that have been studied include  , the estimates obtained by fitting separate models for each variable (Huang and others, 2008), and
, the estimates obtained by fitting separate models for each variable (Huang and others, 2008), and  , the estimates from a regular Lasso procedure (Zhou and others, 2009). The properties of the latter estimates,
, the estimates from a regular Lasso procedure (Zhou and others, 2009). The properties of the latter estimates,  , with
, with 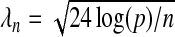 , have been studied and demonstrated to have useful qualities (Zhou and others, 2009). In practice, however, we found that 1/
, have been studied and demonstrated to have useful qualities (Zhou and others, 2009). In practice, however, we found that 1/ performed better, and chose to use those weights in our simulations. For defining
performed better, and chose to use those weights in our simulations. For defining  , we cannot use
, we cannot use 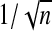 as our cutoff threshold. Instead, we first perform the adaptive Lasso on our data and count the number of coefficients estimated to be non-zero. We then find the threshold, such that by setting all
as our cutoff threshold. Instead, we first perform the adaptive Lasso on our data and count the number of coefficients estimated to be non-zero. We then find the threshold, such that by setting all  below that threshold to 0 and simulating data, the adaptive Lasso on the simulated data estimates a similar number of non-zero coefficients.
below that threshold to 0 and simulating data, the adaptive Lasso on the simulated data estimates a similar number of non-zero coefficients.
3. Results
3.1. Simulation design: comparing λqn and λdn
Our first goal is to offer an example comparing the magnitude and performance of λdn and λqn. As with all simulations here, our objective is not to describe the performance of the estimates  and
and  , but to calculate, describe, and compare the true values of λdn and λqn. We assume that the covariate matrix X is orthogonal and that the outcome Y can be described by linear regression, (2.1), with βj=0.15 if βj∈A and σ2=1. For these examples, we fixed the number of covariates p=50, but let the size of A vary, z∈{0.5,0.7,0.9}. As described below, we used simulation to calculate λdn and λqn, their corresponding lFDR and the proportion of variables that were misclassified, errMC, for a sequence of samples between n=200 and n=2000.
, but to calculate, describe, and compare the true values of λdn and λqn. We assume that the covariate matrix X is orthogonal and that the outcome Y can be described by linear regression, (2.1), with βj=0.15 if βj∈A and σ2=1. For these examples, we fixed the number of covariates p=50, but let the size of A vary, z∈{0.5,0.7,0.9}. As described below, we used simulation to calculate λdn and λqn, their corresponding lFDR and the proportion of variables that were misclassified, errMC, for a sequence of samples between n=200 and n=2000.
Our second goal is to show that results are essentially unchanged when we vary p. For efficiency, we calculated λdn, λqn, lFDR, and errMC at only n=1000 for p∈{100,200,500}, maintaining all of the other assumptions.
Our third goal is to examine whether λqn, calculated assuming that X is orthogonal, was appropriate when there was dependence. Specifically, we repeated the abbreviated analyses assuming that the covariance structure of (Xi1,Xi2,…,Xip) is block diagonal. Correlation ρ within a block was constant, ρ∈{0.3,0.6}, each block contained the same number of influential variables (or possibly no influential variables if there were more blocks than influential variables), and each block contained the same number of total variables. Variables were divided into 2, 5, or 10 groups.
For any combination of n, p, z, and covariance structure, we estimate the values of λdn, λqn, lFDR, and errMC by simulating 200 000 values of X and Y . For each simulation, at a specified set of λ ranging from 0.01 to 100, we calculate the residual deviance and errMC. Furthermore, for the same set of λ, we count the number of true and false positives added to the model when the smoothing parameter was between  and
and  . Then, for each λ, we average the number of true and false positives added, deviance, and errMC over all 200 000 datasets to obtain estimates of each desired value. The lFDR was estimated by the ratio between the average number of false positives added, compared with the total number of variables added to the model. For each combination of n, p, z, and covariance structure discussed, we simulated a new set of 200 000 simulations. To generate a dataset X, we assumed that {Xi1,…,Xip} followed a normal distribution with mean 0 and specified covariance matrix. When X was assumed orthogonal, we used the resulting principal components. All datasets were standardized, so each variable had mean 0 and variance 1.
. Then, for each λ, we average the number of true and false positives added, deviance, and errMC over all 200 000 datasets to obtain estimates of each desired value. The lFDR was estimated by the ratio between the average number of false positives added, compared with the total number of variables added to the model. For each combination of n, p, z, and covariance structure discussed, we simulated a new set of 200 000 simulations. To generate a dataset X, we assumed that {Xi1,…,Xip} followed a normal distribution with mean 0 and specified covariance matrix. When X was assumed orthogonal, we used the resulting principal components. All datasets were standardized, so each variable had mean 0 and variance 1.
3.2. Simulation results: comparing λqn and λdn
First, consider the example when X is orthogonal, p=50, and z=0.7. Figure 1(a) shows that λqn increases linearly with the number of subjects and that the slope is approximately 0.5β2 as (2.11) suggests, except when λnnβ2 is small. The same equation promises that the lFDR-selected λn's, for values q1 and q2, differ by approximately 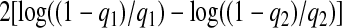 . As the deviance-optimized λn's achieve the oracle properties when X is orthogonal, they must be increasing at a rate less than
. As the deviance-optimized λn's achieve the oracle properties when X is orthogonal, they must be increasing at a rate less than  , and therefore, the representative black line in Figure 1(a) is significantly below those illustrating the smoothing parameters chosen to achieve the specified values of the lFDR.
, and therefore, the representative black line in Figure 1(a) is significantly below those illustrating the smoothing parameters chosen to achieve the specified values of the lFDR.
Fig. 1.

(a) The sequence of λn chosen to minimize the deviance (solid black line) or chosen to achieve a specified lFDR (broken lines) increases with the number of subjects in the study. For these simulations, z=0.7, p=50, β=0.15 for associated variables. (b) The average proportion of variables that are misclassified (error, y-axis), or the number of false positives and false negatives, quickly drops to 0 when λn is chosen to achieve a specified lFDR, but remains above 0 for deviance-optimized smoothing parameters.
The advantage to choosing a sequence λn that increases linearly with the number of the subjects is that the proportion of misclassified variables converges to 0 much quicker. Figure 1(b) shows that when there are 1000 individuals in the study and 35 out of 50 of the SNPs are superfluous, on average, 12% of the variables are misclassified with the deviance-optimized parameters, whereas less than 2.1% are misclassified when using lFDR-selected parameters. The relationship between lFDR and percentage misclassified is not monotone, as it depends on z. Here, setting q=0.5 minimized the proportion misclassified. Figure 2 shows that when λn minimizes deviance, the cost of reducing false positives is very low, or equivalently, the lFDR is high, so there is great benefit in increasing λn. In terms of identifying A exactly, with 1000 individuals, the probability that there is at least one misclassified variable,  , exceeds 0.999 when using deviance-optimized smoothing parameters, whereas that probability is less than 0.64 when using lFDR-selected parameters.
, exceeds 0.999 when using deviance-optimized smoothing parameters, whereas that probability is less than 0.64 when using lFDR-selected parameters.
Fig. 2.

(a) The solid black line shows the probability, 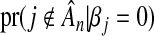 , that a null variable is excluded from
, that a null variable is excluded from  when X is orthogonal. The top curved dashed line shows the probability,
when X is orthogonal. The top curved dashed line shows the probability, 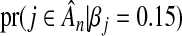 , that a non-null variable is included in
, that a non-null variable is included in  when X is orthogonal, z=0.7, and n=1000. The vertical dashed line farthest to the right indicates λdn. The other pairs of broken lines show the equivalent values when n=500 and n=800. (b) The local FDR, lFDR, is illustrated as a function of λ for the three scenarios above.
when X is orthogonal, z=0.7, and n=1000. The vertical dashed line farthest to the right indicates λdn. The other pairs of broken lines show the equivalent values when n=500 and n=800. (b) The local FDR, lFDR, is illustrated as a function of λ for the three scenarios above.
Table 1 shows that the large difference between λdn and λqn remains for p>50, and, in fact, both λdn and λqn appear to be essentially independent of p when X is orthogonal. When the covariates are correlated, compared with when they are independent, λqn tends to be larger, as more stringent penalty terms are needed to exclude null variables that are correlated with influential variables. Increasing ρ or block size magnifies this effect. Therefore, in practice, we suggest choosing λqn by the bootstrapping method described in Section 2.5. Table 1 also demonstrates the obvious result that as the proportion z of null variables increases, λqn must also increase.
Table 1.
The smoothing parameters designed to achieve lFDR=0.5 are larger than those designed to minimize deviance
| Low correlation |
High correlation |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Independent |
10 | 5 | 2 | 10 | 5 | 2 | |||
| p | z | λdn | λqn | λqn | λqn | ||||
| 100 | 0.9 | 6.31 | 18.52 | 18.72 | 20.32 | 27.33 | 22.32 | 27.63 | 30.23 |
| 100 | 0.7 | 3.7 | 15.02 | 16.22 | 18.32 | 18.32 | 14.92 | 17.12 | 15.22 |
| 200 | 0.9 | 6.21 | 17.92 | 20.72 | 23.63 | 28.33 | 26.23 | 28.13 | 39.44 |
| 200 | 0.7 | 3.7 | 14.82 | 17.02 | 18.72 | 19.82 | 15.02 | 14.92 | 15.42 |
| 500 | 0.9 | 6.21 | 18.12 | 28.73 | 34.84 | 45.15 | 38.44 | 50.56 | 51.66 |
| 500 | 0.7 | 3.7 | 14.22 | 18.62 | 18.92 | 19.52 | 15.42 | 15.42 | 16.02 |
3.3. Simulation design: evaluating the performance of adaptive Lasso with λqn
Our next goal is to evaluate the performance of the adaptive Lasso when using λqn, estimated by our bootstrap approach described in Sections 2.5 and 2.6. This method selects a set of variables that should satisfy the specified lFDR criteria. For comparison, we consider a more traditional method for selecting variables targeting the same criteria. This method, implemented by the R function FDRtool (Strimmer, 2008), inputs the p-values calculated from models including each variable individually. In brief, the method decomposes the overall distribution of p-values into two distributions, representing the p-values from the null and influential variables. Given these two distributions, the traditional method first estimates the p-value thresholds that would result in the specified lFDR and then selects all variables meeting the appropriate threshold.
We consider the lFDR, lFDRAL, resulting from using the bootstrap version of the adaptive Lasso and the rates lFDRTR resulting from the traditional method. We compare these observed rates to the targeted values: q∈{0.1,0.5,0.9}. These comparisons are performed in two types of datasets. When n>p, settings are similar to those in Section 3.1: n=1000, p=500, z=0.9, βj=0.1 if βj∈A and σ2=1. In order for the traditional methods to produce rates below 1, we reduce the number of correlated variables per block to 5. Again ρ∈{0.0,0.3,0.6}. When p>n, specifically n=1000 and p=5000, we increase z to 0.96 and include 10 variables per correlated block. To achieve q=0.1 when p>n, we further increase z to 0.99 and βj to 0.35. We provide an extended set of simulations, exploring other correlation structures and effect distributions, in supplementary material available at Biostatistics online.
For each combination of parameters, we generated 1000 datasets and then averaged the resulting lFDRAL and lFDRTR across all 1000 datasets. For each dataset, we defined the lFDR to be 0 if the last variable selected was influential, 1 otherwise.
3.4. Simulation results: evaluating the performance of adaptive Lasso with λqn
The bootstrap approach proposed in Sections 2.5 and 2.6 selected values of λqn that, when applied to the full dataset, resulted in lFDR values similar to the targeted value. In the example where n>p and ρ=0, the observed lFDR was 0.06, 0.48, and 0.89 when λqn was chosen to achieve lFDR=0.1,0.5, and 0.9. When targeting lFDR=0.1, our method achieved a lower lFDR, and therefore our chosen λq was larger than desired. This inflated λq arises, in part, from a tendency to select too few non-zero 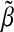 in our bootstrap models. Table 2 and results in supplementary material available at Biostatistics online show that the lFDR estimates were only minimally altered by changing the correlation structure or when considering the p>n.
in our bootstrap models. Table 2 and results in supplementary material available at Biostatistics online show that the lFDR estimates were only minimally altered by changing the correlation structure or when considering the p>n.
Table 2.
A comparison between the newly proposed bootstrap (B) method for obtaining a specified lFDR with the traditional (T) approach
|
ρ=0.0 |
ρ=0.3 |
ρ=0.6 |
||||
|---|---|---|---|---|---|---|
| Target | B | T | B | T | B | T |
| n>p | ||||||
| 0.1 | 0.059 | 0.088 | 0.083 | 0.232 | 0.101 | 0.688 |
| 0.5 | 0.477 | 0.435 | 0.505 | 0.737 | 0.52 | 0.919 |
| 0.9 | 0.893 | 0.804 | 0.905 | 0.94 | 0.909 | 0.967 |
| p>n | ||||||
| 0.1 | 0.008 | 0.075 | 0.019 | 0.298 | 0.105 | 0.904 |
| 0.5 | 0.466 | 0.464 | 0.592 | 0.679 | 0.639 | 0.905 |
| 0.9 | 0.751 | 0.864 | 0.861 | 0.953 | 0.894 | 0.978 |
The traditional approach, based on estimating the p-value distribution of the null and influential variables, performed poorly when there was high correlation between variables (Table 2). When there was high correlation, models with only a single variable assigned low p-values to those null variables associated with influential variables. This resulted in more variables achieving the lFDR threshold, but a higher proportion were false positives. With n>p, ρ=0.6, and a targeted lFDR=0.5, the observed lFDR=0.9.
3.5. Application
In the United States, prostate cancer is the most commonly diagnosed non-cutaneous cancer in men, with approximately 200 000 new diagnoses each year. Because levels of PSA are elevated in the presence of prostate cancer, it is commonly used as a biomarker for early detection. Unfortunately, the specificity of tests based on PSA is often very low, as many healthy individuals also have high levels. Specificity could be greatly improved by a method that can identify individuals with naturally high levels. To this end, there have been large GWASs searching for genetic markers associated with the PSA level. The Prostate, Lung, Colorectal, and Ovarian Cancer Screening Trial, or PLCO, which recorded PSA levels, genotyped 2200 healthy men using an Illumina genotyping platform containing more than 500 000 SNPs (Andriole and others, 2009). We focus on a subset of 530 SNPs in and around the KLK3 gene (Parikh and others, 2010).
Let X be the 2200×530 matrix containing the genotypes for the study population at these 530 SNPs. Genotypes are coded as 0, 1, or 2, indicating the number of minor alleles at that SNP. Let Y be the log-transformed PSA levels. Then we regressed Y on X using a linear model with the adaptive Lasso procedure. We repeated this analysis with the two values of λ: 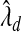 and
and 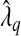 , where
, where 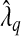 was estimated by the previously defined bootstrap procedure. Unfortunately, the truth is unknown, and therefore we can only use this example to illustrate their relative performance. The estimated values of the smoothing parameter were
was estimated by the previously defined bootstrap procedure. Unfortunately, the truth is unknown, and therefore we can only use this example to illustrate their relative performance. The estimated values of the smoothing parameter were 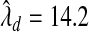 and
and 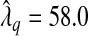 , with q=0.5. As expected,
, with q=0.5. As expected, 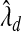 is significantly smaller than that value estimated to achieve lFDR=0.5. As a consequence,
is significantly smaller than that value estimated to achieve lFDR=0.5. As a consequence, 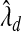 allowed 17 SNPs to have non-zero coefficients, whereas
allowed 17 SNPs to have non-zero coefficients, whereas  allowed only 1 SNP (Table S2 of supplementary material available at Biostatistics online). Although we cannot be certain that either model is correct, it seems doubtful that 17 SNPs in that region are directly associated with PSA levels. To estimate β corresponding to rs2735839 using the two-stage approach, first selecting variables with
allowed only 1 SNP (Table S2 of supplementary material available at Biostatistics online). Although we cannot be certain that either model is correct, it seems doubtful that 17 SNPs in that region are directly associated with PSA levels. To estimate β corresponding to rs2735839 using the two-stage approach, first selecting variables with  and then estimating β using OLS, we calculate
and then estimating β using OLS, we calculate  from a model containing only rs2735839.
from a model containing only rs2735839.
4. Discussion
The adaptive Lasso has become a popular model-building procedure because it shrinks a subset of coefficients to zero, thereby simultaneously performing variable selection and simplifying model interpretation. Although, asymptotically, using the traditional smoothing parameters promises that the adaptive Lasso will achieve consistent variable selection, their use often leaves a large number of false positives in the model when sample size is finite.
The lFDR is usually a form of post-processing, in that we would first perform a statistical procedure to attach a p-value to an estimate of each parameter and then determine the probability that the true value of a parameter with that p-value is the null value. We have adapted the lFDR framework to select smoothing parameters in the adaptive Lasso. Instead of defining an lFDR for a specific p-value, we define it for a specific value of the tuning constant λ. The framework offers an alternative means for selecting the smoothing parameters. When chosen to achieve a specified value of the lFDR, the adaptive Lasso procedure promises both asymptotically consistent variable selection and better control of the false positive rate for finite samples.
By itself, a single-step, adaptive Lasso procedure using λq, the lFDR-selected smoothing parameter, does not achieve the oracle properties. If one believed that the optimal, or best, estimator had to have these properties, then a combined variable selection and model fitting procedure with λq would not be a viable option. However, we do not consider the absence of the second oracle property to be a deterrent to using λq. First, the oracle properties can be regained by a two-step procedure that adds a separate model fitting step, where OLS is applied only to those variables retained by the initial adaptive Lasso. Although the convenience of a one-step procedure is sacrificed, the final estimate would still have the stated properties. Second, the first oracle property, consistent variable selection, is not a statement of optimality. That property makes no claims on the rate at which 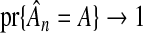 . In some sense, the rate of our two-step procedure is faster than the rate of the single-step procedure. Therefore, there is a benefit to our method, even if it cannot be measured by a characteristic as coarse as the oracle properties.
. In some sense, the rate of our two-step procedure is faster than the rate of the single-step procedure. Therefore, there is a benefit to our method, even if it cannot be measured by a characteristic as coarse as the oracle properties.
We chose to select the smoothing parameters to achieve a desired lFDR, instead of FDR, because we wanted to judge each variable on its own merits, and not the merits of all selected variables. As discussed previously (Efron and others, 2001; Efron and Tibshirani, 2002), if one fit a model with 1000 variables and aimed to achieve an FDR of 0.1, then if the first 90 variables selected were guaranteed to be non-null, the next 10 would be included regardless of the evidence. Note also that in addition to providing examples when lFDR=0.1, we offered examples with an lFDR as high as 0.9, a larger value than that generally used. For the adaptive Lasso procedure, where standard practice has been to choose lFDR=1 and there is often the desire not to omit any non-null variables, aiming for larger lFDR values may be preferred for the Lasso procedure.
5. Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
6. Funding
Sampson's and Chatterjee's research was supported by the Intramural Research Program of the NCI. Chatterjee's research was supported by a gene-environment initiative grant from the NHLBI (RO1-HL091172-01). Müller's research was supported by a grant from the Australian Research Council (DP110101998). Carroll's research was supported by a grant from the National Cancer Institute (R37-CA057030). Carroll was also supported by Award Number KUS-CI-016-04, made by King Abdullah University of Science and Technology (KAUST).
Supplementary Material
Acknowledgements
This study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the NIH, Bethesda, Md. (http://biowulf.nih.gov). Conflict of Interest: None declared.
References
- Andriole G. L., Grubb R. L., Buys S. S., Chia D., Church T. R., Fouad M. N., Gelmann E. P., Kvale P. A., Reding D. J., Weissfeld J. L. Mortality results from a randomized prostate-cancer screening trial. New England Journal of Medicine. 2009;360:1310–1319. doi: 10.1056/NEJMoa0810696. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bach F. R. Bolasso: model consistent lasso estimation through the bootstrap. Proceedings of the Twenty-fifth International Conference on Machine Learning (ICML) 2008 Helsinki, Finland. [Google Scholar]
- Benjamini Y., Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B. 1995;57:289–300. [Google Scholar]
- Cai T., Sun W. Oracle and adaptive compound decision rules for false discovery rate control. Journal of the American Statistical Association. 2007;102:901–912. [Google Scholar]
- Efron B., Tibshirani R. Empirical Bayes methods and false discovery rates for microarrays. Genetic Epidemiology. 2002;23:70–86. doi: 10.1002/gepi.1124. [DOI] [PubMed] [Google Scholar]
- Efron B., Tibshirani R., Storey J. D., Tusher V. Empirical Bayes analysis of a microarray experiment. Journal of the American Statistical Association. 2001;96:1151–1160. [Google Scholar]
- Fan J., Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association. 2001;96:1348–1360. [Google Scholar]
- Hall P., Lee E. R., Park B. Bootstrap-based penalty choice for the lasso achieving oracle performance. Statistica Sinica. 2009;19:449–471. [Google Scholar]
- Hans C. Model uncertainty and variable selection in Bayesian Lasso regression. Statistics and Computing. 2010;20:221–229. [Google Scholar]
- Huang J., Ma S., Zhang C.-H. Adaptive lasso for sparse high dimensional regression models. Statistica Sinica. 2008;18:1603–1618. [Google Scholar]
- Kooperberg C., LeBlanc M., Obenchain V. Risk prediction using genome-wide association studies. Genetic Epidemiology. 2010;34:643–652. doi: 10.1002/gepi.20509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez J. G., Carroll R. J., Muller S., Sampson J. N., Chatterjee N. A note on the effect on power of score tests via dimension reduction by penalized regression under the null. The International Journal of Biostatistics. 2010;6 doi: 10.2202/1557-4679.1231. Article 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parikh H., Deng Z., Yeager M., Boland J., Matthews C., Jia J., Collins I., White A., Burdett L., Hutchinson A. A comprehensive resequence analysis of the KLK15-KLK3-KLK2 locus on chromosome 19q13.33. Human Genetics. 2010;127:91–99. doi: 10.1007/s00439-009-0751-5. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park T., Casella G. The Bayesian Lasso. Technical Report. 2005 [Google Scholar]
- Pötscher B. M., Schneider U. On the distribution of the adaptive lasso estimator. Journal of Statistical Planning and Inference. 2009;139:2775–2790. [Google Scholar]
- Storey J. D. A direct approach to false discovery rates. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 2002;64:479–498. [Google Scholar]
- Strimmer K. fdrtool: a versatile R package for estimating local and tail area-based false discovery rates. Bioinformatics. 2008;24:1461–1462. doi: 10.1093/bioinformatics/btn209. [DOI] [PubMed] [Google Scholar]
- Sun W., Ibrahim J. G., Zou F. Genomewide multiple-loci mapping in experimental crosses by iterative adaptive penalized regression. Genetics. 2010;185:349–359. doi: 10.1534/genetics.110.114280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society Series B. 1996;58:267–288. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the Lasso: a retrospective. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2011;73:273–282. [Google Scholar]
- Wu T. T., Chen Y. F., Hastie T., Sobel E., Lange K. Genome-wide association analysis by Lasso penalized logistic regression. Bioinformatics. 2009;25:714–721. doi: 10.1093/bioinformatics/btp041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou S., van de Geer S., Buhlmann P. Adaptive lasso for high dimensional regression and gaussian graphical modeling. 2009 ArXiv:0903.2515. [Google Scholar]
- Zou H. The adaptive lasso and its oracle properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.