Abstract
Purpose
Fetal MRI volumetry is a useful technique but it is limited by a dependency upon motion-free scans, tedious manual segmentation, and spatial inaccuracy due to thick-slice scans. An image processing pipeline that addresses these limitations was developed and tested.
Materials and methods
The principal sequences acquired in fetal MRI clinical practice are multiple orthogonal single-shot fast spin echo scans. State-of-the-art image processing techniques were used for inter-slice motion correction and super-resolution reconstruction of high-resolution volumetric images from these scans. The reconstructed volume images were processed with intensity non-uniformity correction and the fetal brain extracted by using supervised automated segmentation.
Results
Reconstruction, segmentation and volumetry of the fetal brains for a cohort of twenty-five clinically acquired fetal MRI scans was done. Performance metrics for volume reconstruction, segmentation and volumetry were determined by comparing to manual tracings in five randomly chosen cases. Finally, analysis of the fetal brain and parenchymal volumes was performed based on the gestational age of the fetuses.
Conclusion
The image processing pipeline developed in this study enables volume rendering and accurate fetal brain volumetry by addressing the limitations of current volumetry techniques, which include dependency on motion-free scans, manual segmentation, and inaccurate thick-slice interpolation.
Keywords: Fetal MRI, Brain volumetry, Image reconstruction, Segmentation
Introduction
Background
In-vivo fetal imaging techniques such as ultrasonography and magnetic resonance imaging (MRI) are of paramount importance in evaluating and determining the development of the fetus. Biometric normative values for gestational age (GA) have been established in-vitro by evaluation of fixed brains, and also through measuring large cohorts of same-age fetuses using ultrasonography. Fetal MRI is a relatively newer modality, utilized in the evaluation of high-risk pregnancies in which there is concern for anomalies based on identified risks, such as advanced maternal age, family history, maternal exposures, and anomalies detected by routine prenatal ultrasound.
MRI has been useful in evaluating abnormalities of fetal structures which are difficult to thoroughly assess by prenatal sonography alone, such as those involving the fetal brain, chest, and airway [1–4]. MRI does not involve ionizing radiation, has no known adverse effects on either the pregnant patient or the fetus, and has many advantages over sonography, including that it is less limited by decreased amniotic fluid, maternal obesity, or difficult fetal position.
Fetal cerebral biometry mainly involves length measures which are assessed by obstetric imagers on two-dimensional views. The most commonly obtained measures of fetal brain size include cerebral and skull biparietal diameter (BPD), occipitofrontal diameter (OFD), and head circumference (HC). Transverse cerebellar diameter, vermian depth and height, corpus callosal length, and the size and distance between orbits are also frequently measured [5]. Normative biometric values have been obtained through assessments of very large cohorts of fetal sonographic images. Reference biometric values for the fetal brain have been recently obtained based on large sets of MRI images of 589 fetuses [6].
The advanced imaging technologies beyond 2D sonography, i.e. 3D ultrasound and MRI, lead to more illustrative biometric measures based on the volume and shape of fetal organs and structures. Fetal brain volumetry is considered to be crucial in the evaluation of fetal development [7].
Related work
Many articles have addressed fetal brain volumetry using both MRI and 3D ultrasound [7–16], but little progress has been made in the computation methods used. Most techniques rely on the (modified) Cavalieri method of unbiased volume estimation. On the basis of the Cavalieri principle, an unbiased estimation of the mean total volume of an arbitrary-shaped object can be obtained from the areas on systematic-uniform-random slices (sections). Several methods exist for estimation of the areas of slices, but the most efficient method is considered to be point-counting.
Early MRI-based volumetry methods [10,11] relied on slices as thick as 10 mm which induce too great a measurement error for very small fetal brain sizes (e.g. 50th percentile normal cerebral BPD is 80 mm for a 35 week GA fetus). Similar volumetry techniques based on ultrasonography [7,13] also rely on manual tracing and measurement of the area of 8–10 serial coronal cuts. In these studies, the fetal brain volume is estimated by automatically adding vertical cylindrical slices in between the cuts which resembles a linear interpolation between thick-slice sections. In another investigation based on ultrasound [16], a spherical shape was assumed for fetal head and the estimated volumes were compared to published postmortem data on fetal brain weight matched for GA and the specific gravity of the brain. An estimation factor was hence obtained for brain volumetry.
In other studies [8,12], brain volumetry was performed by selecting the best original single-shot fast spin echo (SSFSE) MRI scans obtained during a single scanning session. Volume calculation was performed in these studies through dedicated software, but again, the computation was based on MRI scans of 4–5 mm slice thickness and use of manual tracing. Volumetry was performed for ten fetuses in [12] and for fifty fetuses of 17–37 weeks GA in [8]. The length of the time required to perform manual tracings has been identified as an important limitation [8].
Purpose
Three critical limitations exist in fetal brain MRI volumetry techniques; first, fetal and maternal motion may significantly degrade the MRI scans and their suitability for volumetry calculation. Although high-quality slices are normally obtained by SSFSE due to short slice acquisition time, severe inter-slice motion-induced differences frequently appear in out-of-plane views. Therefore, the acquired SSFSE scans can rarely be resampled and translated to acceptable volumetric images. Second, thick slices (normally 3–5 mm) are acquired in fetal MRI in order to maintain a high signal-to-noise ratio. This limitation results in considerable approximation errors in resampling and volumetry, specifically when examining tiny sized fetal structures. Third, manually tracing and segmenting fetal brain structures is tedious and time-consuming, significantly reducing interest in the routine use of fetal brain volumetry.
In order to address the limitations of fetal brain MRI volumetry techniques, we have developed an image processing pipeline based on inter-slice motion correction, super-resolution volume reconstruction, intensity non-uniformity correction and supervised segmentation. Our method relies on a recently developed technique for super-resolution volume reconstruction from slice acquisitions [17,18]. The developed technique provides high-resolution volumetric images which represent coherent anatomic boundaries that are not apparent in original SSFSE scans. Therefore, the reconstructed volumetric images allowed us to develop supervised image segmentation techniques in order to improve the accuracy and ease of obtaining precise fetal brain volumetry. In the three sections that follow, the methods are described, experiments and results are reported, and the broad applications, limitations, and possible improvements are discussed.
Methods
Fetal brain MRI involves multiple single-shot fast spin echo (SSFSE) image acquisitions in the orthogonal views of the fetus [19–21] which normally provide high-resolution and high-quality slices in the presence of intermittent fetal and maternal motion. However, due to thick-slice acquisitions and inter-slice motion, these images do not reflect the anatomic details and coherent tissue boundaries in the three-dimensional views thus cannot be effectively used for tissue segmentation and precise brain volumetry. In this section, we present a description of our image processing pipeline based on motion correction, super-resolution volume reconstruction, and supervised brain tissue segmentation which allows accurate fetal brain volumetry.
Volume reconstruction
There have been a few recent studies addressing high-resolution volumetric image reconstruction from multiple multislice MRI scans [22–24]. These techniques rely on inter-slice motion correction and scattered data interpolation (SDI) for volumetric image reconstruction. There are technical differences between these techniques based on motion correction approaches and the SDI methods used [22–24]. Nevertheless, these techniques do not provide an appropriate mathematical formulation to justify that the reconstructed volume is a minimum error representation of the underlying anatomy given the acquired thick-slice scans.
In our recent work on super-resolution volume reconstruction from slice acquisitions [17,18], we developed a mathematical framework for error minimization based on a slice acquisition model. This approach considers a physical model for the SSFSE scans as stacks of thick slices oriented in the three-dimensional space.
The slice acquisition model is a forward model, which describes how the acquired slices are obtained from the imaged object during the MRI slice acquisition procedure. Figure 1 depicts a simple diagram of the slice acquisition model. This model incorporates motion of the imaged object in three-dimensional space and the MRI slice acquisition process which involves slice selection, signal acquisition, quantization and sampling. The output is a digital representation of a thick slice of the imaged object.
Fig. 1.

Block diagram of the slice acquisition model used in volume reconstruction; this model incorporates motion of the object in the three-dimensional space, slice selection profile, signal acquisition, and sampling
In the super-resolution volume reconstruction formulation, a discrete version of this model is considered in which the input is a desired high-resolution volumetric representation of the imaged object. The input and output images are represented by vectors of the image voxels in the lexicographical order. All the image operators between the input and the output can be modeled as matrix operations, thus a linear model representation is achieved. The super-resolution volume reconstruction is thus defined as the inverse problem of finding the desired high-resolution representation of the imaged object given a sufficient number of acquired slice scans. The formulation and solution of this linear inverse problem is thoroughly discussed in [17] and [18].
It is worth noting that relatively accurate models can be obtained for the blocks associated with the MRI signal acquisition process (i.e. slice selection, signal acquisition, and sampling). This is achieved through the physics of MRI. On the other hand, the motion of the object cannot be physically modeled and should be estimated. The motion estimation and volume reconstruction problems are considered to be separable, thus it is assumed in solving the volume reconstruction problem that the motion is accurately estimated. This assumption may not be always correct. We will briefly discuss about the motion estimation and its incorporation in the volume reconstruction algorithm in the section that follows.
Slice motion estimation and scattered data interpolation
Slice motion estimation in fetal MRI is quite difficult. We utilize a slice-to-volume registration technique discussed in [17] and [18]. This technique is similar to the techniques used in [22] and [23]; however, there are implementation differences based on the cost functions used and the optimization techniques. In slice-to-volume registration, the motion parameters of each slice are computed by registering that slice to a reference volume. For each slice, a 6 degree-of-freedom three-dimensional rigid transformation is computed by minimizing the mean square intensity differences (MSD) between that slice and the reference volume. Nevertheless, a high-resolution reference volume is not available for this purpose. Therefore, an approximation of the reconstructed volumetric image is used as the reference for registration. This approximation is initially computed as the average of the resampled SSFSE scans and is improved through iterations of slice motion estimation and super-resolution volume reconstruction. The iterative algorithm is illustrated in Fig. 2.
Fig. 2.

Block diagram of the developed motion correction and super-resolution volume reconstruction algorithm; TC represents the termination condition, which is based on the change in average slice-to-volume registration metrics. When the change in average metric goes below a threshold, the algorithm is terminated
After slice-to-volume registration, the slice image voxels will not be on a regular grid and are considered as scattered data points in the three-dimensional space. Scattered data interpolation (SDI) is required to obtain a first estimation of the reconstructed volume image from this data. The SDI approach utilized here is based on local intensity injection through Gaussian kernels. The scattered data points obtained from motion-corrected slices are mapped to their nearest neighbor grid points in the reconstructed image space, and their intensity values are injected into the neighborhood points through Gaussian kernel weights. This initial estimate of the reconstructed volume is refined through maximum likelihood super-resolution volume reconstruction developed and discussed in [18]. We refer to this entire iterative reconstruction algorithm as ML-SVR here, for maximum likelihood super-resolution volume reconstruction.
Intensity non-uniformity correction
The correction of intensity non-uniformity is crucial prior to automated image segmentation. The intensity non-uniformity artifacts can be severe in fetal images due to weak signal, fetal positioning, cardiac coil placement, and magnetic field bias. We use the fully automatic entropy minimization approach of Mangin for estimating a smooth multiplicative field for intensity non-uniformity correction [25]. The idea is to find the parameters of a regular grid of points with cubic Spline interpolation as a smooth model of the correction field (Fc). The optimal correcting field is defined as the global minimum of a multiterm cost function:
| (1) |
where X is the reconstructed volumetric image, H (Fc X) is the entropy of the corrected image, R (Fc) is a regularization function which measures the field smoothness, and M (Fc X) is a quadratic measure of the distance between the reconstructed volume and the corrected volume. The weighting constants are set as KH = 1, KR = 0.01, and KM = 0.5, and the grid point spacing was set between 32 and 64 mm in our experiments depending on the size of the image and the intensity distortions. We refer to [25] and [26] for the details of the algorithm and implementation.
Segmentation
Segmentation of fetal MRI images is very challenging due to low resolution, low signal contrast, the differences in developing brain tissue types, and motion and intensity non-uniformity artifacts. Therefore, most of the studies on fetal brain volumetry rely on manual tracings for segmentation of original thick-slice SSFSE scans. The super-resolution reconstruction of high-resolution volumetric images discussed earlier allows us to use automated segmentation algorithms more effectively. Since our goal is brain volumetry, we focus on the segmentation of brain tissue and cerebrospinal fluid (CSF). Bone structures such as skull are hypointense and the CSF is hyperintense on T2-weighted fetal MRI images, so if the motion artifacts and intensity non-uniformity are effectively corrected by the algorithms discussed in the previous sections, automated segmentation is feasible.
Nevertheless, due to the complexity and high variability of the developing brain tissue and the differences in contrast due to clinical imaging parameters and the positioning of the fetal brain, it is difficult to establish a set of parameters for automated segmentation of fetal brains for all gestational ages.
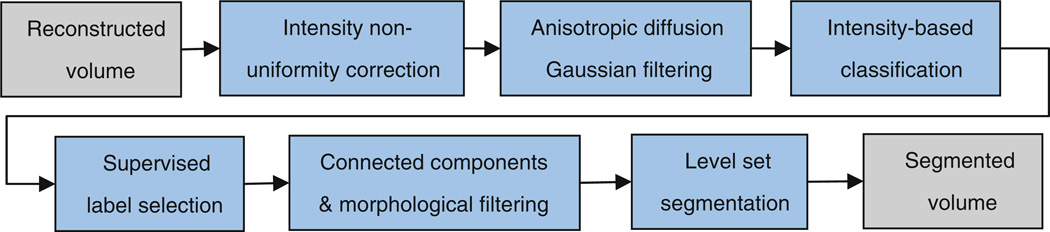
In order to eliminate manual tracing, we developed a supervised automated segmentation algorithm which involves sequential application of intensity-based classification, connected components labeling, morphological filtering, and geodesic active contours level set segmentation. We use the implementation of these components in ITK [27]. An algorithmic overview is shown in Fig. 3. The segmentation is interactively initialized, and no manual tracing is needed. Prior to intensity-based classification, the intensity non-uniformity corrected volumetric image (Xc) is passed through anisotropic diffusion Gaussian filtering for edge-preserving noise reduction.
Fig. 3.
Block diagram of the post-processing and segmentation algorithm for brain volumetry
The first step in segmentation is an intensity-based classification based on multiple Otsu’s histogram thresholding method. This method provides image intensity thresholds that maximize the between-class variances for multiple intensity-based classifications. We use a fast multiple thresholding implementation of this method based on [28]. In order to effectively classify the developing brain tissue types such as gray matter, myelinated and unmyelinated white matter, germinal matrix, CSF, skull, scalp, etc., we use ten intensity thresholds in this stage. However, due to the variability of tissue-type contrast and the lack of references for different gestational ages, these class labels cannot be automatically mapped to the tissue types. Therefore, in this stage the user supervises the results and chooses the labels that represent the brain tissue. This is a simple task that can be done quickly by a trained user.
The desired labels are then passed to the connected components algorithm. In this stage, unique labels are assigned to connected structures in the image based on run length encoding along raster lines. Partial voluming is normally problematic in intensity-based segmentation; therefore, we use morphological operations for eliminating the effects of partial voluming. In specific, a thin layer in the boundary of CSF (hyperintensity) and skull (hypointensity) is often mis-classified as brain parenchyma due on its average intensity value due to partial voluming. This layer is filtered by a morphological erosion operation of one voxel radius size on the outer boundary of CSF.
After connected components and morphological filtering we have approximate connected intensity-based segmentation of different structures of interest. For brain volumetry, two main classes are extracted; CSF and the brain parenchyma which mainly includes white matter, gray matter, and germinal matrix. Although our segmentation method allows the exact computation of CSF and parenchymal volumes separately, the brain volume has in past practice been computed as the volume enclosed by brain parenchyma, including the ventricles. The union of segmented ventricular CSF component and the brain parenchyma undergoes a morphological closing operation (radius of 3 voxels) to achieve a connected brain volume mask.
The final stage in our segmentation algorithm is based on geodesic active contours level set segmentation and is used to refine the segmentation from the previous stages. The reader is referred to [29,30] and [31] for detailed description of the level set image segmentation techniques. The idea is to formulate the boundary of the segmentation as a moving surface starting from an initial contour and propagating through the image based on a speed function (S). The initial contour is defined by the labeled voxels obtained from the previous stages of segmentation. The problem is then formulated by the time evolution of a level set function (ϕ) which is a function of position of the points on the contour (x) and time (t):
| (2) |
The zero level set of this evolving function is always identified with the propagating surface.
The definition of the speed function is very important. The speed of propagation should be slow in the edge regions of the image structures and fast inside the structures with uniform intensity values. In the geodesic active contours, the speed function is simply defined as the edge potential map of the image, which has values close to zero in regions near the edges and values close to one inside the structures. The edge potential map is computed from the image gradient obtained from a derivative of Gaussian operator (∇ * G):
| (3) |
We use an implementation of the fast sparse field level set method developed by Whitaker [32] in ITK [27]. This method performs calculations and updates only in a neighborhood of the zero level set and is quite fast and efficient.
Results
Fetal MRI data
Fetal MRI data were obtained from clinical MRI of patients with diagnosed or suspected cases of fetal anomalies after diagnostic ultrasonography. Clinical fetal MRI was performed using a 1.5-T TwinSpeed Signa system (GE healthcare) and an 8-channel phased-array cardiac coil, without maternal sedation or breath-hold, with the mother in left decubitus position to minimize caval compression. The protocol involved multiple acquisitions in the fetal sagittal, axial and coronal views using half-Fourier acquisition single-shot fast spin echo (SSFSE) magnetic resonance imaging with TR varying between 1,000 and 4,500 ms; TE varying between 80 and 100 ms; variable field of view based on the maternal and fetal body size (between 24 and 40 cm); variable matrix size between 160 and 512; and slice thickness of 3 or 4 mm. Clinical fetal MRI at our institution involves SSFSE scans with different TR and TE values which result in different image contrasts. For the experiments in this study we only use sets of SSFSE scans with the same contrast.
T2-weighted SSFSE is particularly useful in studying brain structure and structural abnormalities as it provides very high in-plane resolution and appropriate contrast for the developing brain in-utero [19,20]. Motion of the fetus does not frequently affect the in-plane slice quality and resolution of SSFSE, but severe inter-slice motion artifacts pose major limitations for the reconstruction of volumetric images from these images. Twenty-five datasets (cases) were obtained from the database. The age range of these fetuses was between 19.28 and 38.43 weeks (mean 28.03, stdev 6.55). Each dataset of the original images consisted of 3–11 (mean 5.88, stdev 2.22) SSFSE scans in fetal sagittal, coronal or axial planes. Table 1 shows the main parameters of these datasets for reconstruction and analysis in this study. These parameters include the gestational age (GA) of the fetus, number of input scans (N), number of slices (n), and finally slice thickness (Δsk) and matrix resolution (Δρ) in millimeters.
Table 1.
The main parameters of the fetal MRI cases considered in this study and the computed parenchymal volumes (PV) and brain volumes (BV)
| GA | N | n | Δsk (mm) | Δp (mm) | |
|---|---|---|---|---|---|
| C1 | 31w3d | 6 | 93 | 5 | 0.78 |
| C2 | 33w2d | 4 | 96 | 4 | 0.7 |
| C3 | 20w6d | 11 | 161 | 4–5 | 0.7 |
| C4 | 27w6d | 9 | 219 | 4 | 0.7 |
| C5 | 31w5d | 8 | 196 | 4 | 0.78 |
| C6 | 19w2d | 5 | 103 | 3 | 0.7 |
| C7 | 19w2d | 5 | 124 | 3 | 0.7 |
| C8 | 24w0d | 3 | 79 | 3 | 0.7 |
| C9 | 35w3d | 6 | 208 | 3 | 0.78 |
| C10 | 29w3d | 3 | 91 | 5 | 0.78 |
| C11 | 36w2d | 4 | 60 | 6 | 0.8 |
| C12 | 19w3d | 5 | 101 | 3 | 0.63 |
| C13 | 27w1d | 4 | 112 | 3 | 0.63 |
| C14 | 35w0d | 7 | 134 | 3–5 | 0.7 |
| C15 | 19w6d | 11 | 158 | 4 | 0.78 |
| C16 | 36w2d | 6 | 218 | 3 | 0.8 |
| C17 | 38w3d | 4 | 73 | 4 | 0.78 |
| C18 | 21w6d | 6 | 86 | 4 | 0.59 |
| C19 | 19w3d | 4 | 107 | 3–4 | 0.78 |
| C20 | 30w5d | 4 | 58 | 5 | 0.78 |
| C21 | 28w1d | 9 | 102 | 3 | 0.63–0.7 |
| C22 | 21w2d | 6 | 109 | 5 | 0.78 |
| C23 | 33w3d | 6 | 93 | 5 | 0.78 |
| C24 | 35w6d | 5 | 120 | 4 | 0.8 |
| C25 | 25w0d | 6 | 125 | 3 | 0.8 |
| Mean | 28.03 | 5.88 | 121.0 | 3.92 | 0.74 |
| Stdev | 6.55 | 2.22 | 47.0 | 0.87 | 0.06 |
Fetal brain volume reconstruction and segmentation
For the 25 fetal MRI cases shown in Table 1, we reconstructed volumetric images with uniform spatial resolution of 0.7–0.8 mm depending on the matrix resolution in the original scans. Figure 4 shows the reconstruction of images for one of the cases (C4). The rows show slices of three orthogonal views, i.e. axial, coronal, and sagittal views. The first three columns show three original SSFSE scans acquired in the axial, coronal, and sagittal planes; Fig. 4d shows the initial estimation of the reconstructed volume based on averaging the SSFSE scans. This estimation was used as the target for slice-to-volume registration in the first iteration of the algorithm; Fig. 4e shows the reconstructed volume after 10 iterations of slice-to-volume registration and reconstruction (ML-SVR algorithm). This volumetric image has a uniform spatial resolution of 0.8 mm and clearly reflects the underlying continuity of tissue boundaries in all three planes. Note that due to the effect of inter-slice motion, thick slice acquisitions, and partial voluming, the original SSFSE scans as well as the initial reconstructed image do not present coherent tissue boundaries, thus cannot be effectively used for tissue segmentation and brain volumetry.
Fig. 4.
Slices of a 27.86 week GA fetus (case C4): axial, coronal, and sagittal views of the acquired a axial, b coronal, c sagittal SSFSE scans; d the initial estimation of a volumetric image by averaging the original SSFSE scans, and e the reconstructed volume after iterations of slice-to-volume registration and super-resolution reconstruction (the ML-SVR technique). a–c Only good representatives of the anatomy in the slice plane views. The volumetric image in (e) is high-resolution in all plane views, is more accurate and much sharper than (d), and presents coherent tissue boundaries in all three planes. Due to the discontinuity of tissue boundaries, the images in (a–d) are not appropriate for automated segmentation or brain volumetry. On the other hand, the reconstructed volume in (e) clearly shows the brain structure and can be used for automated segmentation and brain volumetry
For quantitative evaluation of the performance of volume reconstruction technique, we computed the average root mean square differences (RMSD) of the intensity values between the motion-corrected slices and the reconstructed volumes. It was observed that RMSD reduced during iterations of motion correction and volume reconstruction. Lower RMSD values indicate better slice-to-volume registration (motion correction), which in turn indicate that better reconstructed volumetric images were used as target (reference) for registration. For each fetal MRI experiment, we normalized the RMSD values of the final iteration with respect to the RMSD values in the first iteration. It was observed that RMSD decreased in all 25 cases, and the average of normalized values over all cases was 0.86 ± 0.08 (when compared to 1 for the first iterations).
In addition to RMSD, we computed two image sharpness measures, i.e. the intensity variance measure (M1) and the energy of image gradient measure (M2) for the reconstructed volumes [18]. Both measures are monotonic and robust to noise [33]. We compared these measures for the volumetric images obtained from the volume reconstruction algorithm (ML-SVR) and the averaging of the resampled SSFSE scans, referred to as AVE here. The values of the sharpness measures were normalized for each case with respect to the values obtained for the reconstructed volumes obtained from AVE. It was observed that except for one case for each sharpness measure, the measures were always higher for the volumes reconstructed using ML-SVR. The average of normalized values over all cases was 1.09 ± 0.06 for M1 and 1.33 ± 0.21 for M2. This strongly suggests that sharper images were obtained using the ML-SVR technique which in turn indicates that the motion artifacts were effectively corrected during the iterations of slice-to-volume registration and volume reconstruction.
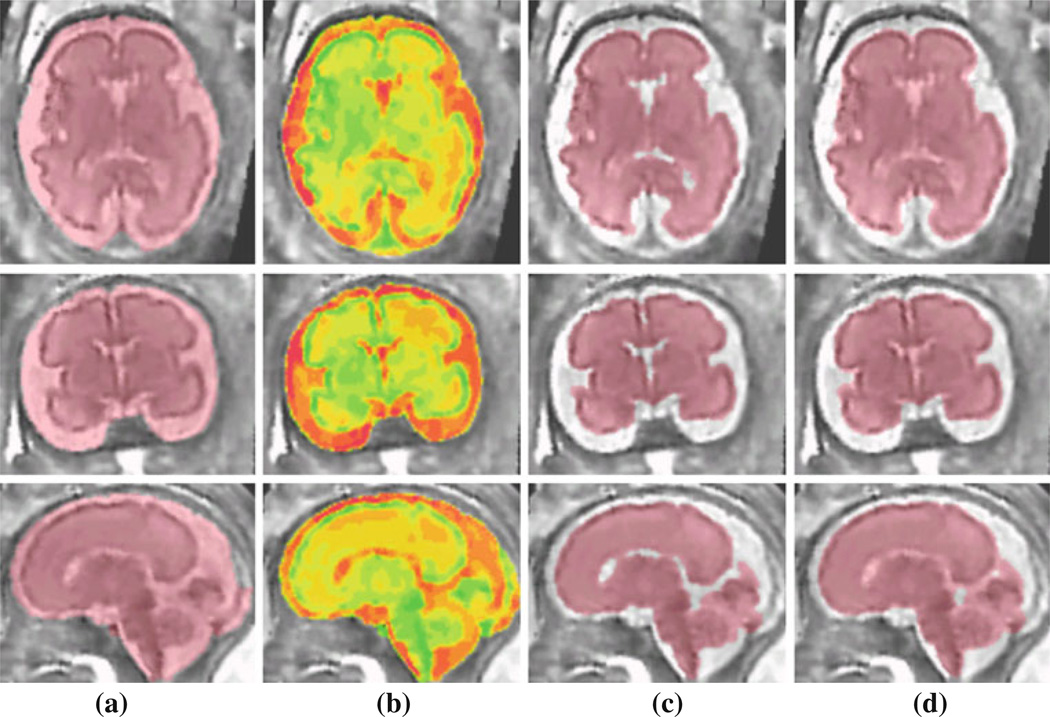
The reconstructed volumetric fetal MRI images were processed by intensity non-uniformity correction and segmentation algorithms discussed in this article. Figure 5 shows different stages of segmentation to achieve brain volumetry. These stages involve intracranial segmentation, tissue classification using multiple intensity-based thresholding, brain parenchyma segmentation based on the tissue classifications using connected components algorithm, morphological filtering, and level set segmentation, and finally brain volume segmentation by adding parenchymal and ventricular volumes processed with morphological filtering (closing operation) and connected components algorithm. The brain volume is segmented with this procedure because in practice the brain volume is computed as the volume enclosed by brain parenchyma including the ventricles. This is shown in Fig. 5d.
Fig. 5.
Segmentation of a fetal brain MRI: a intracranial mask, b tissue classification using multiple threshold intensity-based segmentation; c segmentation of brain parenchyma and cerebro-spinal fluid (CSF) based on tissue classification, connected components algorithm, morphological filtering, and level set segmentation; and d brain volume segmentation for fetal brain volumetry obtained by adding parenchymal and ventricular volumes and applying morphological closing operation and connected components algorithm on (c)
In order to quantitatively assess the accuracy of the supervised segmentation algorithm, we generated manual segmentations of brain parenchyma and brain volume for five randomly chosen fetal brain MRI cases, i.e. cases C3, C6, C11, C13, and C16. Manual segmentation was precisely performed on high-resolution reconstructed volumetric images and was used as the reference for evaluation. We computed the Dice index and the sensitivity and specificity measures for these cases. These measures are shown in Table 2. The results indicate that the supervised segmentation algorithm is accurate and eliminates the need for tedious manual segmentations. In the next section, we will compare the brain volumetry results based on the automated and manual segmentations for these cases.
Table 2.
Quantitative evaluation of fetal brain segmentation algorithm based on manual segmentations of high-resolution reconstructed fetal brain volumetric images for five randomly chosen fetuses from the database
| C3 | C6 | C11 | C13 | C16 | |
|---|---|---|---|---|---|
| Dice | 0.9328 | 0.9206 | 0.9480 | 0.9575 | 0.9700 |
| Sensitivity | 0.9498 | 0.9444 | 0.9205 | 0.9594 | 0.9943 |
| Specificity | 0.9977 | 0.9948 | 0.9984 | 0.9953 | 0.9978 |
Dice index overlap measure and the sensitivity and specificity measures are used to assess the accuracy of brain segmentation with respect to the reference manual segmentations
Fetal brain volumetry
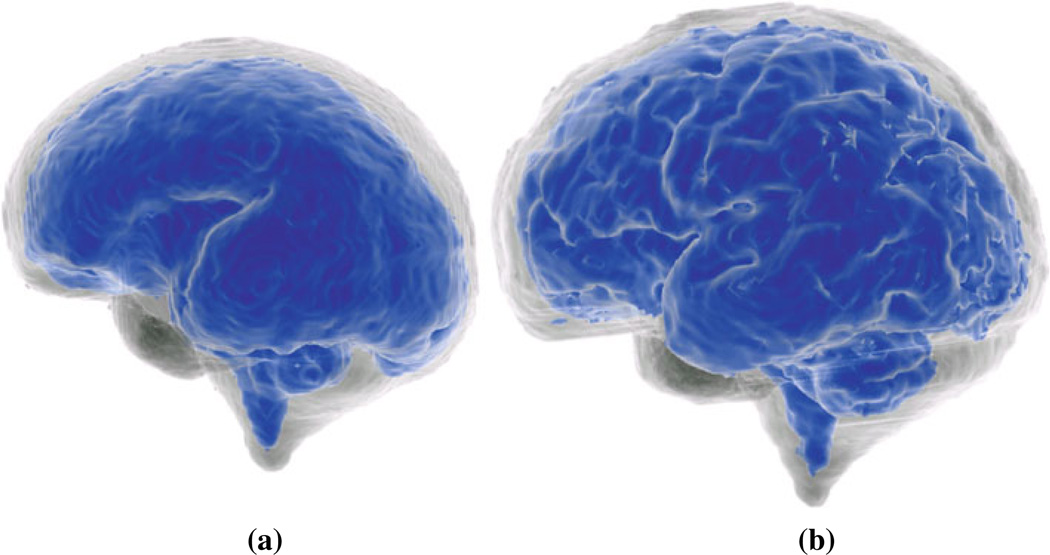
Once the intracranial mask, brain parenchyma, and brain volume segmentations are obtained for the fetuses, brain volumes are simply computed by counting the number of labeled voxels and multiplying to the voxel volumes in milliliters. It is also possible to generate triangular mesh surface model renderings of the cortex and the brain volumes. Figure 6 shows the surface model of the cortex (in blue) and the intra-cranial volume (brain and CSF) of two fetuses in 27.86 and 31.71 weeks GA.
Fig. 6.
Surface model rendering of the cortex (brain parenchyma in blue color) and the intracranial volume (brain and CSF) of a 27.86 week (a) and a 31.71 week fetus (b)
In Table 3, we have shown the computed parenchymal volumes (PV) and brain volumes (BV) based on supervised automated segmentation and the manual segmentations performed for the five fetuses discussed in the previous section. The percentage errors of PV and BV have also been reported in this table. Average of these percentage errors are 3.26 and 2.72% for PV and BV, respectively. These results indicate that brain volumetry based on the developed image reconstruction and segmentation algorithm is accurate and is more efficient than the previous methods based on manual tracing.
Table 3.
Quantitative evaluation of fetal brain parenchyma volumetry (PV) and brain volumetry (BV) based on manual segmentations of high-resolution reconstructed fetal brain volumes for five randomly chosen fetuses from the database
| C3 | C6 | C11 | C13 | C16 | |
|---|---|---|---|---|---|
| PV (estimated) ml | 52.42 | 37.16 | 365.74 | 126.87 | 307.49 |
| PV (manual) ml | 50.58 | 35.33 | 379.50 | 126.36 | 297.21 |
| PV (% error) | 3.65% | 5.17% | 3.62% | 0.40% | 3.46% |
| BV (estimated) ml | 79.01 | 39.14 | 416.96 | 137.96 | 325.50 |
| BV (manual) ml | 77.17 | 38.45 | 416.00 | 133.49 | 313.17 |
| BV (% error) | 2.33% | 1.76% | 0.23% | 3.25% | 3.79% |
The percentages of errors in PV and BV have been reported for automated volumetry as compared to the reference volumetry based on manual segmentation of the high-resolution reconstructed volumes
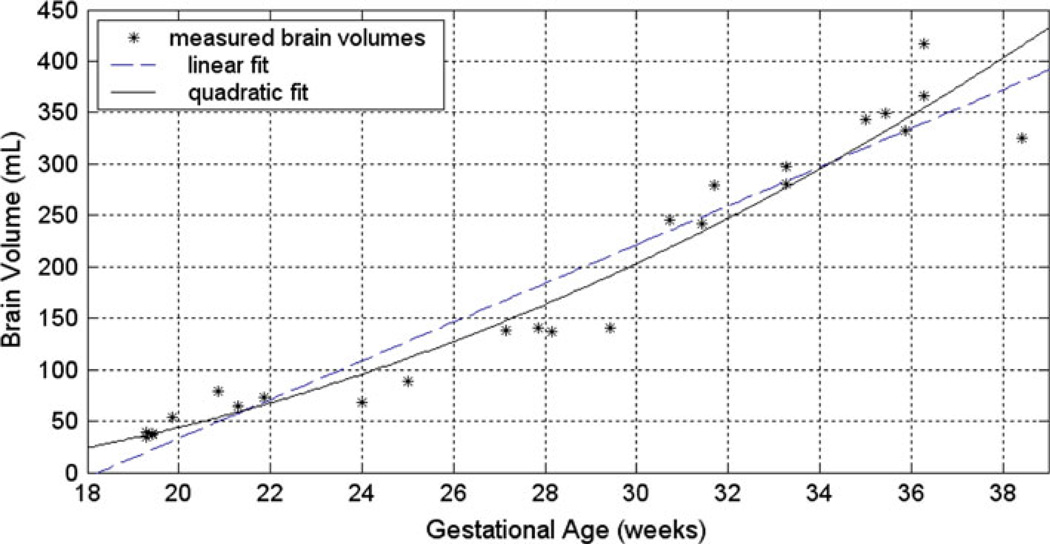
The brain volumes (BV) computed for the 25 fetuses in the database are shown versus the fetuses’ GA (in weeks) in Fig. 7. Linear and quadratic model fits have also been shown in this Figure. Similar analysis was done for intracranial volumes (ICV) and parenchyma volumes (PV). The coefficient of determination (r2), shown in Table 4, measures the goodness of fit of the linear, quadratic, and exponential models for this data. These measures indicate that a quadratic model best describes the ICV, PV, and BV changes versus GA. This supports the previous studies that suggest a quadratic relationship between the fetal brain volume and GA, i.e. [15].
Fig. 7.
Brain volumes measured (in ml) for fetuses in this study versus their GA (in weeks). Linear and quadratic fits have also been shown for this data. According to the goodness-of-fit measures, a quadratic model best describes the fetal brain volume changes versus gestational age
Table 4.
The coefficient of determination (r2) measures for linear, quadratic, and exponential model fittings to the volumetry data obtained for the 25 fetuses in this study
| r2 (ICV) | r2 (BV) | r2 (PV) | |
|---|---|---|---|
| Linear fit | 0.917 | 0.930 | 0.941 |
| Quadratic fit | 0.922 | 0.945 | 0.953 |
| Exponential fit | 0.818 | 0.826 | 0.833 |
The volumetry data involve intracranial volumes (ICV), brain volumes (BV), and parenchymal volumes (PV). This analysis indicates that a quadratic model best describes the fetal ICV, BV, and PV changes versus gestational age (GA)
Discussion
We have developed image reconstruction and segmentation algorithms that provide high-resolution volumetric images and models of fetal brain from thick-slice SSFSE scans. The developed super-resolution reconstruction algorithm is capable of correcting inter-slice motion artifacts if the slice in-plane quality is preserved. Normally the fetus does not move too fast during the entire scanning session; therefore, a set of good quality slices can be obtained for successful super-resolution reconstruction. By incorporating slices from multiple orthogonal scans in the reconstruction, the volumetric image space can be densely sampled thus leading to uniform image spacing of 0.7–1.0 mm which is much better than 3–5 mm slice thickness of the original SSFSE scans. Consequently, the super-resolution volume reconstruction algorithm effectively addresses two of the main limitations of brain volumetry techniques; i.e. the dependency on motion-free scans and the inaccuracies due to thick-slice approximations.
Another important limitation of the volumetry techniques is the need for manual tracing, which significantly reduces the interest in routine use and evaluation of volumetric measures. Manual tracing will be much more tedious if it should be done for accurate segmentation of a high-resolution volumetric image (70 slices with 0.7 mm spacing) instead of 8–10 cuts with 5mm slice thickness. The multistage supervised segmentation algorithm that we examined in this study eliminates the need for tedious manual tracing, and although it is done interactively based on label selection, the time and effort for segmentation are significantly reduced.
The downside of our technique is that it also depends on the quality of the input scans and the motion and intensity non-uniformity artifacts. If the range of fetal motion is larger than the capture range of the registration algorithm, or the number of good quality slices is not sufficient for effective sampling of the volumetric image space, the reconstruction algorithm may not perform well. The capture range of our slice-to-volume registration algorithm depends on several parameters including the quality of the estimated volumetric image used as registration target, as well as the image features which in turn depends on the GA of the fetus and the image contrast. In practice we do not expect the algorithm to capture and correct inter-slice motion of 8 mm or more. If motion artifacts remain in the reconstructed image or the intensity non-uniformity cannot be restored, the segmentation algorithm may fail and volumetry may not be accurate. However, it is expected that with better and faster imaging techniques fetal images of a better quality can be acquired which will lead to increases in the success rate of our algorithm.
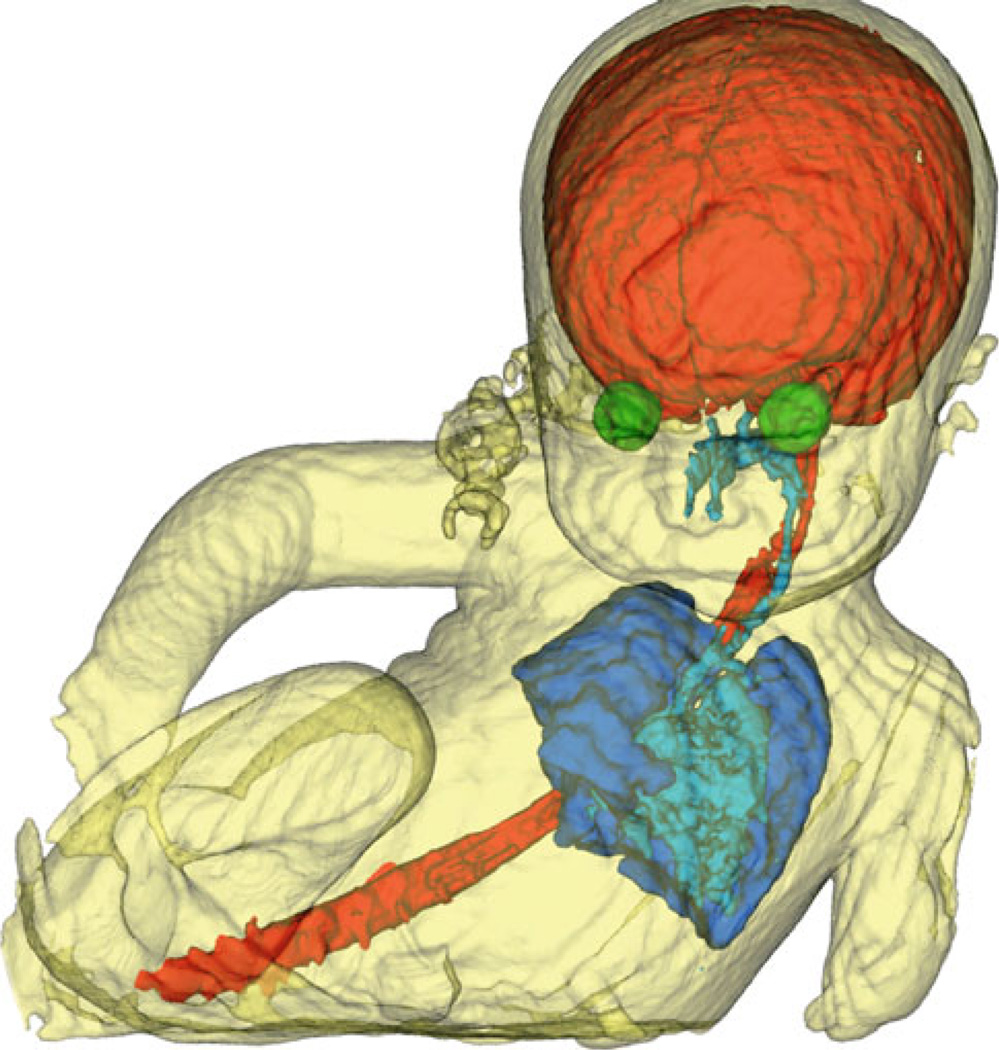
Finally, the developed techniques in this study can be applied to other fetal organs. Here we report a preliminary reconstruction, segmentation, and rendering experiment for a 33.28-week fetus which did not move at the time of acquisition. The fetal body has been extracted from uterus, and the brain (CSF), spinal cord, orbits, airways, and the lungs are also segmented and shown in Fig. 8. In addition to brain and organ volumetry, the image processing techniques developed here can be used for the evaluation and assessment of the shape and structure of fetal body and organs. An excellent quality view of the fetus face (nose and lips), as shown in Fig. 8, can also be used for evaluating craniofacial anomalies such as cleft lip and palate. The most critical issue for the reconstruction of the craniofacial structures and other fetal organs is the non-rigid nature of the motion in those regions. If the motion is negligible or if it can be estimated accurately, reconstruction, segmentation, and visualization will be feasible.
Fig. 8.
Three-dimensional surface model of a fetus body extracted by automated segmentation from uterus and amniotic fluid and rendered by marching cubes triangulation using VTK [27]. The fetal brain, spinal cord, orbits, airways, and lungs are also segmented and shown in this picture. Part of the umbilical cord can also be seen around baby’s neck. The parts which are not shown were not taken by MRI scans due to limited field of view
Acknowledgments
This research was supported in part by NIH grants R01 RR021885, R01GM074068, R01EB008015, and R43MH086984.
Contributor Information
Ali Gholipour, Email: ali.gholipour@childrens.harvard.edu.
Judy A. Estroff, Email: judy.estroff@childrens.harvard.edu.
Carol E. Barnewolt, Email: carol.barnewolt@childrens.harvard.edu.
Susan A. Connolly, Email: susan.connolly@childrens.harvard.edu.
Simon K. Warfield, Email: simon.warfield@childrens.harvard.edu.
References
- 1.Reddy UM, Filly RA, Copel JA. Prenatal imaging: ultra-sonography and magnetic resonance imaging. Obstet Gynecol. 2008;112(1):145–157. doi: 10.1097/01.AOG.0000318871.95090.d9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Coakley FV, Glenn OA, Qayyum A, Barkovich AJ, Goldstein R, Filly RA. Fetal MRI: a developing technique for the developing patient. AJR Am J Roentgenol. 2004;182(1):243–252. doi: 10.2214/ajr.182.1.1820243. [DOI] [PubMed] [Google Scholar]
- 3.Guibaud L. Contribution of fetal cerebral MRI for diagnosis of structural anomalies. Prenat Diagn. 2009;29(4):420–433. doi: 10.1002/pd.2171. [DOI] [PubMed] [Google Scholar]
- 4.Garel C. Imaging the fetus: when does MRI really help. Pediatr Radiol. 2008;3(38 Suppl):S467–S470. doi: 10.1007/s00247-008-0837-6. [DOI] [PubMed] [Google Scholar]
- 5.Garel C. Fetal cerebral biometry: normal parenchymal findings and ventricular size. Eur Radiol. 2005;15(4):809–813. doi: 10.1007/s00330-004-2610-z. [DOI] [PubMed] [Google Scholar]
- 6.Tilea B, Alberti C, Adamsbaum C, Armoogum P, Oury JF, Cabrol D, Sebag G, Kalifa G, Garel C. Cerebral biometry in fetal magnetic resonance imaging: new reference data. Ultrasound Obstet Gynecol. 2009;33(2):173–181. doi: 10.1002/uog.6276. [DOI] [PubMed] [Google Scholar]
- 7.Chang CH, Yu CH, Chang FM, Ko HC, Chen HY. The assessment of normal fetal brain volume by 3-D ultrasound. Ultrasound Med Biol. 2003;29(9):1267–1272. doi: 10.1016/s0301-5629(03)00989-x. [DOI] [PubMed] [Google Scholar]
- 8.Kazan-Tannus JF, Dialani V, Kataoka ML, Chiang G, Feldman HA, Brown JS, Levine D. MR volumetry of brain and CSF in fetuses referred for ventriculomegaly. AJR Am J Roentgenol. 2007;189(1):145–151. doi: 10.2214/AJR.07.2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Roberts N, Garden AS, Cruz-Orive LM, Whitehouse GH, Edwards RH. Estimation of fetal volume by magnetic resonance imaging and stereology. Br J Radiol. 1994;67(803):1067–1077. doi: 10.1259/0007-1285-67-803-1067. [DOI] [PubMed] [Google Scholar]
- 10.Baker PN, Johnson IR, Gowland PA, Hykin J, Adams V, Mansfield P, Worthington BS. Measurement of fetal liver, brain and placental volumes with echo-planar magnetic resonance imaging. Br J Obstet Gynaecol. 1995;102(1):35–39. doi: 10.1111/j.1471-0528.1995.tb09023.x. [DOI] [PubMed] [Google Scholar]
- 11.Gong QY, Roberts N, Garden AS, Whitehouse GH. Fetal and fetal brain volume estimation in the third trimester of human pregnancy using gradient echo MR imaging. Magn Reson Imaging. 1998;16(3):235–240. doi: 10.1016/s0730-725x(97)00281-6. [DOI] [PubMed] [Google Scholar]
- 12.Schierlitz L, Dumanli H, Robinson JN, Burrows PE, Schreyer AG, Kikinis R, Jolesz FA, Tempany CM. Three-dimensional magnetic resonance imaging of fetal brains. Lancet. 2001;357:1177–1178. doi: 10.1016/S0140-6736(00)04375-0. [DOI] [PubMed] [Google Scholar]
- 13.Endres LK, Cohen L. Reliability and validity of three-dimensional fetal brain volumes. J Ultrasound Med. 2001;20:1265–1269. doi: 10.7863/jum.2001.20.12.1265. [DOI] [PubMed] [Google Scholar]
- 14.Kinoshita Y, Okudera T, Tsuru E, Yokota A. Volumetric analysis of the germinal matrix and lateral ventricles performed using MR images of postmortem fetuses. AJNR Am J Neuroradiol. 2001;22(2):382–388. [PMC free article] [PubMed] [Google Scholar]
- 15.Roelfsema NM, Hop WC, Boito SM, Wladimiroff JW. Three-dimensional sonographic measurement of normal fetal brain volume during the second half of pregnancy. Am J Obstet Gynecol. 2004;190(1):275–280. doi: 10.1016/s0002-9378(03)00911-6. [DOI] [PubMed] [Google Scholar]
- 16.Boito S, Struijk PC, Ursem NT, Fedele L, Wladimiroff JW. Fetal brain/liver volume ratio and umbilical volume flow parameters relative to normal and abnormal human development. Ultrasound Obstet Gynecol. 2003;21(3):256–261. doi: 10.1002/uog.54. [DOI] [PubMed] [Google Scholar]
- 17.Gholipour A, Warfield SK. Super-resolution reconstruction of fetal brain MRI. In: C Studholme, F Rousseau., editors. MICCAI Workshop on Image Analysis for the Developing Brain (IADB’2009) London, UK: Sep 24, 2009. pp. 45–52. 2009 [Online]. Available: http://www.crl.med.harvard.edu/ publications/SR-Fetal-Brain-MRI-IADB-MICCAI2009.pdf. [Google Scholar]
- 18.Gholipour A, Estroff JA, Warfield SK. Robust super-resolution volume reconstruction from slice acquisitions: application to fetal brain MRI. IEEE Trans Med Imaging. 2010 doi: 10.1109/TMI.2010.2051680. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rousseau F, Glenn OA, Iordanova B, Rodriguez-Carranza C, Vigneron DB, Barkovich JA, Studholme C. Registration-based approach for reconstruction of high-resolution in utero fetal mr brain images. Acad Radiol. 2006;13(9):1072–1081. doi: 10.1016/j.acra.2006.05.003. [DOI] [PubMed] [Google Scholar]
- 20.Jiang S, Xue H, Glover A, Rutherford M, Rueckert D, Hajnal J. MRI of moving subjects using multislice snapshot images with volume reconstruction (SVR): application to fetal, neonatal, and adult brain studies. IEEE Trans Med Imaging. 2007;26(7):967–980. doi: 10.1109/TMI.2007.895456. [DOI] [PubMed] [Google Scholar]
- 21.Prayer D, Brugger PC, Prayer L. Fetal MRI: techniques and protocols. Pediatr Radiol. 2004;34:685–693. doi: 10.1007/s00247-004-1246-0. [DOI] [PubMed] [Google Scholar]
- 22.Lee S, Wolberg G, Shin S. Scattered data interpolation with multilevel b-splines. IEEE Trans Vis Comput Graph. 1997;3(3):228–244. [Google Scholar]
- 23.Kim K, Habas PA, Rousseau F, Glenn OA, Barkovich AJ, Stud-holme C. Intersection based motion correction of multislice MRI for 3D in utero fetal brain image formation. IEEE Trans Med Imag. 2010;29(1):146–158. doi: 10.1109/TMI.2009.2030679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Levine D, Barnes PD, Robertson RR, Wong G, Mehta TS. Fast MR imaging of fetal central nervous system abnormalities. Radiology. 2003;229:51–61. doi: 10.1148/radiol.2291020770. [DOI] [PubMed] [Google Scholar]
- 25.Mangin J. Entropy minimization for automatic correction of intensity nonuniformity. Proceedings of the of the IEEE workshop on mathematical methods in biomedical image analysis. 2000:162. [Google Scholar]
- 26. http://brainvisa.info/index.html.
- 27. http://itk.org/
- 28.Liao P, Chen T, Chung P. A fast algorithm for multilevel thresholding. J Inf Sci Eng. 2001;17(5):713–727. [Google Scholar]
- 29.Caselles V, Kimmel R, Sapiro G. Geodesic active contours. Int J Comput Vis. 1997;22(1):61–97. [Google Scholar]
- 30.Sethian JA. Level set methods and fast marching methods: evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science. Cambridge University Press; 1999. ISBN 0-521-64557-3. [Google Scholar]
- 31.Malladi R, Sethian JA, Vemuri BC. Shape modeling with front propagation: a level set approach. IEEE Trans Pattern Anal Mach Intell. 1995;17(2):158–175. [Google Scholar]
- 32.Whitaker RT. A level-set approach to 3D reconstruction from range data. Int J Comput Vis. 1998;29(3):203–231. [Google Scholar]
- 33.Subbarao M, Choi T, Nikzad A. Focusing techniques. J Opt Eng. 1992;32:2824–2836. [Google Scholar]