Abstract
We designed and tested a novel hybrid statistical model that accepts radiologic image features and clinical variables, and integrates this information in order to automatically predict abnormalities in chest computed-tomography (CT) scans and identify potentially important infectious disease biomarkers. In 200 patients, 160 with various pulmonary infections and 40 healthy controls, we extracted 34 clinical variables from laboratory tests and 25 textural features from CT images. From the CT scans, pleural effusion (PE), linear opacity (or thickening) (LT), tree-in-bud (TIB), pulmonary nodules, ground glass opacity (GGO), and consolidation abnormality patterns were analyzed and predicted through clinical, textural (imaging), or combined attributes. The presence and severity of each abnormality pattern was validated by visual analysis of the CT scans. The proposed biomarker identification system included two important steps: (i) a coarse identification of an abnormal imaging pattern by adaptively selected features (AmRMR), and (ii) a fine selection of the most important features from the previous step, and assigning them as biomarkers, depending on the prediction accuracy. Selected biomarkers were used to classify normal and abnormal patterns by using a boosted decision tree (BDT) classifier. For all abnormal imaging patterns, an average prediction accuracy of 76.15% was obtained. Experimental results demonstrated that our proposed biomarker identification approach is promising and may advance the data processing in clinical pulmonary infection research and diagnostic techniques.
Keywords: Infectious diseases, Parainfluenza, Pneumonias, NTM, Biomarker, Texture analysis, Lung CT, Feature extraction, AmRMR
1. Introduction
Radiologic interpretation predominantly comes in the form of qualitative reporting and semi-quantitative severity classifications, and clinicians must integrate cognitively with other clinical variables to assess patient care. Even though computational radiology techniques have advanced to yield more quantitative techniques, the use of statistical modeling to integrate quantified image data with clinical variables has lagged behind. Some imaging techniques are inherently quantifiable based on photon counts, like with position emission tomography (PET), while other imaging modalities require further image processing to arrive at quantified results, like with CT. For example, texture analysis – a longstanding approach in image processing for CT when quantifying an array of features – is used to derive a set of statistical characteristics using automatic computer-based platforms. However, mathematically modeling those quantified texture features to integrate with clinical variables is still under significant development and further investigation especially for some diseases other than cancers. Overall, optimized integration of clinical and imaging variables can be useful, especially when identifying biomarkers that have clinical predictive and diagnostic value.
Infectious disease is one particular area of clinical medicine that largely depends on qualitative radiologic interpretation, and it serves as a useful testing ground for systems biology techniques. It is evident by the worldwide disease burden from pulmonary infections that accelerated mathematical modeling of infectious disease is needed to improve clinical and public health response strategies. Because of the often rapid onset and progression of new infections in pandemics and epidemics, pulmonary infections such as swine-origin H1N1 influenza and tuberculosis (TB) can be life threatening [1]. As radiology serves as a primary diagnostic response for assessing pulmonary infections, abnormal radio-graphic imaging and/or symptoms are often the most important part of patient care, especially during diagnosis, monitoring progression, and response to therapy. In this context, CT is widely utilized and provides essential details about anatomic structures; however, a lack of more effective tools to diagnose pulmonary infections at an early stage and to differentiate particular diseases for an accurate therapy plan leads to moderate to high mortality rates. Biomarkers of a disease's existence could facilitate detection of a certain biological disease in populations of individuals with similar symptoms (i.e., infections, memory impairments, etc.) caused by different conditions. In this work, we aimed to identify predictive biomarkers exhibiting a high classification and detection accuracy for six abnormal lung patterns (i.e., linear opacity/thickening (LT), consolidation, tree-in-bud (TIB), pulmonary nodules, pleural effusion (PE), and ground glass opacity (GGO)). These patterns are commonly encountered in lung infections, but they are not exclusive of other lung diseases.
To understand what determines the biomarkers of infectious lung diseases, it is necessary to model the interaction between the pathogen and its host, usually taking the biology of the disease (i.e., clinical features) [2] into account. Recent advances in imaging technology make it possible to import observable quantities (i.e., textural features) into non-linear models of infectious disease [3]. In practice, a pulmonary infection diagnosis using the proposed biomarker identification model could eliminate additional diagnostic tests. However, in most prediction models reported in the literature [2,4–7], parameter estimation methods often lacked robustness – even though deterministic approaches were increasingly augmented with stochastic frameworks that were often important determinants of disease persistence. Likewise, in this study, we used the selection of a feature set based on a novel maximum mutual information based relevancy rule, inspired by the mRMR (max-relevance, min-redundancy) method [8]. By the proposed feature selection method (Adaptive mRMR or AmRMR in short), we ensure that (i) selected image textures or clinical features are relevant to a target class maximally, and (ii) redundant features have been eliminated – we adaptively controlled the degree of target class relevancy using intuitive correlation metrics.
In order to accomplish our aims, we investigated multiple textural features from CT scans and then extracted clinical features from laboratory tests as predictors of abnormality patterns. We also integrated the strength of predictable properties of certain imaging and specific clinical variables through cascaded boosting and decision tree classifiers. We concluded from our prediction model that some of the textural and clinical features may reflect on the underlying abnormal imaging patterns and may serve as biomarkers. Furthermore, we compared the performance of our proposed method to the recently proposed well-grounded MIC (maximal information coefficient) [9] method to show that our design is capable of finding synergistic associations between weakly correlated synergistic data accurately.
2. Materials and methods
2.1. Patients
Our study received approval from the Institutional Review Board (IRB) at the National Institute of Allergy and Infectious Disease (NIAID)at NIH. Retrospective cases of human parainfluenza (HPIV-1, HPIV-2, and HPIV-3), nontuberculous mycobacteria (NTM) (mycobacterium avium complex (MAC), M. abscessus, M. massiliense, M. intracellular), and fungal pneumonias (FPN) (primary cutaneous cryptococcosis (PCC), aspergillus, Fusarius) were collected from our institute. HPIV, NTM, and FPN cases were collected from May 2005 through July 2010, January 2006 through December 2010, and November 2008 through August 2011, respectively. Laboratory confirmed patients with HPIV (n=93), patients with NTM (n=32), patients with FPN (n=35), and control subjects (n=40) were selected for experiments. We classified the subjects with their particular infections if their subsequent laboratory information yielded infected cells. Patient inclusion criteria for this study was a positive test of growth from bronchoalveolar lavage (HPIV), nasopharyngeal washing (HPIV, fungus), or sputum processing (fungus, NTM). One hundred and fifty-six patients were selected for this study, and none of the patients were co-infected with a second pathogen. All selected patients and the control group had no history of malignancy or immune deficiency such as stem cell transplantation and/or the use of immunosuppressive medications. In addition, CT imaging findings (consolidations, nodules, ground glass opacities, tree-in-bud, linear opacity, and pleural effusion) were reported through a visual grading scheme (Table 1), by well-trained three radiologists (i.e., observer 1 and 2 are with more than 10 years of thoracic radiology experience, and observer 3 is with more than 3 years general radiology experience). Typical imaging findings from CT scans for infectious diseases are shown in Fig. 1. Table 2 shows the demographic characteristics of the subjects, the type, and the serotype of diseases.
Table 1.
Visual grading scheme. Scores are given to lung zones for which the left and the right lungs are divided into three zones for local analysis (see Fig. 2). Each zone has its own label indicating the existence of an abnormal imaging pattern for that particular zone.
| Visual scores | Percentage of the abnormality over zones |
Label for the presence of abnormality |
|---|---|---|
| 0 | Absence of abnormality | 0 |
| 1 | 0%–5% | 1 |
| 2 | 5%–25% | 1 |
| 3 | 25%–50% | 1 |
| 4 | 50%–75% | 1 |
| 5 | 75%–100% | 1 |
Fig. 1.
(a) Linear opacity/thickening (LT), (b) ground glass opacity (GGO), (c) tree-in-bud (TIB) patterns, (d) consolidation, (e) nodules and nodular structures, and (f) pleural effusion (PE).
Table 2.
Demographics, disease types and subtypes, and number of CT scan.
| Variable | Total | HPIV | NTM | FPN | Control |
|---|---|---|---|---|---|
| # of patients | 156 | 44 | 37 | 35 | 40 |
| Age range (year) | 7–73 | 11–73 | 11–78 | 7–73 | 22–65 |
| Median age ± SD (year) | 45 ± 716 | 58 ± 18 | 44 ± 18 | 41 ± 11 | |
| Gender | 68 women | 23 women | 31 women | 14 women | 18 women |
| 48 men | 21 men | 6 men | 21 men | 22 men | |
| HPIV-1 | 34 | 29% | – | – | – |
| HPIV-2 | 13 | 12% | – | – | – |
| HPIV-3 | 46 | 59% | – | – | – |
| MAC | 7 | – | 21.8% | – | – |
| M. abscessus | 21 | – | 65.6% | – | – |
| M. massiliense | 3 | – | 9.37% | – | – |
| M. intracellular | 1 | – | 3.12% | – | – |
| PCC | 21 | – | – | 60% | – |
| Aspergillus | 13 | – | – | 37.15% | – |
| Fusarium | 1 | – | – | 2.85% | – |
| # of CT scans | 205 | 93 | 37 | 35 | 40 |
2.2. CT acquisition and measurements of small airway diseases
All patients were imaged at our institution using a 32-detector row Siemens Definition, a 64-detector row Philips Brilliance, or a 320-detector row Toshiba Aquilion CT scanner. The chest CT studies were performed at end-inspiration with 1.0 or 2.0 collimation, obtained at 10 or 20 mm intervals from the base of the neck to upper abdomen [10,11]. The participating radiologists analyzed the disease by visual evaluation framework ( 1 for disease, 0 for normal) (Fig. 1 and Table 1) such that consensus score was obtained from observer 1 and observer 3, and an independent score was obtained from observer 2, who was blinded to the other scores. Note that in Fig. 2, the left and the right lungs are divided into three zones for local analysis, and each zone has its own label indicating the existence of an abnormal imaging pattern for that particular zone. These binary labels were used as a target class identifier. Visual scoring is often accepted as the gold standard for the evaluation, and it is usually reported with intra- and inter-observer agreements. Inter-observer agreement rates were found by Pearson correlation tests, and representative R values were found to be R2 = 0:625 (p=0.028), R2 = 0:86 (p < 0:001), and R2 = 0:89 (p < 0:001) for NTM, FPN, and HPIV, respectively.
Fig. 2.
Lungs are divided into three zones (left). Rough anatomical locations separating zones are shown in coronal (middle) and axial CT slices (right), respectively.
2.3. Extracting clinical features from laboratory tests and imaging features from CT scans
For each subject, we collected 34 clinical features from laboratory tests (Chem 20 panel and complete blood count (CBC)), as demonstrated in Table 3. A blood serum chemistry test was conducted for each subject, and specimen collection instructions were based on the NIH's test guide [12]. Note that apart from general tests (i.e., serum glucose and calcium levels), a liver and kidney function assessment, as well as electrolyte and protein levels, were also considered in the Chem 20 laboratory test. Patients received laboratory tests within 20 days of their CT scans (±10 days from CT scan date).
Table 3.
Physiological (clinical) features extracted from each subject.
| Physiological features | |
|---|---|
| 1 | ALANINEAMINOTRANSFERASE |
| 2 | ALBUMIN |
| 3 | ALKALINEPHOSPHATASE |
| 4 | ASPARTATEAMINOTRANSFERASE |
| 5 | BASOPHILABSOLUTE |
| 6 | BASOPHILS |
| 7 | CALCIUM |
| 8 | CHLORIDE |
| 9 | CREATINEKINASE |
| 10 | CREATININE |
| 11 | EOSINOPHILABSOLUTE |
| 12 | EOSINOPHILS |
| 13 | GLUCOSE |
| 14 | HCT |
| 15 | HGB |
| 16 | LACTATEDEHYDROGENASE |
| 17 | LYMPHOCYTEABSOLUTE |
| 18 | LYMPHOCYTES |
| 19 | MAGNESIUM |
| 20 | MCV |
| 21 | MONOCYTEABSOLUTE |
| 22 | MONOCYTES |
| 23 | NEUTROPHILABSOLUTE |
| 24 | NEUTROPHILS |
| 25 | PHOSPHORUS |
| 26 | PLATELET COUNT |
| 27 | POTASSIUM |
| 28 | RBC |
| 29 | RDW |
| 30 | SODIUM |
| 31 | TOTAL CO2 |
| 32 | UREANITROGEN |
| 33 | URICACID |
| 34 | WBC |
For imaging features, on the other hand, Table 4 shows texture features extracted from the segmented lung regions from CT scans. Further information on imaging features is available in the following subsection.
Table 4.
Texture features extracted from CT scans.
| Histogram based features |
Co-occurrence matrix based Run-length features features |
|
|---|---|---|
| Mean | Energy | Long run emphasis |
| Skewness | Inertia difference | Run length non-uniformity |
| Deviation | Correlation | Low grey-level run emphasis |
| Variance | Average difference | Short run low grey-level emphasis |
| Kurtosis | Entropy difference | Long run low grey-level emphasis |
| Inertia | Short run high grey-level emphasis | |
| Entropy | Long run high grey-level emphasis | |
| Average sum | Short run emphasis | |
| Run grey-level non-uniformity | ||
| Run percentage | ||
2.3.1. Image based features (texture)
Image segmentation is often the first step in computer assisted detection (CAD) systems. In this study, the fuzzy connectedness (FC) image segmentation algorithm was used to achieve a successful lung delineation [13]. The accuracy of the FC method for lung segmentation was tested using Dice similarity coefficient (DSC) (i.e., overlap ratio) based on two observers’ manual reference truths. Average DSC and inter-observer agreement were found to be 0:95%±0:11% and ≈98%, respectively. Mean distance between the borders drawn by two observers was 1.50 mm with a standard deviation of 1.28 mm and the median distance was 1.08 mm. Although we used the FC segmentation method for lung delineation, other lung segmentation methods could also be used for this purpose as long as abnormal patterns are included within lung masks. Once lungs were segmented, lung regions were subdivided into texture blocks, and the characteristic texture features were computed. The default texture block size was 16 × 16 pixels, but our software provides users the flexibility to change the block size if needed – 3D if data is of high resolution [11]. In addition, the feature vector extracted from each texture block was composed of 25 different texture features, including mean intensity and intensity variance features from histogram statistics, energy and correlation features from a co-occurrence matrix [14], and short- and long-run emphasis features from a run-length matrix [15]. Table 4 lists the 25 texture features computed for each texture block. Within that table, intensity mean is an average intensity among the blocks; intensity deviation measures the statistical variability of intensity among the pixels in the blocks; correlation reflects the spatial and intensity-based relationship of adjacent pixels; the average sum is the total number of correlated pixels pairs (with the same sum) in the texture block; the gray level non-uniformity is the orderliness or randomness of the pixel densities among the blocks, which can indicate the degree of structure; and the gray-level run length emphasis measures consecutive pixels of the same intensity along particular orientations, as another representation of structure [11].
2.4. Microbiologic sampling/analysis for characterization of infection
Patients receiving bronchoalveolar lavage (BAL) (HPIV and NTM patients) inhaled lidocaine to anesthetize the upper and lower lung passages. A bronchoscope was then passed into airways and advanced to an involved lung segment, where six 30 mL aliquots of sterile saline were instilled and suctioned into a sterile trap. Nasopharyngeal wash (NPW) (for HPIV patients only) was performed by instilling 7:5 mL of normal saline in each are while the patient leaned forward to allow fluid collection to go into a sterile specimen cup. Both BAL and NPW fluid were sent for microbiologic and cytologic analysis. Cultures of NPW and BAL for respiratory viruses were performed using the shell vial method with A549 cells and Madin-Darby Canine Kidney cells (R-Mix TooTM, Diagnostic Hybrids, Athens, OH). The D3 Ultra Respiratory Staining Kit (Diagnostic Hybrids, Athens, OH) allowed for identification of influenza A and B, respiratory syncytial virus, HPIV types 1,2, and 3, and adenovirus. Sputum was collected once a day for three consecutive days in 5 mL aliquots. The specimen with NaOH/NALC was decontaminated first, and then smears were prepared. After the smears were prepared, the specimen was plated to Middlebrook agar in MGITTM-PANTATM and incubated at 35 1C for six weeks.
2.5. Biomarker identification
Widely used biomarker identification methods, in general, typically rank features such as biological variables or DNA microarrays according to their differential expressions and classification performances and then pick the top-ranked features based on statistical parameters such as F-statistics or Spearman correlations [16]. However, we observed that this approach is not optimal when features are weak in identifying the target class (i.e., a particular imaging abnormality). Features are considered weak when they contain certain redundancies. Eliminating these redundancies by extracting more reliable features that capture broader characteristics of each imaging abnormality is a challenging task. This process is known as biomarker identification. As the clinical and imaging features pertaining to pulmonary infections are usually weak in identifying abnormal imaging patterns, correlations obtained by conventional statistical models are often limited in providing strong associations between features and the targeted classes. With that said, a feature selection method – finding the largest dependency on the target class – is necessary. For this purpose, inspired by the mRMR feature selection method, we proposed to use an adaptive version of mRMR (AmRMR) to selectively identify the most reliable features that contained minimal redundancies and maximal dependencies on the target class. Then, these adaptively determined features were fed into a boosted decision tree (BDT) classifier, where the Boosting algorithm [16] was used to combine many weak classifiers in order to achieve a final strong classifier. Although there have been many recent advances in medical imaging and radiology associating different data sources using machine learning algorithms, to the best of our knowledge, our study is the first attempt to find hidden associations between imaging and clinical features by identifying abnormal imaging patterns pertaining to pulmonary infections.
Fig. 3 illustrates the proposed methodology for the biomarker identification system. The system that we proposed in this study is based on a coarse-to-fine strategy and includes two main steps: (i) coarse selection: we selected the most discriminant features from imaging and clinical features globally by the AmRMR, and (ii) fine selection: we used the Boosting algorithm to refine the decision tree (DT) classifier output over the best individual feature (s) from the coarse selection in the previous step. Globally selected features were used to predict the presence of imaging abnormalities using our proposed method. When the prediction was positive (i.e., particular imaging abnormality existed), clinicians had access to the pre-determined biomarkers with descriptive ranges for the abnormal imaging patterns for a further evaluation.
Fig. 3.
Schematic drawing of the proposed methodology for marker/biomarker identification.
2.6. Adaptive mRMR (AmRMR) feature selection algorithm
Although more sophisticated regression models have been developed [17–20], the feature selection procedure in those models often relies on human intuition with trial-and-error or a distribution extracted from a small set of data points, so a lack of generalizability was inevitable [8]. Simply combining very effective features with other effective features does not always (in most cases) form better feature sets; therefore, a discriminative feature selection method is often required [8]. Indeed, discriminative feature selection is an active research area and widely used in bioinformatics applications for distinguishing cancer tissues from normal tissues or cancer subtypes from other subtypes [8,21,22]. And instead of using all of the available features/attributes, one might selectively choose a subset of features to be used in the prediction and classification. For this reason, we proposed to use AmRMR for the coarse and fine selection of features. Although in conventional mRMR [8], max-relevancy is an alternative criteria to the maximal dependency rule in which a feature set jointly has the largest dependency on the target class, the max-relevancy is usually tuned to an approximation of mean value for all of the mutual information values in pair-wise features and target class. However, in our particular case, we used normalized mutual information (NMI) [23] to reduce any bias of mutual information (MI) toward multi-valued attributes and restricted its value to a [0–1] interval. As we denoted relevance between the feature set S and the target class c, we reformulated the max-relevancy rule as argmax
| (1) |
| (2) |
| (3) |
where x denotes individual features spanning from 1 to m, and NMI between x and target class c is defined as
| (4) |
In this equation, H denotes entropy and MI is obtained typically as
| (5) |
where the joint probability density function (pdf) p(x,y) and marginal pdfs p(x) and p(y) were computed as in [8]. Basically, Eq. (1) reveals that each individual feature is required to have the largest NMI with the target class c. On the other hand, to identify redundant features, mRMR uses the following minimal redundancy condition:
| (6) |
| (7) |
Although this minimal redundancy approach is promising, we modified the minimal redundancy hypothesis with an alternative approach (i.e., adaptive) to reduce the cost of pair-wise computation and provide a statistically sound method. First, we computed correlations (Spearman) among feature sets and constructed a correlation matrix (x). Our motivation in using correlations [24] instead of using direct MI was because MI is built from joint and marginal pdfs of the variables that do not utilize statistics of any grade or order. However, in conventional Spearman or Pearson statistical relation tests, we have a ranking over the feature sets and their relations; therefore, one can select a threshold value to filter out considerably weak features from consideration (and thus, from computation). Second, we provided a thresholding parameter (τ), denoting a default correlation value larger than certain amount (i.e., | τ| > 0.3) to convert the correlation matrix (χ) into an indicator matrix χτ, which is sparse, namely, most of the elements of this matrix is zero based on the selection of the τ, and remaining ones are 1 (see Eq. (10)). Third, we computed NMI between variables if the corresponding value in the indicator matrix was not zero. Mean value of all calculated NMI values between individual features and class were used to define the adaptive minimal redundancy rule as follows:
| (8) |
| (9) |
where indicator sparse matrix (i.e., a matrix populated primarily with zeros) is obtained by thresholding its elements with τ as
| (10) |
Note that χ is defined as a symmetric correlation matrix having correlation coefficients among individual features in its elements (i, j), and it can be formulated as
| (11) |
AmRMR combines two criteria (the normalized mutual information difference criterion: MID, and the normalized mutual information quotient criterion: MIQ), based on the use of NMI and user selected threshold value τ such that
| (12) |
| (13) |
or
| (14) |
| (15) |
Selecting features through maximizing Eqs. (12) or (14) (MIQ or MID) reveals the most important features of the set. It will also reveal a hidden but an important relationship between the features, even if the correlation between those features are weak (i.e., weak features are considered as features having classification accuracy around 50% or less). We show this fact in the results section so that seemingly uncorrelated or weakly correlated features can be used jointly to identify certain abnormal patterns with the AmRMR feature selection procedure.
2.7. Boosted decision tree (BDT) classifier
Once AmRMR selected the clinical and imaging features for the first time (i.e., coarse selection), adaptively determined features were fed into the DT classifier, where the output indicated the presence of abnormal patterns. Because prediction abilities of the selected features were still weak, we used the conventional AdaBoosting algorithm, integrated into the weak DT classifiers to obtain a strong classifier. It is well known that “Boosting” is a general method for producing an accurate prediction rule by integrating rough and moderately inaccurate predictions [25], so for each step of the Boosting algorithm, we refined our classifier, and we selected the most powerful feature set again using the AmRMR method. This procedure continued until the final step of the Boosting procedure, where no significant increment was observed in the prediction accuracy of classifier. Finely selected features (i.e., determined in the last step of the Boosting procedure by AmRMR algorithm) were considered as a biomarker for the particular abnormal imaging pattern. Fig. 3 shows the interconnection of AmRMR and BDT schematically. Further information on BDT classifiers and Boosting methods can be found in [16,26–29].
2.8. Graphical network model for correlation analysis
As graphical models are powerful in representing multivariate probability distributions of features, we used graphical network models [30] to tackle complex relationships between imaging and clinical features with abnormal imaging patterns, determined by the BDT classifier and the AmRMR feature selection algorithm. Statistically significant associations among these features and target class (i.e., abnormal imaging patterns) were indicated by the connected line (i.e., edges). An adaptive feature selection algorithm was applied to features only having edges to target class.
2.9. Computational issues and statistical analysis tools
All data preprocessing, statistical model building, BDT classifier, AmRMR algorithm and statistical analysis were implemented in R (version 2.12.2) and Matlab (version R2010a) platforms. Computer aided measurements and analysis software, including segmentation of the lungs from CT scans, was written by using GNU gcc 4.5 (Copyright 2010 Free Software Foundation) on a Linux platform (Ubuntu).
2.10. Detecting associations among clinical and imaging data through maximal information coefficient (MIC) approach
MIC is a novel measure of dependence that captures linear and non-linear associations between a pair of variables [9]. MIC basically constructs a grid with various sizes and finds the largest mutual information obtained from the pairwise data. Nevertheless, MIC is not an estimate of mutual information, it is a rank order statistic that helps to define the underlying complexity of the data, and it can also be used in a feature selection and for ranking problems [31]. As I denotes the mutual information and G denotes the particular grid, MIC of a set D of pairwise data, with a sample size n and grid size less than B(n), is given by
| (16) |
where
| (17) |
and I*(D,x,y) = max I(D|G) for different distributions of grids G such that B(n) is the maximal grid size. For practical reasons, it is set to n0.6 (see [9] supplementary notes for details).
In addition, MIC has three key properties that were used to explore the non-linear properties of the data and to develop a feature selection procedure. These features are a maximum asymmetry score (MAS), a maximum edge value (MEV), and a minimum cell number (MCN). Given a finite set D of ordered pairs, one may partition the x-values of D into x bins and the y-values of D into y bins, allowing empty bins. Such a pair of partitions is called an x-by-y grid (i.e., each element of the grid is called a cell). MAS is a measure of non-monotonicity, and monotonic functions are those functions that follow a particular order; therefore, monotonic properties are very useful for differentiating individual functions. In general, non-monotonicity is not a desirable property due to a lack of consistency in the functional analysis. On the other hand, MEV is defined as being close to a function, and it measures the degree of which the data set appears to be sampled from a continuous function. MCN is known as a complexity measure that simply counts the number of cells required to reach the MIC score. Although well-defined and monotone functions require less number of cells, non-monotone and parametrically poorly defined functions require a large number of cells to reach MIC. MIC uses these three key components to explore non-linear associations among different data sources, where conventional correlation analysis falls short. Due to its powerful key properties and success in understanding the pairwise relationship of the data set, we compared the performance of MIC data exploration technique to our proposed method in the results section.
3. Results
Experimental results provided quantitative information about the nature of each disease's pathology by our proposed method, which synergistically combined imaging and clinical features and predicted the presence of abnormalities pertaining to infectious lung disease. BDT based classification indicated that combined biomarkers effectively predicted the existence of multiple imaging abnormalities with an average prediction accuracy of 76.15%. The most accurate predictions were obtained when AmRMR eliminated the most redundant features. See Fig. 4 for clinical, imaging, and combined feature selection and abnormality pattern prediction accuracy, respectively.
Fig. 4.
(a) Clinical, (b) imaging, and (c) combined features are used to predict abnormal imaging patterns pertaining to infected lungs. MID and MIQ feature selection of AmRMR were used and prediction accuracies were reported. “All variable” indicates that there was no feature selection step in prediction experiments. The number of total samples evaluated per group is the following: 37 subjects for linear thickening, 57 subjects for TIB, 77 subjects for GGO, 59 subjects for consolidations, 52 subjects for nodules, and 60 subjects for PE.
Highly correlated features for the specific types of abnormalities are shown in Fig. 5. Note that correlations are demonstrated in a network graph, where statistically significant and discriminative features are shown in highlight. For each abnormal pattern, the determined imaging and clinical biomarkers were explained in the following subsections in detail.
Fig. 5.
Determined biomarkers for the abnormal imaging patterns are shown. Blue and red represent imaging and clinical biomarkers, respectively. Significant correlations are shown with orange lines and corresponding Spearman R2 values. TIB: tree in bud, LT: linear thickening, GGO: ground glass opacity, PE: pleural effusion. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)
3.1. Prediction of abnormal patterns
The strongest association between abnormal imaging patterns, predictive variables, and their descriptive ranges are given in Table 5. For LT pattern, the prediction accuracy was found as 64:52%. From all possible biomarkers for this imaging abnormality, the most relevant feature (as found by coarse selection) was chloride. Similarly, the strongest association between PE and the predictive variables was due to chloride and HGB with a prediction accuracy of 82:8%, as verified by the AmRMR. Therefore, chloride and HGB were regarded as possible biomarkers for this abnormal imaging pattern. Predictions of GGO and consolidation were quite accurate when compared with other abnormality types. For instance, while the strongest association between GGO and predictive variables was due to LDH, with a prediction accuracy of 84:95%, the most relevant features for predicting presence of consolidation patterns were platelet count, RDW, and high gray run emphasis with a prediction accuracy of 86:02%. Similar to the consolidation prediction, the combined textural and clinical features resulted in better precision than the clinical features or textural features alone for predicting the existence of TIB patterns. For TIB prediction, on the other hand, the best feature set selected by AmRMR yielded a prediction accuracy of 72:04%; hence, possible biomarkers for this abnormality were MCV and long run emphasis. Lastly, prediction of nodules were mostly obtained through textural features, in particular the summation of average intensities had a prediction accuracy of 63:44%. Overall, textural features had better prediction abilities compared to the clinical features for pulmonary nodule identification. For all abnormal imaging patterns, an average prediction accuracy of 76:15% was obtained.
Table 5.
Determined biomarkers pertaining to the given abnormal patterns are listed with their descriptive ranges.
| Abnormal patterns | Indicators | Ranges for control group | Ranges for unhealthy subjects | Descriptive ranges | Accuracy of descriptor (%) |
|---|---|---|---|---|---|
| LT | Chloride (mmol/L) | [101–111] median=104 | [94–115] median=105 | [94–101) or (111–115] | 64.52 |
| GGO | LDH (U/L) | [114–187] median=144.5 | [81–537] median=241 | [81–114) or (187–537] | 84:95 |
| Nodules | Sum of avg intensities | [205:4–524:1] median=375.6 | [283:9–535:1] median=390 | (524:1–535:1] | 63.44 |
| PE | HGB (g/dL) | [7:1–11:4] median=9.2 | [7:9–13:6] median=10.3 | (11:4–13:6] of HGB level and (111–115] or [98–101) of chloride level | 82:8 |
| Chloride (mmol/L) | [101–111] median: 104 | [98–115] median: 106 | |||
| TIB | MCV (fL) | [79:1–95:7] median: 86.4 | [84–101] median: 91.2 | (95:7–101] of MCV level and [73.9–77.7) of long run emphasis level | 72:04 |
| Long run emphasis | [77.6–127.7] median=102.7 | [73.9–124.8] median=99.7 | |||
| Consolidation | Platelet (K/uL) | [118–337] median: 240 | [1–356] median: 93.5 | [1–118) or (337–356] of platelet level and [10.2–11.7) or (15.7–19.2] and [0.0119–0.0168) or (0.1863–0.2] | 86.02 |
| RDW (%) | [11.7–15.7] median: 13 | [10.2–19.2] median: 14.7 | |||
| High gray run emphasis | [0.01–0.18] median: 0.06 | [0.01–0.2] median: 0.10 |
3.2. Comparison to MIC
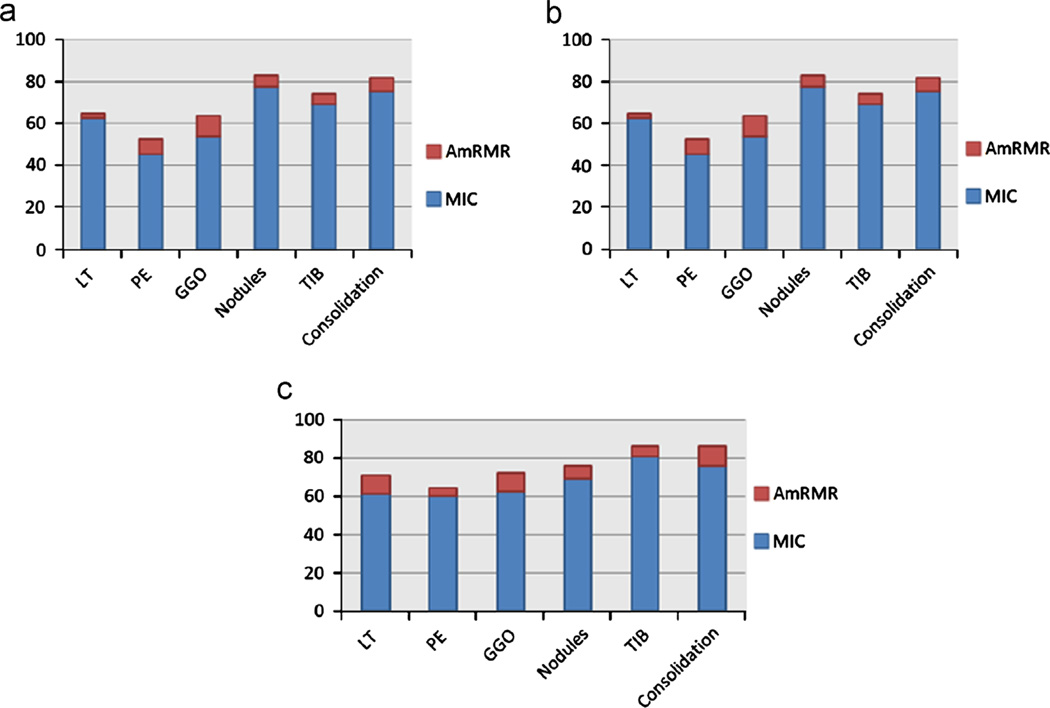
We compared our proposed feature ranking system (AmRMR) to the MIC approach by selecting the most predictive features of both methods and testing their prediction powers using the same classifiers (BDT). Fig. 6 shows the classification rates of clinical features in (a), imaging features in (b), and integrated features in (c), respectively. Notably, in all cases of abnormality patterns, the proposed method was superior to the MIC based feature selection system.
Fig. 6.
Prediction abilities (vertical axis in %) of the features selected by the proposed AmRMR, compared with the MIC method, are shown for clinical features in (a), imaging features in (b), and synergistically integrated imaging and clinical features in (c), respectively.
4. Discussion
Although CT image intensities do not possess a non-standardization, certain calibration may be necessary for studies that use a large number of CTs from different scanners, institutes, and patient groups (in particular patient size). This was not an issue in our study because the CT images used in this study were from the same institution and came from a limited number of scanners with optimized parameters for a routine clinical use. Thus, a calibration was not necessary.
Our study hypothesized that clinical laboratory features and automatically quantified imaging features can be used alone or even integrated to identify potential biomarkers. Note that interpreting the interaction or explaining the variables with the target class (i.e., existence of particular abnormality patterns) has been evaluated in terms of machine learning perspective; therefore, we provided little clinical justification on how the features interact. However, this is mainly due to the limitation of clinical features in the diagnostic decision mechanism and the lack of interpretability owing to lower specificity of the features. To alleviate this problem, one may need to act beyond the range of the existing classification problem.
Although the data presented herein were derived from infectious disease research, the proposed method has a broader application for other medical sub-specialities requiring imaging and laboratory data integration. In this pilot study, we demonstrated how clinical and imaging biomarkers were related to certain abnormal imaging patterns pertaining to infectious lung diseases; therefore, as a possible extension of this work, a correlation study incorporating biopsy results into the proposed framework could further identify the infection type and serotype, in addition to the identification of abnormal imaging patterns. Moreover, DNA microarray analysis of the lung exhibiting the abnormalities may provide additional insights, not only as a secondary validation set of our findings but also by discovering novel sequences as biomarkers too.
Even though a possible increment in data set size will not change the existing and morphological properties of the abnormality patterns observed in CT scans, using a larger data set will lead to a better understanding of variability within the clinical features and their extent. Specifically, subjects pertaining to this study did not include severe secondary illnesses; therefore, the variability of both imaging and clinical features are limited to the observation of the major infection. A broad study including more patients with different infection types and secondary (moderate to severe) illnesses or possibly a multi-center study using standardized, uniformly collected and evaluated clinical and imaging features will provide the academic knowledge to shift our paradigm from infectious lung diseases biomarkers to general lung diseases biomarkers.
5. Conclusions
From the experimental results and quantitative analysis, we concluded that specific alterations in clinical variables and textural features might occur as a result of infection and this could perhaps be retrieved by our proposed biomarker prediction method. More generally, image processing and laboratory data can be analyzed efficiently using the presented techniques that integrate radiologic information from cross-sectional imaging and clinical laboratory measurements. Our proposed method has the potential for a broad application for systems biology approaches that require quantitative radiology features and complex statistical modeling of corresponding clinical information for research purposes and for patient-care.
Summary
Radiology serves as a primary diagnostic method for assessing pulmonary infections. It also functions as an important part of continuous patient care such as monitoring disease progression or response to therapy. In this context, computed tomography is a widely utilized modality that solely provides details on global anatomical information. On the other hand, clinical laboratory measurements such as platelet count or hemoglobin levels elucidate underlying biological mechanisms of a certain disease. However, there is a lack of effective computational and statistical methods which integrate information from imaging modalities with findings from clinical science approaches in order to diagnose pulmonary infections at an early stage. Here we show that synergistically combining statistical imaging features with clinical features can identify abnormal lung patterns pertaining to pulmonary infections. We found that the following variables have interesting relationships with anatomic pulmonary abnormalities: chloride, hemoglobin level, mean corpuscular volume, lactate dehydrogenase, red blood cell distribution width, summation of average intensities, and run-lengths features. By exploring the hidden connection between these clinical and imaging features, we can reliably identify the following abnormal lung patterns with high accuracy: consolidations, pulmonary nodules, tree-in-bud, ground glass opacities, pleural effusions, and linear thickening. Our results demonstrate that revealing connections between seemingly unrelated information spaces can facilitate early detection of an infectious pulmonary disease. We expect that our methods will be used as a foundation for more sophisticated data exploration and identification of unknown relationships in intra-and inter-disciplinary features.
Acknowledgments
We thank Albert Wu and Omer Aras for visual scoring, and T. Palmore for useful information on clinical variables. This research is supported by the Center for Infectious Disease Imaging (CIDI), the Intramural Program of the National Institutes of Allergy and Infectious Diseases (NIAID), and the Intramural Research Program of the National Institutes of Biomedical Imaging and Bioengineering (NIBIB) at the National Institutes of Health (NIH). We thank Brent Foster for useful discussions on the revised paper, and Kristine Evers for editing of this paper.
Footnotes
Conflict of interest statement
None declared.
References
- 1.Bagci U, Bray M, Caban J, Yao J, Mollura DJ. Computer-assisted detection of infectious lung diseases: a review. Comput. Med. Imaging Graphics. 2012;36(1):72–84. doi: 10.1016/j.compmedimag.2011.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Seto WK, Lee CF, Lai CL, Ip PP, Fong DY, Fung J, Wong DK, Yuen MF. A new model using routinely available clinical parameters to predict significant liver fibrosis in chronic hepatitis B. PLoS ONE. 2011;6(8):e23077. doi: 10.1371/journal.pone.0023077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hogg JC, Chu F, Utokaparch S, Woods R, Elliott WM, Buzatu L, Cherniack RM, Rogers RM, Sciurba FC, Coxson HO, Pare PD. The nature of small-airway obstruction in chronic obstructive pulmonary disease. N. Engl. J. Med. 2004;350(26):2645–2653. doi: 10.1056/NEJMoa032158. [DOI] [PubMed] [Google Scholar]
- 4.Beane J, Sebastiani P, Whitfield TH, Steiling K, Dumas YM, Lenburg ME, Spira A. A prediction model for lung cancer diagnosis that integrates genomic and clinical features. Cancer Prev. Res. (Philadelphia) 2008;1(1):56–64. doi: 10.1158/1940-6207.CAPR-08-0011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Moffat BA, Chenevert TL, Meyer CR, McKeever PE, Hall DE, Hoff BA, Johnson TD, Rehemtulla A, Ross BD. The functional diffusion map: an imaging biomarker for the early prediction of cancer treatment outcome. Neoplasia. 2006;8(4):259–267. doi: 10.1593/neo.05844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Frank JI, Paul AR. Feature selection for multiclass discrimination via mixed-integer linear programming. IEEE Trans. Pattern Anal. Mach. Intell. 2003;25:779–783. http://doi.ieeecomputersociety.org/10.1109/TPAMI.2003.1201827. [Google Scholar]
- 7.Jain A, Zongker D. Feature selection: evaluation, application, and small sample performance. IEEE Trans. Pattern Anal. Mach. Intell. 1997;19:153–158. [Google Scholar]
- 8.Peng H, Long F, Ding C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005;27(8):1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- 9.Reshef DN, Reshef YA, Finucane HK, Grossman SR, McVean G, Turnbaugh PJ, Lander ES, Mitzenmacher M, Sabeti PC. Detecting novel associations in large data sets. Science. 2011;334(6062):1518–1524. doi: 10.1126/science.1205438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bagci U, Yao J, Caban J, Suffredini AF, Palmore TN, Mollura DJ. Learning shape and texture characteristics of CT tree-in-bud opacities for CAD systems. Med. Image Comput. Assist. Interv. 2011;14(Pt 3):215–222. doi: 10.1007/978-3-642-23626-6_27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yao J, Dwyer A, Summers RM, Mollura DJ. Computer-aided diagnosis of pulmonary infections using texture analysis and support vector machine classification. Acad. Radiol. 2011;18(3):306–314. doi: 10.1016/j.acra.2010.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.NIH. Department of Laboratory Medicine-Panel Tests [Google Scholar]
- 13.Udupa JK, Saha PK. Fuzzy connectedness and image segmentation. Proc. IEEE. 2003;91(10):1649–1669. [Google Scholar]
- 14.Haralick RM. Statistical and structural approaches to texture. Proc. IEEE. 1979;67(5):786–804. [Google Scholar]
- 15.Liu Y, Srihari SN. Document image binarization based on texture features. IEEE Trans. Pattern Anal. Mach. Intell. 1997;19:540–544. [Google Scholar]
- 16.Roe BP, Yang H-J, Zhu J, Liu Y, Stancu I, McGregor G. Boosted decision trees as an alternative to artificial neural networks for particle identification. Nucl. Instrum. Methods Phys. Res. A. 2005;543:577–584. http://dx.doi.org/10.1016/j.nima.2004.12.018 arXiv:arXiv:physics/0408124. [Google Scholar]
- 17.Bornkamp B, Ickstadt K, Dunson D. Stochastically ordered multiple regression. Biostatistics. 2010;11(3):419–431. doi: 10.1093/biostatistics/kxq001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jackson CH, Best NG, Richardson S. Bayesian graphical models for regression on multiple data sets with different variables. Biostatistics. 2009;10(2):335–351. doi: 10.1093/biostatistics/kxn041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cohen AR, Gomes FL, Roysam B, Cayouette M. Computational prediction of neural progenitor cell fates. Nat. Methods. 2010;7(3):213–218. doi: 10.1038/nmeth.1424. [DOI] [PubMed] [Google Scholar]
- 20.Chibon F, Lagarde P, Salas S, Perot G, Brouste V, Tirode F, Lucchesi C, de Reynies A, Kauffmann A, Bui B, Terrier P, Bonvalot S, Le Cesne A, Vince-Ranchere D, Blay JY, Collin F, Guillou L, Leroux A, Coindre JM, Aurias A. Validated prediction of clinical outcome in sarcomas and multiple types of cancer on the basis of a gene expression signature related to genome complexity. Nat. Med. 2010;16(7):781–787. doi: 10.1038/nm.2174. [DOI] [PubMed] [Google Scholar]
- 21.Van Landeghem S, Abeel T, Saeys Y, Van de Peer Y. Discriminative and informative features for biomolecular text mining with ensemble feature selection. Bioinformatics. 2010;26(18):i554–i560. doi: 10.1093/bioinformatics/btq381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mita T, Kaneko T, Stenger B, Hori O. Discriminative feature co-occurrence selection for object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2008;30(7):1257–1269. doi: 10.1109/TPAMI.2007.70767. [DOI] [PubMed] [Google Scholar]
- 23.Estevez PA, Tesmer M, Perez CA, Zurada JM. Normalized mutual information feature selection. IEEE Trans. Neural Networks. 2009;20(2):189–201. doi: 10.1109/TNN.2008.2005601. [DOI] [PubMed] [Google Scholar]
- 24.Kendall M, Kendall F, Smith B. The distribution of Spearman's coefficient of rank correlation in a universe in which all rankings occur an equal number of times. Biometrika. 1939;30:251–273. [Google Scholar]
- 25.Zhang Y, Yang Y, Zhang H, Jiang X, Xu B, Xue Y, Cao Y, Zhai Q, Zhai Y, Xu M, Cooke HJ, Shi Q. Prediction of novel pre-microRNAs with high accuracy through boosting and SVM. Bioinformatics. 2011;27(10):1436–1437. doi: 10.1093/bioinformatics/btr148. [DOI] [PubMed] [Google Scholar]
- 26.Yoon Y, Lee GG. Subcellular localization prediction through boosting association rules. IEEE/ACM Trans. Comput. Biol. Bioinformatics. 2012;9(2) doi: 10.1109/TCBB.2011.131. http://dx.doi.org/10.1109/TCBB.2011.131. [DOI] [PubMed] [Google Scholar]
- 27.Natarajan S, Khot T, Kersting K, Gutmann B, Shavlik J. Gradient-based boosting for statistical relational learning: the relational dependency network case. Mach. Learn. 2012;86(1):25–56. [Google Scholar]
- 28.Kearns M, Mansour Y. On the boosting ability of top-down decision tree learning algorithms. Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing; ACM Press; 1995. pp. 459–468. [Google Scholar]
- 29.Wozniak M. Boosted decision trees for diagnosis type of hypertension; Springer-Verlag. Proceedings of the 6th International Conference on Biological and Medical Data Analysis, ISBMDA'05; 2005. pp. 223–230. [Google Scholar]
- 30.Stingo FC, Chen YA, Vannucci M, Barrier M, Mirkes PE. A Bayesian Graphical Modeling Approach to MicroRNA Regulatory Network Inference. The Annals of Applied Statistics. 2010;4(4):2024–2048. doi: 10.1214/10-AOAS360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Caban J, Bagci U, Mehari A, Shoaib A, Fontana J, Gregory K, Mollura DJ. Characterizing non-linear dependencies among pairs of clinical variables and imaging data; 34th Annual International IEEE EMBS Conference; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]