Reaction pathway and free energy profile for papain-catalyzed hydrolysis of N-acetyl-Phe-Gly 4-nitroanilide

Abstract

Possible reaction pathways for papain-catalyzed hydrolysis of N-acetyl-Phe-Gly 4-nitroanilide (APGNA) have been studied by performing pseudobond first-principles quantum mechanical/molecular mechanical-free energy (QM/MM-FE) calculations. The whole hydrolysis process includes two stages: acylation and deacylation. For the acylation stage of the catalytic reaction, we have explored three possible paths (A, B, and C) and the corresponding free energy profiles along the reaction coordinates. It has been demonstrated that the most favorable reaction path in this stage is path B consisting of two reaction steps: the first step is a proton transfer to form a zwitterionic form (i.e. Cys-S⁻/His-H⁺ ion-pair), and the second step is the nucleophilic attack on the carboxyl carbon of the substrate accompanied with the dissociation of 4-nitroanilide. The deacylation stage includes the nucleophilic attack of a water molecule on the carboxyl carbon of the substrate and dissociation between the carboxyl carbon of the substrate and the sulfhydryl sulfur of Cys25 side chain. The free energy barriers calculated for the acylation and deacylation stages are 20.0 kcal/mol and 10.7 kcal/mol, respectively. Thus, the acylation is rate-limiting. The overall free energy barrier calculated for papain-catalyzed hydrolysis of APGNA is 20.0 kcal/mol, which is reasonably close to the experimentally derived activation free energy of 17.9 kcal/mol.

Introduction

Cysteine proteases, such as papain and cathepsin, are proteolytic enzymes that were found in a wide variety of living organisms, such as bacteria, plants, and animals.^1–6 Over the past decades, they were identified to play important roles in the degradation of muscular proteins,^7–9 immunopharmacological response,^10–11 the viral reproductive cycle, and other pathological cellular processes etc.^12–15 Deficiency of cysteine proteases can cause many diseases such as cancer,¹⁶ muscular dystrophy,¹⁷ and Alzheimer’s disease.¹⁸ For these fundamental biological functions, understanding the catalytic mechanism of cysteine proteases has attracted extensive attention in both experimental and computational studies.

On one hand, extensive experimental studies have been carried out to explore how the cysteine proteases catalyze the hydrolysis of peptide bond.^19–21 On the other hand, the mechanism of the cysteine proteases-catalyzed hydrolysis has also been studied computationally.^22–25 The overall principles of substrate recognition, catalysis, and inhibition have been documented reasonably, and it is widely accepted that the whole catalytic cycle consists of two stages: acylation and deacylation. However, as discussed below, a couple of crucial mechanistic questions still need to be addressed in the acylation stage.

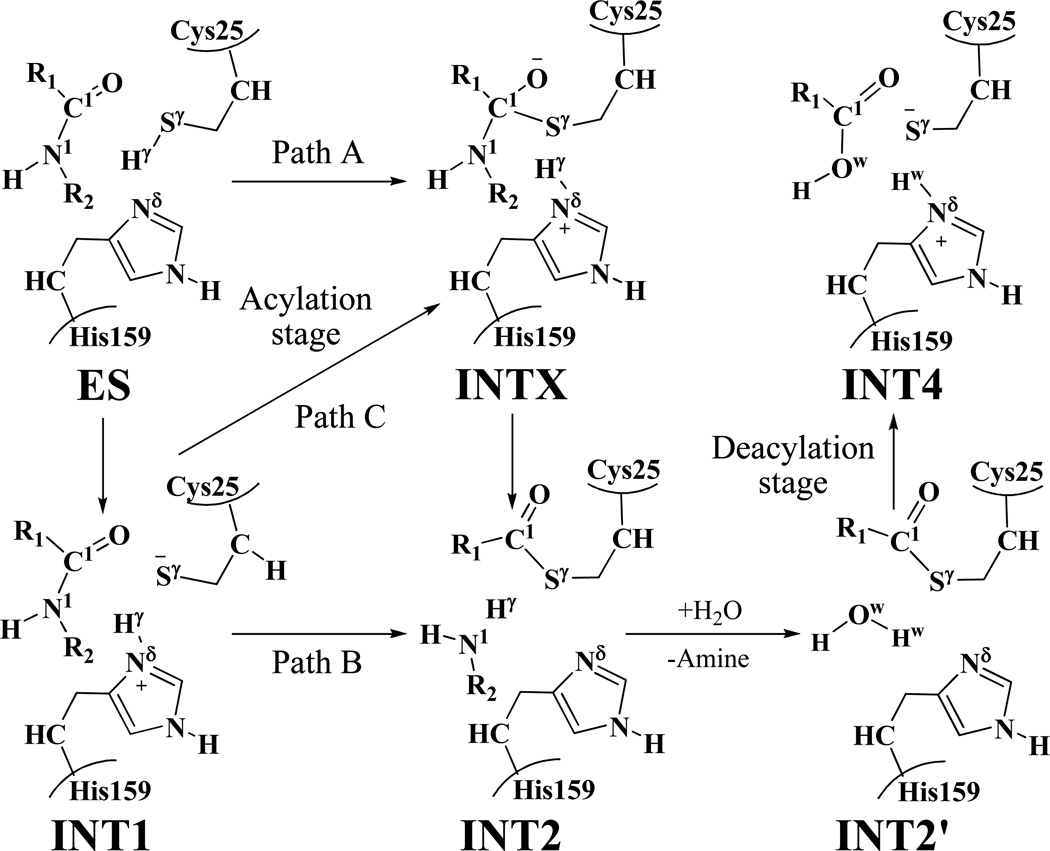
The first question is whether the neutral form (ES, depicted in Scheme 1) or the zwitterionic form (INT1, depicted in Scheme 1) should be the starting point of the catalytic cycle. Generally, the active-site center of a cysteine protease was thought to be present as a zwitterionic form (i.e. the Cys-S⁻/His-H⁺ ion-pair), rather than the neutral form, and almost all of the reported computational studies on the mechanism of the enzyme were based on this preassumption. Notably, Mladenovic et al. recently performed molecular dynamics (MD) simulations on cathepsin B using quantum mechanical/molecular mechanical (QM/MM) potentials.²⁶ Their computational results suggested that the ion-pair is more stable than the neutral form due to the stabilization by a complex hydrogen-bond network in the enzyme environment. However, Lowe and co-workers proposed that papain could exist in a neutral form and suggested a possible reaction pathway for the structural transformation from the neutral form ES to a tetrahedral intermediate INTX (path A, depicted in Scheme 1) in their experimental report.²⁷ To the best of our knowledge, the possibility of path A has never been examined computationally so far. In order to clarify the reaction mechanism in detail, it is necessary to take this possibility into account.

Scheme 1.

The acylation (including three possible paths A, B, and C) and deacylation stages of the cysteine proteases-catalyzed hydrolysis.

The second question is whether the fundamental hydrolysis pathway involves a tetrahedral intermediate (INTX, depicted in Scheme 1) in the acylation stage. Hillier et al. obtained a concerted transition state from the structural transformation of the zwitterion (INT1, depicted in Scheme 1) to the intermediate (INT2, depicted in Scheme 1) in the acylation stage of papain-catalyzed hydrolysis of N-Methylacetamide using a hybrid QM(AM1)/MM and QM(B3LYP/3-21G*)/MM method.²³ These researchers proposed that the proton transfer from residue His159 to the substrate concerted with the nucleophilic attack, proceeding via only one transition state without the intervention of the tetrahedral intermediate INTX for the structural transformation from intermediate INT1 to INT2 (path B, depicted in Scheme 1). More recently, Gao et al.²⁵ carried out molecular dynamics free energy simulations using a combined quantum mechanical and molecular mechanical (AM1/MM) potential to study the catalytic mechanism of human cathepsin K which is highly homologous to papain. Their computational study was performed to study the entire catalytic cycle (including both the acylation and deacylation stages) and, in their calculations, the zwitterion (INT1, depicted in Scheme 1) was used as the starting point of the hydrolysis process. According to their calculated free energy profiles,²⁵ the acylation stage should be rate limiting with a barrier height of 19.8 kcal/mol, and the tetrahedral intermediate (INTX, depicted in Scheme 1) should exist in this step. Based on their computational data, they suggested that the acylation stage should undergo a stepwise mechanism for the structural transformation from intermediate INT1 to INT2 (path C, depicted in Scheme 1), but the overall nucleophilic addition and proton-transfer processes are highly coupled.²⁵

As discussed above, so far, computational studies have been reported only on the two possible reaction paths (paths B and C, depicted in Scheme 1) in the acylation stage of the cysteine proteases-catalyzed hydrolysis. None of the reported computational studies has ever examined and compared all of the possibilities (including paths A, B, and C, depicted in Scheme 1). In the present study, we first aimed to know whether the neutral form (ES) and zwitterionic form (INT1) are all stable structures associated with local minima on the QM/MM potential energy surface. Assuming that both of them were associated with local minima, we also wanted to know which structural form is more stable (with the lowest free energy) in the cysteine protease. Further, we would like to know which reaction path is the most favorable one in the acylation stage. In order to explore the possible reaction paths depicted in Scheme 1 for the cysteine protease-catalyzed hydrolysis, we chose papain-catalyzed hydrolysis of N-acetyl-Phe-Gly 4-nitroanilides (APGNA, depicted in Scheme 2 and Scheme 3) as the representative reaction in our computational study.

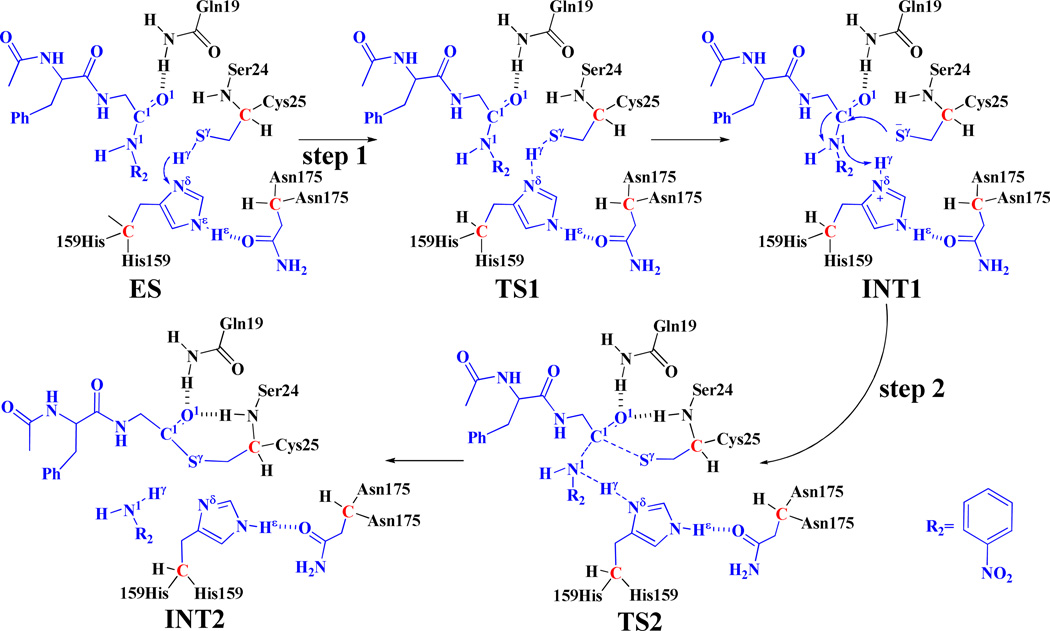
Scheme 2.

The possible reaction pathway (path B) in the acylation stage. Atoms colored in blue are treated by QM method in the pseudobond first-principles QM/MM calculations. Three boundary carbon atoms (colored in red) are treated with the improved pseudobond parameters. All other atoms belong to the MM subsystem.

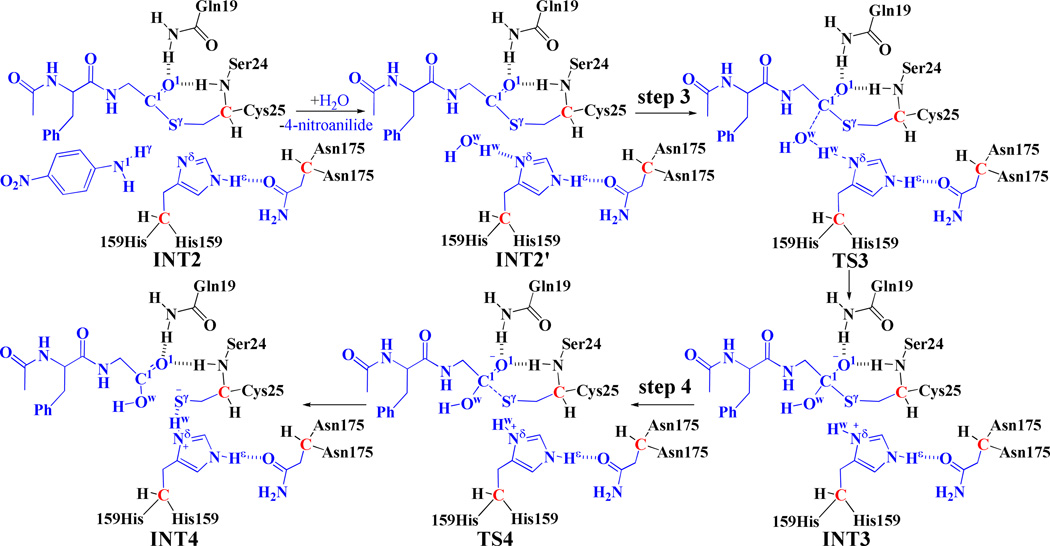
Scheme 3.

Fundamental reaction pathway in the deacylation stage. Atoms colored in blue are treated by the QM method in the pseudobond first-principles QM/MM calculations. Three boundary carbon atoms (colored in red) are treated with the improved pseudobond parameters. All other atoms belong to the MM subsystem.

Thus, we performed pseudobond quantum mechanical/molecular mechanical-free energy (QM/MM-FE) calculations^28–31 to study the detailed reaction pathway for the papain-catalyzed hydrolysis of APGNA. The pseudobond first-principles QM/MM-FE approach^{28–29, 31–32} has been demonstrated to be a powerful tool in simulating a variety of enzymatic reactions,^33–41 and some theoretical predictions^42–43 were subsequently confirmed by experimental studies.^44–46 The computational results have clearly revealed the detailed reaction pathway and the corresponding free energy profile for the papain-catalyzed hydrolysis of APGNA. The rate-determining step is thereby identified, and the roles of essential residues are discussed on the basis of the QM/MM-optimized geometries of the key states existing in the catalytic hydrolysis reaction process.

Computational Details

Preparation of the Initial Structures

The initial structure of the enzyme-substrate (ES) complex was constructed from the X-ray crystal structure of papain-inhibitor complex (PDB ID: 1KHP).⁴⁷ The inhibitor in the active site was replaced by the substrate (APGNA) whose geometry was optimized by performing ab initio quantum mechanical calculations at the HF/6-31G* level using the Gaussian03 program.⁴⁸ The optimized geometry was used to calculate the electrostatic potentials on the molecular surfaces at the HF/6-31G* level. The calculated electrostatic potentials were used to determine the partial atomic charges by using the standard restrained electrostatic potential (RESP) fitting procedure^49–50 implemented in the antechamber module of the AMBER11 program package.⁵¹ The determined RESP charges were used for the calculation of electrostatic energies in the MD simulation processes. The force field parameters for APGNA were developed from the general AMBER force field (GAFF) implemented in the AMBER11 program.⁵¹ Then the constructed model of the neutral form ES (depicted in Figure 1) was solvated in an orthorhombic box of TIP3P water molecules,⁵² with a minimum solute wall distance of 10 Å, and a total of 7 chlorine ions were added to neutralize the solvated system. Once the whole system was set up, a serious of energy minimizations and then a ~2 ns MD simulation was carried out by using the Sander module of AMBER11 program.⁵¹ As shown in Schemes 2 and 3, the papain-catalyzed hydrolysis of the substrate includes acylation and deacylation stages. The 4-nitroanilide leaves the system after the acylation stage. Consequently, we constructed the structure of INT2´ by removing the 4-nitroanilide out of the QM/MM-optimized INT2 structure. The constructed INT2´ structure was then relaxed by performing ~2 ns MD simulation, and was neutralized by adding a total of 7 chlorine ions and solvated in an orthorhombic box with the TIP3P water molecules with a minimum solute-wall distance of 10 Å.

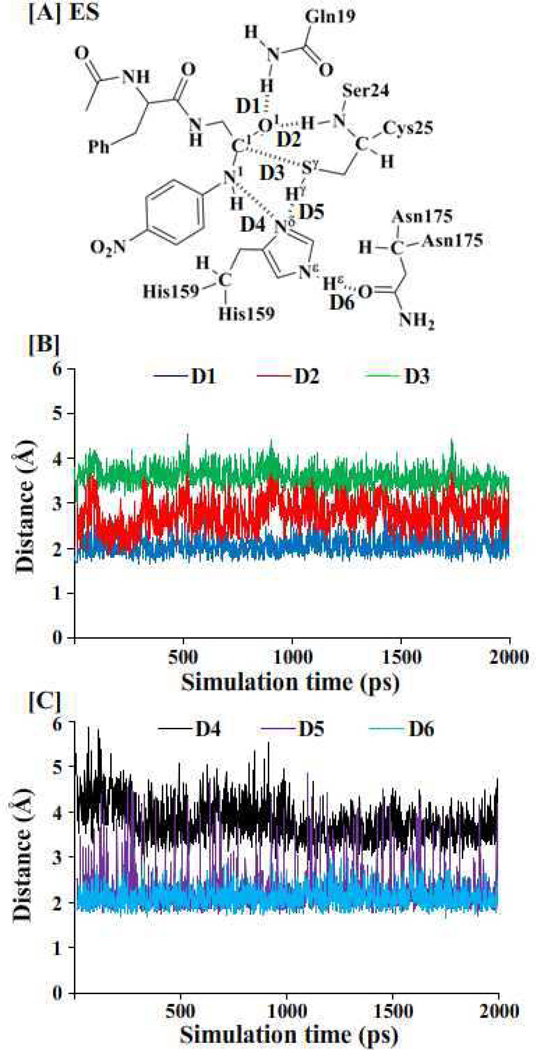
Figure 1.

Key internuclear distances (D1 to D6 defined in panel A) vs the simulation time in the MD-simulated papain-APGNA complex.

For both the acylation and deacylation stages, the last snapshots in the MD simulations were used as the initial structures to prepare pseudobond first-principles QM/MM calculations, as the last snapshots were close to the average structures simulated. Since we were interested in the reaction center, the water molecules beyond 50 Å of the sulfur atom (S^γ in Figure 1) of residue Cys25 were removed, leaving the QM/MM system with 2,439 water molecules and a total of 10,618 atoms for the acylation stage, and 2,948 water molecules and a total of 12,129 atoms for the deacylation stage. The QM-MM interface was described by a pseudobond approach.^{28–29, 32} The boundary atoms of the QM-MM systems were defined in Schemes 2 and 3. Prior to the QM/MM geometry optimizations, each initial reaction system was energy-minimized with the MM method by using the revised AMBER8 program,⁵³ where the convergence criterion was the root-mean-square deviation (rmsd) of the energy gradient being less than 0.1 kcal·mol⁻¹·Å⁻¹.

Minimum-Energy Path of the Enzymatic Reaction

With a reaction-coordinate driving method and an iterative energy minimization procedure,³¹ the possible enzymatic reaction paths were determined by performing the pseudobond QM/MM calculations at the B3LYP/6-31G*:AMBER level. In the QM/MM calculations, the QM calculation was performed at the B3LYP/6-31G* level of theory by using a modified version of Gaussian03⁴⁸ and the MM calculation was performed by using a modified version of the AMBER8 program.⁵³ Normal mode analysis was performed to characterize the enzyme-substrate complex (ES), intermediates (INT), and transition states (TS). In addition, single-point energy calculations were carried out at the QM/MM(B3LYP/6-31++G**:AMBER) level on the QM/MM-optimized geometries to evaluate the energy barriers. Throughout the QM/MM calculations, the boundary carbon atoms were treated with improved pseudobond parameters.²⁸ No cutoff for nonbonded interactions was used in the QM/MM calculations. For the QM subsystem, the convergence criterion for geometry optimizations followed the original Gaussian03 defaults. For the MM subsystem, the geometry optimization convergence criterion was when the rmsd of energy gradient was less than 0.1 kcal·mol⁻¹·Å⁻¹. All atoms within 20 Å of the S^γ atom of residue Cys25 were allowed to move while all the other atoms outside this range were frozen in all the QM/MM calculations. During the QM/MM geometry optimization, the QM and MM subsystems were energy-minimized iteratively. For each step of the iteration, the MM subsystem was energy-minimized when the QM subsystem was kept frozen, whereas the QM subsystem was energy-minimized when the MM subsystem was kept frozen.

Free Energy Perturbation

After the minimum-energy path was determined by the QM/MM calculations, the free energy changes associated with the QM-MM interactions were determined by using the free energy perturbation (FEP) method.³¹ In the FEP calculations, sampling of the MM subsystem was carried out with the QM subsystem frozen at different states along the reaction path. The point charges on the frozen QM atoms used in the FEP calculation are those determined by fitting the electrostatic potential (ESP) in the QM part of the QM/MM calculation.⁵⁴ The FEP calculations enabled us to more reasonably determine relative free energy changes due to the dynamic interactions between and QM and MM subsystems. Technically, the final (relative) free energy determined by the QM/MM-FE calculations is the QM part of the QM/MM energy (excluding the Coulumbic interaction energy between the point charges of the MM atoms and the ESP charges of the QM atoms) plus the relative free energy change determined by the FEP calculations. In the FEP calculations, the time step used was 2 fs, and bond lengths involving hydrogen atoms were constrained. In sampling of the MM subsystem by the MD simulations, the temperature was maintained at 308.15 K. Each FEP calculation consisted of 50 ps of equilibration and 300 ps of sampling, as we did previously for other enzymatic reaction systems.^34–41

Most of the MD simulations were performed on a supercomputer (i.e. the Dell X-series Cluster with 384 nodes or 4,768 processors) at the University of Kentucky’s Computer Center. Some other modeling and computations were carried out on SGI Fuel workstations in our own laboratory at University of Kentucky.

Results and Discussion

Papain-APGNA Binding Structure from MD Simulation

First of all, we performed MD simulation on the papain-APGNA complex for ~2 ns to study the enzyme-substrate (ES) binding. Papain is a globular protein consisting of 212 residues and its active site is a catalytic triad (residues Cys25, His159, and Asn175). Collected in Figure 1 are plots of key internuclear distances vs the simulation time in the MD-simulated ES complex. Trace D1 is the distance between the carbonyl oxygen (O ) atom of the substrate and the closest H atom of the NH2 group on the side chain of residue Gln19. Trace D2 is the distance between the O atom of the substrate and the H atom of the NH group of Ser24 backbone. Trace D3 is the distance between the S^γatom of Cys25 side chain and the carbonyl carbon (C¹) of the substrate. Trace D4 is the distance between the N^δ atom of His159 side chain and the N¹ atom of the substrate. Trace D5 is the distance between the N^δ atom of His159 side chain and the H^γ atom of Cys25 side chain. Trace D6 is the distance between the H^εatom of His159 side chain and the carbonyl oxygen of residue Asn175.

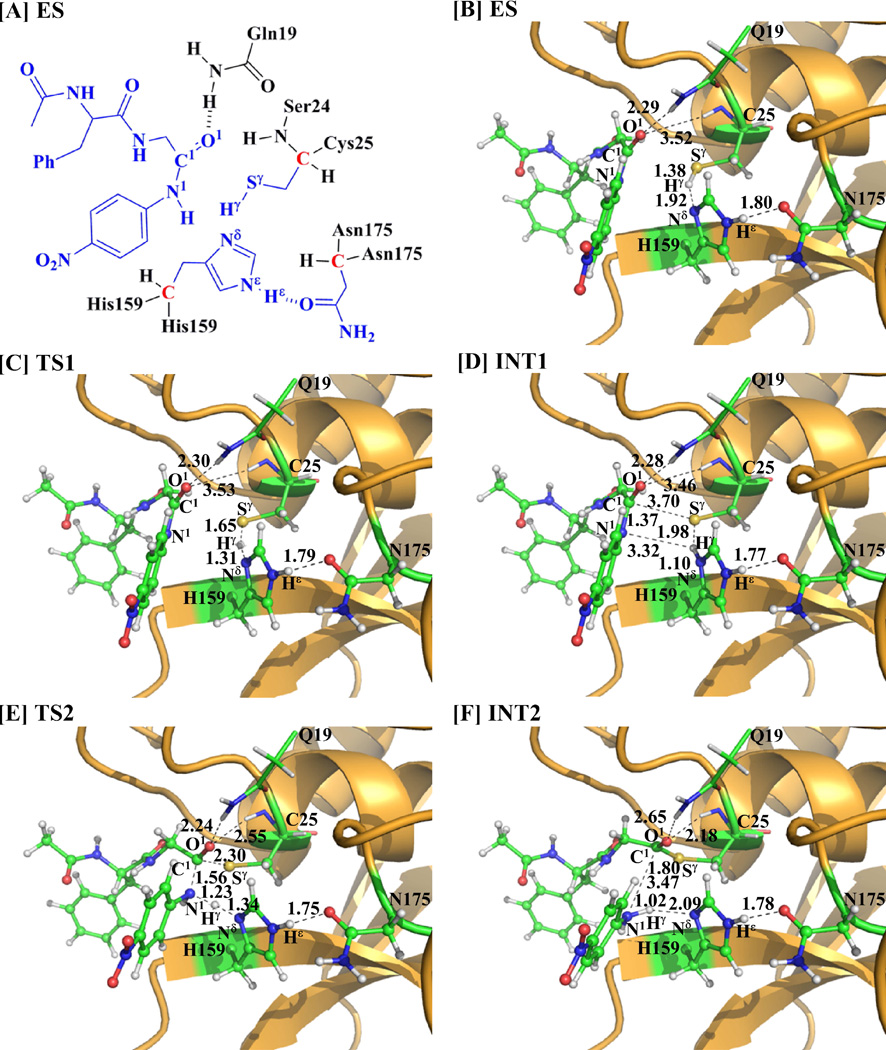
As seen in Figure 1, in the MD-simulated ES complex, the average values of D1 and D2 are ~2.0 and ~2.8 Å, respectively, indicating the existence of the “oxyanion hole”. The average value of D3 (~3.7 Å) is an appropriate distance for the S^γ atom of residue Cys25 to initiate the nucleophilic attack on the carbonyl carbon of the substrate. The average values of D4 and D5 are ~3.6 and ~2.0 Å, respectively, suggesting that the residue His159 is positioned well and ready for facilitating the proton transfer process. The average value of D6 (~2.0 Å) suggests that there is a strong hydrogen bond involving the H^εatom of His159 side chain and the carbonyl oxygen of Asn175. Compared with the ES complex structure optimized at the QM/MM(B3LYP/6-31G*:AMBER) level (Figure 2B), the QM/MM-optimized geometrical parameters D1, D2, D3, D4, D5, and D6 (Figure 1A) are 2.29, 3.18, 3.92, 3.58, 1.92, and 1.80 Å, respectively. The QM/MM-optimized distances are reasonably close to the corresponding average values of the above traces.

Figure 2.

Key states involved in reaction path B of the papain-catalyzed hydrolysis of APGNA. The geometries were optimized at the QM/MM(B3LYP/6-31G*:AMBER) level. The key distances are given in Å. Carbon, oxygen, nitrogen, sulfur, and hydrogen atoms are colored in green, red, blue, yellow, and white, respectively. The backbone of the protein is rendered in orange. The QM atoms are represented as balls and sticks, and the surrounding residues are rendered as sticks or lines.

Fundamental Reaction Pathway for Papain-Catalyzed Hydrolysis of APGNA

Acylation stage

The MD simulation led to a dynamically stable ES complex. Starting from the MD-simulated ES complex, the QM/MM reaction-coordinate calculations were performed at the B3LYP/6-31G*:AMBER level. Below we discuss each of these three possible reaction pathways (paths A, B, and C) in the acylation stage.

As shown in Scheme 1, path A, if it exists, may consist of two reaction steps: the first step would be the formation of the tetrahedral intermediate INTX starting from the initial structure ES via a concerted process, and the second step would be the structural transformation from INTX to INT2. The first step of path A depicted in Scheme 1 would involve the breaking of the S^γ–H^γ bond and the formation of the S^γ–C¹ and N^δ –H^γ bonds. Thus, the distances R_Sγ-Hγ, R_Sγ-C1, and R_Nδ-Hγ were chosen to represent the reaction coordinate as R_Sγ-Hγ – R_Sγ-C1 – R_Nδ-Hγ for the QM/MM reaction-coordinate calculations on this possible concerted reaction pathway. However, the reaction-coordinate calculations actually led to the transition state (TS1) and intermediate (INT1) depicted in Figure 2. So, the QM/MM reaction-coordinate calculations do not support the hypothesis of the concerted reaction pathway for the structural transformation from the intermediate ES to intermediate INTX (i.e. path A).

Concerning path B, starting from the optimized ES complex structure, our QM/MM reaction-coordinate calculations at the B3LYP/6-31G*:AMBER level revealed that path B may also consist of two reaction steps (steps 1 and 2, depicted in Scheme 2). The first step is the proton (H^γ) transfer from S^{γ of} Cys25 side chain to N of His159 side chain and, therefore, the zwitterion INT1 is generated. The variations of the distances R_Sγ-Hγ and R_Nδ-Hγreflect the nature of the proton transfer process. Thus, the reaction coordinate for the step 1 was chosen to be R_Sγ-Hγ – R_Nδ-Hγ. The second step is the nucleophilic attack on the carbonyl carbon of the substrate by the S^γ atom of Cys25 side chain, accompanied with the proton (H^γ) transfer from the N atom of His159 side chain to the N¹ atom of the substrate and the breaking of N¹ –C¹ bond of the substrate. The structural transformation from intermediate INT1 to intermediate INT2 (step 2) involves the breaking of the N¹–C¹ bond and the formation of the S^γ–C¹ , N^δ–H^γ, and N¹–H^γ bonds. So, the distances R_N1-C1, R_Nδ-Hγ, R_Sy-C1, and R_N1-Hγ were chosen to represent the reaction coordinate as R_N1-C1 +R_Nδ-Hγ–R_Sγ-C1–R_N1-Hγ in the QM/MM reaction-coordinate calculations for the step 2. All the geometries of key states in path B (depicted in Scheme 2) were optimized at the QM/MM(B3LYP/6-31G*:AMBER) level, and are shown in Figure 2.

In the first proton transfer step (step 1), the S^γ–H^γ distance changes from 1.38 Å in ES to 1.65 Å in transition state TS1 and then to 1.98 Å in intermediate INT1, while the N^δ–H^γ distance changes from 1.92 Å in ES to 1.10 Å in transition state TS1 and then to 1.31 Å in intermediate INT1, indicating the proton (H^γ) transfer from the S^γ atom of Cys25 side chain to the N^δ atom of His159 side chain. In the second step of path B (step 2), there are three major types of structural changes. One is the formation of S^γ–C¹ bond (R_Sγ-C1 is 3.70 Å in intermediate INT1, 2.30 Å in transition state TS2, and 1.80 Å in intermediate INT2). The second significant structural change is the breaking of N¹–C¹ bond (R_N1-C1 is 1.37 Å in intermediate INT1, 1.56 Å in transition state TS2, and 3.47 Å in intermediate INT2). The other is the proton (H^γ) transfer from the N^δ atom of His159 side chain to the N¹ atom of the substrate (N^δ–H^γ and N¹–H^γ respectively change from 1.10 and 3.32 Å in intermediate INT1 to 1.34 and 1.23 Å in transition state TS2, and then to 2.09 and 1.02 Å in intermediate INT2). A characteristic feature of this process is that the hydrogen-bond interactions of the carbonyl oxygen of the substrate with the oxyanion hole are enhanced in transition state TS2, as revealed by the significant shortening of the distances between the O¹ atom and the H atoms in the oxyanion hole. As seen in Figure 2, the distance between the carbonyl oxygen O¹ of the substrate and an H atom in the NH₂ group of Gln19 side chain shortens from 2.28 Å in intermediate INT1 to 2.24 Å in TS2, while the distance between the carbonyl oxygen O¹ of the substrate and the backbone H of Ser24 shortens from 3.46 Å in INT1 to 2.55 Å in TS2. Thus, the oxyanion hole helps to more favorably stabilize transition state TS2. Noteworthy, the H^ε atom of residue His159 maintains a strong hydrogen-bonding interaction with the carbonyl oxygen of residue Asn175 (with the average distance being ~1.80 Å) in the whole acylation stage.

Regarding path C, the first reaction step would be the same as that of path B. The additional QM/MM reaction-coordinate calculations were carried out starting from the second step of path C (i.e. the structural transformation from intermediate INT1 to the tetrahedral intermediate INTX). The structural transformation from intermediate INT1 to intermediate INTX involves the formation of the S^γ–C¹ bond. Hence, R_Sγ-C1 was used as the reaction coordinate in the QM/MM reaction-coordinate calculations for this possible reaction path. However, the reaction-coordinate calculations actually led to the same transition state (TS2) and intermediate (INT2) depicted in Figure 2. So, the QM/MM reaction-coordinate calculations do not support the hypothesis of the stepwise reaction pathway for the structural transformation from the intermediate INT1 to intermediate INT2 (i.e. path C).

In summary, the QM/MM calculations on the acylation stage have revealed that paths A and C do not exist. Thus, within the three possible reaction paths, only path B is supported by the current QM/MM calculations.

Deacylation stage

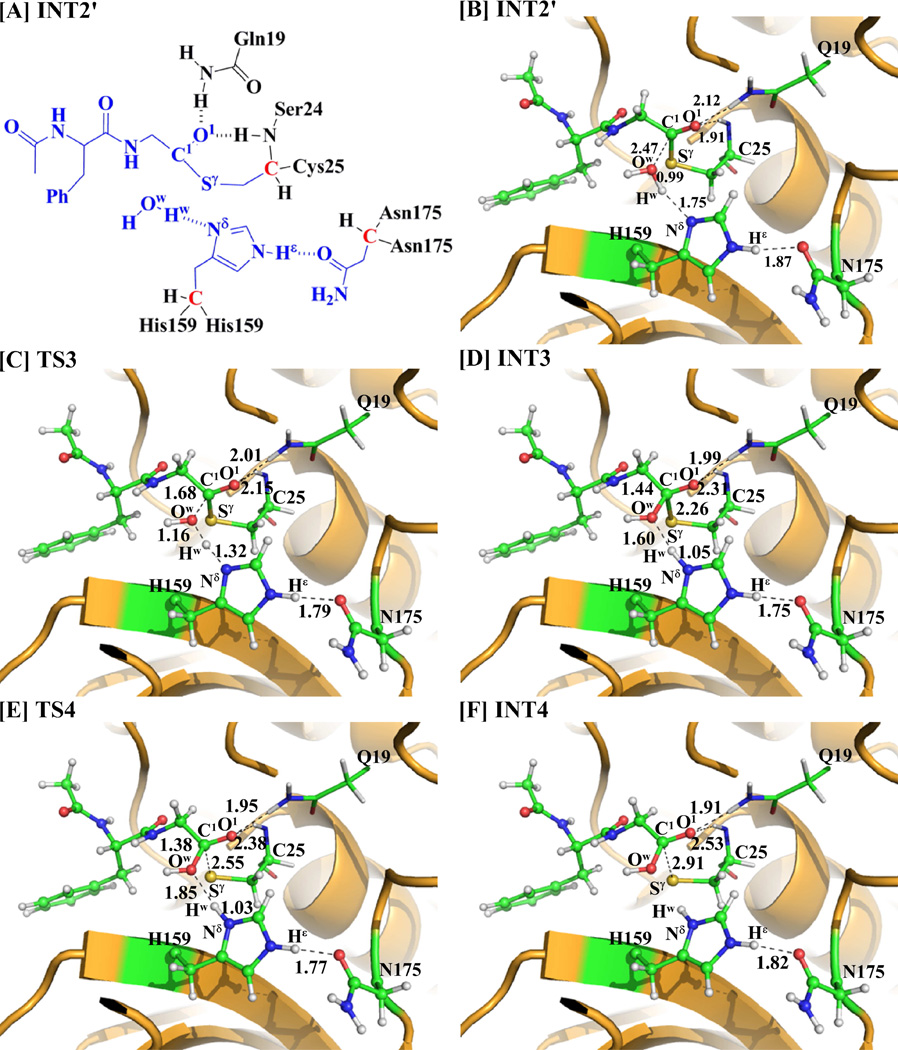
As one can be seen from Scheme 3, 4-nitroanilide was removed from the above-discussed QM/MM-optimized geometry of the intermediate INT2 to construct the structure of the intermediate INT2´, which was then relaxed by performing MD simulation for ~2 ns. A water molecule close to the carbonyl carbon (C¹) of the substrate was selected as the nucleophile and was treated by the QM method. Similar to that in the acylation stage, the carbonyl oxygen O¹ of the substrate is also stabilized by the oxyanion hole. As shown in Figure 3, there are two hydrogen bonds between the carbonyl oxygen (O¹) of the substrate and the oxyanion hole in the intermediate INT2´.

Figure 3.

Key states involved in the deacylation stage of papain-catalyzed hydrolysis of APGNA. The geometries were optimized at the QM/MM (B3LYP/6-31G*:AMBER) level. The key distances in the figure are given in Å. Carbon, oxygen, nitrogen, sulfur, and hydrogen atoms are colored in green, red, blue, yellow, and white, respectively. The backbone of the protein is rendered in orange. The QM atoms are represented as balls and sticks, and the surrounding residues are rendered as sticks or lines.

Starting from the optimized INT2´ structure, our QM/MM reaction-coordinate calculations at the B3LYP/6-31G*:AMBER level revealed that the deacylation stage consists of two reaction steps (steps 3 and 4). For the step 3, accompanied by the nucleophilic attack on the carbonyl carbon C¹ by a water molecule, the proton (H^w) transfers from the O^w atom of the water molecule to the N^δ atom of residue His159 to form a tetrahedral intermediate INT3 via transition state TS3. Hence, the step 3 involves the breaking of the O^w–H^w bond and the formation of the N^δ–H^w and O^w–C¹ bonds. For the step 4, the S^γ–C¹ bond is broken to generate intermediate INT4 via transition state TS4. Interestingly, even though the distances R_Ow-Hw, R_Sγ-C1, R_Ow-C1, and R_Nδ-Hw were chosen to represent the concerted reaction coordinate as R_Ow-Hw + R_Sγ-C1 – R_Ow-C1 – R_Nδ-Hw in the QM/MM reaction-coordinate calculations for steps 3 and 4 together (which is a concerted reaction coordinate), we still obtained the QM/MM results indicating that the deacylation stage occurs in the stepwise manner. Overall, the deacylation stage is stepwise, but the two steps are highly coupled, as shown in Scheme 3.

As shown in Figure 3, the geometries of all intermediates and transition states in the deacylation stage were optimized at the QM/MM(B3LYP/6-31G*:AMBER) level. In the step 3, the O^w–C¹, N^δ–H^w, and O^w–H^w distances change respectively from 2.47, 1.75, and 0.99 Å in intermediate INT2´ to 1.44, 1.05, and 1.60 Å in intermediate INT3 via 1.68, 1.32, and 1.16 Å in transition state TS3. In the step 4, the distance R_Sγ-C1 changes from 2.26 Å in intermediate INT3 to 2.55 Å in transition state TS4 and then to 2.91 Å in intermediate INT4. Meanwhile, the distance between the carbonyl oxygen of the substrate and the backbone hydrogen of residue Ser24 changes from 2.31 Å in intermediate INT3 to 2.38 Å in transition state TS4 and then to 2.53 Å in intermediate INT4. So, the hydrogen bonds are weakened in intermediate INT4.

Free Energy Profile

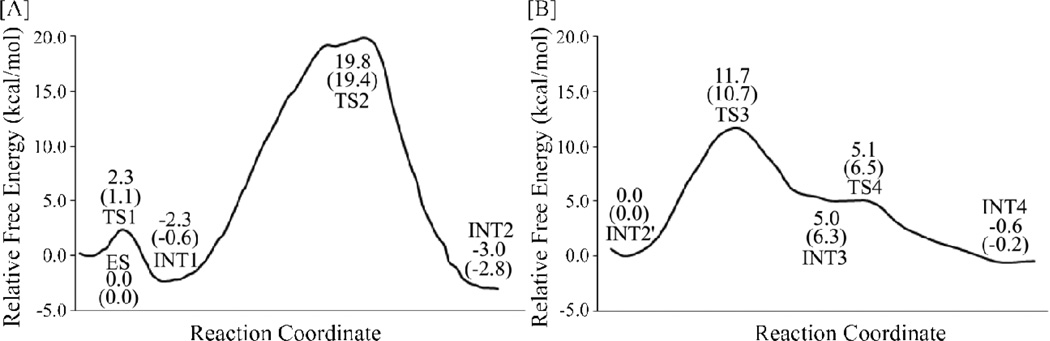
The above QM/MM reaction-coordinate calculations at the B3LYP/6-31G*:AMBER level have revealed that the fundamental papain-catalyzed hydrolysis pathway consists of four reaction steps, including steps 1 to 2 belonging to the acylation stage (path B) and steps 3 to 4 belonging to the deacylation stage. Further, to determine the corresponding free energy profile, single-point QM/MM energy calculations were performed at the B3LYP/6-31++G**:AMBER level on the QM/MM-optimized geometries along the minimum-energy path. For each geometry along the reaction path, the ESP charges determined in the QM part of the QM/MM single-point energy calculation were used in the subsequent FEP simulations to estimate the free energy changes. Depicted in Figure 4A and 4B are the free energy profiles for the fundamental reaction pathway, including the acylation and deacylation stages, that are determined by the QM/MM-FE calculations first without the zero-point and thermal corrections for the QM subsystem, and then with the zero-point and thermal corrections for the QM subsystem (values given in parentheses).

Figure 4.

Free energy profile for the acylation (path B, depicted in Figure 4A) and deacylation (depicted in Figure 4B) of the papain-catalyzed hydrolysis. The relative free energies were determined by the QM/MM-FE calculations at the B3LYP/6-31++G**:AMBER level, excluding the zero-point and thermal corrections for the QM system. Values in the parentheses are relative free energies including the zero-point and thermal corrections for the QM subsystem.

Depicted in Figure 4A is the free energy profile in the acylation stage (path B) of the hydrolysis reaction, determined by the QM/MM-FE calculations at the B3LYP/6-31++G**:AMBER level. As shown in Figure 4A, without the zero-point and thermal corrections for the QM subsystem, the free energy barriers calculated for the steps 1 and 2 are 2.3 and 22.1 kcal/mol, respectively. With the zero-point and thermal corrections for the QM subsystem (the values given in parentheses), the free energy barriers change to 1.1 and 20.0 kcal/mol, respectively.

As shown in Figure 4B, with the zero-point and thermal corrections for the QM subsystem, the free energy barriers calculated for the steps 3 and 4 in the deacylation stage are 11.7 and 0.1 kcal/mol, respectively. With the zero-point and thermal corrections for the QM subsystem, the free energy barriers change to 10.7 and 0.2 kcal/mol, respectively. The highest energy barrier for the deacylation stage (10.7 kcal/mol) is 9.3 kcal/mol lower than that for acylation stage (20.0 kcal/mol), which is consistent with the experimental observation that the acylation stage is rate-limiting.⁵⁵ Further, the experimentally determined catalytic rate constant k_cat (1.3±0.2 s⁻¹)⁵⁵ is associated with an activation free energy of 17.9 kcal/mol according to the conventional transition state theory.⁵⁶ Our calculated overall free energy barrier (20.0 kcal/mol) for the whole papain-catalyzed hydrolysis reaction is only 2.1 kcal/mol higher than the experimentally-derived activation free energy barrier of 17.9 kcal/mol, indicating that the fundamental pathway uncovered in this computational study is reasonable.

Conclusion

In this study, we performed pseudobond first-principles QM/MM-FE study on the entire catalytic cycle of papain-catalyzed hydrolysis of substrate APGNA and determined the corresponding free energy profile. For the acylation stage, three possible reaction pathways (paths A, B, and C) were examined. The computational results demonstrate that path B is the fundamental reaction pathway in the acylation stage, and there are two steps (steps 1 and 2) in the path B. The first step is the proton transfer from the S^γ atom of Cys25 to the N^δ atom of His159 side chain to generate the zwitterionic intermediate INT1 via transition state TS1. The second step is the nucleophilic attack of the S^γ ion on the carboxyl carbon of the substrate, accompanied with the dissociation of 4-nitroanilide (i.e. the structural transformation from intermediate INT1 to intermediate INT2 via the concerted transition state TS2). The deacylation stage also consists of two reaction steps (steps 3 and 4). In the step 3, the O atom of a water molecule initiates the nucleophilic attack on the carboxyl carbon of the substrate, which is accompanied by the proton transfer from the water molecule to the N^δ atom of His159 side chain via transition state TS3. In the step 4, the S^γ–C¹ bond breaks via transition state TS4.

The free energy barriers calculated for the four reaction steps (steps 1 to 4) are 1.1, 20.0, 10.7, and 0.2 kcal/mol, respectively. Thus, for the whole papain-catalyzed hydrolysis process, the rate-limiting reaction step should be the step 2 belonging to the acylation stage (associated with transition state TS2), which is consistent with the reported experimental observation. The overall free energy barrier (20.0 kcal/mol) calculated for the whole papain-catalyzed hydrolysis reaction process is reasonably close to the experimentally-derived activation free energy barrier of 17.9 kcal/mol, which suggests that the computational results are reasonable.