Investigating the Release of a Hydrophobic Peptide from Matrices of Biodegradable Polymers: An Integrated Method Approach

Abstract

The objectives of this work were: (1) to select suitable compositions of tyrosine-derived polycarbonates for controlled delivery of voclosporin, a potent drug candidate to treat ocular diseases, (2) to establish a structure-function relationship between key molecular characteristics of biodegradable polymer matrices and drug release kinetics, and (3) to identify factors contributing in the rate of drug release. For the first time, the experimental study of polymeric drug release was accompanied by a hierarchical sequence of three computational methods. First, suitable polymer compositions used in subsequent neural network modeling were determined by means of response surface methodology (RSM). Second, accurate artificial neural network (ANN) models were built to predict drug release profiles for fifteen polymers located outside the initial design space. Finally, thermodynamic properties and hydrogen-bonding patterns of model drug-polymer complexes were studied using molecular dynamics (MD) technique to elucidate a role of specific interactions in drug release mechanism. This research presents further development of methodological approaches to meet challenges in the design of polymeric drug delivery systems.

1. Introduction

Over the past several decades significant advances in the design and development of drug delivery systems (DDS) were made as a result of the impressive growth of biotechnology. Drug delivery devices and sophisticated formulations that allow controlling the rate and period of drug delivery as well as targeting specific areas of the body attracted special attention of biomedical research [1–3]. Polymeric DDS were used to provide controlled release of drugs and, in the cases of biomolecular delivery, to protect the drug from biological degradation prior to its delivery. The development of polymeric DDS rapidly progressed from non-degradable polymers, which rely exclusively on a diffusion process, to complex biodegradable polymer compositions in which drug release is governed by diffusion, swelling, and erosion. These materials degrade within the body, eliminating the need to remove the DDS after releasing the active agent and thus improving patient acceptance and compliance [1]. Polymer-based controlled DDS has become a possibility for multidisciplinary teams of biologists, chemists, and engineers to make a substantial contribution to human health care.

Polymer design for drug delivery is highly dependent on the specific device application [1]. For ophthalmic indications, drug delivery to eye tissues is particularly problematic despite the fact that the eyes are among the most accessible organs for medical treatment. Studies showed that ocular diseases associated with posterior segment of the eye remain the leading causes of the visual impairment in the industrial countries [4]. Advanced methods of controlled drug delivery for ophthalmic applications include polymeric injections, inserts and implants, nanoparticulates, microencapsulated cells and gene medicines [4]. It needs to be mentioned that each drug type has unique interactions with its surrounding polymeric matrix, and the release profile and other performance characteristics of the DDS should not be generalized. Several reviews [4–6] and original research papers [7–11] devoted to the development of ophthalmic DDS were recently published illustrating the importance of drug type and appropriate polymer compositions. In the present work the family of tyrosine-derived polycarbonates, specifically, compositions comprised of poly(DTE-co-y%DT-co-z% PEG_1K carbonate) which have been extensively studied in the laboratory of J. Kohn for more than fifteen years [12–18], was selected as a suitable material for controlled-release ocular DDS. Voclosporin, a derivative of the immunosuppressant cyclosporine A (CsA), was chosen as the model drug for incorporation into the polymeric matrices to create novel ophthalmic implants with controlled drug release properties. Voclosporin is 3–4 times more potent than its parent compound and it is currently in clinical trials as a next-generation treatment for ocular inflammatory diseases [19, 20].

Understanding the structure-function relationship of the polymeric material is of utmost importance to the design and development of controlled delivery devices [21]. In vitro drug release studies in conjunction with computational modeling reveal the structure-function relationships of the polymer matrices, contribute to the tailoring of polymeric material for optimal design of the DDS, and provide useful insights into the performance of DDS in vivo. However, the quantitative prediction of the performance of DDS is often difficult. A statistical approach such as response surface methodology (RSM) has been used in the development of different types of controlled-release DDS [22–24]. Sun et al. [25] described limitations of this polynomial approach and suggested artificial neural networks (ANN) as an alternative or complementary tool to RSM. ANN models were successful in predicting the properties and responses associated with drug release from polymer matrices, in particular drug release profiles [26–28], mechanisms of drug release [29], dissolution profiles [30], and in vitro release kinetics [31–33]. Sun et al. [25] also reported several examples where a statistical approach was employed in combination with ANN for formulation optimization. In these examples statistical experimental designs were carried out to reduce the number of experiments for data collection and to provide reliable data (with a minimum number of experiments) to train ANN models [25].

It is generally accepted that development of a quantitative understanding of the structure-function relationships in modern materials requires multi-scale modeling and simulations involving an integration of macroscopic and atomistic methods [34]. Molecular dynamics (MD) simulations demonstrated their power to represent real systems and to provide useful insights into molecular structures [35]. MD simulations of polymers have a relatively long and well established history from monitoring protein folding [36, 37] to investigations of mechanical properties of amorphous polymer solids [34, 38], to elucidation of structure and conformations in polymer solutions [39], and to studies of specific interactions in polymer blends and molecular complexes [40–43]. Distinctive features and the character of hydrogen-bonding networks in polymer-containing molecular systems have been the focus of several studies [35, 44–47]. However, only a few authors (Sandoval et al. [45], Molinelli et al. [46], Cilurzo et al. [47]) investigated a role of hydrogen bonding in polymer-polymer and drug-polymer complex formation.

In the present work the investigation of experimentally designed DDS was accompanied by a hierarchical sequence of three computational methods: response surface methodology, neural network modeling and MD simulations. Drug release measurements were carried out for a set of polycarbonate-based polymers. Selection of the most promising polymer compositions was aided and rationalized using the statistical modeling approach. This particular selection allowed us to build accurate neural network models and to predict drug releasing trends for the polymers outside the experimental domain thus providing guidance for the future polymer synthesis. We also hypothesized that hydrogen bonding interactions in drug-polymer complexes belong to the factors that contribute to the rate controlling release mechanism. Indeed, the excellent correlation between propensity of the polymer chains to form “a cage” stabilized by hydrogen bonds and their drug releasing ability in the experimental setting was established. Analysis of computed molecular properties helped us to understand better a role of non-bonded interactions in the drug release mechanism and to explain peculiarities of experimental behavior.

This article is organized as follows. In Section 2, the model drug, experimental methods as well as the computational models and techniques are described. In Section 3, experimental and computational results are presented and discussed. In particular, Section 3.1 is devoted to statistical modeling, drug release kinetics and mechanism; Section 3.2 describes computational analysis of experimental data followed by generation of training and predictive ANN models; Section 3.3 provides insights from MD simulations into thermodynamic behavior of model drugpolymer complexes, corresponding hydrogen-bonding pattern(s) and their possible role in the drug release mechanism. Finally, Section 4 is devoted to our concluding remarks.

2. Materials and methods

2.1 Model drug

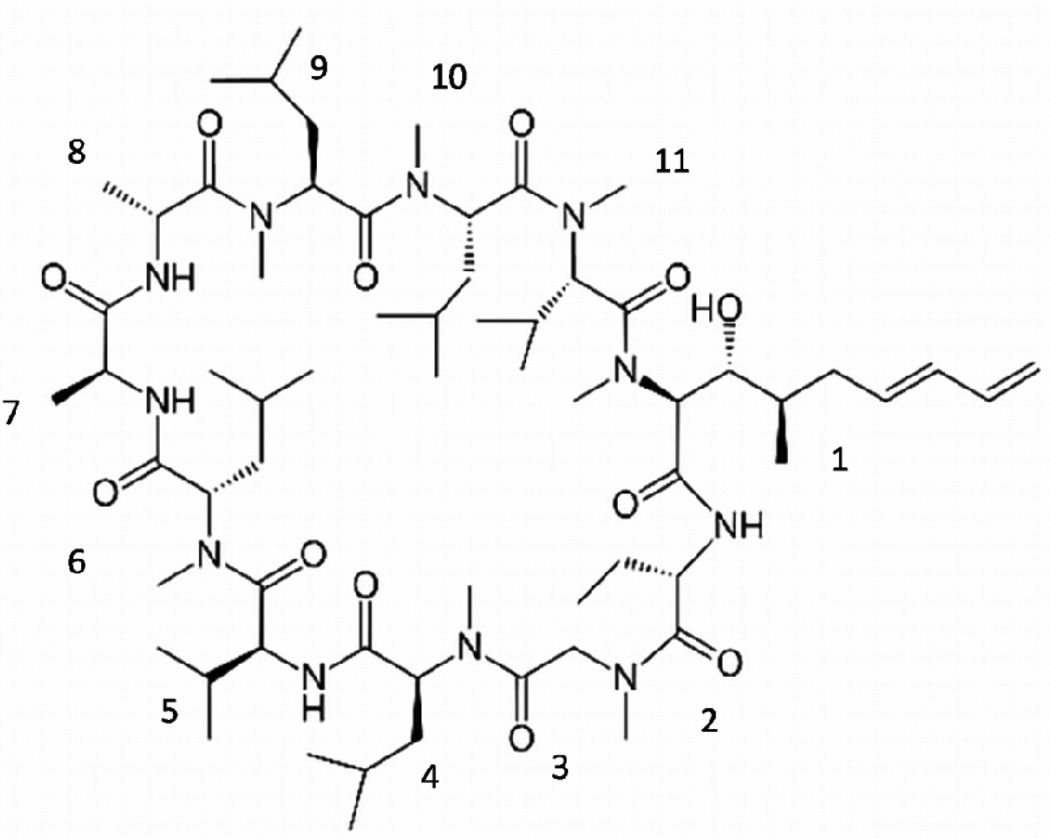
Voclosporin, developed by Isotechnika Inc. (Alberta, Canada) and licensed to Lux Biosciences Inc. (New Jersey, USA), was used in the present work to study polymeric drug delivery. Voclosporin is one of the most active derivatives of the immunosuppressant molecule CsA [48]. It is a cyclic undecapeptide consisting of 11 mainly hydrophobic amino acids that are not normally present in mammalian proteins. Seven amino acids of the 11-membered amino acid rings are N-methylated. The four remaining protonated nitrogen atoms can form intramolecular hydrogen bonds with carbonyl groups, which contribute to the rigidity of the molecular skeleton (see Figure 1).

Figure 1.

Chemical structure of voclosporin; 11 amino acid residues are numbered in a clockwise direction: (4R)-4-[(E)-2-butenyl]-4,N-dimethyl-L-threoneine (MeBmt), α-amino butyric acid (Abu), methylglycine (MeGly), N-methylleucine (MeLeu), valine (Val), MeLeu, L-alanine (Ala), D-alanine (D-Ala), MeLeu, MeLeu, N-methylvaline (MeVal).

2.2 Selection and preparation of polymers

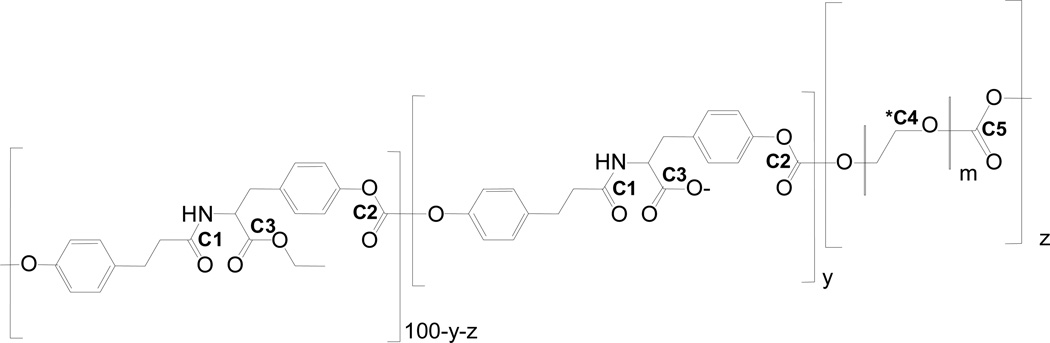
Polymer candidates were selected from the library of tyrosine-derived poly(DTE-co-y% DT-co-z% PEG_1K carbonate)s, where DTE, DT and PEG_1K abbreviate desaminotyrosyl-tyrosine ethyl ester, desaminotyrosyl-tyrosine, and poly(ethylene glycol) of molecular weight of 1kDa, respectively (Figure 2). Throughout this work, polymer compositions were expressed in mole percentage unless it is stated otherwise. Limits of compositions, specifically ‘y’ = 12% and ‘z’ =18% were determined from preliminary studies. Polymer compositions were selected using the 3,3 d-optimal design method available in Design of Experiment (DOE) software, Design-Expert v.7 [49]. The polymers were synthesized by means of a condensation reaction. Voclosporin was incorporated in polymer matrices by dissolving the drug and polymer in dichloromethane followed by film casting. The final test samples were hot compression molded into flat disks. The details of the polymer synthesis and sample preparation were reported in [50] and [51].

Figure 2.

Chemical structure of poly(DTE-co-y%DT-co-z%PEG_1K carbonate)s. The carboxy group of DT is shown in its ionized form. All carbon atoms covalently bonded to possible acceptors of hydrogen bonds are labeled and numbered consequently; *C4 represents all carbon atoms of PEG_1K bonded to oxygen atoms by a single bond.

2.3 Drug release measurements

The experimental conditions, procedure and selected results of drug release measurements (up to 35 weeks) were recently published [51]. In the experimental section of this work and the subsequent semi-empirical modeling the 12-week (84-day) cumulative drug release is presented and discussed since beyond this time point voclosporin was released at a steady rate.

2.4 Computational methods

2.4.1 Molecular models and descriptors

Twenty nine representatives of tyrosine-derived polycarbonates were employed in the modeling part of this study. The actual polymer compositions were approximated by an integer number of repeat units of DTE, DT and PEG and all polymer models were divided into two groups. The first group comprised fourteen unique compositions out of seventeen compounds characterized experimentally (Table 1) and the second group included fifteen “virtual” polymers that were not synthesized (Table 2 of the Supplementary Materials). The length of model polymer chains varied from 609 to 1226 atoms. The terminal hydroxy groups were substituted by hydrogen atoms on the benzyl ring of DTE or DT and by methyl groups on PEG to exclude a contribution of the polar terminals into the hydrogen-bonding network formed by the polymer chains. The carboxy groups of all DT monomers were presented in the ionized form. The order of monomers within each chain was randomized such that each of three repeat units was situated in the middle of a chain at least once.

Table 1.

Polymer compositions and naming conventions

Lattice points	Polymer number	Drug releasea)	Actual compositions, %			Model compositions b)			Model name
			DTE	DT	PEG1K	DTE	DT	PEG1K
Vertex	1	0.0984	100	0	0	13	0	0	pc13-0-0*
Vertex	2	0.0035	88	12	0	12	2	0	pc12-2-0 charge4*
Vertex	3	0.1305	82	0	18	11	0	2	pc11-0-2
Vertex	4	0.1544	70	12	18	9	2	2	pc9-2-2-charge4*
Third-edge	5	0.0489	96	4	0	13	1	0	pc13-1-0
Third-edge	6	0.0119	92	8	0	12	1	0	pc12-1-0
Third-edge	7	0.0148	94	0	6	13	0	1	pc13-0-1
Third-edge	8	0.0966	88	0	12	12	0	2	pc12-0-2
Third-edge	9	0.1108	82	12	6	11	2	1	pc11-2-1
Third-edge	10	0.1336	76	12	12	10	2	2	pc10-2-2-charge4*
Third-edge	11	0.1188	78	4	18	10	1	2	-
Third-edge	12	0.1156	74	8	18	10	1	2	-
Axial	13	0.0093	92.5	3	4.5	12	0	1	pc12-0-1
Axial	14	0.0194	86.5	9	4.5	12	1	1	pc12-1-1-charge2*
Axial	15	0.1179	83.5	3	13.5	11	0	2	-
Axial	16	0.1209	77.5	9	13.5	10	1	2	pc10-1-2
Centroid	17	0.1092	85	6	9	11	1	1	pc11-1-1-charge2*

^a)Average cumulative fractional drug release recorded after 84 days

^b)Model compositions are expressed in number(s) of repeat units where each unit of DTE, DT and PEG_1K contains 49, 42 and 157 atoms, respectively

^*Polymers selected for MD simulations

Table 2.

Expectation-Maximization cluster analysis of drug release data

Polymer	Model name	Time (days)
#		3	10	22	28	36
1	pc13-0-0	LOW	LOW	MEDIUM	MEDIUM	MEDIUM
2	pc12-2-0-charge4	LOW	LOW	LOW	LOW	LOW
3	pc11-0-2	MDIUM	HIGH	HIGH	MEDIUM	MEDIUM
4	pc9-2-2-charge4	HIGH	HIGH	HIGH	HIGH	HIGH
5	pc13-1-0	LOW	LOW	MEDIUM	LOW	LOW
6	pc12-1-0	LOW	LOW	LOW	LOW	LOW
7	pc13-0-1	LOW	LOW	LOW	LOW	LOW
8	pc12-0-2	MEDIUM	MEDIUM	HIGH	MEDIUM	MEDIUM
9	pc11-2-1	MEDIUM	MEDIUM	HIGH	MEDIUM	MEDIUM
10	pc10-2-2-charge4	HIGH	HIGH	HIGH	HIGH	HIGH
13	pc12-0-1	LOW	LOW	LOW	LOW	LOW
14	pc12-1-1-charge2	LOW	LOW	LOW	LOW	LOW
16	pc10-1-2	HIGH	HIGH	HIGH	HIGH	HIGH
17	pc11-1-1-charge2	MEDIUM	MEDIUM	HIGH	MEDIUM	MEDIUM

All polymer models were built using Molecular Operating Environment (MOE) simulation package [52]. For the semi-empirical modeling part of the study, single polymer chains were optimized using OPLS all-atom force field [53, 54] and the entire pool of 184 two-dimensional (2D) molecular descriptors incorporated into MOE software was calculated for each polymer. MOE descriptors were used in previous studies to build several successful semiempirical models and to generate accurate prediction of polymeric gene delivery [55] and bioresponses on a surface of biodegradable polymers from the libraries of polyarylates [56] and polymethacrylates [57]. These descriptors were expected to be sufficiently powerful for the prediction of polymeric drug release profiles.

2.4.2 Semi-empirical modeling

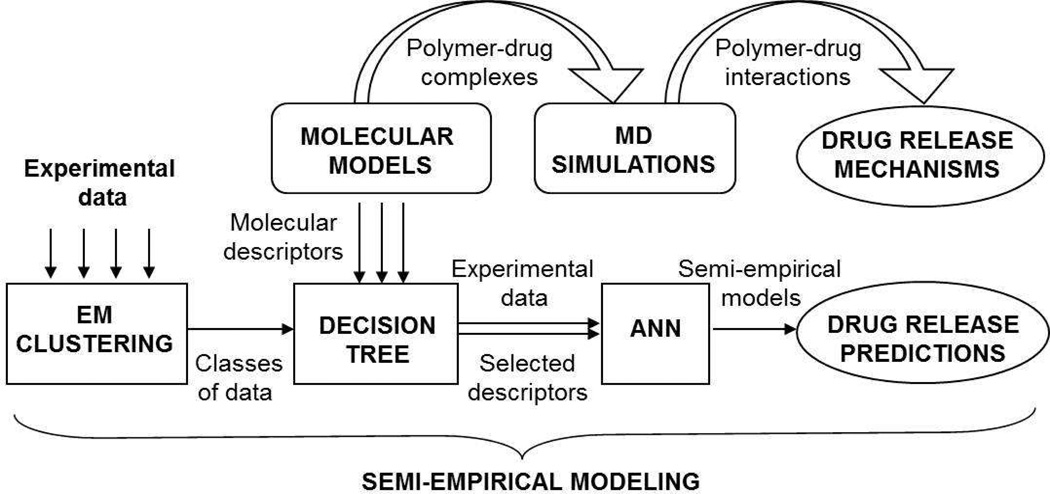
Semi-empirical modeling of polymeric drug release included several consecutive computational steps such as cluster analysis of the raw experimental data, selection of the most significant molecular descriptors by means of a Decision Tree algorithm, and the generation of ANN models to predict drug release profiles (Figure 3). The data-mining package WEKA (Waikato Environment for Knowledge Analysis [12]) was used in this part of the study. Semiempirical models were built using the average (over three experimental trials) values of cumulative drug release for time intervals of 3, 10, 22, 28 and 36 days.

Figure 3.

Schematic representation of the computational modeling procedure.

Expectation-maximization (EM) cluster analysis [58, 59] was employed to categorize the cumulative drug release data for all polymeric systems into three classes (i.e., low, medium, and high). EM is an iterative process consisting of both expectation (E) and maximization (M) steps. During the E step, cluster probabilities were calculated, given the current estimate of the parameters. During the M step, parameters were re-estimated to achieve a maximum likelihood using the distribution information determined in the E step.

Decision Tree algorithms developed for a descriptor analysis generate rules underlying experimental data with hierarchical, sequential structures that recursively divide the data into subsets based upon the best classifying descriptors at each level [56]. The J48 algorithm (C4.5 Decision Tree family [60]) was used to evaluate the significance of each descriptor with respect to the set of experimental drug release data, according to the classes identified by the cluster analysis.

Machine-learning algorithms based on neural networks allow complex, non-linear and parallel analysis of data [61]. In the WEKA data-mining package a feed-forward ANN utilizes a multi-layer perceptron module that includes a set of source nodes (neurons) as an input layer, a set of computational nodes combined into one (hidden) layer, and a set of nodes as an output layer. To build the ANN models of drug release, all input variables were scaled to the unit interval while the learning rate and the momentum applied for updating the weights were 0.3 and 0.2, respectively. Randomization of the initial weights and shuffling of the training data were performed by varying (up to 10 times) the seed of a random number generator to achieve full convergence of the predicted values. A Monte Carlo (MC) approach was used to account for the experimental uncertainty and to improve the accuracy of the results. A series of 100 computerbased pseudo-experiments were generated to randomly perturb the measured values of drug release within a normal distribution defined by the experimental mean and standard deviation.

ANN models of polymeric drug release were built using two, three, and four of the most significant descriptors identified by the J48 Decision Tree. The training set comprised eleven polymers numbered from 1 to 10 and 17 in Table 1. All polymers situated in vertexes, third edges and centroid points of the lattice generated by the DOE software [49] for polycarbonate compositions were used in the training, while polymers located in axial points were used in the validation set. Validation of the model was performed by means of a k-fold cross-validation with 2<k< 11 (i.e., from 50% to 10% left out, respectively). Experimental measurements of drug release were carried out for 3 additional polymers (numbered 13, 14 and 16, Table 1) to provide an external validation and assess the accuracy of the final ANN model. The best ANN model identified in the validation procedure was used to generate predictions for fifteen polymers that were not characterized experimentally and not included in the DOE compositions.

2.4.3 MD simulations

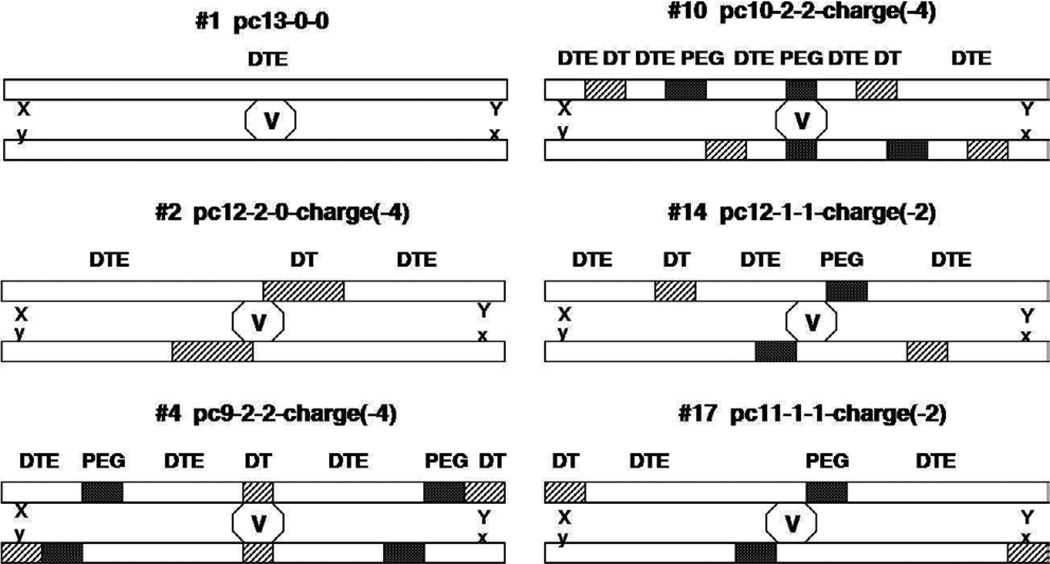
In the MD part of the present work, seven model complexes were built to study drug-polymer and polymer-polymer interactions. First, the experimental crystal structure of CsA, (from a 1CWH PDB file) was computationally modified and optimized to produce voclosporin in its the most potent trans conformation [62]. Then, a molecule of voclosporin was positioned between two anti-parallel polymer chains to mimic a molecular arrangement observed in supramolecular complexes of CsA and cyclophilin species, where CsA was bound to antiparallel (β–barrel of the enzyme [63, 64]. The drug molecule was placed between the polymer chains to maximize the hydrogen-bonding interactions between polar groups of both the drug and middle locations of the polymer chains. This arrangement allowed us to place either the DTE, DT or PEG in the vicinity of the centered drug molecule. A schematic representation of the drugpolymer molecular complexes is given in Figure 4.

Figure 4.

Schematic representation of model systems used in MD simulations.

MD simulations of the molecular complexes were performed using the MacroModel (version 8.5) simulation package [65]. The generalized Born/surface area (GB/SA) implicit solvent model [66] was employed to represent an aqueous environment around each complex. Similar to our previous MD study of tyrosine-derived polyarylates [56] the OPLS all-atom force field was used throughout this work [53]. The molecular systems consisting of the voclosporin molecule located between two polymer chains in extended conformation were minimized in the presence of implicit water by means of the Polak-Ribiere Conjugate Gradient (PRCG) method to eliminate close contacts and unrealistic atomic positions. These minimized complexes were used as starting configurations for constant temperature (NVT) MD simulations performed at 300 K (maintained by a Nose-Hoover thermostat) with an integration time step of 1 fs. Long range electrostatic interactions were handled by means of Bond Dipole Cutoff (BDCO) method incorporated into MacroModel suite. This method was previously tested on charged complexes of biomolecules and demonstrated satisfactory results [64]. Extended cutoff distances of 8Å and 20Å were used for non-bonded and electrostatic interactions, respectively, and the dielectric constant was set to 80. Drug-polymer complexes were pre-equilibrated for 0.5 ns and then equilibrated for 0.7 ns until convergence of the energy was achieved. The total simulation time was 2.5 ns where the latter 1.3 ns was the production stage. The trajectory was sampled over the 2 ps intervals and an average number inter- and intramolecular hydrogen bonds formed within complexes were calculated using the simulation package Mercury [67].

3. Results and discussion

3.1 Polymeric drug release

3.1.1 Statistical model and analysis

A response surface methodology (RSM) was used to estimate the effect of polymer composition(s) on drug release response inside and outside the experimental domain. Design-Expert software v.7 was used to generate the design space and to select a suitable statistical model.

Empirical models were obtained with fractional compositions of DTE (X₁), DT (X₂), and PEG_1K (X₃) in the tyrosine-derived polycarbonates. Limits of experimental compositions were: 70 mole %≤X₁≤100 mole %; 0 mole %≤X₂≤12 mole %; 0 mole %≤X₃≤ mole 18%; and X₁+X₂+X₃=100 mole %. Assignment of the experimental points in the design space is shown in Figure 1 of the Supplementary Materials.

The statistical tests including analysis of variance (ANOVA) were carried out to assess the significance of each model and its coefficients. Sequential model sum of squares was used to identify the highest order polynomial with significant terms that are not aliased [49]. The reduced cubic model was chosen while maintaining hierarchy of the model and a 0.05% level of significance. The corresponding equations in general terms and in terms of real components were:

$$Y=b_1{X}_1+b_2{X}_2+b_3{X}_3+b_{12}{X}_1{X}_2+b_{23}{X}_2{X}_3+b_{13}{X}_1{X}_3+b_{13}(X_{1^{-}}{X}_3),$$

where Y is a dependent variable, namely drug release, b_i are estimated coefficients for the corresponding components X_i namely, polymer compositions, and

$$DR=0.0932X_1+7.0094X_2-51.6300X_3-8.6367X_1{X}_2+88.1201X_1{X}_3+31.4991X_2{X}_3-38.7304X_1{X}_3(X_1-X_3).$$

The regression coefficients of the model (R² =0.88, adjusted R² =0.81, predicted R² =0.52) with residuals randomly distributed around zero confirmed a good correlation between the values of the average cumulative fractional drug release (given in Table 1) and polymer compositions. Conventionally, RSM is employed to optimize a formulation. In the present study, it has been used to rationally design polymer compositions, to gain additional insights into the drug release behavior, and to select representative polymers for subsequent computational modeling.

3.1.2 Influence of polymer composition

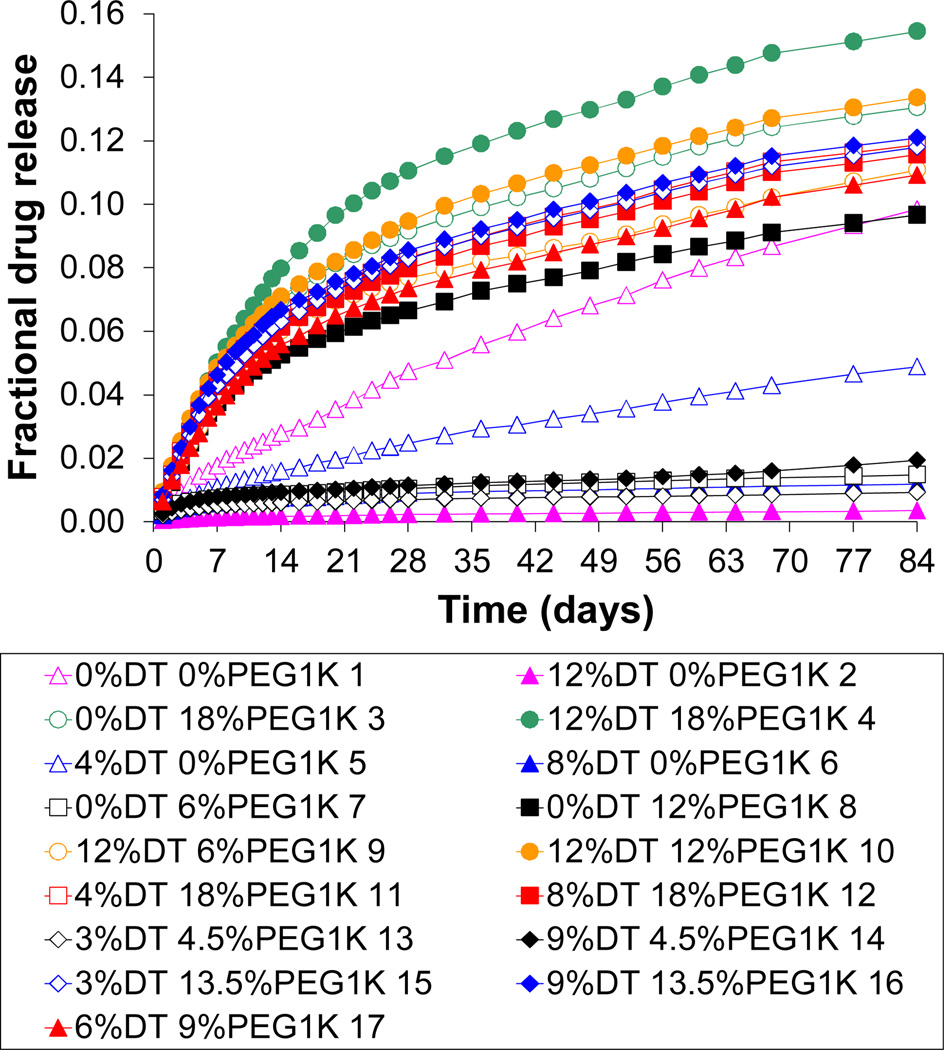
In vitro cumulative fractional release of voclosporin from the selected polycarbonate matrices measured over a period of 84 days is shown in Figure 5. The following compositions exhibited relatively slow drug release: (a) the compositions containing only DTE and DT, (b) the compositions of DTE and PEG_1K, where PEG_1K content was ≤ 6 % and (c) the compositions where DT and PEG_1K content was ≤ 9 % and ≤ 4.5 %, respectively. All other compositions examined in this study, including the homopolymer poly(DTE carbonate), demonstrated a relatively fast release of voclosporin.

Figure 5.

In vitro cumulative fractional release of voclosporin (initial loading of 30 wt. %) from poly(DTE-co-y% DT-co-z% PEG_1K carbonate)s after 84 days in phosphate buffered saline (PBS) at 37°C.

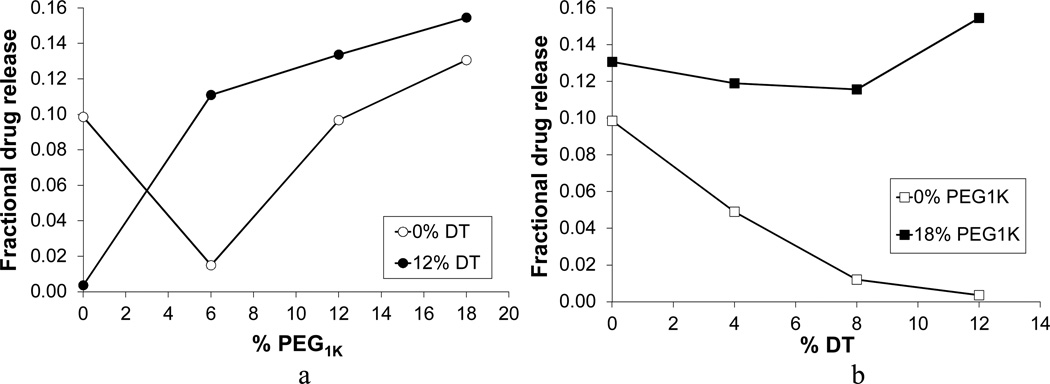
In Figure 6a, a nonlinear increase in drug release is observed as the PEG_1K content increases for the polymer compositions with 0 and 12% of DT, where terpolymers demonstrate higher values of drug release than their respective copolymers without DT. The homopolymer, poly(DTE carbonate), was the only exception: it showed higher release than its respective p(DTE-co-12% DT carbonate) copolymer. This somewhat unexpected behavior is explained in Section 3.3.

Figure 6.

Effect of polymer composition on average cumulative fractional release of voclosporin after 84 days: (a) 0 and 12% of DT with varied PEG_1K content; and (b) 0 and 18% of PEG_1K with varied DT content.

In Figure 6a, a nonlinear increase in drug release is observed as the PEG_1K content increases for the polymer compositions with 0 and 12% of DT, where terpolymers demonstrate higher values of drug release than their respective copolymers without DT. The homopolymer, poly(DTE carbonate), was the only exception: it showed higher release than its respective p(DTE-co-12% DT carbonate) copolymer. This somewhat unexpected behavior is explained in Section 3.3.

The effect of increasing DT content on drug release from the compositions with 0 and 18% of PEG_1K is shown in Figure 6b. For the polymers containing only DTE and DT, there was a substantial decrease in drug release as the DT content increased. This decrease in drug release was not observed in the respective terpolymers with 18 % of PEG_1K, where drug release was invariant, indicating the dominant effect of PEG_1k.

In general, for the studied poly(DTE-co-y% DT-co-z% PEG_1K carbonate)s an increase in the content of PEG_1K led to an increase in the release of voclosporin. Similar to Khan et al. [51], the synergistic influence on the drug release by both DT and PEG_1K components of the terpolymers was observed. The other results reported by the research group of J. Kohn [18], also demonstrated that the simultaneous presence of PEG and DT in the terpolymers has a synergistic effect on accelerating both the rate of degradation (i.e., molecular weight loss) and the rate of resorption (i.e., mass loss).

3.1.3 Drug release rate

Biodegradable polymer matrices typically exhibit multi-phase drug release profiles which include (a) an initial phase (i.e., initial burst) characterized by the rapid delivery of drug upon hydration, (b) a lag phase categorized by a near-zero order rate of release for some period of time, and (c) a final phase where measurable release resumes [68, 69]. It has been reported recently that poly(DTE-co-y% DT-co-z% PEG_1K carbonate)s have drug release profiles equivalent to near-zero order release due to the balancing act between diffusional slowdown and acceleration of the release rate by erosion [50]. Drug delivery systems that exhibit drug release at or near-zero order have drug release coefficients that are essentially unchanged relative to the arithmetic mean over the sustained release phase of drug delivery under physiological conditions. In some cases the release rate of drug from the biodegradable matrix varies by (but no more than) ±5%, ±7%, ±9%, and ±10% over the sustained release phase following the initial burst [50].

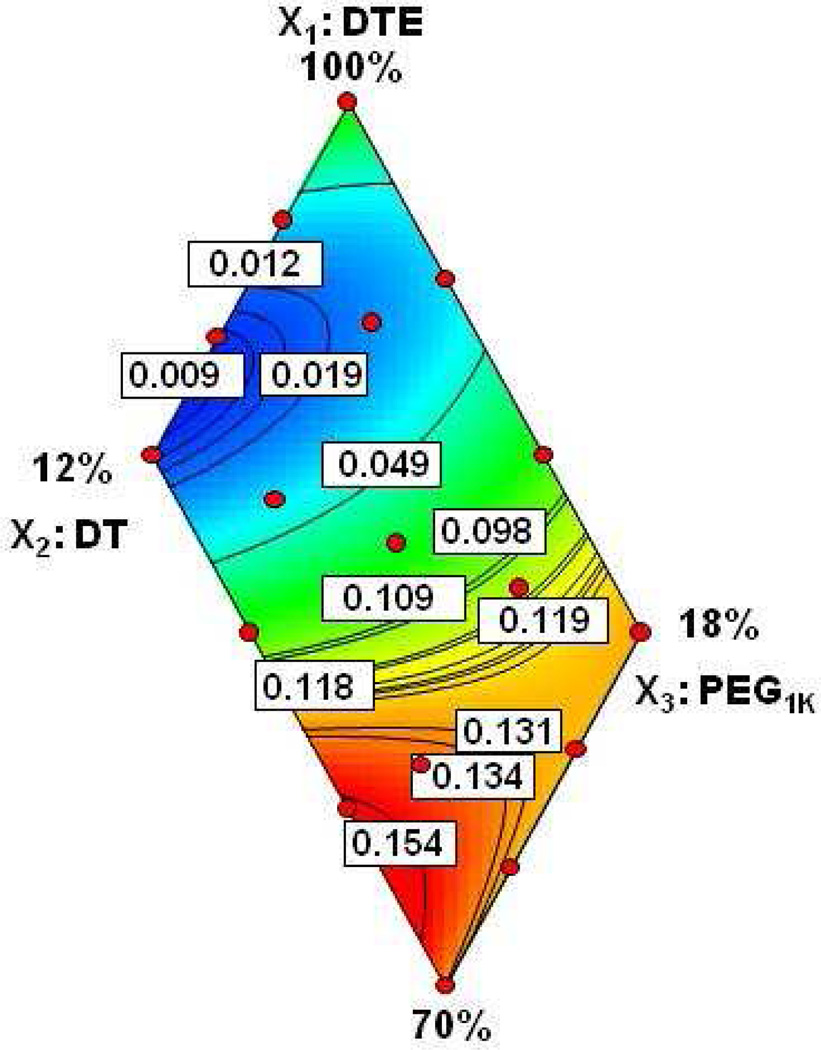
The polynomial equation 2 (Section 3.1.1) was used to generate a two-dimensional response surface map (Figure 7) that illustrates the empirical relationship between the drug release values and the polymer compositions. In Figure 7, the area colored in dark blue represents a near-zero release of voclosporin, i.e., almost complete retention of the drug within the polymer samples.

Figure 7.

Response surface map of in vitro cumulative fractional release of voclosporin measured after 84 days in PBS at 37°C.

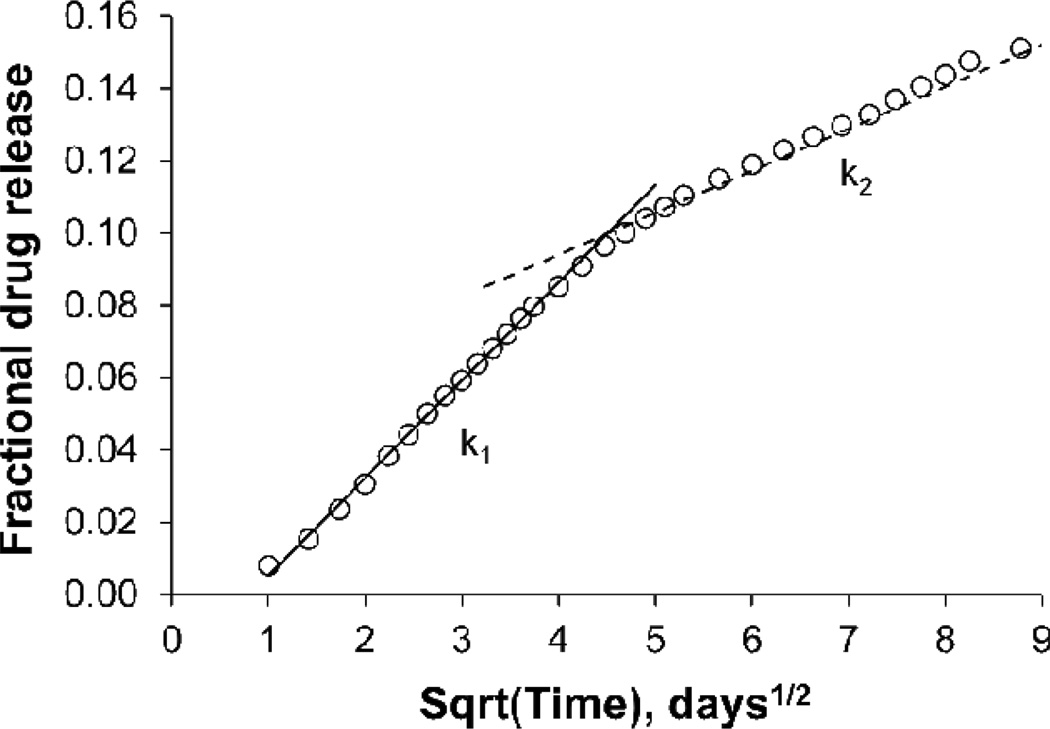
To examine drug release kinetics in more detail a persistence factor, defined as η_p = k₂/k₁, where k₁ is the overall diffusional rate constant in the early-stage drug release and k₂ is the overall diffusional rate constant in the late-stage drug release, was utilized. If k₂ = k₁ then η_p= 1 and drug release persists at the same diffusion rate in both stages of release. This state corresponds to the classical diffusion-controlled release described by Fick’s law. If k₂ = 0 then η_p= 0 and drug is no longer being released. This state is described as full drug retention. If 0≤η_p ≤ 1, the system is in various degrees of drug retention. Most of the experimentally tested terpolymers fall into this category (a typical example is given in Figure 8). If η_p > 1 then the system is predominantly controlled by erosion or swelling.

Figure 8.

Average cumulative fractional release of voclosporin after 84 days in PBS at 37°C. Rate constants k₁ and k₂ corresponding to the diffusion-controlled release are typical for most of the tested terpolymers.

Figure 8 demonstrates the change in a drug release rate for poly(DTE-co-12%DT-co-18%-PEG_1k carbonate)s. The slowdown in the drug release rate, k₂, is apparent. It is interesting to note that polymer erosion in this sample was relatively fast in comparison with the other experimental terpolymers, yet drug release was not predominantly controlled by the erosion. If erosion were dominant, then the experimental data points would deviate to the left of either the k₁ or k₂ line.

3.1.4 Drug release mechanism

It has become a widely accepted point of view that degradable delivery systems control drug release via fundamental phenomena such as diffusion (passive movement of drug), degradation (breakdown of the polymer structure), erosion (mass loss from the polymer matrix) and dissolution (the solubilization of drug) [68, 69]. Since every delivery system has unique physicochemical properties (e.g., in the present case, the drug is a hydrophobic cyclic peptide) a drug release behavior of one polymer system is not predictive of behavior of other polymer systems. Kohn et al. reported that two-component drug-polymer blends providing near-zero order release are uncommon and it is a challenge to formulate polymer compositions in which acceleration by erosion and deceleration by diffusion cancel each other over longer periods of time [50].

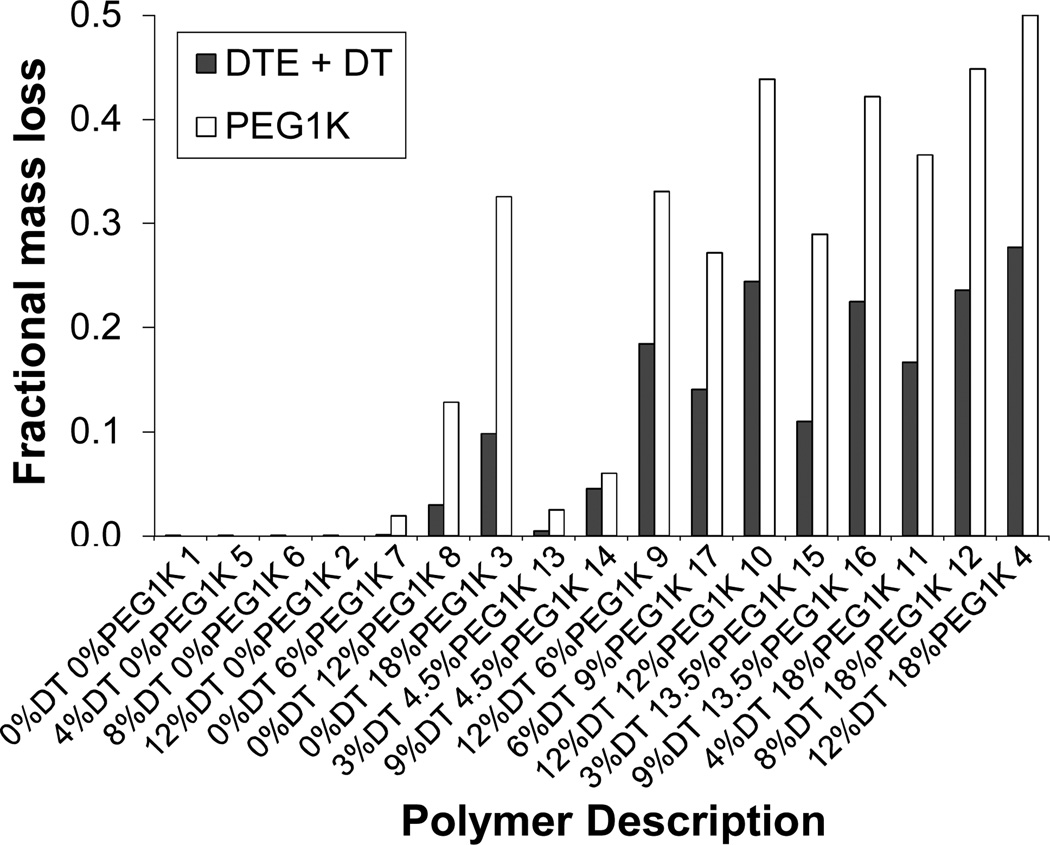
Figure 9 shows the relative fractions of DTE+DT and PEG_1K that eroded from the polymer matrices during a period of three months (84 days). In the terpolymers undergoing erosion, more fractional PEG_1K was lost. This indicates the possibility of preferential hydrolytic chain scission of the polymer backbone at the PEG_1K carbonate bonds. The need of PEG_1K in the polymer backbone to accelerate erosion is also reflected in the Figure 9. The polymers without PEG_1K content (e.g., 1, 5,6, and 2, Table 1) showed no detectable mass loss in three months. A threshold of >6% PEG_1K or a threshold > 3% DT-co-4.5% PEG_1K was required for detectable erosion. These results illustrate once more the synergistic relationship between DT and PEG_1k and the minimum amount of each constituent needed for relatively rapid polymer erosion.

Figure 9.

Cumulative fractional erosion of DT and PEG_1K components of polymer matrices loaded with voclosporin (initial loading 30 wt. %) after 84 days in PBS at 37°C. Numbers at the end of each polymer description correspond to the point assignment in the experimental design space.

Additional comparison of the 84-day cumulative fractional drug release and 84-day cumulative fractional polymer erosion for poly(DTE-co-y%DT-co-z%-PEG_1k carbonates) revealed two distinctive groups: fast eroding polymers with good drug release capability and slow eroding polymers with poor drug release capability. No cross-groups were observed (Figure 2 of Supplementary Materials).

In Figure 7, the response surface map shows a non-linear effect of DT and PEG_1k components on drug release and confirms that the high DT-co-PEG_1k content terpolymers (e.g., 4, 10, 12 and 16, Table 1) are the best drug releasing candidates. This outcome is not surprising, but it is necessary to identify the limits of the polymer compositions that give a desired performance for drug release and concomitant erosion. Analysis of the data allows locating a region on the response surface map (shown as the red region in Figure 7) where polymer erosion and drug release are relatively high for the terpolymer compositions with DT ≥8% and PEG_1k ≥12%. It is possible, however, to have more than one set of parameters that fit the experimental data.

The rate of diffusion and the rate of polymer degradation/erosion are not the only characteristics responsible for a zero or near-zero order release behavior of DDS. The decreasing concentration gradient and increasing diffusion distance counterweighted by increasing porosity associated with erosion as well as the difference in the transport resistance are among the possible factors to be considered [69].

3.2 ANN modeling and validation

3.2.1 Data analysis and selection of the most significant descriptors

EM cluster analysis was initially applied to the entire pool of experimental data recorded after 36 days of drug release. These data were grouped into 6 bins (i.e., instances of similarity in terms of cumulative release were assigned to the same bins), specifically: 1–3; 4–20; 22, 24, 26– 28, and 32–40 days. To simplify the modeling procedure, the most representative data points from the first, second, fifth and sixth groups were selected (i.e., data corresponding to 3, 10, 22, 28, and 36 days of cumulative drug release) and the mean values were further classified as low, medium, and high. Results of the EM clustering are shown in Table 2, where the numerical order given in Table 1 is reproduced. The polymers selected for the test and validation sets were preliminary classified as possessing low (polymers 2, 5, 6, 7, 13 and 14), mainly medium (polymers 1, 3, 8, 9, and 17) and high (polymers 4, 10 and 16) drug releasing capability. Table 2 shows that after the 22nd day of in vitro drug release measurements the observed classification trends become “stabilized” for all polymers in the set.

In the next step, the J48 Decision Tree algorithm was used (a) to reduce the total number of calculated descriptors (184) by removing highly correlated descriptors and those that contain the same information, as well as (b) to identify the most significant descriptors associated with polymeric drug release. The four best descriptors identified by Decision Tree for each time point are summarized in Table 3.

Table 3.

Two-dimensional molecular descriptors selected by Decision Tree

Time (days)	Codea)	Class[52]
3	GCUT_PEOE_2	Distance matrix descriptor
	DTE	Composition of DTE
	PEOE_VSA-5	PEOE partial charge
	PEOE_VSA+5	PEOE partial charge
10	GCUT_PEOE_2	Distance matrix descriptor
	SlogP-VSA7	Subdivided surface area
	PEOE_VSA-1	PEOE partial charge
	PEOE_VSA-5	PEOE partial charge
22	BCUT-SMR_3	Adjacency matrix descriptor
	SlogP_VSA4	Subdivided surface areas
	PEOE_VSA-5	PEOE partial charge
	DT	Composition of DT
28	DTE	Composition of DTE
	GCUT_PEOE_2	Distance matrix descriptor
	PEOE_VSA+5	PEOE partial charge
	PEOE_VSA-5	PEOE partial charge
36	SlogP-VSA7	Subdivided surface areas
	GCUT_PEOE 2	Distance matrix descriptor
	PEOE_VSA-1	PEOE partial charge
	PEOE_VSA-5	PEOE partial charge

^a)Descriptors are given in order of significance

Several of the descriptors were repeated from group to group with a slight variation in their order (i.e., significance). Thus, to relate molecular characteristics of the eleven polymers in the test set with the corresponding cumulative drug release, a “universal” set of four descriptors was selected. These descriptors, in order of relevance, were GCUT_PEOE_2, DTE, PEOE_VSA-5, and SlogP_VSA7 (for detailed description see Ref. [52] and Table 1 of Supplementary Materials). It is not surprising that two descriptors strongly associated with accessible van der Waals surface areas (PEOE_VSA-5 and SlogP_VSA7) were identified as significant for the polymers designed to become potential implants with the surfaces exposed to body fluids. Contributions to PEOE_VSA-5 and SlogP_VSA7 from PEOE partial charges (i.e., atomic partial charges calculated by the Partial Equalization of Orbital Electronegativities method [70]) and SlogP descriptors, respectively, reflects the most prominent chemical features of the DT and DTE monomers, namely the presence of charged oxygen of free carboxylic groups in DT and overall hydrophobic nature of DTE. The influence of hydrophobicity on drug release is also emphasized by selecting the composition of DTE as one of the significant descriptors. The distance matrix descriptor GCUT_PEOE_2, with PEOE partial charges as diagonal elements, highlights the structural specificity of the polymers by taking into account the mutual locations of atoms in polymer chains and the presence of charged group(s). The delicate balance between hydrophobicity, hydrophilicity and accessible surface areas in the experimentally studied polymers was reflected in the corresponding molecular models and encoded in the “universal” set of the four descriptors selected by the Decision Tree algorithm.

3.2.2 Features and sensitivity of ANN models

The ANN models of polymeric drug release were built using the sets of two, three or four “universal” descriptors described in the previous section. Ten models were built for each of the selected points on the drug release profiles to study the effect of a number of random seeds (from 1 to 10) in each model. The model obtained with each seed represents a local optimum, based on the initial weights. Thus, running enough seeds and selecting the best model among them would allow finding the global optimum. It was determined that a sequence of five random seeds is sufficient for achieving a convergence of the predicted drug release values. The final models for each of the selected time points were obtained by averaging over ten such trials. All ANN models were trained on eleven polymers in the training set. The accuracy of the models was evaluated by calculating an average Pearson correlation coefficient, R, and relative absolute error, RAE.

First, performance of each model was tested by the sequential use of two, three and four descriptors. Utilization of three descriptors instead of two improved the correlation coefficient and decreased the RAE. However, only insignificant improvement was observed after utilization of all four descriptors. For all models, the correlation coefficient varied within a range of 0.94–0.98 while the relative absolute error was less than 2.3 times the experimental error (Figure 3a of the Supplementary Materials).

The sensitivity of the ANN models of drug release was further tested by taking into consideration the experimental uncertainty using a Monte Carlo approach. A sequence of 50 and 100 pseudo-experiments was carried out by varying the values of drug release in a random fashion within a normal distribution defined by the experimental mean and standard deviation [71]. The drug release values used in MC calculations were obtained by averaging over 100 MC runs. For all models, the average correlation coefficient was in the range of 0.92±0.03–0.98±0.01 and RAE was less than 2.5 ± 0.5 times the experimental error (Figure 3b of the Supplementary Materials).

The model prediction of three days of voclosporin release, generated using the MC technique described above and the entire set of four descriptors, has a correlation coefficient of 0.98±0.01 and RAE of 19±4%. However, starting from 22 days and beyond, the correlation coefficient and RAE gradually changed to 0.95±0.02 and 33±6%, respectively, as predicted for 36 days of cumulative drug release (Figure 3b of the Supplementary Materials). This observation sheds light on an important issue associated with the utilization of descriptor-based computational models for predicting drug release from biodegradable polymer matrices. After a certain point of in vitro drug release, polymer degradation begins to make a “contribution” to the release profile(s), thereby making the molecular descriptors that encode the original polymer structures less applicable. As the degradation process proceeds the initially derived descriptors gradually lose their predictive power which becomes reflected in the model performance. Routine monitoring of key model parameters would enable us to identify (predict) time points when the in vitro degradation process begins and to define time-dependent limits of applicability for descriptor-based semi-empirical models of polymeric drug release.

The available training set for ANN modeling was relatively small (i.e., eleven polymers). As such, the previously tested and successful 2-fold validation protocol, where 50% of experimental data were used as the training set and the remainder as the test set, was extended to an 11-fold validation procedure. The drug release data collected over 36 days were used for cross-validation of the least accurate of ANN models to estimate possible limits of its applicability. The k-fold validation protocol with k ≥5 provided the best results with a correlation coefficient of 0.74 ± 0.10 and a RAE less than 62 ± 13%, and confirmed the statistical significance of this ANN model.

3.2.3 Prediction of drug release

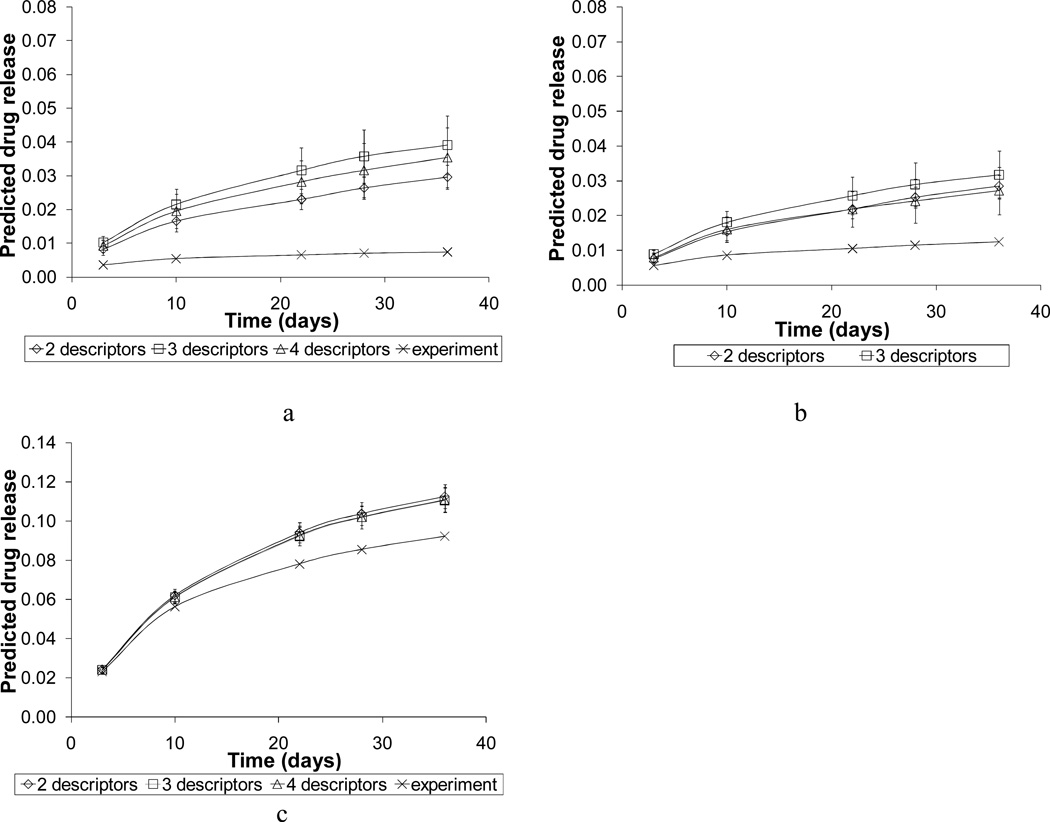
The most accurate ANN models were further validated by predicting drug release profiles for two polymers with low drug release values (pc12-0-1 and pc12-1-1-charge2), and one polymer with high drug release values (pc10-1-2). These three polymers were chosen from the molecular space that was defined by RSM for training ANN models; however they were not used in either the cluster analysis or in the descriptor selection. Figure 10 shows that the correct level of drug release was successfully reproduced for all three polymers and that the predicted values did not exceed experimental estimates by more than 3 %. The predicted release profiles obtained with the set of four descriptors compared more favorably with the experimental results than those calculated with the sets of two or three descriptors.

Figure 10.

Predicted drug release profiles for polymers (a) pc12-0-1, (b) pc12-1-1-charge2, and (c) pc10-1-2 that compose the external validation set. Experimental uncertainty was taken into account by 100 Monte Carlo iterations.

To predict drug release profiles for a set of similar polycarbonates located outside of the molecular space defined by the RSM design (see the unshaded area in Figure 1a of the Supplementary Materials), fifteen virtual polymer compositions ranging from 36–80% for DTE; 0, 3–32% for DT and 0, 20–64% for PEG_1k were built. Their naming convention, model and actual compositions are given in Table 2 of the Supplementary Materials. The aim of this particular selection was two-fold. First, it would provide a comparison between predicted and experimentally determined trends and second, it would exhibit the influence of compositions on drug release kinetics, unknown from the experimental perspective.

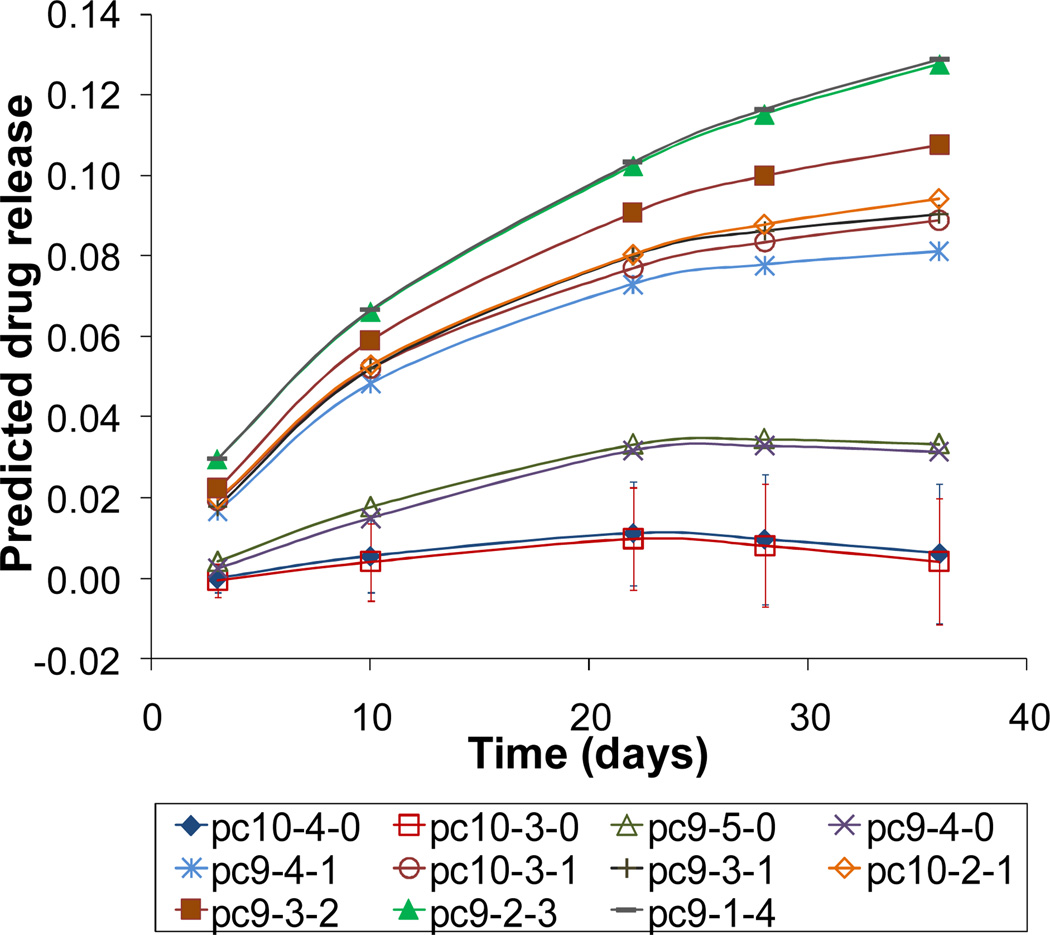
Drug release profiles predicted for the fifteen, design-independent virtual polymers were obtained using the protocol adopted in the training and validation steps. The sets of two, three and four descriptors were employed sequentially and the MC routine was used to get the best estimate of errors. The predictions obtained with all three sets of descriptors correctly reproduced the general trends observed experimentally in copolymers: elevation of drug release values with increasing the PEG_1K content and lowering of release profiles for the high DT compositions. The best representation of the observed trends was achieved using a set of four descriptors as shown in Figure 11. For the sake of clarity, drug release profiles of copolymers pc10-0-3, pc9-0-4, pc9-0-5 and the terpolymer pc10-1-3 are not shown in Figure 11; their release profiles (and corresponding trends) are similar to pc9-2-3 and pc9-1-4.

Figure 11.

Drug release profiles predicted for eleven representatives of the virtual polymers using a set of four descriptors and 100 MC iterations. Error bars are shown only for data points that have negative or near-zero values.

Visual inspection of eleven representative profiles shown in Figure 11 allows identification of two groups of polymers: a group of four copolymers with a relatively high DT and DTE contents (20–32%, 68–87%, respectively) and a group of seven terpolymers with high PEG_1K content (20–47%) and relatively low compositions of DTE (36–67%). In the first group, the experimental trend of lower drug release profiles for high DT containing polymers in the absence of PEG_1K is reproduced (e.g., see the experimental profiles 2 and 6, Figure 5) though slightly overestimated: two data points have negative mean values. Accounting for experimental error allows us to classify two out of these four compositions (specifically pc10-4-0 and pc10-3-0) as polymers that exhibit nearly complete drug retention. In the second group, a gradual nonlinear increase of the PEG_1K content leads to a steady nonlinear increase in drug release values. This trend is associated with the gradual decrease in DT content (i.e., 22%, 17%, 14%, 8%, and 3%) as well as with lowering DTE content from 68% to 40%. Drug release behavior predicted for all polymers with 0% DT and the high composition of PEG_1K (i.e., the model predictions for pc10-0-3, pc9-0-4 and pc9-0-5 in comparison with the experimental profiles 3 and 8, Figure 5) is in excellent agreement with experimentally observed trends.

3.3 Insights from MD simulations

3.3.1. General characteristics of simulated systems

Six molecular systems selected for MD simulations included polymers characterized by low, medium and high drug release. In a framework of each system, a mutual position of two polymer chains, location of monomers in the vicinity of the drug and orientation of the drug with respect to the polymers were rationally randomized to model as closely as possible a natural distribution of the drug in the polymer matrices. Similar to the modeling approach adopted by Cilurzo et al. [47], the polymer matrices were represented by molecular dimers with carboxyl groups of DT in their ionized form (i.e., containing from two to four negatively charged oxygen atoms per dimer) to study the behavior of charged molecular complexes. In several features, the present molecular models were more realistic than those employed by Subashini et al. [43] who reported MD simulations of drug uptake using models consisting of drug molecules interacting with a single polymer chain. In contrast to the studies mentioned above [43, 47], the GB/SA solvent model was used throughout this work to mimic an implicit aqueous environment. Jaud et al. [72] reported MD simulations using the OPLS force field in conjunction with the GB/SA solvation model to circumvent errors inherent in rotational isomeric state (RIS) treatment of polymer nano- and picosecond dynamic, to gain computational speed and to explore longer relaxation times. In addition to the obvious computational gain, this choice allowed us to focus exclusively on drug-polymer and polymer-polymer hydrogen-bonding interactions and their contribution to the process of drug release.

A concept of hydrogen bond balance is applicable not only to individual (i.e., hydrogen bond donating or accepting) sites but also to redistribution of intra- and intermolecular hydrogen bonds within a molecular system of interest. One more reason of excluding explicit contacts with water molecules was to examine (a) what polymers would form hydrogen bonds with a few hydrogen bonding sites of the drug (despite its overall hydrophobic nature), (b) what polymers would interact through hydrogen bonding network with each other forming “a cage” that encapsulates the drug, and (c) what polymers would fold due to preferential intramolecular hydrogen bonding, giving rise to the chain separation and formation of water filled pores observed in the actual experimental environment.

Simulation results for thermodynamic properties of the model systems, specifically the average bond, bond angle, and dihedral angle energies (<U_b>, <U_a>, and <U_d>, respectively), the average van der Waals, electrostatic and solvation energies (<U_vdw>, <U_e>, and <U_s>, respectively), and the total average potential energy (<U>) are given in Table 4. Values of the total average potential energy are positive and of the same order of magnitude (about 1000 kJ/mol) for the majority of systems with exception of systems pc12-2-0-charge4 and pc12-2-0-charge4prp that have negative values of the total potential energy of about 400 kJ/mol. The electrostatic, solvation, and van der Waals energy terms made the largest contribution to the thermodynamic difference between the studied molecular complexes.

Table 4.

Contributions to the total potential energy of model systems at 300K

#	Model name	<Ub>	<Ua>	<Ud>	<UVDW>	<Ue>	<Us>	<U>a)
1	pc13-0-0	2234	2779	1662	−344	−4436	−999	896
2	pc12-2-0-charge4b)	2304	2878	1803	−229	−4467	−2680	−391
2	pc12-2-0-charge4prpb)	2298	2903	1761	−271	−4478	−2664	−451
4	pc9-2-2-charge4	2752	3766	1684	−924	−2894	−3415	969
10	pc10-2-2-charge4	2993	3822	1834	−954	−3377	−3318	1000
14	pc12-1-1-charge2	2693	3433	1779	−650	−4157	−2081	1017
17	pc11-1-1-charge2	2579	3185	1656	−468	−3817	−2102	1033

^a)Units for the potential energy are kJ/mol;

^b)Position of the drug with respect to the polymer chains was varied (parallel and perpendicular alignment)

Interactions between polar groups associated with differences in the chemical composition of polymers, in their folding patterns, and in the position of the drug relative to the polymer chains are among the factors that could influence electrostatic term. Although it is difficult to estimate these factors separately, some correlations can be established.

For example, the model system pc9-2-2-charge4 is the only system that has two very short (10–15 Å) distances between like charges and has the highest value of electrostatic energy, −2894 kJ/mol. One of these distances was initially included in the model and the other distance was formed as a result of polymer folding during MD simulations. In the system pc11-1-1-charge2 two charges of DT were significantly separated at the beginning of the MD run but this distance and the value of electrostatic energy remained almost unchanged by the end of simulations (∼40 Å and −3817 kJ/mol, respectively). One of the possible explanations for this result is a difference in flexibility of polymer chains associated with a difference in the PEG_1k content (refer to Figure 4 of the Supplementary Materials). Indeed, the system pc12-2-0-charge4, in contrast to pc9-2-2-charge4, has the lowest value of electrostatic energy (−4467 kJ/mol) and all six charge-charge distances of ∼20–30 Å unaffected by polymer folding, which can be attributed to the relative stiffness of this molecular system in the absence of PEG_1K. It is also worth mentioning that the position of voclosporin relative to the polymer chains has an insignificant effect on the value of electrostatic term (i.e., −4467 kJ/mol and −4478 kJ/mol for pc12-2-0-charge4 and pc12-2-0-charge4prp, respectively). A tendency for all charged DT groups to be situated on the surface of the molecular complexes facing dielectric continuum was also evident.

Thermodynamic properties given in Table 4 were invariant to the starting position of the drug: the average deviation of their absolute values for the model pc12-2-0-charge4prp did not exceed 3.7 % of the values calculated for the model pc12-2-0-charge4.

To analyze van der Waals (VDW) contributions to the average total potential energy of the model systems, the solvent accessible molecular surfaces (SAS) and the solvent inaccessible polymer-polymer and drug-polymer contact surfaces (S_hid) were calculated. The parameter S_hid was computed as the difference between the total “potential” SAS, given by the sum of SAS of all isolated components (i.e., the drug, polymer 1 and polymer 2) and a “traditional” SAS, i.e., the surface exposed to the solvent (SAS_exp). The estimates of S_hid are given in Table 5 for the 1.3 ns MD run. For each molecular system, Table 5 also shows a portion of drug’s SAS (SAS_drug) that is capable of interacting with polymers. The correlation between S_hid and VDW contributions to the total potential energy of the systems (see Tables 4 and 5) confirms that this calculated parameter is a good approximation of the true internal VDW surface. In the present context, another trend can be revealed. The larger area of the VDW contact in the molecular complex ensures stronger VDW attraction between molecules, which is reflected in the more negative value of the VDW energy term. In Table 4, the largest negative VDW contributions correspond to the molecular systems with the highest content of PEG_1K. This finding offers the additional insight into the molecular role of PEG as a component of complex polymeric systems.

Table 5.

The van der Waals volume and the solvent accessible surface (SAS) areas of model systems at 300K

#	Model name	VVDW Å3	SASexp Å2	Shid Å2	SASdrug %
1	pc13-0-0	10039	6273	6471	48
2	pc12-2-0-charge4	10580	6720	4097	69
2	pc12-2-0-charge4prp	10571	6855	5414	54
4	pc9-2-2-charge4	12298	7365	7655	71
10	pc10-2-2-charge4	12982	7439	7816	60
14	pc12-1-1-charge2	11849	7283	7316	79
17	pc11-1-1-charge2	11168	7233	6133	64

3.3.2 Hydrogen-bonding pattern

Conventional hydrogen bond definitions imply either energetic or geometric criteria [73, 74]. Similar to previous studies [75–77] hydrogen bond definitions based on geometric criteria were used throughout this work. Specifically, a hydrogen bond (D-H…A) formed between donor (D) and acceptor (A) atoms was recognized as a contact if the following conditions were fulfilled: (D…A) < R_D + R_A and the angle D-H…A > 110°, where R_D and R_A are the van der Waal’s radii of the donor and acceptor atoms, respectively. To identify possible correlation(s) between hydrogen bonding observed in the model systems and the experimental results on polymeric drug release, the average number of detected hydrogen bonds was normalized by the number of hydrogen bond donors of molecular system involved in hydrogen bond formation [44]. The results of a general count of intra- and intermolecular hydrogen bonds in the model systems are summarized in Tables 3 and 4 of the Supplementary Materials. All molecular systems have a similar average number of total hydrogen bonds; however, redistribution of inter- and intramolecular hydrogen bonds differs from system to system, depending on corresponding type of drug release.

3.3.2.1 Drug-polymer hydrogen-bonding pattern

The average number of drug-polymer hydrogen bonds formed by the functional groups of polymers and the corresponding bond length are given in Table 6. Only five out of nine functional groups capable of hydrogen bond formation participated in hydrogen bonding between the drug and polymer chains. These were the backbone amino groups, the two backbone carbonyl groups (in Figure 2: C1=O and C2=O of DT and DTE), the carbonyl groups of the side chains (C3=O), and, to a less extent, the oxygen atoms bound to *C4 carbon atoms of PEG_1K-containing repeat unit. Hydrogen bonding involving these amino groups was observed in all model systems with pc10-2-2-charge4 as the only exception. The NH and C2=O groups of the systems pc9-2-2-charge4, pc11-1-1-charge2, and pc12-1-1-charge2 formed approximately the same average number of hydrogen bonds. The system pc10-2-2-charge4, where PEG_1k monomers were the only segments of the polymer directly interacting with voclosporin, had the weakest drug-polymer hydrogen bonds among all simulated systems. These hydrogen bonds were formed exclusively by oxygen atoms of *C4-O motif of the PEG_1k-containing repeat units.

Table 6.

Average number of hydrogen bonds formed by the functional groups of model polymers with voclosporin

#	Model name	Backbone							Side chain		Total
		NH	Length Å(Å)	C1=O	Length Å(Å)	C2= O	Length Å(Å)	*C4-O- C5-O-	C3=O	Length (Å)
1	pc13-0-0	1.0	1.97	-	-	-	-	-	-	-	1.0
2	pc12-2-0-ch4	1.6	2.08	0.4	2.45	-	-	-	0.7	2.22	2.7
2	pc12-2-0-ch4prp	0.8	1.94	0.8	2.11	0.1b	-	-	0.8	2.31	2.5
4	pc9-2-2-ch4	1.1	2.09	-	-	0.9	2.22	-	-	-	2.0
10	pc10-2-2-ch4	-	-	-	-	-	-	0.4a	-	-	0.4
14	pc12-1-1-ch2	0.4	2.04	0.9	2.10	0.6	2.24	-	-	-	1.9
17	pc11-1-1-ch2	0.9	1.89	-	-	0.8	2.21	-	-	-	1.7

^*C4 represents all carbons of the repeat motif of PEG_1K

^{a, b}Weak hydrogen bonds of 2.30 and 2.39 (Å), respectively

Hydrogen bonds that involve hydrogen atoms of the amide groups were short (Table 6) and stable; they were detected in all sampled MD trajectories. Hydrogen bonds formed by C2=O groups of the backbone and C3=O groups of the DTE side chains were slightly longer and also stable, while hydrogen bonds formed by oxygen atoms of the PEG_1k-containing units were formed less frequently and overall had shorter life times. Drug-polymer hydrogen-bonding patterns of the models pc11-1-1-charge2 and pc12-1-1-charge2 were similar because of the similarity in their chemical structure and in the location of voclosporin. Interestingly, in both systems hydrogen bonds were formed by the donor or acceptor groups of DTE and not by PEG despite the fact that PEG_1K monomers were initially placed relatively close to the drug molecule (Figure 4). No drug-polymer hydrogen bonds were formed by charged C3-O⁻ groups of the side chains. All charged groups of DT were situated on the surface of molecular complexes.

To some extent, all residues of voclosporin participated in hydrogen bond formation. Hydrogen atoms of the amide groups of 7-Ala and 8-D-Ala as well as carbonyl oxygen of 5-Val were the most preferable hydrogen-bonding sites. These residues were responsible for about 90% of all detected drug-polymer hydrogen bonds. Residue 8-D-Ala had a tendency to form stable hydrogen bonds with the majority of the model polymers, except pc10-2-2-charge4 and pc13-0-0. Residue 5-Val interacted by stable hydrogen bonds with the polymers of medium- and high-release groups only, while 7-Ala made stable hydrogen bonds mainly with the polymers of low release group and formed less stable hydrogen bonds with pc10-2-2-charge4 of the high release group. The residues of voclosporin, corresponding functional groups and the count of hydrogen bonds are given in Table 5 of the Supplementary Materials.

To answer the question whether a position of voclosporin relative to a position of the polymer chains makes a difference in its hydrogen-bonding pattern or not, the model systems pc12-2-0-charge4 and pc12-2-0-charge4prp were compared. The functional groups of the polymers that formed hydrogen bonds with voclosporin were the same for both models (Table 6). However, different residues or different functional groups of a given residue of voclosporin formed hydrogen bonds with the polymer chains (Table 5 of the Supplementary Materials). This fact confirmed that under the present modeling and simulation conditions, the overall hydrogenbonding pattern of the selected molecular complexes was affected by the initial position of the drug, but the average number of hydrogen bonds or distribution of inter- and intramolecular hydrogen-bonding contacts in these systems remained the same.

In summary, analysis of the drug-polymer hydrogen-bonding patterns revealed that (a) 85% of drug-polymer hydrogen bonds were formed by the functional groups of the polymer backbone and 15% by the functional groups of the side chains; (b) in a framework of this distribution, the backbone amide groups provided 58% of possible hydrogen-bonding sites followed by the backbone carbonyl groups (23%) and the oxygen atoms of PEG_1K (4%); (c) 75% of the detected amide hydrogen bonds were formed by the amino groups. Thus, the preferable hydrogen bonding groups of the model polymers were the backbone amino groups and the backbone carbonyl groups (C1=O, C2=O) among which the amino groups were dominant.

3.3.2.2 Polymer-polymer hydrogen-bonding pattern

To analyze the polymer-polymer hydrogen-bonding network in detail, intermolecular and intramolecular hydrogen-bonding interactions were considered separately. The summary of intra-and intermolecular polymer-polymer hydrogen bonds formed by the functional groups of polymers is given in Table 7 and the corresponding bond lengths are listed in Table 6 of the Supplementary Materials. Table 7 shows that the backbone amide groups formed a large portion of polymer-polymer intermolecular hydrogen bonds. In addition to hydrogen bonds formed by the oxygen atoms of carbonate groups (C2-O-, see Figure 2) that were not observed in the drugpolymer hydrogen-bonding pattern, a slightly increased average number of hydrogen bonds made by the carbonyl oxygen atoms of the carbonate groups (C2=O) were detected. More carbonyl groups of the side chains (C3=O) participated in the polymer-polymer intermolecular hydrogen-bonding in comparison with the drug-polymer case. Three functional groups mentioned above made an approximately equal contribution to the polymer cross-linking by hydrogen bonds.

Table 7.

Average number of intra- and intermolecular polymer (1, 2)-polymer (1, 2) hydrogen bonds formed by the functional groups of model polymers

#	Model name	-NH…acceptor of backbone							-NH…acceptor of side chain				Total intra-	Total inter-
		intra-			inter-				intra-			inter-
		C1=O	C2=O	*C4-O- C5-O-	C1=O	C2-O-	C2=O	*C4-O- C5-O-	C3-O-	C3=O	C3-O−	C3-O
1	pc13-0-0	1.0	0.6	-	1.7	-	1.2	-	-	0.4	-	5.4	2.0	8.3
2	pc12-2-0-ch4	2.7	0.1	-	1.4	-	0.8	-	-	1.7	0.4	-	4.9	2.2
2	pc12-2-0-ch4prp	0.8	0.6	-	0.6	-	0.4	-	-	1.8	0.3	-	3.5	1.0
4	pc9-2-2-ch4	-	-	1.2	1.1	-	0.4	0.5	0.1	1.7	0.2	1.5	3.2	3.5
10	pc10-2-2-ch4	1.0	1.1	-	-	-	2.4	1.6	0.1	-	0.1	0.6	2.3	4.6
14	pc12-1-1-ch2	1.9	-	0.2	-	0.9	1.6	-	-	0.9	-	-	3.0	2.5
17	pc11-1-1-ch2	-	-	2.0	1.0	0.2	-	-	-	0.2	0.2	2.2	2.4	3.4

^*C4 represents all carbons of the repeat motif of PEG₁

The obvious difference between the drug-polymer and polymer-polymer hydrogen-bonding interactions was observed for the model system pc10-2-2-charge4. In this system, stable and strong polymer-polymer hydrogen bonds were formed by the backbone carbonyl groups of the pc10-2-2-charge4 model and the number of strong and relatively stable hydrogen bonds with PEG noticeably increased.

The distinguishing features of the intramolecular polymer 1-polymer 1 and polymer 2-polymer 2 hydrogen-bonding networks included (a) formation of hydrogen bonds between the backbone amino groups and charged C3-O⁻ groups of DT detected for the first time (these contacts were neither abundant nor stable) and (b) the presence of the strong and stable hydrogen bonds between amino hydrogen and carboxyl oxygen of the backbone amide groups in the five out seven model systems. Additionally, for all model polymers the backbone amino groups participated equally in intramolecular hydrogen bonding with the side chain carbonyl groups. In the polymer-polymer intramolecular interactions the hydrogen atoms of amide groups were preferable donors of hydrogen bonds, while all oxygen atoms of the model polymers (to a different extent) acted as hydrogen bond acceptors (refer to Table 7 for details).

3.3.3 Hydrogen-bonding interactions in polymeric drug release

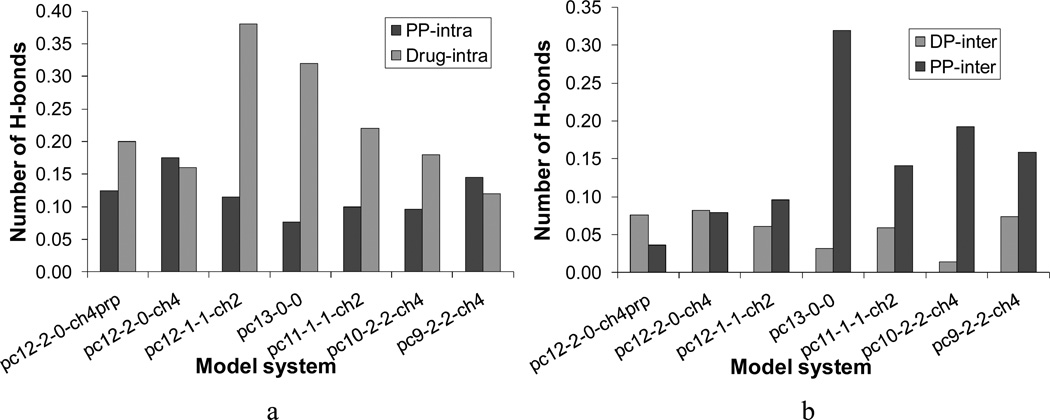
In Figure 12, the normalized average number of drug-polymer and polymer-polymer intra- and intermolecular hydrogen bonds calculated for each model system is shown in the order of increasing the cumulative fractional drug release (see also Figure 5). As seen in Figure 12a, the total number of polymer-polymer intramolecular hydrogen bonds first decreased and then increased, in which sequence the system pc13-0-0 demonstrated the lowest number of polymer-polymer intramolecular hydrogen bonds. Alternatively, the total number of intramolecular hydrogen bonds of voclosporin steadily decreased, with an increasing tendency of drug release. The molecular systems pc12-2-0-charge4 and pc12-2-0-charge4prp were exceptions to this trend.

Figure 12.

Average number of normalized drug-polymer and polymer-polymer (a) intra- and (b) intermolecular hydrogen bonds calculated for each model system. The systems are shown in the order of increasing experimental drug release.

No obvious correlation was found between the total number of hydrogen bonds and experimental drug release in the case of drug-polymer intermolecular interactions (Figure 12b). The molecular systems pc10-2-2-charge4 and pc13-0-0 had the lowest number of drug-polymer hydrogen bonds, but they both exhibited well-developed polymer-polymer intermolecular hydrogen-bonding pattern. The system pc10-2-2-charge4 initially had four monomers of PEG_1k in the close proximity of the drug, while the system pc13-0-0 was the only system that modeled the relatively rigid homopolymer poly(DTE carbonate).

Pairwise comparison of polymer-polymer hydrogen bonding interactions in the systems pc12-2-0-charge4 and pc13-0-0 helped to explain a deviation from the experimental trend that was detected for poly(DTE carbonate) and mentioned in Section 3.1.2. The less rigid copolymer pc12-2-0-charge4 had a smaller number of intermolecular polymer-polymer hydrogen bonds than the homopolymer pc13-0-0 and the lower values of drug release; in the system pc13-0-0 the polymer-polymer hydrogen-bonding network was three times more developed than in pc12-2-0-charge4 and the drug release values were noticeably higher. In addition to identifying the parameters responsible for the deviation in behavior of poly(DTE carbonate), this example established a link between three characteristics: a relative rigidity of the polymer chains, the polymer-polymer hydrogen-bonding pattern(s), and drug release capability.

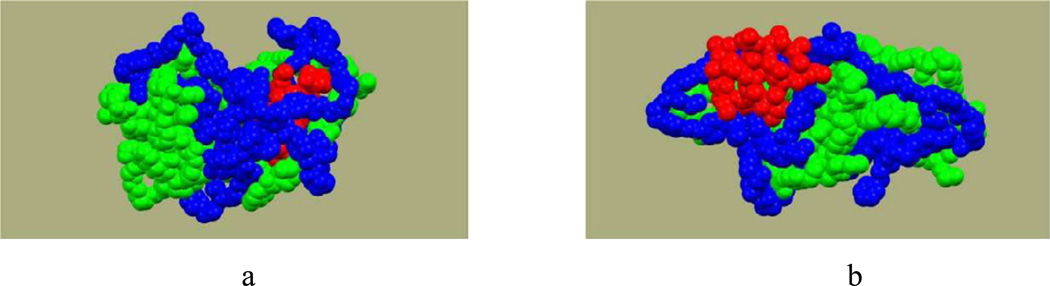
Clearly, the formation of intermolecular hydrogen bonds was more favorable between the rigid polymer chains and intramolecular hydrogen bonds were more preferable in the flexible model polymers. It was also found that the polymer segments situated in the vicinity of the drug affect distribution of hydrogen bonds in the model or experimental DDS. Molecular systems with the higher percentage of SAS_drug such as pc12-2-0-charge4, pc12-1-1-charge2, and pc9-2-2-charge4 (Table 5) had the higher average total number of drug-polymer hydrogen bonds than the rest of the systems. Figure 13 provides additional support to these conclusions; it shows (a) the molecule of voclosporin completely surrounded by the flexible pc12-1-1-charge2 terpolymers and (b) the preferential interactions between the rigid pc13-0-0 homopolymers.

Figure 13.

Final configurations of 1.3 ns MD simulations in implicit water: (a) the model system pc12-1-1-ch2 and (b) the model system pc13-0-0. Drug molecule is colored in red.

Comparative analysis of the average total number of intermolecular hydrogen bonds in the model systems revealed that the hydrophobic drug voclosporin despite its interesting and dynamic picture of hydrogen-bonding interactions with the model polymers was relatively “loosely” hydrogen-bound to the polymer matrices. The number of polymer-polymer hydrogen bonds steadily increased in the systems of co- and terpolymers in the order of increasing drug release. The orientation of the drug in the starting configuration did not influence this trend (e.g, pc12-2-0-ch4prp and pc12-2-0ch4, Figure 12b). This correlation identifies one of the possible processes that may determine the rate controlled mechanism of drug release from the matrices of poly(DTE-co-y% DT-co-z% PEG_1K carbonate)s.

In a recent review devoted to the mechanisms of drug release in poly(lactic-co-glycolic acid), Fredenberg et al. [69] defined the term “true release mechanism” as the way in which the drug is released (e.g., diffusion through water filled pores, diffusion through the polymer, osmotic pumping, and erosion). The authors also defined the process that determines the rate of release (e.g., swelling, drug dissolution, or polymer-drug interactions) as the rate controlling release mechanism and recommended “to first establish the true release mechanisms and then to discuss the rate controlling release mechanisms in more detail” [69]. Our experimental data indicate that the release of voclosporin from polycarbonate matrices relies on the delicate balance between diffusion, erosion and polymer phase separation [48]. It is feasible that the hydrolytic degradation and polymer-polymer hydrogen-bonding interactions are contributing factors in the rate of drug release. These two possible scenarios are not mutually exclusive but interrelated. In an aqueous environment, the polymers with the high polymer-polymer hydrogen-bonding content (e.g., compositions with relatively high PEG_1K content), would participate in hydrogen-bonding interactions with water molecules more aggressively than the polymers with the low hydrogen-bonding content. This could lead to separation of polymer chains and the formation of water filled pores. In parallel, hydrolytic degradation of the polymer begins immediately upon contact with water. This leads to a subsequent decrease in the molecular weight of the polymers, enabling erosion to cause additional drug release. According to Fredenberg et al., several independent studies suggested that the release rate is often diffusion-controlled initially and degradation/erosion-controlled during the final stage of the release period [69].

4. Conclusions

For the first time, an experimental investigation of the release of a hydrophobic peptide from biodegradable polymer matrices was combined with a sequence of judicious computational studies performed on both macroscopic and atomistic levels.

Desirable compositions of poly(DTE-co-y% DT-co-z% PEG_1K carbonate)s were identified by means of a Design of Experiments (DOE) statistical approach. Influence of polymer composition on drug release from the biodegradable polymer matrices was investigated using twelve weeks in vitro release profiles of voclosporin. The trend of increasing drug release with increasing the content of PEG_1K and a synergistic effect of DT and PEG_1K components on drug release kinetics were observed. Near-zero order drug release kinetics maintained by a balance between the diffusion following Fick’s law and polymer erosion was examined using a persistence factor. Both diffusion and erosion were identified as the factors that determine the true drug release mechanism for the selected polycarbonate-based DDS.

The drug release data collected according to recommendations from DOE were used to train and build ANN models. The clustering analysis, Decision Tree and Monte Carlo procedures were employed to test the sensitivity of the ANN models to user-defined parameters and to ensure accuracy of predictions. The predicted values of drug release did not exceed the experimental estimates by more than 3 % for the most accurate ANN models. Due to the rational pre-selection of the training data, the final ANN model was capable of predicting drug release profiles for fifteen model polycarbonates selected from the design-independent molecular space. Despite the relatively small size of the training set, compositional complexity, and structural diversity of these virtual polymers, a good reproducibility of the main trends and distinguishable features of experimentally determined drug release profiles was achieved.

MD simulations were carried out for six rationally designed drug-polymer model systems. Thermodynamic (i.e., various contributions to the total potential energy) and surface properties of molecular complexes were analyzed. A detailed investigation of intra- and intermolecular hydrogen-bonding patterns was performed to elucidate a role of hydrogenbonding in complex formation and stabilization. The correlation between the number of polymer-polymer intermolecular hydrogen bonds and drug release behavior was established. This particular type of hydrogen-bonding interactions was identified as a possible factor involved in the rate controlling drug release mechanism for the poly(DTE-co-y% DT-co-z% PEG_1k carbonate)s.

In addition to achieving the case-specific goals, the present work introduces a new methodological approach to the in vitro design of modern polymeric materials for a wide variety of biomedical applications.